Open Access Article
Open Access ArticleThe structure of a resonance state
A.
García-Vela

Instituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 123, 28006 Madrid, Spain. E-mail: garciavela@iff.csic.es
First published on 6th April 2017
Abstract
The existence of a structure in a resonance state is systematically investigated. A resonance structure is defined as the energy dependence across the resonance width of the fragment state distributions produced upon resonance decay. Different types of resonances, both isolated and overlapping ones, have been explored for this purpose. It is found that isolated resonances do not present an appreciable energy dependence on the product state distributions. On the contrary, overlapping resonances exhibit a clear structure regarding the fragment distributions, which becomes increasingly more pronounced as the intensity of the overlap between the resonances increases. Such an energy dependence of the product distributions arises from the quantum interference between the amplitudes of the overlapping resonances, as demonstrated formally here by the equations derived from the condition of resonance overlap. The application of the present effect to the control of the fragment state distributions produced in a wide variety of molecular processes governed by resonance states is envisioned.
Introduction
Resonance states are very interesting objects of quantum nature that can behave as doorway states from which a variety of molecular processes can be activated.1,2 The predissociation of a molecular system, either in the electronic,3 vibrational,4,5 or rotational6 form, is an example of those resonance-mediated processes. Low-temperature molecular reactions like F + HD,7 F + H2(D2),8–10 and F + CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11,12 are another type of process in which resonances play a central role. Likewise, cold and ultracold non-reactive molecular collisions have recently been shown to be governed by the onset of orbiting resonances13–20 (these resonances, also known as shape resonances, are quasibound states trapped behind a centrifugal barrier). Thus, the effect of resonance states becomes crucial in several of the most common processes involving molecular systems, like photodissociation, reactive, and non-reactive collision dynamics.
11,12 are another type of process in which resonances play a central role. Likewise, cold and ultracold non-reactive molecular collisions have recently been shown to be governed by the onset of orbiting resonances13–20 (these resonances, also known as shape resonances, are quasibound states trapped behind a centrifugal barrier). Thus, the effect of resonance states becomes crucial in several of the most common processes involving molecular systems, like photodissociation, reactive, and non-reactive collision dynamics.
The control of molecular processes is a goal that has been pursued for a long time.21–25 In this sense, the control of resonance-mediated processes is associated with the control of the behavior of the resonance involved. The control of a resonance state behavior essentially implies controlling the main resonance properties, namely the resonance lifetime and the product fragment state distributions produced upon resonance decay. To this purpose, strategies to control both the resonance lifetime26–28 and the product fragment distributions29–31 have been suggested for overlapping and isolated resonance states.
Closely related to the onset of control of the resonance properties is the existence of a resonance structure with respect to those properties. Since a resonance state possesses an energy width, what is meant by a resonance structure is a dependence on the energy of the resonance properties across its width. Clearly, a detailed knowledge of such a structure (whether it exists) would be extremely useful in order to exert control over the resonance behavior, and over the resonance-mediated process of interest. Indeed, a dependence on the energy of the resonance lifetime across the resonance width is well known to occur in all resonances. A resonance state behaves nearly as a bound state in the region of the resonance energy, leading to the longest lifetimes, while it behaves as a continuum state at energies farther away from the resonance energy, leading in this case to the shortest lifetimes. A relevant question is thus whether an energy dependence exists also for the fragment distributions resulting upon resonance decay.
An energy dependence of the state-selected fragment distributions has been found for the unimolecular decomposition of triatomic molecules like CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 and NO2.33–35 The origin of the sensitivity of the distributions to the excitation energy was attributed to an effect of interference between the overlapping resonances excited in those systems. Several theoretical studies investigating the effect of interfering overlapping resonances on the state-selected fragment distributions were reported for different processes in the fields of nuclear36 and chemical physics.37–39 They showed that indeed the energy dependence of the state distributions was directly related to the interference between the overlapping resonances, and to the intensity of the resonance overlap. In general, these studies were applied to model systems which provided a rather qualitative understanding of the mechanisms giving rise to the energy dependence of the fragment distributions when overlapping resonances are involved. Another interesting question that still remains is whether isolated (non-overlapping) resonances can also produce energy-dependent fragment distributions upon decay, and whether this depends or not on how broad they are.
32 and NO2.33–35 The origin of the sensitivity of the distributions to the excitation energy was attributed to an effect of interference between the overlapping resonances excited in those systems. Several theoretical studies investigating the effect of interfering overlapping resonances on the state-selected fragment distributions were reported for different processes in the fields of nuclear36 and chemical physics.37–39 They showed that indeed the energy dependence of the state distributions was directly related to the interference between the overlapping resonances, and to the intensity of the resonance overlap. In general, these studies were applied to model systems which provided a rather qualitative understanding of the mechanisms giving rise to the energy dependence of the fragment distributions when overlapping resonances are involved. Another interesting question that still remains is whether isolated (non-overlapping) resonances can also produce energy-dependent fragment distributions upon decay, and whether this depends or not on how broad they are.
The goal of the present work is to understand in detail the origin and the mechanisms that produce energy-dependent fragment distributions upon the decay of a resonance in a realistic polyatomic system. To this purpose, it has been investigated in a systematic way under which conditions a resonance state can exhibit this type of structure. Different scenarios of resonances have been analyzed, including both isolated and overlapping resonances.
Theoretical background
The vibrational predissociation of the Ne–Br2(B) complex has been chosen as the molecular process subject of this study, because this is a system in which there are different types of resonances. Upon laser excitation, Ne–Br2(X, v′′= 0) + hv → Ne–Br2(B, v′, n′), an intermolecular van der Waals resonance n′ of Ne–Br2(B, v′) is populated. The labels v′′ and v′ denote the vibrational states of Br2 in the X and B electronic states, respectively, while the n′ index labels the energy position of the resonance, with n′ = 0 corresponding to the ground state. The excited resonance then decays to the fragmentation continuum through vibrational predissociation, Ne–Br2(B, v′, n′) → Ne + Br2(B, vf < v′). This process has been studied in detail both experimentally40,41 and theoretically.4,5The process of the Ne–Br2(B, v′, n′) excitation with a laser pulse and the subsequent predissociation of the complex was simulated with a full three-dimensional wave packet method (assuming J = 0) described in detail elsewhere.4,26 In order to assess the quality of the model applied, it is noted that the lifetime calculated with the present theoretical model for the decay of the Ne–Br2(B, v′ = 16) ground intermolecular resonance has been found to be 69 ps,28 while the corresponding lifetime estimated experimentally is 68 ± 3 ps.41 This good agreement with the experimental lifetime implies that both the three-dimensional wave packet method and the potential surfaces used in the present simulations are quite realistic for describing this resonance decay process. Now, in order to investigate whether the Br2(B, vf < v′) fragment vibrational state distribution exhibits an energy dependence, such a distribution has been calculated by projecting out the asymptotic wave packet onto the fragment states for different energies across the resonance width. This has been done for different types of resonances, which include isolated resonances of different widths and overlapping resonances with different overlapping regimes. The excitation of the corresponding Ne–Br2(B, v′) intermolecular resonance is carried out by means of a Gaussian-shaped pump laser field tuned to the resonance energy and with a bandwidth broad enough as to populate the whole resonance width.
Results and discussion
The first case analyzed is the Ne–Br2(B, v′ = 12) ground intermolecular resonance. This is a well isolated resonance, as shown by its Lorentzian line shape displayed in Fig. 1(a), with a rather narrow full width at half maximum (FWHM) of about 0.02 cm−1. The vibrational populations of the Br2(B, vf < v′) fragment in the vf = v′ − 1, v′ − 2 and v′ − 3 final states calculated by projecting out the asymptotic wave packet for different energies across the resonance width are shown in Fig. 1(b). These populations display a similar shape to the spectrum, since the Gaussian-shaped pump laser pulse does not alter this line shape for the resonance population. In order to assess more clearly whether the vibrational populations exhibit an energy dependence, it is more convenient to deal with the normalized vibrational populations of the Br2(B, vf) product fragment, which are defined as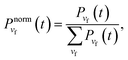 | (1) |
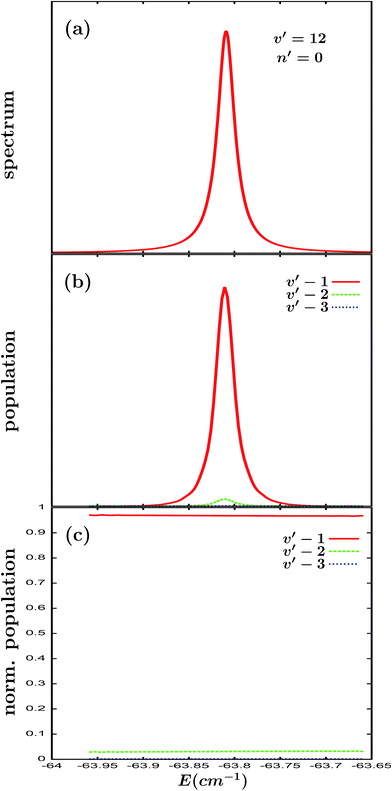 | ||
| Fig. 1 (a) Excitation spectrum of the Ne–Br2(B, v′ = 12) ground intermolecular resonance. (b) Asymptotic Br2(B, vf) fragment vibrational populations in the vf = v′ − 1, v′ − 2, and v′ − 3 final vibrational state, upon the predissociation of the Ne–Br2(B, v′ = 12) ground resonance. (c) The same vibrational populations as in (b), but normalized according to eqn (1) (see the text for details). | ||
Two other isolated resonances were studied, by changing the initial vibrational manifold of the complex to Ne–Br2(B, v′ = 16). Specifically, the n′ = 0 and n′ = 2 intermolecular resonances (i.e., the ground and second excited resonances, respectively) of the v′ = 16 manifold were investigated. The n′ = 0 and n′ = 2 resonances have a FWHM of 0.08 and 0.1 cm−1, respectively. By choosing these two resonances the aim was to change the region of the potential on one side (v′ = 16 is higher in energy than v′ = 12), and to significantly increase the width of the resonance under study on the other side (by a factor of 4 or 5 with respect to the v′ = 12 ground resonance), to elucidate whether these factors might have an effect on the energy dependence of the fragment populations. In these two cases the normalized vibrational populations (not shown) displayed a really weak, practically negligible energy dependence, in line with the results of Fig. 1(c).
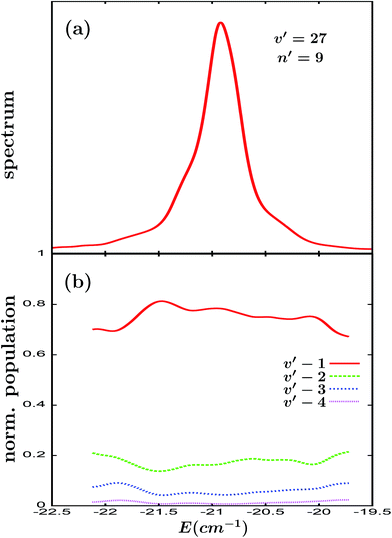
The previous results appear to indicate that fragment state distributions produced upon the decay of isolated resonances do not exhibit a remarkable energy dependence. The question arising now is whether the overlapping resonances present a similar behavior to the isolated ones. In order to analyze this point it is very convenient to change to the v′ = 27 vibrational manifold of Ne–Br2(B). Indeed, it has been shown5,26 that the spectrum of the intermolecular resonances of Ne–Br2(B, v′ = 27) overlaps with the spectrum of the orbiting resonances of Ne–Br2(B, v = v′ − 1 = 26). Since the v = v′ − 1 = 26 spectrum of the orbiting resonances becomes increasingly sparse as the resonance energy increases, the intensity of the overlap between the spectra of v′ = 27 and v = 26 increases (decreases) as we go down (up) in the energy position of the v′ = 27 intermolecular resonance. Thus, by choosing the energy position of the v′ = 27 resonance the intensity of the overlapping regime can be varied in order to study its effect on the possible energy dependence of the Br2(B, vf) fragment vibrational populations. In this work three different resonances supported by the v′ = 27 manifold have been studied, namely n′ = 9, 1, and 0.
The line shape associated with the Ne–Br2(B, v′ = 27, n′ = 9) resonance is shown in Fig. 2(a). This is a Lorentzian line shape distorted by a weak overlap with the v = 26 orbiting resonances. The calculated Br2(B, vf < v′) fragment normalized vibrational populations are displayed in Fig. 2(b) (absolute vibrational populations are not shown to make the figure simpler). Interestingly, the fragment vibrational populations exhibit a relatively weak but appreciable energy dependence across the range of the resonance width, displaying a pattern of undulations. The undulations of the v′ − 1 population have an opposite phase to those of the undulations of the vf < v′ − 1 populations, i.e., the maxima and minima of the v′ − 1 population coincide with the minima and maxima of the vf < v′ − 1 populations, respectively. The reason is that there is competition between the dissociation mechanisms producing the Br2(B, vf = v′ − 1) and Br2(B, vf < v′ − 1) fragments. We will find the same behavior in the pattern of the undulations of the normalized vibrational populations in all of the remaining v′ = 27 resonances investigated in this work.
By moving to the Ne–Br2(B, v′ = 27, n′ = 1) resonance state, the intensity of the overlapping regime is increased significantly. This is reflected in the increase in the distortion of the Lorentzian line shape displayed in Fig. 3(a) with respect to the line shape of Fig. 2(a). Same as in the case of n′ = 9, the populations in Fig. 3(b) display a pattern of undulations, but most interestingly, the dependence on the energy of the populations becomes more pronounced than in Fig. 2(b). Indeed, in the energy range between −44.7 and −43.6 cm−1 where most of the resonance line shape intensity is located, the vf = v′ − 1 population varies from ∼0.7 to 0.8. Even larger changes take place in the populations in the regions of lower line shape intensity (between −45.5 and −44.7 cm−1 and between −43.6 and −43.0).
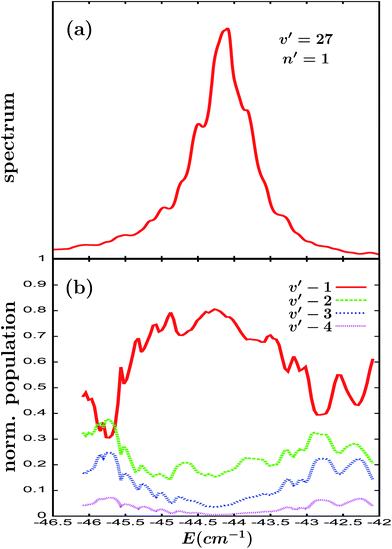 | ||
| Fig. 3 Same as Fig. 2 but for the Ne–Br2(B, v′ = 27, n′ = 1) intermolecular resonance. | ||
The intensity of the resonance overlap can be further increased by moving to the Ne–Br2(B, v′ = 27, n′ = 0) ground intermolecular resonance. The excitation spectrum associated with this resonance is displayed in Fig. 4(a). The most intense peak of the spectrum at −61.8 cm−1 corresponds to the Ne–Br2(B, v′ = 27, n′ = 0) ground resonance, while the peaks located at −60.63 and −59.5 cm−1 correspond to two v = 26 orbiting resonances overlapping with each other and with the Ne–Br2(B, v′ = 27, n′ = 0) resonance. In this case the pump laser pulse used (tuned to excite the energy of −61.0 cm−1) has a bandwidth broad enough to excite the three overlapping resonances. In this way the behavior of the fragment vibrational populations (see Fig. 4(b)) can be analyzed in the energy range of the three resonances.
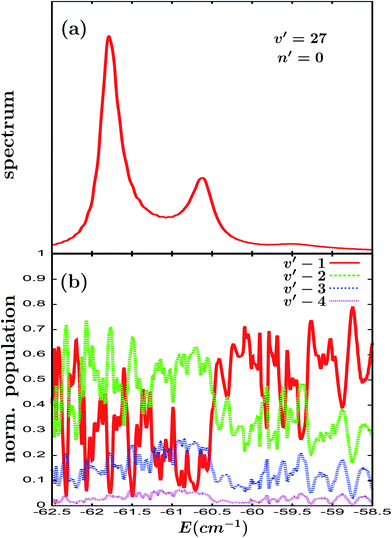 | ||
| Fig. 4 Same as Fig. 2 but for the Ne–Br2(B, v′ = 27) ground intermolecular resonance. | ||
The Br2(B, vf < v′) fragment populations exhibit a strong dependence on energy, displaying a pronounced pattern of oscillations. Not surprisingly, as the energy range is sampled and we move from one resonance to the next one, the overall behavior of the populations typically changes, because each resonance has a specific behavior regarding the dominant dissociation channel (either v′ − 1 or v′ − 2). However, the important results regarding the populations in Fig. 4(b) are the large changes found in the populations within the small energy range of each resonance width. Indeed, in the energy range of the v′ − 27 ground resonance width, for instance, the v′ − 1 population oscillates between ∼0.6 and nearly 0, while the v′ − 2 population oscillates between ∼0.7 and ∼0.3, with the opposite phase. A similar result is found for the other two v = 26 orbiting resonances at higher energies. The implication of this result is that by appropriately choosing the excitation energy and using a narrow bandwidth (or nearly monochromatic) pump laser pulse, the Br2(B, vf < v′) fragment vibrational distribution produced can be drastically different when exciting at different energies within any of the three resonances of Fig. 4(a).
A closer inspection of the oscillating behavior in Fig. 4(b) reveals that it consists of a combination of three oscillation patterns superimposed to produce the overall behavior of the populations across the energy range of the three resonances. Indeed, we can identify a pattern of big peaks separated by a nearly constant amount of energy, and superimposed on each of these peaks there is a secondary pattern of smaller spikes, which actually is a combination of two less intense patterns with two different constant energy separations. The energy separations of the oscillations in the combination of patterns are typically different for each resonance, as expected.
The occurrence of a combination of three patterns can be qualitatively explained as follows. The three resonances in Fig. 4(a) overlap with each other, although with different intensities. This means that when a given energy is excited, the three resonance states are populated simultaneously. Thus they interfere, either constructively or destructively, producing the oscillating behavior of the populations. The interference between each pair of resonances produces a different oscillation pattern. The interference becomes stronger as the resonance overlap is more intense, and therefore the most pronounced pattern of big peaks is produced by the interference between each resonance and its adjacent neighbouring resonance. The two less intense patterns giving rise to the secondary oscillation pattern of the smaller spikes are produced by the interference between the remaining two pairs of resonances, for which the overlap in the energy region of the resonance considered is weaker. This interpretation is confirmed by the result in which the two more separated resonances located at −61.8 cm−1 and −59.5 cm−1, with only one adjacent resonance, show clearly distinct primary and secondary oscillation patterns, while for the resonance at −60.63 cm−1, which is in between two adjacent resonances, the two patterns are significantly less distinct. The origin of the oscillation patterns will be discussed more formally below.
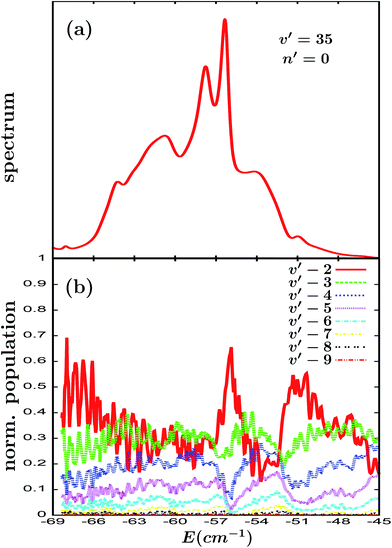
In order to confirm that the results of Fig. 4 were not found by chance, a further resonance state, the Ne–Br2(B, v′ = 35) ground intermolecular resonance, has been investigated. For v′ = 35 the energy position of the ground resonance state lies below the Ne + Br2(B, v = 34, j = 0) dissociation threshold, which implies that for this resonance the vf = v′ − 1 = 34 dissociation channel is closed. As a result, the v′ = 35 ground resonance overlaps with several intermolecular resonances of the v = 34 vibrational manifold. This is reflected in the excitation spectrum of the v′ = 35 ground resonance of Fig. 5(a). The main peak in the spectrum, located at −56.34 cm−1, corresponds to the v′ = 35 ground resonance, and the remaining peaks are associated with the overlapping v = 34 intermolecular resonances. The overlapping regime here is more intense than in the case of Fig. 4(a).
The calculated Br2(B, vf < v′) fragment normalized vibrational populations shown in Fig. 5(b) exhibit a similar behavior as those in Fig. 4(b), namely a strong dependence on energy with essentially two interference patterns (a primary pattern and a secondary one actually composed of two patterns) superimposed to produce the overall behavior. The similarity in the behaviors found for the populations in Fig. 4(b) and 5(b), despite the significantly more intense overlapping regime for v′ = 35, is not very surprising since a given resonance for the v′ = 35 spectrum in Fig. 5(a) essentially overlaps and therefore interferes with its two adjacent resonances (and does so rather weakly with the resonances farther away in energy), thus leading to a similar picture as that for v′ = 27. In this sense, the behavior shown in Fig. 5(b) of the oscillation patterns in the whole energy range is more similar to that associated with the resonance located at −60.63 cm−1 in Fig. 4, with less distinct primary and secondary interference patterns, and further complicated by weak contributions arising from the interference with farther away resonances. However the most relevant result of Fig. 5(b) is that it confirms two interesting points: (a) the energy dependence of the fragment vibrational distribution arises from the interference between the resonance states due to the overlapping between them, and (b) the intensity of this energy dependence is directly related to and increases with increasing intensity of the resonance overlap.
The results presented above show that the isolated resonances exhibit a practically negligible or at most a very weak energy dependence of the fragment state distributions across the resonance width. Such a weak dependence is essentially related to the energy dependence of the coupling of the resonance state to the continuum, which is typically weak, at least for relatively narrow resonances. This result is consistent with the previous findings that a rather weak dependence of the asymptotic Br2(B, vf < v′) fragment vibrational populations was found when the phase of the pump laser field was modulated across the energy range of a superposition of isolated resonances30 and of a single isolated resonance.31
The situation changes drastically, however, when the resonance state is no longer isolated and overlaps with the other resonances, as indicated by the results in Fig. 2–5 for different overlapping regimes. Such results can be rationalized more formally with the aid of the equations resulting from the fragment state distributions when the conditions of resonance overlap are taken into account. Indeed, in a general case one can express the fragment distribution as
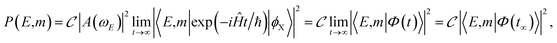 | (2) |
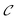 is a constant, ϕX is the ground rovibronic state which is excited to the resonance(s) state(s) by a pump laser with a bandwidth A(ω), and Φ(t) is the wave packet prepared in the excited state by this laser field, that evolves under the action of the Hamiltonian Ĥ. Now, a zeroth-order resonance state ψj can be expressed in terms of the energy eigenstates φE of Ĥ as
is a constant, ϕX is the ground rovibronic state which is excited to the resonance(s) state(s) by a pump laser with a bandwidth A(ω), and Φ(t) is the wave packet prepared in the excited state by this laser field, that evolves under the action of the Hamiltonian Ĥ. Now, a zeroth-order resonance state ψj can be expressed in terms of the energy eigenstates φE of Ĥ as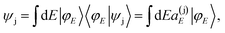 | (3) |
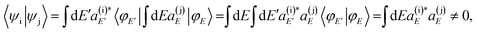 | (4) |
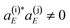 in a range of energies E. The asymptotic wave packet can be expressed as
in a range of energies E. The asymptotic wave packet can be expressed as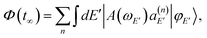 | (5) |
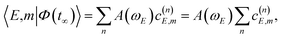 | (6) |
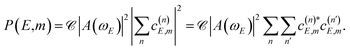 | (7) |
From eqn (7) the quantum interference nature of the oscillation pattern found in the normalized Br2(B, vf < v′) fragment vibrational populations shown in Fig. 2–5 now becomes clear, if we make m = vf. Indeed, when there are two or more overlapping resonances, with n > 1 in eqn (6) (the resonance overlap condition), the complex 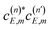 terms of eqn (7) cause constructive and destructive interference in the Br2(B, vf < v′) populations, producing the pattern of oscillations displayed by the results above. Such an interference is not possible in the case of an isolated resonance, where n = 1 in eqn (6), and the energy dependence of the fragment state distribution is only related to the energy dependence of the coupling of the resonance to the continuum, regardless of its resonance width. However, when n > 1 there are two
terms of eqn (7) cause constructive and destructive interference in the Br2(B, vf < v′) populations, producing the pattern of oscillations displayed by the results above. Such an interference is not possible in the case of an isolated resonance, where n = 1 in eqn (6), and the energy dependence of the fragment state distribution is only related to the energy dependence of the coupling of the resonance to the continuum, regardless of its resonance width. However, when n > 1 there are two 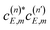 interference terms (i.e.,
interference terms (i.e., 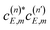 and its complex conjugate) associated with each pair of overlapping resonances, and each couple of interference terms produces a specific interference pattern with an intensity directly related to the amplitude of the two coefficients, which depends on the intensity of the overlap between the two specific resonances involved. For example, in the case of n = 3 in Fig. 4, eqn (7) gives rise to 6 interference terms that produce 3 different interference patterns across the energy range of the three resonances. As the E range is sampled and we move from one resonance to another, the values of the coefficients in eqn (6) change, and therefore the interference terms and the patterns also change, as can be clearly seen in Fig. 4 and 5. The primary, more intense interference pattern is determined by the pair of interference terms between the largest coefficients, and this pattern is responsible for the largest changes in the fragment distributions within a given resonance width, thus allowing for their control. As the amplitude of the coefficients of eqn (6) (at the same energy E) increases, that is, as the overlapping intensity between resonances increases, the magnitude of the interference terms increases correspondingly, thus producing more pronounced interference patterns, as can be found in Fig. 2–5 by increasing the intensity of the resonance overlap.
and its complex conjugate) associated with each pair of overlapping resonances, and each couple of interference terms produces a specific interference pattern with an intensity directly related to the amplitude of the two coefficients, which depends on the intensity of the overlap between the two specific resonances involved. For example, in the case of n = 3 in Fig. 4, eqn (7) gives rise to 6 interference terms that produce 3 different interference patterns across the energy range of the three resonances. As the E range is sampled and we move from one resonance to another, the values of the coefficients in eqn (6) change, and therefore the interference terms and the patterns also change, as can be clearly seen in Fig. 4 and 5. The primary, more intense interference pattern is determined by the pair of interference terms between the largest coefficients, and this pattern is responsible for the largest changes in the fragment distributions within a given resonance width, thus allowing for their control. As the amplitude of the coefficients of eqn (6) (at the same energy E) increases, that is, as the overlapping intensity between resonances increases, the magnitude of the interference terms increases correspondingly, thus producing more pronounced interference patterns, as can be found in Fig. 2–5 by increasing the intensity of the resonance overlap.
The analysis given above through eqn (2)–(7) provides a rigorous basis for a detailed understanding of the origin and specific mechanisms that give rise to the different patterns of fluctuations with the energy of the state-selected fragment distributions produced upon resonance decay. This analysis establishes that such fluctuations are far from being of a random nature,36 and instead they are determined by the interference mechanisms between the specific amplitudes of the overlapping resonances. Knowledge of these amplitudes with their corresponding phases would allow one to predict the specific interference patterns found in the fragment distributions. Thus the present analysis provides a basis for estimating (at least qualitatively) the intensity of the resonance overlap from the experimentally measured energy-dependent state-selected fragment distributions.32–35
Conclusions
The present results and the equations derived above demonstrate that an overlapping resonance state can exhibit a structure in the form of an energy dependence across its energy width, regarding the fragment state distributions produced upon resonance decay. Such a structure arises from the overlap of a resonance with other resonance states, which causes quantum interference between the amplitudes of the overlapping resonances that is reflected in the final fragment state distributions. Therefore, increasing the resonance overlapping intensity causes an increase in the intensity of the resonance interference, and produces a more pronounced resonance structure. This type of structure is not possible in an isolated resonance, regardless of its width.The existence of such a resonance structure opens the door for the control of the fragment state distributions produced upon resonance decay. It should be noted that in order to achieve a control scheme robust enough, the appropriate sensitivity to the energy of the fragment distributions should be found for each specific application, since a very high sensitivity might not favor a control robustness in some cases. Since eqn (2)–(7) are general to any system and to any type of fragment state distributions, the present effect is general to any situation where overlapping resonances are present, regardless of the system or process where it occurs. Thus, the application of this effect for controlling the fragment distributions produced by the decay of resonance states governing a wide variety of molecular processes (photodissociation, low-temperature reactive and non-reactive collisions, etc.) is envisioned.
Acknowledgements
This work was funded by the Ministerio de Economía y Competitividad (MINECO, Spain), Grant No. CTQ2015-65033-P, and COST Action program, Grant No. CM1401 and CM1405. The Centro de Supercomputación de Galicia (CESGA, Spain) is acknowledged for the use of its resources.References
- D. W. Chandler, J. Chem. Phys., 2010, 132, 110901 CrossRef PubMed.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS PubMed.
- G. Balerdi, J. Woodhouse, A. Zanchet, R. de Nalda, M. L. Senent, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2016, 18, 110 RSC.
- A. García-Vela and K. C. Janda, J. Chem. Phys., 2006, 124, 034305 CrossRef PubMed.
- A. García-Vela, J. Chem. Phys., 2008, 129, 094307 CrossRef PubMed.
- C. M. Lovejoy and D. J. Nesbitt, J. Chem. Phys., 1990, 93, 5387 CrossRef CAS.
- R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S. H. Lee, F. Dong and K. Liu, Phys. Rev. Lett., 2000, 85, 1206 CrossRef CAS PubMed.
- M. Qiu, et al. , Science, 2006, 311, 1440 CrossRef CAS PubMed.
- L. Che, et al. , Science, 2007, 317, 1061 CrossRef CAS PubMed.
- J. B. Kim, et al. , Science, 2015, 349, 510 CrossRef CAS PubMed.
- W. Shiu, J. J. Lin and K. Liu, Phys. Rev. Lett., 2004, 92, 103201 CrossRef PubMed.
- T. Westermann, et al. , Angew. Chem., Int. Ed., 2014, 53, 1122 CrossRef CAS PubMed.
- S. Chefdeville, et al. , Phys. Rev. Lett., 2012, 109, 023201 CrossRef PubMed.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234 CrossRef CAS PubMed.
- E. Lavert-Ofir, et al. , Nat. Chem., 2014, 6, 332 CrossRef CAS PubMed.
- S. N. Vogels, et al. , Phys. Rev. Lett., 2014, 113, 263202 CrossRef PubMed.
- S. N. Vogels, et al. , Science, 2015, 350, 787 CrossRef CAS PubMed.
- J. Jankunas, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2015, 142, 164305 CrossRef PubMed.
- A. Bergeat, J. Onvlee, C. Naulin, A. van der Avoird and M. Costes, Nat. Chem., 2015, 7, 349 CrossRef CAS PubMed.
- C. Naulin and M. Costes, Chem. Sci., 2016, 7, 2462 RSC.
- A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber, Science, 1998, 282, 919 CrossRef CAS PubMed.
- R. J. Levis, G. M. Menkir and H. Rabitz, Science, 2001, 292, 709 CrossRef CAS PubMed.
- C. Daniel, J. Full, L. González, C. Lupulescu, J. Manz, A. Merli, S. Vajda and L. Wöste, Science, 2003, 299, 536 CrossRef CAS PubMed.
- B. J. Sussman, D. Townsend, M. I. Ivanov and A. Stolow, Science, 2006, 314, 278 CrossRef CAS PubMed.
- M. E. Corrales, J. González-Vázquez, G. Balerdi, I. R. Solá, R. de Nalda and L. Bañares, Nat. Chem., 2014, 6, 785 CrossRef CAS PubMed.
- A. García-Vela, J. Chem. Phys., 2012, 136, 134304 CrossRef PubMed.
- A. García-Vela, J. Phys. Chem. Lett., 2012, 3, 1941 CrossRef.
- A. García-Vela, Phys. Chem. Chem. Phys., 2015, 17, 29072 RSC.
- A. García-Vela and N. E. Henriksen, J. Phys. Chem. Lett., 2015, 6, 824 CrossRef PubMed.
- A. García-Vela, Phys. Chem. Chem. Phys., 2016, 18, 10346 RSC.
- A. García-Vela, J. Chem. Phys., 2016, 144, 141102 CrossRef PubMed.
- R. L. Miller, S. H. Kable, P. L. Houston and I. Burak, J. Chem. Phys., 1992, 96, 32 Search PubMed.
- J. Miyawaki, K. Yamanouchi and S. Tsuchiya, J. Chem. Phys., 1993, 99, 254 CrossRef CAS.
- S. A. Reid, J. T. Brandon, M. Hunter and H. Reisler, J. Chem. Phys., 1993, 99, 4860 CrossRef CAS.
- S. A. Reid, D. C. Robie and H. Reisler, J. Chem. Phys., 1994, 100, 4256 CrossRef CAS.
- T. Ericson, Ann. Phys., 1963, 23, 390 Search PubMed.
- F. H. Mies, Phys. Rev., 1968, 175, 164 CrossRef CAS.
- U. Peskin, W. H. Miller and H. Reisler, J. Chem. Phys., 1995, 102, 8874 CrossRef CAS.
- E. Narevicius and N. Moiseyev, Phys. Rev. Lett., 1998, 81, 2221 CrossRef CAS.
- J. A. Cabrera, C. R. Bieler, B. C. Olbricht, W. E. van der Veer and K. C. Janda, J. Chem. Phys., 2005, 123, 054311 CrossRef PubMed.
- M. A. Taylor, J. M. Pio, W. E. van der Veer and K. C. Janda, J. Chem. Phys., 2010, 132, 104309 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |