Open Access Article
Open Access ArticleImposing high-symmetry and tuneable geometry on lanthanide centres with chelating Pt and Pd metalloligands†
Mikkel A.
Sørensen
 a,
Høgni
Weihe
a,
Høgni
Weihe
 a,
Morten G.
Vinum
a,
Morten G.
Vinum
 a,
Jesper S.
Mortensen
a,
Linda H.
Doerrer
a,
Jesper S.
Mortensen
a,
Linda H.
Doerrer
 b and
Jesper
Bendix
b and
Jesper
Bendix
 *a
*a
aDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark. E-mail: bendix@kiku.dk
bDepartment of Chemistry, Boston University, 590 Commonwealth Avenue, Boston, Massachusetts 02215, USA
First published on 28th February 2017
Abstract
Exploitation of HSAB preferences allows for high-yield, one-pot syntheses of lanthanide complexes chelated by two Pd or Pt metalloligands, [MII(SAc)4]2− (SAc− = thioacetate, M = Pd, Pt). The resulting complexes with 8 oxygen donors surrounding the lanthanides can be isolated in crystallographically tetragonal environments as either [NEt4]+ (space group: P4/mcc) or [PPh4]+ (space group: P4/n) salts. In the case of M = Pt, the complete series of lanthanide complexes has been structurally characterized as the [NEt4]+ salts (except for Ln = Pm), while the [PPh4]+ salts have been structurally characterized for Ln = Gd–Er, Y. For M = Pd, selected lanthanide complexes have been structurally characterized as both salts. The only significant structural difference between salts of the two counter ions is the resulting twist angle connecting tetragonal prismatic and tetragonal anti-prismatic configurations, with the [PPh4]+ salts approaching ideal D4d symmetry very closely (φ = 44.52–44.61°) while the [NEt4]+ salts exhibit intermediate twist angles in the interval φ = 17.28–27.41°, the twist increasing as the complete 4f series is traversed. Static magnetic properties for the latter half of the lanthanide series are found to agree well in the high temperature limit with the expected Curie behavior. Perpendicular and parallel mode EPR spectroscopy on randomly oriented powder samples and single crystals of the Gd complexes with respectively Pd- and Pt-based metalloligands demonstrate the nature of the platinum metal to strongly affect the spectra. Consistent parametrization of all of the EPR spectra reveals the main difference to stem from a large difference in the magnitude of the leading axial term, B02, this being almost four times larger for the Pt-based complexes as compared to the Pd analogues, indicating a direct Pt(5dz2)–Ln interaction and an arguable coordination number of 10 rather than 8. The parametrization of the EPR spectra also confirms that off-diagonal operators are associated with non-zero parameters for the [NEt4]+ salts, while only contributing minimally for the [PPh4]+ salts in which lanthanide coordination approximates D4d point group symmetry closely.
Introduction
During the last decade and a half, the interest in the coordination chemistry of the lanthanides has been refuelled by the prosperity of mono- and polynuclear 4f metal complexes in the field of molecular magnetism. Polynuclear clusters and extended networks based on especially gadolinium(III) have shown large magnetocaloric effects,1–3 rendering these complexes potentially applicable in low temperature magnetic cooling.4 On the other hand, low nuclearity complexes of anisotropic lanthanide ions have been found to behave as single-molecule magnets with properties superior to those of the archetypal 3d metal clusters of the 1990s.5–8 Notably, complexes containing a single lanthanide ion, so-called single-ion magnets,9 have exhibited remarkably slow spin-lattice relaxation,10–14 with relaxation times reaching up to several 1000 s at liquid helium temperatures.15 These long relaxation times are considered a consequence of relaxation via excited states (Orbach relaxation) within the ground Russell-Saunders (RS) multiplet, which is split by the crystal field experienced by the 4f ion.16,17 Therefore, the optimization of crystal field splittings by appropriate tailoring of ligand environments has been a key preparative target.18 However, despite the achievement of large crystal field splittings, quantum tunnelling of the magnetization (QTM) within the ground state often dominates the low temperature spin relaxation, limiting the timescale of the relaxation events to the order of milliseconds.13,19–21 Therefore, design criteria for obtaining pure crystal field states have also been suggested.22 Low symmetry components of the crystal field serve as to connect the different substates within the ground RS multiplet, thereby increasing tunnelling probabilities causing unwanted, fast spin relaxation. Consequently, the design criteria aimed at maximizing crystal field state purity evolve around tuning of the point group symmetry of the crystal field. The recent dawn of mononuclear lanthanide complexes as molecular spin qubits23,24 adds to the interest in tailoring electronic structures and chemical functionalities allowing for implementation in devices e.g. through surface attachment. All suggested criteria guide the synthetic chemist towards the rational design and control of the crystal field environment and ligand periphery, and in principle, this seems straightforward.Alas, the structural design of lanthanide complexes is less simple than for nd metal complexes for various reasons. Firstly, the high coordination number characteristic of the lanthanides complicates control of the environment if only simple ligands of low denticity are employed. This can either be overcome by using bulky ligands, thereby lowering coordination numbers,25–30 or by coordinatively saturating the metal ion by employing a single31–34 or only few35–38 ligands of high denticity. Secondly, the lack of ligand field stabilization energies renders coordination geometries less predictable and consequently specific symmetries are more easily imposed through the choice of ligand.
The platinum(II) complexes [PtII(SC(O)R)4]2− (R = Me (thioacetate), Ph (thiobenzoate)) have previously been reported on their own (for R = Me),39 and as constituent units of a family of heterobimetallic lantern complexes of formulation [PtIIMII(SC(O)R)4(solv)n] (M = Mg, Ca, Fe, Co, Ni, Zn; solv = solvent molecules),39–42 A[PtIIMII(SC(O)Me)4(NCS)] (A = [Na(15-crown-5)], [Na(12-crown-4)2]; M = Mn, Co, Ni, Zn),43 and [PtIICrIII(SC(O)Ph)4(NCS)]n.43 In the bimetallic lantern compounds, the soft Lewis acidity of platinum(II) allows for selective coordination by the soft sulphur donors, while the harder Lewis acids, that is the divalent ns and 3d metal ions, are selectively coordinated by the oxygen atoms of the thiocarboxylates. This design concept relying on the hard–soft acid–base (HSAB) principle should be expandable to encompass the even harder Lewis acids such as the trivalent lanthanide ions. Herein, we report such an expansion, using the platinum metal complexes [MII(SAc)4]2− (SAc− = thioacetate, M = Pd, Pt) as chelating tetradentate metalloligands. The predictable square-planar geometry of the platinum metal complex facilitates tetragonal symmetry of the resulting [LnIII{MII(SAc)4}2]− complexes, and by selecting appropriate counter cations ([NEt4]+ (for M = Pt: 1Ln, for M = Pd: 1Ln′), [NnPr4]+, or [PPh4]+ (for M = Pt: 2Ln, for M = Pd: 2Ln′)), the tetragonal symmetry can be crystallographically imposed in the solid state. We describe the synthesis as well as the structural, static magnetic, and EPR spectroscopic characterizations of this new family of high-symmetry lanthanide complexes.
Results and discussion
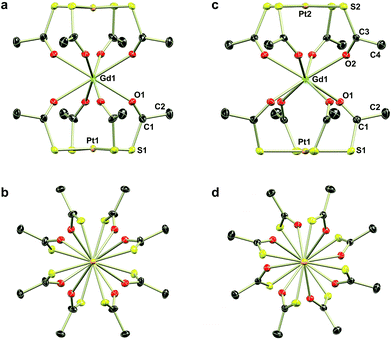
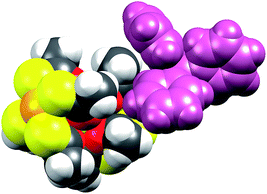
The reaction of thioacetate as its potassium salt with K2[PtCl4] and hydrated trivalent lanthanide chlorides in aqueous solution cleanly yielded the anionic complexes [Ln{Pt(SAc)4}2]−, which could be isolated as either the [NEt4]+ or [NnPr4]+ salts in the presence of an excess of these cations (Scheme 1). This yielded [NEt4][Ln{Pt(SAc)4}2] (1Ln) as golden quadratic plate-shaped single crystals, while near-amorphous powders (as verified by PXRD, not shown) of [NnPr4][Ln{Pt(SAc)4}2] were obtained (see ESI† for synthetic details). It proved possible to synthesize the 1Ln salts (i.e. the [NEt4]+ salts) for all lanthanides (excluding promethium) as well as yttrium by appropriately adjusting the synthetic protocol. The isomorphism of the 1Ln compounds was confirmed by single crystal X-ray diffraction. The crystallographic details and structure of 1Gd are given in Table 1 and Fig. 1, respectively. The crystallographic details for the remainder of the 1Ln compounds are collected in Tables S1–S4 of the ESI.†| 1Gd | 2Gd | |
|---|---|---|
| Formula | C24H44GdNO8Pt2S8 | C40H44GdO8PPt2S8 |
| M r | 1278.56 | 1487.70 |
| T/K | 122(1) | 123(1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Crystal system | Tetragonal | |
| Space group | P4/mcc (no. 124) | P4/n (no. 85) |
| a/Å | 8.6134(3) | 12.6662(5) |
| c/Å | 25.4434(9) | 15.1584(6) |
| V/Å3 | 1887.66(11) | 2431.90(17) |
| Z | 2 | 2 |
| ρ calc/g cm−3 | 2.2493 | 2.0315 |
| μ/mm−1 | 9.612 | 7.508 |
| F 000 | 1214 | 1422 |
| Crystal size/mm3 | 0.10 × 0.10 × 0.040 | 0.12 × 0.12 × 0.080 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Radiation | Mo Kα (λ = 0.71703 Å) | |
| 2θ range/° | 4.72–57.4 | 4.54–57.38 |
| Reflections collected | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 108 |
| Independent reflections | 1263 | 3157 |
| R int, Rσ | 0.0334, 0.0107 | 0.0510, 0.0199 |
| Param/restraints | 91/3 | 139/0 |
| S (on F2) | 1.089 | 1.054 |
| R 1, wR2(I ≥ 2σ(I)) | 0.0164, 0.0522 | 0.0175, 0.0351 |
| R 1, wR2 (all data) | 0.0215, 0.0559 | 0.0248, 0.0375 |
| Δρmax/Δρmin/e Å−3 | 1.43/−0.90 | 2.46/−0.81 |
In the preparation of 1Ln for the full lanthanide series, it was found necessary to modify the employed protocol significantly when moving from the earlier to the later lanthanides. The reactions for especially the earliest lanthanides (La, Ce) had to be carried out at very dilute conditions in order to obtain crystals of a size suitable for structure determination. Upon moving across the series, the concentration of the reaction mixture had to be gradually increased in order to obtain satisfactory yields. For the last four lanthanides, the decrease in the solvent volume rendered the method used for preparing the remainder of the 1Ln complexes inconvenient. Instead, a concentrated solution of the metalloligand was prepared by briefly heating a concentrated aqueous solution of KSAc and K2[PtCl4]. Addition of the relevant lanthanide chloride to this solution resulted in the development of some turbidity, the turbidity being more pronounced the later the lanthanide. For 1Er, 1Tm, and 1Yb the turbidity completely disappeared in the presence of a large excess of [NEt4]Cl, and subsequent gentle heating initiated the formation of square-shaped golden crystals. Also for this procedure, satisfactory yields required much higher concentrations for the latest lanthanides. Addition of solid LuCl3·6H2O to a concentrated solution of the metalloligand resulted in a considerable amount of precipitate rather than the turbidity observed for the larger predecessors. Treatment with excess [NEt4]Cl did not fully redissolve the solid, and despite the remaining solids being filtered off prior to crystallization of the product, 1Lu invariably contained a minor impurity as judged from CHNS elemental analysis and PXRD (see ESI†).
The [NnPr4][Ln{Pt(SAc)4}2] salts are less easily precipitated than the analogous [NEt4]+ salts (1Ln), and consequently the protocol used for the synthesis of the 1Ln compounds for the four latest lanthanides was adapted. Recrystallization of the crude [NnPr4][Ln{Pt(SAc)4}2] products by slow evaporation of a concentrated acetone solution at room temperature yielded single crystals. Structure determination was however impeded by an inherently high mosaicity of the so-obtained crystals.
Direct addition of [PPh4]Cl to aqueous solutions containing [Ln{Pt(SAc)4}2]− precipitates the non-coordinated metalloligand as golden-yellow crystals of formulation [PPh4]2[Pt(SAc)4]·4.5H2O,39 preventing direct preparation of the [PPh4]+ salts. However, facilitated by the reasonable solubility of the near-amorphous crude [NnPr4][Ln{Pt(SAc)4}2] salts in polar organic solvents like acetonitrile, nitromethane, and acetone, golden quadratic single crystals of [PPh4][Ln{Pt(SAc)4}2] (2Ln) could instead be obtained in high yields by the metathesis reaction of crude [NnPr4][Ln{Pt(SAc)4}2] and [PPh4]Cl in MeNO2 (Scheme 1). Single crystal X-ray diffraction revealed the synthesized 2Ln compounds to be isostructural. The crystallographic details and structure of 2Gd are given in Table 1 and Fig. 1, respectively. The crystallographic details of the remaining 2Ln compounds are given in Tables S5 and S6 of the ESI.†
Single crystal X-ray diffraction revealed the tetraethylammonium salts (1Ln) to be isomorphous, a result that was corroborated by PXRD (Fig. S1–S3, ESI†). Due to their isomorphism, the structures of 1Ln will be discussed in comparison to that of 1Gd. The structure solution revealed the coordination of two [Pt(SAc)4]2− complexes to the gadolinium ion through the available oxygen atoms of the thiocarboxylates, yielding an eight-coordinate GdIII centre. The complex can thus be described as the homoleptic metalloligand complex of gadolinium(III) crystallized with one tetraethylammonium counter ion. The salt crystallized in the centrosymmetric tetragonal space group P4/mcc with two formula units in the unit cell. The Gd1, Pt1, and the nitrogen atom of the counter ion (N1) all occupy special positions of four-fold site symmetry, and consequently the asymmetric unit contains only one eighth of a formula unit. As described in the ESI,† the single thioacetate contained in the asymmetric unit is disordered over two positions, the two fragments being equally occupied. A structure determination for 1Gd at room temperature (Table S4, ESI†) revealed an identical disorder (Fig. S4, ESI†), suggesting it to be static in nature. This was corroborated by the electron density map in the region of the oxygen atom positions, showing a clear peanut-shaped electron density rather than an oblate one, indicating two closely spaced but localized positions of the disordered oxygen atom. The oxygen and sulphur atoms belonging to the part of the thioacetate that is omitted in Fig. 1 are labelled with an “a”-extension. Each platinum centre is coordinated by four thioacetates through the sulphur atoms resulting in a square planar geometry, as expected for the 5d8 ion. The planes spanned by either the four S1 or the four S1a atoms are perpendicular to the four-fold axis by symmetry. The platinum atom is shifted slightly out of plane either towards (for the S14 plane) or away from (for the S1a4 plane) the gadolinium centre by 0.086 Å and 0.038 Å, respectively. These out of plane shifts are slightly larger than those observed in the related heterobimetallic lantern complexes,39–43 and significantly larger than for the non-coordinated metalloligand in which the platinum sits exactly in the S4 plane.39
Thiocarboxylates as ligands for lanthanides are uncommon, and to this date only two structurally characterized examples have been reported.44,45 In both these cases, the thiocarboxylates act as chelating bidentate ligands, and the bridging of a lanthanide ion and a transition metal in the μ1,3-fashion observed for 1Gd is hitherto unknown. A related bridging motif is however observed for a series of heterobimetallic dithiooxalate-bridged compounds of formulation [{LnIII(H2O)n}2{NiII(dto)2}3]·xH2O (dto2− = dithiooxalate)46–48 as well as for the systems [MIII{(dto)DyIII(tp)2}3]·4MeCN·2CH2Cl2 (MIII = FeIII, CoIII; tp− = hydrotrispyrazolylborate),49 in which the dithiooxalate ligands selectively coordinate the softer 3d metal ions through the sulphur atoms, while the lanthanide ions are exclusively coordinated by the oxygen atoms of the bridging ligands.
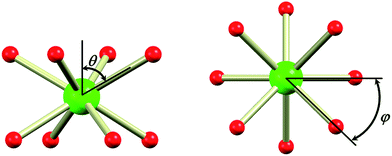
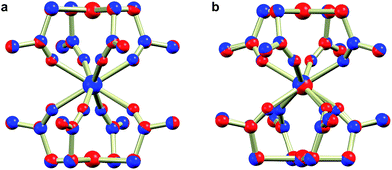
In the evaluation of the nature of the crystal field experienced by the lanthanide ion in the 1Ln salts, two angles are of relevance. Firstly, the compression angle, θ (Fig. 2), defined as the angle between the four-fold axis and the Ln–O bond, describes the axial distortion of the coordination environment. The cube-value of 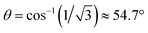 (i.e. half the tetrahedral angle) constitutes the non-compressed scenario, while smaller and larger angles correspond to elongation and compression, respectively. The angle, φ, between the diagonals of the two squares constituted by the two sets of oxygen donor atoms, is illustrated in Fig. 2. This twist angle, also referred to as the skew angle,5,50 is key for determining the point group symmetry at the lanthanide site, which in turn is crucial for appropriately describing the crystal field substate composition of lanthanide complexes. In the case of an axial distortion of the crystal field environment (i.e. for θ ≠ 54.7°), the position of the lanthanide ion belongs to the D4h and D4d point groups for the two extremes φ = 0° (square prism) and 45° (square antiprism), respectively.
(i.e. half the tetrahedral angle) constitutes the non-compressed scenario, while smaller and larger angles correspond to elongation and compression, respectively. The angle, φ, between the diagonals of the two squares constituted by the two sets of oxygen donor atoms, is illustrated in Fig. 2. This twist angle, also referred to as the skew angle,5,50 is key for determining the point group symmetry at the lanthanide site, which in turn is crucial for appropriately describing the crystal field substate composition of lanthanide complexes. In the case of an axial distortion of the crystal field environment (i.e. for θ ≠ 54.7°), the position of the lanthanide ion belongs to the D4h and D4d point groups for the two extremes φ = 0° (square prism) and 45° (square antiprism), respectively.
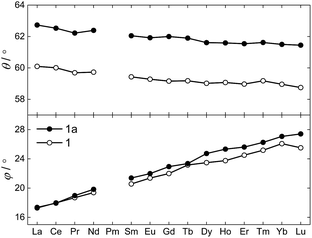
The θ and φ angles were evaluated for the entire 1Ln series and are given in the upper and lower panels of Fig. 3, respectively (excluding 1Y). As a result of the disorder in the thioacetates, two different crystal field environments exist in the crystal, defined by a single type of oxygen atoms (O1 or O1a) for symmetry reasons. As the disorder is 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, so is the distribution between the two crystal field environments. From Fig. 3 it is evident how both angles depend on the lanthanide ion, i.e. the ionic radii. A smooth decrease in the degree of axial compression is observed following the decrease in ionic radius upon going from 1La to 1Lu, the θ values varying between 62.73° (1La, O1a) and 58.87° (1Lu, O1). The difference in degree of axial compression between the two different crystal field environments is on the order of a few degrees for all 1Ln derivatives, the maximum difference being that for 1Gd, in which θO1a − θO1 = 2.84°. The value of φ smoothly increases upon going from 1La to 1Lu, the smallest value being 17.28° for the O1 environment in 1La, and the largest 27.41° for the O1a environment in 1Lu. The difference in the value of the angle for the two different environments for a specific lanthanide is generally small, and never exceeds 1.5°.
50, so is the distribution between the two crystal field environments. From Fig. 3 it is evident how both angles depend on the lanthanide ion, i.e. the ionic radii. A smooth decrease in the degree of axial compression is observed following the decrease in ionic radius upon going from 1La to 1Lu, the θ values varying between 62.73° (1La, O1a) and 58.87° (1Lu, O1). The difference in degree of axial compression between the two different crystal field environments is on the order of a few degrees for all 1Ln derivatives, the maximum difference being that for 1Gd, in which θO1a − θO1 = 2.84°. The value of φ smoothly increases upon going from 1La to 1Lu, the smallest value being 17.28° for the O1 environment in 1La, and the largest 27.41° for the O1a environment in 1Lu. The difference in the value of the angle for the two different environments for a specific lanthanide is generally small, and never exceeds 1.5°.
Despite the highlighted differences, the two crystal field environments found in the crystals of 1Ln are identical from a symmetry point of view. As the twist angles are in between the two extremes of φ = 0° and 45°, the point group symmetry of the lanthanide site lowers to D4 (C4 with disorder, cf. ESI†)
In the crystal packing of 1Gd (Fig. S5, ESI†) all complexes have their Pt–Gd–Pt axis parallel to the c-axis of the unit cell, with the lanthanide complexes being arranged end-to-end along this direction. The shortest Gd⋯Gd distance equals the length of the a-axis (or b-axis) of the unit cell of 8.6134(3) Å. Along the c-axis the shortest Gd⋯Gd distance is half the length of the axis, 12.7217(5) Å. The packing of the cations and anions is CsCl-like with each ion having eight nearest neighbours of the opposite kind.
The shortest intermolecular Pt⋯Pt distance of 5.3240(4) Å rules out any metallophillic Pt⋯Pt interactions similar to those observed for the related heterobimetallic lantern complexes.40,41 Likely, the charge on the complexes and the packing with the counter ions both contribute to suppress Pt⋯Pt interactions. However, the fact that metallophillic interactions have been observed in some of the anionic lantern complexes of the divalent 3d metals,43 points to packing effects involving the counter ions as the main reason. It is conceivable that if the need for the counter ion could be circumvented, e.g. using mixed complexes with an isoelectronic AuIII-based metalloligand, such di- or oligomerization can regain importance.
The synthesis and structural characterization of a full series of isomorphous lanthanide complexes is not a matter of course. Rather, the lanthanide contraction amounting to a ∼15% reduction in ionic radii for the trivalent ions, commonly leads to structural discontinuities across the 4f series. Here, the polydentate, yet flexible nature of the employed metalloligands facilitate the non-trivial preparation of all members of the 1Ln family (with the obvious exception of 1Pm) and hence allows for a detailed study of the full series of lanthanide ions in an identical crystal field environment. Evaluation of the unit cell parameters for the 1Ln complexes determined from single-crystal X-ray diffraction at T = 122 K (Fig. 4) reveals the length of the a-axis and the unit cell volume to conform to the expected trend. The length of the c-axis is found to increase upon reducing the size of the lanthanide ion. Albeit counterintuitive, this lengthening of the c-axis can however also be understood as a result of the lanthanide contraction (a detailed argument for this is presented in the ESI†).
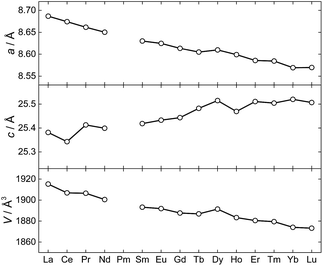 | ||
| Fig. 4 The unit cell parameters for 1Ln at T = 122(1) K determined from the X-ray single crystal structures. | ||
Switching to the salts with tetraphenylphosphonium counter ions (2Ln), the synthesized members of this series were also found to be isostructural from single crystal X-ray diffraction experiments, and this was confirmed by PXRD (Fig. S6, ESI†). Consequently, the description of their structures will take its starting point at the gadolinium derivative. 2Gd crystallized in the centrosymmetric tetragonal space group P4/n with two formula units in the unit cell. The Gd1, Pt1, and Pt2 atoms along with the phosphorus atom belonging to the tetraphenylphosphonium ion all occupy special positions of four-fold site symmetry. As a result of the high symmetry, only a quarter formula unit is contained in the asymmetric unit. As opposed to the structures of the tetraethylammomium salts (1Ln), no disorder of the thioacetates was observed in the structures of 2Ln. The structural characteristics of the complex anion discussed for 1Gd also apply to 2Gd. However, one very important difference between the two salts is observed when evaluating the values of the twist angle φ. The increase of ∼10° in this parameter value for 1Ln observed upon traversing the f-block was discussed above. For those lanthanides for which the analogous 2Ln compounds were prepared, the span of φ angles is from 21.99°/22.94° for 1Gd to 24.50°/25.61° for 1Er. For the tetraphenylphosphonium salts (2Ln) of the same central ions, φ shows a variation as small as 0.09° (44.52–44.61°), much less than the approximately 2.5° variation seen for the analogous 1Ln salts. The pronounced structural invariance observed for the 2Ln can be understood when examining the packing of neighbouring cations and anions in the crystal as illustrated for 2Gd in Fig. 5 (the crystal packing of 2Gd is given in Fig. S7, ESI†). The space-filling model highlights how a phenyl group from the tetraphenylphosphonium ion occupies the void space in between neighbouring thioacetates that are 90° apart around the four-fold axis. By symmetry, all void spaces in between neighbouring CH3C(O)S−-groups are occupied by phenyl groups. While this on its own does not enforce a twist angle of 45°, it seems reasonable to assume that this particular conformation of two metalloligands with respect to each other facilitates the most efficient accommodation of the eight phenyl moieties. The twist angle of ∼45° results in excellent approximation to D4d point group symmetry (which cannot be strictly imposed crystallographically) at the lanthanide site. This is of crucial importance for the description of the electronic structure of these systems, as evidenced by the EPR spectra of the gadolinium derivatives (vide infra). The crystallographic inequivalence of the oxygen atoms O1 and O2 (Fig. 1c) results in two slightly different values of θ. For 2Gd, the angle amounts to 60.03° or 61.23° depending on the oxygen atom chosen as reference. The average of these values, 60.63°, is within uncertainties identical to the average value of θ for the two different crystal field environments found for 1Gd of 60.58°. As for the 1Ln systems, the lanthanide centres in 2Ln are also well separated with nearest neighbour distances of ca. 9.8 Å.
When examining Fig. 5, the build-in soft functionality terminating the lanthanide complexes is immediately evident. The affinity of not only the sulphur atoms but also the platinum centre for soft metal centres (i.e. another platinum centre) has been firmly demonstrated by strong metallophillic interactions in the heterobimetallic complexes already discussed.40–42 The planar nature of the PtS4 units, in principle, renders these extremely well-suited for deposition on softer substrates like gold.
With the prospect of tuning surface interaction strengths and demonstrating the generalizable nature of the chemistry presented here, we synthesized the gadolinium and yttrium derivatives with palladium(II) substituting for platinum(II), giving rise to [NEt4][Ln{Pd(SAc)4}2] (1Ln′), [NnPr4][Ln{Pd(SAc)4}2], and [PPh4][Ln{Pd(SAc)4}2] (2Ln′) with Ln = Gd, Y (see ESI† for synthetic details). The obtained compounds were found to be strictly isostructural with their platinum counterparts (crystallographic data are given in Table S7, ESI†), as evidenced by the structural overlays of the Gd derivatives shown in Fig. 6. Despite their strictly isostructural nature, a few important adjustments were necessary in their preparations. Under reaction conditions employed in the synthesis of the platinum systems, sulphide formation seemed to pose a problem for the preparation of the palladium complexes. This was however avoided by constantly keeping thioacetate in excess. The greater lability of palladium over platinum allowed for a shortening of reaction times, and the [NEt4][Ln{Pd(SAc)4}2] (1Ln′) and [NnPr4][Ln{Pd(SAc)4}2] salts could consequently be precipitated immediately after complete addition of all starting materials to the reaction mixture. The palladium derived complexes are intensely yellow in colour compared to the light golden yellow nature of the platinum based systems. The pronounced difference in the strength of the interaction between the lanthanide ion and the group 10 metal (vide infra), is sufficiently large to possibly influence the optical properties and lead to differences between the platinum and palladium derivatives of the luminescent lanthanide ions.
The crystalline purity and isomorphism of the palladium derivatives was confirmed by PXRD (Fig. S8, ESI†). We note that 1Ln′ and 2Ln′ are the first structurally characterized species containing mono-thiocarboxylates coordinated to palladium.
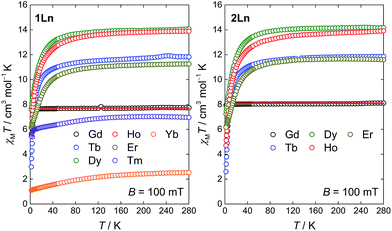
The molar magnetic susceptibilities of the compounds 1Ln (Ln = Gd–Yb) and 2Ln (Ln = Gd–Er) were investigated in an applied magnetic field of B = 100 mT. The temperature dependence of the χMT products is given in Fig. 7. The high temperature values of the χMT products are generally in good agreement with the expected Curie constants (Table S8, ESI†). For all compounds but 1Gd and 2Gd, the value of χMT decreases upon lowering the temperature, as a result of the depopulation of mJ substates within the crystal field split ground J manifold. In general, the powder-averaged susceptibilities and magnetization data (Fig. S9–S15, ESI†) are highly similar when comparing the 1Ln and 2Ln salts. This suggests that whilst the composition of the crystal field states might change significantly upon changing the point group symmetry, the relative energies of the states, and hence the total splitting of the manifold, might be less affected. The plausibility of this is supported by the on-average negligible difference in θ between the two different salts for a given lanthanide, as the axial crystal field parameters are strongly dependent on this parameter but show only slight or no dependence on φ.22 The non-superimposable reduced magnetization isotherms (Fig. S9–S15, ESI†) observed for all compounds but 1Gd and 2Gd indicate the presence of significant anisotropy, low-lying excited states or a combination of the two. For 1Gd and 2Gd a collective fit of the χMT(T) and reduced magnetization data to an isotropic Zeeman Hamiltonian resulted in isotropic g-values of 1.98(3) and 2.03(3) for 1Gd and 2Gd, respectively. Both these values are within error of the expected 2.00.
In order to investigate the importance of the difference in point group symmetry further and probe a possible effect of the Pd/Pt metal centre on the electronic structure of the lanthanide, powder X-band electronic paramagnetic resonance (EPR) spectra of the gadolinium derivatives doped into their respective yttrium hosts at a nominal molar concentration of 2% were recorded. The room temperature spectra of the platinum-based complexes 1Gd and 2Gd doped into their respective host lattices (1Y0.98Gd0.02 and 2Y0.98Gd0.02) recorded with the microwave polarization either perpendicular or parallel to the applied magnetic field are given in the upper panels of Fig. 8 (details on the EPR experiments are given in the ESI†). The structured nature of the spectra calls for the inclusion of crystal field effects, which generate a zero-field splitting of the S = 7/2 ground state. Due to the absence of orbital momentum for the gadolinium(III) centre, the splitting arises from the interactions with higher lying Russell-Saunders multiplets, and the effects are therefore small, as the first excited multiplet is placed approximately 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 away from the ground one.51 The small magnitude of the zero-field splitting of gadolinium(III) makes the frequency characteristic of X-band EPR well-suited for the quantization of said splitting. This contrasts the need for the application of high-field and frequency EPR, which is normally applied for the determination of zero-field splittings in lanthanides with unquenched orbital momentum (i.e. L ≠ 0).52,53 By considering the minimal, common C4 symmetry of the gadolinium site, the appropriate Hamiltonian following the Stevens approach is5
000 cm−1 away from the ground one.51 The small magnitude of the zero-field splitting of gadolinium(III) makes the frequency characteristic of X-band EPR well-suited for the quantization of said splitting. This contrasts the need for the application of high-field and frequency EPR, which is normally applied for the determination of zero-field splittings in lanthanides with unquenched orbital momentum (i.e. L ≠ 0).52,53 By considering the minimal, common C4 symmetry of the gadolinium site, the appropriate Hamiltonian following the Stevens approach is5
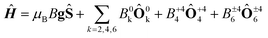 | (1) |
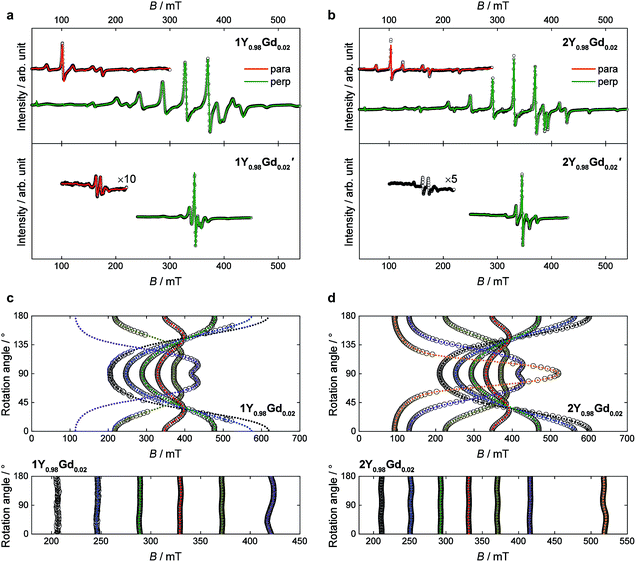
Best fits to the Hamiltonian (1) were found to provide excellent descriptions of the powder spectra of 1Y0.98Gd0.02 and 2Y0.98Gd0.02 for both polarization modes. Despite the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 disorder in the crystal field, characteristic of the 1Ln compounds, it was possible to describe the spectra of 1Y0.98Gd0.02, assuming a single gadolinium site in C4 symmetry. The only manifestation of said disorder is the greater linewidth of the resonance lines for 1Y0.98Gd0.02 over those for 2Y0.98Gd0.02. The best fit parameters are summarized in Table 2. The axial space groups with molecular C4 axes co-parallel facilitate single crystal EPR measurements on doped single crystals of 1Y0.98Gd0.02 and 2Y0.98Gd0.02. These data confirm the validity of the parametrizations, the angular dependence of the resonance lines being well reproduced for various crystal rotations (Fig. 8c and d).
50 disorder in the crystal field, characteristic of the 1Ln compounds, it was possible to describe the spectra of 1Y0.98Gd0.02, assuming a single gadolinium site in C4 symmetry. The only manifestation of said disorder is the greater linewidth of the resonance lines for 1Y0.98Gd0.02 over those for 2Y0.98Gd0.02. The best fit parameters are summarized in Table 2. The axial space groups with molecular C4 axes co-parallel facilitate single crystal EPR measurements on doped single crystals of 1Y0.98Gd0.02 and 2Y0.98Gd0.02. These data confirm the validity of the parametrizations, the angular dependence of the resonance lines being well reproduced for various crystal rotations (Fig. 8c and d).
| 1Y0.98Gd0.02 | 2Y0.98Gd0.02 | 1Y0.98Gd0.02′ | 2Y0.98Gd0.02′ | |
|---|---|---|---|---|
| g ∥ | 1.9865(3) | 1.9880(2) | 1.979(1) | 1.984(1) |
| g ⊥ | 1.98552(4) | 1.98690(7) | 1.9862(8) | 1.9843(1) |
| B 02/cm−1 | 3.2378(5) × 10−2 | 3.0553(5) × 10−2 | 8.8(1) × 10−3 | 1.071(4) × 10−2 |
| B 04/cm−1 | −2.605(4) × 10−4 | −2.480(2) × 10−4 | −2.0(1) × 10−4 | −2.04(3) × 10−4 |
| B 06/cm−1 | −2.8(7) × 10−8 | 4(2) × 10−8 | −1(6) × 10−7 | −5(5) × 10−7 |
| B +44/cm−1 | 1.4(5) × 10−6 | 1.4(2) × 10−6 | 1.9(3) × 10−5 | 6(6) × 10−6 |
| B +46/cm−1 | 1.62(5) × 10−6 | 2.0(3) × 10−7 | N/A | −1.3(7) × 10−6 |
| B −46/cm−1 | −6.1(2) × 10−7 | 3.6(3) × 10−7 | N/A | −2(3) × 10−7 |
As expected, the g-tensors of both compounds are essentially isotropic, and highly comparable. The second and fourth order axial Stevens parameters, B02 and B04, are remarkably similar between the two different salts, the variation being no more than 6%. The value of B06 varies significantly between the two salts, but in both cases, the value is very small, and the effect of this term in the Hamiltonian therefore minimal. The determined value of the real fourth order off-diagonal Stevens parameter B+44 is identical for 1Y0.98Gd0.02 and 2Y0.98Gd0.02, but two orders of magnitude smaller than the parameter value of the axial parameter of the equivalent order, and consequently the contribution of the term in the Hamiltonian (1) associated with the B+44 parameter should be considered small. Rather, the main off-diagonal components of the crystal field are parametrized by the real and imaginary sixth order off-diagonal parameters B+46 (real) and B−46 (imaginary). The determined absolute values of these parameters are larger for 1Y0.98Gd0.02 over 2Y0.98Gd0.02 by factors of 8 and 1.7, respectively. This unambiguously demonstrates the higher symmetry of the 2Ln compounds, the approximation to the axial D4d point group symmetry being significantly better in these salts compared to the 1Ln systems. The parameter values determined from the best fits to the parallel mode spectra (red traces in Fig. 8a and b) agree well with those derived from the perpendicular mode data.
The chelation of the lanthanide centres by the metalloligands combined with the high crystallographic symmetry of the salts, places the filled 5dz2 orbital of platinum along the four-fold axis with radial extension towards the lanthanide ion. In order to assess the possible role of this occupied orbital in defining the environment of the gadolinium(III) ion, similar powder X-band EPR measurements on doped samples were carried out for 1Gd′ and 2Gd′. If important, the reduced radial extension of 4dz2 orbital of palladium should lead to an alteration of the axial zero-field splitting parameters. The room temperature spectra of the palladium-based complexes 1Y0.98Gd0.02′ and 2Y0.98Gd0.02′ recorded with the microwave polarization either perpendicular or parallel to the applied magnetic field are given in the lower panels of Fig. 8a and b.
The visual inspection of the spectra clearly demonstrates the strong influence of the group 10 metal ion, the total width of the spectra of the palladium derivatives being less than half of that of the platinum analogues. The best fits of the perpendicular mode spectra to the Hamiltonian (1) nicely reproduce the data as shown by the green traces in the lower panels of Fig. 8a and b. The fit parameters are summarized in Table 2. As the spectra of 1Y0.98Gd0.02′ and 2Y0.98Gd0.02′ are less rich in detail than those of 1Y0.98Gd0.02 and 2Y0.98Gd0.02, the parameter values are determined with slightly lower fidelity. In the case of 1Y0.98Gd0.02′, the sixth order off-diagonal parameters could not be reliably determined, and consequently the associated terms were excluded from the fit. A fit to the parallel mode spectrum (red trace in Fig. 8a) agrees well with that to the perpendicular mode data for 1Y0.98Gd0.02′, but as for the platinum derivatives, the parameters from the parallel mode fitting come with significant uncertainties.
From the best fits, the main origin of the difference between the platinum and palladium derivatives is found to be the value of the second order axial zero-field splitting parameter, B02. For 1Y0.98Gd0.02′ the determined value is only 27% of the value determined for 1Y0.98Gd0.02, while it for 2Y0.98Gd0.02′ is 35% of that found for 2Y0.98Gd0.02. While the effect is less pronounced for the fourth order axial parameter B04, its value decreases consistently upon exchanging platinum with palladium. As for the platinum derivatives, the term associated with the B06 parameter is found to be relatively unimportant for 1Y0.98Gd0.02′ and 2Y0.98Gd0.02′. These findings strongly indicate a significant interaction between the gadolinium centre and the group 10 metal, suggesting a coordination number of ten, rather than the intuitively assigned eight. Such donation of electron density from Pt(II) to a proximate Lewis acid, i.e. the Ln(III) ion, was recently evidenced in the heterobimetallic lantern complexes based on the alkaline earth metals using 195Pt NMR, thereby demonstrating the Lewis-basic behaviour of the platinum centre.39 The minimization of the off-diagonal terms in the Hamiltonian (1) is again found upon going from 1Y0.98Gd0.02′ to the higher symmetry 2Y0.98Gd0.02′ species. Albeit a direct comparison is hampered by our failure in determining the sixth order off-diagonal parameters for 1Y0.98Gd0.02′, we note that the values of B+44 and B−46 for 2Y0.98Gd0.02′ are found to be equal to zero within error, supporting the notion that the point group symmetry in the 2Ln′ compounds is D4d to a very good approximation.
Conclusions
In summary, we have demonstrated how homoleptic thioacetate complexes of divalent group 10 metal ions can be used as chelating metalloligands in the design of tetragonal complexes of the trivalent lanthanides. Through packing effects with counter cations compatible with four-fold symmetry, the point group symmetry at the lanthanide site in the monoanionic bis metalloligand complexes can be varied between effective C4 in the [NEt4]+ salts and the higher symmetry D4d in the [PPh4]+ salts. This symmetry difference deduced from structural analysis is unequivocally confirmed by detailed electron paramagnetic resonance spectroscopy on the gadolinium derivatives. These EPR studies furthermore demonstrate a significant interaction between the filled ndz2 orbital of the platinum metal and the gadolinium ion, supporting a Lewis-basic nature of the platinum(II) centre. Upon going from the 4dz2 orbital of palladium to the radially more extended 5dz2 orbital of platinum, the leading axial zero-field splitting parameter of Gd3+ quadruples, providing strong evidence for a coordination number of ten rather than eight as otherwise assumed from structural analysis. The fact that the platinum metal can be varied renders this class of lanthanide complexes highly tuneable; not only can the point group symmetry at the lanthanide site be altered, so can the ratio between axial and equatorial components of the crystal field. This unprecedented tunability of chemically otherwise unaltered complexes makes this new family of compounds ideal test subjects for studies of the subtleties governing lanthanide magnetism. The in-detail magnetic investigations of selected members of the series are currently being undertaken, and the results will be communicated in the near future.Acknowledgements
LHD acknowledges support from NSF-CCT EMT 08-517.Notes and references
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606–6609 CrossRef CAS PubMed.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656 CrossRef CAS PubMed.
- K. S. Pedersen, G. Lorusso, J. J. Morales, T. Weyhermüller, S. Piligkos, S. K. Singh, D. Larsen, M. Schau-Magnussen, G. Rajaraman, M. Evangelisti and J. Bendix, Angew. Chem., Int. Ed., 2014, 53, 2394–2397 CrossRef CAS PubMed.
- R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 43–45 CrossRef CAS PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- H. L. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33 CrossRef CAS.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem.–Eur. J., 2014, 20, 9524–9529 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- C. B. P. Finn, R. Orbach and W. P. Wolf, Proc. Phys. Soc., London, 1961, 77, 261–268 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, U.K., 1970 Search PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- A. Watanabe, A. Yamashita, M. Nakano, T. Yamamura and T. Kajiwara, Chem.–Eur. J., 2011, 17, 7428–7432 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- Y.-N. Guo, L. Ungur, G. E. Granroth, A. K. Powell, C. Wu, S. E. Nagler, J. Tang, L. F. Chibotaru and D. Cui, Sci. Rep., 2014, 4, 5471 CAS.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51, 12565–12574 CrossRef PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Chem. Commun., 1972, 349–350 RSC.
- P. G. Eller, D. C. Bradley, M. B. Hursthouse and D. W. Meek, Coord. Chem. Rev., 1977, 24, 1–95 CrossRef CAS.
- W. J. Evans, D. K. Drummond, H. Zhang and J. L. Atwood, Inorg. Chem., 1988, 27, 575–579 CrossRef CAS.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 5864–5868 CrossRef CAS PubMed.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103 RSC.
- P. V. Bernhardt, B. M. Flanagan and M. J. Riley, Aust. J. Chem., 2000, 53, 229–231 CrossRef CAS.
- P. V. Bernhardt, B. M. Flanagan and M. J. Riley, Aust. J. Chem., 2001, 54, 229–232 CrossRef CAS.
- S. Mizukami, H. Houjou, M. Kanesato and K. Hiratani, Chem.–Eur. J., 2003, 9, 1521–1528 CrossRef CAS PubMed.
- K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. Schau-Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe, O. Waldmann, L. F. Chibotaru, J. Bendix and J. Dreiser, Chem. Sci., 2014, 5, 1650–1660 RSC.
- C. Piguet, A. F. Williams, G. Bernardinelli and J.-C. G. Bünzli, Inorg. Chem., 1993, 32, 4139–4149 CrossRef CAS.
- N. Koike, H. Uekusa, Y. Ohashi, C. Harnoode, F. Kitamura, T. Ohsaka and K. Tokuda, Inorg. Chem., 1996, 35, 5798–5804 CrossRef CAS.
- C. Apostolidis, J. Rebizant, B. Kanellakopulos, R. von Ammon, E. Dornberger, J. Müller, B. Powietzka and B. Nuber, Polyhedron, 1997, 16, 1057–1068 CrossRef CAS.
- K. R. Meihaus, S. G. Minasian, W. W. Lukens, S. A. Kozimor, D. K. Shuh, T. Tyliszczak and J. R. Long, J. Am. Chem. Soc., 2014, 136, 6056–6068 CrossRef CAS PubMed.
- F. G. Baddour, A. S. Hyre, J. L. Guillet, D. Pascual, J. M. Lopez-de-Luzuriaga, T. M. Alam, J. W. Bacon and L. H. Doerrer, Inorg. Chem., 2017, 56, 452–469 CrossRef CAS PubMed.
- E. W. Dahl, F. G. Baddour, S. R. Fiedler, W. A. Hoffert, M. P. Shores, G. T. Yee, J.-P. Djukic, J. W. Bacon, A. L. Rheingold and L. H. Doerrer, Chem. Sci., 2012, 3, 602–609 RSC.
- F. G. Baddour, S. R. Fiedler, M. P. Shores, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2013, 52, 4926–4933 CrossRef CAS PubMed.
- F. G. Baddour, S. R. Fiedler, M. P. Shores, J. W. Bacon, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2013, 52, 13562–13575 CrossRef CAS PubMed.
- J. L. Guillet, I. Bhowmick, M. P. Shores, C. J. A. Daley, M. Gembicky, J. A. Golen, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2016, 55, 8099–8109 CrossRef CAS PubMed.
- T. Kanda, M. Ibi, K. Mochizuki and S. Kato, Chem. Lett., 1998, 957–958 CrossRef CAS.
- L. Tian and J. J. Vittal, Cryst. Growth Des., 2006, 6, 822–824 CAS.
- J. C. Trombe, A. Gleizes and J. Galy, Inorg. Chim. Acta, 1984, 87, 129–141 CrossRef CAS.
- M. Siebold, A. Kelling, U. Schilde and P. Strauch, Z. Naturforsch., B: J. Chem. Sci., 2005, 60, 1149–1157 CAS.
- M. Siebold, M. Korabik, U. Schilde, J. Mrozinski and P. Strauch, Chem. Pap., 2008, 62, 487–495 CAS.
- G.-F. Xu, P. Gamez, J. Tang, R. Clérac, Y.-N. Guo and Y. Guo, Inorg. Chem., 2012, 513, 5693–5698 CrossRef PubMed.
- M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479 CrossRef CAS PubMed.
- O. Kahn, Molecular Magnetism, Wiley-VCH, New York, 1993 Search PubMed.
- S. Ghosh, S. Datta, L. Friend, S. Cardona-Serra, A. Gaita-Ariño, E. Coronado and S. Hill, Dalton Trans., 2012, 41, 13697–13704 RSC.
- J. Krzystek and J. Telser, Dalton Trans., 2016, 45, 16751–16763 RSC.
- L. Sorace and D. Gatteschi, in Lanthanides and Actinides in Molecular Magnetism, WILEY-VCH Verlag GmbH & Co. KGaA, 2015, pp. 1–25 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, crystallographic details, additional magnetic data, experimental details on EPR measurements. CCDC 1526314–1526340. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc00135e |
| This journal is © The Royal Society of Chemistry 2017 |