Open Access Article
Open Access ArticleHigh-level ab initio potential energy surface and dynamics of the F− + CH3I SN2 and proton-transfer reactions†
Balázs
Olasz
 ,
István
Szabó‡
,
István
Szabó‡
 and
Gábor
Czakó
and
Gábor
Czakó
 *
*
Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: gczako@chem.u-szeged.hu
First published on 17th February 2017
Abstract
Bimolecular nucleophilic substitution (SN2) and proton transfer are fundamental processes in chemistry and F− + CH3I is an important prototype of these reactions. Here we develop the first full-dimensional ab initio analytical potential energy surface (PES) for the F− + CH3I system using a permutationally invariant fit of high-level composite energies obtained with the combination of the explicitly-correlated CCSD(T)-F12b method, the aug-cc-pVTZ basis, core electron correlation effects, and a relativistic effective core potential for iodine. The PES accurately describes the SN2 channel producing I− + CH3F via Walden-inversion, front-side attack, and double-inversion pathways as well as the proton-transfer channel leading to HF + CH2I−. The relative energies of the stationary points on the PES agree well with the new explicitly-correlated all-electron CCSD(T)-F12b/QZ-quality benchmark values. Quasiclassical trajectory computations on the PES show that the proton transfer becomes significant at high collision energies and double-inversion as well as front-side attack trajectories can occur. The computed broad angular distributions and hot internal energy distributions indicate the dominance of indirect mechanisms at lower collision energies, which is confirmed by analyzing the integration time and leaving group velocity distributions. Comparison with available crossed-beam experiments shows usually good agreement.
Introduction
Bimolecular nucleophilic substitution (SN2) is one of the best-known reaction classes in organic chemistry. The atomic-level description of the back-side attack inversion and front-side attack retention mechanisms of SN2 reactions was already presented in the book of Ingold in 1953.1 According to the simple picture of the X− + CH3Y → XCH3 + Y− [X, Y = F, Cl, Br, I] reactions, the back-side attack Walden-inversion pathway involves a C3v ion–dipole pre-reaction complex (X−⋯H3CY), a central transition state (TS) (X⋯H3C⋯Y)−, and a C3v post-reaction complex (XCH3⋯Y−), whereas the front-side attack pathway goes through a high-energy (H3CXY)− TS, where X directly replaces Y without inversion. However, recent theoretical and experimental studies show that this simple picture is not complete and the dynamics of SN2 reactions are much more complex.2–8 Besides the above described direct pathways, indirect mechanisms play a key role in the dynamics. For the Cl− + CH3I reaction a so-called roundabout mechanism9 was found in 2008 and for the F− + CH3Cl reaction simulations revealed a double-inversion6 pathway in 2015, which was also identified in aqueous solution10 in 2016. Furthermore, in the case of the F− nucleophile a hydrogen-bonded pre-reaction complex (F−⋯HCH2Y) was found to play an important role in the dynamics.5,11 In the case of the F− + CH3Y SN2 reactions, where Y = Cl and I, a recent joint crossed-beam and trajectory study showed that the leaving group can also influence the dynamics, since the F− + CH3Cl reaction was found to be significantly more direct than F− + CH3I.7 This means that the direct rebound mechanism dominates in F− + CH3Cl, whereas slow indirect complex-forming pathways are more likely in the F− + CH3I reaction.The present study focuses on the F− + CH3I reaction, which has been recently investigated both experimentally and theoretically.11–14 Previous reaction dynamics simulations11–13 of the title reaction have been restricted to the use of the direct dynamics approach due to the lack of an analytical potential energy surface (PES). Here, we report such a PES for the F− + CH3I system, which allows efficient quasiclassical trajectory (QCT) computations and opens the door for future quantum dynamics studies. Utilizing the large number of trajectories obtained on the PES, we can compute statistically robust integral and differential cross sections as well as product internal energy distributions allowing quantitative comparisons with previous crossed-beam experiments.11,12,14 We can also determine whether double-inversion trajectories can occur in the F− + CH3I reaction, which have never been seen before in this system even if smaller double-inversion barrier height was recently predicted15 for F− + CH3I than that of F− + CH3Cl. Furthermore, besides the SN2 pathways, a proton transfer between the reactants can also occur. The present study aims to simulate both the SN2 and proton-transfer channels using the newly developed global PES.
Methods
The PES is represented by fitting high-level ab initio energies using the permutationally invariant polynomial approach.16–20 Roughly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy points are computed at the explicitly-correlated CCSD(T)-F12b/aug-cc-pVTZ level of theory21,22 using a relativistic effective core potential and the corresponding aug-cc-pVTZ-PP basis set23 for iodine. Core correlation effects, which can be important for the heavy iodine, are also considered as an additive correction obtained as difference between all-electron and frozen-core energies at the CCSD(T)/aug-cc-pwCVDZ-PP level of theory. The PES is fitted using a 5th order polynomial expansion of Morse-type variables, exp(−rij/a), where rij denotes inter-atomic distances and a = 3 bohr. Note that in many previous studies considering, for example, reactions of atoms with methane, an a value of 2 bohr was used.24 However, in the case of SN2 reactions, where long-range ion–dipole interactions present, a larger a value, i.e., more diffuse fitting basis, is needed. After several test fits with different a values, we have chosen a = 3 bohr, which provides a good description at large distances as shown in Fig. S1 of the ESI.† The number of the linear fitting parameters is 3313, which are determined by a weighted least-squares fit, where each energy, E that is relative to the global minimum, has a weight of E0/(E + E0), where E0 is 0.1 in atomic units. Weights are used to suppress the high-energy data, which are out of the range of chemical importance. Our previous studies5,6 on F− + CH3Cl used E0 = 0.05 a.u.; here a larger E0 is chosen, because F− + CH3I is more exothermic than F− + CH3Cl.
000 energy points are computed at the explicitly-correlated CCSD(T)-F12b/aug-cc-pVTZ level of theory21,22 using a relativistic effective core potential and the corresponding aug-cc-pVTZ-PP basis set23 for iodine. Core correlation effects, which can be important for the heavy iodine, are also considered as an additive correction obtained as difference between all-electron and frozen-core energies at the CCSD(T)/aug-cc-pwCVDZ-PP level of theory. The PES is fitted using a 5th order polynomial expansion of Morse-type variables, exp(−rij/a), where rij denotes inter-atomic distances and a = 3 bohr. Note that in many previous studies considering, for example, reactions of atoms with methane, an a value of 2 bohr was used.24 However, in the case of SN2 reactions, where long-range ion–dipole interactions present, a larger a value, i.e., more diffuse fitting basis, is needed. After several test fits with different a values, we have chosen a = 3 bohr, which provides a good description at large distances as shown in Fig. S1 of the ESI.† The number of the linear fitting parameters is 3313, which are determined by a weighted least-squares fit, where each energy, E that is relative to the global minimum, has a weight of E0/(E + E0), where E0 is 0.1 in atomic units. Weights are used to suppress the high-energy data, which are out of the range of chemical importance. Our previous studies5,6 on F− + CH3Cl used E0 = 0.05 a.u.; here a larger E0 is chosen, because F− + CH3I is more exothermic than F− + CH3Cl.
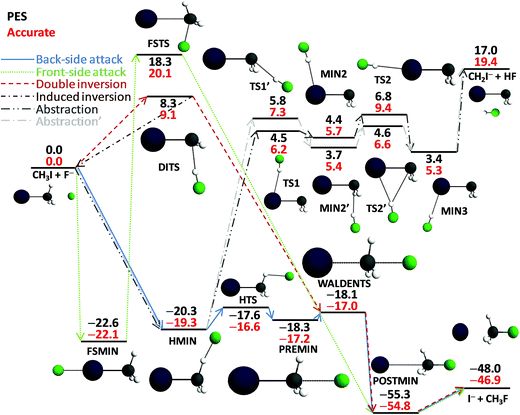
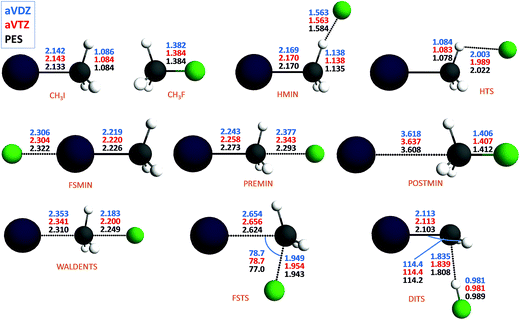
The new PES accurately describes the SN2 channel via the above-mentioned different reaction pathways as well as the proton-transfer channel leading to HF + CH2I−. The energy diagram of the complex PES is shown in Fig. 1, where the relative energies obtained from the PES are compared to high-level benchmark ab initio data. The most important structural parameters of the stationary points obtained at CCSD(T)-F12b with aug-cc-pVDZ-PP and aug-cc-pVTZ-PP basis sets as well as from the PES are shown in Fig. 2 and S2† for the SN2 and abstraction channels, respectively. The benchmark classical relative energies of the stationary points are computed using a composite method based on CCSD(T)-F12b/aug-cc-pVQZ-PP energies and CCSD(T)/aug-cc-pwCVTZ-PP core correlation corrections at CCSD(T)-F12b/aug-cc-pVTZ-PP geometries (Table S1†). The best adiabatic relative energies are determined by adding a harmonic zero-point energy (ZPE) correction, obtained at the CCSD(T)-F12b/aug-cc-pVTZ-PP level of theory, to the classical energies. The CCSD(T)-F12b/aug-cc-pVnZ-PP (n = D and T) and PES harmonic vibrational frequencies of all the stationary points are given in Tables S2 and S3.† All the electronic structure computations are performed with the Molpro package.25
QCT computations are carried out for the F− + CH3I (v = 0) reaction on the new analytical PES using standard normal-mode sampling26 to prepare the initial vibrational ground state (v = 0) of CH3I. Trajectories are run at collision energies (Ecoll) of 1.0, 4.0, 7.4, 10.0, 15.9, 35.3, and 50.0 kcal mol−1 using a time step of 0.0726 fs. The impact parameters, b, are scanned from 0 to bmax with a step size of 0.5 bohr and 5000 trajectories are computed at each b. The bmax values are found to be 30, 20, 17, 15, 13, 10, and 9 bohr for the above collision energies, respectively. Note that bmax values are determined by running trajectories at increasing fixed b values using a step of 0.5 bohr until the reaction probability becomes 0. The final cross sections are obtained by a b-weighted numerical integration of the reaction probabilities over impact parameters from 0 to bmax. This approach is different from that which generates non-uniform b values between 0 and bmax using a Monte Carlo sampling, where the accurate value of bmax is important.27–29 Of course, the two approaches converge to the same results with increasing number of trajectories and decreasing b steps for the former method. The impact parameter dependence of the reaction probabilities for both the SN2 and abstraction channels at all the above collision energies are shown in the ESI (Fig. S3†). The present study considers more than 1 million trajectories. The maximum number of time steps for each trajectory is 5 million (363 ps), but the direct trajectories are only about 0.5–2 ps long and most of the trajectories finish within ∼30 ps (for more details see Fig. S4†). The average CPU time of a trajectory is between 8 and 200 s strongly depending on the collision energy, impact parameter, and computer hardware. Note that the analytical potential ensures that the computation of forces during the trajectory propagation has almost no cost compared to direct dynamics simulations at the same level of theory.
Results and discussion
As shown in Table S1,† the CCSD(T)-F12b energies with aug-cc-pVDZ-PP and aug-cc-pVTZ-PP bases agree within about 0.2 kcal mol−1, the core correlation effects have positive signs and are in the range of 0.0–0.8 kcal mol−1, and the ZPE corrections are ranging from −3.5 to +2.0 kcal mol−1 for all the stationary points shown in Fig. 1. Thus, the ZPE corrections can be significant, since they decrease the exothermicity of the SN2 channel by 1.8 kcal mol−1 and decrease the endothermicity of the abstraction channel by 3.5 kcal mol−1. For the Walden-inversion TS the ZPE effect is negligible, whereas the ZPE correction decreases the abstraction as well as double-inversion barriers by about 2 kcal mol−1. As shown in Fig. 1, the PES reproduces the high-level benchmark energies with 1 kcal mol−1 accuracy for the SN2 pathways and somewhat larger differences of about 2 kcal mol−1 are seen for the abstraction channel. It is important to note that Zhang, Xie, and Hase13 recently reported the same stationary points for the abstraction channel using B97-1/ECP/d/aug-cc-pVDZ level of theory, which usually overestimate the present benchmark values by 0.7 kcal mol−1 on average (the maximum deviation is 1.2 kcal mol−1 for TS1′ using our notation). Thus, our high-level energies confirm the reliability of the B97-1/ECP/d method for direct dynamics studies of the title reaction, at least at not too high energies.Utilizing the benchmark classical relative energies we can characterize the different reaction pathways of the F− + CH3I reaction. The SN2 reaction is highly exothermic (−46.9 kcal mol−1) with a submerged Walden-inversion TS (−17.0, relative to the reactant asymptote), a double-inversion barrier (9.1 kcal mol−1), and a much higher front-side attack barrier (20.1 kcal mol−1). The proton-abstraction channel is endothermic (19.4 kcal mol−1) with several minima and saddle points above the reactants by about 5–10 kcal mol−1, but well below the HF + CH2I− products. It is important to emphasize that the energy level of the proton-abstraction products is significantly above the double-inversion TS and slightly below the front-side attack TS, similar to the F− + CH3Cl reaction, where the double-inversion pathway was discovered.6 Thus, one can expect double-inversion trajectories below the threshold energy of the abstraction and front-side attack SN2 pathways. In the entrance channel of the F− + CH3I reaction we have found several stationary points. Besides the C3v ion–dipole complex (−17.2 kcal mol−1), there is a hydrogen-bonded Cs complex (−19.3 kcal mol−1) which corresponds to a significantly deeper minimum than the C3v complex. The two minima is separated by a TS (−16.6 kcal mol−1) above the Cs and C3v minima by 2.7 and 0.6 kcal mol−1, respectively. Furthermore, a front-side F−⋯ICH3C3v complex (−22.1 kcal mol−1), where F− is connected to the I atom, also exits in the entrance channel. This complex may play a significant role in the dynamics, because the F−⋯ICH3 minimum is deeper by 4.9 and 2.8 kcal mol−1 than the above-mentioned back-side C3v and hydrogen-bonded minima, respectively.
As seen in Fig. 2 and S2 and Tables S2 and S3,† the PES reproduces the benchmark bond lengths and angles as well as the vibrational frequencies with reasonable accuracy. Here we just emphasize a few points. Even if the Walden-inversion barrier of SN2 reactions is usually called “central”, in the present case, the C–I distance is only stretched by 0.2 Å relative to the corresponding equilibrium distance in the reactant molecule, whereas the C–F distance is 0.8 Å longer than that in the product molecule. Thus, for the F− + CH3I reaction we can say that the Walden inversion has an early barrier (reactant-like TS), in accord with the Hammond postulate30 for an exothermic reaction. At the double-inversion TS the H–F distance is stretched by 0.06 Å relative to the bond length of the HF molecule, whereas at the proton-abstraction minima and saddle points the corresponding effects are only around 0.02 Å. Furthermore, the intermolecular H⋯C distance at the double-inversion TS is 1.8 Å, that is much shorter than the corresponding distances of 2.1–2.2 Å at the similar abstraction stationary points. Among the TSs the double-inversion, the front-side attack, and the Walden-inversion saddle points have the largest imaginary frequencies that are 767i, 591i, and 231i, in cm−1, respectively, at the CCSD(T)-F12b/aug-cc-pVTZ-PP level, in good agreement with the corresponding PES values of 775i, 582i, and 206i. Note that the large imaginary frequency of the double-inversion saddle point makes this TS different from the abstraction TSs, which have imaginary frequencies around 100i. Thus, on one hand, there are several properties of the double-inversion TS which separate it from the abstraction TSs. On the other hand, as pointed out by Zhang, Xie, and Hase,13 intrinsic reaction coordinate (IRC) computations show that the double-inversion TS is connected to the proton-transfer TSs. However, trajectories may not follow the IRC reaction path; therefore, the investigation of the role of the TSs in the double-inversion dynamics of the title reaction is an important future research direction.
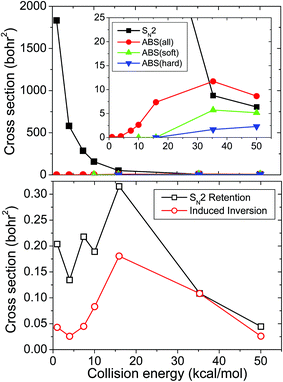
Fig. 3 shows the cross sections as a function of collision energy for the different reaction pathways of the title reaction. The SN2 cross sections are extremely large at low Ecoll and sharply decrease as Ecoll increases, as expected for a highly exothermic barrierless reaction. Applying ZPE constraint, the abstraction channel opens around Ecoll = 15 kcal mol−1 in accord with its endothermicity of 15.9 kcal mol−1. Without ZPE constraint, the abstraction cross sections are significantly larger and do not have a threshold. We consider both soft and hard ZPE constraints. The soft constraint discards trajectories if the sum of the product vibrational energies is less than the sum of ZPEs (obtained in the harmonic approximation), whereas the hard constraint discards trajectories if either HF or CH2I− has less vibrational energy than the corresponding ZPE. Note that a sophisticated alternative of treating the ZPE issue is the use of the one-dimensional Gaussian binning (1GB) method,31–33 but this technique cannot provide realistic absolute cross sections due to the normalization issue, therefore we rely on the simpler soft and hard ZPE constraints. The soft and hard ZPE constraints give similar, physically correct thresholds, but the hard cross sections are substantially smaller as shown in Fig. 3. Recently, Zhang, Xie, and Hase13 reported cross sections of 30.7 ± 7.9 and 7.5 ± 2.9 bohr2 for the SN2 and abstraction channels, respectively, obtained from a DFT/B91-1 direct dynamics computation at Ecoll = 35.3 kcal mol−1. When they applied ZPE constraint for the CH2I− product, the abstraction cross section became 5.4 ± 1.4 bohr2. Our PES gives substantially smaller cross section (8.8 bohr2) for the SN2 channel, which, however, agrees better with an MP2 direct dynamics result of 6.4 ± 1.1 bohr2.34 For the abstraction, the present cross section of 11.7 bohr2 without ZPE constraint is in reasonable agreement with the DFT/B91-1 result of 7.5 ± 2.9 bohr2. Furthermore, our soft constrained cross section (5.7 bohr2) agrees well with the above-cited CH2I− constrained value of 5.4 ± 1.4 bohr2. Note that the error bars of the direct dynamics results reflect the statistical uncertainty of the simulation, which is negligible in our case. The uncertainty due to the inaccuracy of the on-the-fly or analytical PES is hardly predictable, but obviously large especially for the SN2 channel where the B97-1/ECP/d/aug-cc-pVDZ level and the present PES seem to deviate significantly, at least at high energies. The branching ratio between the SN2 and proton-abstraction channels was recently measured by Wester and co-workers.14 In the Ecoll range of 30–50 kcal mol−1 the abstraction channel was found to contribute about 20% to the total reactivity. Without ZPE constraint the present simulation overestimates the abstraction cross sections and gives about 60% contribution. Nevertheless, using the hard ZPE constraint the abstraction cross sections drop to around 20% of the total cross section, in good agreement with experiment. This indicates that the use of the ZPE constraint can be important to get realistic results from a QCT simulation.
Configuration-retaining SN2 cross sections are also shown in Fig. 3. These retention cross sections are about two orders of magnitude smaller than the inversion ones. Examination of many retention trajectories indicates that at low Ecoll all of the retention trajectories occur via the double-inversion mechanism, whereas at collision energies above 20 kcal mol−1 the front-side attack pathway also opens. Double inversion is usually a slow indirect process, whereas the front-side attack is fast and direct. However, we found that one cannot distinguish between the two mechanisms based on simply the integration time, as we did in the case of the F− + CH3Cl, F− + CH3F, and F− + CHD2Cl reactions.6,35,36Fig. 3 also shows the cross sections for the induced inversions of the CH3I reactant, which are not followed by a substitution resulting in an inverted reactant. The Ecoll dependence of the induced and double inversions is similar, both have a maximum at Ecoll = 20 kcal mol−1. At low Ecoll the probability of induced inversion is smaller than that of the double inversion, showing that the first inversion is usually followed by a second inversion. Due to the fact that the adiabatic double-inversion barrier height of the F− + CH3I reaction (7.0 kcal mol−1) is significantly smaller than that of the F− + CH3Cl reaction (14.0 kcal mol−1),6 we predicted15 that the double inversion could be more likely in the F− + CH3I system. The present QCT results support this, since the double-inversion cross sections can be as high as 0.3 bohr2 for F− + CH3I, whereas the corresponding value is only 0.05 bohr2 for F− + CH3Cl.6 Furthermore, the maximum of the double-inversion cross sections, that is at Ecoll = 30 kcal mol−1 for F− + CH3Cl, is at a smaller Ecoll of 20 kcal mol−1 for F− + CH3I.
Comparison of the computed and measured12 differential cross sections as well as product internal energy distributions of the SN2 channel is shown in Fig. 4. The computed scattering angle distributions are broad with forward preference at low Ecoll and slight backward dominance at larger Ecoll. The broad nearly isotropic feature shows the dominance of the indirect reaction pathways in the F− + CH3I SN2 reaction. At low Ecoll up to about 20 kcal mol−1 the CH3F product internal energy distributions are hot peaking at the highest energies showing that most of the available energy transfers into product vibration and rotation which also supports the dominance of the indirect mechanisms. At a higher Ecoll of 35.3 kcal mol−1, the internal energy distributions are broader indicating mixed direct–indirect mechanisms. For the internal energy distributions theory and experiment are in good qualitative or semi-quantitative agreement as shown in Fig. 4. The finding that the maximum internal energy obtained from the simulation is higher by 1–2 kcal mol−1 than the experimental value is due to the fact that the analytical PES overestimates the exothermicity of the SN2 channel by about 1 kcal mol−1. The agreement between the computed and measured angular distributions is excellent at Ecoll = 15.9 kcal mol−1. At Ecoll = 7.4 kcal mol−1, theory shows more forward scattering than experiment, whereas at Ecoll = 35.4 kcal mol−1 theory is more isotropic than the backward-scattered experiment. At this latter Ecoll, the present computed angular distribution shows some agreement with the previous DFT/B91-1 direct dynamics result, which is also isotropic-like.12 We should also note that the MP2 direct dynamics simulation starts to pick up the backward preference of the experiment.34 However, it is clear that more work needs to be done to obtain definitive theoretical predictions for the angular distributions at high collision energies. Furthermore, it is interesting to note that the present angular distributions are much more isotropic and the internal energy distributions are significantly hotter than the corresponding distributions of the F− + CH3Cl reaction. This supports our previous finding that the F− + CH3Cl reaction is more direct than the analogous F− + CH3I reaction showing a significant leaving group effect on the dynamics of SN2 reactions.7
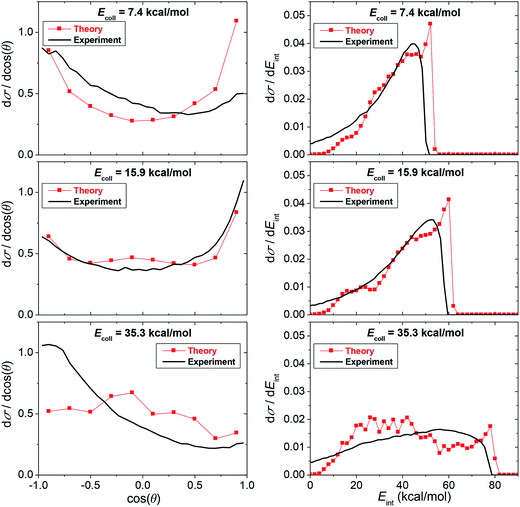 | ||
| Fig. 4 Theoretical (this work) and experimental (ref. 12) normalized scattering angle and product internal energy distributions for the F− + CH3I SN2 reaction at different collision energies. | ||
In order to further investigate the competition between direct and indirect mechanisms, we have determined the direct rebound, direct stripping, and indirect cross sections based on trajectory-integration-time vs. leaving-group-velocity correlation diagrams and scattering angle distributions as shown in more detail in Fig. S5.† The mechanism-specific reaction probabilities at different collision energies are given in Fig. S6.† As seen, the direct reactions proceed with rebound mechanism at small impact parameters and stripping trajectories occur at large b values. The overlaps between the rebound and stripping opacity functions are almost negligible. The indirect reaction probabilities usually decrease with increasing b. At the highest collision energies the indirect reactions vanish at the largest b values and almost solely stripping trajectories are found. The fractions of the rebound, stripping, and indirect cross sections as a function of the collision energy are shown in Fig. 5. At low Ecoll up to about 20 kcal mol−1 the indirect mechanism dominates and at higher Ecoll the direct pathways, especially via the rebound mechanism, become more significant. The computed direct rebound fractions of 17 and 49% at Ecoll = 7.4 and 35.3 kcal mol−1, respectively, are in excellent agreement with the corresponding experimental values of 20 and 52%.12 At Ecoll = 35.3 kcal mol−1 the previous DFT/B91-1 direct dynamics simulation34 gave cross section percentages of 29, 12, and 59 for the direct rebound, direct stripping, and indirect mechanisms, respectively, in disagreement with experiment and the present results of 49, 31, and 20%, respectively. Nevertheless, the agreement with the MP2 direct dynamics results34 of 46, 43, and 11% is much better, which indicates that the DFT/B91-1 method may not give a reasonably accurate description of the PES at high energies. Although both experiment and the present theoretical results show that the direct rebound is the dominant mechanism of the F− + CH3I reaction at high Ecoll, the roughly 50% direct rebound fraction is significantly less than that (∼80%) of the F− + CH3Cl reaction, supporting our previous findings.7
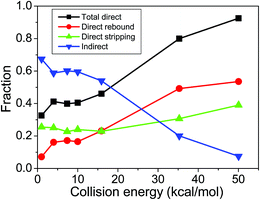 | ||
| Fig. 5 Total direct (rebound + stripping), direct rebound, direct stripping, and indirect F− + CH3I SN2 cross section ratios as a function of collision energy. | ||
Summary and conclusions
We have developed the first analytic global ab initio PES for the title reaction, which accurately describes both the SN2 and proton-transfer channels. QCT simulations on the new PES reveal double-inversion trajectories for the F− + CH3I reaction. Furthermore, the absolute cross sections of F− + CH3I double inversion are found to be larger than those of the F− + CH3Cl reaction. At low collision energies clearly the back-side attack dominates, at high energies the proton-transfer and SN2 channels have similar reactivity. About 1% of the SN2 trajectories occur via the double-inversion and front-side attack pathways. At low collision energies the double-inversion is the dominant retention mechanism, at higher energies the front-side attack pathway opens. The differential cross sections and product internal energy distributions of the F− + CH3I SN2 reaction usually show good agreement with experiment, although some differences can be observed, especially at high collision energies. Some of the results agree well with previous direct dynamics simulations, but there are also differences. The above findings clearly show that the title reaction is a challenging system and the standard single-reference electronic structure methods and effective core potentials used for the iodine atom may not give a good description at high potential energies. Nevertheless, the above-described dynamical results are just certainly the beginning of a fruitful research utilizing the analytical PES reported here for the F− + CH3I reaction. We hope that the new PES will open the door for several future dynamical investigations using quantum37 as well as quasi-classical methods and considering vibrational and/or rotational mode specificity, isotope effects as well as different high-energy reaction channels.Acknowledgements
G. C. thanks the Scientific Research Fund of Hungary (PD-111900) and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences for financial support. We acknowledge the National Information Infrastructure Development Institute for awarding us access to resource based in Hungary at Debrecen and Szeged.References
- C. K. Ingold, Structure and Mechanisms in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953 Search PubMed.
- J. I. Brauman, Science, 2008, 319, 168 CrossRef CAS PubMed.
- P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116, 3061–3080 CrossRef CAS PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969 CrossRef CAS PubMed.
- I. Szabó, A. G. Császár and G. Czakó, Chem. Sci., 2013, 4, 4362–4370 RSC.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151–156 CAS.
- J. Xie and W. L. Hase, Science, 2016, 352, 32–33 CrossRef CAS PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J.-X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183–186 CrossRef CAS PubMed.
- P. Liu, D. Y. Wang and Y. Xu, Phys. Chem. Chem. Phys., 2016, 18, 31895–31903 RSC.
- J. Zhang, J. Mikosch, S. Trippel, R. Otto, M. Weidemüller, R. Wester and W. L. Hase, J. Phys. Chem. Lett., 2010, 1, 2747–2752 CrossRef CAS.
- J. Mikosch, J. Zhang, S. Trippel, C. Eichhorn, R. Otto, R. Sun, W. A. de Jong, M. Weidemüller, W. L. Hase and R. Wester, J. Am. Chem. Soc., 2013, 135, 4250–4259 CrossRef CAS PubMed.
- J. Zhang, J. Xie and W. L. Hase, J. Phys. Chem. A, 2015, 119, 12517–12525 CrossRef CAS PubMed.
- E. Carrascosa, T. Michaelsen, M. Stei, B. Bastian, J. Meyer, J. Mikosch and R. Wester, J. Phys. Chem. A, 2016, 120, 4711–4719 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134–3140 CrossRef PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 CrossRef CAS.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- R. Conte, P. L. Houston and J. M. Bowman, J. Chem. Phys., 2014, 140, 151101 CrossRef.
- R. Conte, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2015, 11, 1631–1638 CrossRef CAS PubMed.
- Y. Wang and J. M. Bowman, Phys. Chem. Chem. Phys., 2016, 18, 24057–24062 RSC.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839–2864 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, MOLPRO, version 2015.1, a package of ab initio programs, see http://www.molpro.net Search PubMed.
- W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407 Search PubMed.
- R. Conte, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 7742–7757 CrossRef CAS PubMed.
- P. L. Houston, R. Conte and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 7758–7775 CrossRef CAS PubMed.
- R. Conte, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 12304–12317 CrossRef CAS PubMed.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- G. Czakó and J. M. Bowman, J. Chem. Phys., 2009, 131, 244302 CrossRef PubMed.
- L. Bonnet and J. Espinosa-García, J. Chem. Phys., 2010, 133, 164108 CrossRef CAS PubMed.
- G. Czakó, J. Phys. Chem. A, 2012, 116, 7467–7473 CrossRef PubMed.
- R. Sun, C. J. Davda, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2015, 17, 2589–2597 RSC.
- I. Szabó, H. Telekes and G. Czakó, J. Chem. Phys., 2015, 142, 244301 CrossRef PubMed.
- I. Szabó and G. Czakó, J. Chem. Phys., 2016, 145, 134303 CrossRef PubMed.
- Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322–3327 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Benchmark classical and adiabatic relative energies (Table S1), vibrational frequencies of all the stationary points (Tables S2 and S3), direct/indirect trajectory separation function parameters (Table S4), entrance-channel potential (Fig. S1), structures of the minima and saddle points corresponding to the abstraction channel (Fig. S2), reaction probabilities (Fig. S3), trajectory integration time distributions (Fig. S4), trajectory integration time vs. I− velocity distributions (Fig. S5), and mechanism-specific reaction probabilities (Fig. S6). See DOI: 10.1039/c7sc00033b |
| ‡ Present address: Department of Chemistry, King's College London, London SE1 1DB, UK. |
| This journal is © The Royal Society of Chemistry 2017 |