Open Access Article
Open Access ArticleRegulating the topology of 2D covalent organic frameworks by the rational introduction of substituents†
Zhong-Fu
Pang
 ,
Tian-You
Zhou
,
Tian-You
Zhou
 ,
Rong-Ran
Liang
,
Rong-Ran
Liang
 ,
Qiao-Yan
Qi
,
Qiao-Yan
Qi
 and
Xin
Zhao
and
Xin
Zhao
 *
*
CAS Key Laboratory of Synthetic and Self-assembly Chemistry for Organic Functional Molecules, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, 345 Lingling Road, Shanghai 200032, China. E-mail: xzhao@sioc.ac.cn
First published on 14th March 2017
Abstract
The topology of a covalent organic framework (COF) is generally believed to be dictated by the symmetries of the monomers used for the condensation reaction. In this context, the use of monomers with different symmetries is usually required to afford COFs with different topologies. Herein, we report a conceptual strategy to regulate the topology of 2D COFs by introducing alkyl substituents into the skeleton of a parent monomer. The resulting monomers, sharing the same C2 symmetry, were assembled with a D2h symmetric tetraamine to generate a dual-pore COF or single-pore COFs, depending on the sizes of the substituents, which were evidenced using PXRD studies and pore size distribution analyses. These results demonstrate that the substituent is able to exert a significant influence on the topology of COFs, which is crucial for their application.
Introduction
Covalent organic frameworks (COFs),1 a variety of crystalline porous materials that are composed of light elements, have drawn considerable attention in the past decade due to their versatile applications in gas storage and separation,2 catalysis,3 sensing,4 drug delivery,5 and electronic devices.6 Compared to other porous organic materials, such as conjugated microporous polymers (CMPs),7 porous polymer networks (PPNs),8 and porous aromatic frameworks (PAFs),9 COFs allow for the atomically precise control of their architectures by changing the structure of their building blocks. In such a way, the shapes and sizes of their pores could be well tuned. Since the first COF was reported in 2005,10 different series of COFs have been constructed. By analyzing the literature, one can conclude that the topology of a COF is dictated by the symmetries of the building blocks used, although the introduction of substituents into the skeletons of the building blocks can result in a change in the size and properties of the pores in a COF.3e,4d,11 It seems that the incorporation of a substituent rarely has an influence on the topology of a COF once the skeleton(s) of the building blocks is/are selected. In most cases, this is reasonable because only one network structure can be predicted for each combination of the building blocks. However, this assertion might not always be true once two or more topologies can be generated from a combination of the same building blocks, a situation that is similar to polymorphism in crystallography. In order to investigate this possibility, a combination of building blocks that can theoretically produce COFs with different topologies must be employed. Although several systems that can meet this criterion have already been recently reported,12 such a possibility has not been demonstrated yet.Very recently, we have reported the construction of a COF with a kagome lattice from the condensation of a monomer with D2h symmetry (4,4′,4′′,4′′′-(ethene-1,1,2,2-tetrayl)tetraaniline, ETTA) and a monomer with C2 symmetry (terephthalaldehyde).12a This COF bears two different kinds of pores; one is hexagonal and the other is triangular. From a topological point of view, a combination of these two monomers may also result in another COF which has only one kind of pore, that is, rhombus-like pores. This feature makes this system an ideal model to investigate the influence of substituents on the topology of COFs. Since the pore size of the triangular pores in the dual-pore (DP) COF is smaller than the size of the pores in single-pore (SP) structure, we envisioned that if suitable substituents are introduced into the skeleton of terephthalaldehyde, steric repulsion between the substituents will arise when they were located inside the triangular pores. As a result, it should block the path for the production of a DP-COF and thus alternatively lead to the formation of a SP structure in which steric repulsion can be significantly alleviated. With this design in mind, in this article, the pristine terephthalaldehyde used in the previous work was replaced with 2,5-dihydroxyterephthalaldehyde (DHTA), and it was further dialkylated using ethyl (2,5-diethoxyterephthalaldehyde, DETA) and n-butyl (2,5-dibutoxyterephthalaldehyde, DBTA). CPK modeling suggested that the size of a triangular pore in the DP-COF was big enough to accommodate three hydroxy groups but it became highly congested when the ethoxy groups were introduced (Fig. S1, ESI†). In the case of the butoxy groups, these were too big to be accommodated by the triangular pores. The experimental results indicate that, while the condensation of DHTA and ETTA gave rise to a COF with a dual-pore structure, the reactions of DETA or DBTA with ETTA led to the formation of COFs with a single-pore topology (Scheme 1). These results reveal that a substituent is able to exert significant influence on the topology of COFs, which has never been observed before.
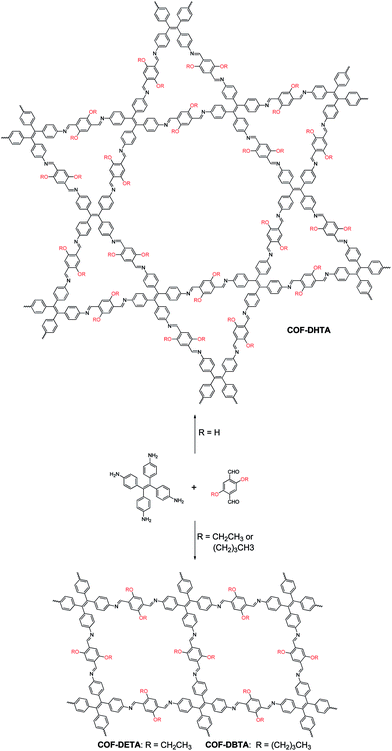 | ||
| Scheme 1 Synthesis of a dual-pore COF and single-pore COFs from ETTA and dialdehyde with different substituents. | ||
Results and discussion
The condensation reactions were carried out by heating the mixtures of ETTA and the corresponding dialdehyde (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in 1,4-dioxane-acetic acid (aq., 6 M) (1/0.1, v/v) in sealed glass ampoules at 120 °C for 72 h and the products were obtained as powders (for details, see the ESI†), which were named COF-DHTA (from DHTA and ETTA), COF-DETA (from DETA and ETTA) and COF-DBTA (from DBTA and ETTA). The as-obtained powders were insoluble in water and common organic solvents, and their colors varied from red to yellow with the increasing chain length of the alkyl substituents. The stretching vibrational band of C
2) in 1,4-dioxane-acetic acid (aq., 6 M) (1/0.1, v/v) in sealed glass ampoules at 120 °C for 72 h and the products were obtained as powders (for details, see the ESI†), which were named COF-DHTA (from DHTA and ETTA), COF-DETA (from DETA and ETTA) and COF-DBTA (from DBTA and ETTA). The as-obtained powders were insoluble in water and common organic solvents, and their colors varied from red to yellow with the increasing chain length of the alkyl substituents. The stretching vibrational band of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N was observed at 1619 cm−1 in Fourier transform infrared (FT-IR) spectra of the powders, which confirmed the existence of C
N was observed at 1619 cm−1 in Fourier transform infrared (FT-IR) spectra of the powders, which confirmed the existence of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N linkages in these materials (Fig. S2, ESI†). Furthermore, the vibration of the NH2 group in ETTA (around 3300 cm−1) was largely attenuated after the condensation reactions, indicating a high degree of polymerization for the polymers. Several peaks in the range of 2850–3000 cm−1 were also observed for COF-DETA and COF-DBTA but not for COF-DHTA, which is consistent with the fact that in the first two materials the alkyl groups were incorporated into their skeletons. The powders were further examined with solid-state 13C cross polarization/magic angle spinning nuclear magnetic resonance (CP/MAS NMR) spectroscopy, which displayed the characteristic 13C resonance signal of C
N linkages in these materials (Fig. S2, ESI†). Furthermore, the vibration of the NH2 group in ETTA (around 3300 cm−1) was largely attenuated after the condensation reactions, indicating a high degree of polymerization for the polymers. Several peaks in the range of 2850–3000 cm−1 were also observed for COF-DETA and COF-DBTA but not for COF-DHTA, which is consistent with the fact that in the first two materials the alkyl groups were incorporated into their skeletons. The powders were further examined with solid-state 13C cross polarization/magic angle spinning nuclear magnetic resonance (CP/MAS NMR) spectroscopy, which displayed the characteristic 13C resonance signal of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N that appeared at 163 ppm for COF-DHTA and at 152 ppm for the other two polymers, which again corroborated the formation of the imine-based polymers (Fig. S3–S5, ESI†). In addition to the signals of C
N that appeared at 163 ppm for COF-DHTA and at 152 ppm for the other two polymers, which again corroborated the formation of the imine-based polymers (Fig. S3–S5, ESI†). In addition to the signals of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and the aromatic carbon atoms, the peaks of the alkyl groups were also identified in the range of 10–70 ppm for COF-DETA and COF-DBTA, clearly indicating the presence of the alkyl substituents in the polymers. Elemental analyses were also performed for these polymers, which revealed that their C, H, and N content was close to that of the corresponding calculated values (see the ESI† for details). As indicated by the thermogravimetric analyses, the as-prepared powders exhibited excellent thermal stabilities. Less than 8% weight losses were observed upon heating them to 400 °C (Fig. S6, ESI†). Scanning electron microscopy (SEM) revealed that they all exhibited irregular morphologies (Fig. S7, ESI†).
N and the aromatic carbon atoms, the peaks of the alkyl groups were also identified in the range of 10–70 ppm for COF-DETA and COF-DBTA, clearly indicating the presence of the alkyl substituents in the polymers. Elemental analyses were also performed for these polymers, which revealed that their C, H, and N content was close to that of the corresponding calculated values (see the ESI† for details). As indicated by the thermogravimetric analyses, the as-prepared powders exhibited excellent thermal stabilities. Less than 8% weight losses were observed upon heating them to 400 °C (Fig. S6, ESI†). Scanning electron microscopy (SEM) revealed that they all exhibited irregular morphologies (Fig. S7, ESI†).
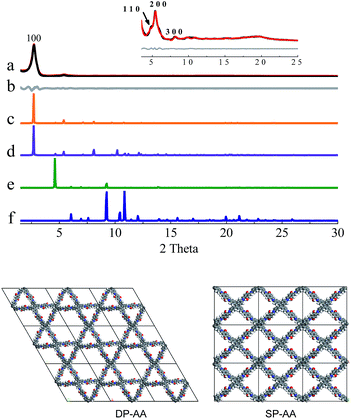
In the next step, theoretical simulations and powder X-ray diffraction (PXRD) experiments were carried out to determine the exact structures of the as-obtained powders (Fig. 1–3 and S8–S10, ESI†). In the simulations, two possible crystalline structures, that is, DP-COF and SP-COF, were constructed. Each crystalline structure was further divided into two stacking models, namely eclipsed packing (AA) and staggered packing (AB). The DP-AA and DP-AB structures were constructed with unit cell parameters of a = b = 37.9 Å, c = 4.5 Å (for DP-AA) or 9.0 Å (for DP-AB), α = β = 90°, and γ = 120°. Similarly, the SP-AA and SP-AB structures were constructed with unit cell parameters of a = 29.2 Å, b = 25.4 Å, c = 4.5 Å (for SP-AA) or 9.0 Å (for SP-AB), and α = β = γ = 90° (see Fig. S9–S12† for details). The powder prepared from DHTA and ETTA was subjected to PXRD analysis and it gave a PXRD pattern similar to that of the previously reported dual-pore COF (Fig. 1a).12a A close comparison of the experimental PXRD pattern with the simulated ones strongly suggests that the powder had a dual-pore structure and eclipsed packing (Fig. 1). Firstly, it exhibits a strong diffraction intensity, indicating the good crystallinity of the powder. Secondly, the experimental PXRD pattern was in good agreement with the simulated PXRD pattern generated from the proposed DHTA-based DP-AA structure. In the experimental PXRD pattern of COF-DHTA, diffraction peaks at 2.72°, 4.83°, 5.40°, 8.10°, and ca. 19.7° are observed, which can be assigned to (100), (110), (200), (300) and (001) diffractions, respectively (Fig. 1a and c). The peak positions and relative intensities could be well reproduced by the simulated PXRD pattern of a DP-COF with AA stacking. In contrast, the simulated PXRD patterns of the structure with single-pore topology exhibited significant differences from the experimentally observed PXRD pattern, suggesting again that the condensation of DHTA and ETTA gave rise to a dual-pore COF, not a single-pore COF. A Pawley refinement reproduced the experimentally observed PXRD peaks quite well and yielded unit cell parameters of a = b = 37.48 Å, c = 4.52 Å, α = β = 90.0°, and γ = 120.0°, with RP = 3.50% and RWP = 4.70%.
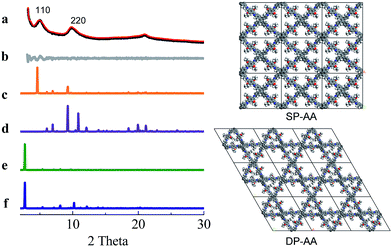
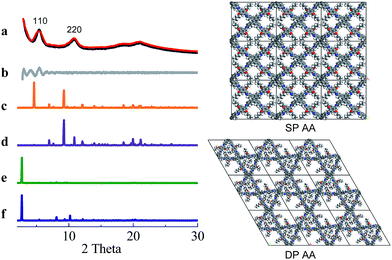
COF-DETA and COF-DBTA exhibited experimental PXRD patterns that were similar to each other. Two broad peaks at 5.0° and 9.9° were observed in the experimental PXRD pattern of COF-DETA (Fig. 2a). Obviously it did not match the simulated PXRD patterns for a dual-pore COF with AA or AB packing (comparing Fig. 2a with 2e and 2f). This result strongly suggested that the condensation of DETA and ETTA did not generate a COF bearing a similar topology as the above dual-pore COF-DHTA. The experimentally observed PXRD pattern was thereupon compared with the ones simulated for a single-pore COF. The simulated PXRD pattern of the DETA-based structure with single-pore topology and AA packing has two major diffraction peaks at 4.62° and 9.24° (Fig. 2b), which are assignable to (110) and (220) diffractions, respectively. At first glance, it seems that the experimental and simulated patterns do not agree very well with each other since the 2-theta values of the diffraction peaks in the experimental PXRD pattern are a little bit larger than those of the simulated one. Further analysis showed that this phenomenon is consistent with previous studies on alkyl modified COFs,11a,b in which the addition of alkyl substituents resulted in a broadening of the diffraction peaks, and a continuous shift of the peaks to a large 2-theta value was also observed with the increase of the alkyl chain length, in comparison with the unsubstituted parent COF. This result was attributed to the presence of alkyl groups which freely rotated within the pores. Therefore, taking this influence of the alkyl substituents on the PXRD of the COF into account, we could conclude that a single-pore COF with eclipsed packing was produced from the condensation of DETA and ETTA. A Pawley refinement was performed, which gave unit cell parameters of a = 29.19 Å, b = 25.40 Å, c = 4.50 Å, α = β = 90.0°, and γ = 90.0°, with RP = 2.01% and RWP = 2.48%. The difference plot between the experimental and the refined XRD patterns indicates that they match each other quite well.
Similarly, the simulated PXRD pattern of the DBTA-based structure with a single-pore topology and AA packing has two major peaks at 4.62° and 9.24°, which are assignable to (110) and (220) diffractions, respectively. The experimental PXRD pattern of COF-DBTA displays two broad diffraction peaks at 5.4° and 10.9° (Fig. 3). A comparison of the experimental PXRD pattern of COF-DBTA with the simulated ones also indicated that it did not match with a dual-pore topology but could match with a single-pore structure when the influence of the butyls on the PXRD pattern was taken into consideration. Therefore, a single-pore COF structure with AA packing was assigned to COF-DBTA. A Pawley refinement gave optimized unit cell parameters of a = 29.26 Å, b = 25.29 Å, c = 4.50 Å, α = 90.10°, β = 90.16°, and γ = 91.44°, with RP = 2.72% and RWP = 3.74%.
The assigned structures for COF-DHTA, COF-DETA, and COF-DBTA were further corroborated using nitrogen adsorption–desorption measurements. The N2 isotherm of COF-DHTA exhibited good reversibility. It did not fit a typical type I model but a hybrid of type I and type IV sorption isotherms (Fig. 4a),13 suggesting that micropores and mesopores coexist in COF-DHTA. The Brunauer–Emmett–Teller (BET) model was applied to the isotherm with P/P0 in the range of 0.05-0.3, which generated a BET surface area of 1869.32 m2 g−1 for COF-DHTA (Fig. S11, ESI†). Its theoretical maximum BET surface area was calculated using the Monte Carlo Metropolis method in Materials Studio,14 which yielded a theoretical surface area of 2103.89 m2 g−1 (Fig. S12, ESI†). This value is quite close to its Connolly surface area (2274.33 m2 g−1). The total pore volume of COF-DHTA was calculated to be 0.90 cm3 g−1 (P/P0 = 0.99). Its pore size distribution curve was generated using nonlocal density functional theory (NLDFT). The two main distributions were observed around 6.3 Å and 26.5 Å, respectively, indicating that two kinds of pores were present in the material (Fig. 4b). These values are very close to the theoretical pore sizes of the dual-pore COF (6.3 and 25.2 Å as estimated by PM3 calculations), confirming again that COF-DHTA holds a dual-pore topology. COF-DETA and COF-DBTA displayed similar N2 isotherms (Fig. 4c and e). On the basis of their N2 isotherm data, their BET surface areas were calculated to be 458.11 and 379.04 m2 g−1, respectively (Fig. S13 and S14, ESI†). We failed to calculate their theoretical maximum BET surface areas due to the fact that no suitable model was available for them. The experimental pore size distribution of COF-DETA shows a narrow peak around 8.4 Å, which is close to the theoretical value of the corresponding SP-COF structure (9.1 Å) (Fig. 4d). Different to COF-DETA, in COF-DBTA the butyl chains are long enough to divide a single rhombus-shaped pore into four parts with very similar pore sizes, which were theoretically estimated to be 6.7 Å (for two of the pores) and 7.0 Å (for the other two pores) (Fig. 4f). Fitting the isotherm data of COF-DBTA using NLDFT revealed a main pore distribution around 6.3 Å, which closely matched with the theoretically predicted pore size. These pore size distribution analyses further confirm that both COF-DETA and COF-DBTA hold a single-pore topology.
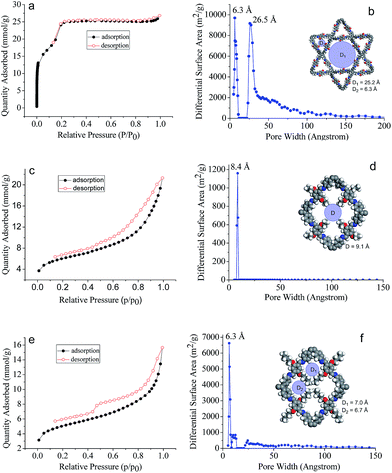 | ||
| Fig. 4 N2 adsorption–desorption isotherms (77 K) of (a) COF-DHTA, (c) COF-DETA and (e) COF-DBTA, and the pore size distribution profiles of (b) COF-DHTA, (d) COF-DETA and (f) COF-DBTA. | ||
Conclusions
In summary, switching the topology of COFs has been successfully achieved through the rational introduction of alkyl substituents into the skeletons of the monomers. Although these monomers share the same symmetry, the presence of different alkyl groups exerts different influences on the formation of the polymeric structures. While a dual-pore COF was obtained from an unsubstituted dialdehyde, the introduction of ethyl or n-butyl groups resulted in COFs with a single-pore topology. The formation of single-pore COFs can be explained by the alleviation of steric repulsion between the substituents. This proof of concept opens up a new route to regulate the topologies of COFs, which in turn will modify their properties and give them new functions.Acknowledgements
We thank the National Natural Science Foundation of China (No. 21472225, 21632004) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB20000000) for financial support. We also thank Mr Yu Fan for his help in calculating the theoretical maximum BET surface areas.Notes and references
- (a) P. J. Waller, F. Gándara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053 CrossRef CAS PubMed; (b) X. Feng, X. Ding and D. Jiang, Chem. Soc. Rev., 2012, 41, 6010 RSC; (c) S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548 RSC; (d) J. L. Segura, M. J. Mancheño and F. Zamora, Chem. Soc. Rev., 2016, 45, 5635 RSC.
- (a) H. Ma, H. Ren, S. Meng, Z. Yan, H. Zhao, F. Sun and G. Zhu, Chem. Commun., 2013, 49, 9773 RSC; (b) C. J. Doonan, D. J. Tranchemontagne, T. G. Glover, J. R. Hunt and O. M. Yaghi, Nat. Chem., 2010, 2, 235 CrossRef CAS PubMed; (c) L. A. Baldwin, J. W. Crowe, D. A. Pyles and P. L. McGrier, J. Am. Chem. Soc., 2016, 138, 15134 CrossRef CAS PubMed; (d) P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450 CrossRef CAS PubMed; (e) Y. Zeng, R. Zou, Z. Luo, H. Zhang, X. Yao, X. Ma, R. Zou and Y. Zhao, J. Am. Chem. Soc., 2015, 137, 1020 CrossRef CAS PubMed; (f) Y. Zeng, R. Zou and Y. Zhao, Adv. Mater., 2016, 28, 2855 CrossRef CAS PubMed; (g) H. Oh, S. B. Kalidindi, Y. Um, S. Bureekaew, R. Schmid, R. A. Fischer and M. Hirscher, Angew. Chem., Int. Ed., 2013, 52, 13219 CrossRef CAS PubMed; (h) Z. Kang, Y. Peng, Y. Qian, D. Yuan, M. A. Addicoat, T. Heine, Z. Hu, L. Tee, Z. Guo and D. Zhao, Chem. Mater., 2016, 28, 1277 CrossRef CAS; (i) S. Kandambeth, B. P. Biswal, H. D. Chaudhari, K. C. Rout, S. H. Kunjattu, S. Mitra, S. Karak, A. Das, R. Mukherjee, U. K. Kharul and R. Banerjee, Adv. Mater., 2017, 29, 1603945 CrossRef PubMed.
- (a) S.-Y. Ding, J. Gao, Q. Wang, Y. Zhang, W.-G. Song, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2011, 133, 19816 CrossRef CAS PubMed; (b) Q. Fang, S. Gu, J. Zheng, Z. Zhuang, S. Qiu and Y. Yan, Angew. Chem., Int. Ed., 2014, 53, 2878 CrossRef CAS PubMed; (c) P. Pachfule, S. Kandambeth, D. D. Díaz and R. Banerjee, Chem. Commun., 2014, 50, 3169 RSC; (d) X. Wang, X. Han, J. Zhang, X. Wu, Y. Liu and Y. Cui, J. Am. Chem. Soc., 2016, 138, 12332 CrossRef CAS PubMed; (e) H.-S. Xu, S.-Y. Ding, W.-K. An, H. Wu and W. Wang, J. Am. Chem. Soc., 2016, 138, 11489 CrossRef CAS PubMed; (f) L. Stegbauer, K. Schwinghammer and B. V. Lotsch, Chem. Sci., 2014, 5, 2789 RSC.
- (a) G. Das, B. P. Biswal, S. Kandambeth, V. Venkatesh, G. Kaur, M. Addicoat, T. Heine, S. Verma and R. Banerjee, Chem. Sci., 2015, 6, 3931 RSC; (b) G. Lin, H. Ding, D. Yuan, B. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302 CrossRef CAS PubMed; (c) Y.-F. Xie, S.-Y. Ding, J.-M. Liu, W. Wang and Q.-Y. Zheng, J. Mater. Chem. C, 2015, 3, 10066 RSC; (d) S.-Y. Ding, M. Dong, Y.-W. Wang, Y.-T. Chen, H.-Z. Wang, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2016, 138, 3031 CrossRef CAS PubMed.
- (a) V. S. Vyas, M. Vishwakarma, I. Moudrakovski, F. Haase, G. Savasci, C. Ochsenfeld, J. P. Spatz and B. V. Lotsch, Adv. Mater., 2016, 28, 8749 CrossRef CAS PubMed; (b) L. Bai, S. Z. F. Phua, W. Q. Lim, A. Jana, Z. Luo, H. P. Tham, L. Zhao, Q. Gao and Y. Zhao, Chem. Commun., 2016, 52, 4128 RSC; (c) Q. Fang, J. Wang, S. Gu, R. B. Kaspar, Z. Zhuang, J. Zheng, H. Guo, S. Qiu and Y. Yan, J. Am. Chem. Soc., 2015, 137, 8352 CrossRef CAS PubMed.
- (a) L. Chen, K. Furukawa, J. Gao, A. Nagai, T. Nakamura, Y. Dong and D. Jiang, J. Am. Chem. Soc., 2014, 136, 9806 CrossRef CAS PubMed; (b) M. Calik, F. Auras, L. M. Salonen, K. Bader, I. Grill, M. Handloser, D. D. Medina, M. Dogru, F. Löbermann, D. Trauner, A. Hartschuh and T. Bein, J. Am. Chem. Soc., 2014, 136, 17802 CrossRef CAS PubMed; (c) S. Wan, F. Gándara, A. Asano, H. Furukawa, A. Saeki, S. K. Dey, L. Liao, M. W. Ambrogio, Y. Y. Botros, X. Duan, S. Seki, J. F. Stoddart and O. M. Yaghi, Chem. Mater., 2011, 23, 4094 CrossRef CAS; (d) C. R. DeBlase, K. E. Silberstein, T.-T. Truong, H. D. Abruña and W. R. Dichtel, J. Am. Chem. Soc., 2013, 135, 16821 CrossRef CAS PubMed; (e) J. I. Feldblyum, C. H. McCreery, S. C. Andrews, T. Kurosawa, E. J. G. Santos, V. Duong, L. Fang, A. L. Ayzner and Z. Bao, Chem. Commun., 2015, 51, 13894 RSC.
- (a) A. I. Cooper, Adv. Mater., 2009, 21, 1291 CrossRef CAS; (b) Y. Xu, S. Jin, H. Xu, A. Nagai and D. Jiang, Chem. Soc. Rev., 2013, 42, 8012 RSC.
- W. Lu, J. P. Sculley, D. Yuan, R. Krishna, Z. Wei and H.-C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 7480 CrossRef CAS PubMed.
- T. Ben and S. Qiu, CrystEngComm, 2013, 15, 17 RSC.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O’Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166 CrossRef PubMed.
- (a) R. W. Tilford, S. J. Mugavero III, P. J. Pellechia and J. J. Lavigne, Adv. Mater., 2008, 20, 2741 CrossRef CAS PubMed; (b) L. M. Lanni, R. W. Tilford, M. Bharathy and J. J. Lavigne, J. Am. Chem. Soc., 2011, 133, 13975 CrossRef CAS PubMed; (c) Z. Li, Y. Zhang, H. Xia, Y. Mu and X. Liu, Chem. Commun., 2016, 52, 6613 RSC.
- (a) T.-Y. Zhou, S.-Q. Xu, Q. Wen, Z.-F. Pang and X. Zhao, J. Am. Chem. Soc., 2014, 136, 15885 CrossRef CAS PubMed; (b) Z.-F. Pang, S.-Q. Xu, T.-Y. Zhou, R.-R. Liang, T.-G. Zhan and X. Zhao, J. Am. Chem. Soc., 2016, 138, 4710 CrossRef CAS PubMed; (c) L. Ascherl, T. Sick, J. T. Margraf, S. H. Lapidus, M. Calik, C. Hettstedt, K. Karaghiosoff, M. Döblinger, T. Clark, K. W. Chapman, F. Auras and T. Bein, Nat. Chem., 2016, 8, 310 CrossRef CAS; (d) Y. Zhu, S. Wan, Y. Jin and W. Zhang, J. Am. Chem. Soc., 2015, 137, 13772 CrossRef CAS PubMed; (e) X. Chen, N. Huang, J. Gao, H. Xu, F. Xu and D. Jiang, Chem. Commun., 2014, 50, 6161 RSC; (f) H. Ding, Y. Li, H. Hu, Y. Sun, J. Wang, C. Wang, C. Wang, G. Zhang, B. Wang, W. Xu and D. Zhang, Chem.–Eur. J., 2014, 20, 14614 CrossRef CAS PubMed; (g) S.-L. Cai, Y.-B. Zhang, A. B. Pun, B. He, J. Yang, F. M. Toma, I. D. Sharp, O. M. Yaghi, J. Fan, S.-R. Zheng, W.-G. Zhang and Y. Liu, Chem. Sci., 2014, 5, 4693 RSC.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquérol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603 CrossRef CAS.
- E. L. Spitler, B. T. Koo, J. L. Novotney, J. W. Colson, F. J. Uribe-Romo, G. D. Gutierrez, P. Clancy and W. R. Dichtel, J. Am. Chem. Soc., 2011, 133, 19416 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Procedure for the preparation of the COFs, IR spectra, solid-state 13C NMR, SEM images, TGA traces, PXRD profiles and simulations, fractional atomic coordinates, and BET plots. See DOI: 10.1039/c6sc05673c |
| This journal is © The Royal Society of Chemistry 2017 |