Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying the efficiency of CO2 capture by Lewis pairs†
Jay J.
Chi
a,
Timothy C.
Johnstone
a,
Dan
Voicu
a,
Paul
Mehlmann
b,
Fabian
Dielmann
 b,
Eugenia
Kumacheva
*a and
Douglas W.
Stephan
b,
Eugenia
Kumacheva
*a and
Douglas W.
Stephan
 *a
*a
aDepartment of Chemistry, University of Toronto, 80 St. George St., Toronto, Ontario M5S 3H6, Canada. E-mail: dstephan@chem.utoronto.ca
bInstitut für Anorganische und Analytische Chemie, Westfälische Wilhelms-Universität Münster, Corrensstrasse 30, 48149 Münster, Germany
First published on 20th February 2017
Abstract
A microfluidic strategy has been used for the time- and labour-efficient evaluation of the relative efficiency and thermodynamic parameters of CO2 binding by three Lewis acid/base combinations, where efficiency is based on the amount of CO2 taken up per binding unit in solution. Neither tBu3P nor B(C6F5)3 were independently effective at CO2 capture, and the combination of the imidazolin-2-ylidenamino-substituted phosphine (NIiPr)3P and B(C6F5)3 was equally ineffective. Nonetheless, an archetypal frustrated Lewis pair (FLP) comprised of tBu3P and B(C6F5)3 was shown to bind CO2 more efficiently than either the FLP derived from tetramethylpiperidine (TMP) and B(C6F5)3 or the highly basic phosphine (NIiPr)3P. Moreover, the proposed microfluidic platform was used to elucidate the thermodynamic parameters for these reactions.
Introduction
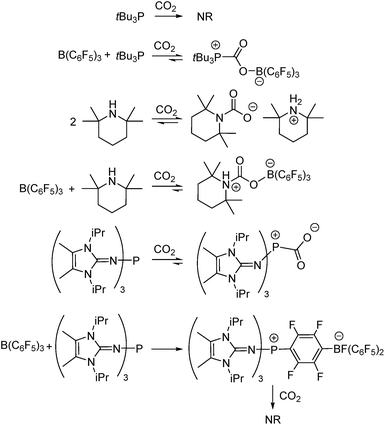
Anthropogenic carbon dioxide (CO2) emissions continue to climb to unprecedented levels and have played a key role in global climate change.1 This worldwide issue has prompted many researchers to explore a wide variety of approaches to both reduce CO2 emissions and lower CO2 concentrations in the atmosphere. Efforts targeting the use of CO2 as a C1 chemical feedstock for conversion to formic acid, carbon monoxide,2 or reusable fuels such as methane or methanol,3 have prompted many studies targeting new catalyst development.4 Although these developments offer the potential for disruptive technologies, it is important to note that the capture of CO2 will be an integral component of any such advancement. A variety of approaches have been explored to capture CO2 including the use of zeolites, silica gels, aluminas, and activated carbons,5 as well as sophisticated metal–organic frameworks (MOFs).6Investigations of the reactions of CO2 with main group reagents have included a variety of amines,7 alkanolamines8 amidines, guanidines,9 and N-heterocyclic carbenes (NHCs).10 A decade ago, the use of frustrated Lewis pairs (FLPs) to capture CO2 emerged with the report of Stephan, Erker, and coworkers who described intramolecular and intermolecular B/P-based FLPs for the capture of CO2.11 Since then, a wide variety of B/N,12 B/P,13 Al/P,14 and Si/P12a,15 systems have been shown to capture or effect stoichiometric or catalytic reduction of CO2. In a very recent development, Dielmann and coworkers described the synthesis of highly basic phosphines, generated by the inclusion of imidazolin-2-ylidenamino substituents.16 These are the first phosphines to be shown to sequester CO2 in the absence of the Lewis acid necessary to form an FLP.17
Although a number of FLP and main group systems have been shown to capture CO2,13c the ability to quantitatively compare the efficiency of such systems remains experimentally challenging. Standard batch-scale characterization methods for reactions at the CO2 gas–liquid interface suffer from long reaction times and are often diffusion controlled.18 Recently, Kumacheva and coworkers developed a microfluidic (MF) platform for the study of gas/liquid reactions.19 The MF methodology was validated for the well-studied CO2 reaction with amine19b and used small amounts of reagents thus providing fast and cost-efficient access to thermodynamic data for gas/liquid reactions (10–15 min per experiment).
In Fig. 1, a gas and a reagent solution are supplied to two inlets of a MF reactor. At a Y-junction, the gaseous stream breaks up in a periodic manner to generate uniformly sized gas plugs that are separated by liquid segments (slugs). As alternating gas plugs and solution slugs flow through the MF channel, the dissolution of the gas and its reaction with reagents in the solution results in a decrease in the volume of gas plugs with time (or the distance from the Y-junction). Analysis of digitized images of the gas plugs allows for the quantification of gas consumption using the ideal gas law.19a,20 After a particular time (directly related to distance in the MF reactor), the dissolved reagents and the gas reach equilibrium, and the gaseous plug volume remains constant. This enables the determination of the equilibrium constant of the reaction, and a study of the reaction at different temperatures enables assessment of the thermodynamic parameters, ΔG°, ΔH°, and ΔS°. The validity of this methodology was demonstrated with the study of the sequestration of CO2 by the FLP, ClB(C6F5)2/tBu3P.19a,20
 | ||
| Fig. 1 (a) Schematic depiction of the MF gas/liquid device. (b) Magnified view of the outlined region shown in (a), which shows the shrinkage of the gas plugs as they flow through the channel. | ||
In the present work, this innovative MF approach has been applied to compare the efficiency of CO2 sequestration in reactions of three Lewis acid–base combinations with CO2. The prototypical FLP tBu3P/B(C6F5)3, as well as the FLP derived from tetramethylpiperidine (TMP)/B(C6F5)3, were investigated. In addition, the extremely basic imidazolin-2-ylidenamino-substituted phosphine (NIiPr)3P was investigated alone and in combination with B(C6F5)3. Although each of these systems is known to bind CO2 (Scheme 1),11,12b,17b the present MF study provides qualitative and quantitative comparisons of this CO2 binding. Such data afford insights that are important for the design of main group systems for CO2 capture.
Results and discussion
The established MF protocol19a was used to determine the thermodynamic parameters associated with the reaction of CO2 with combinations of the Lewis acid B(C6F5)3 and one of the Lewis bases, tBu3P, TMP, or (NIiPr)3P. Bromobenzene was selected as a suitable solvent due to its low volatility and the solubility of the reagents and corresponding CO2 adducts. In an initial reference experiment, physical dissolution of CO2 gas in bromobenzene was characterized by the temporal variation in the concentration of physically dissolved CO2 (i.e., [CO2]dissolved) by analysing the digitized dimensions of alternating slugs of solvent and plugs of CO2 flowing through the MF reactor. By monitoring the decrease in CO2 plug volume and applying the ideal gas law19a (eqn (1) and (2), see ESI, Fig. S1 and S2†), the number of moles of CO2 transferred from the gas plug to the adjacent liquid slug at time t, nCO2(t), was determined. The equilibrium concentration of physically dissolved CO2 (Ctot) was reached after approximately 2 s (Fig. 2).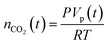 | (1) |
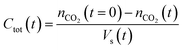 | (2) |
 | ||
Fig. 2 Variation in total concentration of CO2 transferred at 293 K from gas plugs to reagent solution slugs plotted as a function of time. The gaps in the data from 1.5 s to 2.0 s result from the exclusion of microchannel bends outside the region of interest (see ESI, Fig. S1†). (a) Plots for the FLP derived from tBu3P and B(C6F5)3. (b) Plots for the FLP derived from TMP and B(C6F5)3. (c) Plots for the combination of (NIiPr)3P and B(C6F5)3. For C6H5Br alone ( ), Ctot = [CO2]dissolved. Each experimental point represents the average of three experiments conducted under identical conditions, where 300 images were acquired for each experiments with a minimum of 4000 CO2 plugs. ), Ctot = [CO2]dissolved. Each experimental point represents the average of three experiments conducted under identical conditions, where 300 images were acquired for each experiments with a minimum of 4000 CO2 plugs. | ||
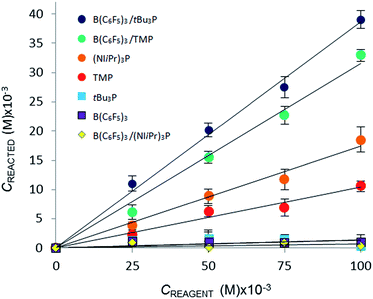
The addition of either B(C6F5)3, or tBu3P independently to the solvent had little effect on the equilibrium concentration of CO2 in the liquid slugs, beyond the dissolution of CO2 in bromobenzene (Fig. 2a). However, combining B(C6F5)3 and tBu3P in solution resulted in increased CO2 uptake, which further increased with elevated FLP concentration. These observations are consistent with the known inability of the individual components to capture CO2, and the established efficacy with which CO2 is captured by this FLP. These observations are also consistent with our earlier MF study of CO2 capture by the related ClB(C6F5)2/tBu3P FLP.19a
Investigation of the FLP derived from B(C6F5)3 and TMP revealed that TMP alone in solution is able to sequester CO2 (Fig. 2b,  ), consistent with the known ability of secondary amines to reversibly bind CO2.12b It is noteworthy, however, that the concurrent presence of B(C6F5)3 in solution results in a significantly enhanced CO2 uptake. Again, increasing concentration of the FLP results in increased CO2 sequestration.
), consistent with the known ability of secondary amines to reversibly bind CO2.12b It is noteworthy, however, that the concurrent presence of B(C6F5)3 in solution results in a significantly enhanced CO2 uptake. Again, increasing concentration of the FLP results in increased CO2 sequestration.
In sharp contrast to tBu3P, increasing concentrations of (NIiPr)3P led to increasing capture of CO2 (Fig. 3). These observations are consistent with the work of Dielmann and coworkers17b who have demonstrated the ability of imidazolin-2-ylidenamino-substituted phosphines to bind CO2. In further contrast, addition of B(C6F5)3 to solutions of (NIiPr)3P inhibited CO2 uptake beyond the physical dissolution of CO2 into the solvent ( vs.
vs. , Fig. 2c). This result indicates an irreversible reaction of (NIiPr)3P with B(C6F5)3. Monitoring of this reaction by NMR spectroscopy supports the formation of several products, including the zwitterionic product (NIiPr)3PC6F4BF(C6F5)2 as the major species (Scheme 1, see ESI†). Analogous products have been previously reported for sterically encumbered, basic phosphines.21 Presumably, the highly basic nature of the phosphine (NIiPr)3P prompts this reactivity with B(C6F5)3 and precludes capture of CO2.
, Fig. 2c). This result indicates an irreversible reaction of (NIiPr)3P with B(C6F5)3. Monitoring of this reaction by NMR spectroscopy supports the formation of several products, including the zwitterionic product (NIiPr)3PC6F4BF(C6F5)2 as the major species (Scheme 1, see ESI†). Analogous products have been previously reported for sterically encumbered, basic phosphines.21 Presumably, the highly basic nature of the phosphine (NIiPr)3P prompts this reactivity with B(C6F5)3 and precludes capture of CO2.
The CO2 uptake caused directly by chemical reaction, Creacted, was determined by subtracting the [CO2]dissolved (for the CO2–bromobenzene system) from the total equilibrium uptake of CO2, Ctot, for each reagent. A plot of Creacted against reagent concentration illustrates the relative efficacy of the reaction of CO2 with the Lewis acid, Lewis base, or Lewis acid–base combination (Fig. 3).
Using the concentration data allows determination of the equilibrium constants (Keq) for each system. In eqn (3), [CO2 adduct] is equal to Creacted (determined from Fig. 3), the [Lewis acid] and [Lewis base] are calculated directly by subtracting Creacted from the initial reagent concentrations, and [CO2]dissolved is the equilibrium concentration of CO2 dissolved in bromobenzene (Fig. 2). In this fashion, the room temperature equilibrium constants for CO2 binding for tBu3P/B(C6F5)3, TMP/B(C6F5)3, and (NIiPr)3P were determined and are collected in Table 1. The data shown in Fig. 3 reveal that the FLP systems derived from tBu3P or TMP with B(C6F5)3 are more efficient at CO2 capture by 29% and 16%, respectively, than the highly basic phosphine, (NIiPr)3P. In this context, efficiency is taken to be the amount of CO2, per binding unit, sequestered by the binding reagents. These data also illustrate that the FLP tBu3P/B(C6F5)3 is 11% more efficient at CO2 uptake than the FLP derived from TMP/B(C6F5)3. Thus, although previously reported NMR experiments demonstrated the ability of these systems to bind CO2, the present MF methodology provides a fast, efficient and high-throughput platform for quantitative ranking of the ability of these systems to bind CO2 at ambient temperature.
| Reagents | K eq (293 K) | ΔH293b kJ mol−1 | ΔS293 J mol−1 K−1 | ΔG293 kJ mol−1 |
|---|---|---|---|---|
| a Additional values for 273 K, 283 K, 303 K, and 313 K are deposited in the ESI (Table S2–S4). b The value for ΔH is determined by the corresponding slope in Fig. 5. | ||||
| tBu3P/B(C6F5)2Cl19a | 223 M−2 | −39.3 | −89.3 | −14.8 |
| tBu3P/B(C6F5)3 | 517 M−2 | −100.0 | −289.3 | −15.2 |
| TMP/B(C6F5)3 | 267 M−2 | −73.8 | −205.4 | −13.6 |
| (NIiPr)3P | 4158 M−1 | −29.1 | −30.8 | −20.0 |
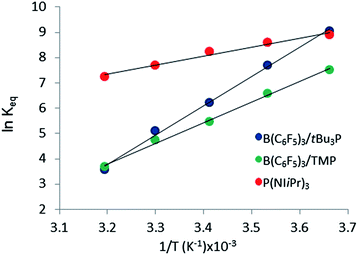
The reactions of tBu3P/B(C6F5)3, TMP/B(C6F5)3, and (NIiPr)3P with CO2 were also studied in the temperature range from 273 to 313 K. A plot of the amount of CO2 captured (Creacted) versus the concentration of either the FLPs or (NIiPr)3P was monotonic and linear. Due to the exothermic nature of the reactions,19a,20 as the reaction systems were cooled, the degree of CO2 capture was enhanced at each of the concentrations of reagents (Fig. 4). Using the values of Keq at different temperatures, the corresponding Gibbs free energy for each reaction can be obtained (eqn (4)). The use of a van't Hoff plot (Fig. 5; eqn (5)) allows the determination of the corresponding enthalpy (ΔH°) and entropy (ΔS°) values (Table 1). The linearity of the association between ln(Keq) and 1/T indicates that enthalpy does not change appreciably within the temperature range investigated. It is noted that the ΔH° of the reaction of B(C6F5)3, tBu3P, and CO2, −100.0 kJ mol−1, is in excellent agreement with the value of −100.4 kJ mol−1 obtained calorimetrically by Autrey and coworkers.22
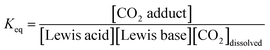 | (3) |
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Keq) ln(Keq) | (4) |
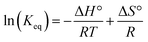 | (5) |
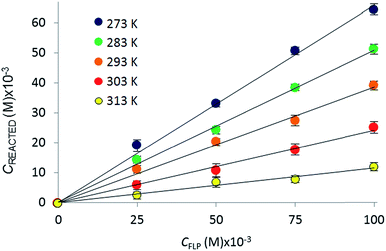 | ||
| Fig. 4 Variation in the equilibrium concentration of captured CO2, plotted as a function of initial FLP (B(C6F5)3 and tBu3P) concentration at T = 273 K, 283 K, 293 K, 303 K, and 313 K (repeated in triplicate analysing 300 images with a range of 4000–7000 plugs of CO2) (see ESI† for plots for the other systems). | ||
To gain further insight, theoretical calculations were performed using Density Functional Theory (DFT) at the M11/6-311G(d,p) level of theory.23 The optimized geometries of B(C6F5)3, tBu3P, CO2, and tBu3PCO2B(C6F5)3 were computed using the integral equation formalism variant of the polarizable continuum model (IEFPCM) to implicitly assess the effects of solvation by bromobenzene.24 Frequency calculations confirmed that each structure was at a minimum on its potential energy surface and provided partition functions from which thermodynamic parameters were computed. The reaction enthalpy obtained at this level of theory, −176 kJ mol−1, was significantly larger than the experimental value of −100.0 kJ mol−1. To further investigate this discrepancy, the calculations were carried out at the B2PLYP-D3/6-311G(d,p) level of theory.25 This double hybrid meta-GGA method includes an empirical long-range dispersion correction and performs well in the evaluation of main group thermochemistry.26 A recent study comparing the ability of M11 and B2PLYP-D3 to evaluate the chemistry of compounds for which dispersive interactions are important found the latter to consistently outperformed the former.27 The internal reaction energy for CO2 capture by the B(C6F5)3/tBu3P FLP was computed to be −129 kJ mol−1 at this double hybrid level of theory. This value more closely approaches the experimental reaction enthalpy. In addition, if this internal reaction energy is used in combination with the reaction entropy obtained at the M11/6-311G(d,p) level of theory, then the Gibbs free energy of the reaction computed at ambient temperature is −15.4 kJ mol−1, in excellent agreement with the experimental value of −15.2 kJ mol−1.28
The experimentally determined thermodynamic parameters illustrate that CO2 binding by the two presently studied FLP systems and the previously studied ClB(C6F5)2/tBu3P system19a is less entropically favoured than that by (NIiPr)3P, consistent with the three-component nature of the FLP reactions. On the other hand, CO2 binding by the FLP systems is more enthalpically favoured than that by (NIiPr)3P, consistent with the formation of two bonds in the FLP products versus only one bond in the reaction with (NIiPr)3P. Given that the phosphine (NIiPr)3P is among the strongest of nucleophiles known to independently bind CO2, it is expected that this phosphine should be more efficient than simple amines, consistent with the presently described results with TMP. The present observations suggest that bidentate binding by an FLP improves the efficiency for CO2 capture.
Of the three systems examined, the tBu3P/B(C6F5)3 FLP is most efficient at CO2 capture at ambient temperatures; however the phosphine (NIiPr)3P has the most negative ΔG293 among the systems studied. Among the FLP systems, tBu3P/B(C6F5)3 has a more exergonic ambient-temperature CO2 binding reaction than TMP/B(C6F5)3, but the thermodynamic parameters predict that, at elevated temperatures (347–365 K), the reaction of TMP/B(C6F5)3 with CO2 will be more exergonic. Nonetheless, these data infer that at room temperature the FLP derived from tBu3P/B(C6F5)3 binds CO2 more effectively that the FLP derived from TMP/B(C6F5)3.
Conclusions
The present study illustrates the power of the time- and labor-efficient MF platform for the qualitative and quantitative assessment of CO2 binding by small molecules and for the determination of the thermodynamic parameters of these reactions. These data form a quantitative basis for comparison of CO2 capture systems at different temperatures. The systems considered in this paper included FLPs, tBu3P/B(C6F5)3 and TMP/B(C6F5)3, and the highly basic phosphine (NIiPr)3P, which effectively span the range known for interactions of CO2 with Lewis acids and bases. The data reveal the FLP derived from tBu3P and B(C6F5)3 to be the most efficient at capturing CO2 at ambient temperature per equivalent of CO2 binding unit. However (NIiPr)3P offers a higher CO2 content by mass. Certainly, these data do infer that further study of FLPs in CO2 capture may uncover new systems that are more readily available (i.e. cheaper) and offer improved efficiency. To this end, we are continuing to employ this innovative MF methodology to assess and design new FLP systems for CO2 capture and ultimately reduction. In addition, the study of other reactions that occur at a gas–liquid interface continues. The results of these studies will be reported in due course.Acknowledgements
D. W. S. and E. K. gratefully acknowledge the financial support from NSERC Canada and the awards of Canada Research Chairs. T. C. J. gratefully acknowledges NSERC Canada for a post-doctoral fellowship. F. D. and P. M. gratefully acknowledge the financial support from the DFG (IRTG 2027, SFB 858) and the FCI. The computational work described in this paper was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: http://www.sharcnet.ca) and Compute Canada.Notes and references
- T. R. Karl and K. E. Trenberth, Science, 2003, 302, 1719–1723 CrossRef CAS PubMed.
- P. G. Jessop, T. Ikariya and R. Noyori, Chem. Rev., 1995, 95, 259–272 CrossRef CAS.
- G. A. Olah, A. Goeppert and G. K. S. Prakash, J. Org. Chem., 2009, 74, 487–498 CrossRef CAS PubMed.
- (a) S. Bontemps, L. Vendier and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2012, 51, 1671 CrossRef CAS PubMed; (b) D. S. Laitar, P. Müller and J. P. Sadighi, J. Am. Chem. Soc., 2005, 127, 17196–17197 CrossRef CAS PubMed; (c) M. Nielsen, E. Alberico, W. Baumann, H.-J. Drexler, H. Junge, S. Gladiali and M. Beller, Nature, 2013, 495, 85–89 CrossRef CAS PubMed; (d) M. S. Sgro and D. W. Stephan, Angew. Chem., Int. Ed., 2012, 51, 11343 CrossRef CAS PubMed.
- K. B. Lee, M. G. Beaver, H. S. Caram and S. Sircar, Ind. Eng. Chem. Res., 2008, 47, 8048–8062 CrossRef CAS.
- (a) R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Science, 2008, 319, 939–943 CrossRef CAS PubMed; (b) J. L. C. Rowsell, E. C. Spencer, J. Eckert, J. A. K. Howard and O. M. Yaghi, Science, 2005, 309, 1350–1354 CrossRef CAS PubMed; (c) A. C. Sudik, A. R. Millward, N. W. Ockwig, A. P. Cote, J. Kim and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 7110–7118 CrossRef CAS PubMed.
- G. T. Rochelle, Science, 2009, 325, 1652–1654 CrossRef CAS PubMed.
- (a) P. D. Vaidya and E. Y. Kenig, Chem. Eng. Technol., 2007, 30, 1467–1474 CrossRef CAS; (b) C. Reller, M. Pöge, A. Lißner and F. O. R. L. Mertens, Environ. Sci. Technol., 2014, 48, 14799–14804 CrossRef CAS PubMed; (c) G. Sartori and D. W. Savage, Ind. Eng. Chem. Fundam., 1983, 22, 239–249 CrossRef CAS.
- (a) C. Villiers, J. P. Dognon, R. Pollet, P. Thuery and M. Ephritikhine, Angew. Chem., Int. Ed., 2010, 49, 3465–3468 CrossRef CAS PubMed; (b) A. Barbarini, R. Maggi, A. Mazzacani, G. Mori, G. Sartori and R. Sartorio, Tetrahedron Lett., 2003, 44, 2931–2934 CrossRef CAS; (c) J. Ma, X. Zhang, N. Zhao, A. S. N. Al-Arifi, T. Aouak, Z. A. Al-Othman, F. Xiao, W. Wei and Y. Sun, J. Mol. Catal., 2010, 315, 76–81 CrossRef CAS; (d) F. S. Pereira, E. R. deAzevedo, E. F. da Silva, T. J. Bonagamba, D. L. da Silva Agostíni, A. Magalhães, A. E. Job and E. R. P. González, Tetrahedron, 2008, 64, 10097–10106 CrossRef CAS; (e) X. Zhang, Y.-B. Jia, X.-B. Lu, B. Li, H. Wang and L.-C. Sun, Tetrahedron Lett., 2008, 49, 6589–6592 CrossRef CAS; (f) X. Zhang, N. Zhao, W. Wei and Y. Sun, Catal. Today, 2006, 115, 102–106 CrossRef CAS.
- (a) J. D. Holbrey, W. M. Reichert, I. Tkatchenko, E. Bouajila, O. Walter, I. Tommasi and R. D. Rogers, Chem. Commun., 2003, 28–29 RSC; (b) L. J. Murphy, K. N. Robertson, R. A. Kemp, H. M. Tuononen and J. A. C. Clyburne, Chem. Commun., 2015, 51, 3942–3956 RSC; (c) H. A. Duong, T. N. Tekavec, A. M. Arif and J. Louie, Chem. Commun., 2004, 112–113 RSC.
- C. M. Mömming, E. Otten, G. Kehr, R. Fröhlich, S. Grimme, D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2009, 48, 6643–6646 CrossRef PubMed.
- (a) A. E. Ashley, A. L. Thompson and D. O'Hare, Angew. Chem., Int. Ed., 2009, 48, 9839 CrossRef CAS PubMed; (b) A. Berkefeld, W. E. Piers and M. Parvez, J. Am. Chem. Soc., 2010, 132, 10660–10661 CrossRef CAS PubMed.
- (a) R. Declercq, G. Bouhadir, D. Bourissou, M.-A. Légaré, M.-A. Courtemanche, K. S. Nahi, N. Bouchard, F.-G. Fontaine and L. Maron, ACS Catal., 2015, 5, 2513–2520 CrossRef CAS; (b) M.-A. Courtemanche, M.-A. Légaré, L. Maron and F.-G. Fontaine, J. Am. Chem. Soc., 2014, 136, 10708–10717 CrossRef CAS PubMed; (c) T. Wang and D. W. Stephan, Chem. Commun., 2014, 50, 7007–7010 RSC.
- (a) M.-A. Courtemanche, J. Larouche, M.-A. Légaré, W. Bi, L. Maron and F.-G. Fontaine, Organometallics, 2013, 32, 6804–6811 CrossRef CAS; (b) G. Ménard and D. W. Stephan, J. Am. Chem. Soc., 2010, 132, 1796–1797 CrossRef PubMed; (c) G. Ménard and D. W. Stephan, Angew. Chem., Int. Ed., 2011, 50, 8396–8399 CrossRef PubMed.
- (a) S. A. Weicker and D. W. Stephan, Chem.–Eur. J., 2015, 21, 13027–13034 CrossRef CAS PubMed; (b) M. Reißmann, A. Schäfer, S. Jung and T. Müller, Organometallics, 2013, 32, 6736–6744 CrossRef.
- M. A. Wünsche, P. Mehlmann, T. Witteler, F. Buß, P. Rathmann and F. Dielmann, Angew. Chem., Int. Ed., 2015, 54, 11857–11860 CrossRef PubMed.
- (a) F. Buß, P. Mehlmann, C. Mück-Lichtenfeld, K. Bergander and F. Dielmann, J. Am. Chem. Soc., 2016, 138, 1840–1843 CrossRef PubMed; (b) P. Mehlmann, C. Mück-Lichtenfeld, T. T. Y. Tan and F. Dielmann, Chem.–Eur. J., DOI:10.1002/chem.201604971.
- S. Bishnoi and G. T. Rochelle, Chem. Eng. Sci., 2000, 55, 5531–5543 CrossRef CAS.
- (a) D. Voicu, M. Abolhasani, R. Choueiri, G. Lestari, C. Seiler, G. Menard, J. Greener, A. Guenther, D. W. Stephan and E. Kumacheva, J. Am. Chem. Soc., 2014, 136, 3875–3880 CrossRef CAS PubMed; (b) W. Li, K. Liu, R. Simms, J. Greener, D. Jagadeesan, S. Pinto, A. Gunther and E. Kumacheva, J. Am. Chem. Soc., 2012, 134, 3127–3132 CrossRef CAS PubMed.
- D. Voicu, D. W. Stephan and E. Kumacheva, ChemSusChem, 2015, 8, 4202–4208 CrossRef CAS PubMed.
- (a) G. C. Welch, R. R. San Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126 CrossRef CAS PubMed; (b) G. C. Welch, L. Cabrera, P. A. Chase, E. Hollink, J. D. Masuda, P. R. Wei and D. W. Stephan, Dalton Trans., 2007, 3407–3414 RSC.
- A. Karkamkar, K. Parab, D. M. Camaioni, D. Neiner, H. Cho, T. K. Nielsen and T. Autrey, Dalton Trans., 2013, 42, 615–619 RSC.
- (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS; (b) R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS; (c) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- (a) S. Grimme, J. Chem. Phys., 2006, 124, 034108–034116 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- L. Goerigk, J. Phys. Chem. Lett., 2015, 6, 3891–3896 CrossRef CAS PubMed.
- Computed thermochemical parameters for the binding of CO2 by (NIiPr)3P afforded values significantly greater than those reported here (ref. 17b). Preliminary follow-up computations suggest that a monotonic relationship between the amount of Hartree–Fock exchange included and the computed internal energy of reaction for CO2 binding to (NIiPr)3P. While we do not as of yet have an explanation for this observation, it is noted that the present computations show better agree with the experimental values derived herein.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc05607e |
| This journal is © The Royal Society of Chemistry 2017 |