Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrogen-adduction to open-shell graphene fragments: spectroscopy, thermochemistry and astrochemistry
Gerard D.
O'Connor
 a,
Bun
Chan
bc,
Julian A.
Sanelli
d,
Katie M.
Cergol
b,
Viktoras
Dryza
d,
Richard J.
Payne
b,
Evan J.
Bieske
d,
Leo
Radom
b and
Timothy W.
Schmidt
*a
a,
Bun
Chan
bc,
Julian A.
Sanelli
d,
Katie M.
Cergol
b,
Viktoras
Dryza
d,
Richard J.
Payne
b,
Evan J.
Bieske
d,
Leo
Radom
b and
Timothy W.
Schmidt
*a
aSchool of Chemistry, UNSW Sydney, NSW 2052, Australia. E-mail: timothy.schmidt@unsw.edu.au; Tel: +61 439 386 109
bSchool of Chemistry, The University of Sydney, Sydney, New South Wales 2006, Australia
cGraduate School of Engineering, Nagasaki University, Bunkyo 1-14, Nagasaki 852-8521, Japan
dSchool of Chemistry, The University of Melbourne, Victoria 3010, Australia
First published on 26th September 2016
Abstract
We apply a combination of state-of-the-art experimental and quantum-chemical methods to elucidate the electronic and chemical energetics of hydrogen adduction to a model open-shell graphene fragment. The lowest-energy adduct, 1H-phenalene, is determined to have a bond dissociation energy of 258.1 kJ mol−1, while other isomers exhibit reduced or in some cases negative bond dissociation energies, the metastable species being bound by the emergence of a conical intersection along the high-symmetry dissociation coordinate. The gas-phase excitation spectrum of 1H-phenalene and its radical cation are recorded using laser spectroscopy coupled to mass-spectrometry. Several electronically excited states of both species are observed, allowing the determination of the excited-state bond dissociation energy. The ionization energy of 1H-phenalene is determined to be 7.449(17) eV, consistent with high-level W1X-2 calculations.
1 Introduction
Graphene is a material consisting of a single layer of carbon atoms bonded in a hexagon lattice.1,2 Its unhybridized pz orbitals conjugate to bring about a structure with fascinating electronic properties. Interest in this material has led to an explosion of research over the past decade due to graphene's many potential applications.1Addition of hydrogen to graphene alters the delocalised π-structure, removing the now sp3 hybridised carbon from the π-system, modifying the electronic and magnetic properties.2–14 The binding energy of a single hydrogen atom on graphene is reported to be just 0.7 eV.15 When graphene is saturated with hydrogen, one obtains the two-dimensional hydrocarbon graphane, an insulator.3,5 Novoselov and Geim showed that graphene hydrogenation to graphane is reversible,5 and, indeed, graphene has been investigated as a potential hydrogen storage material.4,11,15 Graphane's volumetric hydrogen capacity of 0.12 kg H2 per L exceeds the US Department of Energy target of 0.081 kg H2 per L for the year 2015.3
Very recently, it was shown that addition of a single hydrogen atom to graphene results in a measurable magnetic moment.13 Using density functional theory it has been calculated that semihydrogenated graphene (graphone) becomes a ferromagnetic semiconductor with a small indirect gap.7 It has also been shown theoretically that sporadic hydrogenation of graphene nanoribbons can forge new pathways towards carbon-based spintronics applications.9
The optical bandgap of graphene is also sensitive to the state of hydrogenation.10,14 Zhou et al. demonstrated that the electronic and magnetic properties of graphene can be finely tuned by hydrogenation.8 Haberer et al. showed that a tunable gap in quasi-free-standing monolayer graphene on gold can be induced by hydrogenation. The size of the gap reaches ∼1.0 eV for a hydrogen coverage of 8%.10
Chemisorption of hydrogen on graphene fragments is also believed to catalyse the formation of interstellar H2 molecules.16 As such, astronomical abundances of hydrogenated graphene nanoparticles are of fundamental astronomical interest.
Despite the intense interest in hydrogenation of graphene, its size is beyond the reach of chemically accurate calculations. However, smaller relevant systems are accessible to such accurate calculations, and these may be used to benchmark more approximate quantum chemical methods.
The phenalenyl radical consists of 13 carbon atoms and 9 hydrogen atoms arranged in the form of three conjoined six-membered rings bound at a central carbon atom. It is the smallest polycyclic subunit of graphene with an internal carbon atom and has peculiar and interesting electronic properties.17,18 It has been invoked as a building block for single molecule molecular conductors,19,20 and its high stability has led to derivatives having been observed at room temperature in solution and as crystals.21,22
The phenalenyl radical, and its at-first paradoxically aromatic 12-π-electron cation are also excellent candidates as astronomically relevant species, as are polycyclic aromatic hydrocarbons in general.23–28 Indeed, the related cation C60+ has recently been confirmed to carry interstellar absorption features (diffuse interstellar bands, DIBs),29,30 the first and only confirmed DIB identification.
As phenalenyl is the smallest scale model system of open-shell graphene nano-particles, its H-adduction product, 1H-phenalene (Fig. 1), may be considered a starting point in studying the electronic properties of such systems. Furthermore, substituted phenalene species have been studied as the basis of powerful organic superacids.31
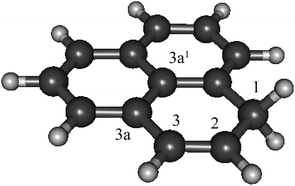 | ||
| Fig. 1 The structure of 1H-phenalene, the result of H-addition to phenalenyl radical (C13H10, B3-LYP/6-311G(d,p)). | ||
In this work, we examine the electronic spectroscopy of the 1H-phenalene molecule and its radical cation. We identify two electronic states of the neutral, and three electronic states of the cation. Several vibrational assignments are made for neutral 1H-phenalene, which are compared with results of density functional theory calculations. We apply state-of-the-art quantum chemical methods to determine the bond dissociation energy of 1H-phenalene and its isomers. This is combined with spectroscopic information to determine the excited-state bond dissociation energy for 1H-phenalene. Our experimentally determined ionization energy is in close agreement with high-level theory. These studies form a rigorous benchmark for calculations performed with more approximate methods on much larger graphene models.
2 Theoretical methods
2.1 Geometries and frequencies
Density functional theory calculations of ground-state and excited-state geometries and vibrational frequencies were carried out at the (TD-)B3-LYP/6-311++G(d,p) level.32–35 Excited-state potential energy surfaces of 1H-phenalene were constructed by computing single-point TD-B3-LYP excited-state energies at geometries distorted by application of the appropriate excited-state vibrational coordinates. The calculated points were then fit with a cubic spline, allowing the variational calculation of (anharmonic) vibrational energy levels from the one-dimensional Schrödinger equation.36 The B3-LYP and TD-B3-LYP calculations were carried out using the Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 suite of software.
37 suite of software.
2.2 Vertical excitation energies
At ground-state geometries obtained by density functional theory (vide supra), vertical excitation energies were calculated using the X-MCQDPT2 method38 in the Firefly package.39,40 The basis sets used were of triple-zeta quality, with two sets of d-type functions for the carbon atoms and one set of p-type functions for the hydrogens. The orbitals employed were obtained at the R(O)HF level, with the active spaces as indicated in the text (n electrons in o π-orbitals, [n, o]). These calculations are taken as indicative of excitation energies, but do not account for zero-point energy differences between states or geometry relaxation in the excited state. Furthermore, the ground-state geometry is calculated at a different level of theory. This method was found previously to slightly underestimate excitation energies for a range of open-shell hydrocarbon species.412.3 Thermochemical calculations
Standard wavefunction and DFT calculations were carried out with the Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 and Molpro 2012
37 and Molpro 2012![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 programs. Geometries were optimized with the B3-LYP/6-31G(2df,p) procedure according to the G3X(MP2)-RAD protocol.43 Following each geometry optimization, harmonic frequency analysis was carried out to confirm the nature of the stationary point as an equilibrium structure. To obtain the zero-point vibrational energies (ZPVEs), we used B3-LYP/6-31G(2df,p) harmonic vibrational frequencies scaled by 0.9854.44 Refined single-point energies were obtained using a number of higher-level procedures. These included B3-LYP/6-311+(3df,3pd), G3X(MP2)-RAD,43 G4(MP2)-6X,44 CCSD(T)-F12b/VDZ,45 and W1X-2.46 The most accurate of these levels is W1X-2, which corresponds to CCSD(T) with an infinite basis set. Calculated ionization energies correspond to 0 K enthalpies, whereas bond dissociation energies are reported as vibrationless values, 0 K enthalpies, as well as 298 K enthalpies.
42 programs. Geometries were optimized with the B3-LYP/6-31G(2df,p) procedure according to the G3X(MP2)-RAD protocol.43 Following each geometry optimization, harmonic frequency analysis was carried out to confirm the nature of the stationary point as an equilibrium structure. To obtain the zero-point vibrational energies (ZPVEs), we used B3-LYP/6-31G(2df,p) harmonic vibrational frequencies scaled by 0.9854.44 Refined single-point energies were obtained using a number of higher-level procedures. These included B3-LYP/6-311+(3df,3pd), G3X(MP2)-RAD,43 G4(MP2)-6X,44 CCSD(T)-F12b/VDZ,45 and W1X-2.46 The most accurate of these levels is W1X-2, which corresponds to CCSD(T) with an infinite basis set. Calculated ionization energies correspond to 0 K enthalpies, whereas bond dissociation energies are reported as vibrationless values, 0 K enthalpies, as well as 298 K enthalpies.
3 Experimental methods
3.1 Preparation of 1H-phenalene
1H-Phenalene was synthesised from commercially available perinaphthenone and reduced with diisobutylaluminum hydride in a one-step process following an established procedure.47MeOH (7 mL) was cooled to 0 °C under Ar in a flask covered in foil and NaBH4 (140 mg, 3.6 mmol, 1.3 eq.) was added as a solid. The resulting mixture was allowed to stir for 5 min before perinaphthenone (500 mg, 2.8 mmol) was added, and the reaction allowed to warm to room temperature for 16 hours (note: exothermic, H2 gas released). 5% aq. HCl (0.7 mL) was added, and then the crude reaction mixture was poured onto water (50 mL) and extracted with diethyl ether (3 times, 50 mL), dried (Na2SO4) and concentrated in vacuo to approximately 4 mL. The crude solution was loaded directly onto a column and was purified by column chromatography (10% Et2O/pentane) to afford the desired compound as a white solid (125 mg, 27%). The work-up of reaction and column chromatography was carried out in the dark.
3.2 1H-Phenalene radical cation excitation spectrum
The excitation spectrum of the 1H-phenalene radical cation was recorded indirectly, through the predissociation spectrum of the weakly bound 1H-phenalene+⋯Ar complex. The spectrum of the argon-tagged cation was recorded using a tandem quadrupole–octupole–quadrupole mass spectrometer equipped with an electron-impact supersonic expansion ion source. The apparatus has been described previously.48–52The 1H-phenalene parent sample was heated in argon behind a pulsed nozzle, seeding the supersonic expansion with 1H-phenalene. 1H-Phenalene radical cations were generated through electron impact near the nozzle orifice and clustered with Ar atoms in the free-jet expansion. The expansion was skimmed and the ions were guided into the first quadrupole mass filter by ion optics.
The first mass filter (preceding an octupole photofragmentation region) was set to m/z 206, corresponding to the 1H-phenalene+⋯Ar cluster, while the second mass filter was set to m/z 166, corresponding to the bare 1H-phenalene radical cation. Ions negotiating both the first and second quadrupole mass spectrometers were detected by a multi-channel plate. When the 1H-phenalene+⋯Ar clusters absorb photons and decompose, signal is observed by the increased flux of bare 1H-phenalene radical cations. The light source was a pulsed optical parametric oscillator (OPO) with a bandwidth of ≈8 cm−1. The OPO power was recorded and all reported spectra are normalized by laser power.
Note that the positions of the 1H-phenalene+⋯Ar absorption bands will be offset compared with the 1H-phenalene+ bands. However, these shifts have been shown to be small for similar molecules49,53,54 and spectra of Ar-tagged molecular cations have proved useful in determining if the observed excitation spectra are relevant to astronomical spectroscopy.
3.3 1H-Phenalene excitation spectrum
The resonance-enhanced multi-photon ionization time-of-flight (REMPI-TOF) spectrometer is identical to that used previously.18,36,55–61 The sample was heated in an argon atmosphere to approximately 390 K, seeding the argon with 1H-phenalene, behind a pulsed nozzle. The nozzle was heated to a slightly higher temperature than the sample to reduce condensation.The pulsed nozzle was used to supersonically expand 1H-phenalene-seeded argon into the source chamber of the REMPI-TOF chamber. The source chamber had an operating pressure on the order of 10−4 Torr. The coldest part of the free jet was passed through a 2 mm skimmer into the differentially-pumped interrogation region, between the electrostatic grids of a Wiley–Mclaren time-of-flight mass spectrometer.62 The excitation spectrum was recorded using a combination of resonant two-photon ionization and resonant two-color two-photon ionization with Nd:YAG-pumped dye lasers.
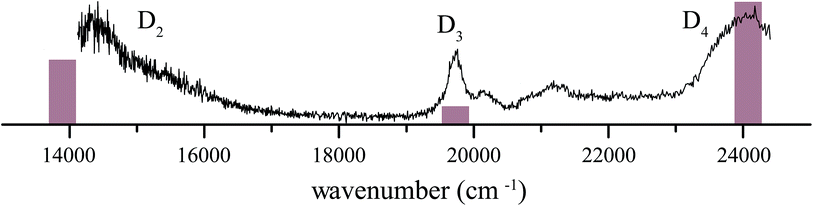
4 1H-Phenalene radical cation excitation spectrum
The resonance-enhanced photodissociation spectrum of the 1H-phenalene+⋯Ar complex is shown in Fig. 2. There are a number of spectral features consistent with the existence of several electronically excited states. As an aid to the assignment of the electronic transitions, a stick spectrum of the region of interest is plotted from the X-MCQDPT2 calculated energies and (relative) intensities (Table 1). The energies for the stick-spectrum are shifted by 1200 cm−1 higher to allow a clearer comparison with the experimental spectrum. While the calculations were carried out for the bare radical cation, it is assumed that the energy shift due to argon-tagging is small compared with the differences in predicted energy, as in past studies.49,52| State | [3, 4] | [5, 5] | [7, 7] | [9, 8] | Experiment |
|---|---|---|---|---|---|
| a [n, o] corresponds to an active space of n electrons in o orbitals. | |||||
| D1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
8742 | 9341 | 9693 | — |
| D2 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 475 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 551 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 704 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357 357 |
| D3 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 915 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
| D4 | — | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 293 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523 523 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 895 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985 985 |
The 1H-phenalene radical cation has been previously observed in a 77 K freon matrix by Bally and co-workers.63 The argon-tagged 1H-phenalene radical cation spectrum reported in this work reproduces all the features observed in the matrix spectrum within the same spectral range. This results in amendments to the previous assignments, since any features observed in the present photofragmentation spectrum must be assigned to cationic species.
The first transition is observed as a broad strong band, which begins before the lower limit of our spectrum, centred on ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 cm−1 with full width at half maximum (FWHM) ∼ 1120 cm−1. The high-energy end of this band appears to consist of unresolved vibronic features. This is similar to the band observed, and assigned as D2 ← D0, by Bally and co-workers.63
360 cm−1 with full width at half maximum (FWHM) ∼ 1120 cm−1. The high-energy end of this band appears to consist of unresolved vibronic features. This is similar to the band observed, and assigned as D2 ← D0, by Bally and co-workers.63
The next transition observed has a Lorentzian-shaped band profile centred at about 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 cm−1 with width 290 cm−1. This feature was previously assigned as being carried by the neutral phenalenyl radical.63 This is an understandable assignment. The strongest vibronic band (ν25) of the 12E′′ ← X2A′′1 (D1 ← D0) transition of the phenalenyl radical had been previously observed in this region by matrix isolation spectroscopy,64 and has been since recorded by us to have a gas-phase frequency of 19
735 cm−1 with width 290 cm−1. This feature was previously assigned as being carried by the neutral phenalenyl radical.63 This is an understandable assignment. The strongest vibronic band (ν25) of the 12E′′ ← X2A′′1 (D1 ← D0) transition of the phenalenyl radical had been previously observed in this region by matrix isolation spectroscopy,64 and has been since recorded by us to have a gas-phase frequency of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 cm−1.18 However, as neutral species such as phenalenyl radical cannot be detected by the tandem quadrupole mass-spectrometer used to record the spectrum in Fig. 2, the carrier of this band must be a cationic species with m/z ≃ 166. As such, the transition is reassigned as the electronic origin of the D3 ← D0 transition of the 1H-phenalene radical cation. The argument could be made that this feature is the 11E′ ← X1A′1 transition of the phenalenyl (closed-shell) cation (C13H9+). However, this is unlikely for several reasons. The intensity of this peak correlates well with the other observed transitions, when compared with the spectrum of Bally and co-workers,63 and between repeated experiments. Additionally, the observed band is significantly lower in energy than our calculations suggest for the strong 11E′ ← X1A′1 transition of the phenalenyl cation (23
560 cm−1.18 However, as neutral species such as phenalenyl radical cannot be detected by the tandem quadrupole mass-spectrometer used to record the spectrum in Fig. 2, the carrier of this band must be a cationic species with m/z ≃ 166. As such, the transition is reassigned as the electronic origin of the D3 ← D0 transition of the 1H-phenalene radical cation. The argument could be made that this feature is the 11E′ ← X1A′1 transition of the phenalenyl (closed-shell) cation (C13H9+). However, this is unlikely for several reasons. The intensity of this peak correlates well with the other observed transitions, when compared with the spectrum of Bally and co-workers,63 and between repeated experiments. Additionally, the observed band is significantly lower in energy than our calculations suggest for the strong 11E′ ← X1A′1 transition of the phenalenyl cation (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 cm−1). Indeed, the calculated 11E′ ← X1A′1 transition energy of phenalenyl cation is in good agreement with the band assigned thus by Bally and co-workers, supporting this assignment. This assignment has been further supported by mass-resolved matrix spectra published by Fulara, Chakraborty and Maier, who assign a feature at 3.16 eV (25
319 cm−1). Indeed, the calculated 11E′ ← X1A′1 transition energy of phenalenyl cation is in good agreement with the band assigned thus by Bally and co-workers, supporting this assignment. This assignment has been further supported by mass-resolved matrix spectra published by Fulara, Chakraborty and Maier, who assign a feature at 3.16 eV (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 cm−1) to the closed-shell cation, and variously calculate that this transition should lie at 3.17 eV (SAC-CI) and 3.49 eV (CASPT2).65 Thus, we retain the assignment of the D3 ← D0 transition of the 1H-phenalene radical cation for the 19
480 cm−1) to the closed-shell cation, and variously calculate that this transition should lie at 3.17 eV (SAC-CI) and 3.49 eV (CASPT2).65 Thus, we retain the assignment of the D3 ← D0 transition of the 1H-phenalene radical cation for the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 cm−1 band. The smaller features at slightly higher energy are assumed to be vibronic features of the same electronic transition.
735 cm−1 band. The smaller features at slightly higher energy are assumed to be vibronic features of the same electronic transition.
The remaining feature is a large band at the high energy end of the scanned region. The OPO power in this region is significantly higher than for the rest of the scan. As such, to eliminate power-broadening effects, a low-power scan was performed for this region. This allowed a Lorentzian to be fitted centred on 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985 cm−1 with a width of 680 cm−1. This peak is assigned as the D4 ← D0 transition of the 1H-phenalene radical cation. Despite the reduced power, this transition is still significantly saturated, and has roughly twice the intensity observed in Fig. 2 (exact quantification of the relative intensity is difficult).
985 cm−1 with a width of 680 cm−1. This peak is assigned as the D4 ← D0 transition of the 1H-phenalene radical cation. Despite the reduced power, this transition is still significantly saturated, and has roughly twice the intensity observed in Fig. 2 (exact quantification of the relative intensity is difficult).
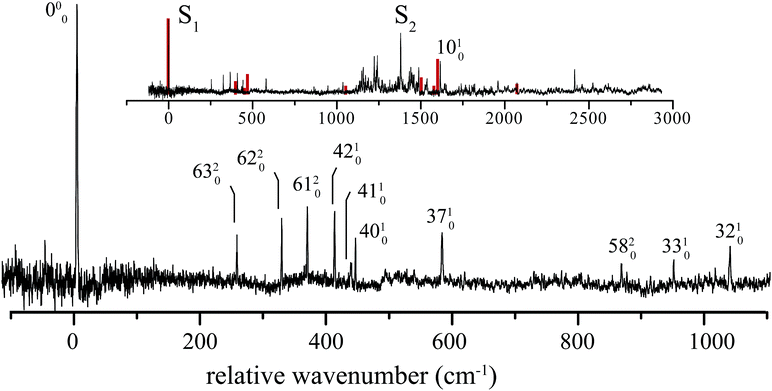
5 1H-Phenalene spectrum
The excitation spectrum of 1H-phenalene is displayed in Fig. 3. The lowest-frequency band in the spectrum was observed at 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 cm−1 (353.2 kJ mol−1). This band is also the strongest band in the spectrum and is assigned as the S1 ← S0 electronic origin band of 1H-phenalene. Other features of the observed spectrum include a number of low-frequency vibrational modes, and a dense region of transitions centred about a strong band with relative frequency 1380 cm−1.
527 cm−1 (353.2 kJ mol−1). This band is also the strongest band in the spectrum and is assigned as the S1 ← S0 electronic origin band of 1H-phenalene. Other features of the observed spectrum include a number of low-frequency vibrational modes, and a dense region of transitions centred about a strong band with relative frequency 1380 cm−1.
Due to the overwhelming number of possible assignments, an assignment of the dense region centred about 1380 cm−1 is not attempted in this work. However, an assignment of the relatively uncluttered low-frequency region was undertaken. This region is displayed, with assignments, in Fig. 3.
In Cs symmetry, the observed S1 ← S0 electronic transition has total symmetry A′ (21A′ ← X1A′). Therefore, under the Franck–Condon approximation, transitions to vibrational states with total symmetry a′ will be allowed. Total symmetry a′ can be the result of any combination of in-plane a′ quanta or an even number of quanta of out-of-plane a′′ modes.
The lowest-frequency vibrational band, with a relative frequency 254 cm−1, is significantly lower in energy than ν42, the lowest-frequency in-plane mode. As such, this band is assigned to the two-quanta excitation of the lowest-frequency out-of-plane mode, ν63, an out-of-plane torsion of the ring containing the sp3 hybridised carbon. As shown in Table 2, the observed frequency of this band is bracketed by the harmonic and anharmonic calculated value. Two-quanta excitations of ν62 and ν61 are also assigned, and for these the anharmonic frequency calculations agree well, with the observed bands lying just 9 cm−1 and 15 cm−1 to higher energy than the respective calculated values. 2ν60 and 2ν59 are predicted to have relative frequencies of 486 cm−1 and 626 cm−1, respectively. No peaks are observed in these regions. However, noise around 486 cm−1 could possibly be hiding 2ν60. A band with relative frequency 864 cm−1 is close in energy to the predicted energy for two quanta of ν58 and is assigned thus.
| Assignment | Exp. | Harm. | Anharm. | Δ |
|---|---|---|---|---|
| a Tentative assignment. | ||||
| 2ν63 | 254 | 224 | 276 | +22 |
| 2ν62 | 325 | 304 | 316 | −9 |
| 2ν61 | 366 | 384 | 351 | −15 |
| 2ν58 | 864 | 886 | 884 | +20 |
| ν 42 | 409 | 401 | 398 | −11 |
| ν 41 | 435 | 420 | 420 | −15 |
| ν 40 | 442 | 453 | 447 | +5 |
| ν 37 | 580 | 602 | 602 | +22 |
| ν 33 | 947 | 964 | +17 | |
| ν 32 | 1036 | 1031 | −5 | |
| ν 10 | 1616 | 1603 | 1606 | −10 |
The peak observed with relative frequency 409 cm−1 is assigned to the lowest-frequency in-plane a′ mode ν42, with a calculated anharmonic frequency of 398 cm−1. Similar assignments are made for modes ν41, ν40, ν37, ν33 and ν32. It can be seen in Table 2 that the in-plane a′ modes are relatively harmonic. As such, relatively inexpensive calculated harmonic frequencies were used for the assignment of a′ modes ν33 and ν32.
In an attempt to assign the more intense peaks at higher energies, TD-B3-LYP/6-311++G(d,p) Frank–Condon (FC) and Frank–Condon–Herzberg–Teller (FCHT) intensities were calculated.37 The FCHT stick-spectrum is displayed in the inset to Fig. 3.
The FCHT calculation correctly predicts the cluster of bands around 400 cm−1, supporting the assignment of the observed bands to single quanta of modes ν42, ν41 and ν40. The FC, FCHT and anharmonic calculations all suggest that ν10 should be strong, and this is assigned to the strong band observed at 1616 cm−1. However, it should be noted that TD-DFT calculations fail to reproduce the correct ordering of electronic states for the related chromophore, naphthalene. In the present chromophore, with reduced symmetry, the results of TD-DFT should be treated with caution. Nevertheless, the band at 1036 cm−1 is closest in energy to the calculated harmonic frequency of ν32. However, ν31 is predicted to be more intense in the FCHT simulation. The original assignment of ν32 is tentatively retained.
None of the simulations predict a strong transition at 1380 cm−1, or indeed any strong vibronic activity in the entire 1200–1500 cm−1 region. Due to the congestion in this region, combination bands are required to explain the sheer number of observed peaks. As such, there are many possible assignments in this region. The intensity of the peak at 1380 cm−1 is suggestive of a progression-forming mode, but there is no evidence of an overtone.
The calculated vertical Sn ← S0 excitation energies are given in Table 3. The calculations, which account for static correlation using an [n, o] active space of n electrons in o π-orbitals, and dynamic correlation using perturbation theory, predict a lowest excitation which is about 1000 cm−1 too high, an acceptable discrepancy. The calculations also clearly predict that the second excited state, S2 should be near-degenerate with S1. In the light of these calculations, we ascribe the feature at 1380 cm−1 to the origin of the S2 ← S0 transition, with the associated thicket of features due to vibronic coupling. The calculated transition dipole moments of these states are not orthogonal, but are disposed at an angle of 33°, indicating that the adjacent double-bond of 1H-phenalene results in an admixture of the La and Lb states of the related naphthalene chromophore.
| State | [4, 4] | [6, 5] | Experiment |
|---|---|---|---|
| S1 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 523 523 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 527 |
| S2 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261 261 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
| S3 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828 828 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
— |
6 1H-Phenalene ionization energy
While recording the one-laser two-photon excitation spectrum, no bands were observed below 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 cm−1 (ν37, relative frequency 580 cm−1). When the 206 nm ionization laser was introduced, lower-frequency bands could be observed.
107 cm−1 (ν37, relative frequency 580 cm−1). When the 206 nm ionization laser was introduced, lower-frequency bands could be observed.
It is proposed that 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 cm−1 photons (the energy of ν40, the next highest energy band) are of insufficient energy to ionize 1H-phenalene from the state of the same energy. The IE of 1H-phenalene can thus be bracketed between twice the energies of the ν37 and ν40 bands, 2 × 29
970 cm−1 photons (the energy of ν40, the next highest energy band) are of insufficient energy to ionize 1H-phenalene from the state of the same energy. The IE of 1H-phenalene can thus be bracketed between twice the energies of the ν37 and ν40 bands, 2 × 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 < IE < 2 × 30
970 < IE < 2 × 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 cm−1, 7.449(17) eV.
107 cm−1, 7.449(17) eV.
We previously demonstrated an approximate method for computationally bracketting the IE of resonance-stabilized hydrocarbon radicals (RSRs).59 For the molecules examined, IEs calculated with the B3-LYP/6-311++G(3df,3pd) and G3X(MP2)-RAD levels of theory were found to bracket the experimental figure for the range of RSRs tested. It is of interest to determine if this approximation also holds for closed-shell molecules such as 1H-phenalene. The IE of 1H-phenalene was calculated using several computational methods, as reported in Table 4. As with our previous studies on radicals, B3-LYP/6-311++G(3df,3pd) and G3X(MP2)-RAD indeed bracket the experimental result, with the highest-level W1X-2 IE of 7.49 eV close to the experimental value of 7.449(17) eV. The related W1X-1 method, when applied to the cyclohexadienyl radical, predicts an IE which is 20 meV too high, a similar discrepancy to the present case,66–68 noting that the experimental IE could lie anywhere within the stated range.
| Method | eV |
|---|---|
| a Experiment brackets result between 7.432 and 7.466 eV. | |
| B3-LYP/6-311++G(3df,3pd) | 7.13 |
| G3X(MP2)-RAD | 7.56 |
| G4(MP2) | 7.41 |
| G4(MP2)-6X | 7.61 |
| CCSD(T)-F12b/A'VDZ | 7.44 |
| W1X-2 | 7.49 |
| Experiment | 7.449(17) |
7 1H-Phenalene bond dissociation energy
The hydrogens are weakly bonded to the sp3 carbon of 1H-phenalene, due to the remarkable resonance-stability of the phenalenyl radical. The reported bond dissociation energy (BDE) is just 272(8) kJ mol−1.69 We have determined the BDE at 0 and 298 K at a range of levels of theory (Table 5). Our most accurate level of theory for all the BDEs is W1X-2, and we find also that G3X(MP2)-RAD and CCSD(T)-F12b/DVZ are generally in good agreement with W1X-2. The best calculations place the BDE close to the experimental figure, which was determined at much higher temperatures.| Vibrationless | 0 K | 298 K | |
|---|---|---|---|
| BDE (1H) | |||
| B3-LYP/6-311++G(3df,3pd) | 271.2 | 239.6 | 244.8 |
| G3X(MP2)-RAD | 286.8 | 255.1 | 260.3 |
| G4(MP2) | 299.4 | 267.7 | 272.9 |
| G4(MP2)-6X | 310.0 | 278.3 | 283.5 |
| CCSD(T)-F12b/VDZ | 288.4 | 256.7 | 261.9 |
| W1X-2 | 289.8 | 258.1 | 263.3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| BDE (2H) | |||
| B3-LYP/6-311++G(3df,3pd) | 47.9 | 27.7 | 31.6 |
| G3X(MP2)-RAD | 68.5 | 48.3 | 52.1 |
| G4(MP2) | 82.2 | 62 | 65.8 |
| G4(MP2)-6X | 84.5 | 64.3 | 68.1 |
| CCSD(T)-F12b/A'VDZ | 60.3 | 40.1 | 43.9 |
| W1X-2 | 58.7 | 38.5 | 42.4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| BDE (3aH) | |||
| B3-LYP/6-311++G(3df,3pd) | −16.8 | −41.5 | −36.7 |
| G3X(MP2)-RAD | 19.2 | −5.5 | −0.7 |
| G4(MP2) | 32.7 | 8 | 12.8 |
| G4(MP2)-6X | 36.4 | 11.7 | 16.5 |
| CCSD(T)-F12b/A'VDZ | 10.1 | −14.6 | −9.7 |
| W1X-2 | 6.3 | −18.4 | −13.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| BDE (3a 1 H) | |||
| B3-LYP/6-311++G(3df,3pd) | 1.7 | −38.9 | −33.6 |
| G3X(MP2)-RAD | −60.9 | −101.5 | −96.3 |
| G4(MP2) | −47.4 | −87.9 | −82.7 |
| G4(MP2)-6X | −40.1 | −80.7 | −75.4 |
| CCSD(T)-F12b/A'VDZ | −58.8 | −99.3 | −94.1 |
| W1X-2 | −59.7 | −100.3 | −95.1 |
The excited-state BDE can also be determined by combining the calculated ground-state BDE with the excitation energies of the neutral phenalenyl radical18 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1, 225.1 kJ mol−1) and 1H-phenalene (29
800 cm−1, 225.1 kJ mol−1) and 1H-phenalene (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 cm−1, 353.2 kJ mol−1), as shown in Fig. 4. Based on the 0 K W1X-2 calculations, the BDE of 1H-phenalene reduces from 258.1 kJ mol−1 to 130.0 kJ mol−1 in the S1 (21A′) excited state.
527 cm−1, 353.2 kJ mol−1), as shown in Fig. 4. Based on the 0 K W1X-2 calculations, the BDE of 1H-phenalene reduces from 258.1 kJ mol−1 to 130.0 kJ mol−1 in the S1 (21A′) excited state.
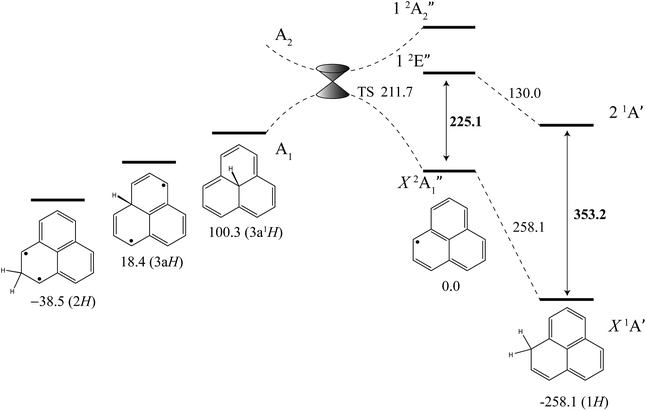 | ||
| Fig. 4 Energies of 1H-phenalene and its isomers (kJ mol−1), relative to the phenalenyl radical, calculated at the W1X-2 level (Table 5). Bold numbers are spectroscopically derived from this and previously published work.18 | ||
Addition of hydrogen at other positions of phenalenyl radical results in phenalenes with much reduced, and in some cases negative, BDEs. The BDE of 2H-phenalene is calculated to be just 38.5 kJ mol−1, while 3aH- and 3a1H-phenalene have negative BDEs. The reduced stabilities are due to a combination of strain, in the cases of 3aH- and 3a1H-phenalene, and the biradical nature of the π-system in the cases of 2H- and 3aH-phenalene. The 12-electron periphery of 3a1H-phenalene is classically anti-aromatic.
Despite the instabilities, these higher-energy isomers are all bound. Inspection of the highest-occupied molecular orbital of phenalenyl radical (a′′1) reveals radical density only at the 1-position and its symmetry-equivalents. As such, only addition to this site is expected to be barrierless. Dissociation of 3a1H-phenalene, maintaining an A1 electronic state in C3v symmetry, will result in a D3h phenalenyl radical of A′′2 symmetry. This is an electronically excited state, which we calculate to lie near 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 205 cm−1 (241.7 kJ mol−1). Since the ground state of phenalenyl radical is of A′′1 symmetry, there will be a crossing of the potential energy curves for adiabatic dissociation in C3v symmetry. Symmetry-breaking will allow these surfaces to form an avoided crossing either side of the actual crossing, at high symmetry, resulting in a conical intersection. The transition structure is located below this point, and is calculated to have an energy of 211.7 kJ mol−1 above the energy of phenalenyl radical (Fig. 4).
205 cm−1 (241.7 kJ mol−1). Since the ground state of phenalenyl radical is of A′′1 symmetry, there will be a crossing of the potential energy curves for adiabatic dissociation in C3v symmetry. Symmetry-breaking will allow these surfaces to form an avoided crossing either side of the actual crossing, at high symmetry, resulting in a conical intersection. The transition structure is located below this point, and is calculated to have an energy of 211.7 kJ mol−1 above the energy of phenalenyl radical (Fig. 4).
8 Astronomical relevance
The S1 ← S0 transition of 1H-phenalene is observed in the UV region, significantly too high in energy to be a carrier of a DIB – all of which are observed in the visible and NIR regions of the spectrum.70,71 Additionally, while having a strong origin transition, the strong vibrational bands would likely be visible in any spectra where the origin could be observed, and therefore 1H-phenalene also violates the non-correlation criteria for the DIBs.721H-Phenalene can be considered the smallest model system for edge addition of hydrogen to radical graphene fragments, altering the edge π-orbital structure. H-Addition to peripheral sp2 carbons of sufficiently larger open-shell graphene fragments will result in species with visible spectra. Given the relatively small FWHM of 1H-phenalene, it is likely that larger edge-H-adducted graphene fragments will have widths appropriate to the DIBs. Whether or not these larger molecules exhibit origin-dominated spectra remains to be seen. Spectroscopically, these H-adducted graphene fragments are unlikely to differ significantly from other large neutral closed-shell PAHs.73,74
Proton addition to aromatic frameworks remains of intrinsic astronomical interest. The recent identification of the C60+ radical cation as a carrier of DIBs has naturally fuelled speculation that related molecules may also be carriers. Indeed, charge-transfer bands of C60H+ and other metal-adducted and substituted fullerenes have been previously suggested as possible DIB carriers.75 The transitions observed in the visible predissociation spectrum of the 1H-phenalene+⋯Ar complex are all significantly too broad to be relevant to the DIBs. However, further experimental work on larger edge-protonated graphene molecules may be warranted.
9 Conclusions
The gas-phase spectra of the 1H-phenalene molecule and its radical cation have been presented for the first time. Multiple electronic states of both species were assigned with the aid of quantum chemical calculations. The previous assignment of 1H-phenalene radical cation in matrix isolation spectra was amended. The ionization energy of 1H-phenalene was determined to reasonable precision (17 meV), and the bond dissociation energy was calculated using high-level theory, allowing the excited-state bond dissociation energy to be determined from spectroscopic measurements. This combination of state-of-the-art spectroscopic and quantum chemical methods on a system both experimentally and theoretically tractable will enable insight into the interactions between hydrogen atoms and much larger open-shell graphene fragments.Acknowledgements
This research was supported under Australian Research Councils Discovery Projects funding scheme (DP120102559, DP120100100 and DP1501425). T. W. S. and R. J. P. acknowledge the Australian Research Council for Future Fellowships (FT130100177 and FT130100150). G. D. O., K. M. C. and J. A. S. acknowledge the receipt of Australian Postgraduate Awards. V. D. acknowledges an Australian Renewable Energy Agency Postdoctoral Fellowship (6-F004) and support from the University of Melbourne's Early Career Researcher Grant Scheme. The National Computational Infrastructure National Facility (NCI NF) is thanked for generous allocations of supercomputer time.References
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef.
- D. W. Boukhvalov, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035427 CrossRef.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- M. Z. S. Flores, P. A. S. Autreto, S. B. Legoas and D. S. Galvao, Nanotechnology, 2009, 20, 465704 CrossRef CAS PubMed.
- J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870 CrossRef CAS PubMed.
- J. Zhou, M. M. Wu, X. Zhou and Q. Sun, Appl. Phys. Lett., 2009, 95, 103108 CrossRef.
- D. Soriano, F. Muñoz Rojas, J. Fernández-Rossier and J. J. Palacios, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165409 CrossRef.
- D. Haberer, D. V. Vyalikh, S. Taioli, B. Dora, M. Farjam, J. Fink, D. Marchenko, T. Pichler, K. Ziegler, S. Simonucci, M. S. Dresselhaus, M. Knupfer, B. Büchner and A. Grüneis, Nano Lett., 2010, 10, 3360–3366 CrossRef CAS PubMed.
- K. S. Subrahmanyam, P. Kumar, U. Maitra, A. Govindaraj, K. P. S. S. Hembram, U. V. Waghmare and C. N. R. Rao, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2674–2677 CrossRef CAS PubMed.
- M. Pumera and C. H. A. Wong, Chem. Soc. Rev., 2013, 42, 5987–5995 Search PubMed.
- H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J.-Y. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437–441 CrossRef PubMed.
- C. Lee, N. Leconte, J. Kim, D. Cho, I.-W. Lyo and E. Choi, Carbon, 2016, 103, 109–114 CrossRef CAS.
- V. Tozzini and V. Pellegrini, Phys. Chem. Chem. Phys., 2013, 15, 80–89 RSC.
- L. Hornekær, E. Rauls, W. Xu, Z. Šljivančanin, R. Otero, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 97, 186102 CrossRef PubMed.
- M. K. Cyrański, R. W. A. Havenith, M. A. Dobrowolski, B. R. Gray, T. M. Krygowski, P. W. Fowler and L. W. Jenneskens, Chem.–Eur. J., 2007, 13, 2201–2207 CrossRef PubMed.
- G. D. O'Connor, T. P. Troy, D. A. Roberts, N. Chalyavi, B. Fückel, M. J. Crossley, K. Nauta, J. F. Stanton and T. W. Schmidt, J. Am. Chem. Soc., 2011, 133, 14554–14557 CrossRef PubMed.
- A. Sarkar, F. S. Tham and R. C. Haddon, J. Mater. Chem., 2011, 21, 1574–1581 RSC.
- T. Kubo, Chem. Rec., 2015, 15, 218–232 CrossRef CAS PubMed.
- K. Goto, T. Kubo, K. Yamamoto, K. Nakasuji, K. Sato, D. Shiomi, T. Takui, M. Kubota, T. Kobayashi, K. Yakusi and J. Ouyang, J. Am. Chem. Soc., 1999, 121, 1619–1620 CrossRef CAS.
- Y. Morita, T. Aoki, K. Fukui, S. Nakazawa, K. Tamaki, S. Suzuki, A. Fuyuhiro, K. Yamamoto, K. Sato, D. Shiomi, A. Naito, T. Takui and K. Nakasuji, Angew. Chem., Int. Ed., 2002, 41, 1793–1796 CrossRef CAS.
- A. Léger and J. L. Puget, Astron. Astrophys., 1984, 137, L5–L8 Search PubMed.
- L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25–L28 CrossRef CAS.
- D. Small, V. Zaitsev, Y. Jung, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Am. Chem. Soc., 2004, 126, 13850–13858 CrossRef CAS PubMed.
- D. Small, S. V. Rosokha, J. K. Kochi and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 11261–11267 CrossRef CAS PubMed.
- V. Zaitsev, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Org. Chem., 2006, 71, 520–526 CrossRef CAS PubMed.
- Y. M. Rhee, T. J. Lee, M. S. Gudipati, L. J. Allamandola and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5274–5278 CrossRef CAS PubMed.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- G. A. H. Walker, D. A. Bohlender, J. P. Maier and E. K. Campbell, Astrophys. J., Lett., 2015, 812, L8 CrossRef.
- R. Vianello and Z. B. Maksić, Tetrahedron, 2005, 61, 9381–9390 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 72 Search PubMed.
- D. O'Connor, G. B. Bacskay, G. V. G. Woodhouse, T. P. Troy, K. Nauta and T. W. Schmidt, J. Phys. Chem. A, 2013, 117, 13899–13907 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision A.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- A. Granovsky, Firefly version 8.0.0, http://classic.chem.msu.su/gran/firefly/index.html Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- G. D. O'Connor, G. V. Woodhouse, T. P. Troy and T. W. Schmidt, Mol. Phys., 2015, 113, 2138–2147 CrossRef.
- H. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242 CrossRef CAS.
- D. J. Henry, M. B. Sullivan and L. Radom, J. Chem. Phys., 2003, 118, 4849 CrossRef CAS.
- B. Chan, J. Deng and L. Radom, J. Chem. Theory Comput., 2011, 7, 112 CrossRef CAS PubMed.
- T. B. Adler, G. Knizia and H. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2012, 8, 4259 CrossRef CAS PubMed.
- B. Stulgies, D. P. Pigg Jr, P. Kaszynski and Z. H. Kudzin, Tetrahedron, 2005, 61, 89–95 CrossRef CAS.
- D. A. Wild and E. J. Bieske, Int. Rev. Phys. Chem., 2003, 22, 129–151 CrossRef CAS.
- V. Dryza, N. Chalyavi, J. A. Sanelli and E. J. Bieske, J. Chem. Phys., 2012, 137, 204304 CrossRef PubMed.
- V. Dryza, J. A. Sanelli, E. G. Robertson and E. J. Bieske, J. Phys. Chem. A, 2012, 116, 4323–4329 CrossRef CAS PubMed.
- S. Hansen, S. J. Blanksby, N. Chalyavi, E. J. Bieske, J. R. Reimers and A. J. Trevitt, J. Chem. Phys., 2015, 142, 014301 CrossRef PubMed.
- N. Chalyavi, K. J. Catani, J. A. Sanelli, V. Dryza and E. Bieske, Mol. Phys., 2015, 113, 2086–2094 CrossRef CAS.
- T. Pino, N. Boudin and P. Bréchignac, J. Chem. Phys., 1999, 111, 7337–7347 CrossRef CAS.
- H. Friha, G. Féraud, T. Troy, C. Falvo, P. Parneix, P. Bréchignac, Z. Dhaouadi, T. W. Schmidt and T. Pino, J. Phys. Chem. A, 2013, 117, 13664–13672 CrossRef CAS PubMed.
- N. J. Reilly, D. L. Kokkin, M. Nakajima, K. Nauta, S. H. Kable and T. W. Schmidt, J. Am. Chem. Soc., 2008, 130, 3137–3142 CrossRef CAS PubMed.
- N. J. Reilly, M. Nakajima, T. P. Troy, N. Chalyavi, K. A. Duncan, K. Nauta, S. H. Kable and T. W. Schmidt, J. Am. Chem. Soc., 2009, 131, 13423–13429 CrossRef CAS PubMed.
- N. Chalyavi, T. P. Troy, M. Nakajima, B. A. Gibson, K. Nauta, R. G. Sharp, S. H. Kable and T. W. Schmidt, J. Phys. Chem. A, 2011, 115, 7959–7965 CrossRef CAS PubMed.
- N. Chalyavi, G. B. Bacskay, A. S. Menon, T. P. Troy, N. J. L. K. Davis, L. Radom, S. A. Reid and T. W. Schmidt, J. Chem. Phys., 2011, 135, 124306 CrossRef PubMed.
- T. P. Troy, N. Chalyavi, A. S. Menon, G. D. O'Connor, B. Fückel, K. Nauta, L. Radom and T. W. Schmidt, Chem. Sci., 2011, 2, 1755–1765 RSC.
- N. Chalyavi, T. P. Troy, G. B. Bacskay, K. Nauta, S. H. Kable, S. A. Reid and T. W. Schmidt, J. Phys. Chem. A, 2012, 116, 10780–10785 CrossRef CAS PubMed.
- T. P. Troy, M. Nakajima, N. Chalyavi, K. Nauta, S. H. Kable and T. W. Schmidt, J. Phys. Chem. A, 2012, 116, 7906–7915 CrossRef CAS PubMed.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- T. Bally, Z. Zhu, J. Wirz, M. Fulscher and J. Hasegawa, J. Chem. Soc., Perkin Trans. 2, 2000, 2311–2318 RSC.
- W. P. Cofino, S. M. van Dam, D. A. Kamminga, G. P. Hoornweg, C. Gooijer, C. MacLean and N. H. Velthorst, Mol. Phys., 1984, 51, 537–550 CrossRef CAS.
- J. Fulara, A. Chakraborty and J. P. Maier, Angew. Chem., 2016, 128, 3485–3488 CrossRef.
- O. Krechkivska, Y. Liu, K. L. K. Lee, K. Nauta, S. H. Kable and T. W. Schmidt, J. Phys. Chem. Lett., 2013, 4, 3728–3732 CrossRef CAS.
- O. Krechkivska, C. Wilcox, G. D. O'Connor, K. Nauta, S. H. Kable and T. W. Schmidt, J. Phys. Chem. A, 2014, 118, 10252–10258 CrossRef CAS PubMed.
- O. Krechkivska, C. M. Wilcox, T. P. Troy, K. Nauta, B. Chan, R. Jacob, S. A. Reid, L. Radom, T. W. Schmidt and S. H. Kable, Phys. Chem. Chem. Phys., 2016, 18, 8625–8636 RSC.
- M. Gerst and C. Rüchardt, Chem. Ber., 1993, 126, 1039–1045 CrossRef CAS.
- L. M. Hobbs, D. G. York, T. P. Snow, T. Oka, J. A. Thorburn, M. Bishof, S. D. Friedman, B. J. McCall, B. Rachford, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2008, 680, 1256 CrossRef CAS.
- L. M. Hobbs, D. G. York, J. A. Thorburn, T. P. Snow, M. Bishof, S. D. Friedman, B. J. McCall, T. Oka, B. Rachford, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2009, 705, 32 CrossRef CAS.
- B. J. McCall, M. M. Drosback, J. Thorburn, D. G. York, S. D. Friedman, L. M. Hobbs, B. L. Rachford, T. P. Snow, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2010, 708, 1628 CrossRef CAS.
- D. A. Amirav, U. Even and J. Jortner, J. Chem. Phys., 1981, 75, 3770–3793 CrossRef.
- L. Kokkin, T. P. Troy, M. Nakajima, K. Nauta, T. D. Varberg, G. F. Metha, N. T. Lucas and T. W. Schmidt, Astrophys. J., 2008, 681, L49 CrossRef.
- H. W. Kroto and M. Jura, Astron. Astrophys., 1992, 263, 275–280 CAS.
| This journal is © The Royal Society of Chemistry 2017 |