Open Access Article
Open Access ArticleA quantitative mechanistic PK/PD model directly connects Btk target engagement and in vivo efficacy†
Fereidoon
Daryaee‡
a,
Zhuo
Zhang‡
a,
Kayla R.
Gogarty
a,
Yong
Li
a,
Jonathan
Merino
a,
Stewart L.
Fisher
*b and
Peter J.
Tonge
 *a
*a
aInstitute for Chemical Biology & Drug Discovery, Department of Chemistry, Stony Brook University, Stony Brook, NY 11794-3400, USA. E-mail: peter.tonge@stonybrook.edu
bC4 Therapeutics, Cambridge, MA 02142, USA. E-mail: stewfisher@slfisherconsulting.com
First published on 14th March 2017
Abstract
Correlating target engagement with in vivo drug activity remains a central challenge in efforts to improve the efficiency of drug discovery. Previously we described a mechanistic pharmacokinetic–pharmacodynamic (PK/PD) model that used drug–target binding kinetics to successfully predict the in vivo efficacy of antibacterial compounds in models of Pseudomonas aeruginosa and Staphylococcus aureus infection. In the present work we extend this model to quantitatively correlate the engagement of Bruton's tyrosine kinase (Btk) by the covalent inhibitor CC-292 with the ability of this compound to reduce ankle swelling in an animal model of arthritis. The modeling studies include the rate of Btk turnover and reveal the vulnerability of Btk to engagement by CC-292.
Introduction
Drug design and discovery is dominated by the use of thermodynamic parameters such as IC50 or Ki values to select and optimize lead candidates. These metrics are used to predict in vivo drug pharmacodynamics (PD) based on the assumption that drugs are at equilibrium with their targets.1 However, drug concentration at the target site is often not constant, due to dynamic events such as absorption, distribution, metabolism and excretion, and thus drug and target are unlikely to be at equilibrium.1–4 Instead, a complete description of drug–target binding requires the inclusion of drug–target kinetics which can be used to better predict time-dependent changes in drug activity.1,2,4–9 This has led to the development of mechanistic pharmacokinetic/pharmacodynamic (PK/PD) models that include the on and off rates for binding of the drug to the target, an approach that makes implicit predictions concerning the relationship between target occupancy (TO) and PD.10,11 Direct links between target occupancy and in vivo drug PK are keenly sought, since the amount of target that has to be complexed with drug to elicit the desired PD has a direct bearing on the vulnerability of the target. In this study, the mechanistic PK/PD models reported previously by our group10,11 have been modified to integrate drug PK, drug binding kinetics and target turnover (target degradation and resynthesis), in order to simulate PD based on the combinatorial effects of TO and target vulnerability. This model has been used to understand the relationship between drug concentration and drug efficacy of CC-292, an irreversible inhibitor of Bruton's tyrosine kinase (Btk), in a rat model of rheumatoid arthritis (RA).Btk is a non-receptor tyrosine kinase in the B-cell antigen receptor (BCR) signalling pathway, which is involved in a signal transduction cascade that regulates B cell development, differentiation and functioning.12–14 B cells are known to play an important role in RA,15–17 an auto-immune disease which is characterized by recognition of normal proteins in the joints as autoantigens and infiltration of lymphocytes into the joints that will finally lead to joint damage,18 and there have been extensive efforts to develop Btk inhibitors as potential therapeutics for RA.19 In particular, a subset of Btk inhibitors including ibrutinib and CC-292 (Fig. 1) form a covalent bond with a conserved cysteine (Cys-481) in the active site,20,21 and these compounds are valuable chemical tools for evaluating the relationship between TO and PD, and for assessing the predictive power of our PK/PD model, since probes can be developed to quantify Btk TO as a function of inhibitor concentration. In this regard, Evans, et al.21 used a biotinylated analogue of CC-292 to measure Btk TO by CC-292 in Ramos cells as well as in mice and humans. Although a quantitative relationship between TO and PD was not reported, higher doses of CC-292 resulted in increased occupancy of Btk and resulted in increased efficacy in a mouse RA model. In addition, Honigberg, et al. used a covalent fluorescent probe derived from ibrutinib to quantify the Btk occupancy achieved by ibrutinib treatment in mice with RA.20 The same probe was used in a recently published study by Bradshaw, et al. to quantify target occupancy achieved by a series of reversible covalent Btk inhibitors.22 However, neither study attempted to quantify the relationship between drug concentration, TO and efficacy. Conversely, Liu, et al. correlated the concentration of a reversible Btk inhibitor GDC-0834 with Btk phosphorylation, and with efficacy against RA using a traditional PK/PD model.23 In this case, TO was not measured and this study employed an empirical PK/PD model in which drug concentration and Btk phosphorylation, as well as Btk phosphorylation and drug efficacy, were described by sigmoidal equations in which a rapid equilibrium was assumed to exist between drug concentration and Btk phosphorylation. Such PK/PD models cannot be used for drugs with slow binding kinetics, particularly those that dissociate slowly from, or form irreversible covalent bonds with, their targets and thus that have sustained TO.
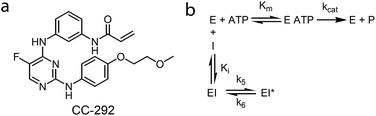 | ||
| Fig. 1 (a) Structure of CC-292. (b) Inhibition of Btk by an ATP-competitive inhibitor that binds through a two-step mechanism. For irreversible inhibitors such as CC-292, k6 = 0. | ||
In the present study, we have used a covalent fluorescent probe to quantify the in vitro and in vivo occupancy of Btk following CC-292 treatment. The PK of CC-292 was determined and the efficacy of CC-292 was evaluated in a rat model of RA. Subsequently, the quantitative relationship between Btk occupancy and PD was analysed using a mechanistic PK/PD model that integrates drug–target binding kinetics and target turnover, thus providing insight into the vulnerability of Btk. Target vulnerability, viz. the level of target occupancy required to elicit the desired pharmacological outcome, is a critical factor in determining dosing drug regimens. Thus, the ability to determine target vulnerability and use this information prospectively is expected to have a profound effect on the drug discovery cascade by informing target selection and designing optimal dosing regimens that maximize the impact of sustained target engagement.
Results
PK/PD model
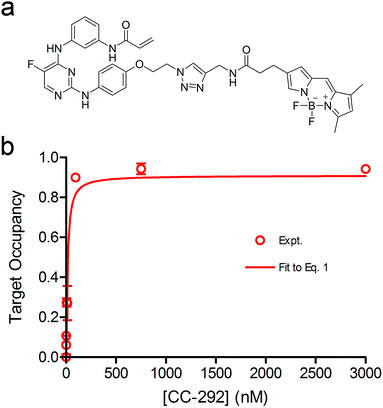
We previously derived a PK/PD model that was used to predict drug activity in an animal model of infection.10 This model was subsequently modified to enable target occupancy to be explicitly calculated, enabling an estimate of target vulnerability.11 In the present work we have adapted the PK/PD model to predict the PD of a Btk inhibitor. Since CC-292 is an irreversible Btk inhibitor we can explicitly quantify intracellular Btk engagement as a function of CC-292 concentration. In addition, as Btk is present in B cells, we can thus explicitly calculate in vivo Btk engagement as a function of plasma drug concentration, rather than relying on a permeability function as we did in the previous models. Finally, since CC-292 is an irreversible inhibitor, the only way that the effect of Btk inhibition can be overcome is by new target synthesis. Thus, in the present model we now include an estimate of Btk turnover.Our approach is based on the use of in vitro drug target kinetic data to calculate target engagement as a function of drug concentration and time. The interaction of CC-292 with Btk is shown in Fig. 1 where Ki is the equilibrium dissociation constant for the initial EI complex, and k5 is the maximum rate of inactivation (kinact). For irreversible inhibitors, the ratio of k5/Ki (kinact/Ki) is the second-order rate constant that quantifies the efficiency of inactivation when E + I is in rapid equilibrium with EI relative to the rate of the second step (k5 or kinact).24 To calculate the engagement of Btk by CC-292, estimates are required for k5 and Ki. This was achieved by fitting the experimentally observed TO of Btk in Ramos cells, obtained as a function of CC-292 concentration, to an equilibrium TO model (eqn (1)) (ESI Appendix, eqn (S3)†).
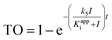 | (1 S3) |
The equilibrium TO of Btk in Ramos cells was determined with a covalent fluorescent-probe assay,20,22 using BDP-CC-292, a probe synthesized by us from CC-292 (Fig. 2a and ESI Appendix Scheme S1†). Briefly, after exposing cells to CC-292 for 1 h, the cells were lysed and the lysate treated with high concentrations of BDP-CC-292 to capture unreacted Btk. After SDS-PAGE, the amount of BDP-CC-292 bound Btk was quantified by fluorescence scanning while the total amount of Btk was quantified by western blotting (ESI Appendix, Fig. S1 and S2 and Table S1†). The concentration of CC-292 required for 50% target occupancy was 22.3 ± 5.4 nM (Hill coefficient = 1), which is similar to the value of 8 nM reported previously.21 The data were then fit to eqn (1) to obtain values for k5 and Kappi of 2.41 ± 0.67 h−1 and 40 nM, respectively (Fig. 2b).
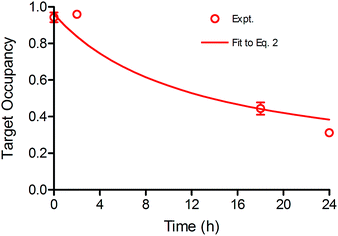
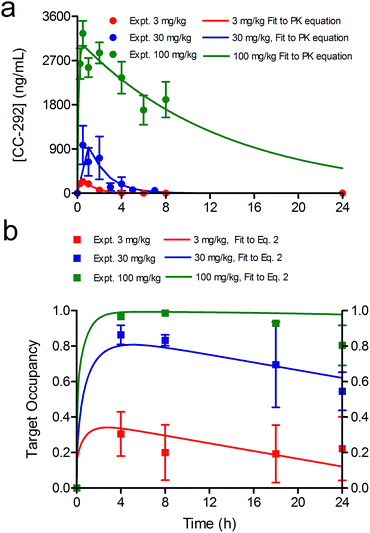
Time dependent changes in TO are modulated by both drug–target binding kinetics, as well as the rate of target degradation and re-synthesis. In this study Btk degradation and re-synthesis have been incorporated into our model by using a linear turnover parameter ρ that modulates target occupancy by enlarging the total Btk pool. The time-dependent change in Btk occupancy TOt is given by eqn (2) (ESI Appendix, eqn (S16)†) where ρ is the rate of target turnover, and ES is the concentration of active Btk at time t calculated based on the kinetic mechanism shown in Fig. 1.
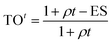 | (2 S16) |
To assess the impact of target turnover on TO, Ramos cells were incubated with 750 nM CC-292 for 1 h to ensure complete Btk engagement and then free drug was removed by washing. TO was then quantified as a function of time following washout (ESI Appendix, Fig. S3 and Table S2†), showing that engagement of Btk by CC-292 had dropped to 30% after 24 h, and enabling ρ to be determined by fitting the data to the TO model that incorporates turnover (eqn (2), Fig. 3). In addition to values for k5 and Kappi (Fig. 1), the ratio of KM/[S] (M = KM/[S]) is also needed to fit the data using eqn (2). The KM value of ATP for Btk has previously been measured (25 µM),23 and assuming the concentration of ATP is 500 µM, which is within the reported intracellular ATP concentration range,25 this gives M of 0.05. Subsequent data fitting (Fig. 3) returned values of M = 0.1 and ρ = 0.079 h−1.
Our PK/PD model integrates dynamic drug concentration into predictions of TO and PD. Consequently, we performed a PK study in Lewis rats to determine the time course of CC-292 concentration following oral doses of 3, 30 and 100 mg kg−1. The time course of plasma drug concentration is shown in Fig. 4a and a traditional one-compartment PK model was used to fit the data giving the PK parameters reported in Table S3 (ESI Appendix†). Btk is found in circulating B lymphocytes,13,14 and thus plasma drug concentration can be used directly for the in vivo TO and PD models (below).
 | ||
| Fig. 4 CC-292 PK and occupancy of Btk in rats. (a) The time course of plasma drug concentration (circles) and the fit to a one-compartment PK model (solid lines) gave the PK parameters reported in Table S3 (ESI Appendix†). (b) Btk target occupancy as a function of time following a single oral 3, 30 or 100 mg kg−1 dose of CC-292. Experimental data are shown as squares and the fit to the model is shown as solid lines. | ||
The values of k5, Kappi, ρ and M obtained from the in vitro cellular experiments were further optimized by evaluating the time-dependent occupancy of Btk by CC-292 in rat lymphocytes following administration of three oral doses (3, 30 and 100 mg kg−1) (ESI Appendix, Fig. S4†). Both the plasma drug concentration and the TO peaked 1–2 h after dosing, indicating rapid permeation of the drug into B lymphocytes and binding to Btk. Subsequently, TO decreased much more slowly compared to plasma drug concentration (Fig. 4a and b). Analysis of the data using the in vivo TO model (eqn (2)) but now using the plasma drug concentration from the PK data as the input for [I] gave the fitted curves shown in Fig. 4b. The input seed values for the parameters required to fit the data to eqn (2) were taken from the in vitro experiments. The parameters were allowed to float during fitting and it was found that Kappi, k5 and M remained essentially constant, whereas ρ changed by 5 fold (Table 1), suggesting that the target synthesis rate is slower in vivo than that observed in cell culture.
| Parameter | Input | Output | Ratio |
|---|---|---|---|
| a R 2 = 0.97. | |||
| K M/[S] (M) | 0.10 | 0.17 | 1.7 |
| k 5 (h−1) | 2.4 | 2.5 | 1.0 |
| K appi (nM) | 40 | 79 | 2.0 |
| ρ (h−1) | 0.079 | 0.013 | 0.2 |
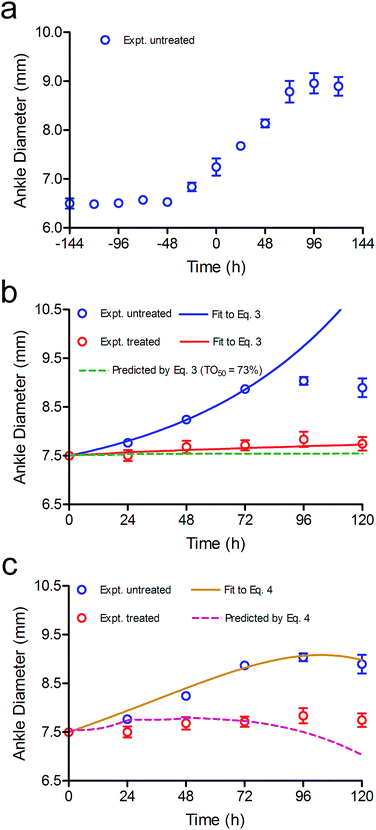
A critical goal of this work is to develop and evaluate a PK/PD model that describes the relationship between dynamic drug concentration at the site of efficacy, target engagement and PD. To achieve this goal, we used a collagen-induced arthritis (CIA) model of RA in rats, which has previously been shown to respond to inhibition of Btk. Progression of disease was quantified by determining ankle diameter (AD) as a function of time. Previously, Liu et al. analyzed the relationship between the inhibition of Btk phosphorylation and the anti-arthritis effect of GDC-0834, a reversible inhibitor of Btk. They reported that 73% inhibition of Btk phosphorylation was required for 50% of the maximum effect and that the relationship between Btk inhibition and efficacy had a Hill coefficient of 24. Assuming that a one-to-one correlation exists between Btk occupancy and the inhibition of phosphorylation, a PK/PD model was developed, shown in eqn (3) (ESI Appendix, eqn (S17)†).
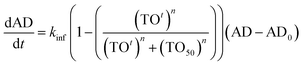 | (3 S17) |
In eqn (3), kinf is the rate constant for the logarithmic increase in AD caused by arthritis, AD0 is the ankle diameter in healthy rats, TOt is the occupancy of Btk as a function of time defined by eqn (2), TO50 is the target occupancy that results in 50 percent of the maximum efficacy and n is Hill coefficient that defines how steeply target occupancy and efficacy are correlated.
Rats typically started to show signs of ankle swelling 10 to 15 days after initiating the disease (4 to 9 days after the second booster injection), in accordance with previous reports.26–31 Progression of the disease was then quantified by determining ankle diameter (AD), which increased in untreated animals for 5 days after which it plateaued and then started to decrease (Fig. 5a).26–31 In our study, the observation of a 2% increase in ankle diameter over a 24 h period was used to define the onset of RA (t = 0). Subsequently, data from the untreated disease group were analysed using the dynamic PD model (eqn (3)) to estimate the intrinsic rate of disease development by constraining TOt to 0 since no drug was administered (Fig. 5b, control), yielding a value for kinf of 0.015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD (h−1).
AD (h−1).
 | ||
| Fig. 5 Modelling CC-292 efficacy in the rat CIA model. (a) Development of RA in the rat CIA model based on ankle diameter. (b) In vivo efficacy of CC-292. The data from untreated animals were fit to eqn (3) (blue line) to determine kinf and eqn (3) was then used to simulate the efficacy of CC-292 (red dots) assuming TO50 and n of 73% and 24 (green dashed line). Subsequently, the experimental data were fit to eqn (3) allowing TO50 and n to vary (red solid line), giving values for TO50 and n of 69% and 7, respectively. (c) The data from untreated animals were fit to eqn (4) (gold line), which includes a feedback loop to model spontaneous remission, and eqn (4) was then used to simulate the efficacy of CC-292 (purple dashed line) using the values of TO50 (69%) and n (7) determined by fitting the data to eqn (3) in (b). | ||
Subsequently, efficacy was simulated using eqn (3) where the concentration of CC-292 at each time point ([I]) was provided by the free fraction of compound determined by the PK analysis. The kinf value of 0.015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD h−1 determined above was used for the simulation together with an AD0 value of 6.8 mm and the values for M, ρ, k5 and Kappi obtained from the in vitro experiments and modified by the analysis of in vivo target occupancy (M = 0.17, ρ = 0.013 h−1, k5 = 2.5 h−1, Kappi = 79 nM; Table 1). Finally, the values for TO50 and n of 73% and 24, respectively reported by Liu et al. were also used in the simulation (Fig. 5b, green dash line).
AD h−1 determined above was used for the simulation together with an AD0 value of 6.8 mm and the values for M, ρ, k5 and Kappi obtained from the in vitro experiments and modified by the analysis of in vivo target occupancy (M = 0.17, ρ = 0.013 h−1, k5 = 2.5 h−1, Kappi = 79 nM; Table 1). Finally, the values for TO50 and n of 73% and 24, respectively reported by Liu et al. were also used in the simulation (Fig. 5b, green dash line).
In Fig. 5b it can be seen that model overestimates the actual efficacy of CC-292 (red dots) using the reported values for TO50 and n (green dashed line). Consequently, we repeated the analysis this time fitting the experimental data to the PD model whilst allowing TO50 and n to float, yielding values for TO50 and n of 69% and 7, respectively (Fig. 5b, red solid line). TO50 and n define the vulnerability function for Btk engagement, and in Fig. 6 we compare the vulnerability function obtained in the present work with that reported by Liu et al. (Fig. 6).23
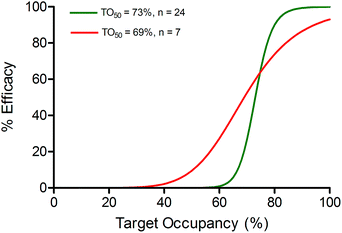 | ||
| Fig. 6 Vulnerability of Btk. Target vulnerability defines the correlation between target occupancy and efficacy. Here a sigmoidal function is assumed which is defined by TO50 and the Hill coefficient n. The vulnerability function based on the values of TO50 (73%) and n (24) determined by Liu et al.23 is shown as a green line. Vulnerability determined from Liu et al. assumes that the level of Btk occupancy and inhibition of Btk phosphorylation are identical. Vulnerability determined by fitting the efficacy data to the PK/PD model eqn (3) is shown as a red line (TO50 of 69% and n of 7). | ||
The increase in ankle diameter of the untreated group is accurately described by the linear function for the first 4 days of CIA. However, ankle diameter plateaued after day 4 due to the spontaneous remission that is characteristic of the rodent CIA model, which differs from human disease by lacking a chronic component.32,33 We were thus curious to explore the contribution of this self-resolution to the modelling of the treated data. A negative feedback loop is often introduced to account for disease remission either as a correction factor for kinf,28,29 or by including a rate constant for self-resolution of the disease (kout) together with a transit function that modulates the magnitude of kout over time.23 We thus re-analysed the data using a modified version of eqn (3) that included kout (eqn (4), ESI Appendix eqn (S23)†).
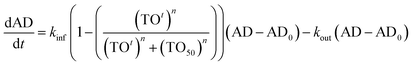 | (4 S23) |
The transit model used to derive eqn (4) requires an input value for kout and we used 0.001 h−2 (R) from Liu et al.23 Fitting of the untreated data to this more complex form of the PD model was able to accurately account for the start of disease remission, with values for kinf of 0.0031 h−1 and a value of 0.012 h−1 for the transit rate constant k (Fig. 5c, gold line). We then used eqn (4) in an attempt to predict the time course of ankle diameter in the treated group. However, this approach grossly overestimated the efficacy of CC-292 (Fig. 5c, purple dashed line) at later time points, indicating that self-resolution played a smaller role in the time course of CIA in treated than untreated animals. This may be because CC-292 treatment reduces the production of anti-inflammatory cytokines that are thought to be involved in the host response to CIA.26,27
To extend our study and further validate our model, the efficacy of two additional doses of CC-292 was predicted by eqn (3). In Fig. 7 we show efficacy data obtained with doses of CC-292 at 3 and 100 mg kg−1 together with simulations of the predicted efficacy generated using the relevant PK data and values for TO50 and n of 69% and 7, respectively. As shown in Fig. 7, the model was able to accurately simulate the experimental efficacy, indicating that the model can reliably predict the efficacy of multiple drug doses.
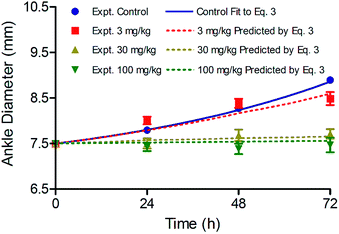 | ||
| Fig. 7 Simulation of CC-292 efficacy at three different doses using eqn (3) and values of 69% and 7 for TO50 and n, respectively, to define vulnerability. | ||
Subsequently, we validated our modelling parameters by calculating TO50 and n separately using experimental PD data and TO values obtained at different doses. Briefly, the TO at 24, 48 and 72 h for each dose was calculated using eqn (2), and plotted against the PD at the same time points for the same doses relative to the PD of 100 mg kg−1 at 72 h (Fig. 8). The data were fit to a Hill equation to calculate TO50 and n. It was found that TO50 was 69% and n was 6.8, which are consistent with the values for these parameters generated by our initial modelling.
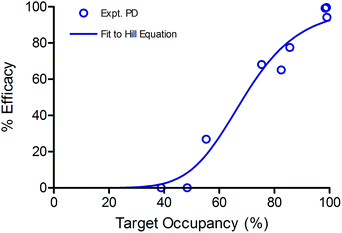 | ||
| Fig. 8 Sigmoidal correlation between Btk occupancy and experimentally observed efficacy. The data were fit to the Hill equation giving values for TO50 = 69% and n = 6.8. | ||
Discussion
The present study highlights some of the key parameters that are involved in the translation of target occupancy to PD. Clearly a quantitative knowledge of this relationship is a critical factor in the initial selection of drug targets, and the subsequent identification and optimization of drug leads to modulate the activity of those targets. Below we discuss the importance of several key parameters including the values for the kinetic and thermodynamic parameters k5 and Ki, the rate of target turnover ρ, the ratio of KM to substrate concentration (KM/[S] = M), and the vulnerability of Btk. Further, we investigated the impact of covalent modification by assuming that the Btk inhibitor binds reversibly to Btk with a residence time of 2, 20 or 100 h, in order to highlight the role that the rate of drug target dissociation can play in translating time-dependent enzyme inhibition to PD.In Fig. 9a and b we have predicted the response to CC-292 therapy after varying k5 and Ki, the rate of target turnover ρ, and the value of M by a factor of 5 in each direction. The corresponding changes to TOt (ESI Appendix, Fig. S5†) demonstrate that an increase in affinity of CC-292 for Btk (0.2 × Ki) or an increase in the rate of formation of the covalent bond with Btk (5 × k5) causes only a slight improvement in the predicted efficacy of CC-292, indicating that CC-292 is highly optimized for Btk modification. In contrast, a 5-fold change in either of these parameters in the opposite direction (5 × Ki or 0.2 × k5) significantly reduces the predicted efficacy due to a dramatic reduction in TOt (ESI Appendix, Fig. S5†), consistent with the observation that sustained, high levels of TO are required for efficacy.
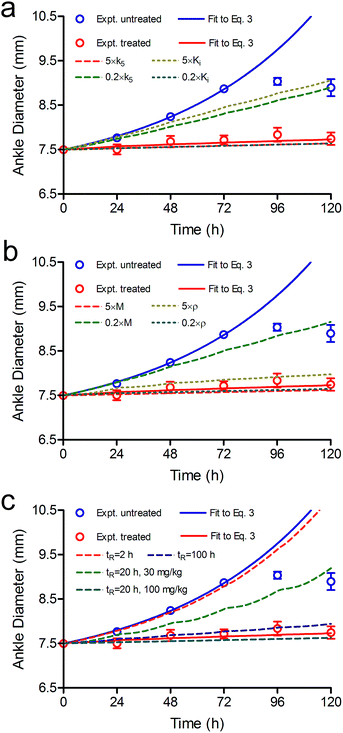 | ||
| Fig. 9 Effect of k5, Ki, ρ, M and tR on the predicted efficacy of CC-292. Experimental data are shown as dots and the solid lines are fits of the experimental data to the PK/PD model (eqn (3)) (blue, untreated; red, treated with CC-292) (Fig. 5). The dashed lines are the simulated efficacy resulting from 5-fold changes in each parameter. This leads to either under or overestimates in the predicted efficacy which is given as % change relative to the red line at day 3. (a) 5 × k5 (red), overestimates efficacy 6%; 0.2 × k5 (green) underestimates efficacy 54%; 5 × Ki (gold) underestimates efficacy 66%; 0.2 × Ki (blue) overestimates efficacy 6%. (b) 5 × M (red) overestimates efficacy 7%; 0.2 × M (green) underestimates efficacy 70%; 5 × ρ (yellow) underestimates efficacy 16%; 0.2 × ρ (green) overestimates efficacy 5%. (c) The dashed lines are simulated efficacy using a reversible inhibitor with tR values of 2 (red), 20 (green), and 100 h (purple). This reduces efficacy by 94, 51 and 9%, respectively. Note that the experimental data were obtained at 37 °C and thus the parameters used for the modelling are also assumed be at 37 °C. Use of parameters determined at RT for modelling could have larger effects: for example, the tR values for inhibitors of Lpxc are 3–9 fold shorter at 37 °C than at RT.10 | ||
The rate of target turnover ρ can also have a significant impact on the coupling between TOt and the duration of the PD effect since the synthesis of new target will alleviate the pharmacological impact of target engagement. By fitting the in vivo TO data to eqn (2) we obtained a value for ρ of 0.013 h−1 (Fig. 4, Table 1), which is in the range of values reported for human proteins (2 × 10−5 h−1 to 5.4 h−1).34 The value of ρ is also similar to that estimated from the effect of cyclohexamide treatment on Btk-drug residence time (0.043 h−1),22 or from the time dependent change in cellular Btk (0.045 and 0.037 h−1).21 To evaluate the sensitivity of the data modelling to the value of ρ, we simulated the efficacy of CC-292 when ρ was fixed at 5× or 0.2× the output value obtained from in vivo TO modelling (Fig. 9b), and observed that a 5-fold increase in ρ underestimates the efficacy of CC-292 by 16% at day 3 whereas a 5-fold decrease in ρ overestimates the efficacy of CC-292 by 5%. In contrast, simulations revealed that while the maximum TO did not change significantly, the occupancy of Btk decreased much more slowly when ρ was reduced (ESI Appendix, Fig. S5†). These observations indicate that protein resynthesis is a key driver in pharmacological outcome, and elevated rates would significantly impact the durability of the pharmacological response.
CC-292 is an ATP-competitive inhibitor, and thus Btk occupancy depends on both the affinity of ATP for Btk and the cellular concentration of ATP which is accounted for in the modelling by including the term M(KM/[S]). Initially we used a value of 0.05 for M(25/500), which increased to 0.1 when we analysed the time-dependent occupancy of Btk in B cells by CC-292, suggesting that either the intracellular concentration of ATP is lower than assumed or the KM value larger. Simulations to explore the dependence of efficacy on M showed that a reduction in the ability of ATP to compete for Btk caused by an increase in M resulted in an increase in the predicted efficacy, whereas a reduction in M had the opposite effect (Fig. 9b). Analysis of the simulated in vivo Btk occupancy showed that while the time-dependent TO did not change dramatically, the maximum TO either decreased or increased at 0.2 × M or 5 × M, respectively, as expected for a competitive inhibitor (ESI Appendix, Fig. S5†).
In addition to the ATP concentration, the intracellular concentration of CC-292 also affects the level of Btk inhibition. When we previously modelled the efficacy of the antibacterial LpxC and FabI inhibitors, we included a permeability factor to account for the difference in drug concentration between the free fraction in plasma and the concentration of drug in the bacteria.10,11 For Btk we can directly estimate the concentration differential between CC-292 in plasma and that in B cells since there is no tissue barrier through which the drug has to permeate. The apparent enzyme–inhibitor dissociation constant, Kappi (Table 1) was determined using the extracellular concentration of CC-292 (eqn (1), Fig. 2). Kappi thus correlates the extracellular concentration of inhibitor to the amount of intracellular enzyme–inhibitor complex. This parameter was used for PK/PD modelling rather than the value of Ki (0.5 nM),21 determined by measuring the binding of CC-292 to purified Btk. By comparing the value of Kappi with that of Ki, we can estimate that the concentration of CC-292 in the Ramos cells is 80-fold (40/0.5) lower than that outside the cells.
CC-292 is an irreversible inhibitor and thus the only way to generate active Btk is through new protein synthesis. However, many drugs, including other inhibitors of Btk, bind reversibly to their targets. In the limiting situation where turnover is 0 and drug rebinding does not occur, then the rate of active Btk formation from inhibited enzyme will be determined by the residence time (tR) of the drug bound to Btk. To estimate the impact of reversible inhibition on Btk drug efficacy, we repeated the PK/PD modelling with a compound that had tR values of 2, 20 and 100 h on Btk. This necessitated the inclusion of a rate constant (k6) for breakdown of the Btk–inhibitor complex (Fig. 1), where TOt in eqn (2) is defined by eqn (S21) (ESI Appendix, eqn (S21)†). Fig. 9c shows that a drug with tR = 2 h provides no therapeutic benefit whereas the 100 h tR compound gives almost the same predicted efficacy as that for CC-292 (ESI Appendix, Fig. S5†).
While there are many factors that contribute to the translation of residence time to PD, it may initially be surprising that replacement of an irreversible inhibitor with one that has a 20 h residence time results in a significant decrease in efficacy. However, target vulnerability plays a critical role, and as we described above fitting the efficacy data to the PK/PD model resulted in TO50 and n values of 69% and 7, respectively, indicating that Btk must be completely engaged by drug to elicit the full pharmacological impact of drug treatment. In addition, once the level of engagement has fallen below 40% then Btk inhibition has no impact on the development of disease. The model predicts that a dose of 100 mg kg−1 would be needed to achieve efficacy comparable to the 30 mg kg−1 dose of CC-292 if a residence time of 20 h is assumed (Fig. 9c, cyan dash line). Since higher drug doses could lead to increased engagement of off-target proteins and thus greater potential for safety issues, this analysis exemplifies the potential benefit of increased residence time for targets that must be continuously suppressed to achieve the desired pharmacological outcome.
Based on our analysis it can be concluded that Btk is a relatively low vulnerability target where high levels of engagement must be maintained to achieve a beneficial therapeutic outcome. On a broader level, these studies demonstrate the potential for mechanistic PD modelling in the prediction of in vivo pharmacological responses. In addition to quantitative predictions of inhibitor efficacy in humans, these models, based largely on in vitro measurements, can be used for the improved design, selection and optimization of covalent inhibitors.
Experimental
Material and methods
Human recombinant His-tagged Btk was purchased from Thermo Fisher Scientific and CC-292 (AVL-292) (98%) was purchased from Ontario Chemicals Incorporated. A covalent fluorescent Btk probe, BDP-CC-292 (Fig. 1), was synthesized from CC-292 (ESI Appendix, Scheme S1†). This method involved the synthesis of an azide intermediate from CC-292 that was subsequently coupled to an alkyne analog of the fluorescent dye BODIPY using click chemistry.Btk occupancy in Ramos cells
Ramos cells (human B lymphocytes, Burkitt's lymphoma) were grown in RPMI-1640 media supplemented with 2 mM glutamine and 10% fetal bovine serum (FBS) at 37 °C in 5% CO2. The cell density was maintained at ∼1 × 106 cells per mL until needed, at which point the cell density was accurately determined using a hemocytometer and the ratio of live cells to dead cells was determined using trypan-blue. Cells were harvested from 300 mL culture by centrifugation and the cell pellets were washed three times with serum-free RPMI-1640 by resuspension and re-centrifugation (15 min, 6000g). Subsequently, the cells were re-suspended in 35 mL serum-free RPMI-1640 containing streptomycin–penicillin (35 mL medium, containing 100 units per mL penicillin and 100 µg mL−1 streptomycin). One mL of new cell culture was used to seed each well of several 12-well plates to give a cell density of 1.3 × 107 cells per mL. CC-292 was dissolved in sterile DMSO and added to each well to give final concentrations of 0.37, 1.46, 5.86, 11.72, 93.75, 750 and 3000 nM, respectively. A vehicle-only control was also included. The cells were incubated for 1 h at 37 °C in 5% CO2, after which 1 mL of cell culture from each well was transferred to 1.5 mL Eppendorf tubes, and cells were collected by centrifugation at 1800g (5 min). The cell pellets were washed twice with 100 mM phosphate buffer by resuspension and re-centrifugation, after which the cell pellets were re-suspended in 60 µL of lysis buffer (CelLytic M, Sigma, C2978) containing 3 µL protease inhibitors (Sigma Cat#P2714). The mixture was vortexed and then kept on ice for 10 min, a process which was repeated 3 times. Subsequently, the cell debris was removed by centrifugation at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g for 45 min and the supernatant was collected after centrifugation and stored at −80 °C prior to analysis.
000g for 45 min and the supernatant was collected after centrifugation and stored at −80 °C prior to analysis.
The occupancy of Btk by CC-292 was quantified using a fluorescent probe derived from CC-292 (BDP-CC-292) (ESI Appendix, Table S1†). BDP-CC-292 was added to cell lysates to give a final concentration of 24 µM, after which the mixtures were incubated at RT for at least 1 h in the dark. Subsequently, 10 µL of denaturing buffer was added and the samples were boiled for 10 min and then subjected to electrophoresis on 4–20% Mini-PROTEAN® TGX™ Precast Protein Gels (Bio-Rad) at 4 °C (85 V, 270 min). The amount of BDP-CC-292 bound to Btk was quantified using a GE Typhoon scanner (excitation: 480 nm laser; absorbance: 520 nm), after which the gel was transferred to a cellulose membrane for western blotting. The cellulose membrane was incubated with Mouse Anti-Human Btk antibody (BD Transduction Laboratories™, Cat#: 611116) and then with a secondary HRP-conjugated F(AB)2-goat anti-mouse IgG antibody (Novex by life technologies, Cat#: A24476). After incubation the HRP substrate was added and total Btk was quantified using the GE typhoon scanner (ImageQuant software). Several concentrations of pure recombinant human Btk incubated with BDP-CC-292 were included on each gel to generate standard curves. All experiments were performed in at least triplicate.
Btk turnover in Ramos cells
Ramos cells were prepared in 12 well plates as described above. Subsequently CC-292 was added to each well to give a final concentration of 750 nM to ensure complete target engagement. The cells were incubated for 1 h at 37 °C in 5% CO2. Subsequently, 1 mL from each well was transferred into 1.5 mL Eppendorf tubes, and cells were collected by centrifugation at 1800g for 5 min. The cell pellets were washed with serum-free RPMI two times by resuspension and re-centrifugation, and cell pellets were then collected and re-suspended in 10 mL serum-free RPMI. The cells were incubated at 37 °C in 5% CO2 for 2, 18 or 24 h, after which the cells were collected by centrifugation and lysed and quantified for CC-292:BTK-occupancy as described above (ESI Appendix, Table S2†). All experiments were performed in triplicate.Pharmacokinetics (PK) of CC-292 in rats
All experiments involving live animals were performed in compliance with the relevant laws and institutional guidelines. The experimental protocol for both the PK studies and the pharmacodynamics studies (below) was approved by the Institutional Animal Care and Use Committee (IACUC) at Stony Brook University.The PK of CC-292 was determined using 6 to 8 week old female Lewis rats (Charles River Laboratory). Three rats were dosed by oral gavage with 3, 30 and 100 mg kg−1 CC-292 suspended in 1 mL 2% CMC saline solution. Blood samples were collected at 0.25, 0.5, 1, 2, 4, 6, 8 and 24 h post dosing by retro orbital bleeding. A pre-dose blood collection was performed 1 day before drug dosing. Plasma proteins were precipitated by the addition of acetonitrile and drug concentration in the supernatant was quantified by LC-MS/MS. The pharmacokinetic profile was analyzed using a single-compartment model using WinNonlin (Pharsight Corporation, Mountain View, CA, USA) (ESI Appendix, Table S3†).
Btk occupancy and turnover in rats
Six to 8 week old female Lewis rats (Charles River Laboratory) were used for the in vivo target occupancy and turnover experiments. The rats were dosed via oral gavage with 3, 30 or 100 mg kg−1 CC-292 (6 mg per rat) suspended in 1 mL 2% CMC saline solution. After 2, 4, 8, 18 and 24 h, animals (n = 3) were euthanized by CO2 inhalation and blood samples (3–4 mL) were obtained by cardiac puncture and placed in a heparin-coated tube. A target occupancy analysis control group (n = 3) was euthanized prior to drug administration.Lymphocytes were isolated from the whole blood using Ficoll-Paque PLUS (GE Healthcare). Briefly, 2 mL blood was mixed with 2 mL pre-made balanced salt buffer in a 15 mL Falcon tube. Then 2 mL Ficoll-Paque PLUS was layered carefully on the top of the mixture without disturbing it. The mixture was centrifuged at 400g for 40 min at 20 °C, resulting in the formation of four layers in the tube. The top layer (plasma) was discarded, and the second layer containing the lymphocytes was re-suspended in 3 mL pre-made balanced salt buffer in a second 15 mL Falcon tube. The new mixture was centrifuged at 100g for 10 min, and the resulting pellets were re-suspended in 1 mL balanced salt buffer and transferred to a 1.5 mL Eppendorf tube. Cells were collected by centrifugation (1800g, 5 min) and re-suspended in 60 µL of lysis buffer (CelLytic M, Sigma, C2978) containing 3 µL protease inhibitors. The mixture was vortexed and then placed on ice for 10 min. Vortexing and incubation on ice was repeated three times after which the cell debris was removed by centrifugation at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g for 45 min. The resulting supernatant was used immediately for quantitative target occupancy analysis as described above. The target occupancy was quantified by calculating the percentage of fluorescent-labeled Btk from the drug treated sample relative to the control sample after the fluorescence signal was normalized by western blot.
000g for 45 min. The resulting supernatant was used immediately for quantitative target occupancy analysis as described above. The target occupancy was quantified by calculating the percentage of fluorescent-labeled Btk from the drug treated sample relative to the control sample after the fluorescence signal was normalized by western blot.
Total protein quantification
Total protein was quantified using a Pierce BCA assay kit (Thermo Scientific). A sample of cell lysate (20 µL) was combined with 80 µL of lysis buffer in a 15 mL Falcon tube and then 2.0 mL of premixed working buffer was added to each tube. The absorbance at 562 nm, obtained after incubating the samples at 37 °C for 30 min, was used to calculate total protein based on a bovine serum albumin standard curve.Efficacy of CC-292 in a CIA rat model
A Collagen Induced Arthritis (CIA) model was used to assess the efficacy of CC-292 towards RA.27,29,35,36 Briefly, an emulsion of Incomplete Freund's Adjuvant and Bovine Type II Collagen (Chondrex Inc.) (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture) was prepared by homogenization. The emulsion was injected into 6 to 8 week female Lewis rats to induce RA. Two doses of the emulsion were injected twice at day 0 and day 6. The injection sites included the base of the tail (subcutaneous injection, 0.20 mL of the emulsion) and two sites on the back (subcutaneous injection, 0.15 mL each side), and ankle diameters were subsequently monitored using a caliper. Ankle diameter was measured every 2nd day up to day 6, and then daily, and body weight was recorded after each ankle diameter measurement.
1 mixture) was prepared by homogenization. The emulsion was injected into 6 to 8 week female Lewis rats to induce RA. Two doses of the emulsion were injected twice at day 0 and day 6. The injection sites included the base of the tail (subcutaneous injection, 0.20 mL of the emulsion) and two sites on the back (subcutaneous injection, 0.15 mL each side), and ankle diameters were subsequently monitored using a caliper. Ankle diameter was measured every 2nd day up to day 6, and then daily, and body weight was recorded after each ankle diameter measurement.
Typically, rats started to show signs of ankle swelling and redness around day 11. Animals were placed into treatment groups after observing either a continuous 2% increase in ankle diameter over 2 days or a greater than 10% increase in ankle diameter in a single day. In the treatment groups, rats were dosed with either 3, 30 or 100 mg kg−1 CC-292 suspended in 1 mL 2% CMC saline solution by oral gavage each day for 5 days. In the control group rats were dosed with 1 mL 2% CMC saline solution at the same frequency. The time of initial administration of CC-292 or vehicle was defined as time 0 for the study and the ankle diameter of each rat was monitored daily at the same time for 5 days.
Modeling target occupancy and efficacy
The full derivation of the equations used for calculating target occupancy are given in the ESI.† The PK/PD model eqn (3) (ESI Appendix, eqn (S17)†) predicts efficacy by calculating the occupancy of CC-292 as a function of time based on the plasma drug concentration (free fraction) determined from the PK studies. Calculation of target occupancy requires the kinetic parameters Ki and k5, an estimate of the ability of CC-292 to compete for Btk with ATP (M = KM/[S]), the rate of Btk turnover (ρ), and the vulnerability of Btk (TO50 and n). Initially the occupancy of Btk was directly measured under equilibrium conditions using the fluorescent probe. Fitting of the occupancy data to eqn (1) (ESI Appendix, eqn (S3)†) in MATLAB yielded values of k5 and Kappi, where the latter is the extracellular Ki enabling the plasma concentration of CC-292 to be directly related to Btk occupancy. Subsequent global fitting of the in vivo Btk occupancy data to eqn (2) (ESI Appendix, eqn (S16)†) in MATLAB yielded values of ρ and M together with optimized values for k5 and Kappi. Values for k5, Kappi, ρ and M where then used to predict efficacy based on the plasma drug concentration with the eqn (3) (ESI Appendix, eqn (S17)†) in Mathematica.Conflict of interest
The authors declare no competing financial interest.Acknowledgements
This research was funded by NIH/NIGMS (PJT GM102864).Notes and references
- H. Lu and P. J. Tonge, Curr. Opin. Chem. Biol., 2010, 14, 467–474 CrossRef CAS PubMed.
- R. A. Copeland, D. L. Pompliano and T. D. Meek, Nat. Rev. Drug Discovery, 2006, 5, 730–739 CrossRef CAS PubMed.
- D. C. Swinney, Pharm. Med., 2008, 22, 23–34 CrossRef.
- R. A. Copeland, Nat. Rev. Drug Discovery, 2016, 15, 87–95 CrossRef CAS PubMed.
- D. C. Swinney, Curr. Top. Med. Chem., 2006, 6, 461–478 CrossRef CAS PubMed.
- P. J. Tummino and R. A. Copeland, Biochemistry, 2008, 47, 8465 CrossRef CAS.
- D. C. Swinney, Curr. Opin. Drug Discovery Dev., 2009, 12, 31–39 CAS.
- R. Zhang and F. Monsma, Curr. Opin. Drug Discovery Dev., 2009, 12, 488–496 CAS.
- R. A. Copeland, Nat. Chem. Biol., 2015, 11, 451–452 CrossRef CAS PubMed.
- G. K. Walkup, Z. You, P. L. Ross, E. K. Allen, F. Daryaee, M. R. Hale, J. O'Donnell, D. E. Ehmann, V. J. Schuck, E. T. Buurman, A. L. Choy, L. Hajec, K. Murphy-Benenato, V. Marone, S. A. Patey, L. A. Grosser, M. Johnstone, S. G. Walker, P. J. Tonge and S. L. Fisher, Nat. Chem. Biol., 2015, 11, 416–423 CrossRef CAS PubMed.
- F. Daryaee, A. Chang, J. Schiebel, Y. Lu, Z. Zhang, K. Kapilashrami, S. G. Walker, C. Kisker, C. A. Sotriffer, S. L. Fisher and P. J. Tonge, Chem. Sci., 2016, 7, 5945–5954 RSC.
- J. A. Di Paolo, T. Huang, M. Balazs, J. Barbosa, K. H. Barck, B. J. Bravo, R. A. Carano, J. Darrow, D. R. Davies, L. E. DeForge, L. Diehl, R. Ferrando, S. L. Gallion, A. M. Giannetti, P. Gribling, V. Hurez, S. G. Hymowitz, R. Jones, J. E. Kropf, W. P. Lee, P. M. Maciejewski, S. A. Mitchell, H. Rong, B. L. Staker, J. A. Whitney, S. Yeh, W. B. Young, C. Yu, J. Zhang, K. Reif and K. S. Currie, Nat. Chem. Biol., 2011, 7, 41–50 CrossRef CAS PubMed.
- W. N. Khan, Immunol. Res., 2001, 23, 147–156 CrossRef CAS PubMed.
- A. J. Mohamed, L. Yu, C. M. Backesjo, L. Vargas, R. Faryal, A. Aints, B. Christensson, A. Berglof, M. Vihinen, B. F. Nore and C. I. Smith, Immunol. Rev., 2009, 228, 58–73 CrossRef CAS PubMed.
- L. Martinez-Gamboa, H.-P. Brezinschek, G. R. Burmester and T. Dörner, Autoimmun. Rev., 2006, 5, 437–442 CrossRef CAS PubMed.
- P. J. Mease, J. Rheumatol., 2008, 35, 1245–1255 CAS.
- G. J. Silverman and D. A. Carson, Arthritis Res. Ther., 2003, 5(suppl. 4), S1–S6 Search PubMed.
- F. A. Cooles and J. D. Isaacs, Curr. Opin. Rheumatol., 2011, 23, 233–240 CrossRef CAS PubMed.
- J. A. Whang and B. Y. Chang, Drug Discovery Today, 2014, 19, 1200–1204 CrossRef CAS PubMed.
- L. A. Honigberg, A. M. Smith, M. Sirisawad, E. Verner, D. Loury, B. Chang, S. Li, Z. Pan, D. H. Thamm, R. A. Miller and J. J. Buggy, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13075–13080 CrossRef CAS PubMed.
- E. K. Evans, R. Tester, S. Aslanian, R. Karp, M. Sheets, M. T. Labenski, S. R. Witowski, H. Lounsbury, P. Chaturvedi, H. Mazdiyasni, Z. Zhu, M. Nacht, M. I. Freed, R. C. Petter, A. Dubrovskiy, J. Singh and W. F. Westlin, J. Pharmacol. Exp. Ther., 2013, 346, 219–228 CrossRef CAS PubMed.
- J. M. Bradshaw, J. M. McFarland, V. O. Paavilainen, A. Bisconte, D. Tam, V. T. Phan, S. Romanov, D. Finkle, J. Shu, V. Patel, T. Ton, X. Li, D. G. Loughhead, P. A. Nunn, D. E. Karr, M. E. Gerritsen, J. O. Funk, T. D. Owens, E. Verner, K. A. Brameld, R. J. Hill, D. M. Goldstein and J. Taunton, Nat. Chem. Biol., 2015, 11, 525–531 CrossRef CAS PubMed.
- L. Liu, J. Di Paolo, J. Barbosa, H. Rong, K. Reif and H. Wong, J. Pharmacol. Exp. Ther., 2011, 338, 154–163 CrossRef CAS PubMed.
- R. A. Copeland, Evaluation of enzyme inhibitors in drug discovery: a guide for medicinal chemists and pharmacologists, Wiley, Hoboken, N.J., 2nd edn, 2013 Search PubMed.
- H. Huang, X. Zhang, S. Li, N. Liu, W. Lian, E. McDowell, P. Zhou, C. Zhao, H. Guo, C. Zhang, C. Yang, G. Wen, X. Dong, L. Lu, N. Ma, W. Dong, Q. P. Dou, X. Wang and J. Liu, Cell Res., 2010, 20, 1372–1385 CrossRef CAS PubMed.
- L. Marinova-Mutafchieva, C. Gabay, K. Funa and R. O. Williams, Clin. Exp. Immunol., 2006, 146, 287–293 CrossRef CAS PubMed.
- J. C. Earp, D. C. Dubois, D. S. Molano, N. A. Pyszczynski, C. E. Keller, R. R. Almon and W. J. Jusko, J. Pharmacol. Exp. Ther., 2008, 326, 532–545 CrossRef CAS PubMed.
- J. C. Earp, D. C. Dubois, R. R. Almon and W. J. Jusko, Pharm. Res., 2009, 26, 196–203 CrossRef CAS PubMed.
- H. K. Lon, D. Liu, D. C. DuBois, R. R. Almon and W. J. Jusko, J. Pharmacokinet. Pharmacodyn., 2013, 40, 701–712 CrossRef CAS PubMed.
- Y. Wang, S. Wang, Y. Li, J. Jiang, C. Zhou, C. Li, D. Li, L. Lu, P. Liu, M. Huang and X. Shen, Transl. Res., 2015, 165, 704–716 CrossRef CAS PubMed.
- Q. Liu, J. Zhao, R. Tan, H. Zhou, Z. Lin, M. Zheng, E. Romas, J. Xu and N. A. Sims, Scand. J. Rheumatol., 2015, 44, 182–191 CrossRef CAS PubMed.
- L. Bevaart, M. J. Vervoordeldonk and P. P. Tak, Arthritis Rheum., 2010, 62, 2192–2205 CrossRef CAS PubMed.
- A. Karatas, S. S. Koca, M. Ozgen, A. F. Dagli, F. Erman, N. Sahin, K. Sahin and A. Isik, Inflammation, 2015, 38, 9–15 CrossRef CAS PubMed.
- M. K. Doherty, D. E. Hammond, M. J. Clague, S. J. Gaskell and R. J. Beynon, J. Proteome Res., 2009, 8, 104–112 CrossRef CAS PubMed.
- J. C. Earp, D. C. Dubois, D. S. Molano, N. A. Pyszczynski, R. R. Almon and W. J. Jusko, J. Pharmacol. Exp. Ther., 2008, 326, 546–554 CrossRef CAS PubMed.
- Y. A. Levine, F. A. Koopman, M. Faltys, A. Caravaca, A. Bendele, R. Zitnik, M. J. Vervoordeldonk and P. P. Tak, PLoS One, 2014, 9, e104530 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Derivation of PK/PD models, supplemental methods, analytical data. See DOI: 10.1039/c6sc03306g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |