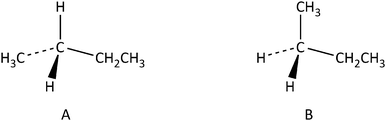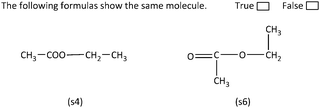Changes in visual/spatial and analytic strategy use in organic chemistry with the development of expertise

Abstract

We present two studies that investigated the adoption of visual/spatial and analytic strategies by individuals at different levels of expertise in the area of organic chemistry, using the Visual Analytic Chemistry Task (VACT). The VACT allows the direct detection of analytic strategy use without drawing inferences about underlying mental processes. The first study examined the psychometric properties of the VACT and revealed a structure consistent with the hypothesis that it consists of two sub-scales: visual/spatial and analytic. The second study investigated the performance of 285 participants with various levels of expertise in organic chemistry on the VACT. The results showed that the adoption of analytic strategies in organic chemistry, and specifically in molecular structure, was difficult and was systematically used only by the more expert participants. The implications of this research for the teaching of chemistry are discussed.

---

Introduction

In recent years we have seen an explosion of research on spatial reasoning and its relation to success in STEM disciplines in general and chemistry in particular. Compared to students with low spatial skills, students with high spatial skills have consistently been found more likely to demonstrate better performance in STEM disciplines (Mathewson, 1999; Wai et al., 2009; Newcombe and Frick, 2010; Uttal et al., 2013; Hegarty, 2014) including chemistry (Bodner and McMillen, 1986; Carter et al., 1987; Pribyl and Bodner, 1987; Harle and Towns, 2011). These findings have led to the development of many training studies in spatial reasoning (Harle and Towns, 2011; Merhant et al., 2012; Stull et al., 2012, 2016; Newcombe, 2013; Al-Balushi and Al-Hajri, 2014; Cohen and Hegarty, 2014; Carlisle et al., 2015; Kornkasem and Black, 2015; Stieff and Uttal, 2015; Barrett and Hegarty, 2016; Salah and Alain, 2016; Stieff et al., 2016; Stull and Hegarty, 2016).

Undeniably, chemistry is a discipline that demands the use of spatial reasoning in order for individuals to be able to represent three dimensional objects from their two dimensional appearance, to imagine how an object will appear from different perspectives, to visualize the effects of operations such as rotation, reflection, and inversion, to mentally manipulate objects, and to apprehend and identify a visual pattern in the presence of distracting stimuli (Barnea and Dori, 1999; Wu and Shah, 2004). However, in addition to visual/spatial strategies, the application of analytic strategies is also of great importance for successful scientific problem solving in chemistry particularly as expertise in chemistry develops (Stieff, 2007).

Analytic strategies make it possible to lower the cognitive load of visual/spatial thinking by applying rules and heuristics on spatial information extracted from a diagram or a verbal statement (Hegarty et al., 2013). For example, an individual who applies a visual/spatial strategy in order to decide whether the two representations of butane, A and B, (Fig. 1) depict the same molecule or two enantiomers, can rotate representation A and check whether it can be superimposed on to representation B. An individual who applies an analytic strategy, on the other hand, can solve the same problem without mental rotation by following the rule “if a molecule has two identical substitutes, it cannot have an enantiomer”. Since the two representations in Fig. 1, have two identical substitutes (–H), we can immediately deduce that they cannot be enantiomers. By employing this analytic rule, problems such as the above can be solved more efficiently and precisely.

Fig. 1 3D representations of butane.

The use of visual and analytic strategies has often been approached in the literature from an individual difference point of view. Several studies investigate the relation between strategy choice and spatial ability or gender and on how strategy choice is influenced by instruction, (Stieff et al., 2010a, 2010b, 2012, 2014; Hegarty et al., 2013; Stieff, 2013). However, the use of visual and analytic strategies is also critically related to the development of domain expertise. Experts are much more likely than novices to use analytic strategies in chemistry (Stieff, 2007; Hegarty et al., 2013). In a study conducted in a large research university, Stieff (2007) showed that undergraduate students, enrolled in the sixth week of instruction in organic chemistry, were more likely than expert chemical scientists, who were employed as university professors, to use visual/spatial strategies and mental rotation to solve stereochemistry tasks despite the fact that they had received instruction from texts and lectures recommending the use of an analytic strategy. Students switched from mental rotation to the analytic strategy only after direct instruction. On the contrary, the analytic strategy was consistently used by the expert chemists.

Another difference between novices and experts is that unlike novices, experts are more likely to exhibit flexible strategy use when solving problems. For example, Stieff and Raje (2008) investigated the problem solving strategies employed by ten faculty members at primarily research universities in the mid-Atlantic region of the United States. They showed that expert organic chemists employed a range of imagistic and analytic strategies for solving undergraduate organic chemistry assessment tasks although they preferred, on average, to use analytic strategies. Stieff and Raje (2010) extended their research in a study that documents how science experts use both algorithms and imagistic reasoning to solve problems. The experts employed algorithms to solve the majority of spatial tasks, reserving imagistic strategies to solve only a class of tasks that required translation between representations. The strategies applied varied widely depending on experts and tasks. On the contrary, university students enrolled in a two-semester organic chemistry course at a research university in the United States relied on one primary strategy alone for solving in-class examination tasks, while, like the experts, employed spatial reasoning almost exclusively in order to translate between representations (Stieff, 2011).

The above suggest that there is a shift in the application of visual vs. analytic strategies in organic chemistry with the acquisition of expertise. This strategy shift is found in other domains of science and in mathematics, and we would like to suggest that it is the result of considerable conceptual changes that need to happen as individuals progress in their learning of science and mathematics (Vosniadou and Skopeliti, 2014). With the acquisition of expertise, problem solving increasingly relies on specialized, domain-specific, rule-based, analytic approaches compared to visual, perceptual information and mental rotation. For example, in geometry, reliance on visuo/spatial strategies is characteristic only of early levels of geometrical knowledge. As geometry expertise develops, individuals must increasingly rely on formal analytic strategies and geometrical thinking is increasingly characterized by the formal manipulation of the logical systems that geometry represents (Kospentaris et al., 2016).

The issues regarding the relationship between analytic strategy use and chemistry expertise are important both theoretically and in terms of their implications for instruction and require further investigation. Is there indeed a systematic shift in the use of analytic strategies in chemistry with the acquisition of expertise? How does this take place? What is the relationship between spatial reasoning and the development of analytic thinking? Do visual strategies continue to exist after analytic procedures have been developed? The answers to these questions can have important implications for learning and instruction in chemistry. If experts use predominately analytic strategies why do we have to train individuals in spatial reasoning in order to improve their success in chemistry? What is the best way to develop expertise in chemistry?

The purpose of the present research is to start by trying to answer the first question, namely to investigate if there is a shift in the use of visual vs. analytic strategies with the acquisition of expertise, using a Visual/Analytic Chemistry Task (VACT) specifically developed for this purpose.‡

A variety of methods and tasks have been used to study strategy use in chemistry so far. Stieff (2007) has developed two tasks based on a canonical psychometric approach that permits the detection of the use of mental rotation when examining three-dimensional objects. According to this approach, individuals have to characterize objects in a pair as identical or mirror images. Between the objects of each pair there is an angular disparity, which increases from pair to pair. A positive linear relationship between the response time and the angular disparity between the objects indicates that mental rotation is used for making similarity judgments. Stieff (2007) has applied this approach in the development of the tasks containing object pairs of either three-dimensional block shapes or dash-wedge molecular formulas. He hypothesized that the absence of a positive linear relationship between angular disparity and response time would suggest the use of an analytic strategy. Because this approach cannot directly detect the use of analytic strategies, Stieff asked participants, additionally, to complete a written retrospective self-report in order to confirm the above hypothesis.

Think aloud protocols have also been used as a method to identify problem solving strategies adopted by students and experts (Stieff and Raje, 2008, 2010; Stieff, 2011). Stieff and Raje (2010) based on prior research by Lean and Clements (1981) developed an instrument which contained organic chemistry problems and lists of strategies applicable to each problem. This instrument was used to assess students' strategies in many studies in chemistry by asking students to solve the chemistry problems and indicate the strategy they used from the lists of strategy descriptions. If the methods that the students had used were not listed, students were instructed to describe their strategies in writing, giving as many details as possible (Stieff et al., 2010b, 2012, 2014; Hegarty et al., 2013).

Although these methodologies allow us to make some inferences about the kind of strategies individuals use during problem solving, they also have limitations. Stieff's methods to detect mental rotation cannot directly assess the use of analytic strategies requiring additional retrospective self-reports that are time consuming and unreliable (Stieff, 2007). With respect to the use of think aloud protocols, their application involves risks concerning data validity and has limitations such as the requirement of time and resources. Moreover, in many cases, individuals may not be capable of accurately verbalizing their thoughts or may not be conscious of internal cognitive processes many of which happen automatically (Chiu and Shu, 2010). Concerning the method that uses strategy-lists in chemistry, Stieff and co-workers (2014) have argued that it might be unreliable and that it has to be used in addition to more objective measures. Another limitation of existing materials is that they deal only with concepts from the areas of stereochemistry, stereoselectivity and regiochemistry and cannot be applied to assess strategy use in students who have been taught only introductory organic chemistry and only two-dimensional molecular structures of organic compounds.

The purpose of creating the Visual Analytic Chemistry Task (VACT) used in the present research was to avoid some of the above mentioned limitations. The VACT is different from existing tasks used to assess strategy use in chemistry in a number of ways: As a paper and pencil test the VACT can be completed in short period of time (about 30 min). Its content makes it appropriate for application to a wide range of participants, from novice students to expert chemists. Most importantly, however, the VACT is designed to directly investigate individuals’ use of visual/spatial and/or analytic strategies without trying to make inferences about underlying internal reasoning processes. Rather, in order to detect strategy use, the VACT contains items that can be solved correctly applying either visual/spatial or analytic strategies and items that require for their correct solution the application of analytic strategies and where the adoption of a visual strategy would lead in error. Thus, the VACT enables us to capture the possible changes in the use of strategies, and in particular the use of analytic strategies, with the acquisition of expertise.

In the present paper we will describe two studies. In the first study we examined the construct validity and reliability of the VACT, and tested the hypothesis that the items that require the application of analytic strategies will be more difficult to be solved compared to the items that can be solved with visual/spatial strategies alone. The second study used the VACT to investigate strategy change in individuals with different levels of expertise in organic chemistry. So far, existing research has revealed differences between novices and experts with reference to the kind of strategies they use during chemistry problem solving. With the second study we attempted to investigate strategy use while acquiring expertise by examining individuals of different levels of expertise in organic chemistry. Summing it up, the two studies presented bellow attempted to answer the following research questions:

(1) Does VACT consist of two distinct sub-scales, visual/spatial and analytic, in accordance to its design? (Study 1)

(2) Does the novices' performance differ on items of the VACT that can be solved correctly by applying visual/spatial strategies, and on items that require the application of analytic strategies for their correct solution? (Study 1)

(3) Do individuals of different levels of expertise in the area of organic chemistry differ in their performance on items of the VACT that can be solved correctly by applying visual/spatial strategies and on items that require for their correct solution the application of analytic strategies? (Study 2)

Study 1

The purpose of study 1 was to investigate the construct validity and reliability of the VACT. Based on the design of the VACT, we expected that it would consist of two distinct sub-scales: sub-scale I would contain the items that can be solved correctly applying visual/spatial strategies, and sub-scale II would contain the items that require for their correct solution the application of analytic strategies. The purpose of study 1 was also to examine the hypothesis that students who were novices in chemistry would find the items that can be solved with the use of visual/spatial strategies easier than the items that require for their correct solution the reliance on analytic strategies.

Method

Participants. There were three groups of participants. The first two groups were used to validate the VACT. The third group was used to test the hypothesis that the items in sub-scale I (visual/spatial strategies) would be easier than the items in sub-scale II (analytic strategies) for students, novices in chemistry. The first group consisted of six chemistry teachers who had a basic degree in chemistry and taught chemistry to 11th grade students in Greek schools. Their experience ranged from 9 to 22 years of teaching. The second group consisted of 34 11th grade Greek students attending their fifth month of instruction in organic chemistry on a twice-weekly basis and who had attended introductory chemistry classes during the three previous years. The third group of participants consisted of 132 (63 males and 69 females) 11th grade students (age range = 16.50–18.55, mean = 17.05, SD = 0.34) who were in their fifth month of instruction in organic chemistry (twice a-week, two teaching hours in total). These students had attended introductory chemistry classes during the three previous years.

Materials. The VACT is a paper and pencil task in which the participants must decide whether two structural formulas represent the same molecule or not. It consists of 20 items (see examples in Table 1) equally divided into two sub-scales, I and II. The first sub-scale consists of items that can be solved correctly using visual/spatial strategies but their solution is consistent with the use of analytic strategies also.

Table 1 Sample items from the Visual Analytic Chemistry Task

Item's Category		Item's example
Sub-scale I Consistent: appearance corresponds to reality	A Appear +/Real +
	B Appear −/Real −
Sub-scale II Inconsistent: appearance does not correspond to reality	C Appear +/Real −
	D Appear −/Real +

---

The first 5 items of sub-scale I belong to Category A, “Appearance +/Reality +” where the two given formulas both appear to be and are indeed representations of the same molecule (Table 1, Category A sample item). The remaining 5 items belong to Category B, “Appearance −/Reality −” where in each item the two given formulas neither appear to be nor are representations of the same molecule (Table 1, category B sample item). Sub-scale I will be referred to as the “Consistent” sub-scale of the VACT, since the solution of these 10 items is consistent with the solution imposed by their visual appearance.

Sub-scale II shall be referred to as the “Inconsistent” sub-scale of the VACT, because it includes items the solution of which is inconsistent with the use of visual/spatial strategies alone and require reliance on chemical knowledge and the adoption of analytic strategies. Five of the items of sub-scale II belong to Category C, “Appearance +/Reality −”, where in each item the two given formulas appear to be but are not representations of the same molecule (Table 1, category C sample item). The rest 5 items belong to category D, “Appearance −/Reality +”, where in each item the two given formulas, although they do not seem to represent the same molecule, they actually do (Table 1, Category D sample item). These two Categories of items in the VACT Inconsistent sub-scale can be used to investigate individuals' ability to use analytic strategies. Furthermore, these items investigate individuals' ability to apply analytic strategies in counter-intuitive situations in which the response strongly suggested by visual inspection is incorrect. This applies particularly to the solution of items in Category C, where the use of visual/spatial strategy is likely to lead to error.

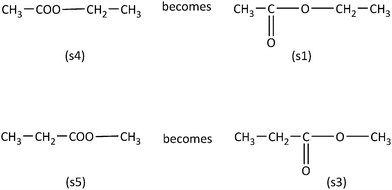
In the case of the Consistent items (sub-scale I, Table 1) the conclusion that the two chemical formulas are identical (Category A sample item) or not (Category B sample item) can derived through the use of visual/spatial strategies alone (Fig. 2). For example, with respect to Category A sample item, if an individual flips the molecule (s1) horizontally will see that the arisen molecule (s2) is tantamount to (s1). In the case of Category B sample item, even if a number of different orientations of molecule (s3) are examined, none of the arisen molecules will be equivalent to molecule (s1).

Fig. 2 Solution of Category B sample item by the application of a visual/spatial strategy.

Category A and B sample items can also be solved by using analytic strategies based on chemical knowledge. For example, if the molecule chains (s1) and (s2) are numbered according to IUPAC rules, could easily note that every carbon in the chain of molecule (s1) is identical with the equivalent carbon of molecule's (s2) chain (Fig. 3).

Fig. 3 Solution of Category A sample item by the application of an analytic strategy.

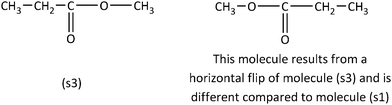
However, in the case of the Category B sample item in Fig. 4, we observe that the carbonyl carbon of the ester group occupies the second position of the (s1) molecule chain, while in the (s3) the carbonyl carbon occupies the third position.

Fig. 4 Solution of Category B sample item by the application of an analytic strategy.

In the case of the Inconsistent items, usage of analytic strategies is required, as the application of visual/spatial strategies will lead to an erroneous response. With respect to Category C sample item, the expanded structural formulas for the condensed structural formulas (s4) and (s5) must be drawn. To do this, the problem solver needs to know the expanded formula of the ester group (Fig. 5). Subsequently, the dissimilarity of the arisen molecules (s1) and (s3) can be concluded by the application of a visual or an analytic strategy (as in the former examples in Fig. 2 and 4), suggesting that the molecules (s4) and (s5) are different.

Fig. 5 Solution of Category C sample item by the application of an analytic strategy.

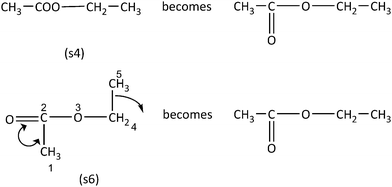
Regarding Category D sample item, the analytic strategy can take place in two stages. First, expansion of the condensed formula (s4) is required, followed by rearrangement of the carbon chain, in order to form a straight chain. In particular, expansion of molecule's (s4) ester group is needed, while in the second stage rearrangement of the atoms in (s6) is required (Fig. 6). As shown the arisen molecules are identical, suggesting that the structural formulas (s4) and (s6) represent the same molecule.

Fig. 6 Solution of Category D sample item by the application of an analytic strategy.

The VACT was constructed by a team of researchers consisting of four experts in chemistry and in chemistry education and three experts in cognitive psychology. In order to validate the content of the VACT, a single version of this task containing the items in a randomized order was administered to the first two groups of participants mentioned earlier: the group of 6 experienced chemistry teachers, and the group of 34 11th grade Greek students. Both groups received the VACT as a paper and pencil test and were interviewed while solving it. They were asked to examine the degree of difficulty of the various questions, the suitability of the items with regard to our purposes, to report any possible misunderstandings due to the way the questions were phrased, and to comment on whether questions were clearly phrased. The comments of the two groups of participants were taken into consideration and resulted in the rephrasing of some of the items of the VACT.

Two versions of the revised VACT were created, each containing the same 20 items in a different randomized order to eliminate any possible carry-over effect.

Procedure. The VACT was tested using the third group of participants (132 11th grade students). Testing took place in the students' school (a public urban area high school). The head teacher of the school and the teachers' association were informed about the goals and the procedure of the research and approved its conduct and the use of the resulting data for our study. The students and their parents were also informed about the goals of the present study and parents gave their consent to use students' responses. The students participated in the research with a code name in order to ensure their anonymity (Taber, 2014). Each student received one of the two versions of the task from the chemistry teacher in the classroom during chemistry class. The participants were told that the task referred to the similarity between two structural formulas. They were asked to judge whether the two structural formulas of each item of the VACT represented the same molecule or not. Students were also instructed to use whichever method they believed appropriate in order to solve the items accurately. Testing lasted 30 minutes.

Results and discussion

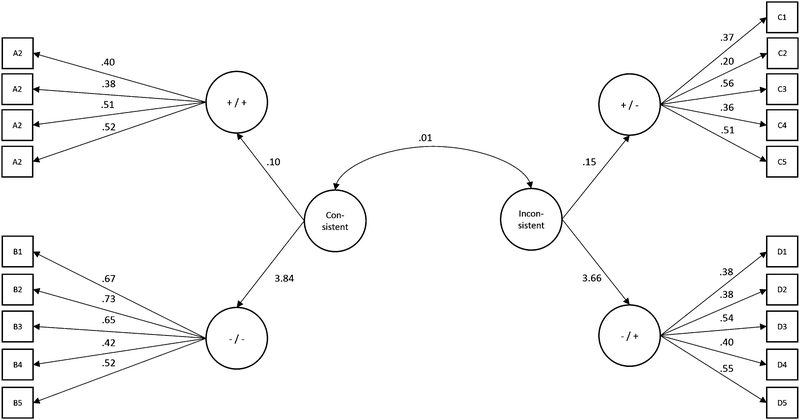
In order to test the construct validity of the VACT, a Confirmatory Factor Analysis was applied on the data: one factor standing for each Category (A, B, C, and D) was regressed on mean performance on the corresponding items. A second-order factor, standing for the Consistent sub-scale, was regressed on factors A and B, and another second-order factor, standing for the Inconsistent sub-scale, was regressed on factors C and D. These second-order factors were allowed to correlate (see Fig. 7). The fit of this model was very good, χ²(149) = 174.934, p > 0.05, χ²/df = 1.174, CFI = 0.892, RMSEA = 0.04 (0.00–0.06), SRMR = 0.078, Model AIC = 256.934.

Fig. 7 The structure of VACT, χ²(149) = 174.934, p > 0.05, χ²/df = 1.174, CFI = 0.892. RMSEA = 0.04 (0.00–0.06), SRMR = 0.078, Model AIC = 256.934. Note: item A1 was excluded from the analysis due to ceiling effect on performance.

The values of Cronbach's α of the Consistent and Inconsistent sub-scale were 0.68 and 0.62 respectively. These values are in the range of “0.60 to 0.69” and are considered as “undesirable to minimally acceptable” (DeVellis, 2003), supporting the reliability of the two VACT constructs.

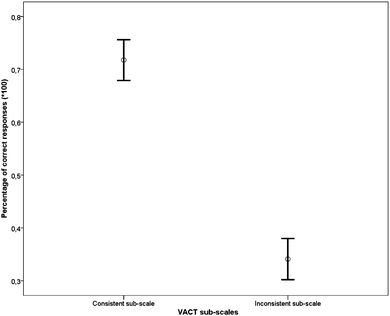
The results of a t-test analysis showed a statistically significant difference between the Consistent and Inconsistent sub-scales [t(123) = 13.62, p < 0.001, d = 1.72]. Performance on items in the VACT Consistent sub-scale (range: 0.20–1.00, mean = 0.71, SD = 0.21) was more accurate compared to performance on the items in the VACT Inconsistent sub-scale, (range: 0.00–0.90, mean = 0.34, SD = 0.22) (Fig. 8), confirming our hypothesis.

Fig. 8 Error bar chart for percentages (95% CIs) of correct responses in VACT sub-scales (study 1).

In summary, the VACT exhibited good psychometric qualities and the CFA revealed a structure consistent with the hypothesis that it consists of two distinct sub-scales. Sub-scale I containing items that can be solved correctly using visual/spatial strategies, and sub-scale II containing items that require the use of analytic strategies for their correct solution. The results confirmed the hypothesis that novices in organic chemistry would find it more difficult to solve the items in sub-scale II compared to the items in sub-scale I. The low success rate (34%) achieved by the students in solving correctly the sub scale II items indicates that the majority of the students were not able to use chemistry knowledge and apply strategies other than visual inspection. This lack of use of alternate strategies by the students in sub-scale II was confirmed during the interviews that took place after the testing of the second group of 34 11th grade students. In order to further investigate the changes in the use of visual and analytic strategies with the development of expertise, study 2 was conducted.

Study 2

The purpose of study 2 was to compare the adoption of visual/spatial and analytic strategies in individuals of different levels of expertise in the area of organic chemistry. We also wanted to examine the use of analytic strategies in situations in which visual inspection strongly favored the application of visual/spatial strategies. This was achieved by comparing the performance of the participants in the Category C and D items of the VACT Inconsistent sub-scale. Both Category C and D items were purposely constructed so that their correct solution could be achieved only by applying analytic strategies based on chemistry knowledge. However, the items in Category C were more perceptually similar to each other than the items in Category D, making it more likely that the participants would adopt a visual/spatial strategy that would lead them to an erroneous response.

Based on existing research (Stieff, 2007; Stieff and Raje, 2008, 2010) we hypothesized that novices would rely on the use of visual/spatial strategies despite the fact that they had been instructed in the use of analytic strategies. Experts, on the other hand, were expected to use both visual/spatial and analytic strategies as appropriate. As mentioned earlier, analytic strategies based on rules and heuristics help in reducing the cognitive load of visual/spatial thinking resulting in more successful problem solving in chemistry (Stieff, 2007). Thus we hypothesized that correct performance on the items that require reliance on chemical knowledge and the adoption of analytic strategies (sub-scale II items) would increase with the development of expertise.

Method

Participants. Four groups of a total of 285 individuals, indicating four different levels of expertise, participated in this research. The first group consisted of 127 (56 males and 71 females) 11th grade students (age range = 16.36–18.36, mean = 16.90, SD = 0.37) in an urban secondary school. At the time of data collection, the students had attended chemistry courses for three years (from 8th to 10th grade) and they had been taught organic chemistry for five months (during the 11th grade).

The second and the third groups consisted of 132 university students majoring in chemistry (71 first year and 61 third year). The first-year university students, 18 males and 53 females, (age range = 18.34–20.66, mean = 18.98, SD = 0.46 years) had been exposed to chemistry for five years at secondary education. They took part in the present research during the first month of their studies at the university, while enrolled in an inorganic chemistry course. The third-year university students, 24 males and 37 females, (age range = 20.62–24.79, mean = 21.43, SD = 0.86 years) were in their third and last semester of instruction in organic chemistry.

The fourth group consisted of 26 chemistry teachers, 10 males and 16 females (age range from 26 to 53) who had a basic degree in chemistry. At the time of data collection they taught chemistry to 11th grade students in private and public secondary education schools. These teachers had a wide range of experience ranging from 4 to 26 years of teaching.

Materials. The two versions of the revised Visual Analytic Chemistry Task (VACT) were used, as described in Study 1.

Cronbach's α scores of the Inconsistent sub-scale of the VACT were “respectable” (α = 0.79) (DeVellis, 2003), indicating that this scale had internal consistency across samples. Cronbach's α was also good for the Category C and Category D items (0.74 and 0.73 respectively), whereas Cronbach's α for the Consistent sub-scale was “undesirable to minimally acceptable” (DeVellis, 2003) in this sample (α = 0.60), probably due to high percentages of correct responses in the items of this sub-scale.

Procedure. The VACT was administered to 11th grade students and to 1st and 3rd year university students in the form of a paper and pencil test and was completed within approximately 30 minutes. The secondary school students received the VACT as an assessment test during chemistry class, while the university students completed the test during laboratory classes in inorganic and organic chemistry respectively. The chemistry teachers received the VACT via e-mail and completed it during a training course on educational software under the presence of one of the researchers. The administration of the VACT was in accordance to the ethical standards (Taber, 2014), as described in study 1.

Results and discussion

One-way Multivariate Analyses of Variance were applied to determine whether there were any differences in the performance of the different groups: (i) on the VACT Consistent and Inconsistent sub-scales and (ii) on the Category C and the Category D items of the VACT Inconsistent sub-scale. The dependent variables in the first analysis were accuracy performance on the VACT Consistent and Inconsistent sub-scales, and in the second analysis accuracy performance on the Category C and the Category D items of the VACT Inconsistent sub-scale. In both cases group type was the independent variable.

(i) Performance on the VACT Consistent and Inconsistent sub-scales

The analysis showed a statistically significant effect for group type [F(6, 558) = 16.78, p < 0.001, Wilk's Λ = 0.718, η_p² = 0.15]. The groups with greater expertise in chemistry had better scores than the groups with less expertise (Table 2).

Table 2 Mean responses in the VACT Consistent and Inconsistent sub-scale as a function of group type

Group type	N	VACT Consistent sub-scale		VACT Inconsistent sub-scale
		Mean	SD	Mean	SD
11th grade students	126	0.90	0.15	0.53	0.25
1st year university students	71	0.91	0.14	0.54	0.23
3rd year university students	61	0.97	0.06	0.75	0.23
Teachers	26	0.98	0.05	0.97	0.06

---

A statistically significant main effect for group type was obtained in both the Consistent [F(3, 280) = 5.97, p = 0.001, η_p² = 0.06] and the Inconsistent sub-scales [F(3, 280) = 35.38, p < 0.001, η_p² = 0.28] of the VACT, indicating that performance on both sub-scales was influenced by the level of expertise in chemistry. Group type differences in the Consistent sub-scale were rather small and the effect size was moderate (η_p² = 0.06) indicating that only 6% of the variance in performance could be attributed to the group effect. On the contrary, group type had a larger effect on performance in the Inconsistent sub-scale (η_p² = 0.28). Indeed, success on the items of the Inconsistent sub-scale increased with expertise, confirming our hypothesis.

Table 2 presents the scores of each group in the VACT Consistent and Inconsistent sub-scales.

Multiple comparisons using Tukey's HSD post hoc tests on the Consistent sub-scale showed that the chemistry teachers had better performance than the 11th grade students (mean difference = 0.07, p = 0.039, d = 0.52). Third year university students performed better than 11th grade students (mean difference = 0.07, p = 0.003, d = 0.53) and 1st year university students (mean difference = 0.07, p = 0.016, d = 0.61), whereas the two latter groups did not differ significantly (mean difference = 0.00, p = 0.999, d = 0.02).

On the Inconsistent sub-scale of the VACT the teachers performed better than all other groups [11th grade students' (mean difference = 0.45, p < 0.001, d = 1.91), 1st year university students' (mean difference = 0.44, p < 0.001, d = 2.16) and 3rd year university students’ (mean difference = 0.29, p < 0.001, d = 1.15)]. Third year university students scored better than 11th grade students (mean difference = 0.22, p < 0.001, d = 0.88) and 1st year university students (mean difference = 0.21, p < 0.001, d = 0.90), whereas no statistically significant differences were observed between 11th grade and 1st year university students (mean difference = 0.01, p = 0.993, d = 0.04). This last finding could be attributed to the fact that the 1st year university students did not receive instruction in organic chemistry for more than six months, whereas high school students were attending a course in organic chemistry during the period of the research.

The application of the parametric criterion t for dependent samples indicated a statistically significant difference between the Consistent and Inconsistent sub-scales of the VACT for: the 11th grade students [t(125) = 17.38, p < 0.001, d = 1.79], the 1st year university students [t(70) = 13.43, p < 0.001, d = 1.94] and 3rd year university students [t(60) = 8.07, p < 0.001, d = 1.31]. For these three groups, performance on the Consistent sub-scale was better than on the Inconsistent sub-scale. The magnitude of mean differences between the two sub-scales of the VACT was large (d > 0.8) for all the student groups. On the contrary, there was no significant difference in the performance of the teachers on these two sub-scales [t(25) = 0.27, p = 0.788, d = 0.07], indicating that the teachers performed equally highly in the two VACT sub-scales. The above results are shown in Fig. 9.

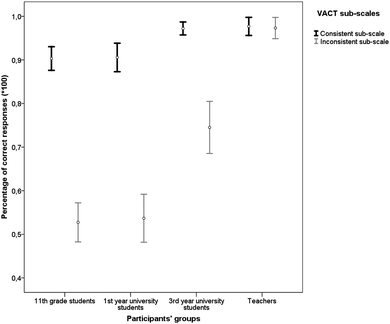Fig. 9 Error bar chart for percentages of correct responses (95% CIs) on the VACT sub-scales for each group type.

The above results confirmed our hypothesis that the accuracy on the Inconsistent sub-scale of the VACT would increase with the development of expertise. They also showed that the adoption of analytic strategies is very difficult to be achieved, even by students in their third year of university study.

The results are in agreement with the literature reporting that novice students continue to use visual/spatial strategies, such as mental rotation, even after having been instructed in analytic strategies (Stieff, 2007), while experts employ a range of visual/spatial and analytic strategies and prefer, on average, to use analytic strategies (Stieff, 2007; Stieff and Raje, 2008). They further add to the literature by confirming that it is very difficult to systematically adopt analytic strategies and by showing that individuals become gradually more competent in their use of analytic strategies with the acquisition of expertise.

(ii) Performance on categories C and D of the VACT inconsistent sub-scale

A One-Way MANOVA showed statistically significant differences in the performance of the various groups when comparing responses in the Category C and Category D items of the VACT Inconsistent sub-scale [F(6, 556) = 17.41, p < 0.001, Wilk's Λ = 0.709, η_p² = 0.16]. Additionally, performance on both Category C [F(3, 279) = 28.81, p < 0.001, η_p² = 0.24] and Category D [F(3, 279) = 18.37, p < 0.001, η_p² = 0.17] was influenced by group type and increased with expertise (see Table 3).

Table 3 Mean responses in the Categories C and D of the Inconsistent sub-scale of the VACT as a function of group type

Group type	N	Category C of the VACT Inconsistent sub-scale		Category D of the VACT Inconsistent sub-scale
		Mean	SD	Mean	SD
11th grade students	125	0.41	0.29	0.65	0.33
1st year university students	71	0.43	0.31	0.64	0.29
3rd year university students	61	0.62	0.32	0.88	0.23
Teachers	26	0.95	0.12	0.99	0.04

---

Tukey's HSD post hoc tests on Category C items showed that teachers performed better than all the other groups [3rd year university students (mean difference = 0.34, p < 0.001, d = 1.21), 1st year university students (mean difference = 0.52, p < 0.001, d = 1.92) and high school students (mean difference = 0.54, p < 0.001, d = 1.99)]. Third year university students performed better than 1st year university students (mean difference = 0.19, p = 0.002, d = 0.59) and high school students (mean difference = 0.20, p < 0.001, d = 0.67). There were no statistically significant differences between high school and 1st year university students (mean difference = 0.02, p = 0.981, d = 0.06).

Multiple comparisons on Category D items performance showed that there was no statistically significant difference between teachers and 3rd year university students (mean difference = 0.12, p = 0.290, d = 0.61), but teachers had better performance than 11th grade students (mean difference = 0.34, p < 0.001, d = 1.14) and 1st year university students (mean difference = 0.35, p < 0.001, d = 1.41). Similarly, 3rd year university students performed better than 11th grade students (mean difference = 0.23, p < 0.001, d = 0.75) and 1st year university students (mean difference = 0.23, p < 0.001, d = 0.88), whereas the two latter groups did not differ significantly (mean difference = 0.01, p = 0.999, d = 0.02).

Paired samples t-tests showed that the performance on Category D items was significantly better than on Category C items for 11th grade students [t(124) = 7.26, p < 0.001, d = 0.77], 1st year university students [t(70) = 4.78, p < 0.001, d = 0.70] and 3rd year university students [t(60) = 6.56, p < 0.001, d = 0.93]. There was no statistically significant difference in the teachers’ performance on the two Categories of the VACT Inconsistent sub-scale [t(25) = 1.55, p = 0.134, d = 0.44]. The performances of all the groups are summarized in Fig. 10.

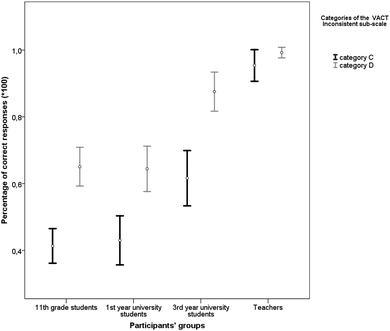Fig. 10 Error bar chart for percentages of correct responses (95% CIs) on the Categories of VACT Inconsistent sub-scale for each group type.

The results indicated that the difference between the Categories C and D of the VACT Inconsistent sub-scale influenced performance. More specifically, they showed that the participants found it difficult to ignore or inhibit the strong perceptual similarity between the two stimuli being compared in the Category C items. Under these circumstances they were led into the adoption of a visual/spatial strategy, which results in an erroneous response. This was the case even if they had in their repertoire at least some of the chemistry knowledge required to use an analytic strategy instead. This is suggested by the finding that the 3rd year university students, who failed in the Category C items, nevertheless succeeded in solving correctly the Category D items. Only the chemistry teachers were not influenced by the perceptual similarity of the Category C items and used chemical knowledge and analytic strategies in order to answer both Category C and D items.

In conclusion, the difference in performance on Categories C and D shows that the adoption of analytic strategies can be hindered in situational contexts where a visual/spatial strategy is highly supported by the superficial similarity of the items, and that many years of expertise are required before such contextual influences are systematically overcome.

General discussion and implications for instruction

The present research introduces the VACT as a new diagnostic instrument capable of detecting the development of analytic competence in organic chemistry. The VACT has good psychometric qualities and its items can be differentiated into two sub-scales, each of them consisting of two Categories. Sub-scale I contains items that can solved using either visual/spatial or analytic strategies, while the second sub-scale consists of items that can be solved correctly only when an analytic strategy is employed. The purpose of the VACT is not to investigate the growing ability to use visual/spatial strategies but rather to detect the use of analytic strategies. The strength of the VACT is in the analytic domain, i.e., in sub-scale II, the items of which require the application of analytic strategies and the use of chemical knowledge. The important advantage of VACT is that it permits the direct detection of analytic strategies in ways that do not require drawing inferences about underlying internal reasoning processes, as other methods do (Stieff, 2007, 2011; Stieff and Raje, 2008, 2010). The VACT is not time-consuming and unlike previous tasks it can be administered to a wide range of academic levels, something that makes it an appealing tool.

The use of the VACT allowed us to investigate changes in the use of analytic strategies by individuals at different levels of expertise in organic chemistry for the first time. The results indicate that the adoption of analytic strategies in organic chemistry is a particularly difficult process that requires the systematic acquisition of organic chemistry knowledge, adding and enriching the existing literature (Stieff, 2007; Stieff and Raje, 2008). The results are consistent with the argument that there is a systematic shift in strategy use with the acquisition of expertise.

Another important finding of the present research pertains to the differences in the students’ performance on the Categories C and D of sub-scale II of the VACT. The results showed that the students were more likely to apply analytic strategies in order to solve correctly the Category D items compared to the Category C items. This difference was particularly pronounced in the case of the 3rd year university students. The difference between these two Categories lies in the degree of their visual/perceptual similarity. The items in Category C consist of pairs that are more perceptually similar compared to the pairs in the Category D items. It appears that this perceptual similarity leads the students into erroneously applying a visual/spatial strategy, which leads to an incorrect response. When this similarity in appearance is not present, as in the case of D items, the participants are more likely to apply an analytic strategy. In other words, many individuals fail to use analytic strategies in chemistry not because of lack of knowledge, but because they find it difficult to inhibit the response suggested by visual inspection; they are misled by the situational context when the latter favors a visual/spatial approach.

The finding that students, even the university students specializing in chemistry who had received many years of instruction did not do well in the analytic sub-scale of the VACT, shows that chemistry instruction is not very successful. Despite the fact that the instruction in the country in which this research was conducted focuses primarily on analytic strategies, students continue to face considerable difficulty in understanding and applying the rules and heuristics they have been taught. This is not an entirely new finding, as it is consistent with the findings of existing educational research in chemistry (Stieff, 2007). Some researchers have suggested that the change from visual to analytic strategies is difficult because it requires changes in students underlying mental representations and mental models (Hegarty et al., 2013). We agree with this suggestion and suggest that it might be profitable to investigate the visual/analytic shift from the lenses of a more general, conceptual change approach in order to understand in greater detail the underlying changes in knowledge organization and representation that it may entail.

The difference in students’ performance in the two Categories (C and D) of the VACT Inconsistent sub-scale highlights another issue on which instruction needs to focus, namely, the role played by the situational context in the adoption of analytic strategies. As was discussed earlier, the adoption of analytic strategies might be easier in some contexts compared to others. Thus, it might be advisable for educators to include in their instruction and in the educational materials they use explicit examples of contexts where the responses suggested by visual inspection are incorrect and where only an analytic approach can lead to the correct solution. Also, assessment tests and homework exercises might contain items that would make students reflect on their strategy use, after revision and feedback. As an educational outcome, students should understand that the immediate application of a visual/spatial strategy might lead them to errors and should learn to check themselves by also employing an analytic strategy to ensure the accuracy of their responses.

Finally, the present results raise some questions about the role of training in spatial reasoning in order to achieve success in STEM in general (Newcombe, 2013; Cohen and Hegarty, 2014; Kornkasem and Black, 2015; Stieff and Uttal, 2015) and chemistry in particular (Harle and Towns, 2011; Merhant et al., 2012; Stull et al., 2012, 2016; Al-Balushi and Al-Hajri, 2014; Carlisle et al., 2015; Barrett and Hegarty, 2016; Salah and Alain, 2016; Stieff et al., 2016; Stull and Hegarty, 2016). If the acquisition of expertise in many areas of STEM, including chemistry, requires the development of analytic strategies, what exactly is the role of spatial reasoning training? What is the relationship between spatial reasoning early on in science learning and the adoption of analytic strategies later, as domain expertise is acquired? Existing research suggests that the best approach to instruction in chemistry might be one that uses both visual/spatial and analytic strategies in strategic combination (Stull and Hegarty, 2016). However, more research is needed to investigate why this is the case and in what exact way training in spatial reasoning might be used to support the subsequent development of analytic strategies.

Limitations and future directions

The present research is only the beginning of a larger investigation that needs to take place to better understand how the visual/analytic shift takes place in chemistry and in other domains of knowledge. One of the limitations of the present study is that it did not investigate the spatial reasoning abilities of the participants, something that we are in the process of doing in ongoing research. It is important to find out if the development of expertise in analytic strategies depends only on chemistry knowledge or whether it also draws on spatial reasoning abilities, or maybe, on more developed analytic reasoning skills.

It is also important to investigate individual differences in students who performed better in the VACT, and especially in the Category C items of sub-scale II. Did they differ in their knowledge of chemistry? Where there any individual differences in their spatial reasoning abilities? Did they differ in other important cognitive skills such as analytic reasoning and executive function skills and in particular in the ability to inhibit familiar responses? These are all important questions for future research.

Acknowledgements

This research has been co-financed by the European Union (European Social Fund – ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF) – Research Funding Program: Thales. Investing in knowledge society through the European Social Fund. The research team thanks the secondary education teachers Dr Vafiadis Anastasios and Med Nalbantis Konstantinos for their help to administer the tests to their students.

References

1. Al-Balushi S. M. and Al-Hajri S. H., (2014), Associating animations with concrete models to enhance students' comprehension of different visual representations in organic chemistry, Chem. Educ. Res. Pract., 15, 47–58.
2. Barnea N. and Dori Y. J., (1999), High-school chemistry students' performance and gender differences in a computerized modelling learning environment, J. Sci. Educ. Technol., 8(4), 257–271.
3. Barrett T. J. and Hegarty M., (2016), Effects of interface and spatial ability on manipulation of virtual models in a STEM domain, Comput. Hum. Behav., 70, 1–9.
4. Bodner G. M. and McMillen T. L. B., (1986), Cognitive restructuring as an early stage in problem solving, J. Res. Sci. Teach., 23(8), 727–737.
5. Carlisle D., Tyson J. and Nieswandt M., (2015), Fostering spatial skill acquisition by general chemistry students, Chem. Educ. Res. Pract., 16, 478–517.
6. Carter C. S., LaRussa M. A. and Bodner G. M., (1987), A study of two measures of spatial ability as predictors of success in different levels of general chemistry, J. Res. Sci. Teach., 24(7), 645–657.
7. Chiu I. and Shu L. H., (2010), Potential limitations of verbal protocols in design experiments, ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Montreal, pp. 287–296.
8. Cohen C. A. and Hegarty M., (2014), Visualizing cross sections: training spatial thinking using interactive animations and virtual objects, Learn. Individ. Differ., 33, 63–71.
9. DeVellis R. F., (2003), Scale development: theory and applications, 2nd edn, Thousand Oaks, CA: Sage.
10. Harle M. and Towns M. J., (2011), A review of spatial ability literature, its connection to chemistry, and implications for instruction, J. Chem. Educ., 88(3), 351–360.
11. Hegarty M., (2014), Spatial thinking in under graduate science education, Spat. Cogn. Comput., 14(2), 142–167.
12. Hegarty M., Stieff M. and Dixon B. L., (2013), Cognitive change in mental models with experience in the domain of organic chemistry, J. Cogn. Pshchol., 25(2), 220–228.
13. Kornkasem S. and Black J. B., (2015), Formation of spatial thinking skills through different training methods, Cogn. Process., 16, 281–285.
14. Kospentaris G., Vosniadou S., Kazi S. and Thanou E., (2016), Visual and Analytic Strategies in Geometry, Frontline Learning Research, 4 (1), 40–58.
15. Lean G. and Clements M. A., (1981), Spatial ability, visual imagery, and mathematical performance, Educ. Stud. Math., 12, 267–299.
16. Mathewson J. H., (1999), Visual-spatial thinking: an aspect of science overlooked by educators, Sci. Educ., 83(1), 33–54.
17. Merhant Z., Goetz E. T., Keeney-Kennicutt W., Kwok O., Cifuentes L. and Davis T. J., (2012), The learner characteristics, features of desktop 3D virtual reality environments, and college chemistry instruction: a structural equation modeling analysis, Comput. Educ., 52(2), 551–568.
18. Newcombe N. S., (2013), Seeing Relationships: Using Spatial Thinking to Teach Science, Mathematics, and Social Studies, Am. Educ., 37(1), 26–31.
19. Newcombe N. S. and Frick A., (2010), Early education for spatial intelligence: why, what, and how, Mind Brain Educ., 4(3), 102–111.
20. Pribyl J. R. and Bodner G. M., (1987), Spatial ability and its role in organic chemistry: a study of four organic courses, J. Res. Sci. Teach., 24(3), 229–240.
21. Salah B. M. and Alain D., (2016), To what degree does handling concrete molecular models promote the ability to translate and coordinate between 2D and 3D molecular structure representations? A case study with Algerian students, Chem. Educ. Res. Pract., 17, 862–877.
22. Stieff M., (2007), Mental rotation and diagrammatic reasoning in science, Learn. Instr., 17, 219–234.
23. Stieff M., (2011), When is a molecule three dimensional? A task-specific role for imagistic reasoning in advanced chemistry, Sci. Educ., 95(2), 310–336.
24. Stieff M., (2013), Sex differences in the mental rotation of chemistry representations, J. Chem. Educ., 90, 165–170.
25. Stieff M. and Raje, S., (2008), Expertise & Spatial Reasoning in Advanced Scientific Problem Solving, Proceedings of the 8th international conference on International conference for the learning sciences, vol. 2, pp. 366–373.
26. Stieff M. and Raje S., (2010), Expert algorithmic and imagistic problem solving strategies in advanced chemistry, Spat. Cogn. Comput., 10, 53–81.
27. Stieff M. and Uttal D., (2015), How Much Can Spatial Training Improve STEM Achievement? Educ. Psychol. Rev., 27(4), 607–615.
28. Stieff M., Hegarty M. and Dixon B., (2010a), Alternative strategies for spatial reasoning with diagrams, Diagrammatic Representation and Inference, LNAI, 6170, 115–127.
29. Stieff M., Ryu M. and Dixon B., (2010b), Students' use of multiple strategies for spatial problem solving, ICLS ’10 Proceedings of the 9th International Conference of the Learning Sciences, vol 1, pp. 765–772.
30. Stieff M., Ryu M., Dixon B. and Hegarty M., (2012), The role of spatial ability and strategy preference for spatial problem solving in organic chemistry, J. Chem. Educ., 89, 854–859.
31. Stieff M., Dixon B. L., Ryu M., Kumi B. and Hegarty M., (2014), Strategy training eliminates sex differences in spatial problem solving in a stem domain, J. Educ. Psychol., 106(2), 390–402.
32. Stieff M., Scopelitis S., Lira M. E. and Desutter D., (2016), Improving Representational Competence with Concrete Models, Sci. Educ., 100(2), 344–363.
33. Stull A. T. and Hegarty M., (2016), Model manipulation and learning: Fostering representational competence with virtual and concrete models, J. Educ. Psychol., 108(4), 509–527.
34. Stull A. T., Hegarty M., Dixon B. and Stieff M., (2012), Representational Translation with Concrete Models in Organic Chemistry, Cogn. Instruct., 30(4), 404–434.
35. Stull A. T., Gainer M., Padalkar S. and Hegarty M., (2016), Promoting Representational Competence with Molecular Models in Organic Chemistry, J. Chem. Educ., 93(6), 994–1001.
36. Taber K. S., (2014), Ethical considerations of chemistry education research involving ‘human subjects’, Chem. Educ. Res. Pract., 15, 109–113.
37. Uttal D. H., Miller D. I. and Newcombe N. S., (2013), Exploring and enhancing spatial thinking links to achievement in science, technology, engineering and mathematics? Curr. Dir. Psychol. Sci., 22(5), 367–373.
38. Vosniadou S. and Skopeliti I., (2014), Conceptual Change from the Framework Theory Side of the Fence, Sci. Educ., 23 (7), 1427–1445.
39. Wai J., Lubinski D. and Benbow C. P., (2009), Spatial ability for STEM domains: aligning over 50 years of cumulative psychological knowledge solidifies its importance, J. Educ. Psychol., 101 (4), 817–835.
40. Wu H. K. and Shah P., (2004), Exploring visuospatial thinking in chemistry learning, Sci. Educ., 88, 465–492.

---

Footnotes

† Current address: School of Education, Flinders University, GPO Box 2100, Adelaide 5001, South Australia, Australia.

‡ The VACT will be available from the authors upon request.

---