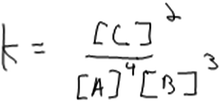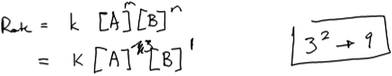Engaging students in analyzing and interpreting data to construct mathematical models: an analysis of students’ reasoning in a method of initial rates task
Nicole M.
Becker
 *,
Charlie A.
Rupp
and
Alexandra
Brandriet
*,
Charlie A.
Rupp
and
Alexandra
Brandriet
E355 Chemistry Building, Iowa City, Iowa 52242-1294, USA. E-mail: nicole-becker@uiowa.edu
First published on 5th July 2017
Abstract
Models related to the topic of chemical kinetics are critical for predicting and explaining chemical reactivity. Here we present a qualitative study of 15 general chemistry students’ reasoning about a method of initial rates task. We asked students to discuss their understanding of the terms rate law and initial rate, and then analyze rate and concentration data in order to construct a rate law. We also asked participants to critique rate laws constructed by hypothetical students. We discuss five patterns in the students’ approach to the method of initial rates task, ranging from the use of surface-features, such as stoichiometric coefficients in the construction of a rate law, to more sophisticated interpretations and mathematization of the trends in the data. Findings highlight specific difficulties with inter-related competences required to engage in the task, such as interpreting data and reasoning mathematically, and provide insight into assessment strategies for similar tasks.
Introduction
For practicing chemists, mathematical models related to chemical kinetics are indispensable for predicting and explaining chemical reactivity. Rate laws, for instance, are mathematical models that describe how concentrations of reactant species will influence the rate of a reaction (Holme et al., 2015). This type of mathematical model is useful for not only predicting the rate at which a reaction will occur, but also for understanding inferences about the atomic-molecular mechanism of a reaction (Holme and Murphy, 2012; Holme et al., 2015).The American Chemical Society Exams Institute’s Anchoring Concept Content Map (ACCM) cites being able to reason about the rate and rate laws as an essential component of the undergraduate general chemistry curriculum (Murphy et al., 2012; Holme et al., 2015). Here, the central idea of chemical kinetics is that chemical reactions have a timescale over which they occur, which is referred to as an “anchoring concept” because it is one that extends throughout the undergraduate chemistry curriculum. Sub-ideas pertaining to chemical kinetics are referred to as “enduring understandings” in the ACCM and include the idea that empirically derived rate laws summarize the dependence of reaction rates on the concentration of reactants and temperature and that the “order” of reaction relates to the exponent used for that species in the rate law. The method of initial rates is highlighted as one route toward constructing (and evaluating) rate laws in the chemistry context and is the focus of our present study. Once known, rate laws are useful in predicting, quantitatively, the rate of a reaction.
The study reported here examines how students navigate the interrelated concepts and skills required to construct rate laws in a method of initial rates task. From the students’ perspective, constructing rate laws can be a complex task. To use the method of initial rates to construct a rate law, students must recognize the empirical basis of rate laws, and understand how to interpret initial rate and concentration data. Students must also think about the mathematical relationship between reactant concentration and initial rate to infer the order of reaction, that is, the exponent in the rate law.
Our focus on the method of initial rates contexts is motivated in part by the widespread use of this type of task within the general chemistry curriculum, both in lecture and in lab. To experts, the method of initial rates provides an opportunity to engage students in the process of model building, a fundamental part of scientific inquiry (National Research Council, 2012) and one that has been shown to improve learning outcomes (Schuchardt and Schunn, 2016).
However, there has long been evidence that students tend to approach quantitative problem solving in general chemistry courses algorithmically, with limited attention to the concepts underlying the math (Nurrenbern and Pickering, 1987). Thus, we have reason to doubt the assumption that method of initial rates tasks might support students in gaining rich insights into the model-building enterprise, at least as they are typically framed in typical large enrollment chemistry courses. However, at a minimum we conjecture that such tasks might provide some opportunities for supporting students’ abilities to interpret data and reason mathematically about patterns in data, competencies that have been highlighted as foundational to more advanced modeling competencies (Pasley et al., 2016). By understanding how students engage in and reason about method of initial rates tasks, our goal is to generate a firmer evidence base that might support curricular reforms aimed at more authentic engagement in science practices in undergraduate chemistry classrooms. This study addresses the following research questions:
RQ1: How do students conceptualize rate laws?
RQ2: How do students construct rate laws based on numerical data in a method of initial rates task?
RQ3: How do students evaluate the appropriateness of a rate law?
To situate this work, we focus our discussion of the literature on how students interpret, construct, and use rate laws when thinking about chemical kinetics. We direct the reader to reviews by Bain and Towns (2016) and Justi (2002) for more comprehensive discussions of the research on student reasoning about kinetics concepts.
Review of related literature
Students’ abilities to analyze and interpret data
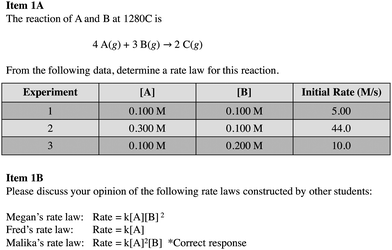
Empirical evidence is fundamental to science, and scientists garner meaning from data as a result of the analysis and interpretation of it (National Research Council, 2012; Osborne, 2014). Scientists use several tools that aid in analysis and interpretation, such as graphs, tables, and statistics, and these tools can help make sense of the patterns and relationships that exist between variables (National Research Council, 2012). The National Research Council (2012) describes analyzing and interpreting data as an important science practice that is highly intertwined with other practices, such as constructing models and mathematical and computational thinking. For instance, scientists might distinguish patterns between variables and construct mathematical models that are predictive of those trends.We see science practices as similarly intertwined in the context of method of initial rates tasks, such as that shown in Fig. 1. Optimally, in determining a rate law for the data shown in Fig. 1, Task A, students would realize that they need to use a control of variables strategy to aid in their analysis of data. That is, students might hold the concentration of one reactant species constant so as to make it possible to investigate the impact of a second variable on the reaction rate. Students must then identify and interpret relevant patterns in the data and attempt to mathematically model those patterns using exponents to generate a rate law in the form, rate = k[A]m[B]n, where m and n are the so-called “reaction orders” representing relationships identified in the data.
We see several potential areas of difficulty with method of initial rates tasks, including difficulties in using the control of variable strategy, challenges in identifying relevant patterns in data, and difficulty mathematically representing the relationship between reactant concentrations and rate. We briefly review the key literature pertaining to each of these areas.
Studies have found that the control of variables strategy may be difficult for undergraduate students (Boudreaux et al., 2008; Zhou et al., 2016). For instance, Boudreaux et al. (2008) asked introductory physics students to analyze a table of data from an experiment performed to investigate whether certain variables (e.g. length of string, mass of bob) affect the number of swings of a pendulum at a specified time interval. While most students recognized the need to compare trials in which the variable tested was changed, some did not hold other variables constant, and as such, students drew conclusions based on confounded experiments. Others that assumed that only one variable could influence a system at a time arrived at incorrect interpretations of the data.
In analyzing data, students may also struggle to identify which aspects of the data are the most salient and important to their analysis and may focus on aspects that experts would consider surface features. In doing so, novices may neglect important interpretations of the data (Cakmakci et al., 2006; Heisterkamp and Talanquer, 2015).
For instance, in a chemical kinetics context, Cakmakci and colleagues (Cakmakci, 2005; Cakmakci et al., 2006) asked students to infer whether a plot of concentration versus time showing a linear decrease in concentration of nitrogen monoxide (NO) was consistent with a scientist’s claim that the rate law for the reaction 2NO(g) → N2(g) + O2(g) would be ‘Rate = k[NO]0’. Many undergraduate general chemistry students (33%, n = 16) focused on surface features of the graph, such as where the graph began or ended, rather than the fact that a constant slope indicates a zeroth-order reaction. For instance, one student concluded that the reaction was in fact zeroth-order, because the graph ended at a concentration of zero. An additional 29% of students (n = 14) gave what the authors refer to as incomprehensible responses, perhaps underscoring the difficulty of the task.
Students’ abilities to mathematically model relationships between variables
Analysis of data and mathematical thinking are closely intertwined in this task. In particular, after identifying a pattern in the data students must decide what the relationship between the concentration and rate is, and they must express that relationship using exponents in the rate law. Research in mathematics education has shown that students may struggle to differentiate between different types of relationships, for instance in distinguishing proportional relationships from other types of relationships (Izsák and Jacobson, 2017). Furthermore, students may encounter difficulty in mathematizing relationships and quantities using algebraic notation. For instance, MacGregor and Stacey (1997) found that high school students commonly misused algebraic notation when attempting to mathematically represent a quantity, for instance, using x3 to model a quantity more appropriately described by 3x. It is thus reasonable to believe that students may encounter similar difficulties when attempting to mathematize relationships between concentration and rate in chemistry contexts.Students’ conceptions of rate laws
A significant body of research has focused on documenting alternative conceptions of concepts related to chemical kinetics (Cakmakci, 2010; Yan and Subramaniam, 2016) or addressing alternative conceptions through instruction (Van Driel, 2002; Cakmakci and Aydogdu, 2011). Reviews by Bain and Towns (2016) and Justi (2002) summarize a large body of this research and we direct readers here for a comprehensive overview of prior work in this area.Prior work has shown that students may hold alternative conceptions of reaction rate, including the idea that the reaction rate is the time required for the reaction to reach completion and that the reaction rate is related to the yield of a reaction (Kousathana and Tsaparlis, 2002; Yalçιnkaya et al., 2012).
Although to date there is limited research on students’ conceptualizations of the term rate law, there is some evidence that students may struggle to understand the nature and purpose of rate laws (i.e. that rate laws are experimentally determined and can be used to predict changes in reaction rates).
A study by Turányi and Tóth (2013) highlights that students may not recognize the empirical basis of rate laws. Turányi and Tóth designed a multiple-choice assessment that asked Hungarian physical chemistry students (n = 424) to predict what would happen to the reaction rate if the concentration of hydrogen gas were doubled for the reaction N2(g) + 3H2(g) → 2NH3(g). Only 31% of chemistry majors in this sample correctly identified that without more information (i.e. empirical data), a rate law for the balanced chemical equation could not be determined. Incorrect responses to this task included the prediction that the reaction rate would double or that the rate would increase by a factor of 8 (the prediction that would be obtained if stoichiometric coefficients were used as reaction orders).
Several additional studies have also documented students’ use of stoichiometric coefficients as exponents of rate (Cakmakci et al., 2006; Cakmakci and Aydogdu, 2011; Turányi and Tóth, 2013). This approach may reflect confusion about when to apply the Law of Mass Action, in which stoichiometric coefficients may be used to construct a rate law for a proposed elementary reaction step (Cakmakci and Aydogdu, 2011; Turányi and Tóth, 2013).
In addition to the difficulty in recognizing the empirical basis of rate laws, undergraduate chemistry students may also not recognize when and how to use rate laws, that is, rate laws can be used to predict changes in rates as a function of concentration (Cakmakci et al., 2006; Kurt and Ayas, 2012). For instance, Cakmakci et al. (2005, 2006) found that students may not recognize that rate laws can be used to make predictions about how changes in concentration impact the reaction rate and instead may rely on generalized rules or intuitive ideas. In a follow-up question to the nitrogen monoxide probe, undergraduate general chemistry students were asked to predict the impact of increasing the concentration of NO on the reactant rate for the reaction 2NO(g) → N2(g) + O2(g). Half of general chemistry participants in this study ignored the provided data and the rate law and instead based their predictions on general rules (e.g. “rate of a reaction is directly proportional to the concentration of reactants”) or prototypical real-world scenarios (e.g. putting more sugar in water would make it dissolve slower).
Indeed, these tendencies have been noted in other studies of students’ approach to analyzing data as grounds for predictions of chemical properties. For instance, in a case study of a freshman chemistry students’ approach to explaining patterns in ionization energy and boiling point data, Heisterkamp and Talanquer (2015) observed that the student tended to hybridize chemical and intuitive knowledge to explain trends in the data or apply ideas in an unconstrained fashion.
In summary, there is evidence from the way in which students engage with tasks that require them to construct or use rate laws, and that students may have limited understandings about how rate laws are constructed or how they may be used. Suggested reasons for students’ difficulties in constructing rate laws include the observation that students might conflate different mathematical expressions, for instance, between equilibrium constants and rate laws or the distinction between rate laws for an overall process versus for proposed elementary steps in a reaction (Turányi and Tóth, 2013).
Theoretical perspectives
Our perspective on student learning is informed by Hammer and Elby’s (2003) Resources Perspective, which was developed to describe conceptual resources students bring to learning physics. Such cognitive resources may include, for instance, procedural knowledge such as how to represent an exponential relationship, epistemological ideas such as information about how models are developed and tested in science, or conceptual knowledge. They may also include ideas akin to what diSessa (1993) termed phenomenological primitives (or “p-prims”), primitive ideas that in many cases may arise through generalization of experiences with physical phenomena.Resources in and of themselves are not inherently correct or incorrect; given an unfamiliar problem, students may search through their store of resources, perhaps even trying several before arriving at one that seems to be useful. Although they may make errors in applying resources, it does not necessarily mean that a resource is itself invalid. Indeed, in another context, the resource could be a productive tool for making sense of the world. Furthermore, the expression of non-productive resources does not necessarily mean that students lack productive resources entirely, only that those resources for whatever reason were not activated in a given context. By examining what ideas students are able to activate in response to instructional tasks, educators may gain insight as to how they may scaffold students’ use of more productive resources, for instance through bridging analogies or targeted instruction.
Framing students’ difficulties in terms of alternative conceptions provides some insight into how to address these difficulties through instruction. However, overall, this research direction provides relatively little insight as to how instructors can scaffold students’ engagement in more complex and authentic tasks. Descriptions of student reasoning during such tasks can aid in gauging students' levels of understanding and helping them to use their knowledge in a more coherent manner.
Our work draws on an approach known as the BEAR assessment system (BAS), which views learning and assessments with a developmental perspective (Wilson, 2005, 2009). Fundamental to BAS is an assessment structure that measures the qualitatively distinct but increasingly sophisticated nature of students’ responses to an assessment item. In this perspective, students’ responses go beyond being correct or incorrect, and rather, students’ knowledge and skills lie somewhere on a continuum. As a result, students’ knowledge and skill progress from lower to higher levels of sophistication and are anchored in their prior knowledge and skills. In order to appropriately scaffold students’ learning, we must develop models that can characterize the range of students’ knowledge and skills (Wilson, 2009).
Many studies have used sophistication of students’ responses to characterize different performance levels (Briggs et al., 2006; Mohan et al., 2009; Gunckel et al., 2012). As an example, Mohan et al. (2009) evaluated K-12 students’ written assessment and interview responses about what happens during different carbon transformation processes. Four levels emerged from the data that accounted for a range of sophistication in students’ reasoning. At the lowest level, students recognized processes in terms of macroscopic accounts of the events with the goal of fulfilling their natural tendencies. In comparison, the highest level responses were able to use atomic/molecular accounts that provided a mechanism that explained the processes.
However, there are relatively few in-depth descriptions of how students coordinate conceptual knowledge of chemical kinetics (such as the meaning of terms like first order, rate of reaction, etc.) with mathematical knowledge to engage in more complex tasks, such as constructing and using rate laws. In our study, we characterized the level of sophistication in students’ arguments using a method of initial rates task. Our study expands upon previous studies by providing an in-depth description of how students analyze data to construct rate laws. Characterizing students’ reasoning using such a task can help facilitate the development of instructional interventions and related assessments that could help students engage in the science practices of analyzing data and constructing models.
Methods
Research setting
Participants of this study were drawn from the second-semester of a two-semester introductory chemistry course for STEM majors at a large Midwestern university. Students in this introductory chemistry course were required to enroll in three course components: a lecture section that met three times per week, a discussion section that met once per week, and a laboratory section. Discussion and laboratory sections were led by graduate teaching assistants and typically featured guided problem solving and occasional small-group activities led by graduate teaching assistants. The course used a commercially available text (Brown et al., 2014).The topic of chemical kinetics was introduced early in the second-semester. At the time of this study, students had completed a laboratory activity on the kinetics of H2O2 decomposition and had been assessed on the chapter on chemical kinetics. The method of initial rates had been explicitly covered in lecture, and students had solved similar problems on both the homework assignments (MasteringChemistry) and the multiple-choice chapter exam.
Interview guide design
Here, we discuss student responses to the portion of the interview guide that addressed participants’ understanding of reaction rates and their approach to reasoning about a method of initial rates task. We began by asking students to describe their understanding of terms such as the rate of reaction and rate law. When introduced by participants, we probed understanding of related terms and concepts, such as “order of reaction” or “first order”.Next, we gave participants a table of initial rate and concentration data for a generic reaction and asked them to construct a rate law for the reaction, explaining their thinking as they did so. After working through the task, we asked students to summarize their reasoning about the task (Fig. 1). We used a generic task because in our pilot tests with similar tasks students tended to become fixated on irrelevant details when presented with real systems and focused on features such as the structure of the molecule and mechanism of the reaction. A generic system enabled us to focus our attention on students’ analysis of the data.
We considered the rate law task in 1A to be comprised of two subtasks: determination of reaction orders of reactants A and B. We expected subtask A to be more difficult than B (first-order), because A is second order and required students to reason about an increase in concentration resulting in a squared increase in the rate. Furthermore, we intentionally selected data that would give a non-integer value if students used an algorithmic approach to determine order in A. We did this because we wanted to see how students interpreted the outcome of calculations and how they thought about models as representing simplifications and approximations of the target system.
In the second interview question (Task 1b), we asked participants to examine rate laws constructed by three hypothetical students (Megan, Fred, and Malika) (Fig. 1) and to argue for their choice of the best rate law. We conjectured that students who struggled with the first task might find it easier to interpret, rather than construct rate laws, and thus, this component was intended, in part, to scaffold students who found 1a difficult.
Institutional Review Board approval was obtained for the study and all interview participants were informed of their rights as research participants. The interviews were video recorded and Livescribe pens (http://www.livescribe.com) were used to record written work and audio.
Data analysis
We analyzed student responses to probes about their interpretation of terms such as “rate law” as well as responses to Item 1B (Fig. 1) using an inductive, constant comparative approach (Corbin and Strauss, 2008).For responses to Item 1A (the method of initial rates task), we considered students' attempts to justify their selection of an exponent for each reactant in the main rate law task as the articulation of an argument. Our initial analysis was informed by Toulmin’s (1958) model of argumentation, which considers the basic structure of an argument to be composed of three main components: a claim, evidence, and reasoning.
We identified the claims students made regarding the exponent denoting reaction order for each reactant and the evidence they used to support their claims, which was typically either data from the table or information from the balanced chemical equation. We then identified how their interpretation of the data was connected to their claim about the exponent (reasoning). In some student responses, reasoning about the reaction order was implied or disconnected from the student’s selection of an exponent and thus we observed some responses that contained only claim and evidence (not reasoning).
In defining qualitatively distinct “levels” of reasoning, the correctness of students’ overall rate law played a minor role. Instead, we looked for progression in the evidence and reasoning students presented in support of their rate law. For instance, we examined what evidence students used in support of their proposed rate law and saw a progression from surface features to using the empirical data, with varying degrees of interpretation of the trend in the data (Levels 1–3, as described in findings). For those students who identified the appropriate evidence and interpreted the pattern in the data appropriately, we looked for progression in their ability to mathematize the trend in the data to determine an exponent for the rate law (Levels 4 and 5, as described in findings). Overall, our analysis suggested five main types of arguments about rate laws and we present these as the five main themes in the findings section.
Inter-rater agreement
After establishing a coding scheme related to specific ideas functioning as claim, evidence, and reasoning within the data, two raters independently applied the coding scheme to the 15 transcripts. Initial percent agreement was 88.2% for the reasoning pertaining to the order of A and 79.5% for the order of B. The raters then discussed discrepancies and negotiated a consensus set of argument components for subsequent coding.The five main themes we will present reflect what we see as trends in the combinations of evidence and reasoning used by students to support claims about the exponents used in the rate law (reaction orders). To examine reliability of the five main themes pertaining to the overall argument type, we conducted a second inter-rater agreement analysis. Two raters (the first author and a graduate student who was not involved with the initial development of the code categories) independently coded combinations of claim and evidence for the complete dataset. Initial agreement was 91% (94% for passages pertaining to reaction order in B, 80% for passages pertaining to order in A). Minor clarifications to code definitions were made following the second inter-rater reliability analysis.
Findings
Participants’ ideas about the meaning of the term “rate law”
Our first research question addresses students’ understanding of the nature and purpose of rate laws. At the beginning of our semi-structured interviews, we asked students to discuss their understanding of the term rate law and to discuss why one might want to construct a rate law. We also probed students’ understanding of terms such as “order of reaction” when these were introduced by the participants.The term rate law was familiar to all participants and all associated it with some type of mathematical expression they had used in their course. The majority of students recalled the correct functional form of a rate law though a few seemed to conflate rate laws with equilibrium expressions (Elliott, Jenna, Melvin).
Beyond this, however, most participants' discussions of what the term “rate law” meant to them was limited to simple associations between concepts. Some of the more canonical associations with concepts pertaining to chemical kinetics included the idea that rate laws have to do with the rate or speed of a reaction (nine participants), and the rate as relating to the appearance of products with respect to time (Marjorie). Others used the terms rate and rate law interchangeably or gave responses suggestive of alternative conceptualizations of rate, such as the idea that the rate law is the speed that a reaction reaches equilibrium (Antonio).
Three of our fifteen participants appropriately discussed how rate laws reflect the dependence of reaction rate on concentration (Alicia, Callie, Penelope). In response to probes addressing participants' understanding of the term “order of reaction”, three additional participants discussed how the exponent in the rate law is selected to model the relationship between concentration and rate (Kameron, Marjorie, Yeliz).
Four participants reflected on the experimental nature of rate laws (Aaron, Kameron, Penelope, Yeliz). However, the depth that they understood how or why rate laws are experimentally determined varied. Yeliz, for instance, commented that she remembered that at a review session, her instructor told her that a common error made by students was to use coefficients from the balanced equation rather than experimental data. Thus, her mention of experimental determination of the rate laws seems to be rooted in her understanding of how to successfully construct a rate law for the purposes of her general chemistry course rather than in deeper recognition of the empirical basis of these models.
Participants’ approach to the method of initial rates task
Our participants exhibited a range of approaches to constructing rate laws from initial rate and concentration data. Of the 15 participants, 3 constructed the “correct” rate law for this task, while 12 constructed alternative rate laws. We identified five themes in the reasoning students presented to support their rate laws. We have ordered these themes (Levels 1–5) in what we will argue to be a progression towards greater overall sophistication and deeper engagement in the dimensions of analyzing and interpreting data and mathematical thinking. Table 1 includes brief descriptions and examples of all themes. An additional category, Level 0, was used to designate instances in which participants responded “I don’t know” or did not attempt to construct a rate law.| Level | Description | Example |
|---|---|---|
| 5 | Students examine the experimental data by selecting two trials such that one variable is held constant; they correctly describe the pattern in the data verbally (e.g. concentration doubles, rate quadruples) and appropriately use exponents in the rate law expression to model observed changes. Responses may include some explicit reflections as to how the selected exponent models change in the reaction rate. | Looking at this from here to here [examines trial 1 and trial 3]… B doubles and this [rate] doubles, so that would be first order. So, B to the one power so it’d be itself. [Katie] |
| 4 | Students select two trials such that concentration of one variable is constant; they may correctly describe some aspects of the pattern in the data verbally (e.g. rate doubles, concentration doubles). However, they either (1) use incorrect heuristic-focused reasoning and therefore select an incorrect exponent for the rate law or (2) make an error in translating their interpretation of the trend in the data into an exponent for the rate law. Students’ reasoning at this level often does not include elaborating how the trend in the data relates to the selected exponent. | When [B] doubles, the rate doubles, so it would be second order [Susan] |
| 3 | Students select two trials such that one variable is held constant; they discuss the impact of changing reactant concentration on the change in the initial rate and attempt to interpret the trend in the data using languages such as “doubles”, “triples”, and “increases by more than double”. Students’ interpretations of either rate or concentration may be incorrect or too vague to serve as an appropriate foundation for determining a reaction order. If the student selects an exponent, they typically do so without a clear relation to the pattern in the data. That is, there is no explicit reasoning. | When [A] triples, the rate gets really big, so it’s probably higher than second order [Callie] |
| 2 | Students examine the experimental data and use an algorithmic approach to find the orders of the reactants. They describe what they did, but not why they did it or how the outcome of the calculation relates to the general pattern in the data. They do not discuss how the selected exponents model the trend in the data. | You can put one rate experiment on top of the other and the k’s cancel out, the B’s cancel out, and then you just have two things to compare [Alana] |
| 1 | Students use the stoichiometric coefficients as the exponents in the rate law; they do not use the rate data and do not discuss holding one variable constant to see the impact of concentration on the rate. | [the rate law] is concentration of products over reactants with the little exponent is the coefficient [Elliott] |
Level 1 responses: recalling the algorithmic approach using stoichiometric coefficients
At a minimum, construction of a rate law from method of initial rates data requires that students recognize the importance of using empirical data. Three of our 15 interview participants did not, in fact, recognize the need for empirical data and instead used stoichiometric coefficients from the balanced chemical equation as exponents in the rate law and hence as the “order” of the species. In the case of one of these participants, Elliott, there was a clear confusion between rate laws and equilibrium constant expressions (Fig. 2).Elliott: “Um, my first reaction would be to remember what the rate law equation would be… which I think is concentration of products over reactants with the little exponent is the coefficient.”
Other students’ reasons for using this approach were less clear. Another student, Fergus, wrote the rate law expression shown in Fig. 3 by using coefficients from the balanced equation as exponents in his rate law. He then described how he would use data from the table to compute the rate of reaction.
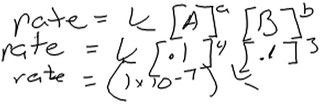 | ||
| Fig. 3 Fergus’s rate law and written work for the rate of the reaction; the rate is calculated using data from experiment 1 (Level 1 reasoning). | ||
Fergus: “Rate equals the constant times the concentration of A to the coefficient times the concentration of B to the coefficient. So just plug in the numbers.”
Fergus’s use of stoichiometric coefficients as exponents in his rate law seemed to preclude deeper analysis of the data and reflection on how the mathematical expression relates to the data. He may have recalled using a similar approach in his general chemistry class, for instance when constructing elementary reactions to help infer the mechanism of a reaction. However, neither Fergus nor any of our other participants mentioned reaction mechanisms or elementary steps or gave any indication that they recognized that this approach would be valid only if thinking about elementary reaction steps.
Level 2 response: low-level use of data in conjunction with an algorithmic approach
Two participants, Aaron and Alana, did recognize the need to use empirical data in the construction of their rate laws, but did so by using an algorithmic approach in which they set up generic rate law expressions and, using concentration and rate data from two trials, took the ratio of the expressions to solve for the unknown exponents. This approach was taught in the participants’ introductory chemistry course and is potentially useful when the order of reaction cannot be easily inferred by inspection of the data alone. And, in contrast to students who used a Level 1 approach, this approach suggests that participants recognized, at a basic level, the need to use empirical data to construct a rate law and the need to control variables as they examine the impact of concentration on rate.While some participants who initially used an algorithmic approach (e.g. Alana) were able to explain the results of their calculation when probed to do so (that is, they were able to provide reasoning in support of their selected exponent), this was not the case for one participant, Aaron. We discuss his approach here because we believe his reasoning to be distinct from those of the other participants and potentially representative of a significant trend if a larger population of students were to be examined.
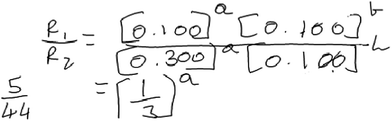
When approaching the method of initial rates task in 1a, Aaron used this algorithmic approach seemingly with little understanding of what the objective of the task was and he did not reflect on the appropriateness of the results. To illustrate Aaron’s reasoning, consider the following excerpt from his interview (Fig. 4).
Aaron: “To find the value of A we’ll use experiment 1 and experiment 2 now. So, rate 1 divided by rate 2 equals to—I won’t write the formula again, I’ll just put the values. It would be 0.100 raised to A multiplied by 0.100 raised to B the entire thing upon 0.300 raised to A and 0.100 raised to B. And this will cancel out so we’ll basically have the value of R1 [the rate for experiment 1] is 5 and R2 is 44. So, 5 by 44 and on the other side 1 by 3 raised by A. So, I’m not sure how this goes after this because it’s 44. Yeah I can’t get it down to 1 by 3.”
Aaron selected data from experiments 1 and 2 in his attempt to construct a rate law. He noted that the concentration of B was the same for both trials, enabling him to examine the effect of one reactant at a time on the reaction rate. His approach and earlier discussion of the term rate law, in which he noted that rate laws are constructed using experimental data, suggest some recognition of the empirical basis of rate laws as well as the necessity of controlling the concentration of one reactant species to examine the impact of the other on the rate.
Aaron did happen to determine the order of B correctly. However, he struggled with determining the order in A. He seemed to be stuck on the fact that when he solved for the expression in Fig. 4 for “a” (the order for A), the left-hand side of his expression in Fig. 4 (5/44) could not be reduced to an integer value that he could easily interpret.
Indeed, in our design of the interview protocol, we intentionally included values of the initial rate and concentration that would generate a non-integer value of the exponent if an algorithm was applied. We believed this would provide an opportunity to assess whether students could (a) reason about the fact that rate laws model a general pattern in the data rather than a specific change between two trials and (b) that experimental error may lead to deviations from a general trend. Though Aaron explicitly commented on the fact that rate laws are experimentally derived, his difficulties may reflect a shallow understanding of what this means in practice.
Level 3: interpretation of patterns in data
In what we refer to as Level 3 responses, students used empirical data in the construction of their rate laws, attempted to interpret the patterns in the data, and used those patterns to select an exponent for the rate law. This interpretation of the data is critical to enabling students to reason mathematically about the relationship in the trend in the data. However, students who gave what we refer to as Level 3 responses stopped short of connecting their interpretation of the data to the selected exponent; that is, they did not provide explicit reasoning. In some cases, students’ reasoning reflected difficulty with certain aspects of the task, such as handling the approximation or in recognizing mathematical relationships beyond linear (first order) relationships. Not surprisingly, students typically guessed at an exponent and gave no explicit reasoning (mathematical or otherwise) for how the selected exponent enabled the rate law to fit the data. Five participants used this type of reasoning when attempting to determine order in A. To illustrate, consider Susan’s reasoning about the rate law task.Susan: “Okay so the concentration from [experiment] 1 to [experiment] 2 A triples. So, you would see what happens with the rate and that would give you your exponent kind of. I don’t remember how to write it out, but okay since that triples, oh geez that doesn’t triple.”
Earlier, Susan noted that her intent in selecting data from experiments 1 and 2 was to ensure that [B] remained constant so that she could examine only the impact of changing [A] on rate. She described the change in A as “A triples”, but struggled to specify the extent of the increase in rate (“oh geez, that doesn’t triple”). She wrote the expression shown in Fig. 5, but did not reflect on what an exponent of 0 would mean (that changing [A] would not affect the rate) and whether the expression fits what she observed in the data.
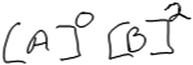 | ||
| Fig. 5 Susan’s rate law (reasoning classified as Level 3 for the reaction order in A, Level 4 for the reaction order in B). | ||
Susan later remarked that part of her difficulty in determining order in A was that the rate across trials 1 and 2 did not increase by an integer factor.
Susan: “It just seemed odd to me that when the concentration of A tripled and B remained the same, the rate did something that didn’t seem to correlate in my mind. So, there’s either something that I’m forgetting or something because it did more than triple. But it also wasn’t an even division, so I wasn’t sure what to do with that.”
Here, Susan referred to an earlier attempt at dividing the rates from trials 1 and 2, noting that “it wasn’t an even division”, which we interpreted to mean that the result of the division was not an integer value (44.0/5.00 = 8.8). Additionally, her confusion about A tripling while the rate more than tripled suggested that she may have been expecting the rate to increase proportionally with concentration.
Level 4: mathematizing trend in data but with incorrect reasoning
Participant responses classified as Level 4 involved the appropriate use of evidence and appropriate interpretation of the trends in the concentration and rate data. Students also provided some explicit reasoning about how their selected exponent modeled the trend in the data. The distinction between Level 4 and the remaining types of reasoning we observed (Level 5) is that Level 4 responses included incorrect reasoning about the relationship between the exponent and data. For example, Penelope reasoned about order in A as follows:Penelope: “Looking at A you see from here to here A triples while [B] is constant and rate goes up by nine. So that would be A to the third power I think, because how much it goes up by is three squared which in nine [writes 32 → 9], which is why it gets nine time faster.”
Penelope wrote the expression 32 → 9 while working through the task. An expert might interpret this expression by observing that 3 represents the 3-fold increase in the concentration of A, 9 represents the 9-fold increase in the reaction rate, and 2 represents the exponent selected to model the relationship between the concentration and rate. Penelope seemed to misinterpret this expression, however, and identified 3 as the order for A (Fig. 6), perhaps because she did not see the relationship between the expression she wrote and the rate law.
Later in her interview, she seemed to recognize that her rate law as written would not enable her to replicate the trend in the data, but she remained firm in her assertion that the order in A would be third order.
Penelope: “If [concentration in A] doubled and [rate] got nine times faster that would explain the jump from here to here as third order, and I know it’s not first. So, it has to be between those two even if I don’t remember the math of how exactly to work it out because I don’t remember.”
For other participants, incorrect reasoning was the result of the application of heuristics beyond their appropriate scope. To illustrate, consider the following vignette from Susan’s interview as she reasoned about the order in B. Earlier we presented her reasoning for the order in A as an example of a Level 3 response.
Susan: “From experiment 1 to 3, [B] definitely doubles and the rate doubles. I don’t remember exactly how this correlates to the exponent for the rate law, but I know it does because I remember the rate law having something to do with the concentration of A and some exponent, which often times could be 1 and the concentration of B. I believe the exponent should be squared because [concentration] is doubled. But I don’t remember what to do here because I don’t know the exact correlation.”
Susan identified a trend in the data (“[B] doubles and the rate doubles”) and used the notion that “doubling means 2” to select an exponent of 2 for B in the rate law. We consider the idea that “doubling means 2” to be a heuristic or “common-sense” idea (Talanquer, 2006). This idea may work well for modeling relationships in some circumstances, for instance, modeling a linear increase in concentration by selecting a concentration multiplier. However, Susan did not seem to recognize that the approach was not valid when selecting an exponent for the rate law. Overall, Susan clearly tried to connect rate, concentration, and the exponent in some reasoned way. Perhaps because she did not understand what the rate law is for (modeling the relationship between rate and concentration), she did not go beyond application of this heuristic to realize that her rate law as written would in fact, predict that the rate would quadruple, rather than double, when concentration doubles, which does not fit the data.
We observed similar reasoning patterns as students reasoned about the order in A, with common errors including students selecting an exponent of 3 with the analogous reasoning that “tripling means 3”.
Level 5: mathematizing trend in data with appropriate reasoning
Responses categorized as Level 5 included the correct aspects of previous levels, for instance, the appropriate selection of two experimental trials such that concentration of one reactant is held constant and an appropriate interpretation of the trend in the data. In addition, Level 5 responses also included correct reasoning about the relationship between the change in rate and concentration. To illustrate, consider Penelope’s reasoning for the order of B (previously, her discussion of order in A was discussed as an example of Level 4 reasoning).Penelope: “The way I understood rate law is rate equals the constant times sometimes the concentration of the reactants. And to find out how the reactants affect it [rate] you have to use experimental data. And so, I’d look at this [points to data in table] and I’d look every time the concentration doubles what it does to the actual rate…Looking at this from here to here [examines trial 1 and trial 3] let’s see- … B doubles and this [rate] doubles, so that would be first order. So, B to the one power so it’d be itself.”
Penelope wrote an exponent of 1 for B in her rate law expression (Fig. 6) and reflected on the appropriateness of this exponent in terms of how well it enabled her rate law to model the observed changes in concentration and rate (“So B to the one power, so it’d be itself”). Overall, her approach to determining the order of reaction in B and her responses to follow-up prompts suggests a relatively sophisticated level of understanding of both the nature of rate laws as experimentally determined models, and of how to analyze and interpret data, and mathematically reason about the relationship between concentration and rate.
Some responses characterized as Level 5 did not involve formal mathematical reasoning and instead appealed to more general rules that did fit in this particular instance. Marjorie, for instance, recognized a linear relationship between the rate and B, which she associated with a first order relationship and an exponent of 1 in the rate law.
Marjorie: “If you look at the rate, the rate doubles, so B is first order.”
Interviewer: “Okay, what does that term mean to you? First order?”
Marjorie: “…When I think of first order I think of a linear line.”
The use of non-mathematical reasoning was especially common in participants’ discussion of order in B (6 of 9 participants whose responses were classified as Level 5), perhaps due to the relatively simple relationship between rate and concentration.
The role of metaknowledge of modeling in students’ reasoning
It is important to note that some responses categorized as Level 5 still reflect limited understanding of the nature and purpose of rate laws. To an expert, construction and use of mathematical models such as rate laws are guided by a deeper understanding of the nature and purpose of models within the scientific inquiry (Schwarz and White, 2005). Such ideas have been referred to as “metamodeling ideas” and include, for instance, the idea that models may be experimentally determined, may be revised on the basis of new evidence, or that models capture key features or trends but are not equivalent to the system they represent (Treagust et al., 2002; Schwarz and White, 2005).From participants’ responses to our probes addressing the meaning of the term rate law and the rate law task, we saw some evidence that students may miss key aspects of metamodeling knowledge and that the lack of robust metamodeling knowledge may hinder students’ reasoning about rate laws. For instance, students who reasoned at Level 1 did not use the data at all and relied instead on a recalled algorithm. As we have discussed, this type of reasoning may reflect confusion about when a particular algorithm is applicable (equilibrium constants or elementary reaction steps). Alternately, this approach may suggest a lack of recognition that rate laws are empirically derived.
Even some of the most sophisticated responses (Level 5) were suggestive of difficulties with certain aspects of the tasks, such as the approximation necessary for inferring the order in A. Katie’s response, for example, was characterized as Level 5. She constructed an appropriate rate law (Fig. 7), but qualified that she “guessed” and was still troubled by the approximation aspect of the task.
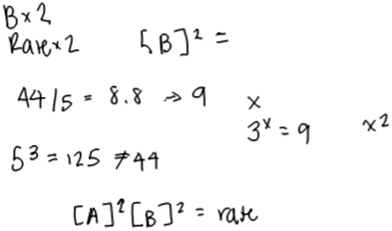 | ||
| Fig. 7 Katie’s written work for the rate law task (response classified as Level 4 for B and Level 5 for A). | ||
Katie: “So A triples and then I need to see the relationship between 44 and 55. Wait 44 and 5. Oh, gosh. There is no clear relationship…Like five cubed is 125.” “…44 divided by 5 is 8.8 and then I don’t really know what to do with that number since it’s not a solid number. If it was like 9 then I could do something with that.”
Here, Katie expressed uncertainty as to how to interpret the outcome of her calculation, since it was not an integer. She described how, if this were an exam, she would select 2 as the order in A.
Katie: “I would probably just guess on a test… I would probably go with [points to where she had written a 2 as the exponent of A] because 8.8 is kind of close to 9 so I would say [writing rate law] [A] squared and [B] squared equals rate.”
Katie was frank about the fact that she knew how to “do the math” to get a rate law, but didn’t feel that she deeply understood rate laws at a conceptual level. Earlier in her interview, when asked to discuss her understanding of the term “rate law”, Katie commented that rate laws are:
Katie: “How fast the reactions gonna go to product. And which reactant gets used faster maybe. I never really understood it. I just know how to do the math then that’s it.”
Her discussion of how she understands the term “rate law”, together with her problem-solving approach, suggests a limited understanding of the ideas that (1) mathematical models such as rate laws predict patterns in the data, but not necessarily individual observations and that (2) experimental error may contribute to deviations from a general pattern. Both of these ideas are key understandings about the nature of scientific inquiry that would support students in the method of initial rates task.
Our analysis highlights that the ability to engage in the practices of mathematical thinking and analyzing and interpreting data are necessary competencies, but are not sufficient for full engagement in model-based reasoning. Thus, a deeper understanding of the nature and purpose of specific models, ideas that we refer to as meta-knowledge of modeling, is also critical for the development of an expert-like understanding of how and when to use mathematical models in chemistry contexts (Schwarz and White, 2005).
Comparison of student reasoning about the order in A compared to the order in B
Fig. 8 and 9 summarize our characterization of students’ final responses across the two subtasks.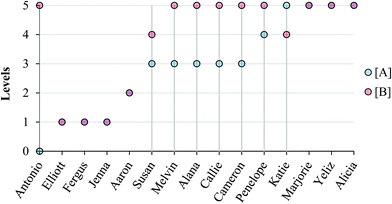 | ||
| Fig. 8 Summary of final student responses to Task 1a to five levels of reasoning; vertical lines highlight students who reasoned differently about the reaction order in (A) compared to (B). | ||
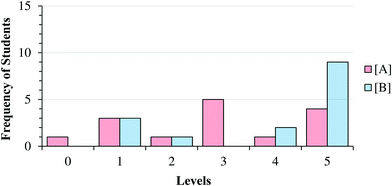 | ||
| Fig. 9 Frequency of final student responses to Item 1A; Level 0 represents participants who did not select an exponent for the task (e.g. “I don’t know”). | ||
As can be seen in Fig. 8 and 9, students who reasoned higher on our progression (Levels 4 and 5) commonly used lower level reasoning (especially Level 3) about the order in task A, suggesting that determining the order in A was, as intended, more challenging.
Participants’ approach to the critiquing rate laws task
In Task 1b, we asked students to comment on the appropriateness of three rate laws constructed by hypothetical students (Fig. 1). We initially conjectured that this task would promote deeper reflections about the appropriateness of the rate law than Task 1a and might support students who used the “coefficients as exponents” approach (Level 1) in a more critical reflection on the empirical basis of rate laws. However, our analysis suggests that this was not necessarily the case. All participants at Levels 1 and 2 and some at Level 3 evaluated the “goodness” of the hypothetical student rate laws by comparing how close the rate laws were to those that they had constructed. Fergus, for instance, decided that the third response (Malika’s) was the best of the three because the exponents used were numerically the closest to the stoichiometric coefficients.Fergus: “They don’t really make sense. She [Megan] has an exponent of 1 for A and 2 for B, but from the equation says, 4A + 3B yields 2C. So, I don’t know where they would even think of that. And this one [Fred’s rate] only has [A]. So that’s like saying there was no B in [the reaction] at all.”
In general, our lower-level participants did not seem to recognize the grounds upon which a rate law should be critiqued, namely based on the ability to model the trend in the data.
Only participants who reasoned at Levels 3 and 4 (and who were already attending to the data) critiqued the rate law by discussing how well the given expression fits the data, and only three of our 15 participants resolved their previous difficulties in response to Task 1b. For instance, Cameron’s initial reasoning about the order in A was classified as Level 3. She recognized the need to interpret the data, but struggled to model the relationship between concentration and rate mathematically and ultimately guessed at a coefficient, after noting that:
Cameron: “A is weird. When you triple it [concentration of A]. It [rate] doesn’t triple though…”
In part, Cameron’s difficulty seemed to lie in deciding whether approximation or rounding was appropriate when trying to determine an exponent for the rate law. Upon seeing Malika’s rate law in 1b, she recognized that she could model the change in rate using an exponent of 2 and clearly articulated how she would use the data to do so. While the hypothetical student rate laws enabled her to more conclusively move forward with approximation, there was still limited discussion as to why approximation would be appropriate here.
Another participant, Antonio approached the method of initial rates task in 1a by exploring with the idea of using coefficients from the balanced reaction as exponents. He ultimately declined to select a coefficient for A as he was uncertain as to the appropriateness of this approach. In Task 1b, he concluded that Malika’s response (second order in A, first order in B) was the best and provided evidence and reasoning for this assertion by discussing the trend in the data and how an exponent of 2 for [A] would replicate the pattern in the data (Level 5 reasoning). Thus, for Antonio, the critiquing task seemed to be a somewhat useful scaffold in that it helped him remember what rate laws are and how they are constructed.
Lastly, Aaron used an algorithmic approach to determine a correct exponent for B in response to Item 1a (Level 2). His discussion of 1a suggested a basic understanding that rate laws are empirical models, but his discussion provided minimal evidence that he could reason about the appropriateness of his exponent for modeling the trend in the data. His critique of Megan’s response in 1b suggested that he was indeed able to reason about how his initial response (first order in B) fits the trend in the data and articulate a rationale for his selected exponent. His reasoning for the order in A, however, remained unchanged, which is perhaps not surprising since the mathematical relationship between the rate and concentration of A was more challenging. Thus, for Aaron, the value of the critiquing task lies in promoting greater articulation of his reasoning.
In summary, our critiquing task proved of limited utility in promoting reflection on the empirical basis of rate laws for students who initially reasoned at Level 1. However, for students who struggled with the mathematical aspect of the task, in some instances, the task seemed to be useful in supporting students in their efforts to interpret data and think mathematically about trends in the data. Overall, participants’ responses to this task suggest that more instructional support for helping students understand how models are constructed and evaluated is needed.
Limitations and ongoing challenges
It is important to remind the reader at this point that our characterizations of students’ reasoning reflect participants’ final responses to the method of initial rates task. Commonly, we observed that students would work through multiple iterations of a solution, often reasoning at lower levels before self-evaluating and changing approach. This is consistent with other researchers’ observations that participants’ reasoning tends to be highly dynamic and context-dependent (Gupta et al., 2010).Our focus on participants’ final response is a limitation because due to our smaller sample size, some of our proposed categories included few final responses, most notably Level 2. We decided to discuss Aaron’s response as representative of what we call “Level 2” reasoning because we suspect his use of an algorithmic approach with limited reflection on the meaning of the results would be representative of a significant number of students in the broader population. We observed similar reasoning patterns with other participants in the course in their attempt to construct a rate law; however, other participants, unlike Aaron, eventually engaged in reflection that moved them beyond rote application of an algorithm. In a forthcoming manuscript, we will report findings from a follow-up study in which we administer an online survey based on the tasks reported here. The larger sample size of the follow-up study will support further examination of the representativeness of these themes, including Level 2.
Our findings must also be interpreted in light of the fact that the framing of the tasks, i.e. in a relatively “traditional” format, plays a large role in how students approach the task. All students were familiar with the format of the method of initial rates task; as we have noted, they received explicit instruction on how to solve this type of problem in lecture. Additionally, an analogous multiple choice task was included in the participants’ unit exam and was framed such that students were asked to select the correct order of reaction for a given reactant species. How students interpreted the task, for instance as one of “getting the right answer” versus one of constructing an empirical argument for a mathematical model certainly played a role in the type of reasoning students perceived as appropriate.
Alternative framings that use more novel task structures may support students such as Aaron, who are accustomed to providing the “right” answer, to reframe the task in a way that is better aligned with the broader scientific practices of analyzing and interpreting data. Shifting framing of assessment tasks is one route towards this, but more systemic shifts (i.e. towards including classroom support for these competencies) are also critical for engaging students more meaningfully with mathematical models in chemistry contexts.
Conclusions and implications
The topic of chemical kinetics broadly, and more specifically the method of initial rates, affords rich opportunities for students to analyze and interpret data and reason mathematically about relationships in the data. All our participants were familiar with method of initial rates tasks, which is not surprising since the method of initial rates appears in most commercially available texts and was featured prominently in the class’s discussion of chemical kinetics.However, our qualitative study of students’ reasoning about a method of initial rates task suggests that after instruction, there is considerable variation in how students approach this type of task. Here, we have described five themes on how our participants justified their construction of a rate law, in order of what we consider to be a progression in how students analyzed data and presented their reasoning about the fit between the mathematical relationships in the rate law they constructed and the data. In what we refer to as a Level 1 response, students used coefficients from the balanced chemical equation as exponents in the rate law. In Level 2 responses, we saw progression towards the use of the data and control of variables, but in conjunction with an algorithmic approach and with limited reasoning addressing the fit between the model and data. In Level 3 responses, participants attempted to interpret the pattern in the data and the relationship between rate and concentration; however, their interpretation of the data was either disconnected from their selection of an exponent for the rate law or suggestive of difficulties in interpreting the trend in the data. Only in Levels 4 and 5 responses did we see participants attempting to reason about the appropriateness of the mathematical form of the rate law. Responses classified as Level 4 were characterized by errors in mathematical reasoning or application of heuristics beyond their appropriate scope. Level 5 responses, in contrast, were characterized by appropriate interpretation of the data and appropriate reasoning. It is noteworthy that even Level 5 responses could reflect difficulties in understanding the nature and purpose of rate laws and difficulties handling certain aspects of the tasks, such as the approximation necessary to infer the reaction order for A.
The ability to construct and evaluate models has been highlighted as a key competency in STEM fields (National Research Council, 2012). However, our findings from the critiquing rate law task (1b) suggest that without explicit instructional support for this competency, a significant proportion of students may not develop these skills. When asked to critique rate laws constructed by hypothetical students, participants with lower level reasoning in the method of initial rates task attended only to the closeness of exponents in the given rate laws to those they selected, suggesting a lack of recognition of the empirical basis of rate laws. We suggest that such responses reflect a broader challenge that is limited understanding of key ideas about the nature and purpose of models in science, ideas that have been referred to as metamodeling (Schwarz and White, 2005; White et al., 2011). Such metamodeling ideas include the notion that rate laws are constructed based on empirical data and that mathematical models are evaluated based on how well they model trends in empirical data. As such, more explicit attention towards these ideas in instructional settings is warranted.
Our participants’ challenges with the method of initial rates are certainly influenced by our instructional context. As is typical in large-enrollment introductory chemistry courses, students’ abilities to reason with and about rate laws were assessed largely through the use of multiple-choice assessments. Typical questions asked, for instance, were that students identify the correct reaction order for a particular reactant in a rate law or that they select the correct rate law from a list of options. The challenge with such tasks is that they provide little evidence of the extent to which students are able to engage in inter-related practices, such as analyzing data and modeling trends in data mathematically. And certainly, the algorithmic approaches and test-wiseness strategies that are commonly used with such tasks do little to promote reflection on these aspects of the tasks.
If we are to support students’ engagement with complex practices, such as constructing and evaluating models and interpreting data, it is essential that we design assessments that specifically probe these competencies and provide formative feedback to students and instructors. We see our characterization as one route towards supporting researchers and instructors in thinking about how to better support student reasoning.
References
- Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17, 246–262 10.1039/C5RP00176E.
- Boudreaux A., Shaffer P., Heron P. and McDermott L., (2008), Student understanding of control of variables: deciding whether or not a variable influences the behavior of a system, Am. J. Phys., 76, 163–170 DOI:10.1119/1.2805235.
- Briggs D. C., Alonzo A. C., Schwab C. and Wilson M., (2006). Diagnostic assessment with ordered multiple-choice items, Educ. Asses., 11(1), 33–63 DOI:10.1207/s15326977ea1101_2.
- Brown T. E., LeMay H. E., Bursten B. E., Murphy C., Woodward P. and Stoltzfus M. E., (2014), Chemistry: The Central Science, 13 edn, Boston: Pearson.
- Cakmakci G., (2005), A cross-sectional study of the understanding of chemical kinetics among Turkish secondary and undergraduate students, England: University of Leeds.
- Cakmakci G., (2010), Identifying alternative conceptions of chemical kinetics among secondary school and undergraduate students in Turkey, J. Chem. Educ., 87, 449–455 DOI:10.1021/ed8001336.
- Cakmakci G. and Aydogdu C., (2011), Designing and evaluating an evidence-informed instruction in chemical kinetics, Chem. Educ. Res. Pract., 12, 15–28 10.1039/C1RP90004H.
- Cakmakci G., Leach J. and Donnelly J., (2006), Students’ ideas about reaction rate and its relationship with concentration or pressure, Int. J. Sci. Educ., 28, 1795–1815 DOI:10.1080/09500690600823490.
- Corbin J. and Strauss A., (2008), Basics of qualitative research: Techniques and procedures for developing grounded theory, 3rd edn, Thousand Oaks, CA: Sage Publications.
- diSessa A. A., (1993), Toward an epistemology of physics, Cogn Instr., 10(2/3), 105–225.
- Gunckel K. L., Covitt B. A., Salinas I. and Anderson C. W., (2012), A learning progression for water in socio-ecological systems, J. Res. Sci. Teach., 49(7), 843–868 DOI:10.1002/tea.21024.
- Gupta A., Hammer D. and Redish E. F., (2010), The case for dynamic models of learners’ ontologies in physics, J. Learn. Sci., 19, 285–321 DOI:10.1080/10508406.2010.491751.
- Hammer D. and Elby A., (2003), Tapping epistemological resources for learning physics, J. Learn. Sci., 12(1), 53–90 DOI:10.1207/S15327809JLS1201_3.
- Heisterkamp K. and Talanquer V., (2015), Interpreting Data: The Hybrid Mind, J. Chem. Educ., 92, 1988–1995 DOI:10.1021/acs.jchemed.5b00589.
- Holme T. and Murphy K., (2012), The ACS Exams Institute Undergraduate Chemistry Anchoring Concepts Content Map I: General chemistry, J. Chem. Educ., 89, 721–723 DOI:10.1021/ed300050q.
- Holme T., Luxford C. and Murphy K., (2015), Updating the General Chemistry Anchoring Concepts Content Map, J. Chem. Educ., 92, 1115–1116 DOI:10.1021/ed500712k.
- Izsák A. and Jacobson E., (2017), Preservice teachers' reasoning about relationships that are and are not proportional: A Knowledge-in-Pieces Account, Journal for Research in Mathematics Education, 48, 300–339.
- Justi R., (2002), Teaching and learning chemical kinetics, in Gilbert J. K., de Jong O., Justi R., Treagust D. F. and Driel J. H. V. (ed.), Chemical education: Towards research-based practice, The Netherlands: Kluwer, pp. 293–315.
- Kousathana M. and Tsaparlis G., (2002), Students’ errors in solving numerical chemical equilibrium problems, Chem. Educ. Res. Pract., 3, 5–17 10.1039/B0RP90030C.
- Kurt S. and Ayas A., (2012), Improving students’ understanding and explaining real life problems on concepts of reaction rate by using a four-step constructivist approach, Energy Educ. Sci. Technol., Part B, 4, 979–992.
- MacGregor M. and Stacey K., (1997), Students’ understanding of algebraic notation: 11–15, Educ. Stud. Math., 33(1), 1–19.
- Mohan L., Chen J. and Anderson C. W., (2009), Developing a multi-year learning progression for carbon cycling in socio-ecological systems, J. Res. Sci. Teach., 46(6), 675–698 DOI:10.1002/tea.20314.
- Murphy K., Holme T., Zenisky A., Caruthers H. and Knaus K., (2012), Building the ACS Exams Anchoring Concept Content Map for Undergraduate Chemistry, J. Chem. Educ., 89, 715–720 DOI:10.1021/ed300049w.
- National Research Council., (2012), A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, D.C.: National Academies Press.
- Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: is there a difference? J. Chem. Educ., 64, 508 DOI:10.1021/ed064p508.
- Osborne J., (2014), Teaching scientific practices: meeting the challenge of change, J. Res. Sci. Teach., 25(2), 177–196 DOI:10.1007/s10972-014-9384-1.
- Pasley J. D., Trygstad P. J. and Banilower E. R., (2016), What does Implementing the NGSS Mean? Operationalizing the science practices for K–12 classrooms, Chapel Hill, NC: Horizon Research, Inc.
- Schuchardt A. M. and Schunn C. D., (2016), Modeling Scientific Processes With Mathematics Equations Enhances Student Qualitative Conceptual Understanding and Quantitative Problem Solving, Sci. Educ., 100(2), 290–320 DOI:10.1002/sce.21198.
- Schwarz C. V. and White B. Y., (2005), Metamodeling Knowledge: Developing Students’ Understanding of Scientific Modeling, Cogn Instr., 23(2), 165–205 DOI:10.1207/s1532690xci2302_1.
- Talanquer V., (2006), Commonsense chemistry: a model for understanding students’ alternative conceptions, J. Chem. Educ., 83, 811–816 DOI:10.1021/ed083p811.
- Toulmin S., (1958), The uses of argument, Cambridge, MA: Cambridge University Press.
- Treagust D. F., Chittleborough G. and Mamiala T. L., (2002), Students’ understanding of the role of scientific models in learning science, Int. J. Sci. Educ., 24(4), 357–368 DOI:10.1080/09500690110066485.
- Turányi T. and Tóth Z., (2013), Hungarian university students’ misunderstandings in thermodynamics and chemical kinetics, Chem. Educ. Res. Pract., 14, 105–116 10.1039/C2RP20015E.
- Van Driel J. H., (2002), Students’ corpuscular conceptions in the context of chemical equilibrium and chemical kinetics, Chem. Educ. Res. Pract., 3, 201–213 10.1039/B2RP90016E.
- White B. Y., Collins A. and Frederiksen J. R., (2011), The Nature of Scientific Meta-Knowledge, in Khine M. S. and Saleh I. M. (ed.), Models and Modeling, Springer: Netherlands, pp. 41–76 DOI:10.1007/978-94-007-0449-7_3.
- Wilson M., (2005), Constructing measure: an item response modeling approach, Mahwah, NJ: Lawrence Erlbaum Associates, Inc.
- Wilson M., (2009), Measuring progressions: assessment structures underlying a learning progression, J. Res. Sci. Teach., 46(6), 716–730 DOI:10.1002/tea.20318.
- Yalçιnkaya E., Taştan-Kιrιk Ö., Boz Y. and Yιldιran D., (2012), Is case-based learning an effective teaching strategy to challenge students’ alternative conceptions regarding chemical kinetics? Res. Sci. Technol. Educ., 30, 151–172 DOI:10.1080/02635143.2012.698605.
- Yan Y. K. and Subramaniam R., (2016), Diagnostic appraisal of grade 12 students’ understanding of reaction kinetics, Chem. Educ. Res. Pract., 17, 1114–1126 10.1039/C6RP00168H.
- Zhou S., Han J., Koenig K., Raplinger A., Pi Y., Li D., Bao L., (2016), Assessment of Scientific Reasoning: The Effects of Task Context, Data, and Design on Student Reasoning in Control of Variables, Think. Skills Creat., 19, 175–187 DOI:10.1016/j.tsc.2015.11.004.
| This journal is © The Royal Society of Chemistry 2017 |