 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy transfer in single phase Eu3+-doped Y2WO6 phosphors
J. Llanos *a,
D. Espinozaab and
R. Castilloa
*a,
D. Espinozaab and
R. Castilloa
aDepartamento de Química, Universidad Católica del Norte, Casilla 1280, Antofagasta, Chile. E-mail: jllanos@ucn.cl; Tel: +56 55 2 355615
bDepartamento de Química, Universidad de Chile, Las Palmeras 3425, Santiago, Chile
First published on 7th March 2017
Abstract
Inorganic phosphors based on monoclinic Y2WO6 doped with Eu3+ ions were prepared via conventional solid-state reactions at high temperature. A total of five samples were obtained with different Eu3+ concentrations (0–9%). The purity of the as-prepared phases was checked by powder X-ray diffraction (PXRD). Through the Rietveld refinement, at low concentrations Eu3+ ions are found to occupy preferentially the Y2 (2f) sites in the host compound. However, for higher dopant concentrations, the occupancy of the (2e) and (4g) sites becomes relevant. The excitation, emission, and time-resolved emission spectra were examined in detail. Efficient energy transfer from the (WO6)6− groups to the Eu3+ activators was observed. The decay curves for the Eu3+ 5D0 → 7F4 transition show a non-exponential behavior that is enhanced with increasing Eu3+ concentration. The experimental decay curves were fitted to the Inokuti–Hirayama model to gain some insight into the mechanism of the interaction between the Eu3+ ions in these phosphors.
1. Introduction
In the last decades there has been great interest in the synthesis of inorganic phosphors doped with rare-earth cations mainly because of their uses as luminescent materials in solid-state lighting devices (SSLD), plasma display panels, solar cells, optical sensors, and more recently, for applications in the new fields of nanotechnology and biotechnology.1–6 The trivalent europium ion (Eu3+) is widely used as an activator ion in many phosphors due to its characteristic red emission upon irradiation with UV light, arising from the 5D0 → 7FJ (J = 0,4) transitions.7–9 The 5D0 → 7F1 transition is a magnetic dipole (MD) transition and, hence, its intensity is largely independent from the chemical environment of the Eu3+ cation in the host matrix. In contrast, the electric dipole (ED) 5D0 → 7F2 transition is one of the so-called “hypersensitive transitions”, which means that its appearance and intensity is greatly influenced by the local symmetry of the Eu3+ ion. It is well known that the asymmetric ratio (R) between the intensities of the two ED and MD transitions, 5D0 → 7F2/5D0 → 7F1, can be used as a probe of the local symmetry of the Eu3+ ions in a host material.10,11 For example, in BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eu3+, R > 1 indicates that the proportion of Eu3+ ions in non-centrosymmetric sites is larger than that in centrosymmetric ones, which is in good agreement with the distortion of the lattice found in Eu-doped samples resulting in a change in the local symmetry from octahedral (Oh) to a non-centrosymmetric C4v symmetry.12
Eu3+, R > 1 indicates that the proportion of Eu3+ ions in non-centrosymmetric sites is larger than that in centrosymmetric ones, which is in good agreement with the distortion of the lattice found in Eu-doped samples resulting in a change in the local symmetry from octahedral (Oh) to a non-centrosymmetric C4v symmetry.12
Inorganic phosphors typically consist of an inert host material, normally either oxides, nitrides/oxynitrides, or sulfides/oxysulfides, doped with a small concentration of activator ions. In particular, metal oxides containing d0 transition metal ions, such as VO43−, MoO42−, or WO42− have attracted much attention as host lattices in inorganic phosphors. Tungstates with different stoichiometries, such as Y2WO6, have been studied less extensively, probably due to their rich crystallographic variation. Depending on the synthetic method, Y2WO6 can crystallize in a tetragonal (S.G. P4/nmm), monoclinic (S.G. P2/c), or orthorhombic (S.G. P21ab) form.13–16 On the other hand, Borchardt identified Y2WO6 as a bright photoluminescent material that emitted a pale blue light under ultraviolet excitation17 showing that the excited tungstate groups can effectively transfer energy to doping activator ions.
In the past few years, we have been actively involved in the preparation and characterization of new red-emitting phosphors.18–20 In this paper, Y2−xEuxWO6 red phosphors were synthesized via solid-state reactions and their photoluminescent features were studied. We have carried out a detailed analysis of the energy transfer process between the luminescent excited levels of the dopant Eu3+ ions as a function of their concentration and the interaction between these ions and the host lattice structure. The energy transfer process is found to be well described by the Inokuti–Hirayama model.
2. Experimental
2.1. Synthesis
All Y2−xEuxWO6 samples in this study were prepared at high temperature using solid-state reactions21 starting from a thoroughly ground mixture of the corresponding oxides, Y2O3, Eu2O3, and WO3, in stoichiometric proportions. These mixtures were placed in an alumina boat and heated at 973 K for 10 h before being cooled to below 400 K. The samples were then removed from the crucible, ground into a powder, and reheated for 10 h at 1273 K. The procedure was repeated and the sample was finally heated to 1373 K for another 10 h. Optical inspection of the products showed homogeneous powders with a white color. All of the above synthetic processes were performed under an air atmosphere.2.2. Characterization
To verify the purity of the phases, powder X-ray diffraction (PXD) data were collected using a Bruker D8 Advance diffractometer fitted with a graphite monochromator. The spectra were collected across the range 10° ≤ 2θ ≤ 60°, using Cu Kα radiation (λ = 1.54057 Å) generated at 40 kV and 30 mA. The excitation spectra were measured using a JASCO FP-6500 spectrofluorometer with a 150 W xenon lamp as the excitation source. The emission spectra were obtained by exciting the samples at 300 nm using a 400 W Oriel xenon lamp. The spectra were recorded with a system of two convex lenses that collimated and focalized the Eu3+ emission into an optical fiber coupled to a 0.3 m single grating spectrometer (Andor Shamrock-3031-B). The final measurement was done using a cooled CCD detector (Newton DU920 N) with a resolution of 0.7 nm and an integration time of 2 s. For the lifetime measurements, a tunable optical parameter oscillator (OPO) was used as the excitation source (10 Hz repetition rate, 8 ns pulse temporal width) and the time resolved emission was focused on the entrance slit of a monochromator (Triax 180) coupled with a photomultiplier (Hamamatsu r928). The signal was acquired and averaged by an oscilloscope (Lecroy Wavesurfer 424). All measurements were carried out at room temperature.Thermogravimetry (TG) and differential scanning calorimetry (DSC) analyses were carried out on a STA 448 Jupiter F3 type simultaneous thermal analyzer (Netzsch). The samples used for TG and DSC were powders of about 69 mg in weight. The sample cells were aluminum oxides pans. The parent reagents were heated up to 1373 K at a heating rate of 5 K min−1 under flowing of nitrogen atmosphere at 20 mL min−1.
3. Results and discussion
Samples for a total of five different compositions were synthesized in the Y2−xEuxWO6 system with x ≅ 0, 0.02, 0.06, 0.14 and 0.18. The powder X-ray diffraction patterns for these compounds are similar to those for the monoclinic Y2WO6 phase previously reported in the ICSD (Inorganic Crystal Structure Data) database and by Efremov et al.,22,23 indicating that all samples crystallized isostructurally adopting the monoclinic Y2WO6 structure belonging to the P2/c space group (no. 13). In this structure there are three different crystallographic sites for the Y3+ ion. Two of them are eight-fold coordinated by O− atoms, whereas in the third one, the lanthanide ion is seven-fold coordinated by oxygen atoms (Fig. 1). Upon doping, the trivalent europium ions are expected to occupy the yttrium sites in Y2WO6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eu3+ since the ionic radii of Eu3+, r = 106.6 pm (C.N. = 8) and r = 101.0 pm (C.N. = 7), are only slightly larger than those of Y3+, r = 96 pm (C.N. = 8) and 101.9 pm (C.N. = 7).24 The values of the cell parameters, confirmed by a Le Bail refinement,25,26 for all compounds are given in Table 1, together with their standard deviations. The variation of the unit cell with the Eu3+ content confirms the existence of a range of solid solutions represented by the formula Y2−xEuxWO6 (x ≅ 0.02, 0.06, 0.14 and 0.18).
Eu3+ since the ionic radii of Eu3+, r = 106.6 pm (C.N. = 8) and r = 101.0 pm (C.N. = 7), are only slightly larger than those of Y3+, r = 96 pm (C.N. = 8) and 101.9 pm (C.N. = 7).24 The values of the cell parameters, confirmed by a Le Bail refinement,25,26 for all compounds are given in Table 1, together with their standard deviations. The variation of the unit cell with the Eu3+ content confirms the existence of a range of solid solutions represented by the formula Y2−xEuxWO6 (x ≅ 0.02, 0.06, 0.14 and 0.18).
| Compound | a (Å) | b (Å) | c (Å) | β (°) | Vol. (Å)3 | Ref. |
|---|---|---|---|---|---|---|
| Y2WO6 | 7.578(9) | 5.330(8) | 11.361(18) | 104.36(9) | 444.6(12) | 22 and 23 |
| Y1.98Eu0.02WO6 | 7.578(14) | 5.331(10) | 11.364(2) | 104.36(11) | 444.8(14) | |
| Y1.94Eu0.06WO6 | 7.578(8) | 5.331(10) | 11.365(1) | 104.33(6) | 444.8(12) | |
| Y1.90Eu0.10WO6 | 7.579(1) | 5.333(7) | 11.367(1) | 104.32(7) | 445.2(12) | |
| Y1.86Eu0.14WO6 | 7.578(1) | 5.333(7) | 11.368(2) | 104.31(1) | 445.2(14) | |
| Y1.82Eu0.18WO6 | 7.581(15) | 5.335(10) | 11.372(2) | 104.32(12) | 445.7(16) |
Rietveld refinements for the Y2−xEuxWO6 (x ≅ 0.0, 0.02, 0.18) structures were carried out using the Jana 2006 software.27 The calculated patterns are consistent with the experimental data (see Fig. 2). The occupation factors, refinement parameters and refined compositions are shown in Table 2. As seen, the crystallographic volume of the samples increases with increasing Eu3+ content, while the lattice parameters change only slightly.
 | ||
| Fig. 2 Rietveld refinement results for (a) Y2WO6; (b) Y1.98Eu0.02WO6 and (c) Y1.82Eu0.18WO6. The blue line shows the difference between observed and calculated data. | ||
| Compound | Y2WO6 | Eu0.02Y1.98WO6 | Eu0.18Y1.82WO6 |
| a/Å | 7.578(12) | 7.578(14) | 7.581(15) |
| b/Å | 5.330(8) | 5.331(10) | 5.335(10) |
| c/Å | 11.361(18) | 11.364(2) | 11.372(2) |
| β/(°) | 104.36(9) | 104.36(11) | 104.32(12) |
| V/Å3 | 444.6(12) | 444.8(14) | 445.7(16) |
| Site occupancy | |||
| Y1/Eu1 (2e) | 1.00(4) | 1.00(3)/0.00(3) | 0.83(7)/0.17(7) |
| Y2/Eu2 (2f) | 1.00(5) | 0.95(7)/0.05(7) | 0.86(7)/0.14(7) |
| Y3/Eu3 (4g) | 1.00(3) | 0.98(5)/0.02(5) | 0.90(5)/0.10(5) |
| Rp/(%) | 13.51 | 13.87 | 12.77 |
| Rwp/(%) | 20.41 | 20.89 | 20.13 |
| RF/(%) | 5.89 | 7.03 | 6.57 |
| Refined composition | Y2.00(5)WO6 | Eu0.04(3)Y1.96(3)WO6 | Eu0.25(9)Y1.75(9)WO6 |
Changes in the cell parameters are correlated with the occupation of the Eu3+ ions in the Y3+ positions. One can see that at low concentrations Eu3+ ions occupy preferentially the Y2 (2f) sites, while the occupancy of the Y1 (2e) and Y3 (4g) sites becomes relevant as the concentration of Eu3+ ions increases. This trend in the occupancy of the different sites explains some of the irregularities in the variation of the unit cell parameters for the doped phases (vide supra). On the other hand, the refined compositions obtained through the Rietveld refinement are in good agreement with the TG-DSC experiments (Fig. 3) ruling out the possibility of volatilization of WO3 during the synthesis process.
The emission spectrum of un-doped Y2WO6 under 300 nm UV radiation is shown in Fig. 4. As it has been previously described, tungstate based materials emit blue light (450 nm) themselves under ultraviolet radiation.28 The excitation spectrum of the 450 nm emission for the un-doped sample is dominated by a broad band that can be attributed to the absorption by (WO6)6− groups with a peak centered at about 300 nm (Fig. 4). The decay curve of the blue emission under pulsed laser excitation (300 nm) shown in the inset of Fig. 4 is non-exponential with an intrinsic lifetime of τ = 6.65 μs.
 | ||
| Fig. 4 Emission (λex = 300 nm) and excitation spectra (λem = 450 nm) of Y2WO6. The inset shows the decay curve of the emission band of the un-doped host structure. | ||
PLE spectra of the Eu-doped samples are similar to those previously reported.15 They exhibit a broad band centered at about 300 nm along with very weak f–f transitions at about 395 nm (7F0 → 5L6), 465 nm (7F0 → 5D2), and 540 nm (7F0 → 5D1). The broad, intense band consists of overlapping O2−–Eu3+ and O2−–W6+ charge transfer bands.
Room temperature emission spectra of the Y2−xEuxWO6 (x = 0.0, 0.02, 0.06, 0.14, and 0.18) samples are shown in Fig. 5. The intra-configurational 4f–4f transitions of the Eu3+ ions originating from the 5D0 → 7Fj (J = 0–4) transitions were identified. The most intense emission corresponds to the electric dipole 5D0 → 7F2 transition centered at approximately 610 nm. The emission spectra are also characterized by the band at about 450 nm, originating from the (WO6)6− groups of the host matrix. This emission band disappears when the concentration of the dopant ion is increased. The variation of the emission intensity at 450 nm with the dopant concentration is shown in the inset of Fig. 6. It is observed that while the intensity of the band at 450 nm decreases, that of the band at 610 nm increases for concentrations up to x = 0.14. This phenomenon implies that an energy transfer from the (WO6)6− groups to the Eu3+ ions must occur. At the same time, we observe that the PL intensity decreases when x exceeds 0.14 due to concentration quenching, related to an energy transfer between activator centers. For a good characterization of the PL behavior in this system it is therefore necessary to determinate the critical distance between donors (activator) and acceptors (quenching site) that can be estimated using the equation proposed by Blasse et al.:29
 | (1) |
In order to evaluate the efficiency of the energy transfer (ηET) from the host matrix to the Eu3+ ions, we estimated the emission intensities of the matrix in the presence (Is) and absence (Is0) of the activator ion, using these values to calculate ηET using the following expression:30–32
 | (2) |
The quantum efficiency of the activator ions (QE) ηEu3+ can be calculated using the relevant emission spectra and the following expression:
 | (3) |
| Compound | ηET (%) | ηEu3+ (%) |
|---|---|---|
| Y1.98Eu0.02WO6 | 89.3 | 27.7 |
| Y1.94Eu0.06WO6 | 91.1 | 47.5 |
| Y1.86Eu0.14WO6 | 94.8 | 63.1 |
| Y1.82Eu0.18WO6 | 96.6 | 61.2 |
These results are in good agreement with those reported by Z. Zhao et al. where the optimal concentration of Eu3+ in the Y2WO6 matrix is found to be x = 0.13 (ref. 33) and with those reported by Li. et al., where x = 0.09.16 The behavior found for the Y2WO6 matrix is quite different from that found for the KLa(WO4)2 matrix, for example, where the critical concentration is reached when the Eu3+ concentration is about 40% at.34
As shown in Fig. 6, room temperature emission decay curves upon excitation at 300 nm were measured for the Eu3+ doped samples with different concentrations of the rare-earth ion. Our studies are focused mainly in the 5D0 → 7F4 transition, because the broad emission band of the matrix overlaps the emission corresponding to the 5D0 → 7F2 transition at 610 nm. The decay curves for the Eu3+ 5D0 → 7F4 transition emission show a non-exponential behavior that is enhanced with increasing Eu3+ concentration. The non-exponential character of the decay curves can be explained by taking into account the fact that at intermediate doping concentrations the Eu3+ and the Y3+ ions are randomly distributed in the Y3+ sites in Y2WO6.35 According to Collins et al.36 there are three different regimes of donor decay: (i) no diffusion, where the energy transfer occurs between donor and acceptor with little or no diffusion among donors; (ii) diffusion limited decay, where there is significant diffusion among donors before donor–acceptor energy transfer occurs; and (iii) fast diffusion, during which the diffusion among donors is so fast that the excited atom rapidly comes close enough to an acceptor to allow for a donor–acceptor energy transfer. The non-exponential behavior of the decay curves reveals that the energy transfer process occurs with little or no diffusion among the donors. Hence we use the Inokuti–Hirayama model in order to analyze the decay curves.37 In this model, it is assumed that the activator ions are randomly distributed in the host structure. The Inokuti–Hirayama equation can be formulated as follows:
 | (4) |
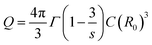 | (5) |
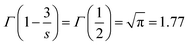 . The energy transfer parameter (Q) can also be described as follows:
. The energy transfer parameter (Q) can also be described as follows:
 | (6) |
 | (7) |
The unit ‘number of ions per cm3’ is used to describe the concentration of both donor and acceptors ions and the intrinsic lifetime of a single ion, τ = 0.85 ms, was obtained from the sample with the lowest concentration of Eu3+ (vide supra). By replacing (R0)3 in eqn (5) by the expression R03 = 3/(4πc0) and rearranging the equation, we get the following expression:
 | (8) |
 | ||
| Fig. 7 Plot of C/C0 vs. (4πC/3). The C/C0 values are taken from the fitting results of dipolar interaction. | ||
4. Conclusions
We prepared Y2WO6 based phosphors doped with different concentrations of Eu3+ via a classic solid-state reaction at high temperature. The luminescent properties of the resultant compounds were investigated. The excitation spectrum is dominated by a broad band consisting of the overlapping O2−–Eu3+ and O2−–WO66+ charge transfer bands, as well as three bands corresponding to the excitations of electrons from the Eu3+ ground state to different excited 4f levels. The emission spectra have a characteristic peak caused by the electric dipole 5D0 → 7F2 transition centered at 610 nm. An emission band centered at about 450 nm originating from the (WO6)6− groups of the host structure is also observed. Moreover, it is found that while the intensity of the band at 450 nm decreases, that of the band at 610 nm increases for dopant concentrations up to x = 0.14 implying the presence of an energy transfer from the host to the Eu3+ ions.The measured decay curves are quite well described by the Inokuti–Hirayama model assuming a dipole–dipole interaction. All results indicate that Eu3+ ions are localized randomly in the structure ruling out the possibility of cluster formation.
Acknowledgements
This work was financially supported by a grant from FONDECYT (Chile) No. 1130248; D. E. Acknowledges CONICYT for providing a doctoral fellowship.References
- T. Jüstel, H. Nikols and C. Ronda, Angew. Chem., Int. Ed., 1998, 37, 3084 CrossRef.
- J. T. Ingle, R. P. Sonekar, S. K. Omanwar, Y. Wang and L. Zhao, J. Alloys Compd., 2014, 608, 235 CrossRef CAS.
- H. Höppe, Angew. Chem., Int. Ed., 2009, 48, 3572 CrossRef PubMed.
- J.-C. Bünzli, Chem. Rev., 2010, 110, 2729 CrossRef PubMed.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301 RSC.
- L. Zhou, J. Huang, F. Gong, Y. Lan, Z. Tong and J. Sun, J. Alloys Compd., 2010, 495, 268 CrossRef CAS.
- J. Llanos, R. Castillo, D. Espinoza, R. Olivares and I. Brito, J. Alloys Compd., 2011, 509, 5295 CrossRef CAS.
- F. Meng, H. Zhang, C. Chen, S. I. Kim and H. J. Seo, J. Alloys Compd., 2016, 671, 150 CrossRef CAS.
- H. Marzougui, I. R. Martín, S. Attia-Essaies, D. B. Hassen-Chehimi, E. Lalla and S. B. F. León-Luis, Opt. Mater., 2015, 46, 339 CrossRef CAS.
- U. Rambabu and S.-D. Han, RSC Adv., 2013, 3, 1368 RSC.
- G. Gao and L. Wondraczek, Opt. Mater. Express, 2014, 4, 480 CrossRef.
- S. Fuentes, N. Barraza, E. Veloso, R. Villarroel and J. Llanos, J. Alloys Compd., 2013, 569, 52 CrossRef CAS.
- J. Huang, J. Xu, H. Li, H. Luo, X. Yu and Y. Li, J. Solid State Chem., 2011, 184, 843 CrossRef CAS.
- R. Hao, Q. Meng, W. Liu and H. Liu, J. Rare Earths, 2013, 31, 864 CrossRef CAS.
- J. Llanos, D. Olivares, V. Manríquez, D. Espinoza and I. Brito, J. Alloys Compd., 2015, 628, 352 CrossRef CAS.
- X. Shi, J.-G. Li, Q. Zhu, X. Li and X. Sun, J. Alloys Compd., 2017, 695, 1984 CrossRef CAS.
- H. J. Borchardt, J. Chem. Phys., 1963, 2, 170 CAS.
- J. Llanos and R. Castillo, J. Lumin., 2009, 129, 465 CrossRef.
- J. Llanos and R. Castillo, J. Lumin., 2010, 130, 1124 CrossRef CAS.
- J. Llanos, R. Castillo, I. R. Martin, L. L. Martin, P. Haro-González and J. González-Platas, J. Lumin., 2014, 145, 553 CrossRef CAS.
- Z. Zhang, W. Wang, M. Shang and W. Yin, J. Hazard. Mater., 2010, 177, 1013 CrossRef CAS PubMed.
- V. A. Efremov, A. V. Tyulin, V. K. Trunov, O. V. Kudin, V. K. Yanosvskii and V. I. Voronkoba, Kristallografiya, 1984, 29, 904 CAS.
- Inorganic Crystal Structure Database, ICSD, Fachinformationzentrum Karlsruhe, Release 1/2016, Coll. Code. #20955.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- A. L. Bail, Powder Diffr., 2005, 20, 316 CrossRef.
- A. L. Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447 CrossRef.
- V. Petricek, M. Dusek and L. Palatinus, J. Crystallogr., 2014, 229, 345 CAS.
- X.-Y. Chen, Z.-J. Zhang, L.-L. Zhu, M. Xu, H. Wang, A.-G. Li and J.-T. Zhao, Appl. Surf. Sci., 2014, 317, 730 CrossRef CAS.
- G. Blasse, Philips Res. Rep., 1969, 24, 131 CAS.
- U. Caldiño, J. Hernández-Pozos, C. Flores, A. Speghini and M. Bettinelli, J. Phys.: Condens. Matter, 2005, 17, 7297 CrossRef.
- U. Caldiño, A. Speghini and M. Bettinelli, J. Phys.: Condens. Matter, 2006, 18, 3499 CrossRef.
- G. Ju, Y. Hu, L. Chen, X. Wang, Z. Mu, H. Wu and F. Kang, J. Lumin., 2012, 132, 1853 CrossRef CAS.
- J. Li, Z. Wu, X. Sun, X. Zhang, R. Dai, J. Zuo and Z. Zhao, J. Mater. Sci., 2017, 52, 3110 CrossRef CAS.
- M. Kavi Rasu, D. Balaji and S. Moorthy Babu, J. Lumin., 2015, 170, 547 CrossRef.
- P. Vergeer, T. J. H. Vlugt, M. H. F. Kox, M. I. den Hertog, J. P. J. M. van der Erden and A. Meijerink, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014119 CrossRef.
- J. Collins, M. Geen, M. Bettinelli and B. Di Bartolo, J. Lumin., 2012, 132, 2626 CrossRef CAS.
- M. Inokuti and F. Hirayama, J. Chem. Phys., 1965, 43, 1978 CrossRef CAS.
- X. Zhang, Z. Zhang, S. I. Kim, Y. M. Yu and H. J. Seo, Ceram. Int., 2014, 40, 2173 CrossRef CAS.
- K.-S. Sohn, Y. G. Choi, Y. Y. Choi and H. D. Park, J. Electrochem. Soc., 2000, 147, 3552 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |




