Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles study of Zr–N crystalline phases: phase stability, electronic and mechanical properties†
Shuyin Yu *ab,
Qingfeng Zengab,
Artem R. Oganovbcde,
Gilles Frapperf,
Bowen Huangf,
Haiyang Niuc and
Litong Zhanga
*ab,
Qingfeng Zengab,
Artem R. Oganovbcde,
Gilles Frapperf,
Bowen Huangf,
Haiyang Niuc and
Litong Zhanga
aScience and Technology on Thermostructural Composite Materials Laboratory, Northwestern Polytechnical University, Xi'an, Shaanxi 710072, China. E-mail: yushuyin2014@gmail.com
bInternational Center for Materials Discovery, Northwestern Polytechnical University, Xi'an, Shaanxi 710072, China
cDepartment of Geosciences, Center for Materials by Design, Institute for Advanced Computational Science, State University of New York, Stony Brook, NY 11794-2100, USA
dSkolkovo Institute of Science and Technology, 3 Nobel Street, Skolkovo 143025, Russia
eMoscow Institute of Physics and Technology, Dolgoprudny, Moscow Region 141700, Russia
fIC2MP UMR 7285, Université de Poitiers, CNRS, 4, rue Michel Brunet, TSA 51106, 86073 Poitiers Cedex 9, France
First published on 17th January 2017
Abstract
Using a variable-composition ab initio evolutionary algorithm, we investigate stability of various Zr–N compounds. Besides the known ZrN and Zr3N4, new candidate structures with Zr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratios of 2
N ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 6
3, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 8
5, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 15
7, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, 7
16, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and 4
8 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 are found to be ground-state configurations, while Zr3N2 has a very slightly higher energy. Besides Zr2N, the newly discovered ZrxNy compounds adopt rocksalt structures with ordered nitrogen or zirconium vacancies. The electronic and mechanical properties of the zirconium nitrides are further studied in order to understand their composition–structure–property relationships. Our results show that bulk and shear moduli monotonically increase with decreasing vacancy content. The mechanical enhancement can be attributed to the occurrence of more Zr–N covalent bonds and weakening of the ductile Zr–Zr metallic bonds. These simulations could provide additional insight into the vacancy-ordered rocksalt phases that are not readily apparent from experiments.
5 are found to be ground-state configurations, while Zr3N2 has a very slightly higher energy. Besides Zr2N, the newly discovered ZrxNy compounds adopt rocksalt structures with ordered nitrogen or zirconium vacancies. The electronic and mechanical properties of the zirconium nitrides are further studied in order to understand their composition–structure–property relationships. Our results show that bulk and shear moduli monotonically increase with decreasing vacancy content. The mechanical enhancement can be attributed to the occurrence of more Zr–N covalent bonds and weakening of the ductile Zr–Zr metallic bonds. These simulations could provide additional insight into the vacancy-ordered rocksalt phases that are not readily apparent from experiments.
1 Introduction
Group IVB transition metal (TM = Ti, Zr and Hf) nitrides have been widely used in cutting tools and as wear-resistant coatings, because of their excellent properties such as high hardness and strength, high melting points, excellent thermal conductivity, and good chemical stability.1–4 Formally, their mononitrides adopt the rocksalt structure, but may show significant variation in composition, both towards cation and anion enrichment.1 Such nonstoichiometry widely exists in group IV/V transition metal oxides, nitrides and carbides, due to the formation of structural vacancies.5 The concentration of vacancies can be up to 50 at%. Their microstructures are usually controlled by the co-precipitation of nonstoichiometric phases, and the mechanical behavior is dependent on the vacancy concentration.Unlike carbides, not only nonmetal vacancies exist, but structure can also tolerate metal atom vacancies since metal atom oxidation state can reach +4.6 Experimental investigations of nonstoichiometric TM nitrides (TM = Ti, Zr, Hf, V, Nb and Ta) have been conducted intensely for more than thirty years.7–10 About twenty ordered carbides and nitrides have been found.1 However, it has not yet been possible to construct a single phase diagram of TM–C or TM–N systems at low temperatures (most of the available phase diagrams have been constructed above 1300–1500 K). In this paper, we explore stable compounds in the Zr–N system at ambient pressure and finite temperatures. To date, there is no comprehensive and inclusive computational investigation of phase stability in the Zr–N system.
Zirconium nitrides represent a rich family of phases where the stability and microstructures are still not completely understood. According to the phase diagram provided by Gribaudo et al.,11 ZrN and Zr3N4 can be stable at ambient conditions. In 2003, c-Zr3N4 with a Th3P4 structure was synthesized by Zerr et al. using diamond-anvil cell experiments at 16 GPa and 2500 K.12 This compound was expected to exhibit a very high Vickers hardness around 30 GPa, similar to that of γ-Si3N4. However, Kroll showed that hardness is just slightly harder than 14 GPa.13 Besides c-Zr3N4, an orthorhombic Pnma modification of Zr3N4 has been proposed.14 First-principles calculations show that o-Zr3N4 is energetically more stable than c-Zr3N4.15 However, both structures are metastable considering decomposition into ZrN and N2.13 Besides, two nitrogen-rich phases ZrNx (1.06 < x < 1.23) with NaCl-type structures have been claimed by Juza et al. in 1964.16 However, precise stoichiometries and crystal structures are not known for their synthesized samples.
Here, we apply recently developed evolutionary algorithm USPEX to extensively explore the crystal structures and stoichiometries in the Zr–N system at ambient conditions, and then their phase stability at finite temperatures are evaluated. Furthermore, the electronic and mechanical properties of stable ZrxNy compounds are studied using density functional theory. Our work should provide guidance for experimental groups aiming to synthesize these new technologically useful materials.
2 Computational details
Searches for low-energy crystalline Zr–N structures were performed using evolutionary algorithm (EA) methodology implemented in the USPEX code17–19 in its variable-composition mode.20 The energies and structural optimizations (including lattice shape, volume and atomic positions) were calculated by VASP package based on density-functional theory.21 The first generation contained 80 randomly produced candidate structures, which were produced under the following constraints: (1) all possible stoichiometries were allowed, (2) the maximum number of atoms is 30 in the primitive cell. In the subsequent generations, each generation contained 60 structures, which were produced by applying heredity (50%), atom transmutation (20%), lattice mutation (15%) operators, while some structures were still randomly (15%). These are typical parameters for USPEX calculations, with which efficiency is known to be very high. Besides, we also performed a fixed-composition search for Zr15N16 which has 31 atoms in its primitive cell.First-principles electronic structure calculations were carried out within the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof form.22 The interactions between ions and electrons were described by the projector-augmented wave method23 with a cutoff energy of 600 eV. Uniform Γ-centered k-points meshes with a resolution of 2π × 0.03 Å−1 and Methfessel–Paxton electronic smearing24 were adopted for the integration in the Brillouin zone. These settings ensure convergence of the total energies to within 1 meV per atom. Structure relaxation proceeded until all forces on atoms were less than 1 meV Å−1 and the total stress tensor was within 0.01 GPa of the target value.
Theoretical phonon spectra were calculated with the supercell method using the PHONOPY package.25 Hellmann–Feynman forces exerted on all atoms in supercells (2 × 2 × 2 of the unit cell) were calculated by finite atomic displacements of each symmetrically nonequivalent atom. Phonon dispersion relations were then obtained by the diagonalization of the dynamical matrix. We used the quasiharmonic approximation to calculate the free energy of zirconium nitrides at finite temperatures. Free energy of a crystal was obtained as a sum of the static total energy, vibrational energy and configurational energy. Computational details are described in ESI.†
3 Results and discussion
3.1 Phase stability of the Zr–N system at finite temperatures
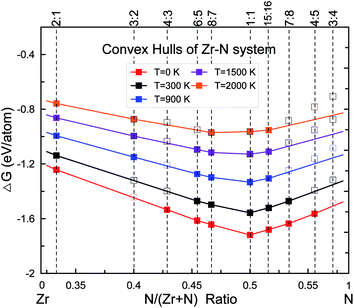
Thermodynamic stability of zirconium nitrides in the temperature range of 0–2000 K was quantified by constructing the thermodynamic convex hull, which is defined as the Gibbs free energy of formation of the most stable phases at each composition:| ΔG(ZrxNy) = [G(ZrxNy) − xG(Zr) − yG(N)]/(x + y) | (1) |
Any phase located on the convex hull is considered to be thermodynamically stable (at T = 0 K, G = H) and at least in principle synthesizable.26 In the case of zirconium nitrides, a series of stable compounds at various Zr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratios, i.e. 2
N ratios, i.e. 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 6
3, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 8
5, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 1
7, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 15
1, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, 7
16, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, 4
8, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 have been discovered by our evolutionary searches at 0 K, shown in Fig. 1. The rocksalt ZrN with space group (SG) Fm
5 have been discovered by our evolutionary searches at 0 K, shown in Fig. 1. The rocksalt ZrN with space group (SG) Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m was found to have the lowest enthalpy of formation. Besides ZrN, substoichiometric Zr2N (SG: P42/mnm), Zr4N3 (SG: C2/m), Zr6N5 (SG: C2/m) and Zr8N7 (SG: C2/m) have also been found to be thermodynamically stable. For the missing composition Zr3N2, the lowest-energy structure is Immm with the enthalpy of formation lying very close to the convex hull at only 0.005 eV per atom, i.e. Zr3N2 is a metastable phase at 0 K.
m was found to have the lowest enthalpy of formation. Besides ZrN, substoichiometric Zr2N (SG: P42/mnm), Zr4N3 (SG: C2/m), Zr6N5 (SG: C2/m) and Zr8N7 (SG: C2/m) have also been found to be thermodynamically stable. For the missing composition Zr3N2, the lowest-energy structure is Immm with the enthalpy of formation lying very close to the convex hull at only 0.005 eV per atom, i.e. Zr3N2 is a metastable phase at 0 K.
Additionally, Juza et al. in 1964 have discovered two nitrogen-rich phases ZrNx (1.06 < x < 1.23) with rocksalt structures.16 The synthesized sample had a dark blue color and turned into metallic ZrN upon heating. Unfortunately, detailed stoichiometries and crystallographic information were not determined. Subsequent studies even questioned the existence of these two compounds.11 From our evolutionary searches, we found these two compounds could be Zr15N16 (x = 1.07, SG: P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and Zr4N5 (x = 1.25, SG: C2/m). Their structures are composed of edge-sharing ZrN6 and □N6 (□ means Zr vacancy) octahedra, similar to the rocksalt ZrN structure. To the best of our knowledge, such nitrogen-rich nitrides have never been reported in other TM–N systems. For Zr3N4, the most stable structure has the orthorhombic Pnma symmetry,27 which is energetically more favorable than the Th3P4-type structure by ∼0.019 eV per atom at 0 GPa and 0 K. We found it is thermodynamic metastable considering decomposition into ZrN and N2 at ambient conditions. First-principles calculation shows that o-Zr3N4 will transform into c-Zr3N4 at ∼2 GPa (Fig. S2†).
) and Zr4N5 (x = 1.25, SG: C2/m). Their structures are composed of edge-sharing ZrN6 and □N6 (□ means Zr vacancy) octahedra, similar to the rocksalt ZrN structure. To the best of our knowledge, such nitrogen-rich nitrides have never been reported in other TM–N systems. For Zr3N4, the most stable structure has the orthorhombic Pnma symmetry,27 which is energetically more favorable than the Th3P4-type structure by ∼0.019 eV per atom at 0 GPa and 0 K. We found it is thermodynamic metastable considering decomposition into ZrN and N2 at ambient conditions. First-principles calculation shows that o-Zr3N4 will transform into c-Zr3N4 at ∼2 GPa (Fig. S2†).
We have carefully calculated the temperature contribution to the phase stability of the new discovered zirconium nitrides from 0 K to 2000 K within the quasiharmonic approximation, as shown in Fig. 1. Note that for each stoichiometry, the space group/structure found at 0 K is kept for higher temperatures. The free energies of formation increase with increasing temperatures for all phases but at different rates, yielding a convex hull which changes with temperature. Our results show that Zr2N, Zr8N7, ZrN and Zr15N16 will not lose their stability in the whole studied temperature range. The unstable Zr3N2 at 0 K will become stable at temperatures higher than ∼900 K, while for Zr4N3, Zr6N5, Zr7N8 and Zr4N5, the temperature contributions have negative effect on their structural stability. For example, the formation enthalpy of reaction 2Zr4N5 (s) → 8ZrN (s) + N2 (g) will become negative above 300 K, which means Zr4N5 should decompose into ZrN and N2 gas at roughly room temperature if associated kinetic barrier allows this process, perfectly consistent with the results of Juza et al.16
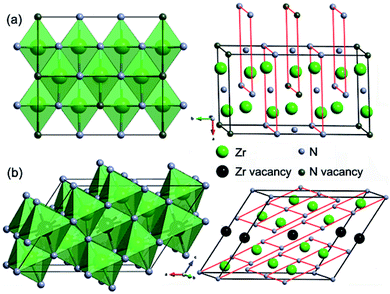
Crystal structures of the representative zirconium-rich Zr6N5 and nitrogen-rich Zr4N5 are schematically shown in Fig. 2, while other structures and their corresponding phonon dispersion curves are shown in Fig. S3 and S4.† No imaginary phonon frequencies are found, indicating their dynamical stability. The detailed crystallographic data, enthalpies and zero-point energies are listed in Table S1.† From Table S1,† we can find the computed lattice parameters for ZrN and Zr3N4 are in good agreement with those obtained from other theoretical and experimental investigations, which confirms the accuracy of our calculations. From the structural point of view, ZrN has the ideal cubic rocksalt structure, while Zrn+1Nn (n = 2, 3, 5, 7) and ZrmNm+1 (m = 4, 7, 15) are versions of the rocksalt structure with ordered nitrogen or zirconium vacancies (Zr2N has rutile-type structure).
In the structures of Zr-rich phases, the metal atoms form hexagonal close-packed (hcp) sublattices with N atoms filled in the octahedral voids, thus each N atom is coordinated by six Zr atoms, forming NZr6 octahedra. However, the concentration of filled octahedral voids in various Zrn+1Nn structures is different. Two thirds of them are filled in Zr3N2; while seven eighths in Zr8N7. Similar nitrogen vacancy-ordered structures were also reported earlier to be stable for transition metal carbides Mn+1Cn (M = Hf and n = 2, 5;28 M = Zr and n = 1, 2, 3, 6;29 M = Ti and n = 1, 2, 5 (ref. 30)) and nitrides Mn+1Nn (M = Ti and n = 1, 2, 3, 5 (ref. 31)). For N-rich phases, one eighth of the metal atoms are replaced with vacancies in Zr7N8, while one fifth in Zr4N5.
The formation of such N-rich phases could be attributed to the enhanced stability of the +4 oxidation state of Zr and Hf compared to Ti due to the relativistic effects,32 leading to the coexistence of +3 in MN and +4 in M3N4, while in the Ti–N system, TiN has the highest nitrogen content under normal conditions. In the structures of Zr3N4, the hcp metal framework of the rocksalt structure is significantly distorted. For o-Zr3N4, there are three nonequivalent types of Zr atoms, one of them is octahedrally coordinated to six N atoms, one resides at the center of a trigonal prism, and the last one is located inside of a heavily distorted octahedron (Fig. S3†). Thus, the second and third nonequivalent Zr atoms are sevenfold coordinated, while in c-Zr3N4, each Zr atom is coordinated to eight N atoms.
3.2 Electronic properties and chemical bonding
We calculated the electronic properties (density of states, DOS, see Fig. 3) of zirconium nitrides at ambient conditions in order to study their chemical bonding. Let us start first with Zr3N4 and then discuss the effect of zirconium or nitrogen vacancies on the electronic properties of rocksalt based-structures. In DOS of o-Zr3N4 displayed in Fig. 3a, three main regions may be described with three kinds of molecular orbital overlaps: nonbonding, bonding and antibonding.33 Firstly, a rather sharp peak at roughly −13 eV appears and it is mainly of N(2s) character although with some Zr(4d) character. This sharp peak reflects the localized character of the nonbonding N(2s)-based levels; secondly, from −6 eV to 4 eV, a very broad structure with two well-defined main peaks originates from mixing of Zr(4d) and N(2p) orbitals. The lower peak corresponds to the bonding states, and the antibonding counterparts appear just above the Fermi level. These bonding and antibonding peaks exhibit a clear mixing of metal 4d and nitrogen 2p states, although the latter has a stronger Zr(4d) character. In o-Zr3N4, the gap separates bonding and antibonding states, thus Zr3N4 is a semiconductor and possesses a remarkable stability. Its calculated band gap (0.68 eV) is consistent with previous theoretical results.6,13 These findings are understandable if one considers the following Zintl picture: Zr is in a formal oxidation state of +4 (Zr4+, d0), and N3− follows the octet rule.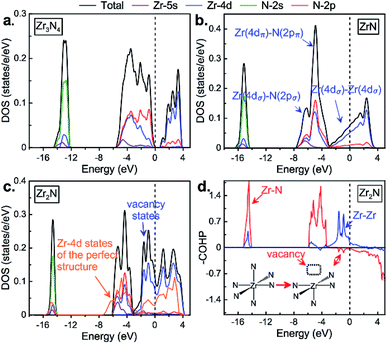 | ||
| Fig. 3 The calculated electronic density of states of (a) o-Zr3N4, (b) ZrN and (c) Zr2N. (d) Crystal orbital Hamilton population (–COHP) curves of Zr2N. | ||
For the well-known stoichiometric rocksalt ZrxNy, we will first briefly discuss their electronic properties, then analyze the electronic perturbation due to the creation of nitrogen or zirconium vacancies – empty octahedral sites in the fcc network – leading to symmetry-broken Zrn+1Nn and ZrmNm+1 structures. Similarly to o-Zr3N4, DOS of ZrxNy phases can be decomposed into three well-separated energy regions as shown in Fig. 3 and S5,† but here no gap separates the valence and conducting bands: (1) a deep lowest valence band, sN; (2) hybridized Zr(4d)/N(2p) band, dMpN; (3) a partially filled higher-energy Zr(4d) band, dM. The sN band is dominated by the 2s orbitals of the nitrogen atoms and is nonbonding. The next group of valence bands, dMpN, results from strong hybridization of the 4d states of zirconium atoms with 2p states of nitrogen atoms. Also, one may see that for ZrxNy the bottom of the dM band, dominated by 4d orbitals of zirconium atoms, responsible for metallicity.
When nitrogen vacancies are created in substoichiometric Zrn+1Nn (n = 1, 2, 3, 5 and 7), notice that obviously the formal oxidation state of Zr decreases as the number of nitrogen vacancies increases, going from Zr3+ d1 in ZrN to Zr1.5+ d2.5 in Zr2N. Therefore, one may expect the occupation of the Zr 4d levels in substoichiometric Zrn+1Nn compounds. This is what happens: Zr–Zr bonding and nonbonding (slightly antibonding) Zr–N levels appear just below the Fermi level, mainly metal 4d in character (see Fig. 3d and S6†). In Zrn+1Nn, Zr atoms are no longer all in the MN6 octahedral environment; some of them are in MN5 square pyramidal configurations. Therefore, one may expect the stabilization of antibonding Zr–N levels when going from formally octahedral ZrN6 to square pyramidal ZrN5 environment due to the lack of a Zr(4d)–N(2p) antibonding component. The occupation of these Zr–N nonbonding levels may explain the mechanical properties of these substoichiometric Zrn+1Nn compounds.
Fig. 3c displays the total and projected DOS of Zr2N, but also the projected d states of a hypothetical ZrN structure within the Zr2N structure (all N vacancies are filled in the so-called perfect structure). One can see that nitrogen vacancies give rise to additional states just below the Fermi level compared to its corresponding perfect structure, which originates from the Zr–Zr bonds passing through a nitrogen vacancy site. Such “vacancy states” usually lead to a drastic increase in the density of states at the Fermi level (0.076 in ZrN; 0.090 in Zr6N5; 0.112 in Zr2N, states per eV per electron). The increasing density of the d state at the Fermi level can be interpreted as an increase in the Zr(4dσ)–Zr(4dσ) bonding or metallic bonds between the zirconium atoms.
3.3 Mechanical properties
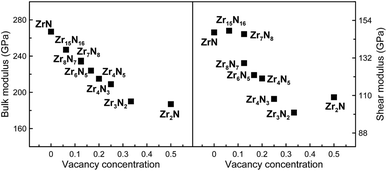
We further studied mechanical properties of the Zr–N compounds. The calculated elastic constants are shown in Table 1. All structures satisfy the Born–Huang stability criteria,40 confirming their mechanical stability. From the calculated elastic constants, we can find ZrN holds the largest C11, C22 and C33 values among the ZrxNy compounds, which indicate the very high compressibility along the axis directions. o-Zr3N4 has the smallest C11 and C44 values. The bulk modulus B, shear modulus G, Young's modulus E and Poisson's ratio ν were further obtained using the Voigt–Reuss–Hill averaging,41 shown in Table 1. The calculated B values of zirconium nitrides are comparable with many other transition metal carbides, nitrides and borides, such as Fe3C (224 GPa (ref. 42)), TiN (294 GPa (ref. 31)) and TiB2 (213 GPa (ref. 43)), but much lower than diamond (437 GPa (ref. 44)). Among these ZrxNy compounds, ZrN has the largest bulk and shear moduli, although Zr7N8 has a practically identical shear modulus (see Table 1).| Phase | C1 | C12 | C13 | C15 | C22 | C23 | C25 | C33 | C35 | C44 | C46 | C55 | C66 | B | G | E | ν | B/G | AU | HS | HC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a B = 249,34 G = 157,35 Hv = 16.36b B = 203,37 238,38 Hv = 12.4.37c B = 224,37 Hv = 11.7,39 11.4.37 | |||||||||||||||||||||
| Zr2N | 305 | 142 | 108 | 362 | 119 | 114 | 187 | 109 | 274 | 0.256 | 1.721 | 0.116 | 14.8 | 13.5 | |||||||
| Zr3N2 | 293 | 132 | 130 | 325 | 93 | 384 | 112 | 96 | 84 | 190 | 100 | 255 | 0.276 | 1.896 | 0.170 | 15.5 | 11.0 | ||||
| Zr4N3 | 336 | 147 | 140 | 8 | 349 | 127 | 2 | 371 | 13 | 127 | −10 | 95 | 109 | 209 | 108 | 277 | 0.280 | 1.931 | 0.091 | 15.2 | 11.3 |
| Zr6N5 | 376 | 135 | 159 | −25 | 384 | 153 | 29 | 364 | 2 | 118 | 25 | 134 | 145 | 224 | 122 | 309 | 0.270 | 1.845 | 0.233 | 15.3 | 13.2 |
| Zr8N7 | 394 | 137 | 171 | −28 | 396 | 162 | 31 | 385 | 2 | 131 | 35 | 154 | 147 | 235 | 129 | 328 | 0.267 | 1.815 | 0.301 | 13.3 | 14.1 |
| ZrNa | 556 | 123 | 113 | 267 | 147 | 372 | 0.268 | 1.818 | 0.534 | 15.6 | 15.4 | ||||||||||
| Zr15N16 | 437 | 153 | 155 | −16 | 467 | 117 | 1 | 468 | 20 | 154 | −13 | 130 | 161 | 247 | 148 | 369 | 0.251 | 1.673 | 0.323 | 15.5 | 17.3 |
| Zr7N8 | 422 | 132 | 146 | 30 | 421 | 157 | −30 | 396 | 2 | 150 | 28 | 166 | 160 | 234 | 146 | 362 | 0.242 | 1.605 | 0.199 | 15.5 | 18.2 |
| Zr4N5 | 338 | 120 | 159 | −11 | 425 | 116 | −9 | 378 | 21 | 139 | −12 | 106 | 118 | 215 | 120 | 303 | 0.264 | 1.789 | 0.211 | 15.0 | 13.7 |
| o-Zr3N4b | 209 | 159 | 164 | 469 | 167 | 422 | 95 | 63 | 130 | 214 | 91 | 239 | 0.314 | 2.359 | 1.043 | 12.4 | 7.3 | ||||
| c-Zr3N4c | 423 | 146 | 133 | 238 | 135 | 341 | 0.261 | 1.761 | 0.002 | 11.0 | 15.2 | ||||||||||
The effect of vacancy concentration on bulk and shear moduli of the rocksalt ZrxNy structures is shown in Fig. 4. It can be seen that bulk and shear moduli monotonically decrease with increasing vacancy concentration. When N vacancies increase in a rocksalt structures, the number of Zr–N bonds obviously decreases. Moreover, the computed Zr–N separations are increasing when N vacancies increase, i.e. from 2.24 to 2.27 Å in Zr8N7 and Zr2N, reflecting the weakening of the Zr–N bonding. Therefore, one may understand our findings, i.e. the loss of B and G is mainly attributed to the disappearance of some strong covalent Zr–N bonds.
For brittle materials, B/G ratio is smaller than 1.75 (ref. 45) (for example, for diamond B/G = 0.8). From Table 1, we can find that B/G values decreases in the following sequence: o-Zr3N4 > Zr4N3 > Zr3N2 > Zr6N5 > ZrN > Zr8N7 > Zr4N5 > c-Zr3N4 > Zr2N > Zr15N16 > Zr7N8. B/G values of Zr2N (1.721), Zr15N16 (1.673) and Zr7N8 (1.605) are smaller than 1.75, which indicate that these are brittle or borderline materials. For the other compounds, B/G values are larger than 1.75, which suggest that they are ductile materials. For ZrN, B/G value is slightly larger than 1.75, making a good compromise between hardness and ductility, which is mainly due to a peculiar interplay between metallicity and covalency. Besides, we can find that B/G values of Zr-rich phases are larger than N-rich ones except Zr2N and o-Zr3N4. Obviously, the higher metal content, the more ductile the material. Surprisingly, semiconducting o-Zr3N4 has the largest B/G value (2.359) due to the low C11 and C44, and o-Zr3N4 also possesses remarkable elastic anisotropy. Here, we used the Ranganathan and Ostoja-Starzewski method46 to estimate anisotropy:
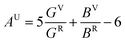 | (2) |
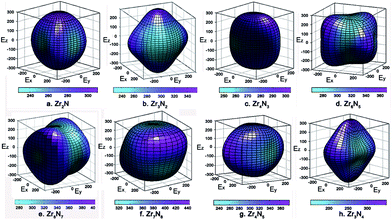
The calculated anisotropy parameters AU of ZrxNy phases are listed in Table 1. Elastic anisotropy decreases in the following sequence: o-Zr3N4 > ZrN > Zr15N16 > Zr8N7 > Zr6N5 > Zr4N5 > Zr7N8 > Zr3N2 > Zr2N > Zr4N3 > c-Zr3N4. Fig. 5 shows the directional dependence of Young's moduli for the selected ZrxNy compounds (see eqn (8) in ESI†). For an isotropic system, one would see a spherical shape. The degree of elastic anisotropy can be directly reflected from the degree of deviation in shape from a sphere. From Fig. 5, we can find that Young's modulus is more anisotropic in o-Zr3N4, while Zr4N3 and Zr2N show more isotropic features. The anisotropy of o-Zr3N4 is due to low C11 and high C22, C33 values, resulting in a flat shape of Young's modulus.
The Vickers hardness of zirconium nitrides was estimated by using Chen's model,47 as follows:
| HC = 2(κ2G)0.585 − 3 | (3) |
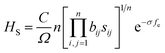 | (4) |
4 Conclusions
By using the variable-composition ab initio evolutionary algorithm USPEX, we explored stable and metastable compounds in the Zr–N system at ambient pressure. Our calculations revealed that ZrN, Zr2N, Zr4N3, Zr6N5, Zr8N7, Zr15N16, Zr7N8 and Zr4N5 are thermodynamically stable compounds at low temperatures, while Zr3N2 is marginally metastable and could be stable at high temperatures. Particularly, we found the two controversial compounds discovered by Juza et al. could be Zr15N16 and Zr4N5. The newly discovered compounds have defective rocksalt structures with ordered nitrogen or zirconium vacancies. The calculated elastic constants of zirconium nitrides are in good agreement with available experimental values. Our results show that bulk and shear moduli monotonically increase with decreasing vacancy content. This can be attributed to the occurrence of more Zr–N covalent bonds and weakening of the ductile Zr–Zr metallic bonds. Besides, we found hardness of bulk Zr3N4 is below ∼15 GPa.Acknowledgements
We thank the National Natural Science Foundation of China (No. 51372203 and 51332004), the Foreign Talents Introduction and Academic Exchange Program (No. B08040), the GDRI RFCCT CNRS (DNM-evol program) and the Hubert Curien Partnerships PHC XU GUANGQI 2015 (No. 34455PE) part of the French Ministry of Foreign Affairs, the Région Poitou-Charentes (France) for a PhD fellowship, and the Government of the Russian Federation (No. 14.A12.31.0003) for financial support. We also acknowledge the High Performance Computing Center of NWPU (China), and TGCC/Curie GENCI (France) under project no. 2016087539 for allocation of computing time on their machines. We would like to thank an anonymous referee to point out Zr15N16 as a potential candidate.References
- H. O. Pierson, Handbook of refractory carbides and nitrides: properties, characteristics, processing and applications, Noyes Publication, New York, 1996, pp. 163–180 Search PubMed.
- H. Holleck, J. Vac. Sci. Technol., A, 1986, 4, 2661–2669 CAS.
- K. Inumaru, T. Ohara, K. Tanaka and S. Yamanaka, Appl. Surf. Sci., 2004, 235, 460–464 CrossRef CAS.
- D. J. Kim, Y. R. Cho, M. J. Lee, J. M. Hong, Y. K. Kim and K. H. Lee, Surf. Coat. Technol., 1999, 116, 906–910 CrossRef.
- A. I. Gusev and A. A. Rempel, Phys. Status Solidi A, 1997, 163, 273–304 CrossRef CAS.
- D. I. Bazhanov, A. A. Knizhnik, A. A. Safonov, A. A. Bagaturyants, M. W. Stoker and A. A. Korkin, J. Appl. Phys., 2005, 97, 044108 CrossRef.
- R. Niewa and F. J. DiSalvo, Chem. Mater., 1998, 10, 2733–2752 CrossRef CAS.
- A. Kafizas, C. J. Carmalt and I. P. Parkin, Coord. Chem. Rev., 2013, 257, 207–2119 CrossRef.
- A. Salamat, A. L. Hector, P. Kroll and P. F. McMillan, Coord. Chem. Rev., 2013, 257, 2063–2072 CrossRef CAS.
- S. V. Didziulis and K. D. Butcher, Coord. Chem. Rev., 2013, 257, 93–109 CrossRef CAS.
- L. Gribaudo, D. Arias and J. Abriata, J. Phase Equilib., 1994, 15, 441–449 CrossRef CAS.
- A. Zerr, G. Miehe and R. Riedel, Nat. Mater., 2003, 2, 185–189 CrossRef CAS PubMed.
- P. Kroll, Phys. Rev. Lett., 2003, 90, 125501 CrossRef PubMed.
- M. Chhowalla and H. E. Unalan, Nat. Mater., 2005, 4, 317–322 CrossRef CAS PubMed.
- W. H. Baur and M. Lerch, Z. Anorg. Allg. Chem., 1996, 622, 1729–1730 CrossRef CAS.
- R. Juza, A. Gabel, H. Rabenau and W. Klose, Z. Anorg. Allg. Chem., 1964, 329, 136–145 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, A. O. Lyakhov, M. Valle, C. Gatti and Y. Ma, Rev. Mineral. Geochem., 2010, 71, 271–298 CrossRef CAS.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2012, 184, 1172–1182 CrossRef.
- G. Kresse and J. Furthmller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- H. Tang, A. Van der Ven and B. L. Trout, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045420 CrossRef.
- M. Lerch, E. Füglein and J. Wrba, Z. Anorg. Allg. Chem., 1996, 622, 367–372 CrossRef CAS.
- Q. F. Zeng, J. H. Peng, A. R. Oganov, Q. Zhu, C. W. Xie, X. D. Zhang, D. Dong, L. T. Zhang and L. F. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 4269–4275 Search PubMed.
- X. X. Yu, C. R. Weinberger and G. B. Thompson, Comput. Mater. Sci., 2016, 112, 318–326 CrossRef CAS.
- C. Jiang and W. S. Jiang, Phys. Status Solidi B, 2014, 251, 533–536 CrossRef CAS.
- S. Y. Yu, Q. F. Zeng, A. R. Oganov, G. Frapper and L. T. Zhang, Phys. Chem. Chem. Phys., 2014, 17, 11763–11769 RSC.
- J. E. Huheey, Inorganic chemistry: principles of structure and reactivity, Harpar & Row, 1993, vol. 156, pp. 907–914 Search PubMed.
- R. Hoffmann, Solids and surfaces: a chemist's view of bonding in extended structures, Wiley-VCH, New York, 1988, pp. 18–21 Search PubMed.
- Z. Q. Chen, J. Wang and C. M. Li, J. Alloys Compd., 2013, 575, 137–144 CrossRef CAS.
- C. Sarioglu, Surf. Coat. Technol., 2006, 201, 707–717 CrossRef CAS.
- F. Lévy, P. Hones, P. Schmid, R. Sanjinés, M. Diserens and C. Wiemer, Surf. Coat. Technol., 1999, 120, 284–290 CrossRef.
- F. M. Gao, Chin. Phys. Lett., 2011, 28, 076102 CrossRef.
- W. Y. Ching, Y. N. Xu and L. Z. Ouyang, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 126–130 CrossRef.
- F. M. Gao, R. Xu and K. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 2103 CrossRef.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- W. Zhou, L. J. Liu, B. L. Li, P. Wu and Q. G. Song, Comput. Mater. Sci., 2009, 46, 921–931 CrossRef CAS.
- C. Jiang, S. G. Srinivasan, A. Caro and S. A. Maloy, J. Appl. Phys., 2007, 103, 3654–3660 Search PubMed.
- V. Milman and M. Warren, J. Phys.: Condens. Matter, 2001, 13, 5585 CrossRef CAS.
- Y. C. Liang, W. L. Guo and Z. Fang, Acta Phys. Sin., 2007, 56, 4847–4855 CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- A. Šimúnek, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 172108 CrossRef.
- A. Zerr, G. Miehe and R. Riedel, Nat. Mater., 2003, 2, 185–189 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27233a |
| This journal is © The Royal Society of Chemistry 2017 |