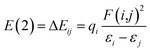Open Access Article
Open Access ArticleA DFT study on lignin dissolution in imidazolium-based ionic liquids†
Yaqin Zhangab,
Hongyan He*ac,
Kun Donga,
Maohong Fanc and
Suojiang Zhang *a
*a
aBeijing Key Laboratory of Ionic Liquids Clean Process, Key Laboratory of Green Process and Engineering, State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China. E-mail: hyhe@ipe.ac.cn; sjzhang@ipe.ac.cn
bSino-Danish College, University of Chinese Academy of Sciences, Beijing 100190, China
cDepartment of Chemical and Petroleum Engineering, University of Wyoming, Laramie, Wyoming 82071, USA
First published on 22nd February 2017
Abstract
Density functional theory (DFT), atoms in molecules (AIM) theory, natural bond orbital (NBO) analysis, and reduced density gradient (RDG) analysis were employed to investigate the mechanism of lignin dissolution in imidazolium-based ionic liquids (ILs). Lignin was modeled with guaiacyl glycerol-β-guaiacyl ether (GG), which is one type of β-O-4 linked dimers. Hydrogen bonds (H-bonds) are studied specifically and characterized by different methods to evaluate the strength of interaction between ILs and the lignin model compound. From the theoretical results, it is observed that H-bonds between anions and the GG model are stronger than those between cations and the GG model. Also, anions have the strongest interaction at the α-OH position of GG, while cations have the strongest interaction at the γ-OH position of GG. In addition, anions Cl, OAc and MeSO4 have much stronger H-bonding ability than PF6, and the length of the alkyl chain does not have a significant influence on the cation–GG interaction. This work also simulates the interaction between the GG model and ion pairs, with the results suggesting that anions in ion pairs play a key role in forming H-bonds, and cations have a π-stacking interaction with GG. The calculation data provide the interaction mechanism of lignin dissolution in ILs to some extent.
1. Introduction
Second to cellulose, lignin is the most abundant bio-renewable and bio-degradable polymer in nature.1,2 Its complicated structure is derived from coniferyl (G unit), sinapyl (S unit), and p-coumaryl (H unit) alcohols, which are linked by various types of C–O and C–C bonds, including β-O-4, α-O-4, 4-O-5, β-5 and β–β linkages. β-O-4 is the dominant linkage among these, constituting more than half of the linkage units of lignin in both softwoods and hardwoods.3 G units constitute approximately 90% of softwood, whereas roughly equal proportions of G unit and S unit appear in hardwood.4 It has been proved that H-bonds between neighboring carboxylic groups, hydroxyl groups and ether groups, and π–π interactions between aromatic moieties are responsible for the associated and complicated structures of lignin.5–8 Based on the above features, lignin may be used as a potential source of phenolic compounds in order to substitute for petroleum-derived chemicals, and its prospects for creating high value-added chemicals are obvious. However, in order to separate lignin from biomass, traditional processes using acid, alkali, and organic solvents have the disadvantages of pollution, corrosion, odor, high temperature, high pressures and high water use.9,10 In general, such reagents are incompatible with green chemistry.Recently, room temperature ionic liquids (RTILs)11–14 composed entirely of cations and anions have drawn the attention of chemists as promising green media for synthesis, catalysis and separation.15–17 Rogers et al. have shown that some of the RTILs can dissolve cellulose,18 and Gomes et al.19–21 extended many works both experiment and simulation to understand the solvation and dissolution of cellulose in BmimOAc in the presence of cosolvent. It is worth mentioning that some gases, such as CO2, SO2 and CH4, show great solubility in functional ILs.22–27 Their use may be extended to lignocellulose composites.28,29 These experiments proved that RTILs have effectively promoted the dissolution and catalytic conversion of biomass materials. Since then, many experimental efforts have been devoted to developing novel ILs in order to dissolve lignin. Fort28 found BmimCl was capable of dissolving both cellulose and lignin simultaneously, and cellulose was easily regenerated by adding co-solvent. Lee30 reported that EmimOAc was able to selectively extract lignin from wood flour, with a highly concentrated solution of chemically unmodified lignin obtained in the recovery of the solvent. Pu et al.73 reported that the solubility of residual softwood kraft pulp lignin in BmimCl reached 13.9 g L−1, while reaching 344 g L−1 and 312 g L−1 in MmimMeSO4 and BmimMeSO4 respectively; it was also reported in this work that lignin was insoluble in BmimPF6. It seems that ILs with Cl, OAc, MeSO4 anions are better solvents for lignin dissolution, while PF6-based ILs are unfavorable. However, it is unclear why different anions result in the dramatically different solubility.
Besides reliable results from experiments, molecular simulations provide specific interaction information that reveals deeper mechanism while reducing manual work and experimental costs.31 Using the COSMO-RS model, Balaji32 computed Hildebrand solubility parameters for 34 cations and 34 anions, and found that high Hildebrand parameters of imidazolium, pyridinium, pyrrolidinium and ammonium-based ILs suggested higher potential for dissolving lignin than other ILs. The energetic contribution of entropic and enthalpy were used to estimate the dissolution mechanism of gases in ILs,27 and free energy was closely related to solubility of polymers19 and crystals,33 thus the thermodynamics of lignin dissolution are speculated to be correctly estimated with these terms. In addition, excess enthalpy of IL/lignin mixtures affects the affinity of lignin with different ILs. Casas34 proved that strong exothermic excess enthalpy was beneficial for lignin dissolution, and that FTIR spectroscopy of regenerated lignin solids further demonstrated good performance of the selected ILs. To study the mechanism of lignin dissolution in ILs, a new prospective different from macroscopic thermodynamic properties is used to reveal the interactions between ILs and polymers at the molecular level, typically Density Functional Theory (DFT) calculations.35,36 Ji et al.37 concluded that stronger H-bonding interaction in AmimCl–LigOH than in LigOH–LigOH was responsible for lignin dissolution, with the regenerability of lignin in water explained by the reduced H-bonds in AmimCl–LigOH when adding water to this system. Recently, Janesko5 performed comprehensive work to elucidate the noncovalent interactions between various ILs and lignocellulose. They highlighted the importance of IL cations in tuning the relative solubilities of lignin and cellulose. Furtherly, they found that ILs with π-conjugated cations are favorable for enhancing lignin solubility. The above studies have shown that the conformers' binding energy is effective to reveal the dissolution mechanism, and demonstrated that the components of the cation and anion in the ILs can be fine-tuned. However, they were mainly focused on the multiple structures and energies of ILs-lignin conformers. To the best of our knowledge, there are few works concerning NBO, AIM and RDG analysis to study the mechanism of lignin dissolution, and very few computational studies shed light on the question why different anion-typed ILs give lignin dramatically different solubility,38 as well as the influences of alkyl substituents on the performance of ILs.
Thus, our work aims at exploring the detailed interactions, especially H-bonding interactions between ILs and the lignin model compound. Due to limited computational capacity, lignin is modeled by the dimer guaiacyl glycerol-β-guaiacyl ether (GG, Fig. S1†), which consists of G units connected with β-O-4 linkages, and whose structure is thought to represent the building blocks of natural lignin. Furthermore, efficiently cleaving the β-O-4 linkage could be of critical importance for the degradation and decomposition of lignin.3 In the present work, the interaction between the GG model and a series of imidazolium-based cations (Mmim, Emim, Bmim and Hmim), anions (Cl, OAc, MeSO4, PF6) and ion pairs are studied to reveal the dissolution mechanism by employing theoretical calculations. Cations and anions are used to study the effects of alkyl chain length39 and coordination ability on the strength of the interaction. Interaction sites are studied to figure out which position is helpful for cleavage of the β-O-4 linkage. Interaction energy is used to estimate approximately the most efficient solvent among the studied ILs at the molecular level. Natural bond orbital (NBO) analysis, atoms in molecules (AIM) theory, and reduced density gradient (RDG) are used in combination to specifically investigate the hydrogen bonds (H-bonds) and π-stacking interactions.
2. Computational details
All calculations are performed with the Gaussian 09 package.40 The DFT method with the Becke's three-parameter functional and the nonlocal correlation of Lee, Yang, and Parr (B3LYP)41 together with the 6-31++g** is used for all calculations. Here, we also highlight many studies got reasonable results in correspondence with experiments by using the same level of theory.14,42–44 All the obtained structures are confirmed by frequency analysis to ensure no imaginary frequencies. It is known that the B3LYP/6-31++g** level is an excellent compromise between computational cost and accuracy of the computational results; further, the 6-31++g** basis set was thought to be effective for considering the double-ξ quality for valence electrons with the consideration of certain diffuse functions.45 Therefore, the basis set is suitable for the ILs and lignin system.46–48 To get comparable results with Janesko,5 dispersion-corrected49–52 DFT is applied to determine the significant π-stacking interactions at the B3LYP-D3/6-311+g**,41 and several reasonable geometries are also performed using M06-2X/6-311+g** level of theory.27,53 In these calculations, the electrostatic potential (ESP) method is used to predict the most plausible sites for electrophilic and nucleophilic attack;54 the initial configurations of the cation–GG, anion–GG, and ion pairs with GG are structured based mainly on the ESP (Fig. S2†) on the isosurface of cations, anions and GG. The most stable conformer in this work is obtained by comparing the electron energies of different initial structures designed and optimized in the calculations. The interaction energy (ΔE) is defined as the energy difference between the conformer and the corresponding isolated ions.| ΔE = 2625.5 × (Eab − Ea − Eb), kJ mol−1 |
Natural bond orbital (NBO) analysis, atoms in molecules (AIM) theory and reduced density gradient (RDG) analysis are performed with the software Multiwfn,55 VMD56 and CYL view57 at the same level to confirm the existence of H-bonds. In the NBO analysis, E(2) is used to describe the intensity of orbital interaction between electron donors and electron acceptors well within the equation.
The higher the value of E(2), the more electrons tend to transfer from the donor.58 Where εi and εj are diagonal elements, qi is the donor orbital occupancy and F(i,j) is the off-diagonal NBO Fock matrix element.
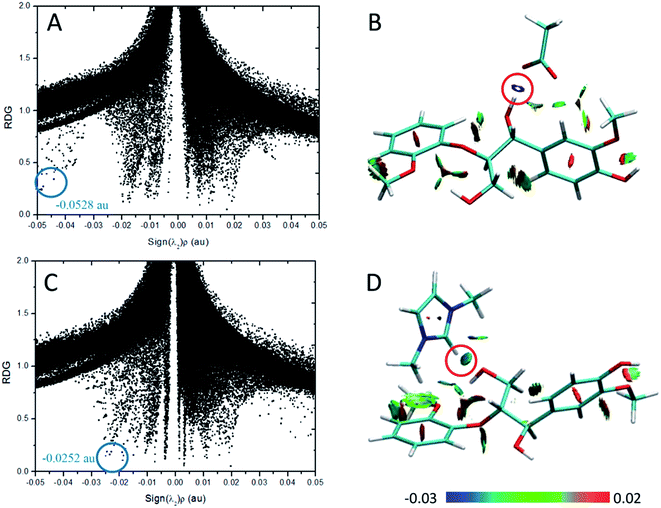
According to the AIM theory, the electron density (ρBCP) and its Laplacian value (∇2ρBCP)59,60 are used to indicate the strength and nature, respectively, of H-bonds at the bond critical point (BCP). The H-bonds and ionic bonds are characterized by ∇2ρBCP > 0 in the closed shell interactions, while the covalent bonds are characterized by ∇2ρBCP < 0; the extremely strong H-bonds can also have negative Laplacian value. RDG scatter plots and isosurfaces visualize55,61,62 all non-covalent interaction in the system, as indicated in Fig. S3.†
3. Results and discussion
3.1 Interaction between cations/anions and GG
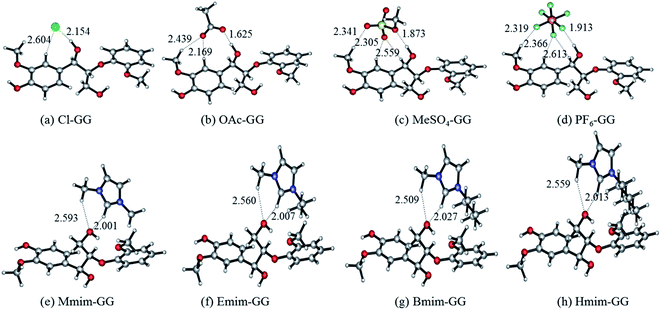 | ||
| Fig. 1 Optimized anion–GG conformers (a–d), and cation–GG conformers (e–h) at the level of 6-31++g**. H-Bonds are indicated by dashed lines. | ||
| Structure | H-Bond | Length (Å) | Angle (°) | ΔE (kJ mol−1) | |
|---|---|---|---|---|---|
| Fig. 1(a) | Cl–GG | Cl⋯H43–O42 | 2.154 | 166.92 | −95.21 |
| Cl⋯H9–C6 | 2.604 | 139.29 | |||
| Fig. 1(b) | OAc–GG | O50⋯H43–O42 | 1.625 | 175.97 | −121.46 |
| O49⋯H9–C6 | 2.169 | 153.97 | |||
| O49⋯H15–C13 | 2.439 | 141.06 | |||
| Fig. 1(c) | MeSO4–GG | O48⋯H43–O42 | 1.873 | 172.46 | −81.98 |
| O45⋯H15–C13 | 2.341 | 139.02 | |||
| O46⋯H9–C6 | 2.305 | 149.38 | |||
| Fig. 1(d) | PF6–GG | F50⋯H43–O42 | 1.913 | 172.13 | −61.69 |
| F49⋯H15–C13 | 2.319 | 169.75 | |||
| F48⋯H9–C6 | 2.366 | 144.49 | |||
| F48⋯H18–C17 | 2.613 | 135.13 | |||
| Fig. 1(e) | Mmim–GG | O35⋯H50–C46 | 2.001 | 155.75 | −72.93 |
| O35⋯H53–C52 | 2.593 | 144.70 | |||
| Fig. 1(f) | Emim–GG | O54⋯H7–C3 | 2.007 | 155.72 | −70.76 |
| O54⋯H18–C16 | 2.560 | 144.86 | |||
| Fig. 1(g) | Bmim–GG | O60⋯H7–C3 | 2.027 | 152.66 | −68.46 |
| O60⋯H17–C15 | 2.509 | 146.41 | |||
| Fig. 1(h) | Hmim–GG | O66⋯H7–C3 | 2.013 | 154.36 | −67.94 |
| O66⋯H17–C15 | 2.559 | 145.43 | |||
Fig. 1 shows two important features of these geometries: (i) α-OH-involved H-bonds (e.g. 2.154 Å in structure (a)) have shorter bond lengths than other H-bonds (e.g. 2.604 Å in structure (a)) formed between GG model compound and anions; and (ii) the C2–H of cations gets closer to γ-OH than the methyl group of cations (e.g. 2.001 Å and 2.593 Å of the two H-bonds in the structure (e)). All of these optimized conformers show that the optimal interaction site for anion–GG interaction is the α-OH group of GG, and the γ-OH of GG for cation–GG interaction. Comparing the interaction energies of these structures, the order of anions to form H-bonds with GG follows: OAc > Cl > MeSO4 > PF6, with the sequence of cations being: Mmim > Emim > Bmim > Hmim. It can be found that increasing alkyl chain length leads to a decrease of interaction energy between cations and GG, but the change is not obvious. Hart64 demonstrated that the proportion of lignin in saturated solutions of lignin in EmimMeSO4 was nine times that of EmimPF6, where the low H-bonding basicity of PF6 means that it cannot dissolve lignin (the theoretical results are consistent with those obtained by the experiments). Therefore, we speculate that these intermolecular H-bonds are expected to be a key factor resulting in the solubility of lignin in ILs. Furthermore, anions may play more important roles than cations in the dissolution of lignin because of stronger interaction with the lignin model compound. These results also may be used to show that lignin cannot be dissolved in PF6-based ILs because of weak interaction in the PF6–GG conformers.
| Structure | Donor (i) | Acceptor (j) | E(2), kJ mol−1 |
|---|---|---|---|
| Cl–GG | Lp Cl44 | σ* C6–H9 | 20.43 |
| Lp Cl44 | σ* O42–H43 | 91.67 | |
| OAc–GG | Lp O49 | σ* C6–H9 | 29.97 |
| Lp O49 | σ* C13–H15 | 8.62 | |
| Lp O50 | σ* O42–H43 | 244.92 | |
| MeSO4–GG | Lp O45 | σ* C13–H15 | 6.82 |
| Lp O46 | σ* C6–H9 | 16.62 | |
| Lp O46 | σ* O42–H43 | 72.88 | |
| PF6–GG | Lp F48 | σ* C6–H9 | 8.92 |
| Lp F48 | σ* C17–H18 | 3.14 | |
| Lp F49 | σ* C13–H15 | 11.64 | |
| Lp F50 | σ* O42–H43 | 41.27 | |
| Mmim–GG | Lp O35 | σ* C46–H50 | 52.91 |
| Lp O35 | σ* C52–H53 | 3.85 | |
| Emim–GG | Lp O54 | σ* C3–H7 | 51.61 |
| Lp O54 | σ* C16–H18 | 3.77 | |
| Bmim–GG | Lp O60 | σ* C3–H7 | 47.05 |
| Lp O60 | σ* C15–H17 | 5.65 | |
| Hmim–GG | Lp O66 | σ* C3–H7 | 50.11 |
| Lp O66 | σ* C15–H17 | 4.60 |
| Structure | H-Bond | ρBCP | ∇2ρBCP | HBCP (10−3 a.u.) |
|---|---|---|---|---|
| Cl–GG | Cl⋯H43–O42 | 0.0285 | 0.0587 | −1.6143 |
| Cl⋯H9–C6 | 0.0128 | 0.0392 | 1.3348 | |
| OAc–GG | O50⋯H43–O42 | 0.0528 | 0.1439 | −2.7072 |
| O49⋯H9–C6 | 0.0183 | 0.0504 | −0.3137 | |
| O49⋯H15–C13 | 0.0101 | 0.0334 | 0.7030 | |
| MeSO4–GG | O46⋯H43–O42 | 0.0315 | 0.1010 | −0.9943 |
| O45⋯H9–C6 | 0.0132 | 0.0412 | 0.3625 | |
| O45⋯H15–C13 | 0.0092 | 0.0310 | 0.7458 | |
| PF6–GG | F50⋯H43–O42 | 0.0219 | 0.0711 | −0.8172 |
| F48⋯H9–C6 | 0.0098 | 0.0387 | 0.9949 | |
| F48⋯H18–C17 | 0.0060 | 0.0261 | 1.2580 | |
| Mmim–GG | O35⋯H50–C46 | 0.0252 | 0.0671 | −0.9019 |
| O35⋯H53–C52 | 0.0074 | 0.0266 | 0.9087 | |
| Emim–GG | O54⋯H7–C3 | 0.0248 | 0.0663 | −0.8775 |
| O54⋯H18–C16 | 0.0074 | 0.0263 | 0.9106 | |
| Bmim–GG | O60⋯H7–C3 | 0.0238 | 0.0641 | −0.8031 |
| O60⋯H17–C15 | 0.0089 | 0.0303 | 0.7937 | |
| Hmim–GG | O66⋯H7–C3 | 0.0235 | 0.0658 | −0.8407 |
| O66⋯H17–C15 | 0.0080 | 0.0280 | 0.8634 |
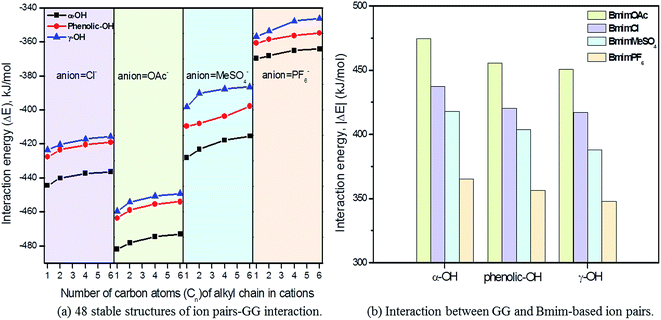
3.2 Interaction between ion pairs and GG
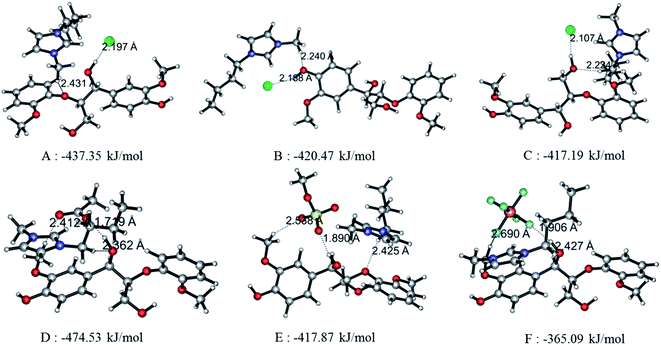
Since the interaction between GG and single anion/cation has been calculated, and because anions and cations appear in the form of ion pairs in the real structure of ILs, it is therefore of great importance to study the structural behavior between model compound and ion pairs which is essential to reveal the dissolution mechanism. The conformers formed between ion pairs and GG model compound were optimized at B3LYP/6-31++g** level. In this part, the interaction energies of 48 possible conformers are compared in Fig. 3(a), wherein we see that increasing the length of the alkyl chain results in a decrease of interaction energies between ion pairs and GG; these changes are not obvious, but are more apparent for anions in ion pairs. Therefore, four Bmim-based ion pairs with different anions are selected to analyze the interaction between GG and ion pairs at different sites in Fig. 3(b). These have much stronger interaction at α-OH of GG, which suggests that anions in ion pairs play a key role in lignin dissolution. The following analysis is performed for the conformers BmimCl–GG, BmimOAc–GG, BmimMeSO4–GG and BmimPF6–GG at the α-OH position.| Structure | H-Bond | Length (Å) | Angle (°) | ΔE (kJ mol−1) | |
|---|---|---|---|---|---|
| Fig. 4(A) | BmimCl–GG | Cl69⋯O42–H43 | 2.197 | 161.59 | −437.35 |
| O21⋯C58–H59 | 2.431 | 138.58 | |||
| Fig. 4(B) | BmimCl–GG | Cl69⋯O10–H11 | 2.188 | 152.34 | −420.47 |
| O10⋯C58–H59 | 2.240 | 171.65 | |||
| Fig. 4(C) | BmimCl–GG | Cl69⋯O35–H36 | 2.107 | 167.44 | −417.19 |
| O35⋯C52–H54 | 2.224 | 164.17 | |||
| Fig. 4(D) | BmimOAc–GG | O74⋯O42–H43 | 1.719 | 168.21 | −474.53 |
| O42⋯C52–H54 | 2.362 | 167.41 | |||
| O75⋯C13–H15 | 2.412 | 166.41 | |||
| Fig. 4(E) | BmimMeSO4–GG | O71⋯O42–H43 | 1.890 | 165.18 | −417.87 |
| O70⋯C13–H15 | 2.538 | 144.92 | |||
| O21⋯C52–H54 | 2.425 | 149.71 | |||
| Fig. 4(F) | BmimPF6–GG | F73⋯O42–H43 | 1.906 | 159.03 | −365.09 |
| O42⋯C52–H54 | 2.427 | 170.77 | |||
| F71⋯C13–H15 | 2.690 | 136.34 | |||
As described before, the interaction of ion pairs–GG is more intensive at α-OH than at γ-OH and p-OH. Also, the binding energies for cation–GG and anion–GG at the B3LYP/6-31++g** level can well explain the H-bonding interactions in this system. The above results reveal that the electrostatic interactions play a key role in the system when there exists only one ion (Section 3.1). The electronegative position of anion tends to attack the –OH groups of GG, and C2–H of imidazolium cations prefer forming H-bonds with O atoms of GG. All of these results are a bit different from Janesko's work.5 Nevertheless, we also confirm there exist π-stacking effects in the conformers of ion pairs–GG as they reported previously. As tested by Grimme's,49 B3LYP-D3 is considered to be an ideal choice to investigate large molecular system, taking the dispersion interaction into account to enhance its capability for noncovalent interaction. The improvement of the B3LYP-D3/6-311+g** level is indicated by the changes in H-bond distances and angles (Table S12 in ESI†). In Table 5, 16 kinds of conformers of ion pair–GG are studied at B3LYP/6-31++g** and B3LYP-D3/6-311+g** levels of theory. As can be observed, the binding energies for ion pairs are −382.12 kJ mol−1, −378.22 kJ mol−1, −374.99 kJ mol−1 and −373.85 kJ mol−1 at the B3LYP/6-31++g** level for MmimCl, EmimCl, BmimCl, and HmimCl, respectively. That increase the alkyl chain of substituent results in a decrease of the interaction energies between cations and anions. The rule is applied for ΔE1,CA of other anion-typed ILs, and the similar results are obtained (Table 5). The elongation of alkyl chain leads to the increase of the ion volume, promoting charge distribution to a greater extent, which leads to a decline of binding energies interaction between cations and anions, i.e. ΔE1,CA and ΔE2,CA. Refer to the data of ΔE1,CA–GG, BmimMeSO4–GG system has relatively higher binding energy, −64.15 kJ mol−1, while the other three's binding energies are −62.36 kJ mol−1 (BmimCl–GG), −61.72 kJ mol−1 (BmimOAc–GG), and −44.01 kJ mol−1 (BmimPF6–GG), respectively. This result can explain the solubilities of lignin in different ILs in some degree. MeSO4 anion based ILs have good H-bond basicity and multiple electron donors, possessing superior ability to dissolve lignin, while PF6 anion based ILs is too sluggish to dissolve lignin.
| Structures | B3LYP/6-31++g**, kJ mol−1 | B3LYP-D3/6-311+g**, kJ mol−1 | ||||
|---|---|---|---|---|---|---|
| ΔE1,CA | ΔE1,CA–GG | ΔE1,C–A–GG | ΔE2,CA | ΔE2,CA–GG | ΔE2,C–A–GG | |
| MmimCl–GG | −382.12 | −62.37 | −444.49 | −391.21 | −116.72 | −507.92 |
| EmimCl–GG | −378.22 | −61.98 | −440.20 | −389.77 | −117.87 | −507.64 |
| BmimCl–GG | −374.99 | −62.36 | −437.35 | −386.98 | −121.53 | −508.51 |
| HmimCl–GG | −373.85 | −62.56 | −436.41 | −385.79 | −124.13 | −509.92 |
| MmimOAc–GG | −421.44 | −60.55 | −481.99 | −434.10 | −121.75 | −555.85 |
| EmimOAc–GG | −416.53 | −61.77 | −478.30 | −429.77 | −127.03 | −556.79 |
| BmimOAc–GG | −412.81 | −61.72 | −474.53 | −428.94 | −129.28 | −558.22 |
| HmimOAc–GG | −411.52 | −61.61 | −473.13 | −427.60 | −132.34 | −559.93 |
| MmimMeSO4–GG | −363.00 | −65.06 | −428.06 | −392.37 | −123.91 | −516.28 |
| EmimMeSO4–GG | −356.81 | −66.40 | −423.21 | −386.54 | −131.81 | −518.35 |
| BmimMeSO4–GG | −353.72 | −64.15 | −417.87 | −384.77 | −135.21 | −519.98 |
| HmimMeSO4–GG | −352.53 | −62.94 | −415.47 | −383.58 | −138.85 | −522.43 |
| MmimPF6–GG | −324.77 | −45.05 | −369.82 | −354.59 | −100.18 | −454.77 |
| EmimPF6–GG | −323.32 | −44.92 | −368.24 | −356.29 | −97.85 | −454.14 |
| BmimPF6–GG | −321.08 | −44.01 | −365.09 | −357.15 | −99.44 | −456.59 |
| HmimPF6–GG | −319.98 | −44.24 | −364.22 | −356.61 | −102.33 | −458.94 |
The interaction energy sequence of ΔE1,CA–GG follows MmimMeSO4–GG > MmimCl–GG MmimOAc–GG > MmimPF6, which is inconsistent with the H-bond ability.67 According to the previous work,69,70 we further consider the substituent and π–π stacking effects on ILs–GG system by reoptimizing those obtained geometries at B3LYP-D3/6-311+g** level, which are expected to have great contribution to the total interaction. It is observed that interaction energies of ion pairs (ΔE2,CA) are nearly 10–30 kJ mol−1 higher than ΔE1,CA, and ΔE2,CA–GG and ΔE2,C–A–GG are increased by 54–76 kJ mol−1 and 63–107 kJ mol−1, respectively, showing D3 term can fairly well consider the dispersion effects in ion pairs–GG system. Owing to the dominant electrostatic interactions between cations and anions, the values of ΔE1,CA and ΔE2,CA do not show such great differences, while the large increased values of ΔE1,C–A–GG and ΔE2,C–A–GG show a big proportion of electrostatic interaction between them. Refer to ΔE2,CA and ΔE2,CA–GG of the conformers (MmimMeSO4–GG, EmimMeSO4–GG, BmimMeSO4–GG and HmimMeSO4–GG), there is a weakening of cation–anion interaction with the elongation of alkyl substituent (ΔE2,CA), accompanied by increased binding energies (ΔE2,CA–GG) because ILs can provide larger spaces to contact with lignin GG model. However, it is clear from the data that increasing alkyl chain is not significant enough to influence the interaction energies of the four conformers. As reported by Janesko,5 cations are more important for lignin dissolution than cellulose, but anions still play key roles in governing the dissolution process, which also has been proved by experiment.71 Moreover, other factors, such as the steric hindrance and viscosity72 of ILs would affect the dissolution of lignocellulose. In addition, the previous basis B3LYP/6-31++g** may not be as accurate as B3LYP-D3/6-311+g** for thoughtless of dispersion interaction, which still gives a reasonable tendency in consistent with experimental results. The interaction energy is a metric that should be as an approximation to solubility in the lack of a better metric such as the free energy. We believe that the descriptor of interaction energy can provide an interesting prospective at the molecular level to understand the dissolution mechanism.
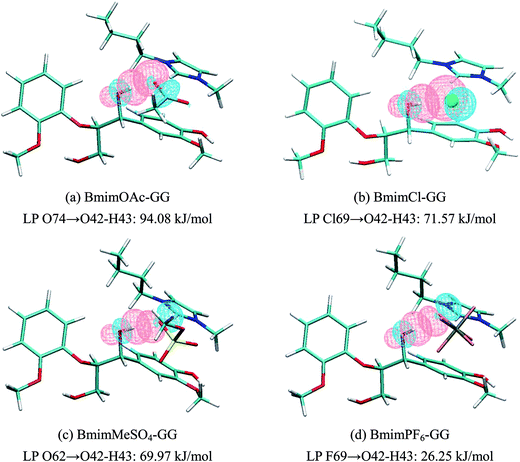
| Structure | π-Stacking interaction, kJ mol−1 | H-Bond interaction, kJ mol−1 | ||||
|---|---|---|---|---|---|---|
| Donor | Acceptor | E(2) | Donor | Acceptor | E(2) | |
| Fig. 5(a) | π C1–C2 | π* C46–N47 | 2.77 | Lp O74 | σ* O42–H43 | 94.08 |
| π C1–C2 | σ* C52–H54 | 0.84 | Lp O75 | σ* C13–H15 | 7.27 | |
| π C44–C45 | π* C3–C4 | 0.63 | Lp O42 | σ* C52–H54 | 6.59 | |
| Fig. 5(b) | π C1–C2 | π* C46–N47 | 3.77 | Lp Cl69 | σ* O42–H43 | 71.57 |
| π C44–C45 | π* C3–C4 | 0.81 | Lp Cl69 | σ* C13–H15 | 5.08 | |
| σ C62–H64 | π* C22–C24 | 0.60 | Lp O42 | σ* C52–H54 | 2.86 | |
| Fig. 5(c) | π C1–C2 | π* C46–N47 | 1.47 | Lp O62 | σ* O42–H43 | 69.97 |
| π C44–C45 | π* C3–C4 | 0.92 | Lp O61 | σ* C13–H15 | 9.70 | |
| π C1–C2 | σ* C52–H54 | 0.67 | Lp O60 | σ* C6–H9 | 7.52 | |
| Fig. 5(d) | σ C1–C2 | π* C46–N47 | 3.36 | Lp F69 | σ* O42–H43 | 26.25 |
| π C1–C2 | σ* C52–H54 | 0.67 | Lp O42 | σ* C52–H54 | 14.66 | |
| π C44–C45 | π* C3–C4 | 0.67 | Lp F73 | σ* C13–H15 | 4.28 | |
| Structure | H-Bond | ρBCP | ∇2ρBCP | HBCP (10−3 a.u.) |
|---|---|---|---|---|
| BmimOAc–GG | O42–H43⋯O74 | 0.045 | 0.141 | −3.531 |
| C13–H15⋯O75 | 0.013 | 0.044 | 1.506 | |
| C52–H54⋯O42 | 0.012 | 0.037 | 1.002 | |
| BmimCl–GG | O42–H43⋯Cl69 | 0.029 | 0.068 | −1.025 |
| C13–H15⋯Cl69 | 0.006 | 0.016 | 0.684 | |
| C52–H54⋯O42 | 0.011 | 0.033 | 0.962 | |
| BmimMeSO4–GG | O42–H43⋯O62 | 0.036 | 0.127 | −0.311 |
| C13–H15⋯O61 | 0.012 | 0.037 | 1.146 | |
| C6–H9⋯O60 | 0.012 | 0.038 | 1.118 | |
| BmimPF6–GG | O42–H43⋯F69 | 0.022 | 0.091 | 1.596 |
| C52–H54⋯O42 | 0.016 | 0.052 | 1.479 | |
| C13–H15⋯F73 | 0.010 | 0.037 | 1.129 |
4. Conclusion
Structures and electron properties in the interactions between ILs and lignin model compound are studied using a density functional theory at B3LYP/6-31++g** level and dispersion corrected DFT at B3LYP/6-311+g** level. Lignin is modeled with guaiacyl glycerol-β-guaiacyl ether (GG), and the interactions between single anion/cation and GG, and ion pairs and GG, are taken into consideration. B3LYP/6-31++g** method generally provides reasonable results for the interaction between ILs and GG model, and B3LYP-D3/6-31++g** method gives more desirable calculations in consideration of the dispersion effects and electrostatic interactions. H-Bond interactions are particularly investigated and characterized by interaction energy (ΔE), NBO analysis, AIM analysis and RDG method to judge the strength of interactions. On the basis of geometries, NBO, AIM and RDG analyses, we find that both cations (Mmim, Emim, Bmim, Hmim) and anions (Cl, OAc, MeSO4, PF6) can form H-bonds with GG model. The analyses also show that anions have the strongest interactions at the α-OH position of GG and cations have the strongest interactions at γ-OH of GG. Furthermore, anions–GG interactions are stronger than cations–GG interactions, and the changing lengths of alkyl chains of cations do not significantly influence H-bond interactions in all of the cations–GG interactions. Anions with electronegative atoms or conjugated electrons are favorable for H-bonds, and non-coordinating anions do not have strong interactions with lignin. In the ion pairs–GG interactions, anions still play a key role in providing H-bond interactions, and cations can afford a π-stacking interaction with model compound GG and from H-bonds with anions simultaneously. NBO and RDG analysis show the importance of π-stacking interactions in lignin dissolution, but its effect is not as significant as anions do. In all, the calculation data explain the dissolution mechanism to some extent, and H-bond is of great importance to facilitate the dissolution of lignin in ILs, which is in consistent with the experimental evidence. Thus, to design an efficient IL solvent for lignin, anions with good H-bond basicity, smaller volume and forming more H-bonds are favorable for lignin dissolution. The long alkyl substituent may result in higher viscosity and steric effect, thus causing reduction of dissolution ability. Cations with too short alkyl chain also have strong association with anions, thus we need come to a balance between chain length and solubility in practices.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21406230), the Key Program of National Natural Science Foundation of China (Grant No. 21336002), the Open Research Fund of State Key Laboratory of Multiphase Complex Systems, IPE, CAS (Grant No. MPCS-2014-D-04), and by the Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (second phase).References
- F. H. Isikgor and C. R. Becer, Polym. Chem., 2015, 6, 4497–4559 RSC.
- V. K. Thakur and M. K. Thakur, Int. J. Biol. Macromol., 2015, 72, 834–847 CrossRef CAS PubMed.
- F. S. Chakar and A. J. Ragauskas, Ind. Crops Prod., 2004, 20, 131–141 CrossRef CAS.
- B. Kamm, P. R. Gruber and M. Kamm, Biorefineries–Industrial Processes and Products, Wiley Online Library, 2007 Search PubMed.
- B. G. Janesko, Phys. Chem. Chem. Phys., 2011, 13, 11393–11401 RSC.
- G. Cheng, M. S. Kent and L. He, et al., Langmuir, 2012, 28, 11850–11857 CrossRef CAS PubMed.
- X. Qiu, Q. Kong and M. Zhou, et al., J. Phys. Chem. B, 2010, 114, 15857–15861 CrossRef CAS PubMed.
- Y. Deng, X. Feng and M. Zhou, et al., Biomacromolecules, 2011, 12, 1116–1125 CrossRef CAS PubMed.
- S. S. Y. Tan, D. R. MacFarlane and J. Upfal, et al., Green Chem., 2009, 11, 339 RSC.
- N. Sun, H. Rodriguez and M. Rahman, et al., Chem. Commun., 2011, 47, 1405–1421 RSC.
- J. S. Wilkes and M. J. Zaworotko, J. Chem. Soc., Chem. Commun., 1992, 965–967 RSC.
- P. Walden, Bull. Russ. Acad. Sci., 1914, 8, 405–422 Search PubMed.
- A. A. Fannin Jr, D. A. Floreani and L. A. King, et al., J. Phys. Chem., 1984, 88, 2614–2621 CrossRef.
- H. He, H. Chen and Y. Zheng, et al., Chem. Eng. Sci., 2015, 121, 169–179 CrossRef CAS.
- L. J. Conceiçao, E. Bogel-Łukasik and R. Bogel-Łukasik, RSC Adv., 2012, 2, 1846–1855 RSC.
- J. G. Huddleston, H. D. Willauer and R. P. Swatloski, et al., Chem. Commun., 1998, 1765–1766 RSC.
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS PubMed.
- R. P. Swatloski, S. K. Spear and J. D. Holbrey, et al., J. Am. Chem. Soc., 2002, 124, 4974–4975 CrossRef CAS PubMed.
- J. M. Andanson, A. A. H. Padua and M. F. Costa Gomes, Chem. Commun., 2015, 51, 4485–4487 RSC.
- J.-M. Andanson, E. Bordes and J. Devemy, et al., Green Chem., 2014, 16, 2528–2538 RSC.
- S. Velioglu, X. Yao and J. Devémy, et al., J. Phys. Chem. B, 2014, 118, 14860–14869 CAS.
- H. Wu and E. J. Maginn, Fluid Phase Equilib., 2014, 368, 72–79 CrossRef CAS.
- S. Budhathoki, J. K. Shah and E. J. Maginn, Ind. Eng. Chem. Res., 2015, 54, 8821–8828 CrossRef CAS.
- J. L. Anthony, J. L. Anderson and E. J. Maginn, et al., J. Phys. Chem. B, 2005, 109, 6366–6374 CrossRef CAS PubMed.
- J. L. Anthony, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2002, 106, 7315–7320 CrossRef CAS.
- C. Cadena, J. L. Anthony and J. K. Shah, et al., J. Am. Chem. Soc., 2004, 126, 5300–5308 CrossRef CAS PubMed.
- G. B. Damas, A. B. A. Dias and L. T. Costa, J. Phys. Chem. B, 2014, 118, 9046–9064 CrossRef CAS PubMed.
- D. A. Fort, R. C. Remsing and R. P. Swatloski, et al., Green Chem., 2007, 9, 63–69 RSC.
- N. Sun, M. Rahman and Y. Qin, et al., Green Chem., 2009, 11, 646–655 RSC.
- S. H. Lee, T. V. Doherty and R. J. Linhardt, et al., Biotechnol. Bioeng., 2009, 102, 1368–1376 CrossRef CAS PubMed.
- A. K. Sangha, L. Petridis and J. C. Smith, et al., Environ. Prog. Sustainable Energy, 2012, 31, 47–54 CrossRef CAS.
- C. Balaji, T. Banerjee and V. V. Goud, J. Solution Chem., 2012, 41, 1610–1630 CrossRef CAS.
- A. Lüttge, J. Electron Spectrosc. Relat. Phenom., 2006, 150, 248–259 CrossRef.
- A. Casas, J. Palomar and M. V. Alonso, et al., Ind. Crops Prod., 2012, 37, 155–163 CrossRef CAS.
- R. S. Payal, R. Bharath and G. Periyasamy, et al., J. Phys. Chem. B, 2012, 116, 833–840 CrossRef CAS PubMed.
- B. B. Cao, J. Y. Du and D. M. Du, et al., Carbohydr. Polym., 2016, 149, 348–356 CrossRef CAS PubMed.
- W. Ji, Z. Ding and J. Liu, et al., Energy Fuels, 2012, 26, 6393–6403 CrossRef CAS.
- J. Zakzeski, P. C. Bruijnincx and A. L. Jongerius, et al., Chem. Rev., 2010, 110, 3552–3599 CrossRef CAS PubMed.
- P. Sista, B. Xue and M. Wilson, et al., Macromolecules, 2012, 45, 772–780 CrossRef CAS.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- K. Dong, Y. Cao and Q. Yang, et al., Ind. Eng. Chem. Res., 2012, 51, 5299–5308 CrossRef CAS.
- K. Dong, Y. Song and X. Liu, et al., J. Phys. Chem. B, 2012, 116, 1007–1017 CrossRef CAS PubMed.
- K. Dong and S. Zhang, Chem.–Eur. J., 2012, 18, 2748–2761 CrossRef CAS PubMed.
- W. G. Cheng, F. Xu and J. Sun, et al., Synth. Commun., 2016, 46, 497–508 CrossRef CAS.
- Z. D. Ding, Z. Chi and W. X. Gu, et al., Carbohydr. Polym., 2012, 89, 7–16 CrossRef CAS PubMed.
- J. Guo, D. Zhang and C. Liu, J. Theor. Comput. Chem., 2010, 9, 611–624 CrossRef CAS.
- X. Zhang, W. Yang and W. Blasiak, Energy Fuels, 2011, 25, 4786–4795 CrossRef CAS.
- S. Grimme, J. Antony and S. Ehrlich, et al., J. Chem. Phys., 2010, 132, 1–19 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Mol. Model., 2013, 19, 5387–5395 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- R. Fu, T. Lu and F. Chen, Acta Phys.–Chim. Sin., 2014, 30, 628–639 CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- H. Guernon and C. Y. Legault, Organometallics, 2013, 32, 1988–1994 CrossRef CAS.
- B. Miehlich, A. Savin and H. Stoll, et al., Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- R. F. W. Bader, in Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd, 2002 Search PubMed.
- J. Cioslowski, Science, 1991, 252, 1566–1568 CrossRef PubMed.
- J. Contreras-Garcia, E. R. Johnson and S. Keinan, et al., J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan and P. Mori-Sanchez, et al., J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- W. E. S. Hart, J. B. Harper and L. Aldous, Green Chem., 2015, 17, 214–218 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CrossRef CAS.
- R. G. Parr, in Horizons of Quantum Chemistry, Springer, 1980, pp. 5–15 Search PubMed.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- B. J. Cox, S. Jia and Z. C. Zhang, et al., Polym. Degrad. Stab., 2011, 96, 426–431 CrossRef CAS.
- A. L. Ringer and C. D. Sherrill, J. Am. Chem. Soc., 2009, 131, 4574–4575 CrossRef CAS PubMed.
- W. Gao, Y. Tian and X. Xuan, J. Mol. Graphics Modell., 2015, 60, 118–123 CrossRef CAS PubMed.
- J. Zakzeski, P. C. Bruijnincx and A. L. Jongerius, et al., Chem. Rev., 2010, 110, 3552–3599 CrossRef CAS PubMed.
- K. C. Badgujar and B. M. Bhanage, Bioresour. Technol., 2015, 178, 2–18 CrossRef CAS PubMed.
- Y. Pu, N. Jiang and A. J. Ragauskas, J. Wood Chem. Technol., 2007, 27, 23–33 CrossRef CAS.
- S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS PubMed.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27059j |
| This journal is © The Royal Society of Chemistry 2017 |