Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the stacking behaviour of a 2D covalent organic framework through non-covalent interactions†
F.
Haase
ab,
K.
Gottschling
ab,
L.
Stegbauer‡
ab,
L. S.
Germann
a,
R.
Gutzler
a,
V.
Duppel
a,
V. S.
Vyas§
a,
K.
Kern
ac,
R. E.
Dinnebier
 a and
B. V.
Lotsch
*ab
a and
B. V.
Lotsch
*ab
aMax Planck Institute for Solid State Research, 70569 Stuttgart, Germany. E-mail: b.lotsch@fkf.mpg.de
bLudwig Maximilians University of Munich, 81377 Munich, Germany
cInstitut de Physique, École Polytechnique Fédérale de Lausanne, Lausanne CH-1015, Switzerland
First published on 8th February 2017
Abstract
Two-dimensional covalent organic frameworks (COFs) are crystalline porous materials composed of organic building blocks that are connected via covalent bonds within their layers, but through non-covalent interactions between the layers. The exact stacking sequence of the layers is of paramount importance for the optoelectronic, catalytic and sorption properties of these polymeric materials. The weak interlayer interactions lead to a variety of stacking geometries in COFs, which are both hard to characterize and poorly understood due to the low levels of crystallinity. Therefore, detailed insights into the stacking geometry in COFs is still largely elusive. In this work we show that the geometric and electronic features of the COF building blocks can be used to guide the stacking behavior of two related 2D imine COFs (TBI-COF and TTI-COF), which either adopt an averaged “eclipsed” structure with apparent zero-offset stacking or a unidirectionally slip-stacked structure, respectively. These structural features are confirmed by XRPD and TEM measurements. Based on theoretical calculations, we were able to pinpoint the cause of the uniform slip-stacking geometry and high crystallinity of TTI-COF to the inherent self-complementarity of the building blocks and the resulting donor–acceptor-type stacking of the imine bonds in adjacent layers, which can serve as a more general design principle for the synthesis of highly crystalline COFs.
Introduction
Covalent organic frameworks (COFs) have risen from obscurity in recent years.1 They show great promise for many applications,2–4 especially since their structures,5,6 properties7–9 and functionalities can be engineered.10–12 However, much of the inherent potential of COFs to rationally design their structures is impeded by their relatively low crystallinity as compared to the related metal–organic frameworks (MOFs).13 The hallmark of COFs, namely their strong covalent bonds combined with their low-temperature synthesis through the utilization of reversible reactions by dynamic covalent chemistry, often leads to a compromise between framework stability and crystallinity.14,15 COFs made by highly reversible reactions such as the nitrosyl dimerization can be obtained in single crystalline form, but they suffer from comparatively low stability due to the intrinsic weakness of these ON–NO bonds.16 Compromising reversibility for stability leads to reduced crystallinity, i.e. disorder and small crystallite sizes.14,17 Two-dimensional COFs rely on van der Waals and other non-covalent interactions in addition to covalent interactions to form a three-dimensional solid. The weak non-covalent interactions often cause the formation of 2D crystals where large deviations from the ideal stacking geometry are possible in the third dimension, leading to complex or ill-defined polytypes. While local analytical techniques such as solid-state NMR are largely insensitive to the stacking sequence, X-ray powder diffraction (XRPD) of COFs with moderate crystallinity returns average structures with no or little information about the layer arrangement. As this is a common challenge in 2D COFs, several design principles have been proposed to improve, control, or alter their stacking behavior. These include for example the use of non-flat, propeller-shaped building blocks that induce stacking without offset and lead to preferred, “locked-in” configurations,18,19 as well as the use of donor and acceptor (DA) molecules that can stack in an alternating fashion,20 or the manipulation of the dipole of the linkers, which can lead to energetic minimum structures through dipolar alignment.21,22 In all cases, however, high crystallinity is a key prerequisite to derive the 3D structure of COFs by means of XRPD.In addition to the experimental difficulties in obtaining highly crystalline COFs, the determination of the exact stacking geometry is challenging and early attempts mainly differentiated between staggered and the so-called eclipsed stacking.23–25 It has been predicted that a perfectly eclipsed stacking is energetically not favorable for π-stacked, flat COFs as the energetic minima lie off-center.26–28 Truly slip-stacked structures based on flat building blocks however have not been identified by XRPD so far, possibly due to stacking disorder and crystallite size effects, which lead to line broadening, precluding the exact determination of the stacking structure. Instead, the higher symmetry structure based on eclipsed layer stacking is usually assumed as an average structure model.3,23,29
Inspired by the existing design principles, we have synthesized a COF in which the stacking can be rationally adjusted based on the geometry and non-covalent interactions of the building blocks. We demonstrate that individual layers can self-assemble to form DA-type stacks where imine bond polarization or similar interlayer interactions may be efficient in determining the polytype. To add evidence for our hypothesis, we “turned off” the possibility of DA stacking in a closely related system by introducing a propeller-shaped building block that causes the formation of an averaged eclipsed geometry. These two very similar systems allow us to gauge the influence of symmetry, geometry and polarity of the building blocks on the stacking characteristics of the COF. The stacking of the COFs was analysed experimentally and theoretically and we provide first evidence of well-defined slipped stacking in a COF based on a combination of Rietveld refinement of XRPD data and transmission electron microscopy (TEM). We thus demonstrate that careful analysis of the stacking mode can serve as a design principle to direct and control disorder and crystallization in COFs.
Results
Two imine COFs based on the triphenyl aryl unit were synthesized through the reaction of a triamine with a trialdehyde under solvothermal conditions in mesitylene/dioxane 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and aqueous acetic acid as a catalyst (Fig. 1).30 The difference between these COFs lies in the nitrogen content of the triamine precursor, which is based on a central phenyl ring or a triazine ring in case of the TBI-COF or the TTI-COF, respectively. The successful condensation reaction was confirmed via the disappearance of N–H and C
1 and aqueous acetic acid as a catalyst (Fig. 1).30 The difference between these COFs lies in the nitrogen content of the triamine precursor, which is based on a central phenyl ring or a triazine ring in case of the TBI-COF or the TTI-COF, respectively. The successful condensation reaction was confirmed via the disappearance of N–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrations and the appearance of C
O vibrations and the appearance of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N vibrations through IR spectroscopy (Fig. S1, ESI†). The porosity of the structures was determined via argon physisorption (Fig. S2, ESI†), which showed BET surface areas of 1108 m2 g−1 for the TBI and 1403 m2 g−1 for the TTI-COF (Fig. S3, ESI†).
N vibrations through IR spectroscopy (Fig. S1, ESI†). The porosity of the structures was determined via argon physisorption (Fig. S2, ESI†), which showed BET surface areas of 1108 m2 g−1 for the TBI and 1403 m2 g−1 for the TTI-COF (Fig. S3, ESI†).
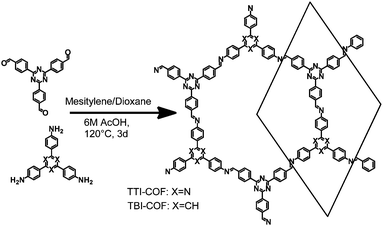 | ||
| Fig. 1 Schematic representation of the synthesis of TTI-COF and TBI-COF from a triamine and a trialdehyde. | ||
While both networks are crystalline (Fig. 2), the TTI-COF has narrower line widths and shows a pronounced splitting of the [100], [110], [020] and [120] diffraction peaks as well as a discernable stacking peak (Fig. 2) showing that this COF is highly crystalline. This unusual diffraction pattern of TTI-COFs is distinct from previously reported, highly symmetrical frameworks.
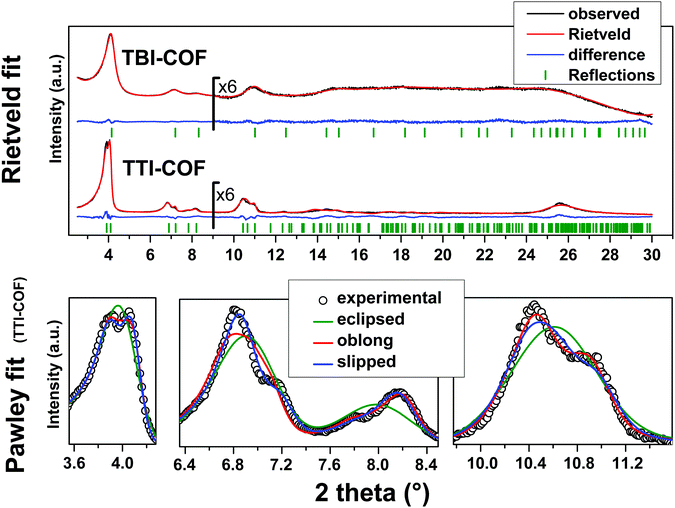 | ||
| Fig. 2 Top: XRPD patterns (λ = Cu Kα1) of the TBI-COF and the TTI-COF (black) with the final Rietveld fits of the COFs (red) and their respective difference curves (blue). Rwp (Rietveld) (see eqn (S1) in ESI†) values for the TTI-COF and the TBI-COF are 7.138 and 2.744, respectively. Bottom: XRPD pattern (λ = Cu Kα1) of the TTI-COF with eclipsed, oblong and slipped Pawley refinements with detail view of the reflections showing the reduction in symmetry. | ||
To determine the structure of the two COFs, several structural models were considered to explain the observed powder patterns. We developed three models based on different stacking modes influencing the overall symmetry as well as the molecular conformations, which were compared to the experimental powder patterns using Pawley refinement31 and Rietveld analysis.32 The initial values of the cell parameters were obtained from the force field optimized structures, which were constructed based on geometrical considerations, and the in-plane connectivity was derived from the topology of the molecular building blocks. All models are based on a honeycomb structure with a hcb net33 (Fig. 1).
High symmetry case: eclipsed stacking
For the eclipsed model C3 symmetry was chosen for the in-plane structure. These individual layers were then stacked in a perfectly eclipsed fashion to form a one-layer cell with P3 symmetry and cell parameters a = b ≠ c and α = β = 90°, γ = 120°. This type of model is simplistically assumed for most COFs in the absence of detailed structural information from the X-ray powder patterns.23,26,28 While these COFs have an apparent high symmetry due to disorder,23 only some COFs stack without any lateral offset between layers.18 When this high symmetry cell is applied to the observed XRPD pattern of TTI-COF, stark differences between the simulated and the observed pattern are obvious and most prominently reflected by the different numbers of reflections (Fig. 2, Rwp: 9.319, see eqn (S1) in ESI†). We therefore explored lower symmetry models for the TTI-COF. For the case of the TBI-COF the eclipsed model yielded a good fit (Rwp: 1.365), as no symmetry reduction is apparent.Low symmetry layers: oblong pores
As a first lower symmetry model, the in-plane C3 symmetry was removed and varying the conformation of the imine bonds lead to oblong pores (Fig. S4, ESI†), while the eclipsed layer stacking was retained. This structural modification leads to a Pm symmetry unit cell with a ≠ b ≠ c and α = β = 90°, γ = 120°. Pawley refinement of the oblong model shows a relatively good fit (Rwp: 5.359) to the observed powder pattern of the TTI-COF (Fig. 2). However, when the structural model was constructed and the cell parameters were applied based on the Pawley refinement (Table S1, ESI†), the structure was compressed in the b direction, resulting in aromatic C–C bond lengths as small as 1.36 Å. The oblong model is only able to fit the experimental XRPD pattern with a marked reduction of the cell parameter b with respect to a, more than would be expected by the conformational changes of the imine bonds. This strain disfavors the oblong model as a cause for the experimentally observed reduction in symmetry.Shifted layer model: slipped stacking
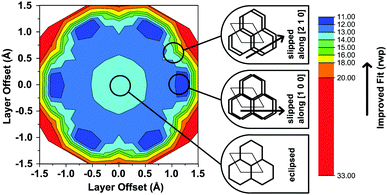
Another conceivable way to lower the symmetry of the unit cell is to shift the individual pseudohexagonal layers along one direction. This model follows previous calculations on boronate ester COFs predicting that a slipped configuration in flat 2D COFs is energetically much more favorable than eclipsed stacking, which lacks experimental confirmation so far.26,27 This model was implemented in a P1 unit cell with the constraints a = b ≠ c and α = β, γ = 120°. Pawley refinement with the slipped model showed the best fit (Rwp (Pawley): 4.461, Fig. 2, bottom) of the three applied models (Table S1, ESI†). The lattice parameters of the slipped model Pawley refinement were implemented and showed no signs of strain such as unrealistically small bond lengths or angles. The one-layer geometry optimized unit cell was then refined using Rietveld analysis. Initially, the slipping direction was fixed with the constraint a = b. To explore other possible slipping directions, the parameter space of different directions and magnitudes of slipping at constant layer-layer distance was used for refinement and plotted against the layer offset (Fig. 3). The obtained “landscape” of stacking maps the hexagonal symmetry of the individual layers and reflects the fact that not all slipping directions fit the powder pattern equally well when comparing constant lateral offsets. The preferred slipping direction in this COF is along [100] and all equivalent directions ([110], [010], [![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 00], [
00], [![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif)
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 0], [0
0], [0![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 0]) (Fig. 3).
0]) (Fig. 3).
The obtained models for the TTI-COF and the TBI-COF differ considerably despite the similarity of both COFs. To further confirm the models we performed periodic boundary condition DFT calculations in which the unit cells and atomic positions of the COFs were relaxed (Table S2, ESI†). These showed a minimum for a slipped TTI-COF and a slipped TBI-COF. While the slipping in the TTI-COF is seen in the XRPD by the symmetry reduction, no such indication of slipping can be seen in the XRPD of the TBI-COF. In these DFT calculations the TTI-COF slips along [100], just as observed in the XRPD refinement. The DFT based structure of the TBI-COF is slipped along [120], which is in contrast to the observed XRPD pattern showing P3 symmetry. In order to understand the difference between the DFT based structure and the observed powder pattern we performed DIFFaX simulations to find an explanation for the apparent higher symmetry obtained from the XRPD pattern (Fig. 4).
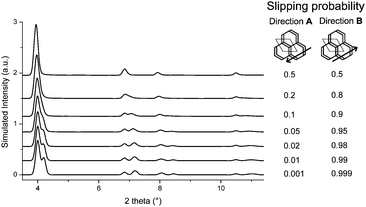 | ||
| Fig. 4 DIFFaX simulated XRPD pattern with varying degrees of disorder in the slipping direction [120] for the TBI-COF. | ||
In the simplified model used in our simulations, subsequent layers of the structure had a chosen probability to slip in either one direction or the opposite, while the magnitude and the stacking offset was kept constant. When the probabilities of slipping in either direction become equal (0.5–0.5), the apparent symmetry of the simulated XRPD pattern increases to P3. Thus, with this simple model we are already able to rationalize the observed higher symmetry of the XRPD of TBI-COF, which can be attributed to disorder in the stacking of the TBI-COF. This confirms the often observed higher apparent symmetry of COFs, which results from an average structure due to the equal probability of energetically similar or equivalent slipping directions.23,26–28
We performed TEM and scanning electron microscope (SEM) experiments to confirm the results from XRPD and to gain further insights into the local structural features of these COFs.
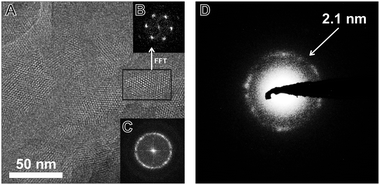
TEM images of the TBI-COF (Fig. 5) show crystalline domains with domain sizes in the range of 30 nm up to 80 nm, which exhibit the hexagonal symmetry of the pores. The fast Fourier transform (FFT) and the selected area electron diffraction (SAED) patterns show the expected repeat distance of 2.1 nm that matches the 100 reflection obtained from the structural model based on the XRPD data. The morphology of the TBI-COF as observed in the SEM and TEM resembles individual slabs that are composed of smaller crystallites (Fig. S5, ESI†).
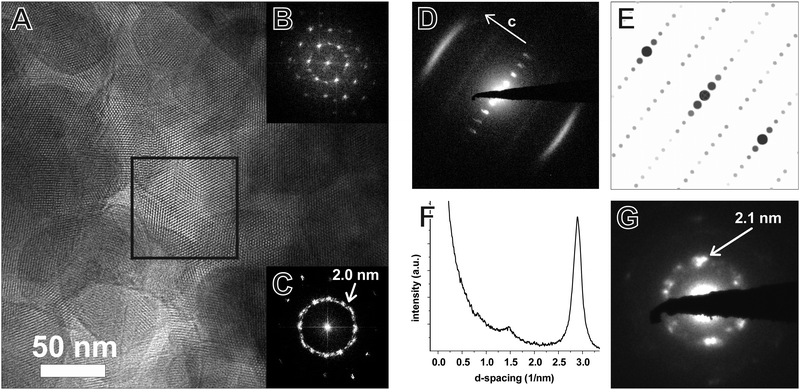
TEM of the TTI-COF shows significantly larger crystalline domains than the TBI-COF with crystallite sizes in the range of 50 nm up to 200 nm. The pseudo-hexagonal symmetry of the pores is apparent along the [001] zone axis, while the pore channels are visible when viewing in the direction along the a–b plane (Fig. 6). The FFT and the SAED of the TTI-COF both show lattice spacings close to the values expected from XRPD. The microscopic morphology of the TTI-COF exposes large polycrystalline rods in which some crystallites show bending along the direction of the channels (Fig. S5 and S6, ESI†).
The FFT shows the hexagonal pore structure of the COF along [001] (Fig. 6B) as well as zone axes allowing the observation of 00l and h![[k with combining overline]](https://www.rsc.org/images/entities/i_char_006b_0305.gif) 0 reflections simultaneously such as [110] (Fig. 6D). In addition to the sharp reflections from the (1
0 reflections simultaneously such as [110] (Fig. 6D). In addition to the sharp reflections from the (1![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 0) and higher order reflections, a prominent streak along hk1 is visible at a distance of 2.90 nm−1 (3.5 Å) which is in excellent agreement with the expected layer-to-layer distance. Close inspection of the SAED reveals a further streak at the distance of 1.45 nm−1 (6.85 Å), which indicates the existence of two individual layers per unit cell along c. The simulated SAED of a two-layer model fits well to the experimentally obtained SAED (Fig. 6D and E; model: Fig. 8, right). In contrast to the simulation, the reflections hk1 and hk2 are smeared out to form streaks. The direction of these streaks indicates in-plane disorder as the cause of this diffuse reflection, since stacking disorder would cause streaks along c. A possible cause of in-plane disorder might be a random variation of the conformation of the imine linkages such as described in the oblong model. Since the SAED indicates two layers per unit cell, we developed possible models with different stacking geometries of imines with two layers per unit cell based on the structures of known molecular imines. From the crystal structures of molecular imine compounds three major geometric motifs are conceivable for the TTI-COF (Fig. 7). Molecular imines have a variety of stacking modes, where sometimes one molecule exhibits different kinds of stacking in one crystal or differently stacked polymorphs exist for a single compound.34 Ordered geometries include the direct slipped geometry where the imine orientation is the same for all molecules that are stacking (Fig. 7A),35 and the antiparallel geometry with the imine orientation changing with a twofold axis from one layer to the next (Fig. 7B).36 These motifs are present in imines with different substituents and the influence of these might guide the stacking behavior.34 A common motif for molecular imines with identical substituents is the disordered stacking leading to a pseudo inversion center on the imine bond (Fig. 7C).37–39 The symmetric substitution in the TTI-COF would point toward the disordered stacking, which however is not compatible with the observed SAED with clearly discernable streaks along (hk1) and (hk2).
0) and higher order reflections, a prominent streak along hk1 is visible at a distance of 2.90 nm−1 (3.5 Å) which is in excellent agreement with the expected layer-to-layer distance. Close inspection of the SAED reveals a further streak at the distance of 1.45 nm−1 (6.85 Å), which indicates the existence of two individual layers per unit cell along c. The simulated SAED of a two-layer model fits well to the experimentally obtained SAED (Fig. 6D and E; model: Fig. 8, right). In contrast to the simulation, the reflections hk1 and hk2 are smeared out to form streaks. The direction of these streaks indicates in-plane disorder as the cause of this diffuse reflection, since stacking disorder would cause streaks along c. A possible cause of in-plane disorder might be a random variation of the conformation of the imine linkages such as described in the oblong model. Since the SAED indicates two layers per unit cell, we developed possible models with different stacking geometries of imines with two layers per unit cell based on the structures of known molecular imines. From the crystal structures of molecular imine compounds three major geometric motifs are conceivable for the TTI-COF (Fig. 7). Molecular imines have a variety of stacking modes, where sometimes one molecule exhibits different kinds of stacking in one crystal or differently stacked polymorphs exist for a single compound.34 Ordered geometries include the direct slipped geometry where the imine orientation is the same for all molecules that are stacking (Fig. 7A),35 and the antiparallel geometry with the imine orientation changing with a twofold axis from one layer to the next (Fig. 7B).36 These motifs are present in imines with different substituents and the influence of these might guide the stacking behavior.34 A common motif for molecular imines with identical substituents is the disordered stacking leading to a pseudo inversion center on the imine bond (Fig. 7C).37–39 The symmetric substitution in the TTI-COF would point toward the disordered stacking, which however is not compatible with the observed SAED with clearly discernable streaks along (hk1) and (hk2).
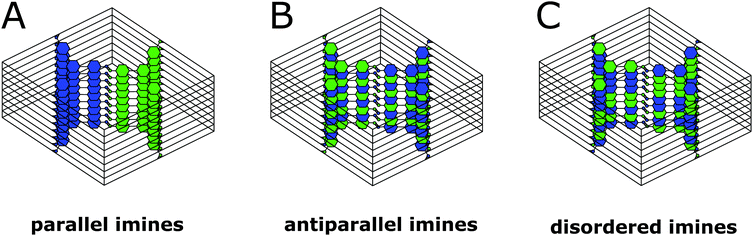 | ||
| Fig. 7 Three of the possible stacking motifs of the TTI-COF, where blue and green represent the amine and aldehyde building blocks, respectively. | ||
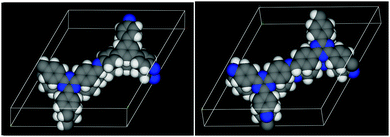 | ||
| Fig. 8 The DFT optimized structures of the TBI-COF (left, parallel) and the TTI-COF (right, antiparallel). Carbon atoms are shown in grey, nitrogen in blue and hydrogen in white. | ||
To further narrow down the possible stacking geometries, we performed periodic boundary DFT calculations on two layer unit cells and compared whether the alignment of the imine bonds (Fig. 7A) or the antiparallel imine bond (Fig. 7B) are energetically more favorable. We relaxed the structures of the antiparallel imine and the parallel imine models and obtained two closely resembling slipped structures that match the obtained lattice parameters from Pawley refinement of the XRPD well (Table S2, ESI†). The difference in total energy of these two structures was calculated and showed that the antiparallel configuration is more stable by approximately 0.32 eV (30.9 kJ mol−1) per unit cell. This is not surprising, as an antiparallel stacking from one layer to the next leads to donor–acceptor (DA) interactions between the more electron rich triazine triphenyl amine (TT-NH2) and the electron poorer triazine triphenyl aldehyde (TT-CHO) across the layers, which is a well-known phenomenon for two flat molecules that have electron poor as well as electron rich character.40 In addition, the antiparallel stacking creates antiparallel aligned dipoles, which stabilize the structure. The comparison of the parallel and the antiparallel stacking in the TBI-COF yielded only a negligible energetic difference of 0.04 eV (3.9 kJ mol−1), which could be explained by a competition of the favorable DA stacking and the unfavorable geometric mismatch between the propeller-shaped triphenyl benzene core (TB) and the flat triphenyl triazine core (TT).
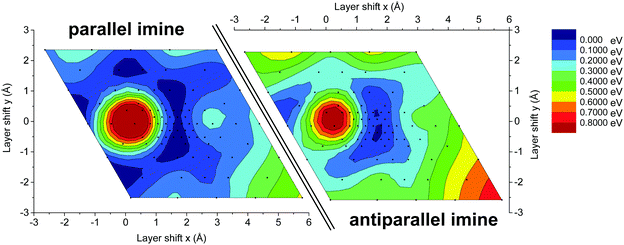
To investigate the origin of the high crystallinity and the unidirectionally slipped geometry of the TTI-COF, we compared the energy landscape of stacking the layers with different offsets of the antiparallel and parallel imines (Fig. 9), determined by DFT. In both energy landscapes, eclipsed stacking, corresponding to zero offset, is energetically non-favorable in contrast to the slipped geometry. The “parallel imine” stacking landscape shows a shallow and widespread minimum with multiple symmetry-related minima with a pseudo-hexagonal structure. Such an energy landscape might be expected to yield a random direction offset in stacking. In contrast, the “antiparallel imine” stacking landscape shows reduced symmetry, which can be attributed to the slight out-of-plane torsion of phenyl rings, which is more pronounced in the antiparallel imine case than in the parallel imine case (Fig. S7, ESI†). This torsion reduces the symmetry of one individual layer, but at the same time is able to propagate the preferential slipping direction to the next layer, providing a rationale to the observed reduction in the symmetry of the unit cell. The comparison of both energy landscapes shows that in the case of the antiparallel imine bonds the minimum is steeper and less distributed than in the case of the parallel imine bonds. A steep minimum likely directs the crystallization process during the synthesis of the TTI-COF and therefore may be linked to the observed slipped stacking mode and the high crystallinity of the TTI-COF.
As the antiparallel stacked TTI-COF is the most stable configuration according to DFT, this structural model was used for the Rietveld refinement. The crystal structure consisting of two independent layers was refined using Rietveld methods, by refining the lattice parameters, atomic coordinates using rigid bodies for the layers and their shift with respect to each other. The final TTI-COF model is shown in Fig. 8 and the corresponding refinement in Fig. 2.
Discussion
As outlined above, the particular slip-stacking mode seen in the TTI-COF can be explained by an interplay of several factors that are different in the TBI-COF. Most notably, the TTI-COF is a relatively flat system, which allows the individual layers to slip, in contrast to propeller like out of plane elements, which can cause locking in of a structure.18,19 However, the flat structure alone does not seem to be sufficient for introducing unidirectional slipping, since many COFs are flat, but do not show the same layer offset in only one direction and hence, symmetry reduction, as observed in the TTI-COF.7,23,26 Therefore, another factor influencing the stacking might be the self-complementarity of the TTI-COF, which means that individual layers can form DA stacks just by alternation of the different building blocks along the c-direction (Fig. 7). This feature is fairly unique, since it requires the use of two linkers with C3-symmetry that have the same size, geometry, but different electronic structures. Generally, the parallel stacking of imines can be seen as a valid model for most imine COFs since conditions for self-complementary antiparallel stacking as outlined above are rarely met. If the size of the building blocks is different, then the contact during alternation would not be that intimate and the dipole of the imine bonds could not be aligned in a close, antiparallel fashion to enable favorable dipole–dipole interactions.21,22 In addition, the planarity of TTI-COF favors the DA stacking, which is in contrast to TBI-COF. The TBI-COF could be expected to stack with no offset between the layers (eclipsed) since it bears a propeller-shaped building block.18 However, the DFT calculations showed an energy minimum for an offset structure, which is why an averaged structure with an apparent zero layer offset is more likely for this COF. In principle, the TBI-COF could be expected to show an even more pronounced stacking in a DA fashion since a benzene core is more electron rich than the triazine core. However, the out-of-plane twisting of the TB system is likely to make efficient contact to the TT core in an adjacent layer difficult. Therefore, the lower crystallinity and the different observed stacking geometry of the TBI-COF is largely linked to the disturbance of planarity.Conclusion
In conclusion, we have synthesized two imine-COFs with similar molecular connectivity but distinctly different stacking geometries. While the TBI-COF adopts the archetypical random layer off-set as seen for most 2D COFs, giving rise to an average higher symmetry structure which is isostructural with eclipsed layer stacking, the TTI-COF shows an unusual slip-stacked geometry with uniform direction of the layer offset in each subsequent layer. SAED in conjunction with DFT calculations revealed a two-layer unit cell of the TTI-COF with antiparallel imines as a preferred stacking mode. The observed stacking preference of the TTI-COF directly translates into significantly increased domain sizes and crystallinity as compared to TBI-COF. DFT based energy landscapes for the stacking of the TTI-COF suggest that the alternate imine stacking creates steeper and deeper minima, which can be seen as the rationale for the unidirectional offset-stacking and the resulting improved overall crystallinity. In conclusion, the observed interlayer donor–acceptor type stacking interactions in TTI-COF may be used as a more general design principle based on non-covalent interactions that facilitate crystallization.Acknowledgements
The authors thank Christine Stefani for measuring the high-resolution XRPD patterns. This work has been funded by the Federal Ministry of Education and Research (BMBF, Germany) in the project StickLiS (FKZ: 03XP0030C). B. V. L. acknowledges financial support by an ERC Starting Grant (project COFLeaf, grant number 639233), the Max Planck Society as well as by the cluster of excellence /Nanosystems Initiative Munich/ and the Center for Nanoscience (CeNS). Open Access funding provided by the Max Planck Society.Notes and references
- J. Jiang, Y. Zhao and O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 3255–3265 CrossRef CAS PubMed.
- S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard, 3rd, J. Am. Chem. Soc., 2008, 130, 11580–11581 CrossRef CAS PubMed.
- C. J. Doonan, D. J. Tranchemontagne, T. G. Glover, J. R. Hunt and O. M. Yaghi, Nat. Chem., 2010, 2, 235–238 CrossRef CAS PubMed.
- L.-M. Yang and R. Pushpa, J. Mater. Chem. C, 2014, 2, 2404–2416 RSC.
- A. P. Cote, H. M. El-Kaderi, H. Furukawa, J. R. Hunt and O. M. Yaghi, J. Am. Chem. Soc., 2007, 129, 12914–12915 CrossRef CAS PubMed.
- G. H. V. Bertrand, V. K. Michaelis, T.-C. Ong, R. G. Griffin and M. Dincă, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4923–4928 CrossRef CAS PubMed.
- V. S. Vyas, F. Haase, L. Stegbauer, G. Savasci, F. Podjaski, C. Ochsenfeld and B. V. Lotsch, Nat. Commun., 2015, 6, 8508 CrossRef CAS PubMed.
- S. Duhović and M. Dincă, Chem. Mater., 2015, 27, 5487–5490 CrossRef.
- S. Chandra, T. Kundu, S. Kandambeth, R. BabaRao, Y. Marathe, S. M. Kunjir and R. Banerjee, J. Am. Chem. Soc., 2014, 136, 6570–6573 CrossRef CAS PubMed.
- M. S. Lohse, T. Stassin, G. Naudin, S. Wuttke, R. Ameloot, D. De Vos, D. D. Medina and T. Bein, Chem. Mater., 2016, 28, 626–631 CrossRef CAS.
- L. Stegbauer, M. W. Hahn, A. Jentys, G. Savasci, C. Ochsenfeld, J. A. Lercher and B. V. Lotsch, Chem. Mater., 2015, 27, 7874–7881 CrossRef CAS.
- N. Huang, X. Chen, R. Krishna and D. Jiang, Angew. Chem., Int. Ed., 2015, 54, 2986–2990 CrossRef CAS PubMed.
- J. Jiang, Y. Zhao and O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 3255–3265 CrossRef CAS PubMed.
- S. Kandambeth, D. B. Shinde, M. K. Panda, B. Lukose, T. Heine and R. Banerjee, Angew. Chem., Int. Ed., 2013, 52, 13052–13056 CrossRef CAS PubMed.
- P. Pachfule, S. Kandmabeth, A. Mallick and R. Banerjee, Chem. Commun., 2015, 51, 11717–11720 RSC.
- D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830–834 CrossRef CAS PubMed.
- S. Chandra, S. Kandambeth, B. P. Biswal, B. Lukose, S. M. Kunjir, M. Chaudhary, R. Babarao, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2013, 135, 17853–17861 CrossRef CAS PubMed.
- L. Ascherl, T. Sick, J. T. Margraf, S. H. Lapidus, M. Calik, C. Hettstedt, K. Karaghiosoff, M. Döblinger, T. Clark, K. W. Chapman, F. Auras and T. Bein, Nat. Chem., 2016, 8, 310–316 CrossRef CAS.
- F. Auras, L. Ascherl, A. H. Hakimioun, J. T. Margraf, F. C. Hanusch, S. Reuter, D. Bessinger, M. Doblinger, C. Hettstedt, K. Karaghiosoff, S. Herbert, P. Knochel, T. Clark and T. Bein, J. Am. Chem. Soc., 2016, 138, 16703–16710 CrossRef CAS PubMed.
- X. Chen, M. Addicoat, S. Irle, A. Nagai and D. Jiang, J. Am. Chem. Soc., 2013, 135, 546–549 CrossRef CAS PubMed.
- H. Xu, J. Gao and D. Jiang, Nat. Chem., 2015, 7, 905–912 CrossRef CAS PubMed.
- L. M. Salonen, D. D. Medina, E. Carbo-Argibay, M. G. Goesten, L. Mafra, N. Guldris, J. M. Rotter, D. G. Stroppa and C. Rodriguez-Abreu, Chem. Commun., 2016, 52, 7986–7989 RSC.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef CAS PubMed.
- R. W. Tilford, W. R. Gemmill, H. C. zur Loye and J. J. Lavigne, Chem. Mater., 2006, 18, 5296–5301 CrossRef CAS.
- X. Ding, L. Chen, Y. Honsho, X. Feng, O. Saengsawang, J. Guo, A. Saeki, S. Seki, S. Irle, S. Nagase, V. Parasuk and D. Jiang, J. Am. Chem. Soc., 2011, 133, 14510–14513 CrossRef CAS PubMed.
- E. L. Spitler, B. T. Koo, J. L. Novotney, J. W. Colson, F. J. Uribe-Romo, G. D. Gutierrez, P. Clancy and W. R. Dichtel, J. Am. Chem. Soc., 2011, 133, 19416–19421 CrossRef CAS PubMed.
- B. T. Koo, W. R. Dichtel and P. Clancy, J. Mater. Chem., 2012, 22, 17460–17469 RSC.
- B. Lukose, A. Kuc and T. Heine, Chem. – Eur. J., 2011, 17, 2388–2392 CrossRef CAS PubMed.
- Y. S. Meng, G. Ceder, C. P. Grey, W. S. Yoon, M. Jiang, J. Bréger and Y. Shao-Horn, Chem. Mater., 2005, 17, 2386–2394 CrossRef CAS.
- V. S. Vyas, M. Vishwakarma, I. Moudrakovski, F. Haase, G. Savasci, C. Ochsenfeld, J. P. Spatz and B. V. Lotsch, Adv. Mater., 2016, 28, 8749–8754 CrossRef CAS PubMed.
- G. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361 CrossRef CAS.
- H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- Y.-F. Xie, S.-Y. Ding, J.-M. Liu, W. Wang and Q.-Y. Zheng, J. Mater. Chem. C, 2015, 3, 10066–10069 RSC.
- C. R. Ojala, W. H. Ojala, W. B. Gleason and D. Britton, J. Chem. Crystallogr., 1999, 29, 27–32 CrossRef CAS.
- C. R. Ojala, W. H. Ojala, W. B. Gleason and D. Britton, J. Chem. Crystallogr., 2001, 31, 377–386 CrossRef CAS.
- C. Ojala, W. Ojala and D. Britton, J. Chem. Crystallogr., 2011, 41, 464–469 CrossRef CAS.
- J. Bernstein and I. Izak, J. Cryst. Mol. Struct., 1975, 5, 257–266 CrossRef CAS.
- C. R. Ojala, W. H. Ojala and D. Britton, J. Chem. Crystallogr., 2010, 41, 464–469 CrossRef.
- J. Bernstein and G. M. J. Schmidt, J. Chem. Soc., Perkin Trans. 2, 1972, 951, 10.1039/p29720000951.
- T. Marszalek, M. Li and W. Pisula, Chem. Commun., 2016, 52, 10938–10947 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis of the COFs, methods details, crystallographic information, IR, sorption data, SEM and additional TEM images. See DOI: 10.1039/c6qm00378h |
| ‡ Current address: Northwestern University, Materials Science and Engineering, Evanston, IL 60208, USA. |
| § Current address: Department of Chemistry, Marquette University, Milwaukee, Wisconsin 53201-1881, USA. |
| This journal is © the Partner Organisations 2017 |