Li2CdGeSe4 and Li2CdSnSe4: biaxial nonlinear optical materials with strong infrared second-order responses and laser-induced damage thresholds influenced by photoluminescence†
Abstract
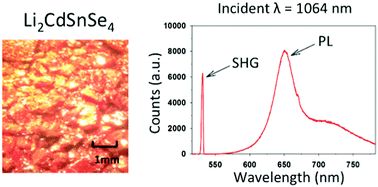
Two new biaxial, diamond-like semiconductors, Li2CdGeSe4 and Li2CdSnSe4, were prepared via high-temperature, solid-state synthesis. Single crystal X-ray diffraction and X-ray powder diffraction coupled with Rietveld refinement were used to refine the crystal structures and assess the phase purity, respectively. Both compounds adopt the lithium cobalt(II) silicate structure type. Strong second-order nonlinear optical (NLO) susceptibility, phase matchability, relatively high thermal stability, and excellent transparency deem both materials potential infrared (IR) NLO candidates. Li2CdGeSe4 and Li2CdSnSe4 display optical bandgaps of approximately 2.5 and 2.2 eV, respectively. Li2CdSnSe4 exhibits a strong, red-light emission under 1064 nm excitation, allowing the compound to release energy that accumulates by two-photon absorption under Nd:YAG laser radiation. Therefore, Li2CdSnSe4 shows a high laser-induced damage threshold (LIDT) of 0.7 GW cm−2. This special phenomenon is remarkable and may open a new avenue in searching for promising IR NLO materials with large LIDTs.
- This article is part of the themed collections: In honour of Mercouri G. Kanatzidis for his contributions to Inorganic Chemistry for over 30 years and Inorganic Chemistry Frontiers HOT articles for 2017


 Please wait while we load your content...
Please wait while we load your content...