Labelled sunscreen SPFs may overestimate protection in natural sunlight
Abstract
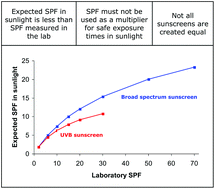
Limited evidence exists to indicate that sunscreen protection factors determined in the laboratory are higher than those in natural sunlight. In this article we propose an explanation for this difference and estimate the expected SPFs of sunscreen products in natural sunlight and those expected from laboratory testing. Our results indicate that the labelled SPF, determined by in vivo assay using a UV solar simulator, overestimates the SPF that would be expected in natural sunlight to the extent that for products labelled SPF50+, it may not be possible to achieve a protection against sunlight of more than 25-fold. The popular interpretation of the SPF that it can be thought of as how much longer skin covered with sunscreen takes to burn in sunlight compared with unprotected skin, can no longer be defended.


 Please wait while we load your content...
Please wait while we load your content...