Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intramolecular hydrogen bonding in conformationally semi-rigid α-acylmethane derivatives: a theoretical NMR study†
Antonio J.
Mota
 *a,
Jürgen
Neuhold
b,
Martina
Drescher
c,
Sébastien
Lemouzy
c,
Leticia
González
*a,
Jürgen
Neuhold
b,
Martina
Drescher
c,
Sébastien
Lemouzy
c,
Leticia
González
 *b and
Nuno
Maulide
*b and
Nuno
Maulide
 *c
*c
aDepartment of Inorganic Chemistry, Faculty of Sciences, Avda. Fuentenueva s/n, 18002 Granada, Spain. E-mail: mota@ugr.es
bUniversity of Vienna, Institute of Theoretical Chemistry, Währinger Strasse 17, 1090 Vienna, Austria. E-mail: leticia.gonzalez@univie.ac.at
cUniversity of Vienna, Institute of Organic Chemistry, Währinger Strasse 38, 1090 Vienna, Austria. E-mail: nuno.maulide@univie.ac.at
First published on 18th August 2017
Abstract
Conformational mobility is a core property of organic compounds, and conformational analysis has become a pervasive tool for synthetic design. In this work, we present experimental and computational (employing Density Functional Theory) evidence for unusual intramolecular hydrogen bonding interactions in a series of α-acylmethane derivatives, as well as a discussion of the consequences thereof for their NMR spectroscopic properties.
Introduction
Conformational flexibility is an intrinsic trait of most organic compounds.1 The remarkable ability of molecules to adopt multiple possible conformations is usually accompanied by a defined preference for certain of those conformations, a property that resides at the core of molecular interactions and molecular recognition.2 Although the distribution of conformational states can be strongly influenced by solvent effects,3 intramolecular attractive or repulsive interactions are often decisive factors that lead molecules to “choose” a specific spatial arrangement of atoms.4 Much, if not all, of the chemical machinery that sustains life as we know it hinges on subtle interactions of small thermodynamic value but enormous structural importance. Such interactions are deployed in multidirectional fashion and can on occasion result in robust, macroscopic 3D molecular scaffolds. Often, unforeseen attractive interactions can become important design elements with applications ranging from synthesis5 to catalysis6 and, ultimately, biology.7N-Acyloxazolidinones, popularized through the seminal, textbook work of Evans and others8 remain, even in the 21st century, as cornerstone reagents for aldol- and related transformations. This is largely due, as in most cases of successful asymmetric induction (be it stoichiometric or catalytic), to their adoption of predictable conformations in solution as governed (at a given temperature) by either chelation or dipole attraction/repulsion effects.
Herein, we present experimental and computational evidence for an unusual intramolecular hydrogen bonding interaction in a series of N-acyloxazolidinones and other α-acylmethane derivatives, with striking consequences to their NMR spectroscopic properties. The study also includes theoretical (density functional theory, DFT) 1H- and 13C-NMR determinations. Theoretical NMR determinations are often used in cases of problematic and dubious NMR assignments9 and should be more frequently used as a tool to enable correct NMR analyses.
Results and discussion
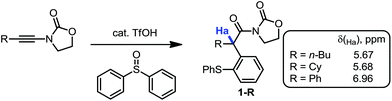
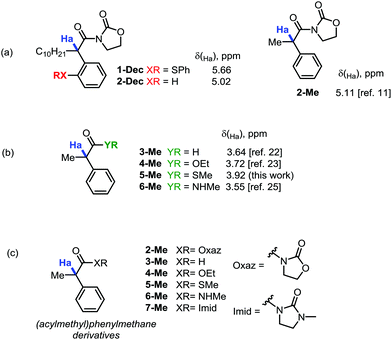
During our recent studies on redox-neutral reactions of N-alkynyloxazolidinones (ynamides),10 leading to the preparation of various α-arylated acyloxazolidinone products (1, Scheme 1), we noted the consistently and unusually low field 1H-NMR shifts of the hydrogen marked in blue as Ha. For instance, in product 1-nBu (R = nButyl) the signal for Ha appeared at δ = 5.67 ppm, at 5.68 ppm for 1-Cy (R = Cyclohexyl), and for 1-Ph (R = Phenyl), the signal goes to 6.96 ppm, lying practically within the aromatic region.In order to eliminate any possible effect of the sulfur residue on the aromatic ring, we compared the known compound 1-Dec (R = Decyl) with its desulfurated analogue 2-Dec. A decrease in chemical shift of 0.64 ppm (from 5.66 to 5.02 ppm, respectively) was found, whereas an equally high chemical shift value of δ = 5.11 ppm has been reported11 for the desulfurated methyl derivative 2-Me (cf.Fig. 1a).
This far exceeds, for instance, the predicted value for this structure obtained by simple NMR-predicting software (the ChemOffice 13.0 suite,12 for example, predicts a chemical shift, δ, of just 3.52 ppm). The value is all the more striking if one compares the acyloxazolidinone 2-Me with other carbonyl analogues (cf.Fig. 1b). Indeed, the aldehyde 3-Me (which could be expected to exert a comparable electron-withdrawing effect on the C–H bonds in α-position with respect to an acyloxazolidinone moiety), the ethylester 4-Me, the methylthioester 5-Me or the N-methylcarboxamide 6-Me are all known compounds reported to have chemical shifts for Ha inside a narrow window not exceeding a δ value of 3.92 ppm (vide infraTable 1).
| 1H-NMR chemical shifts | 2-Me (R1 = Oxaz) | 3-Me (R1 = H) | 4-Me (R1 = OEt) | 5-Me (R1 = SMe) | 6-Me (R1 = NHMe) | 7-Me (R1 = Imid) |
|---|---|---|---|---|---|---|
| a This work (see ESI). | ||||||
| B3LYP | 5.23 | 3.69 | 3.68 | 3.88 | 3.26 | 5.43 |
| B3LYP-D3 | 5.02 | 3.70 | 3.68 | 3.91 | 3.33 | 5.17 |
| CAM-B3LYP | 5.16 | 3.62 | 3.63 | 3.85 | 3.21 | 5.36 |
| M06-2X | 5.12 | 3.79 | 3.82 | 4.22 | 3.48 | 5.20 |
| LC-ωPBE | 5.10 | 3.64 | 3.64 | 3.92 | 3.30 | 5.29 |
| Experimental | 5.11 (ref. 11) | 3.64 (ref. 23) | 3.72 (ref. 24) | 3.92a (ref. 25) | 3.55 (ref. 26) | 5.28a |
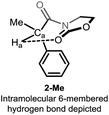
Detailed analysis of the structure of acyloxazolidinones 1-R/2-R revealed the possible intervention of an intramolecular hydrogen bonding interaction through a 6-membered ring ranging from the electron-rich oxazolidinone (Oxaz) carbonyl oxygen to the methinic hydrogen Ha, giving rise to the conformer shown in Fig. 2. We recognised that this structure-specific interaction might lie at the heart of the unusually high chemical shift observed for this particular compound (which is absent in the other derivatives, cf. Fig. 1b).
To validate this assumption, we required a tool to accurately model the two extreme conformational situations where this hydrogen bond is present and absent, compare their relative stability and simulate the NMR spectrum of both forms. We resorted to high-level DFT calculations since it is well-known that general purpose, theoretical 1H-NMR spectra could be reliably covered by this level of theory.13 This required accuracy aims not only at reliably reproducing the already known experimental data but also predict new values for unknown derivatives or non-detectable conformers. The latter is a crucial requirement as we need to compare experimentally assessed H-bonded situations with non-measurable conformers for which no H-bonding is operative and experimental quantification by NMR is not accessible.
We will initially focus on desulfurated α-acylmethane derivatives, i.e., the known compounds 2-Me–6-Me (cf.Fig. 1c). We further added an unknown compound, the N-methylimidazolidinone (Imid) 7-Me, to enlarge the predictability test of our model, and resynthesized 5-Me to ascertain the 1H-NMR chemical shift for Ha, since calculations found a discordant value with that reported in literature (see below in ref. 24).
Computational details
Calculations were performed using the GAUSSIAN09 suite of programs.14 Initial lowest-energy conformations were optimized by density functional theory (DFT) using the well-known hybrid B3LYP functional15 with the Pople's diffuse, polarized, split-valence, double-zeta 6-31+G* basis set.16 From these geometries, the corresponding 1H-NMR isotropic magnetic shielding values were calculated reoptimizing them with the larger triple-zeta 6-311+G(d,p) basis set17 (necessary to get a high accuracy in the determination of chemical shifts,13 see the ESI,† for geometries) combined with different functionals. These include the hybrids B3LYP, which gives reliable 1H-NMR chemical shifts for the most common compounds, their empirical dispersion, B3LYP-D3,18 and long-range corrected, CAM-B3LYP,19 versions, and the Minnesota M06-2X functional,20 which accounts for non-covalent interactions. We have also included for comparison the non-hybrid GGA-functional LC-ωPBE,21a the long range corrected version of PBE21b (another widely used functional for general purposes). All the calculations have been carried out including implicit solvent (in which the corresponding experimental spectra have been recorded, see below) through a Polarizable Continuum Model (PCM).22 Results obtained from these calculations for the chemical shift (in ppm) of the Ha hydrogen of the selected, lowest-energy conformers for compounds 2-Me–7-Me (Fig. 1c) are summarized in Table 1.It should be noted that the precision in the 1H-NMR chemical shift determination is fairly high along the different methods employed. Yet, for this set of molecules, the LC-ωPBE functional performs extremely well, achieving δ values in very close agreement to the experimental ones (see the ESI† for details), therefore we elected the LC-ωPBE functional for further analyses.
Interestingly, the calculated lowest-energy conformations for 2-Me and 7-Me correspond to that depicted in Fig. 2, in which a 6-membered hydrogen bond27 is established between Ha and the carbonyl group of the heterocyclic moiety. We had originally postulated that this was at the origin of the unusual chemical shift values for Ha. With the help of DFT calculations, we are able to consider conformations in which the hydrogen bonding event is absent and recalculate the chemical shift associated to Ha in the same solvent (chloroform). Results for the two limiting conformations in each case (hydrogen bonded, 2-Me and 7-Me, and non-hydrogen bonded, 2b-Me and 7b-Me) are presented in Table 2. An important drop (about 1.5 ppm to high field) is observed affecting the δ value of Ha of the conformer in which the hydrogen bonding is not operating with respect to the one in which the hydrogen bond is established (lowest-energy conformer).
Since the free-energy difference (ΔG) between the two limiting conformations (B3LYP/6-31+G(d)) is 4.46 kcal mol−1 for 2-Me and 5.44 kcal mol−1 for 7-Me, a conformational equilibrium of conformers 2b-Me and 7b-Me (without hydrogen bonding) can be excluded. This means that, besides other possible, energetically accessible conformations, the apparent chemical shifts of Ha for 2-Me and 7-Me should be very close to the theoretical calculated values, as it is evidenced in Table 2.
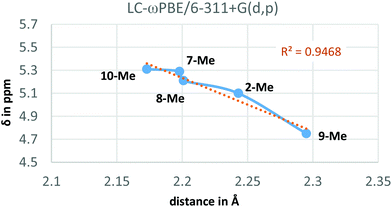
At this juncture, we wished to dive into simulated spectra, with the aim to modulate the strength of the intramolecular H-bond by the calculated value for Ha. Accordingly, we elected several ad hoc unreported derivatives: the permethylated 8-Me and the perfluorinated 9-Me oxazolidinone analogues, and the acylcarbamate 10-Me, which constitutes the ring-strainless open-chain version of the oxazolidinone derivative 2-Me (Fig. 3). Calculations made on these compounds were performed for the conformations for which the 6-membered, intramolecular hydrogen bond is expected to be operative and gave rise to the set of δ values for Ha collected in Table 3 along with the calculated O⋯Ha distances.
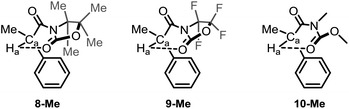 | ||
| Fig. 3 Ad hoc structures created for the study of the 6-membered, intramolecular hydrogen bond in this series of compounds. | ||
| Parameters | 2-Me (R1 = Oxaz) | 7-Me (R1 = Imid) | 8-Me (R1 = Oxaz(Me4)) | 9-Me (R1 = Oxaz(F4)) | 10-Me (R1 = open Oxaz) |
|---|---|---|---|---|---|
| a O⋯Ha distances were extracted from the corresponding 1H-NMR calculations (LC-ωPBE/6-311+G(d,p) in chloroform (PCM)). | |||||
| δ (in ppm) | 5.10 | 5.29 | 5.21 | 4.75 | 5.31 |
| Distance (in Å)a | 2.243 | 2.198 | 2.201 | 2.295 | 2.173 |
From Table 3, it could be pointed out that, concerning the deshielding of Ha, the ureido derivative 7-Me and the open acylcarbamate 10-Me appear to be the more effective compounds establishing the intramolecular hydrogen bond, given the enhanced Lewis basicity (and hence stronger hydrogen bond-donor ability) of the carbonyl oxygen interacting with Ha. Contrarily to this, the fluorinated 9-Me derivative leads to a less electron-rich carbonyl, weakening the hydrogen bond and observing the corresponding δ value of Ha at higher field (by about 0.6 ppm, see Table 3). Interestingly, the incorporation of four methyl groups in 8-Me did not substantially affect the chemical shift of Ha with respect to the pure oxazolidinone moiety (2-Me). On the other hand, the hydrogen bonds (if available) expected to be stronger when presenting a higher δ value for Ha, also present, in general, shorter distances (Table 3).
Additionally, the LC-ωPBE chemical shifts correlate fairly well with the O⋯Ha equilibrium distances in compounds 2-Me and 7-Me–10-Me (see Fig. 4), with some small variations for shorter distances.28
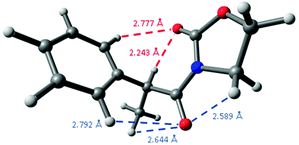
A comparison of these distances with the sum of the corresponding van der Waals radii for hydrogen and oxygen atoms, that is, 2.70 Å,29 constitutes another observation pointing to the presence of intramolecular hydrogen bonding because its short distance,30 as the oxazolidinone carbonyl group establishes another weak C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–Ph interaction in 2-Me at 2.777 Å, a distance slightly higher than the sum of the corresponding van der Waals radii. Interestingly, the remaining carbonyl group establishes three different close interactions: at 2.589 (C
O⋯H–Ph interaction in 2-Me at 2.777 Å, a distance slightly higher than the sum of the corresponding van der Waals radii. Interestingly, the remaining carbonyl group establishes three different close interactions: at 2.589 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯CH2), 2.644 (C
O⋯CH2), 2.644 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Me) and 2.792 Å (C
O⋯Me) and 2.792 Å (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–Ph) (Fig. 5), all them around the expected van der Waals distance.
O⋯H–Ph) (Fig. 5), all them around the expected van der Waals distance.
In order to characterize this special interaction and evaluate its strength, we applied the quantum theory of atoms in molecules (QTAIM)31 over derivatives 2-Me and 7-Me–10-Me (from the corresponding LC-ωPBE/6-311+G(d,p) calculations) using the Multiwfn suite.32 This theory is a topological analysis able to identify bonding interactions within a molecule by means of the gradient vector field of the charge density, ρ(r). Typical ρ(r) values in shared interactions are 0.722, 0.551, and 0.252 a.u. for N2, O2, and C–C bond in ethane molecules, respectively, whereas in closed-shell interactions they are 0.046 and 0.036 a.u. for LiCl molecules and NaCl molecules, respectively.31a,33 These bonding interactions can be classified in terms of the properties of the Laplacian of the electron density, ∇2ρ(r), into two broad general classes: shared (∇2ρ(r) < 0, i.e. covalent bonds) and closed-shell (∇2ρ(r) > 0, i.e. hydrogen bonds) interactions.34 Concerning our study, the well-known criteria of the hydrogen bonding on the basis of AIM theory at the bond critical point (BCP), where the gradient vector field, ∇ρ(r), vanishes, are: (i) ρ(r) between 0.002 and 0.034 a.u., and (ii) ∇2ρ(r) between +0.024 and +0.139 a.u.35 Mata et al.36 correlated the hydrogen-bonding energy, EHB, with the Lagrangian kinetic energy, G(r), at the BCP as EHB = 0.429 × G(r).
Therefore, we calculated the BCPs and searched for those with a positive value of ∇2ρ(r), finding a BCP in all cases in between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ha path (2-Me, as an example, in Fig. 6). Laplacians of the electron density, ∇2ρ(r), charge densities, ρ(r), and Lagrangian kinetic energies, G(r), at each C
O⋯Ha path (2-Me, as an example, in Fig. 6). Laplacians of the electron density, ∇2ρ(r), charge densities, ρ(r), and Lagrangian kinetic energies, G(r), at each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ha BCP, Ha chemical shifts, C
O⋯Ha BCP, Ha chemical shifts, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ha equilibrium distances, and calculated EHB energies are summarized in Table 4.
O⋯Ha equilibrium distances, and calculated EHB energies are summarized in Table 4.
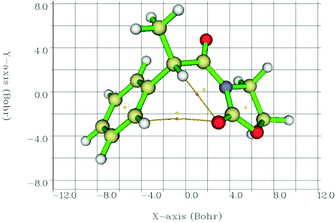 | ||
| Fig. 6 Interatomic bond critical points (orange circles) identified by QTAIM and the corresponding paths between the concerned atoms. Circles in yellow correspond to ring critical points. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ha BCP, Ha chemical shifts, O⋯Ha equilibrium distances, and calculated EHB energies for derivatives 2-Me and 7-Me–10-Me
O⋯Ha BCP, Ha chemical shifts, O⋯Ha equilibrium distances, and calculated EHB energies for derivatives 2-Me and 7-Me–10-Me
| Parameters | 2-Me (R1 = Oxaz) | 7-Me (R1 = Imid) | 8-Me (R1 = Oxaz(Me4)) | 9-Me (R1 = Oxaz(F4)) | 10-Me (R1 = open Oxaz) |
|---|---|---|---|---|---|
a In parenthesis, the B3LYP/6-31+G(d) calculated energy difference between the limiting conformations (those following an intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯ Ha hydrogen bonding scheme and those that does not). Note that most part of this energy difference corresponds to the hydrogen bonding event. O⋯ Ha hydrogen bonding scheme and those that does not). Note that most part of this energy difference corresponds to the hydrogen bonding event.
|
|||||
| ∇2ρ(r) (in a.u.) | 0.06209 | 0.06791 | 0.06790 | 0.05658 | 0.07821 |
| ρ(r) (in a.u.) | 0.01745 | 0.01899 | 0.01878 | 0.01586 | 0.02069 |
| G(r) (in a.u.) | 0.01359 | 0.01493 | 0.01484 | 0.01234 | 0.01712 |
| δ (in ppm) | 5.10 | 5.29 | 5.21 | 4.75 | 5.31 |
| distance (in Å) | 2.243 | 2.198 | 2.201 | 2.295 | 2.173 |
| E HB (in kcal mol−1) | 3.66 (4.46)a | 4.02 (5.44)a | 3.99 | 3.32 | 4.61 (5.14)a |
The data in Table 4 corroborates the presence of hydrogen bonds in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ha paths for oxazolidinone- (2-Me and 8-Me–9-Me), imidazolidinone-based (7-Me) and the open-chain 10-Me compounds. The strongest hydrogen bond can be found in the latter structure 10-Me, with a rather short O⋯H distance, whereas the weakest one, as expected, appeared in the fluorinated derivative 9-Me.
O⋯Ha paths for oxazolidinone- (2-Me and 8-Me–9-Me), imidazolidinone-based (7-Me) and the open-chain 10-Me compounds. The strongest hydrogen bond can be found in the latter structure 10-Me, with a rather short O⋯H distance, whereas the weakest one, as expected, appeared in the fluorinated derivative 9-Me.
Based on both the energy (EHB) and the O⋯Ha distances, these hydrogen bonds are positioned in the limit in between medium and weak and, hence, they present a bond contribution mostly electrostatic.27b,37 As a reference, the calculated CCSD(T) interaction energy for a water dimer, a HF dimer, or a HCl dimer is 4.92, 4.52 and 1.90 kcal mol−1, respectively.38 Although the hydrogen-bond energy (EHB) could be well correlated with the O⋯Ha distance (Fig. 7a), the best correlating descriptor with EHB is the corresponding charge density (ρ(r)) at the BCP,39 as it is showed in Fig. 7b.
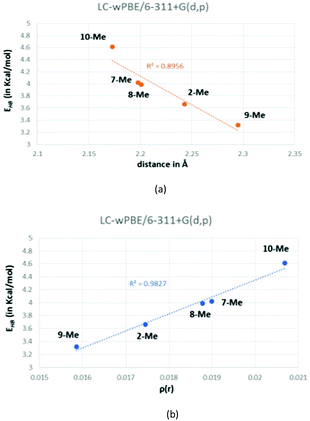 | ||
| Fig. 7 Correlation between the calculated energy of the hydrogen bond (EHB) and either the O⋯Ha distance (a) or the charge density (b). | ||
Solvent is usually an important parameter in NMR theoretical calculations and must be considered in order to accurately reproduce experimental NMR spectra.3,40 In hydrogen bonding, the election of the solvent for spectroscopic properties is not innocent, since high-polar solvents can theoretically disrupt or even break these types of interactions.41 Thus, expecting that we could achieve different chemical shifts for Ha in polar solvents and have access to other molecular conformations than those stabilized by hydrogen bonding, we experimentally and theoretically (LC-ωPBE/6-311+G(d,p)) studied the corresponding 1H-NMR spectra for 7-Me (R1 = Imid) in deuterated methanol and dimethylsulfoxide (Table 5).
Nevertheless, the conclusion that is drawn from Table 5 is that no solvent effect is observed in the chemical shift of Ha, even in the presence of methanol, a polar protic solvent. Therefore, since in Table 2 was clearly shown that the non-hydrogen bonded form of 7-Me (7b-Me) presented a chemical shift of 3.53 ppm, we must conclude that, even with polar solvents, the conformational equilibrium at room temperature keeps this specially stabilized conformation the most part of the time, avoiding the expected shielding of the chemical shift of Ha.
Traditionally, organic chemists rely mostly on 1H-NMR spectra, with relatively little attention being paid to 13C-NMR analysis. However, 13C-NMR constitutes a crucial axis to determining and ascertaining structures mainly due to the fact that it presents a much larger window allowing the appreciation of even small variations and rendering the collapsing of two different signals unlikely. In addition, H–H coupling often leading to broad/multiplet bands and often complicating assignment is absent in 13C-NMR. Therefore, 13C-NMR provides, from a theoretical point of view,13d,42 an ideal ground where many organic products could be unambiguously characterized by a unique fingerprint. We thus set out to complete our findings and reinterpret the problem at hand based on 13C-NMR data for the Ca carbon (the methinic carbon to which Ha is bonded), see Fig. 1 and 3.
Table 6 compiles the chemical shift values for Ca for compounds 2-Me and 2b-Me, 3-Me–6Me, and 7-Me and 7b-Me, using the five functionals initially considered (Table 1). Nevertheless, the basis set used was Pople's polarized split-valence double-zeta 6-31G(d,p),16 since it is known that Pople's double-zeta basis sets perform better than the triple-zeta ones for 13C-NMR calculations, probably due to some cancellation errors.43
| 13C-NMR chemical shifts | B3LYP | B3LYP-D3 | CAM-B3LYP | M06-2X | LC-ωPBE | Experimental |
|---|---|---|---|---|---|---|
| a Carbon non-assigned in the experimental spectrum. b Non-applicable. c This work (see ESI). | ||||||
| 2-Me | 45.86 | 46.16 | 44.33 | 48.59 | 43.08 | 42.6 (ref. 11a) |
| 42.8a (ref. 11b) | ||||||
| 2b-Me | 51.18 | 51.17 | 49.38 | 53.20 | 47.55 | –b |
| 3-Me | 57.22 | 56.91 | 55.23 | 58.89 | 52.94 | 53.2 (ref. 23a) |
| 53.11 (ref. 23b and c) | ||||||
| 4-Me | 49.15 | 48.82 | 47.39 | 50.03 | 45.46 | 45.59 (ref. 24a) |
| 45.5 (ref. 24b) | ||||||
| 5-Me | 58.00 | 57.75 | 55.75 | 60.32 | 53.46 | 54.23c |
| 6-Me | 51.61 | 50.73 | 49.72 | 51.68 | 47.23 | 47.2 (ref. 26a) |
| 7-Me | 45.45 | 45.67 | 43.91 | 47.83 | 42.61 | 42.69c |
| 7b-Me | 50.63 | 50.71 | 48.91 | 52.47 | 47.14 | –b |
Table 6 also reflects a traditional problem associated with the theoretical determination of 13C-NMR chemical shifts, namely that the obtained values are very sensitive to the functional used. This variability is perhaps the main reason why theoretical calculations on 13C-NMR spectra are less common. In this case, although CAM-B3LYP and LC-ωPBE are again the more reliable functionals, LC-ωPBE clearly outperforms, delivering chemical shifts very close to the experimental values.
Furthermore, it is important to highlight the difference of ca. 11 ppm between the chemical shifts calculated for Ca in the imidazolidinone (7-Me) and the methylthio (5-Me) derivatives. This showcases the large spectral window made possible by 13C-NMR.
Calculations for the ad hoc structures 8-Me–10-Me led to the results collected in Table 7. Owing to the fact that 13C-NMR is quite sensitive to steric factors (about an order of magnitude more than 1H-NMR)44 the reported δ values calculated for Ca do not correlate with any property treated in this text. This is in the line presented just above, for which 13C-NMR determinations are better oriented to the unambiguous assignment of spectroscopic data and, hence, the accurate prediction of spectra for unknown products.
| 13C-NMR chemical shifts | 2-Me | 7-Me | 8-Me | 9-Me | 10-Me |
|---|---|---|---|---|---|
| a Structures referred here were calculated at the LC-ωPBE/6-31G(d,p) level of theory and using chloroform as solvent (PCM). | |||||
| δ (in ppm) | 43.08 | 42.61 | 44.63 | 45.57 | 45.44 |
Finally, and as expected given the results achieved for 1H-NMR, solvent effects on compound 7-Me were almost negligible, as it could be drawn from Table 8, indicating that the hydrogen-bonded conformer should be largely favoured within the timescale of the experiment.
Conclusions
In summary, we have presented experimental and computational evidence for an unusual intramolecular hydrogen bonding interaction in a series of N-acyloxazolidinones and other α-acylmethane derivatives, with striking consequences to their NMR spectroscopic properties. In the course of this study, theoretical (DFT) 1H- and 13C-NMR determinations, along with QTAIM analysis, were employed to clearly identify the nature of such special interaction, among others found in these structures. Of special interest is the finding of the reliability and accuracy of the LC-ωPBE functional, which works fairly well in this domain, at least for this kind of derivatives. Crucial has been the possibility to calculate conformers not accessible by synthesis and that emphasize the stronger interaction involved in this series of compounds. Therefore, results presented here hint at possible general applications to the prediction of highly accurate NMR spectral properties for organic compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the ERC (FLATOUT 278872), and the University of Vienna. Calculations were partially performed at the Vienna Scientific Cluster (VSC). We also would like to thank the Centro de Supercomputación de la Universidad de Granada (Alhambra, CSIRC) for computation resources.Notes and references
- (a) E. L. Eliel, N. L. Allinger, S. J. Angyal and G. A. Morrison, Conformational Analysis, Interscience Publishers, New York, 1965 Search PubMed; (b) D. Barton, Nobel Lecture 1967, Nobel Lectures, Chemistry 1963–1970, Elsevier Publishing Company, Amsterdam, 1972 Search PubMed; (c) R. Hubert, Nature, 1979, 280, 538 CrossRef; (d) F. G. Ridell, The conformational analysis of heterocyclic compounds, Academic Press, London, 1980 Search PubMed; (e) G. W. Gokel and A. Nakano, Feeble Forces and Flexible Frameworks, in Crown Compounds: Toward Future Applications, ed. S. Cooper, Verlag Chemie, 1992, ch. 1 Search PubMed; (f) C. Gilon, C. Mang, E. Lohof, A. Friedler and H. Kessler, Synthesis of Cyclic Pepetides, in Houben-Weyl Methods of Organic Chemistry Vol. E 22b, 4th Edition Supplement: Synthesis of Peptides and Peptidomimetics, ed. A. Felix, L. Moroder and C. Toniolo, Georg Thieme Verlag, Stuttgart, 2004 Search PubMed; (g) M. C. Misuraca, T. Grecu, Z. Freixa, V. Garavini, C. A. Hunter, P. W. N. M. van Leeuwen, M. D. Segarra-Maset and S. M. Turega, J. Org. Chem., 2011, 76, 2723 CrossRef CAS PubMed; (h) Structure Elucidation in Organic Chemistry: The Search for the Right Tools, ed. M. -M. Cid and J. Bravo, John Wiley & Sons, Weinheim, 2015 Search PubMed; (i) V. M. Burger, D. J. Arenas and C. M. Stultz, Sci. Rep., 2016, 6, 29040 CrossRef CAS PubMed; (j) B. Szyszko, M. J. Białek, E. Pacholska-Dudziak and L. Latos-Grażyński, Chem. Rev., 2017, 117, 2839 CrossRef CAS PubMed.
- (a) D. J. Chadwick and K. Widdows, Host-Guest Molecular Interactions: From Chemistry to Biology, Ciba Foundation Symposium, John Wiley & Sons, Chichester, 1991 Search PubMed; (b) H.-J. Böhm and G. Klebe, Angew. Chem., Int. Ed. Engl., 1996, 35, 2588 CrossRef; (c) R. A. Laskowski, N. M. Luscombe, M. B. Swindells and J. M. Thornton, Protein Sci., 1996, 5, 2438 CAS; (d) K. K. Frederick, M. S. Marlow, K. G. Valentine and A. J. Wand, Nature, 2007, 448, 325 CrossRef CAS PubMed; (e) P. Hobza and J. Řezáč, Chem. Rev., 2016, 116, 4911 CrossRef CAS PubMed; (f) D. Chatterji, Basics of Molecular Recognition, CRC Press, Boca Raton, 2016 Search PubMed.
- (a) K.-J. Liu and J. L. Parsons, Macromolecules, 1969, 2, 529 CrossRef CAS; (b) Reviews in Computational Chemistry II, ed. K. B. Lipkowitz and D. B. Boyd, John Wiley & Sons, New York, 1991 Search PubMed; (c) Carbohydrates: Structures, Syntheses and Dynamics, ed. P. Finch, Springer Science+Business Media, Dordrecht, 1999 Search PubMed; (d) Ch. Cappelli, S. Corni and J. Tomasi, J. Phys. Chem. A, 2001, 105, 10807 CrossRef CAS; (e) Handbook of solvents, ed. G. Wypych, ChemTec Publishing, Toronto-New York, 2001 Search PubMed; (f) Zh. Xu, Hs. Tsai, Hs.-L. Wang and M. Cotlet, J. Phys. Chem. B, 2010, 114, 11746 CrossRef CAS PubMed; (g) P. I. Nagy, J. Phys. Chem. A, 2012, 116, 7726 CrossRef CAS PubMed; (h) Ch. Wang, F. Ying, W. Wu and Y. Mo, J. Org. Chem., 2014, 79, 1571 CrossRef CAS PubMed; (i) I. V. Alabugin, Stereoelectronic Effects: A Bridge Between Structure and Reactivity, John Wiley & Sons, Chichester, 2016 Search PubMed.
- (a) M. Oki, The Chemistry of Rotational Isomers, Springer-Verlag, Berlin-Heidelberg, 1993 Search PubMed; (b) J. E. Anderson, V. Bru-Capdeville, P. A. Kirsch and J. S. Lomas, J. Chem. Soc., Chem. Commun., 1994, 1077 RSC; (c) Y. Cheng, Y. Qi, Y. Tang, Ch. Zheng, Y. Wan, W. Huang and R. Chen, J. Phys. Chem. Lett., 2016, 7, 3609 CrossRef CAS PubMed.
- (a) C. Altavilla and E. Ciliberto, Inorganic Nanoparticles: Synthesis, Applications and Perspectives, CRC Press, Boca Raton, 2011 Search PubMed; (b) Ch. F. Chen and Y.-X. Ma, Yptycenes Chemistry: From Synthesis to Applications, Springer-Verlag, Berlin-Heidelberg, 2013 Search PubMed.
- (a) Food Proteins: Properties and Characterization, ed. Sh. Nakai and H. W. Modler, Wiley-VCH, New York, 1996 Search PubMed; (b) M. N. Khan, Micellar catalysis, CRC Press, Boca Raton, 2007 Search PubMed.
- (a) D. Leckband and J. Israelachvili, Q. Rev. Biophys., 2001, 34, 105 CrossRef CAS PubMed; (b) J. McMurry, Organic Chemistry with Biological Applications, Brooks/Cole CENGAGE Learning, 2010 Search PubMed; (c) M. J. R. Yunta, Using Molecular Modelling to Study Interactions Between Molecules with Biological Activity, in Bioinformatics, ed. H. Pérez-Sánchez, CC by 3.0 license, 2012, ch. 8 Search PubMed.
- Modern Rhodium-Catalyzed Organic Reactions, ed. P. A. Evans, Wiley-VCH, Weinheim, 2005 Search PubMed.
- (a) S. D. Rychnovsky, Org. Lett., 2006, 8, 2895 CrossRef CAS PubMed; (b) F. Sánchez-Izquierdo, P. Blanco, F. Busqué, R. Alibés, P. de March, M. Figueredo, J. Font and T. Parella, Org. Lett., 2007, 9, 1769 CrossRef PubMed.
- (a) B. Peng, X. Huang, L.-G. Xie and N. Maulide, Angew. Chem., Int. Ed., 2014, 53, 8718 CrossRef CAS PubMed; (b) L.-G. Xie, S. Niyomchon, A. J. Mota, L. González and N. Maulide, Nat. Commun., 2016, 7, 10914 CrossRef PubMed; (c) D. Kaldre, B. Maryasin, D. Kaiser, O. Gajsek, L. González and N. Maulide, Angew. Chem., Int. Ed., 2017, 56, 2212 CrossRef CAS PubMed.
- (a) E. Coulbeck and J. Eames, Tetrahedron: Asymmetry, 2007, 18, 2313 CrossRef CAS; (b) A. Bigot, A. Williamson and M. J. Gaunt, J. Am. Chem. Soc., 2011, 133, 13778 CrossRef CAS PubMed.
- ChemOffice suite v. 13.0. CambridgeSoft, PerkinElmer Inc., 2012 Search PubMed.
- (a) G. Schreckenbach and T. Ziegler, Theor. Chem. Acc., 1998, 99, 71 CrossRef CAS; (b) E. Y. Pankratyev, A. R. Tulyabaev and L. M. Khalilov, J. Comput. Chem., 2011, 32, 1993 CrossRef CAS PubMed; (c) I. A. Konstantinov and L. J. Broadbelt, J. Phys. Chem. A, 2011, 115, 12364 CrossRef CAS PubMed; (d) M. Elyashberg, A. Williams and K. Blinov, Contemporary Computer-Assisted Approaches to Molecular Structure Elucidation, Royal Society of Chemistry, 2011 Search PubMed; (e) D. Fleig, M. Maurer, M. Hanni, K. Braunger, L. Kick, M. Thubauville and Ch. Ochsenfeld, J. Chem. Theory Comput., 2014, 10, 572 CrossRef PubMed; (f) D. E. Hill, N. Vasdev and J. P. Holland, Comput. Theor. Chem., 2015, 1051, 161 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- (a) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS; (b) V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976 CrossRef CAS.
- (a) K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef; (b) D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed.
- (a) Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425 CrossRef CAS PubMed; (b) T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- (a) O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- (a) S. Miertus, E. Scrocco and J. Tomasi, J. Chem. Phys., 1981, 55, 117 CAS; (b) R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 1449 CrossRef CAS; (c) J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027 CrossRef CAS.
- (a) R. Srirambalaji, S. Hong, R. Natarajan, M. Yoon, R. Hota, Y. Kim, Y. H. Ko and K. Kim, Chem. Commun., 2012, 48, 11650 RSC; (b) A. T. Straub, M. Otto, I. Usui and B. Breit, Adv. Synth. Catal., 2013, 355, 2071 CrossRef CAS; (c) S. H. Christensen, E. P. K. Olsen, J. Rosenbaum and R. Madsen, Org. Biomol. Chem., 2015, 13, 938 RSC.
- (a) D. Katayev, V. Matousek, R. Koller and A. Togni, Org. Lett., 2015, 17, 5898 CrossRef CAS PubMed; (b) P. H. Gehrtz, V. Hirschbeck and I. Fleischer, Chem. Commun., 2015, 51, 12574 RSC.
- For spectral data for 5-Me in CCl4, see: (a) D. Seebach and R. Bürstinghaus, Synthesis, 1975, 461 CrossRef CAS. For a prior misassigned spectrum of 5-Me in deuterated chloroform, see: (b) M. Clericuzio, I. Degani, S. Dughera and R. Fochi, Synthesis, 2002, 921 CrossRef CAS . See the ESI† for 1H- and 13C-NMR spectra of 5-Me, in chloroform, newly synthesized for this work.
- (a) Sh. Hanada, T. Ishida, Y. Motoyama and H. Nagashima, J. Org. Chem., 2007, 72, 7551 CrossRef CAS PubMed; (b) J. L. Barneto, M. Avalos, R. Babiano, P. Cintas, J. L. Jiménez and J. C. Palacios, Org. Biomol. Chem., 2010, 8, 857 RSC.
- (a) J. Catalán, J. C. del Valle, J. Palomar, C. Díaz and J. L. G. de Paz, J. Phys. Chem. A, 1999, 103, 10921 CrossRef; (b) G. R. Desiraju and T. Steiner, The weak hydrogen bond in structural chemistry and biology, Oxford University Press, Oxford, 1999 Search PubMed; (c) J. Chen, P. G. Willis, S. Parkin and A. Cammers, Eur. J. Org. Chem., 2005, 171 CrossRef; (d) S. J. Grabowski, Challenges and advances in Computational Chemistry and Physics, 3: Hydrogen Bonding – New Insights, Springer, Dordrecht, 2006 Search PubMed; (e) Y.-Y. Zhu, G.-T. Wang, R.-X. Wang and Zh.-T. Li, Cryst. Growth Des., 2009, 9, 4778 CrossRef CAS; (f) P. S. Kalsi, Organic Reactions and their Mechanisms, New Age International, 2009 Search PubMed; (g) L. Quiquempoix, E. Bogdan, N. J. Wells, J.-Y. Le Questel, J. Graton and B. Linclau, Molecules, 2017, 22, 518 CrossRef PubMed.
- It should be noted that 1H chemical shift values could be influenced by different factors others than pure inductive effect of the surrounding groups or the chosen solvent, i.e. anisotropy, van der Waals deshielding (steric factors), other hydrogen bonding-like or electrostatic interactions. See: L. D. S. Yadav, Organic Spectroscopy, Springer Science+Business Media, Dordrecht, 2005 Search PubMed.
- S. Alvarez, Dalton Trans., 2013, 42, 8617 RSC.
- P. A. Kollman and L. C. Allen, Chem. Rev., 1972, 72, 283 CrossRef CAS.
- (a) R. F. W. Bader, Atoms in Molecules - A quantum theory, Oxford University Press, New York, 1990 Search PubMed; (b) P. S. V. Kuma, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- Y. Aray, J. Rodríguez and D. Vega, J. Phys. Chem. B, 2000, 104, 4608 CrossRef CAS.
- R. F. W. Bader and H. Essen, J. Chem. Phys., 1984, 80, 1943 CrossRef CAS.
- (a) U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747 CrossRef CAS; (b) D. Mani and E. Arunan, Noncovalent Forces, Challenges and Advances in Computational Chemistry and Physics Series, ed. J. Leszcznski, Springer Int'l Pub., Switzerland, 2015, vol. 19 Search PubMed; (c) J. H. Lee, J.-H. Lee, E.-H. Kong and H. M. Jang, Sci. Rep., 2016, 6, 21687 CrossRef CAS PubMed.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185 CrossRef CAS.
- A. Nangia, CrystEngComm, 2002, 4, 93 RSC.
- K. Wendler, J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. A, 2010, 114, 9529 CrossRef CAS PubMed.
- A. T. Ayoub, J. Tuszynski and M. Klobukowski, Theor. Chem. Acc., 2014, 133, 1520 CrossRef.
- M. Dračínský and P. Bouř, J. Chem. Theory Comput., 2010, 6, 288 CrossRef PubMed.
- Hydrogen Bonding and Transfer in the Excited State, ed. K.-L. Han and G.-J. Zhao, John Wiley & Sons, Chichester, 2011 Search PubMed.
- (a) Calculation of NMR and EPR Parameters. Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 2004 Search PubMed; (b) C. Timmons and P. Wipf, J. Org. Chem., 2008, 73, 9168 CrossRef CAS PubMed.
- D. J. Giesen and N. Zumbulyadis, Phys. Chem. Chem. Phys., 2002, 4, 5498 RSC.
- G. W. Buchanan, J. B. Stothers and G. Wood, Can. J. Chem., 1973, 51, 3746 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ob01834g |
| This journal is © The Royal Society of Chemistry 2017 |