Open Access Article
Open Access ArticleThe role of spin states in the catalytic mechanism of the intra- and extradiol cleavage of catechols by O2†
S.
Stepanović
a,
D.
Angelone
 b,
M.
Gruden
b,
M.
Gruden
 *c and
M.
Swart
*c and
M.
Swart
 *bd
*bd
aCenter for Chemistry, Institute of Chemistry, Technology and Metallurgy, University of Belgrade Njegoseva 12, 11001 Belgrade, Serbia
bInstitut de Química Computacional i Catàlisi (IQCC) and Departament de Química, Universitat de Girona, Campus Montilivi (Ciències), 17003 Girona, Spain
cFaculty of Chemistry, University of Belgrade, Studentski trg 12-16, 11001 Belgrade, Serbia. E-mail: gmaja@chem.bg.ac.rs
dICREA, Pg. Lluís Companys 23, 08010 Barcelona, Spain. E-mail: marcel.swart@icrea.cat
First published on 29th August 2017
Abstract
Iron-dependent enzymes and biomimetic iron complexes can catalyze the ring cleavage of very inert, aromatic compounds. The mechanisms of these transformations and the factors that lead either to extradiol cleavage or intradiol cleavage have not been fully understood. By using density functional theory we have elucidated the mechanism of the catalytic cycle for two biomimetic complexes, and explained the difference in the experimentally obtained products.
Introduction
The microbial aerobic degradation of aromatic pollutants, which are widespread contaminants in soils and ground-waters, obviously represents an intense research area in the scientific community.1,2 A key step in the biodegradation of aromatic compounds is the oxidative cleavage of catechol derivatives and is facilitated by a class of enzymes known as catechol dioxygenases.3,4 Two different groups of enzymes play an essential role in the ring cleavage of catechol derivatives: extradiol- and intradiol-cleaving dioxygenases.5 These two enzyme groups have different active sites, and thus catalyse different metabolic transformations.6 In the case of extradiol enzymes, one of the oxygens from O2 is incorporated next to one of the hydroxyl groups (see Fig. 1). On the other hand, in the intradiol dioxygenases, the insertion of the oxygen takes place between the two hydroxyl groups of catechol.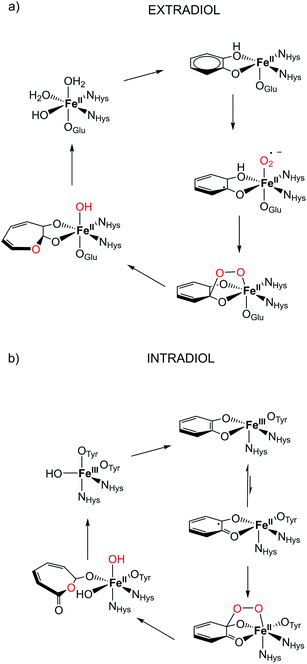 | ||
| Fig. 1 Proposed catalytic cycle in the active site for (a) extradiol and (b) intradiol cleaving catechol dioxygenases.7,8 | ||
The most remarkable feature of these two enzymes is the use of different oxidation states of iron in them. Extradiol-cleaving dioxygenases use FeII in their active site, coordinated by a 2-His-1-carboxylate facial triad in an octahedral environment. The vacant sites are occupied by solvent molecules that can be easily replaced by the substrate and oxygen in the catalytic process, see Fig. 1. In the subsequent step the formation of an alkyl peroxide is followed by a homolytic cleavage of the O–O bond and the insertion of an oxygen atom into the catechol ring occurs. On the other hand, the active site of intradiol dioxygenases consists of FeIII coordinated by two histidines and two tyrosines, and one hydroxide anion.
One of the proposed mechanistic pathways suggested that for an intradiol enzyme, first, FeIII has to oxidize the aromatic ring to a catechol radical, thereby enabling the coordination of oxygen and the subsequent formation of an alkyl peroxide. It is believed that the incorporation of an oxygen atom into the catechol ring proceeds via a concerted process, the so-called Criegee rearrangement.6,9,10
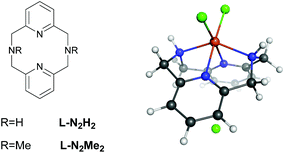
Despite many studies on intra/extradiol enzymes, many questions still remain concerning the details of the reaction mechanisms of these enzymes along with the factors that determine the intra- versus extradiol specificity.6 This is in particular true because of the finding that biomimetic complexes based on FeIII showed both intra- and extradiol activities.11 Previous experimental investigations on iron complexes with rigid L-N2H2 (2,11-diaza[3.3](2,6)pyridinophane) and L-N2Me2 (N,N′-dimethyl-2,11-diaza[3.3](2,6)pyridinophane) ligands (see Fig. 2) have shown that the complexation with L-N2Me2 mainly follows the intradiol pathway (as expected for a FeIII complex),12 while for the complex with L-N2H2 both pathways are being followed.11 Previous experimental and theoretical DFT studies indicated that the formation of an alkyl peroxide is the rate determining step in both cases.10 The selection of one or the other pathway might involve the inclusion of different spin states during the reaction, and therefore, we have studied in detail the influence of the spin-state on the energetics and the mechanism of these reactions.
The relatively small size of biomimetic complexes compared to the enzymes enables both a facile and well-controlled adaptation of the ligand structure, and an in-depth inspection by means of quantum mechanical (QM) modelling; this provides meaningful guidelines for the investigation of the functioning of complicated enzymatic systems.6,13–15 In theory, there is a wide variety of QM levels that can be applied to biomimetic complexes, ranging from semi-empirical methods to high level ab initio (post-Hartree Fock) approaches,16,17 and including a plethora of Density Functional Approximations (DFAs).18,19 The DFAs offer a fast and easy way to calculate the properties of medium-to-large sized molecules, considering their good compromise between the accuracy and the computational efficiency. However, even though DFA methods are in general very accurate for structures and energies, the reliable prediction of spin state splitting in transition metal compounds becomes a difficult challenge.20 There are a large number of studies21–29 devoted to the validation of Density Functional Approximation (DFA) for accurate description of relative spin state energetics, although the prediction of the ground state in complicated systems requires special caution.20,23,30–34 LDA and early GGA DFAs show intrinsic preferences for the low spin (LS) state, while hybrid DFAs systematically favour high spin (HS) states, which is a consequence35 of the inclusion of HF exchange that does not address the correlation between electrons with different spins in a proper way.36 There has not yet been a generally accepted level of theory for the diversity of complicated transition metal systems, although there is a clear preference for DFAs that are spin-state consistent in their design.19 However, so far, almost all studies on enzyme active sites and their small molecule mimics have used hybrid DFAs.9,10,37–42 As mentioned before, because of the inclusion of the HF exchange in the hybrid DFAs, a tendency to overestimate the stability of high spin states is present in them.23,32 Recently, new spin-state consistent DFAs (SSB-D,43 S12g44 and S12h44) have been designed, showing good performance for spin state energetics and reaction barriers.19 Furthermore, Perdew has recently reported a non-empirical meta-GGA ‘Made Very Simple’ (MGGA-MVS),45 which could also perform well.46
Computational details
All DFT calculations were performed with the Amsterdam Density Functional (ADF) program suite.47,48 MOs were expanded in an uncontracted set of Slater type orbitals (STOs) of triple-ζ quality containing diffuse functions (TZ2P)49 and two sets of polarization functions. Core electrons (1s for the 2nd period, 1s2s2p for 3rd–4th periods) were not treated explicitly during the geometry optimization (frozen core approximation), as it was shown to have a negligible effect on the obtained geometries.50 An auxiliary set of s, p, d, f, and g STOs was used to fit the molecular density and represent the Coulomb and exchange potentials accurately for each SCF cycle. Electronic energies were used without any thermochemistry correction throughout the paper, with Gibbs free energies available in the ESI.†The geometries were optimized using the QUILD program51 (as implemented in the ADF2016 suite) using adapted delocalized coordinates52 until the maximum gradient component was less than 10−4 a.u. The energies and gradients were calculated by the S12g44 DFA, using a Becke grid53,54 with a numerical accuracy of very good quality. The COSMO55–57 dielectric continuum model was used for implicit treatment of the environment (with methanol as a solvent).58,59 Scalar relativistic corrections have been included self-consistently by using the zeroth-order regular approximation (ZORA).60–62 The nature of the stationary points is confirmed by calculating analytical Hessians. The subsequent single point calculations that use all-electron basis sets have been performed on all optimized geometries with the S12g, SSB-D,43 M06-L,13,63 MVS45 and S12h44 levels of theory (see the ESI†).
Results and discussion
General mechanism
The proposed mechanism for both the extradiol and intradiol cleavages of an iron catechol complex is shown in Fig. 3 (with the N2H2 ligand, it is assumed that the same pathways are being followed using the N2Me2 ligand). This mechanism represents stepwise progression via multiple local minima. In the examined biomimetic complexes, iron is coordinated by four nitrogen atoms from the chelate ligand, having two adjacent sides accessible for the coordination of the catechol which donates two oxygen atoms to the iron in the resting state (0), see Fig. 3.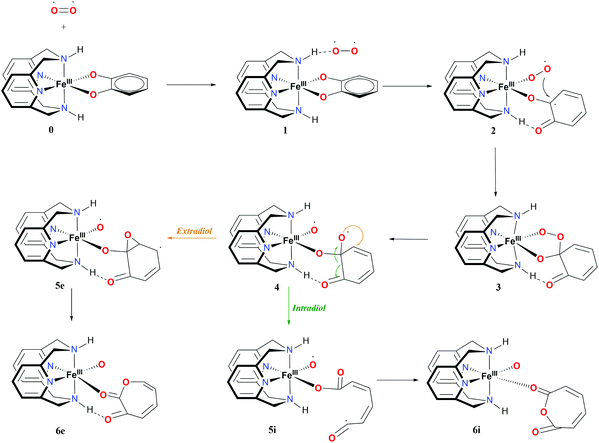 | ||
| Fig. 3 Proposed mechanism and nomenclature for intra- and extradiol catechol cleavages catalyzed by the L-N2H2 iron(III) complex. | ||
After binding of O2, in the first step a weakly-bound van der Waals complex 1 is obtained. Subsequent electron transfer from the catechol, via iron(III) to oxygen, and coordination of the latter, occur via a concerted process,9 forming intermediate 2 (see Fig. 3). In the next step, the coordinated superoxide attacks the catechol, which results in a bridging alkyl peroxide 3. The O2 bond is cleaved homolytically, leading to intermediate 4, which immediately decays in one of the two possible routes: intradiol or extradiol. This intermediate 4 is therefore the branching point where the selectivity for one of the two routes is decided.
The intradiol pathway leads to the open chain radical intermediate 5i, via breaking of the C–C bond and subsequently, the insertion of the oxygen to leads to the cyclization product 6i (see Fig. 3). The extradiol pathway involves the formation of cyclic epoxide 5e, and then breaking of the C–C bond, and the insertion of the oxygen leads to structure 6e. It should be noted that 6i and 6e dissociate forming two isomers, a muconic anhydride and a seven-membered ring lactone, respectively.
Iron(III) complexes have three possible spin-states: high-spin (HS) with five unpaired electrons on the metal; intermediate-spin (IS) with three unpaired electrons on the metal; and low-spin (LS) with one unpaired electron on the metal. In order to fully understand the proposed mechanism, the spin-state splittings of all intermediates and transition states involved in the reaction mechanisms shown in Fig. 3 were investigated. The spin-state splittings of 0, 6i and 6e at S12g/TZ2P are given in Table 1, while those with SSB-D, S12h, M06-L and MVS45 can be found in Tables S1–S8.†
| Ligand molecule | L-N2H2 | L-N2Me2 | ||||
|---|---|---|---|---|---|---|
| 0 | 6i | 6e | 0 | 6i | 6e | |
| LS | 0 | −28.3 | −15.0 | 0 | −25.8 | −12.6 |
| IS | 5.0 | −28.7 | −15.5 | 4.3 | −26.5 | −13.3 |
| HS | 4.5 | −30.0 | −16.8 | 4.1 | −27.4 | −21.7 |
There are a number of experimentally available crystal structures of the complexes that are related to the investigated catalytic cycle.11,12,64,65 They are either precursors of complex 0 with chloride ions instead of catechol with L-N2H2 and L-N2Me2 ligands, or 0 itself (only characterized structurally with L-N2Me2). The calculated bond distances for all complexes show reasonable agreement with the experimentally determined bond lengths (see Table S9†). Experimental studies have concluded (based on the bond lengths of similar systems) that all of these complexes are in the HS ground state.9,10 The calculated electronic energies show that the chloride precursors are in the HS ground state, which corroborates the experimental conclusions. However, for the complex with catechol, the LS state is obtained as the ground state. Similar results are obtained previously at the B3LYP* level of theory.10 This indicates that the spin ground-state for this complex is not determined by the electronic energies, but instead a significant effect is to be expected from enthalpy and entropy corrections that systematically favour the HS state. Irrespective of the coordinated ligand (L-N2H2 or L-N2Me2), the HS intradiol product is thermodynamically favoured, see Table 1.
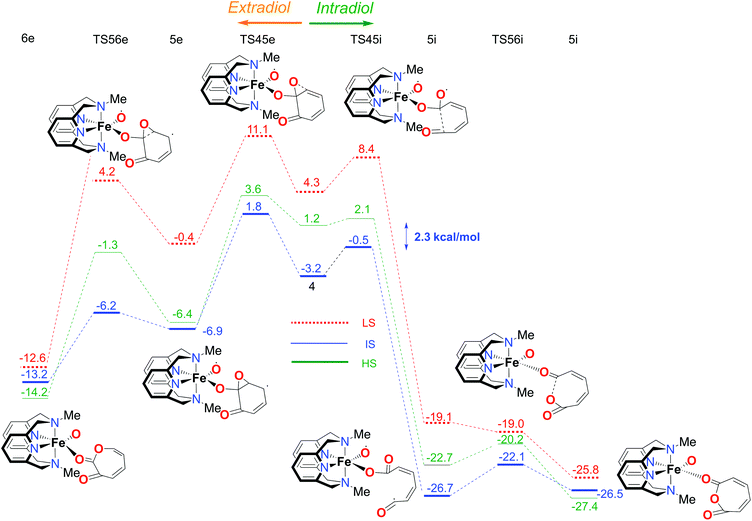
Reaction path with the L-N2H2 ligand
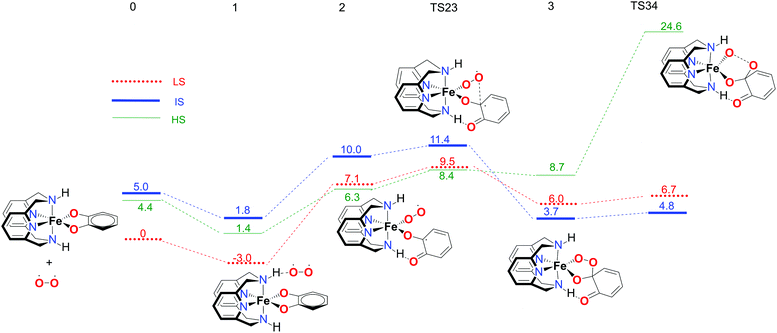
The first part of the energy landscape for the catalytic cycle of the complex with the L-N2H2 ligand (before branching into intradiol and extradiol pathways) is represented in Fig. 4. The splitting of the pathways after branching point 4 is shown in Fig. 5. For the sake of clarity, only the S12g results are given. Some of the specific details are different using SSB-D, M06-L, S12h and MVS, but the overall conclusions regarding the spin state that governs the mechanism and product distribution are the same (see Tables S1–S8†).Following the schematic representation shown in Fig. 1, the complete catalytic dioxygenation reaction for all the available spin states is calculated, starting from a [Fe(LN4H2)(Cat)]+ complex 0, Fig. 4. As mentioned earlier, the initial structure 0 is suggested to be in the HS state. Close lying LS and the HS states are obtained using S12g, with the LS slightly lower in energy. The reaction proceeds with the initial formation of the van der Waals complex 1 that has a negligible effect on the relative spin state energies. Since complex 1 is coordinatively saturated, the subsequent coordination of molecular oxygen needs to be accompanied by decoordination of one part of catechol, in an endothermic process, leading to structure 2. The oxygen that moved away is now able to form an H-bond with the ligand, thereby fixating its position during the reaction. This step is a complex set of events that include catechol oxidation coupled with the iron mediated electron transfer to the O2 molecule, accompanied by the large structural changes. As a result, the spin state ordering in intermediate 2 has changed, with the sextet state now being the lowest in energy. This result is in accordance with experimental results for the enzymatic reaction66 and similar iron superoxo intermediates.67
In the next step, after the catechol is attacked by the superoxo moiety, an intermediate with a five-membered ring (3) is formed. This corroborates the scattered experimental results for the enzymatic process.68 During the formation of the peroxo intermediate, the quartet state becomes the lowest in energy, and remains so until the final point where the muconic anhydride and seven-membered ring lactone dissociate from the iron centre. After the formation of intermediate 3, the O–O bond weakens, and subsequently it breaks, leading the reaction profile to the branching point region in which it can continue either along the intradiol or the extradiol pathway. The reaction profile that follows the cleavage of the O–O bond in intermediate 3 is depicted in Fig. 5. The intradiol pathway is presented on the right, while the extradiol pathway is shown in the same figure on the left. These two mechanisms are characterized by distinct structural transformations, reaction courses and final products.
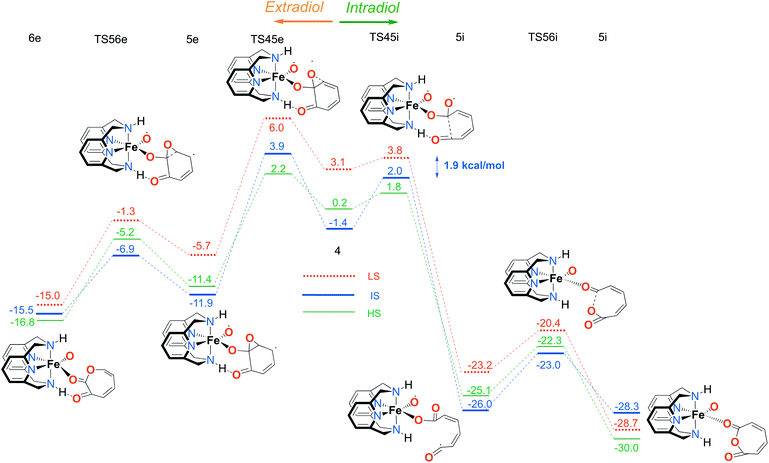
Our calculations indicate that the intradiol mechanism starts with the breaking of the C–C bond, which is then followed by a rearrangement and cyclization, creating the final product, a seven-membered ring lactone. The extradiol pathway is initiated by the formation of the cyclic epoxide, followed by the breaking of a different C–C bond to give the extradiol product, muconic anhydride (see Fig. 5). However, in most of the previous studies concerning the mechanism of intradiol catechol dioxygenase6 and its biomimetics,9,10 a concerted mechanism was found for the formation of seven-membered lactone, whereas in this study the C–C bond breaking occurs first.
The ratio of the products is determined by the barriers for the two pathways, i.e. the relative energies of two transition states TS45i and TS45e. In the IS state, the energy difference between TS45i and TS45e is 1.9 kcal mol−1, favouring the intradiol pathway. However, much smaller barriers are found in the sextet state, with a difference between TS45i and TS45e of only 0.4 kcal mol−1. Since a spin-state switch from IS to HS itself also involves a small barrier (through a so-called minimum-energy crossing point, MECP),69,70 no attempt was made here to localize this MECP because of the small barriers involved. It indicates that both products should in principle be formed, which is in excellent agreement with the experiment.11 The inspection of the reaction landscape shows that the quartet and sextet states are almost equi-energetic in many cases, see Fig. 5, and hence two-state reactivity71–73 seems to play a role here to govern the reaction until the dissociation of the seven-membered ring products and the formation of a five-coordinate iron–oxo complex occur. This is in good agreement with previous studies9 which concluded that iron–oxo complexes tend to be in close lying spin states, with the dominant HS state in a penta-coordinated environment, and IS when hexa-coordinated.
Reaction path with the L-N2Me2 ligand
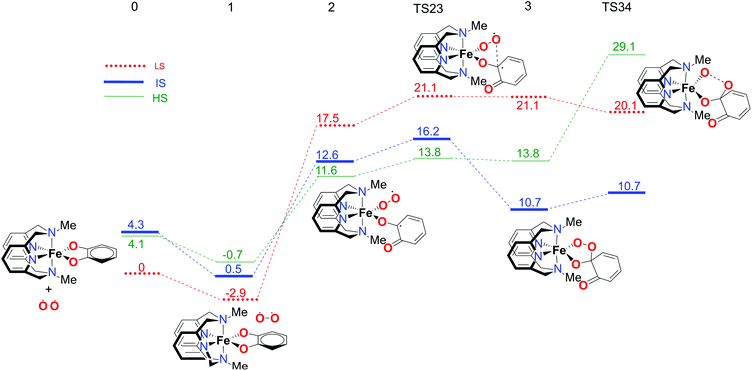
In order to fully understand the behaviour and intrinsic properties of the spin state governed reactions, calculations have also been carried out for the FeIII complex with the L-N2Me2 ligand. The observed reaction profile with S12g is shown in Fig. 6 and 7 (SSB-D, M06-L, S12h and MVS results are given in Tables S1–S8†).The overall reaction pathway is very similar to the catalytic cycle of the complex with the L-N2H2 ligand. The sextet state is the ground state for the superoxo intermediate 2, as well as for the final product, a five-coordinate iron–oxo complex. The quartet state governs the reaction mechanism and product distribution due to the fact that the barrier for the O–O bond dissociation TS34 is very high in energy on a sextet PES.
However, there are two notable differences. First, the step for the coordination of O2, 1 → 2, is more endothermic for the L-N2Me2 ligand. The obvious reason for this is easily found to be the absence of a H-bond donor here (see Fig. 7), to which the decoordinating catechol oxygen can bind (unlike the situation for the L-N2H2 ligand, see Fig. 4).
Secondly and most importantly, the differences in the reaction barriers (TS45ivs.TS45e) after the branching point 4 were twice as large (2.8 kcal mol−1) for the L-N2Me2 ligand compared to those for the L-N2H2 ligand (1.4 kcal mol−1). This corroborates the experimental findings that the iron(III)-complex with the L-N2Me2 ligand selectively cleaves the catechol in an intradiol pathway.12
The difference in the product selectivity with FeIII complexes from L-N2H2 and L-N2Me2 ligands
The overall selectivity of the catalytic cycle is determined by the differences in the energies of the transition states for the two reaction pathways, TS45i for the intradiol and TS45e for the extradiol routes. The difference in the intradiol/extradiol barriers can be explained in terms of the relative orientation of the substrate toward the bridging peroxide.10 The extradiol pathway has a higher barrier, probably due to the necessity of reorientation of the O2p orbital originating from the O–O cleavage.10 The reason for the difference in the product selectivity of the two complexes, i.e. barrier heights at the branching point, can be found in the inspection of H-bonding towards the catechol substrate with the L-N2H2 ligand. During the intradiol pathway, the H-bond with the L-N2H2 ligand is lost in the 4 → 5i step, as a consequence of the breaking of the C–C bond. This does not occur during the extradiol reaction path, explaining why the intradiol pathway is higher in energy and closer to the extradiol alternative with the L-N2H2 ligand. Similarly, the larger reaction rate for the L-N2H2 ligand compared to L-N2Me2 results from the smaller endothermicity for binding of O2 with L-N2H2 because of the capability to form H-bonds (see Fig. 4). In addition, it seems that the methyl groups on the ligand tend to further stabilize the intermediate spin if we compare intermediate 4 with the two ligands. Although on an absolute scale the barrier of the extradiol pathway remains almost identical (ca. 5 kcal mol−1) the barrier for the intradiol path is ca. 1 kcal mol−1 lower for the L-N2Me2 ligand. The origin of this change in the barrier height can be found in L-N2Me24 where the IS state shows an increased bond distance between iron and the catechol oxygen. At the same time a higher Mulliken spin-density charge is observed on the oxygen and carbon atoms that are involved in the cleavage. The Fe core also seems to have a higher spin density in the L-N2Me2 ligand than the L-N2H2 one, and therefore, the geometry and the spin densities of the L-N2Me2 complex in the IS state are more similar to a HS electronic configuration, while in the case of 4 with the L-N2H2 ligand the geometry and electronic configuration are closer to a low spin electronic configuration.Conclusions
Density functional theory calculations have been performed for the reaction mechanism of the catechol cleaving dioxygenase biomimetic iron complexes with L-N2H2 and L-N2Me2 ligands. The complete details of the catalytic cycle, with all accessible spin states and two possible pathways, intradiol and extradiol, were determined. Our calculations show that the formation of both intradiol and extradiol products is substantially exothermic, but the intradiol product formation is thermodynamically more favourable. For the L-N2H2 ligand, H-bonding plays an important role, both in stabilizing the binding of O2, and in making the reaction barriers after the branching point 4 more equal (and hence reducing the preference for an intradiol pathway). Several spin states are involved throughout the reaction mechanism, where again for the L-N2H2 ligand in the critical steps a two-state reactivity seems to be present. On the other hand, for the L-N2Me2 ligand only the quartet state is shown to be involved in an energetically plausible mechanism, completely determining the product distribution. Finally, the difference in the intradiol/extradiol barriers is explained with the change in the H-bonding of the catechol substrate with the L-N2H2 ligand during the intradiol pathway. The obtained results and rationalizations can assist in the design of more selective catechol dioxygenation mimics.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The following organizations are thanked for financial support: the Ministerio de Economia y Competitividad (MINECO, projects CTQ2014-59212-P and CTQ2015-70851-ERC) and the DIUE of the Generalitat de Catalunya (project 2014SGR1202, and Xarxa de Referència en Química Teòrica i Computacional). Financial support was provided by MICINN and the FEDER fund (European Fund for Regional Development) under grant UNGI10-4E-801, and the Serbian Ministry of Education and Science (Grant No. 172035). This work was performed in the framework of COST Action CM1305 “Explicit Control Over Spin-states in Technology and Biochemistry (ECOSTBio)” (STSM reference: COST-STSM-CM1305-21136).References
- M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986 CrossRef CAS PubMed.
- C. K. Brown, M. W. Vetting, C. A. Earhart and D. H. Ohlendorf, Annu. Rev. Microbiol., 2004, 58, 555–585 CrossRef CAS PubMed.
- S. J. Lippard and J. M. Berg, Principles of bioinorganic chemistry, University Science Books, 1994 Search PubMed.
- J. J. R. Fraústo da Silva and R. J. P. Williams, The Biological Chemistry of the Elements, Oxford University Press, 2001 Search PubMed.
- K. Ray, F. F. Pfaff, B. Wang and W. Nam, J. Am. Chem. Soc., 2014, 136, 13942–13958 CrossRef CAS PubMed.
- A. Company, J. Lloret-Fillol and M. Costas, in Comprehensive Inorganic Chemistry II, ed. J. R. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 487–564. DOI:10.1016/B978-0-08-097774-4.00323-5.
- E. G. Kovaleva, M. B. Neibergall, S. Chakrabarty and J. D. Lipscomb, Acc. Chem. Res., 2007, 40, 475–483 CrossRef CAS PubMed.
- T. Borowski and P. E. M. Siegbahn, J. Am. Chem. Soc., 2006, 128, 12941–12953 CrossRef CAS PubMed.
- R. Jastrzebski, M. G. Quesne, B. M. Weckhuysen, S. P. de Visser and P. C. A. Bruijnincx, Chem. – Eur. J., 2014, 20, 15686–15691 CrossRef CAS PubMed.
- V. Georgiev, H. Noack, T. Borowski, M. R. A. Blomberg and P. E. M. Siegbahn, J. Phys. Chem. B, 2010, 114, 5878–5885 CrossRef CAS PubMed.
- N. Raffard, R. Carina, A. J. Simaan, J. Sainton, E. Rivière, L. Tchertanov, S. Bourcier, G. Bouchoux, M. Delroisse, F. Banse and J.-J. Girerd, Eur. J. Inorg. Chem., 2001, 2001, 2249–2254 CrossRef.
- W. O. Koch and H.-J. Krüger, Angew. Chem., Int. Ed. Engl., 1996, 34, 2671–2674 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. K. Panda, A. John, M. M. Shaikh and P. Ghosh, Inorg. Chem., 2008, 47, 11847–11856 CrossRef CAS PubMed.
- S. Chatterjee, D. Sheet and T. K. Paine, Chem. Commun., 2013, 49, 10251–10253 RSC.
- C. Daul, M. Zlatar, M. Gruden-Pavlovic and M. Swart, in Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity, ed. M. Swart and M. Costas, Wiley, Oxford, 2015, pp. 7–34. DOI:10.1002/9781118898277.ch2.
- C. Sousa and C. de Graaf, in Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity, ed. M. Swart and M. Costas, Wiley, Oxford, 2015, ch. 3, pp. 35–57. DOI:10.1002/9781118898277.ch3.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- M. Swart and M. Gruden, Acc. Chem. Res., 2016, 49, 2690–2697 CrossRef CAS PubMed.
- M. Swart, Int. J. Quantum Chem., 2013, 113, 2–7 CrossRef CAS.
- H. Paulsen, L. Duelund, H. Winkler, H. Toftlund and A. X. Trautwein, Inorg. Chem., 2001, 40, 2201–2203 CrossRef CAS PubMed.
- M. Reiher, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, J. Phys. Chem. A, 2004, 108, 5479–5483 CrossRef CAS.
- J. Conradie and A. Ghosh, J. Phys. Chem. B, 2007, 111, 12621–12624 CrossRef CAS PubMed.
- K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365 CrossRef CAS PubMed.
- L. M. Lawson Daku, A. Vargas, A. Hauser, A. Fouqueau and M. E. Casida, ChemPhysChem, 2005, 6, 1393–1410 CrossRef PubMed.
- B. J. Houghton and R. J. Deeth, Eur. J. Inorg. Chem., 2014, 2014, 4573–4580 CrossRef CAS.
- W. C. Isley III, S. Zarra, R. K. Carlson, R. A. Bilbeisi, T. K. Ronson, J. R. Nitschke, L. Gagliardi and C. J. Cramer, Phys. Chem. Chem. Phys., 2014, 16, 10620–10628 RSC.
- P. Verma, Z. Varga, J. E. M. N. Klein, C. J. Cramer, L. Que Jr. and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC.
- S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774 CrossRef CAS PubMed.
- M. Swart, M. Güell and M. Solà, in Quantum Biochemistry, Wiley-VCH, 2010, pp. 551–583. DOI:10.1002/9783527629213.ch19.
- M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066 CrossRef CAS PubMed.
- M. Gruden-Pavlovic, S. Stepanovic, M. Peric, M. Güell and M. Swart, Phys. Chem. Chem. Phys., 2014, 16, 14514–14522 RSC.
- S. Stepanovic, L. Andjelkovic, M. Zlatar, K. Andjelkovic, M. Gruden-Pavlovic and M. Swart, Inorg. Chem., 2013, 52, 13415–13423 CrossRef CAS PubMed.
- M. Swart, Inorg. Chim. Acta, 2007, 360, 179–189 CrossRef CAS.
- J. N. Harvey, Struct. Bonding, 2004, 112, 151–183 CrossRef CAS.
- A. T. P. Carvalho, A. Barrozo, D. Doron, A. V. Kilshtain, D. T. Major and S. C. L. Kamerlin, J. Mol. Graphics Modell., 2014, 54, 62–79 CrossRef CAS PubMed.
- M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Chem. Rev., 2014, 114, 3601–3658 CrossRef CAS PubMed.
- S. P. de Visser, in Comprehensive Inorganic Chemistry II, ed. J. R. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 619–634. DOI:10.1016/B978-0-08-097774-4.00928-1.
- D. Li, Y. Wang and K. Han, Coord. Chem. Rev., 2012, 256, 1137–1150 CrossRef CAS.
- S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2009, 110, 949–1017 CrossRef PubMed.
- S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS PubMed.
- M. Swart, M. Solà and F. M. Bickelhaupt, J. Chem. Phys., 2009, 131, 094103 CrossRef PubMed.
- M. Swart, Chem. Phys. Lett., 2013, 580, 166–171 CrossRef CAS.
- J. Sun, J. P. Perdew and A. Ruzsinszky, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 685–689 CrossRef CAS PubMed.
- F. Feixas and M. Swart, unpublished data, 2017.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. V. Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, T. Heine, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, 2016 Search PubMed.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- M. Swart and J. G. Snijders, Theor. Chem. Acc., 2003, 110, 34–41 CrossRef CAS . Erratum: M. Swart and J. G. Snijders, Theor. Chem. Acc., 2003, 111, 156 Search PubMed.
- M. Swart and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 724–734 CrossRef CAS PubMed.
- M. Swart and F. M. Bickelhaupt, Int. J. Quantum Chem., 2006, 106, 2536–2544 CrossRef CAS.
- M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553 CrossRef CAS.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- M. Swart, E. Rösler and F. M. Bickelhaupt, Eur. J. Inorg. Chem., 2007, 2007, 3646–3654 CrossRef.
- C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- W. O. Koch, V. Schünemann, M. Gerdan, A. X. Trautwein and H.-J. Krüger, Chem. – Eur. J., 1998, 4, 686–691 CrossRef CAS.
- W. O. Koch, V. Schünemann, M. Gerdan, A. X. Trautwein and H.-J. Krüger, Chem. – Eur. J., 1998, 4, 1255–1265 CrossRef CAS.
- M. M. Mbughuni, M. Chakrabarti, J. A. Hayden, E. L. Bominaar, M. P. Hendrich, E. Münck and J. D. Lipscomb, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16788–16793 CrossRef CAS PubMed.
- C.-W. Chiang, S. T. Kleespies, H. D. Stout, K. K. Meier, P.-Y. Li, E. L. Bominaar, L. Que, E. Münck and W.-Z. Lee, J. Am. Chem. Soc., 2014, 136, 10846–10849 CrossRef CAS PubMed.
- C. J. Knoot, V. M. Purpero and J. D. Lipscomb, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 388–393 CrossRef CAS PubMed.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
- J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1–14 CrossRef CAS.
- S. Shaik, S. P. de Visser, F. Ogliaro, H. Schwarz and D. Schroder, Curr. Opin. Chem. Biol., 2002, 6, 556–567 CrossRef CAS PubMed.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed.
- D. Usharani, B. Wang, D. A. Sharon and S. Shaik, in Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity, ed. M. Swart and M. Costas, Wiley, Oxford, 2015, pp. 131–156. DOI:10.1002/9781118898277.ch7.
Footnote |
| † Electronic supplementary information (ESI) available: Relative energies and XYZ coordinates. See DOI: 10.1039/c7ob01814b |
| This journal is © The Royal Society of Chemistry 2017 |