Self-assembly of Au@Ag core–shell nanocuboids into staircase superstructures by droplet evaporation†
Xianzhong
Yang
ab,
Jing
Li
c,
Yuxin
Zhao
d,
Jianhua
Yang
e,
Liyan
Zhou
ab,
Zhigao
Dai
f,
Xiao
Guo
ab,
Shanjun
Mu
d,
Quanzhen
Liu
d,
Chunming
Jiang
d,
Mengtao
Sun
 *g,
Jianfang
Wang
*g,
Jianfang
Wang
 e and
Wenjie
Liang
e and
Wenjie
Liang
 *ab
*ab
aBeijing National Laboratory for Condensed Matter Physics, Beijing Key Laboratory for Nanomaterials and Nanodevices, Institute of Physics, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: wjliang@iphy.ac.cn
bSchool of Physical Sciences, University of Chinese Academy of Sciences, Beijing, 100049, China
cKey Laboratory of Photochemical Conversion and Optoelectronic Materials, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, 100190, China
dState Key Laboratory of Safety and Control for Chemicals, SINOPEC Research Institute of Safety Engineering, No. 339, Songling road, Laoshan District, Qingdao, China
eDepartment of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong SAR, China
fLaboratory of Printable Functional Nanomaterials and Printed Electronics, School of Printing and Packaging, Wuhan University, Wuhan, 430072, China
gBeijing Key Laboratory for Magneto-Photoelectrical Composite and Interface Science, School of Mathematics and Physics, University of Science and Technology Beijing, Beijing, 100083, China. E-mail: mengtaosun@ustb.edu.cn
First published on 31st October 2017
Abstract
Plasmonic nanomaterials, along with their assemblies, provide numerous applications due to their profound optical properties. In this work, we report the self-assembly of Au@Ag core–shell nanocuboids (NCs) into staircase superstructures in both vertical and horizontal orientations through two-stage droplet evaporation. Each stair is composed of a uniform well-aligned monolayer of NCs. The gap distance between NCs can be greatly shrunk to boost the corresponding surface-enhanced Raman scattering (SERS) performance using an ethanol wash method. The SERS performance of the assembled NCs is calculated by finite-difference time-domain (FDTD) simulation, and studied against the step number using 4-mercaptobenzoic acid as a Raman reporter molecule. The increasing EF with the increase of layer number proves that the plasmon mode propagates well in our uniformly aligned assemblies.
Introduction
Noble metal nanoparticles with different shapes,1 such as nanospheres,2 nanotriangles,3 nanocubes,4 and nanorods,5–9 have attracted increasing attention owing to their widespread applications in catalysis,10 biomedical technologies,11 plasmon-enhanced spectroscopy,12–14 solar cells15 and so on. Due to their highly tunable optical properties,16 Au nanorods are one of the most studied anisotropic nanoparticles. If these nanorods are placed adjacent to each other to form ordered assemblies, their localized surface plasmon resonances (LSPRs) will couple together through electromagnetic interactions, which brings numerous interesting collective plasmon responses, such as extremely large electric field enhancements and distinct collective plasmon modes. In recent years, increasing interest has been shown in assembling Au nanorods into ordered superstructures and characterizing their optical properties. A number of techniques, including Langmuir–Blodgett deposition,17,18 assembly via chemical modification,19,20 and droplet evaporation,5,21–23 have been used to obtain the related assemblies. Among them, droplet evaporation has been extensively investigated because of its operability, cost-effectiveness, and wide compatibility with various functional nanomaterials.24Recently, the assembly of Au nanorods into monolayer vertical arrays has been achieved.12,25 And Li et al. have succeeded in acquiring a thick-layer assembly by regulating the surface properties of Au nanorods.24 However, as far as we know, layer by layer assembly of thin layer Au nanorods by evaporation has not been achieved yet. And as a particular kind of nanorod, nanocuboids haven't been studied thoroughly, especially in the area of assembly. Herein, we demonstrate a simple yet robust 2-stage droplet evaporation25 approach to directionally assemble Au@Ag core–shell nanocuboids (NCs) into staircase-like alignments. These alignments are assembled layer by layer in both vertical and horizontal orientations. Furthermore, we successfully tune the NCs’ coupling via adjusting their spacing. Then the optical properties of the obtained superstructures are examined through FDTD calculation. Finally, the SERS properties of the NCs are investigated with 4-mercaptobenzoic acid (4-MBA) as the analyte molecule26 and a high SERS enhancement and a high propagation are demonstrated.
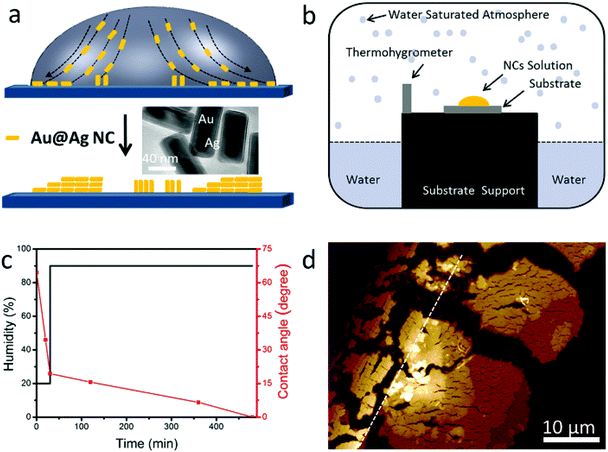
The assembly of NCs takes advantage of the “coffee ring” effect (see Fig. 1a).5,23,27–29 One drop of NC dispersion is cast onto a silicon substrate and dried under certain conditions.
During drying, the contact line at the edge will be pinned. The solvent from the interior replenishes the solvent evaporating from the edge due to the higher evaporation rate at the edge. The resulting edgeward flow carries NCs toward the edge and deposits them in the vicinity of the contact line forming a ring-like pattern. The evaporation process is affected by several parameters, such as NC concentration, surfactant, evaporation speed (temperature, humidity), NC aspect ratio, substrate, and so on. All of these have to be well controlled to obtain the desired assembly geometry. Our control of assemblies follows a 2-stage evaporation method similar to that reported by Xie et al.25 We are interested in the assembly of dilute NC solution (10–50 pM) and in the end, the solution would be depleted and almost all NCs would be assembled at the very edge of the contact line.
Au@Ag core (Au)–shell (Ag) nanocuboids were prepared by the method reported before (see Methods in the ESI†).15,30 Briefly, the uncoated Au nanorods were synthesized using a seed-mediated growth method in aqueous solutions and were stabilized with cetyltrimethylammonium bromide (CTAB). Then the surface of Au nanorods was coated with Ag by adding AgNO3 and ascorbic acid in solution. The as-prepared nanocuboid solution was centrifuged and re-dispersed in a different volume of deionized water with 2.5 mM CTAB. The aspect ratio of the NCs is about 2.4 (total length: 80 ± 4 nm, width: 34 ± 2 nm, shell thickness: 7 nm, see the TEM image in the inset of Fig. 1a). The absorption spectrum of NC solution is shown in Fig. S1a.† The plasmon peaks located at 630 and 465 nm are attributed to the longitudinal and transverse dipolar modes, respectively. And the plasmon peaks at 401 and 341 nm are assigned to an octupolar mode of NCs.30–33 For our 2-stage evaporation, the droplet was left in an atmospheric environment for 30 minutes in the first stage, in which the droplet edge was pinned. Then the droplet on the substrate was transferred to a homemade chamber which is schematically illustrated in Fig. 1b. The high humidity inside the chamber guarantees enough time for the gradual assembly of NCs. The black and red lines in Fig. 1c show the humidity and contact angle change during the whole evaporation process, respectively, which reveal the fast and slow evaporation speeds (see also Fig. S1b†). After the evaporation, a ring made up of NC assemblies was observed on the substrate (see Methods in the ESI†). A representative atomic force microscopy (AFM) image of a random corner of the ring is shown in Fig. 1d, where two well separated types of NC assemblies can be clearly recognized. NCs next to the drying edge (the black dotted line in Fig. 1d) assemble in the horizontal direction and stack in a staircase fashion, accumulating more layers toward the direction of the droplet center. While for the area far from the drying edge (on the right of the white dotted line in Fig. 1d), vertical alignment of NCs was achieved, and the staircases of the layers are also clear (this will be discussed in detail in the following section). These assemblies could only be observed within tens of micrometers near the contact line. We don't observe any NCs or assemblies far away from this region.
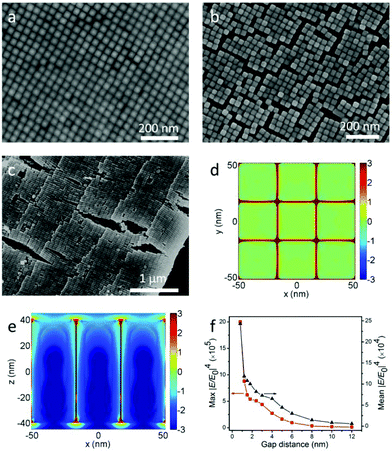
Although the self-assembly of NRs into monolayer and 3D structures has been achieved using different methods,12,24,25 the staircase-like superstructure of NCs has never been reported. In order to systematically study the stair-like arrays, scanning electron microscopy (SEM) and AFM were used to carefully examine the morphology. The assembly results of NCs from 50 pM solution are presented in Fig. 2. Fig. 2a–c and d–f correspond to horizontal and vertical alignments respectively. A high magnification SEM image of the horizontal assembly shows that NCs indeed form a stair-like structure (Fig. 2a). On each stair, NCs assemble into a rectangular lattice, with the long axial direction pointing to the stair edge. In between different stairs, NCs make a perfect match with the NCs of the front stair, showing a single crystal ordering if the stair edges could be ignored. Each stair shows an almost identical stair width, which is about a length of 9 NCs or around 720 nm. The period of 9 NCs of this assembly gives rise to an additional symmetry, and the high quality of this ordering can refer to the fast Fourier transforms (FFT) in Fig. S2.† The white arrows in Fig. 2a and c point to the center of the coffee ring, namely, the drying direction. It's found from Fig. 2a–c that almost all NCs are parallel to the drying directions. As aforementioned, the NCs are transported from the interior to the edge during evaporation. Only parallel to the drying directions, can the NCs be subject to the least resistance.
The cross-sectional view of one sample is shown in Fig. 2b, from which 5 and 6 layers of assembled NCs can be distinguished on the two sides of the stair edge (white dotted line). That the layer numbers change only by one at the staircase edge confirms that the arrays are assembled layer by layer.
It can be seen from Fig. 2b that the stacking of NCs along the vertical direction tilts toward the drying direction, and the tilt angle is about 70° from the horizon. Fig. 2c shows low magnification of AFM image of horizontal arrays. The inset of Fig. 2c shows the height profile along two line traces (dotted lines A and B) of the same assembly at different positions. The plateaus from A and B overlap together very well, showing that the whole assembly is uniform. The continuous numbers of layers are labeled on the right of each plateau, which also indicate that the NCs are assembled horizontally layer by layer. The average height of each layer is about 34 nm which is consistent with the width of a single nanocuboid.
Similar results are also valid for vertical arrays far away from the drying edge. The NCs assemble into a tetragonally packed superstructure (see the FFT in Fig. S2b and c†) with a handful of deformations in Fig. 2d. Fig. 2e shows the cross-sectional view of vertical arrays, where 3–4 layers can be recognized, and the NCs in different layers stack on top of each other. So we can conclude that the NCs are vertically assembled layer by layer. Actually the so-called vertical arrays are not perpendicular but inclined to the substrate. And the inclination angle is also about 70°, the same as the horizontal case, which reduces the height of each layer by about 5 nm. Fig. 2f shows the AFM image of multilayer vertical arrays. The height profile along the dotted white line shown in the inset reveals that the arrays are stacked from 2 to 5 layers. The mean height of each layer is about 75 nm, which is in agreement with the 70° inclination. This 70° inclination of the vertical arrays can be observed in all the examined samples. However, the even spacing of the vertical step that happens for the horizontal alignments is unfortunately missing. The diverse width of each vertical stair is of several micrometers.
Different concentrations of NC solutions are used to investigate the staircase-like assemblies. Six layers of horizontal arrays are acquired when the concentration is 10 pM (see Fig. 3a), and the number of layers increases to 16 as the solution concentration increases to 50 pM (see Fig. 3b). The first layer locates at the pinned line of the droplet, and it is quite disordered because of the instability of the external environment. The steps tend to be orderly and uniform from the second step. Both arrows in Fig. 3a and b point to the drying directions. Comparing Fig. 3a and b, it can be found that all NCs align parallel to the drying direction, and the size of each step is around a length of 9 NCs. So the direction and average width of each step have nothing to do with the solution concentration. Analogously, the thicknesses of vertical arrays also change with the solution concentration. For 10 pM solution, most of the vertical arrays are monolayer except for few bilayers at the domain boundaries (see Fig. 3c and Fig. S3a†), and the mean area of one domain is about 100 μm2. Multilayer vertical arrays shown in Fig. 3d are formed when we increased the droplet concentration to 50 pM. Besides, the average area can be as large as 200 μm2 (see Fig. 1d).
 | ||
| Fig. 3 SEM images of step-like horizontal arrays evaporated from (a) 10 PM, (b) 50PM NCs solution. SEM images of vertical arrays evaporated from (c) 10 PM, (d) 50 PM NCs solution. | ||
The highest stair numbers on the ring are the same for different samples from the same solution concentration, which are about 6 and 16 for the 10 pM and 50 pM solutions, respectively. The stair sizes of the horizontal arrays are surprisingly uniform for all samples. An analogous step-like arrangement was observed in the assembly of Au polyhedra,5 while the exact mechanism is not yet clear. If NCs are packed side by side perfectly along the circumference, a simple estimation (see Methods) reveals that 10 pM and 50 pM solution would give 5–6 layers and 12–13 layers of horizontal stair-like superstructures, respectively, which are a little smaller than the experimental results. Actually, horizontal and vertical arrays coexist on the ring, and there is a lot of space between aligned islands. The concentration dependent stair numbers of both horizontal and vertical assemblies prove that the depletion of all NCs at the drying edge plays an important role in the unique stair-like superstructures.
The 70° inclination indicates the universal influence of the fluidic flow. The spatial separation of horizontal and vertical alignment regions suggests that different assembly mechanisms are dominant at different locations. At the very edge where NCs are confined in a quite limited space with a high flow rate, NCs are aligned parallel to the fluidic flow direction. The flow rate decreases in the area relatively far from the pinned edge, and there is more room for NCs to adjust their orientation for assembly and so they prefer vertical alignment which further increases the binding energy by exposing less surface area.
The stair-like packing and well-aligned nature between different layers give support to the fact that assembly happens on the substrate instead of in the solution or at the air/liquid interface. Otherwise the orientations of horizontal alignments would be random. The uniform staircase structure may appear from the slow retreat of the pinned line, and the movement of 720 nm is hard to observe in the contact angle system (Fig. S1†). The contact line moves in a stick-slip34 fashion and the shape of the assembly at the drying edge follows exactly this movement, giving a vivid horizontal superstructure with a stable width. The space between the very edge and the pinned first layer in Fig. 3a is approximately 720 nm, which is equal to the width of each stair. This also confirms the stick-slip movement in another way. While for the region far from the drying edge, the vertical assembly loosely follows the drying speed, giving a stair-like superstructure with a random step width. The later argument is further supported by the fact that the heights of the horizontally aligned superstructures and vertically aligned superstructures roughly match each other (see Fig. 1d). The layer number of the horizontal staircase to that of the vertical staircase is about 6 to 2 (10 pM) and 16 to 5 (50 pM), basically matching our NC aspect ratio of 2.4. This matching suggests that the assembly of horizontal and vertical superstructures is indeed layer by layer and finishes about the same time when NCs are depleted.
As mentioned above, the LSPRs of NCs couple together through electromagnetic interactions when they are placed adjacent to each other. And the strength of coupling is closely dependent on the distance between the NCs. However, NCs grown by seed-mediated methods are covered with bilayer CTAB, which makes the NCs’ surface positively charged.7 The CTAB not only prevents the aggregation of NCs in solution, but also governs the gap distance between NCs in the assembly. It was reported that UV ozone could be used to dramatically narrow the gap distance in Au nanorod monolayer arrays.12 While for Au@Ag NCs, this way is impractical, because the surface of Ag is so easy to oxidize by ozone. In consideration of the dissolvability of CTAB in ethanol, the substrate with horizontal and vertical arrays was soaked in ethanol for 5 min and dried under N2. Assemblies before and after the soaking are shown in Fig. 4a, b, Fig. S3–S5,† and the FFT of Fig. 4a is shown in Fig. S2d.† The gap distance of vertical arrays significantly decreases from 6 nm to 0.8 nm (see Fig. S6a and b†). As a result, a lot of cracks turn up. By comparing the NCs’ morphologies on both sides of the cracks, we can see that there are no NCs escaping from the substrate during the wash. Analogously, the average gap distance of the horizontal arrays shrinks from 6.3 nm to 2.6 nm (see Fig. 2a, Fig. 4c and Fig. S6c, d†). The shrinking of the gap distance is due to the vanishing of electrostatic repulsive forces after the dissolving of CTAB. Then the van der Waals forces pull the NCs closer. Besides the decrease of gap distance, the cleaning of CTAB by ethanol is also helpful for AFM characterization. This is very crucial for obtaining the precise height of each layer. All the AFM images in Fig. 1d and 2 are from the washed samples.
To study the coupling effects of NCs, FDTD simulation12,35,36 was introduced to investigate the electric field enhancement for monolayer vertical arrays. The electrical field intensity distributions of vertical arrays with 0.8 nm gap distance in the horizontal plane (x–y) and the vertical plane (x–z) are shown in Fig. 4d and e, respectively. It can be clearly seen that the localized electric field is mainly confined to the nanogap between adjacent nanocuboids. And the maximum localized electric fields are around the cuboid vertices. Moreover, Fig. 4f shows the variation for the maximum and average electric field enhancement factors (|E/E0|4) with the change of the gap distance, where |E/E0|4 increases nonlinearly with the decrease of the gap. The maximum |E/E0|4 values are around 9.5 × 104 and 2.0 × 106 when the gap distances are 6 nm and 0.8 nm respectively, which indicates that the close packing of NC arrays induced by ethanol wash significantly improves the electric field enhancement about 21 times. And the average |E/E0|4 values improve about 8 times (from 3 × 104 to 2.4 × 105).
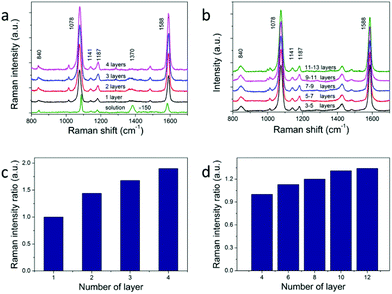
The calculated large electric field enhancement represents the enhanced coupling effect in the vertical arrays and it will benefit the SERS enhancement. 4-Mercaptobenzoic acid (4-MBA) was used as the Raman reporter molecule.26,31,37 NC superstructures were immersed in a 1 mM 4-MBA ethanol solution for about 3 h, rinsed thoroughly with ethanol, and dried with nitrogen for SERS measurement. The excitation wavelength was 785 nm with an estimated power density of 5.9 × 108 W m−2. The monolayer vertical arrays were used to acquire the enhancement factor (see Fig. 5a). The SERS and Raman spectra are dominated by two strong bands at about 1078 and 1588 cm−1, which are assigned to the v(CC) benzene ring-breathing modes.38 The relatively weak peak at 840 cm−1 is due to the bending mode δ(COO−),37 and the two peaks at 1141 cm−1 and 1187 cm−1 are due to the mode δ(CH).26,39 The band at about 1370 cm−1 corresponds to vs(COO−),37 which points to the presence of dissociated COO− groups. And this peak becomes more obvious in solution (the green line in Fig. 5a) because of the addition of ammonium hydroxide. We use the intensity of the peak at 1078 cm−1 to evaluate the SERS performance of NCs. According to previous reports, self-assembled monolayers (SAM) would be formed when NC arrays were soaked in 10−3 M 4-MBA solution.26 The surface plasmon enhancement factor (EF) can be calculated using the following expression:
| EF = [ISERS]/[Isolution] × [Nsolution]/[NSERS] | (1) |
Here, ISERS and Isolution are the SERS signals from 4-MBA SAMs on a closely packed NC vertical array and that from 0.8 M 4-MBA solution. NSERS and Nsolution are the molecule number sampled in the SERS experiments and solution respectively. NSERS comes from multiplying the volume occupied by the nanoparticles in the illuminated laser spot by the bonding density of 4-MBA molecules in a SAM, ∼0.5 nmol cm−2.26 The diameter of the laser spot is estimated using the following equation: Ddiameter = (λ/NA) × 1.22,31 in which the NA of the 50× objective lens of the Raman spectrometer is 0.5, and the wavelength of the excitation laser is 785 nm. For the solution, the penetration depth of the 785 nm laser beam is about 6.53 μm. NSERS and Nsolution are 6.11 × 106 and 9.05 × 109 respectively.40ISERS and Isolution are 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 and 43, respectively, which have been normalized by the accumulation time. We obtain EF ∼ 3.87 × 105. This EF is comparable to the calculated average |E/E0|4 of 2.4 × 105 with a gap distance of 0.8 nm (Fig. 4f), and also agrees with that in previous studies on Ag nanostructures.41–43 The EF observed in our experiments is comparatively more modest compared with the high EF in previous studies.26,44,45 This is mainly attributed to the non-resonant excitation wavelength chosen for SERS measurements, and we may not obtain a full monolayer molecule coverage for the limited soaking time (3 h).
244 and 43, respectively, which have been normalized by the accumulation time. We obtain EF ∼ 3.87 × 105. This EF is comparable to the calculated average |E/E0|4 of 2.4 × 105 with a gap distance of 0.8 nm (Fig. 4f), and also agrees with that in previous studies on Ag nanostructures.41–43 The EF observed in our experiments is comparatively more modest compared with the high EF in previous studies.26,44,45 This is mainly attributed to the non-resonant excitation wavelength chosen for SERS measurements, and we may not obtain a full monolayer molecule coverage for the limited soaking time (3 h).
Self-assembled arrays of NCs are crucial for future applications of optoelectronics and enhanced spectroscopy. One key question for 3D assemblies of NC arrays is how many layers of the arrays would actually contribute to the enhancement of the signals. The previous attempt of utilizing horizontally aligned Ag nanowire arrays in woodpile-like platforms shows that up to 4 layers of the assemblies would contribute to SERS signals.17 We argue that the enhancement of multiple layers depends on how plasmon modes and optical signals propagate between different layers. Not only the NCs within the superstructures should be monodispersed, but also the NCs in adjacent layers should have the same orientation and align to each other. We studied the layer dependent SERS spectra of horizontal and vertical assemblies. The results are shown in Fig. 5a and b. We measured SERS intensities from 4 layers of NCs up to 12 layers of NCs in horizontal arrays and 1 layer to 4 layers in vertical arrays. The observed SERS signals keep increasing against layer numbers in both cases (Fig. 5c and d). The same effect is observed in all samples in which we did layer-dependent SERS studies. It can be seen that the SERS intensities increase almost linearly with layer number for the first several layers in Fig. 5c and d. The SERS intensity of 4-layer vertical arrays is about 1.9 times larger than that of monolayer arrays. This increase is obvious evidence of the increasing hot spot number for multilayers. The fact that we don't see SERS intensity saturation versus layer number clearly proves that plasmon modes and SERS signals propagate very well in our NC staircase superstructures, hence providing more hot spots than other configurations for SERS applications.
The enhancement effect in the current study is far from satisfactory. But careful error analysis gives 1.7% to 6.8% signal variation for measurement on the same layer (ESI, Fig. S7†), which is far below our measured increase against the layer number. We attribute this low number mainly to the lack of efficient coverage of 4-MBA reporter molecules inside the superstructures. Our soaking time in 4-MBA solution was limited to 3 hours, mainly due to structure stability concerns. Unfortunately 3 hours would barely be long enough to form SAM on monolayer Ag NCs. The diffusion of 4-MBA through the close-packed superstructure would not be sufficient. We test this by measuring SERS of our staircase-like superstructure after soaking in 4-MBA solutions for different periods of time. The signal ratio of the deep layer to that of the surface layer linearly increases with soaking time, the thicker the layer, the higher the increase. Further efforts on optimizing the assembly method and loading SERS molecules are needed to solve this insufficient coverage problem.
Conclusion
In summary, by using a two-step droplet evaporation method, we achieved the self-assembly of Au@Ag NCs in a staircase superlattice fashion for both horizontal alignment and vertical alignment. The assemblies are formed layer by layer with monolayer stepping. Horizontally-aligned NC stairs have a stable 720 nm step size and vertically aligned NC stairs have step sizes of micrometers, both of which are adequate for layer by layer optical investigation. The gap distance between the NCs in the staircase was tuned by a simple ethanol wash method. The EF for monolayer vertical arrays is about 3.87 × 105, which agrees well with the average enhancement from FDTD simulation. The layer dependent SERS performance shows that plasmon modes and SERS signals propagate well within these perfectly aligned staircase superstructures. This makes it an ideal system to study the optical properties of plasmonic materials in fields such as SERS, optoelectronics and solar cells.Methods
Methods and any associated references are available in the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC, Grant No. 11374342, 11374353, 91436102, 61307065, 61701543 and 51601131), the Sinopec Innovation Scheme (A-381), the Hubei Provincial Natural Science Foundation (2016CFB166), and the Hong Kong Research Grants Council (GRF, Ref. No. 14305314).References
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS PubMed.
- H. Wang, C. S. Levin and N. J. Halas, J. Am. Chem. Soc., 2005, 127, 14992–14993 CrossRef CAS PubMed.
- L. Scarabelli, M. Coronado-Puchau, J. J. Giner-Casares, J. Langer and L. M. Liz-Marzan, ACS Nano, 2014, 8, 5833–5842 CrossRef CAS PubMed.
- Y. G. Sun and Y. N. Xia, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- T. Ming, X. Kou, H. Chen, T. Wang, H. L. Tam, K. W. Cheah, J. Y. Chen and J. Wang, Angew. Chem., Int. Ed., 2008, 47, 9831–9836 CrossRef.
- A. Guerrero-Martinez, J. Perez-Juste, E. Carbo-Argibay, G. Tardajos and L. M. Liz-Marzan, Angew. Chem., Int. Ed., 2009, 48, 9484–9488 CrossRef CAS PubMed.
- H. Chen, L. Shao, Q. Li and J. Wang, Chem. Soc. Rev., 2013, 42, 2679–2724 RSC.
- X. Huang, S. Neretina and M. A. El-Sayed, Adv. Mater., 2009, 21, 4880–4910 CrossRef CAS PubMed.
- A. Gole and C. J. Murphy, Chem. Mater., 2004, 16, 3633–3640 CrossRef CAS.
- X. Yang, H. Yu, X. Guo, Q. Ding, T. Pullerits, R. Wang, G. Zhang, W. Liang and M. Sun, Mater. Today Energy, 2017, 5, 72–78 CrossRef.
- R. A. Alvarez-Puebla, A. Agarwal, P. Manna, B. P. Khanal, P. Aldeanueva-Potel, E. Carbo-Argibay, N. Pazos-Perez, L. Vigderman, E. R. Zubarev, N. A. Kotov and L. M. Liz-Marzan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8157–8161 CrossRef CAS PubMed.
- B. Peng, G. Y. Li, D. H. Li, S. Dodson, Q. Zhang, J. Zhang, Y. H. Lee, H. V. Demir, X. Y. Ling and Q. H. Xiong, ACS Nano, 2013, 7, 5993–6000 CrossRef CAS PubMed.
- B. Peng, Z. Li, E. Mutlugun, P. L. Hernandez Martinez, D. Li, Q. Zhang, Y. Gao, H. V. Demir and Q. Xiong, Nanoscale, 2014, 6, 5592–5598 RSC.
- P. Guo, D. Sikdar, X. Huang, K. J. Si, W. Xiong, S. Gong, L. W. Yap, M. Premaratne and W. Cheng, Nanoscale, 2015, 7, 2862–2868 RSC.
- S. Liu, R. Jiang, P. You, X. Zhu, J. Wang and F. Yan, Energy Environ. Sci., 2016, 9, 898–905 CAS.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS.
- M. Chen, I. Y. Phang, M. R. Lee, J. K. Yang and X. Y. Ling, Langmuir, 2013, 29, 7061–7069 CrossRef CAS PubMed.
- P. D. Yang, Nature, 2003, 425, 243–244 CrossRef CAS PubMed.
- K. Liu, N. Zhao and E. Kumacheva, Chem. Soc. Rev., 2011, 40, 656–671 RSC.
- S. T. S. Joseph, B. I. Ipe, P. Pramod and K. G. Thomas, J. Phys. Chem. B, 2006, 110, 150–157 CrossRef CAS PubMed.
- B. Nikoobakht, Z. L. Wang and M. A. El-Sayed, J. Phys. Chem. B, 2000, 104, 8635–8640 CrossRef CAS.
- T. K. Sau and C. J. Murphy, Langmuir, 2005, 21, 2923–2929 CrossRef CAS PubMed.
- A. Martin, C. Schopf, A. Pescaglini, J. J. Wang and D. Iacopino, Langmuir, 2014, 30, 10206–10212 CrossRef CAS PubMed.
- P. Li, Y. Li, Z. K. Zhou, S. Tang, X. F. Yu, S. Xiao, Z. Wu, Q. Xiao, Y. Zhao, H. Wang and P. K. Chu, Adv. Mater., 2016, 28, 2511–2517 CrossRef CAS PubMed.
- Y. Xie, S. Guo, C. Guo, M. He, D. Chen, Y. Ji, Z. Chen, X. Wu, Q. Liu and S. Xie, Langmuir, 2013, 29, 6232–6241 CrossRef CAS.
- C. J. Orendorff, A. Gole, T. K. Sau and C. J. Murphy, Anal. Chem., 2005, 77, 3261–3266 CrossRef CAS PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef CAS PubMed.
- P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Nature, 2011, 476, 308–311 CrossRef CAS PubMed.
- R. B. Jiang, H. J. Chen, L. Shao, Q. Li and J. F. Wang, Adv. Mater., 2012, 24, OP200–OP207 CAS.
- Y. Liu, J. Zhou, B. Wang, T. Jiang, H. P. Ho, L. Petti and P. Mormile, Phys. Chem. Chem. Phys., 2015, 17, 6819–6826 RSC.
- Y. Ma, W. Li, E. C. Cho, Z. Li, T. Yu, J. Zeng, Z. Xie and Y. Xia, ACS Nano, 2010, 4, 6725–6734 CrossRef CAS PubMed.
- Y. Okuno, K. Nishioka, A. Kiya, N. Nakashima, A. Ishibashi and Y. Niidome, Nanoscale, 2010, 2, 1489–1493 RSC.
- J. X. Huang, A. R. Tao, S. Connor, R. R. He and P. D. Yang, Nano Lett., 2006, 6, 524–529 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- E. D. Palik, Handbook of optical constants of solids, Academic Press, 1998 Search PubMed.
- A. Michota and J. Bukowska, J. Raman Spectrosc., 2003, 34, 21–25 CrossRef CAS.
- H. Park, S. B. Lee, K. Kim and M. S. Kim, J. Phys. Chem., 1990, 94, 7576–7580 CrossRef CAS.
- D. He, B. Hu, Q.-F. Yao, K. Wang and S.-H. Yu, ACS Nano, 2009, 3, 3993–4002 CrossRef CAS PubMed.
- Y. He, S. Su, T. Xu, Y. Zhong, J. A. Zapien, J. Li, C. Fan and S.-T. Lee, Nano Today, 2011, 6, 122–130 CrossRef CAS.
- S. Zhou, J. Li, K. D. Gilroy, J. Tao, C. Zhu, X. Yang, X. Sun and Y. Xia, ACS Nano, 2016, 10, 9861–9870 CrossRef CAS PubMed.
- M. Rycenga, X. Xia, C. H. Moran, F. Zhou, D. Qin, Z. Y. Li and Y. Xia, Angew. Chem., Int. Ed., 2011, 50, 5473–5477 CrossRef CAS PubMed.
- Y. H. Lee, C. K. Lee, B. Tan, J. M. Rui Tan, I. Y. Phang and X. Y. Ling, Nanoscale, 2013, 5, 6404–6412 RSC.
- P. H. Camargo, M. Rycenga, L. Au and Y. Xia, Angew. Chem., Int. Ed., 2009, 48, 2180–2184 CrossRef CAS PubMed.
- B. N. Khlebtsov, Z. Liu, J. Ye and N. G. Khlebtsov, J. Quant. Spectrosc. Radiat. Transfer, 2015, 167, 64–75 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr05767a |
| This journal is © The Royal Society of Chemistry 2018 |