A two-dimensional TiB4 monolayer exhibits planar octacoordinate Ti†
Abstract
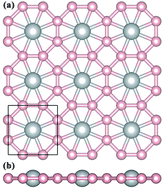
At present, the concept of planar hypercoordination in chemistry meets the fast development of two-dimensional (2D) nanomaterials, leading to considerable interest in searching for 2D materials with planar hypercoordinate atoms. In this work, by means of the swarm-intelligence structure search method and first-principles calculations, we predict a hitherto unknown 2D TiB4 monolayer with a planar octacoordinate Ti moiety, in which each Ti atom binds to eight B atoms with equal distances in a perfect plane, and has the highest coordination of Ti known for 2D materials thus far. Systematic ab initio calculations demonstrate the superior thermodynamic and dynamic stabilities of the predicted TiB4 monolayer, indicating the high feasibility for experimental synthesis. The stabilization of this perfect planar structure originates from the geometric fit between the atomic radius of Ti and the size of the 8-membered B ring, as well as the electron transfer from Ti to B atoms which compensates the electron deficiency of the full sp2 hybridized B network. Motivated by the unforeseen geometry of the TiB4 monolayer, a series of other 2D transition metal borides (TMB4, TM = V, Cr, Mo, W and Os) with quasi-planar octacoordinate TM atoms are further designed and discussed. The present work provides a useful roadmap for the discovery of 2D hypercoordinate materials.


 Please wait while we load your content...
Please wait while we load your content...