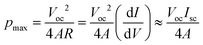DOI:
10.1039/C7NR04387B
(Paper)
Nanoscale, 2017,
9, 12068-12076
Thermal dependence of nanofluidic energy conversion by reverse electrodialysis†
Received
19th June 2017
, Accepted 21st July 2017
First published on 31st July 2017
Abstract
The thermal dependence of salinity-gradient-driven energy conversion by reverse electrodialysis using a mesoporous silica thin film with pores ca. 2–3 nm in diameter was studied in a temperature range of 293–333 K. As the temperature increases, the surface charge density of mesopores increases owing to an increase in the zeta potential of the pore walls, which in turn increases the concentration of counter-ions in the electrical double layer. The ion mobility also increases with increasing temperature owing to a decrease in the liquid viscosity. As a result, the temperature increase improves the ion conductance of mesopores both in the surface-charge-governed regime at low ion concentrations and in the bulk regime at high ion concentrations. However, further increases in temperature induce bubble nucleation. In particular, in highly concentrated salt solutions, hydrophobic patches appear on the pore surfaces because of the salting-out effect and mask the surface charge. The weakened polarity in mesopores allows more co-ions to enter them, decreasing the potential difference across the film, resulting in a serious deterioration of the energy conversion efficiency. The thermal dependence of the performance characteristics of mesoporous-silica-based nanofluidic devices was also evaluated.
Introduction
Functional nanostructured-material-based energy conversion systems can be exploited as reliable alternative energy sources for emerging miniaturized electrical devices.1–3 In particular, the nanofluidic-based power generator using concentration-gradient-driven ion-selective transport, which is also known as the reverse electrodialysis (RED) power generator (Fig. 1a), has recently attracted increasing attention and is intensively studied to improve its performance characteristics such as open-circuit voltage (Voc), short-circuit current (Isc), maximum power density (pmax), and maximum energy conversion efficiency (ηmax). To boost the device performance, the dimensions of the nanofluidic channels/pores4 and the thicknesses of the membranes5,6 have been optimized, the surface charge density has been tuned by pH variation of the working solutions,7 and ionic species with different diffusion coefficients8 have been employed. Furthermore, beyond the conventional 1D nanofluidic systems, a membrane-scale nanofluidic device with asymmetric structure, chemical composition, and surface charge polarity such as an ionic diode membrane (IDM) and 2D nanofluidic channels embedded in a layered graphene oxide membrane (GOM) has been reported.9,10
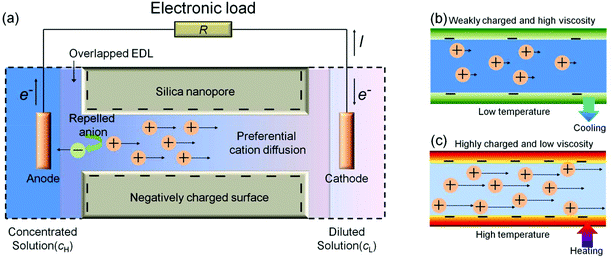 |
| | Fig. 1 Schematic diagrams of (a) preferential cation diffusion across a negatively charged silica mesopore between two reservoirs containing diluted and concentrated solutions, respectively. Cation transport characteristics at (b) low and (c) high temperatures. | |
However, the thermal effect has not yet been extensively studied. In silica–aqueous solution systems, a temperature increase can affect not only the equilibrium constants of the dissociation and protonation reactions of silanol groups, but also the dissociation constant of water, the ion diffusivity, and the liquid viscosity. All of these changes can affect the conductance of the nanofluidic channels/pores.11 As the temperature increases, the surface charge density of the silica mesopores increases,12–15 and thus the concentration of the counter-ions in the electrical double layer (EDL) increases. In addition, as the temperature increases, the liquid viscosity decreases and the ion diffusivity increases,16 and thus the ion mobility increases (Fig. 1b and c). The increases in the density and the mobility of counter-ions enhance the conductance of the nanofluidic channels/pores. However, further increases in temperature may induce bubble nucleation.17 In particular, in highly concentrated salt solutions, hydrophobic patches are formed on the pore surfaces by the salting-out effect and they mask the charged surface. The weakened polarity in mesopores may allow more co-ions to enter the mesopores, decreasing the potential difference across the film. The decreased potential difference can cause a serious deterioration in the performance of the nanofluidic-based-power generator. Increases in temperature may have both positive and negative effects on the energy conversion.
In this study, a mesoporous silica (MPS)-based nanofluidic device, which has uniaxially aligned mesopores ranging from 2 to 3 nm in size, was fabricated, and the thermal dependence of the salinity-gradient-driven energy conversion by RED across an MPS thin film was studied in a temperature range of 293–333 K.
Materials and experimental methods
Synthesis of MPS thin film
A highly ordered MPS thin film was synthesized on a Si substrate by the evaporation-induced-self-assembly method (EISA). A coating solution containing tetraethyl orthosilicate as a silica source and triblock copolymer Pluronic P123 as a structure-directing agent was deposited onto the Si substrate using the dip-coating method.18 The Si substrate used underwent sequential 10 min cleanings with n-hexane, acetone, and pure water in an ultrasonic bath. The substrates were then soaked in piranha solution for 30 min and rinsed with pure water to remove contaminants and make them wettable with a water/ethanol solution. They were then cleaned with 2-propanol for 1 h and dried in air. The precursor solution was prepared as follows: tetraethylorthosilicate (TEOS; 1.50 g) as the silica source, EtOH (15.0 g), pure water (0.78 g), and 0.1 M HCl (0.15 g) were stirred at room temperature for 1 h in a capped vial. Triblock copolymer Pluronic P123 (0.30 g), as the structure-directing agent, and EtOH (14.25 g) were stirred at room temperature for 1 h in a separate capped vial. After stirring, the two different solutions were mixed and then stirred at room temperature for 1 h. The final TEOS/P123/EtOH/H2O/0.1 M HCl molar ratio of the precursor solution was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0072
0.0072![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.2
88.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.17
7.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0021. The prepared precursor solution was then deposited on a Si substrate using the dip-coating method, as follows: the cleaned Si substrate was vertically immersed in the precursor solution, withdrawn at a rate of 3.0 mm s−1 and then aged for 24 h. The coating processes were performed at 298 K at a relative humidity (RH) of 60% inside a glove box. Subsequently, the as-prepared thin films were dried at 343 K for 1 h and calcined to remove the block copolymer surfactant at 773 K for 5 h in air at a very slow ramping rate (<0.5 K min−1) to minimize deformation caused by thermal stress.
0.0021. The prepared precursor solution was then deposited on a Si substrate using the dip-coating method, as follows: the cleaned Si substrate was vertically immersed in the precursor solution, withdrawn at a rate of 3.0 mm s−1 and then aged for 24 h. The coating processes were performed at 298 K at a relative humidity (RH) of 60% inside a glove box. Subsequently, the as-prepared thin films were dried at 343 K for 1 h and calcined to remove the block copolymer surfactant at 773 K for 5 h in air at a very slow ramping rate (<0.5 K min−1) to minimize deformation caused by thermal stress.
Measurement of ionic current at various temperatures
Before the ionic current was measured, the MPS thin film was degassed for 24 h at 0.05 MPa inside desiccators connected to a vacuum pump and two reservoirs were completely filled with different KCl aqueous solutions with a pH range of 5.6–5.8. Then a Ag/AgCl electrode produced by a chemical method using a sodium hypochlorite solution (NaClO) was inserted into each reservoir. An electric potential bias was applied between two electrodes, and the corresponding ionic current passing through the mesopores was measured using an electrochemical measurement system with the femtoammeter option (Modulab system, Solartron Analytical, UK) at different ion concentrations and different temperatures. The temperature of the MPS thin film was precisely controlled by a thermoelectric cooler consisting of a Peltier cooling unit (SLVPU-20T, VICS, Japan), a temperature sensor, a controller (VTH-2000, VICS, Japan), and a DC power supply. A Peltier element surrounded by Al plates was mounted on top of the Peltier cooling unit, and the MPS nanofluidic device was placed on the unit. Although the surface temperature of the Peltier element was precisely controlled, the temperature of the MPS nanofluidic device could be slightly different. Therefore, a type-K thermocouple was attached to the top surface of the MPS nanofluidic device, that is, the top surface of the SiO2 layer 100 nm above the MPS thin film, to measure the temperature of the MPS thin film precisely. Two more type-K thermocouples were additionally inserted into each reservoir to measure the temperature of the aqueous solution. All measurements were conducted in a shielding box (Faraday cage) to eliminate the influence of any external electromagnetic field.
Results and discussion
MPS-based nanofluidic device
Fig. 2a shows a scanning electron microscopy (S-4800, Hitachi High-Technologies, Japan) image of a cross-sectional area of the as-prepared MPS thin film. The MPS thin film has a pore diameter of ca. 2–3 nm and a thickness of ca. 55 nm. The mesopores are uniaxially aligned with two-dimensional pore arrays throughout the thin film. Fig. 2b shows a schematic illustration of the MPS-based nanofluidic device with the thermoelectric cooler to control the temperature of the MPS thin film. The fully packaged nanofluidic device for energy conversion studies was prepared by combining a rectangularly patterned MPS thin film obtained by photolithography with a microstructured poly(dimethylsiloxane) (PDMS) chip embossed by the replica micromolding method. Before the microstructured PDMS chip was bonded, a SiO2 layer ca. 100 nm in thickness was deposited using plasma chemical vapor deposition on the entire area, including the patterned MPS thin film, and then two reservoirs (1 mm in width × 2 mm in length × 1 μm in depth) were formed on both sides of the patterned MPS thin film. The distance between the two reservoirs was 100 μm, which is identical to the length of the mesopores. The details of the device fabrication process are reported in ref. 19.
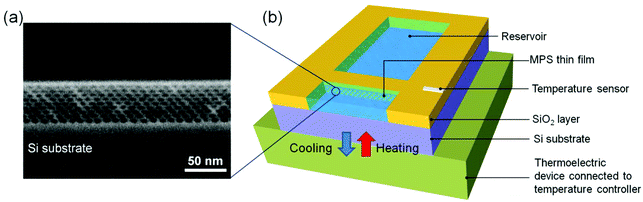 |
| | Fig. 2 (a) Cross-sectional scanning electron microscopy (SEM) image of the MPS thin film and (b) the schematic illustration of the MPS-based nanofluidic device with the thermoelectric cooler. The details of the device fabrication process are reported in ref. 19. | |
Temperature dependence of ionic conductance characteristics
To measure the ionic conductance passing through the MPS thin film, the mesopores were completely filled with KCl aqueous solutions in the ionic concentration range between 10−5 and 1 M and in a pH range of 5.6–5.8. Fig. 3 shows the measured ionic conductance versus aqueous solution concentration (G–c) curves in a temperature range of 283–323 K. The curves show the typical ionic conductance behavior of nanopores with respect to the ion concentration and a gradual increase in the ionic conductance with respect to the temperature in the entire ion concentration range. The ion selectivity of nanopores depends on the thickness of the EDL created at the interface between the solid wall and the aqueous solution. The thickness of the EDL can be characterized by the Debye screening length λD, which is given by| | 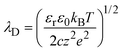 | (1) |
where εr is the dielectric constant of the solvent, ε0 is the permittivity of vacuum, kB is the Boltzmann constant, T is the absolute temperature, c is the concentration of the ionic solution, z is the valence of the ion, and e is the electron charge.20
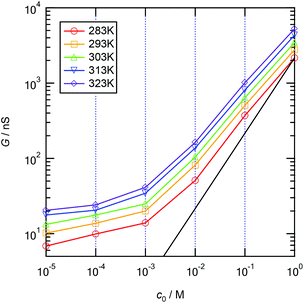 |
| | Fig. 3 Experimental ionic conductance vs. aqueous solution concentration (G–c) curves obtained in a temperature range of 283–323 K. A black solid line represents the bulk conductance at 283 K. | |
As shown in Fig. 3, the ionic conductance apparently deviates from the predicted line (black solid line) in the bulk state at 283 K in the concentration range from 10−5 M to 10−1 M KCl. This indicates that λD is larger than or equal to the diameter of the nanopores up to 10−1 M, and thus the conductance should be governed by the surface charge density up to 10−1 M. Note that the conductance also increases linearly with increasing temperature in the bulk regime between 10−1 and 1 M. An increase in the conductance in the bulk regime by pH modulation was never observed.21,22 An increase in the temperature leads not only to an increase in the surface charge density but also to an increase in the ionic mobility owing to the reduction in the liquid viscosity, as illustrated in Fig. 1c. The reduction in the liquid viscosity plays a crucial role in the enhancement of the ionic conductance, especially in the bulk regime at high concentrations.
The enhanced ionic conductance with increasing temperature can be theoretically modeled. Assuming a silica surface in contact with a 1 M KCl aqueous solution, the surface charge density σs was predicted as a function of the pH of the solution and the temperature according to the site-binding model23,24 (see S1 in the ESI†). Fig. 4a shows the analytically deduced σsversus pH curves for various temperatures. The calculated σs becomes increasingly negative with increasing temperature at a given pH value. This suggests that higher ionic conductance of the MPS thin films can be obtained at higher pH and higher temperature when the EDLs are overlapped (in the surface-charge-governed regime) owing to the requirement of electroneutrality.
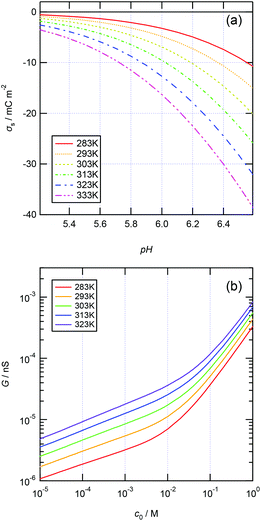 |
| | Fig. 4 (a) Analytically deduced surface charge density σsvs. pH at various temperatures and 1 M KCl. (b) Analytical ionic conductance vs. aqueous solution concentration (G–c) curves obtained in a temperature range of 283–323 K. The ionic conductance is calculated at pH = 5.6. | |
According to the analytical model presented by Schoch et al.21 and Smeets et al.,25 the ionic conductance of a single cylindrical pore, G, as a function of temperature T and bulk concentration c is given by
| | 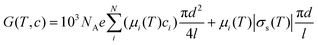 | (2) |
where
d and
l are the pore diameter and the pore length, and
μi(
T) and
σs(
T) are the ionic mobility and the surface charge density as a function of temperature, respectively. Here, the ion mobility can be expressed as a function of temperature:
16| | 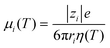 | (3) |
where
ri is the ion radius,
rK+ = 0.141 nm, and
rCl− = 0.141.
26 Furthermore,
η(
T) is the water viscosity as a function of temperature and is given by
27| | 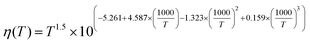 | (4) |
As the temperature increases, the viscosity decreases (eqn (4)), and the ionic mobility increases (eqn (3)); thus, the ionic conductance should increase (eqn (2)). This suggests that higher ionic conductance of the MPS thin films can be obtained at higher temperatures in both the surface-charge-governed and bulk regimes. Fig. 4b shows the ionic conductance versus aqueous solution concentration (G–c) curves calculated using the analytical model at pH = 5.6 in a temperature range of 283–323 K for a single cylindrical pore with d = 2.3 nm and l = 100 μm. The calculated G–c curves show the same characteristics as those measured with temperature variations.
Temperature dependence of energy conversion characteristics
In this nanofluidic device, electrical power can be created by applying an ion concentration gradient, that is, by filling two reservoirs with aqueous solutions at different concentrations. To evaluate the energy conversion characteristics of this device, the open-circuit voltage (Voc, i.e., V at I = 0), also known as the transmembrane or diffusional potential in biological cells; the short-circuit current (Isc, i.e., I at V = 0); the cationic transference number (t+); and the maximum power density (pmax) were systematically investigated under a series of concentration gradient combinations in a temperature range of 293–333 K. A diluted solution (cL) is fixed at 10−4 M, and a concentrated one (cH) is gradually elevated from 10−3 M to 1 M; that is, the concentration gradient changes by a factor of 104.
Fig. 5a and b show the current versus electric potential (I–V) curves obtained at cH = 10−3 and 1 M, respectively. I decreases linearly with increasing V at every temperature; thus, a linear approximation, that is, Ohm's law,4,19 can be used to evaluate the power generation characteristics of this device. In this study, V is obtained as the output voltage from a source meter, Vout, minus the potential difference between two reservoirs with different concentrations, Vredox; that is, V = Vout − Vredox. Vredox is measured experimentally as a function of temperature. The measured Vredox is compared to that calculated using the Nernst equation considering the Pitzer model to predict the temperature-dependent activity coefficient28–30 (see S2 and S3 in the ESI†). At a low concentration gradient, cH = 10−3 M, Isc increases continuously with increasing temperature because of the increased surface charge density and the reduced viscosity of the solution. Isc increases by a factor of ca. 4.5 when the temperature increases from 293 to 333 K (Isc = 0.25 nA at 293 K and 1.14 nA at 333 K). Voc increases with increasing temperature up to 303 K owing to the increase in the surface charge density, but as the temperature increases further, it decreases slightly. Voc decreases by ca. 5.9% when the temperature increases from 293 to 333 K (Voc = 42.7 mV at 293 K and 40.2 mV at 333 K). In contrast, at a high concentration gradient, cH = 1 M, as the temperature increases, Voc decreases more markedly than at cH = 10−3 M, and Isc also decreases above 333 K. Voc decreases by ca. 64% when the temperature increases from 293 to 333 K (Voc = 76.92 mV at 293 K and 28.06 mV at 333 K).
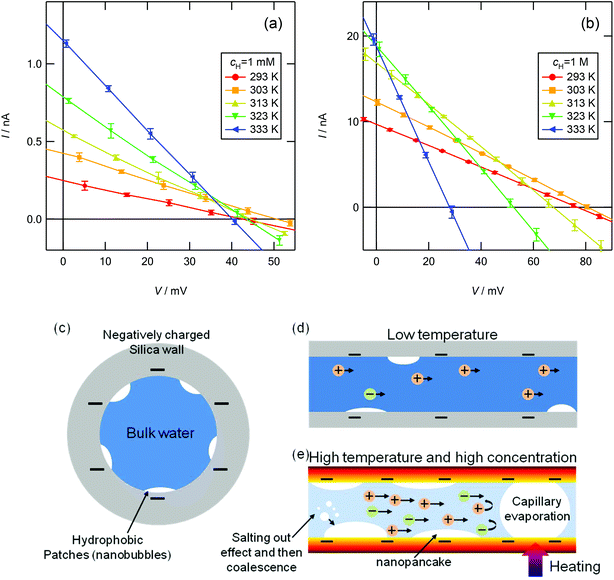 |
| | Fig. 5 Current vs. electric potential (I–V) curves for osmotic energy conversion at (a) cH = 10−3 M and (b) cH = 1 M in a temperature range of 293–333 K. The mean values of four different measurements are plotted in the I–V curves. The error bars represent the standard deviations. Schematic illustration of nanobubbles created around hydrophobic patches at the mesopore surface: cross-sectional views in the (c) radial and (d) axial directions of the cylindrical nanopore at a low temperature, and (e) growth mechanism of nanobubbles at high temperature and high ion concentration. | |
For the osmotic energy conversion system, the ionic current I passing through a mesopore and Voc are defined as follows:4
| | 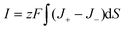 | (5) |
| | 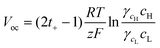 | (6) |
where
t+ is the transference number for the cation, which represents the ratio of the cation flux to the entire ion flux, that is,
t+ =
J+/(
J+ +
J–). Here,
J+ and
J– are the cation and anion flux, respectively. Note that
t+ = 1 and
t+ = 0 indicate ideal cation and anion selective nanopores, respectively.
R,
F, and
γ are the gas constant, the Faraday constant, and the activity coefficient, respectively. Note that
t+ = 1 and
t+ = 0 represent completely cation- and anion-selective mesopores, respectively, whereas
t+ ≈ 0.5 represents non-ion-selective mesopores when the diffusion coefficients of cations and anions are similar. If the surface charge density increases with increasing temperature,
t+ will increase owing to the enhancement of the repulsive force between the anions and the negative surface, and thus
Voc will also increase according to
eqn (6). However,
Fig. 5a and b show that the measured
Voc decreases with increasing temperature. This indicates that the surface charge density should decrease with increasing temperature.
One possible reason for the surface charge density decreasing with increasing temperature is bubble nucleation at the silica surface. The density of water confined in porous materials with pores less than ca. 4 nm in diameter is reportedly 11%–12% smaller than that of bulk water because hydrophobic patches (small cavities composed of gases several angstroms in thickness) are distributed on the pore surface, as shown in Fig. 5c and d.31–33 These small cavities may be negligible in microchannels/pores, but they are not negligible in extremely small pores. The solubility of gases in water decreases with increasing temperature; thus, a larger amount of gas is extracted from water with increasing temperature. In addition, the solubility of gases decreases with increasing ionic strength of the solutions, which is known as the salting-out effect;34 thus, a larger amount of gas is extracted from water with increasing ion concentration. The extracted gases could enlarge the size of the hydrophobic patches, especially the lateral size,35 and the charged surface could be gradually covered with nanopancake-like gas layers, or the nanopores could be occupied by nanobubbles, which is known as capillary evaporation (Fig. 5e; see S4 in the ESI†). As a result, more anions can enter the pores, and thus t+ decreases.
This hypothesis can be qualitatively supported by the analytical results of a two-dimensional nanopore-bridged system with two fluid reservoirs using the Poisson–Nernst–Planck equations and modified Stokes equation. The governing equations are as follows:36
| | 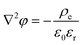 | (7) |
| | | 0 = −∇p + η∇2u − ρe∇φ | (10) |
where
φ,
u, and
p are the electrical potential, velocity vector of the fluids, and pressure, respectively. Here,
ρe is the net charge density and is expressed as
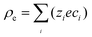
, where
ci,
zi, and
e are the concentration and valence of ion species
i and the electronic charge, respectively.
Ji is the flux of ion species
i and is expressed as
| | 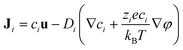 | (11) |
where
Di is the diffusion coefficient of ion species
i. The boundary conditions are given as follows:
| | 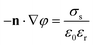 | (12) |
where
n denotes the unit outward normal vector. Furthermore,
σs is assumed to be negative for the pore walls and zero for the reservoir walls. In addition, the dielectric constant and the diffusion coefficient are given as a function of temperature:
37,38| | 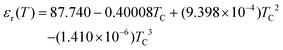 | (15) |
| | 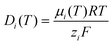 | (16) |
where
Tc is the temperature in degrees celsius, and the temperature-dependent
μi(
T) is given by
eqn (3). The current of each ion species can be calculated by integrating the ion flux density in a cross-sectional area of the mesopore and is given by
| | 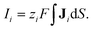 | (17) |
Here, we consider a cylindrical mesopore 2.3 nm in diameter and 100 nm in length bridging cylindrical fluid reservoirs 3.6 μm in diameter and 3.0 μm in length. Because the reservoir is large enough compared to the mesopores, the influence of the reservoir size on the ion flux passing through the mesopore is marginal. The concentration gradient between the two reservoirs is 104 fold because a 0.1 mM KCl solution is placed on one side of the nanopore, and a 1 M KCl solution is placed on the other side. Here, we tried to reproduce the measured I–V curves shown in Fig. 5b by tuning only the surface charge density 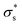 . The
. The 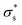 value at 293 K is assumed to be the same as the analytically deduced σs value at pH = 5.6 and 293 K as shown in Fig. 4a. The assumed values of
value at 293 K is assumed to be the same as the analytically deduced σs value at pH = 5.6 and 293 K as shown in Fig. 4a. The assumed values of 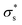 at 303, 313, 323, and 333 K are summarized in Table 1. The analytically deduced σs values at pH = 5.6 for various temperatures shown in Fig. 4a are also listed in Table 1. Fig. 6 shows the I–V curves calculated assuming
at 303, 313, 323, and 333 K are summarized in Table 1. The analytically deduced σs values at pH = 5.6 for various temperatures shown in Fig. 4a are also listed in Table 1. Fig. 6 shows the I–V curves calculated assuming 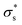 .
.
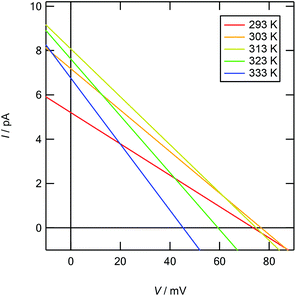 |
| | Fig. 6 Calculated current vs. electric potential (I–V) curves for osmotic energy conversion in a temperature range of 293–333 K. A cylindrical nanopore 2.3 nm in diameter and 100 nm in length bridges cylindrical liquid reservoirs. The reservoirs are filled with cL = 10−4 M and cH = 1 M KCl aqueous solutions, respectively. The surface charge density is given as a function of temperature, as shown in Table 1. | |
Table 1 Surface charge density used in the simulation
|
σ
s is the analytically deduced surface charge density at pH = 5.6 in Fig. 4a.
|
|
T [K] |
293 |
303 |
313 |
323 |
333 |
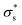 [mC m−2] [mC m−2] |
−2.04 |
−2.2 |
−1.8 |
−1.4 |
−0.6 |
|
σ
s [mC m−2]a |
−2.04 |
−3.0 |
−4.26 |
−5.87 |
−7.85 |
As the temperature increases to 303 K, Voc increases, after which it decreases significantly. Because the calculated Voc and given 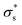 show similar trends with respect to the temperature, the calculated Voc is the direct result of the given
show similar trends with respect to the temperature, the calculated Voc is the direct result of the given 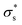 . In contrast, Isc increases gradually with increasing temperature up to 313 K and then decreases slightly. Because the mobility also increases with increasing temperature, the temperature dependence of Isc can be attributed to both the carrier density
. In contrast, Isc increases gradually with increasing temperature up to 313 K and then decreases slightly. Because the mobility also increases with increasing temperature, the temperature dependence of Isc can be attributed to both the carrier density 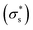 and the carrier mobility (μK+). The measured I–V curves can be reasonably interpreted if we assume that the effective surface charge density
and the carrier mobility (μK+). The measured I–V curves can be reasonably interpreted if we assume that the effective surface charge density 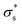 increases with increasing temperature up to ca. 303 K and then decreases as the temperature increases further.
increases with increasing temperature up to ca. 303 K and then decreases as the temperature increases further.
Fig. 7a–d show the power generation characteristics of the MPS-based nanofluidic device as a function of the logarithmic concentration ratio between the two reservoirs, log(cH/cL), at different temperatures.
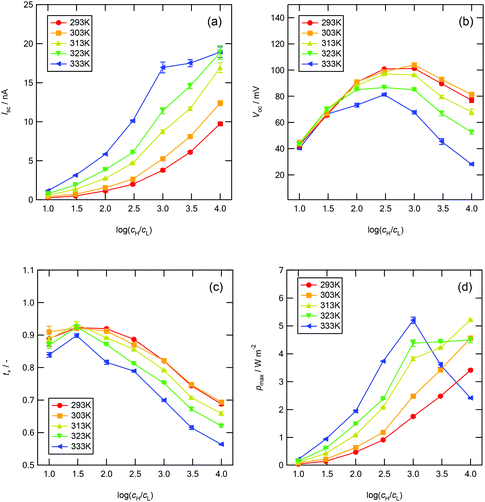 |
| | Fig. 7 Power generation characteristics with respect to log(cH/cL) at different temperatures between 293 and 333 K. (a) Short-circuit current Isc, (b) open-circuit voltage Voc, (c) cationic transference number t+, and (d) maximum power density pmax. | |
In Fig. 7a, Isc increases with increasing log(cH/cL) and temperature. In Fig. 7b, Voc increases with increasing log(cH/cL) up to log(cH/cL) = 2.5–3.0 and then decreases. At low concentration gradients [below log(cH/cL) = 1.5], Voc is independent of temperature, whereas at high concentration gradients, Voc decreases dramatically with increasing temperature. When the temperature is higher than 313 K, the decrease in Voc is especially prominent. In Fig. 7c, the t+ value calculated using eqn (6) decreases significantly as log(cH/cL) increases. Voc and t+ show similar trends with respect to log(cH/cL). The maximum energy conversion efficiency, ηmax, which can be defined as ηmax = (2t+ − 1)2/2, decreases greatly with increasing temperature at high concentration gradients. Here, ηmax is only defined by the ion-selectivity and the heating power factor of the system is not considered. The power analysis considering the heating power of the energy harvesting system is an important task that must be conducted for practical applications. In a real full-scale RED system, a heat exchanger to recover some of the heat transferred across the membrane–solution interface should be also included to improve the overall efficiency and thus thermal insulation plays an important role in evaluating the system efficiency, because the amount of the heating power required to maintain the temperature of the membrane depends on how fast the heat dissipates in the system. However, as the purpose of the current work is to study a fundamental mechanism of the ion-selectivity transport in extremely small nanopores (sub-3 nm) with temperature variations, the energy harvesting system used in this work is not a full-scale closed-loop system with the thermal insulation. For example, at log(cH/cL) = 4.0, ηmax decreases from 7.06% to 0.81% as the temperature increases from 293 to 333 K. Fig. 7d shows the calculated maximum power generation of this device. In the equivalent circuit model, the maximum power density pmax is defined as19
| | 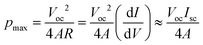 | (18) |
where
A is the cross-sectional area of the membrane (1 mm in width × 55 nm in thickness), and
R is the internal resistance of the nanopores. Because the resistance of the microfluidic channels is several orders of magnitude smaller than
R, it is negligible. Up to 323 K,
pmax increases monotonically with increasing log(
cH/
cL), whereas it decreases sharply above log(
cH/
cL) = 3.0, in particular at 333 K. This behavior can be attributed to the large decrease in
Voc despite the modest increase in
Isc from
eqn (18). This thermal dependence of the power generation characteristics could be the result of bubble nucleation at the silica surface. In this work, the maximum
pmax is 5.22 W m
−2 at 313 K, log(
cH/
cL) = 4 and the corresponding
ηmax is 5.05%. This performance would depend on the pore size-dependent ion-selectivity. Furthermore, the performance can be enhanced by increasing the wettability of the silica surface using a higher pH (<8.0) of the solution, because the increased wettability makes it difficult to produce bubbles by reducing the number of hydrophobic patches.
Conclusions
The temperature sensitivity of the energy conversion characteristics of a RED power generator using an MPS thin film with a pore diameter of 2–3 nm was investigated. The measured ionic current increases gradually with increasing temperature in the range of 283–323 K, and the corresponding ionic conductance increases with increasing temperature in the entire KCl concentration range of 10−5–1 M. The increase in the conductance with the increasing temperature can be attributed to the increased surface charge density and the decreased viscosity of the aqueous solutions.
Regarding the power generation characteristics, the measured short-circuit current Isc increases monotonically with increasing ion concentration gradient log(cH/cL) at all temperatures, but Isc does not increase as much at high temperature and high ion concentration. The measured open-circuit voltage Voc decreases with increasing temperature, especially at large log(cH/cL). These results suggest that the ionic current increases with increasing temperature owing to the increased carrier density and carrier mobility, but when the temperature and the ion concentration are very high, hydrophobic patches grow owing to the extraction of gases from the solution and mask the mesopore surface. The weakened polarity in the mesopores allows more co-ions to enter into them, decreasing the potential difference across the mesopores. As a result, the maximum power density of this MPS-based nanofluidic device pmax increases monotonically with increasing log(cH/cL) when the temperature is lower than 323 K, whereas it decreases sharply above log(cH/cL) = 3 when the temperature is higher than 323 K.
Acknowledgements
This work was supported by a Grant-in-Aid for Young Scientists (B), KAKENHI Grant Number JP16K18024 from the Japan Society for the Promotion of Science (JSPS).
Notes and references
- A. Siria, P. Poncharal, A. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455 CrossRef CAS PubMed.
- Z. L. Wang and J. Song, Science, 2006, 312, 242 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643 CrossRef CAS PubMed.
- D. K. Kim, C. Duan, Y. F. Chen and A. Majumdar, Microfluid. Nanofluid., 2010, 9, 1215 CrossRef CAS.
- L. Cao, F. Xiao, Y. Feng, W. Zhu, W. Geng and J. Yang, Adv. Funct. Mater., 2017, 27, 1604302 CrossRef.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197 CrossRef CAS PubMed.
- W. Guo, L. Cao, J. Xia, F. Q. Nie, M. Wen, J. Xue, Y. Song, D. Zhu, Y. Wang and L. Jiang, Adv. Funct. Mater., 2010, 20, 1339 CrossRef CAS.
- L. Cao, W. Guo, W. Ma, L. Wang, F. Xia, S. Wang, Y. Wang, L. Jiang and D. Zhu, Energy Environ. Sci., 2011, 4, 2259 CAS.
- J. Gao, W. Guo, D. Feng, H. Wang, D. Zhao and L. Jiang, J. Am. Chem. Soc., 2014, 136, 12265 CrossRef CAS PubMed.
- J. Ji, Q. Kang, Y. Zhou, Y. Feng, X. Chen, J. Yuan, W. Guo and L. Jiang, Adv. Funct. Mater., 2017, 27, 1603623 CrossRef.
- M. Taghipoor, A. Bertsch and P. Renaud, ACS Nano, 2015, 9, 4563 CrossRef CAS PubMed.
- P. M. Reppert and F. D. Morgan, J. Geophys. Res., 2003, 108, 2546 CrossRef.
- P. M. Reppert, J. Geophys. Res., 2003, 108, 2547 CrossRef.
- P. Somasundaran and R. D. Kulkarni, J. Colloid Interface Sci., 1973, 45, 591 CrossRef CAS.
- R. Ramachandran and P. Somasundaran, Colloids Surf., 1986, 21, 355 CrossRef CAS.
-
P. Atkins and J. B. De Paula, Atkins's Physical Chemistry, Oxford University Press, Oxford, 10th edn, 2014 Search PubMed.
- S. Jones, Adv. Colloid Interface Sci., 1999, 80, 27 CrossRef CAS.
- J. Hwang, N. Shoji, A. Endo and H. Daiguji, Langmuir, 2014, 30, 15550 CrossRef CAS PubMed.
- J. Hwang, S. Kataoka, A. Endo and H. Daiguji, Lab Chip, 2016, 16, 3824 RSC.
- R. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839 CrossRef CAS.
- R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86, 253111 CrossRef.
- D. Stein, M. Kruithof and C. Dekker, Phys. Rev. Lett., 2004, 93, 35901 CrossRef PubMed.
- D. E. Yates, S. Levine and T. W. Healy, J. Chem. Soc., Faraday Trans. 1, 1973, 70, 1807 RSC.
- A. Revil and P. W. J. Glover, Phys.
Rev. B: Condens. Matter, 1997, 55, 1757 CrossRef CAS.
- R. M. M. Smeets, U. F. Keyser, D. Krapf, M.-Y. Wu, N. H. Dekker and C. Dekker, Nano Lett., 2006, 6, 89 CrossRef CAS PubMed.
- Y. Marcus, J. Solution Chem., 1983, 12, 271 CrossRef CAS.
- P. M. Kampmeyer, J. Appl. Phys., 1952, 23, 99 CrossRef CAS.
- K. S. Pitzer, J. Phys. Chem., 1973, 77, 268 CrossRef CAS.
- K. S. Pitzer and G. Mayorga, J. Phys. Chem., 1973, 77, 2300 CrossRef CAS.
- L. F. Silvester and K. S. Pitzer, J. Phys. Chem., 1977, 81, 1822 CrossRef CAS.
- V. Kocherbitov and V. Alfredsson, J. Phys. Chem. C, 2007, 111, 12906 CAS.
- S. Jähnert, F. Vaca Chávez, G. E. Schaumann, A. Schreiber, M. Schönhoff and G. H. Findenegg, Phys. Chem. Chem. Phys., 2008, 10, 6039 RSC.
- P. J. Branton, P. G. Hall, M. Treguer and K. S. W. Sing, J. Chem. Soc., Faraday Trans., 1995, 91, 2041 RSC.
- Á. Pérez-Salado Kamps, E. Meyer, B. Rumpf and G. Maurer, J. Chem. Eng. Data, 2007, 52, 817 CrossRef.
- X. H. Zhang, G. Li, Z. H. Wu, X. D. Zhang and J. Hu, Chin. Phys., 2005, 14, 1774 CrossRef CAS.
- H. Daiguji, Chem. Soc. Rev., 2010, 39, 901 RSC.
- B. B. Owen, R. C. Miller, C. E. Milner and H. L. Cogan, J. Phys. Chem., 1961, 65, 2065 CrossRef CAS.
-
B. Hille, Ion channels of Excitable Membranes, Sinauer Associates Inc., Sunderland, MA, 3rd edn, 2001 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Theoretical model of surface charge density. Activity coefficient with respect to temperature. Redox potential with respect to temperature. Nonconductive state above the threshold temperature. See DOI: 10.1039/c7nr04387b |
|
| This journal is © The Royal Society of Chemistry 2017 |
 Open Access Article
Open Access Article *a,
Tatsuki
Sekimoto
a,
Wei-Lun
Hsu
*a,
Tatsuki
Sekimoto
a,
Wei-Lun
Hsu
 a,
Sho
Kataoka
a,
Sho
Kataoka
 b,
Akira
Endo
b and
Hirofumi
Daiguji
a
b,
Akira
Endo
b and
Hirofumi
Daiguji
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0072
0.0072![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.2
88.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.17
7.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0021. The prepared precursor solution was then deposited on a Si substrate using the dip-coating method, as follows: the cleaned Si substrate was vertically immersed in the precursor solution, withdrawn at a rate of 3.0 mm s−1 and then aged for 24 h. The coating processes were performed at 298 K at a relative humidity (RH) of 60% inside a glove box. Subsequently, the as-prepared thin films were dried at 343 K for 1 h and calcined to remove the block copolymer surfactant at 773 K for 5 h in air at a very slow ramping rate (<0.5 K min−1) to minimize deformation caused by thermal stress.
0.0021. The prepared precursor solution was then deposited on a Si substrate using the dip-coating method, as follows: the cleaned Si substrate was vertically immersed in the precursor solution, withdrawn at a rate of 3.0 mm s−1 and then aged for 24 h. The coating processes were performed at 298 K at a relative humidity (RH) of 60% inside a glove box. Subsequently, the as-prepared thin films were dried at 343 K for 1 h and calcined to remove the block copolymer surfactant at 773 K for 5 h in air at a very slow ramping rate (<0.5 K min−1) to minimize deformation caused by thermal stress.

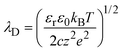

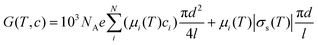
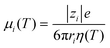
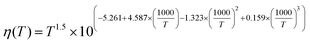
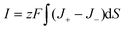
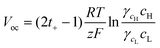
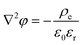
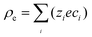 , where ci, zi, and e are the concentration and valence of ion species i and the electronic charge, respectively. Ji is the flux of ion species i and is expressed as
, where ci, zi, and e are the concentration and valence of ion species i and the electronic charge, respectively. Ji is the flux of ion species i and is expressed as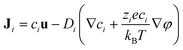
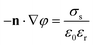
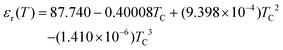
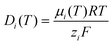
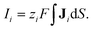
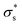 . The
. The 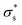 value at 293 K is assumed to be the same as the analytically deduced σs value at pH = 5.6 and 293 K as shown in Fig. 4a. The assumed values of
value at 293 K is assumed to be the same as the analytically deduced σs value at pH = 5.6 and 293 K as shown in Fig. 4a. The assumed values of 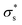 at 303, 313, 323, and 333 K are summarized in Table 1. The analytically deduced σs values at pH = 5.6 for various temperatures shown in Fig. 4a are also listed in Table 1. Fig. 6 shows the I–V curves calculated assuming
at 303, 313, 323, and 333 K are summarized in Table 1. The analytically deduced σs values at pH = 5.6 for various temperatures shown in Fig. 4a are also listed in Table 1. Fig. 6 shows the I–V curves calculated assuming 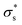 .
.
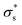 show similar trends with respect to the temperature, the calculated Voc is the direct result of the given
show similar trends with respect to the temperature, the calculated Voc is the direct result of the given 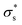 . In contrast, Isc increases gradually with increasing temperature up to 313 K and then decreases slightly. Because the mobility also increases with increasing temperature, the temperature dependence of Isc can be attributed to both the carrier density
. In contrast, Isc increases gradually with increasing temperature up to 313 K and then decreases slightly. Because the mobility also increases with increasing temperature, the temperature dependence of Isc can be attributed to both the carrier density 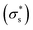 and the carrier mobility (μK+). The measured I–V curves can be reasonably interpreted if we assume that the effective surface charge density
and the carrier mobility (μK+). The measured I–V curves can be reasonably interpreted if we assume that the effective surface charge density 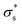 increases with increasing temperature up to ca. 303 K and then decreases as the temperature increases further.
increases with increasing temperature up to ca. 303 K and then decreases as the temperature increases further.