Full-spectrum volumetric solar thermal conversion via photonic nanofluids
Abstract
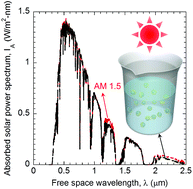
Volumetric solar thermal conversion is an emerging technique for a plethora of applications such as solar thermal power generation, desalination, and solar water splitting. However, achieving broadband solar thermal absorption via dilute nanofluids is still a daunting challenge. In this work, full-spectrum volumetric solar thermal conversion is demonstrated over a thin layer of the proposed ‘photonic nanofluids’. The underlying mechanism is found to be the photonic superposition of core resonances, shell plasmons, and core–shell resonances at different wavelengths, whose coexistence is enabled by the broken symmetry of specially designed composite nanoparticles, i.e., Janus nanoparticles. The solar thermal conversion efficiency can be improved by 10.8% compared with core–shell nanofluids. The extinction coefficient of Janus dimers with various configurations is also investigated to unveil the effects of particle couplings. This work provides the possibility to achieve full-spectrum volumetric solar thermal conversion, and may have potential applications in efficient solar energy harvesting and utilization.

 Please wait while we load your content...
Please wait while we load your content...