Size dependent structural and polymorphic transitions in ZnO: from nanocluster to bulk

Abstract

We report on an extensive survey of (ZnO)_N nanostructures ranging from bottom-up generated nanoclusters to top-down nanoparticles cuts from bulk polymorphs. The obtained results enable us to follow the energetic preferences of structure and polymorphism in (ZnO)_N systems with N varying between 10–1026. This size range encompasses small nanoclusters with 10s of atoms and nanoparticles with 100s of atoms, which we also compare with appropriate bulk limits. In all cases the nanostructures and bulk systems are optimized using accurate all-electron, relativistic density functional theory based calculations with numeric atom centered orbital basis sets. Specifically, sets of five families of (ZnO)_N species are considered: single-layered and multi-layered nanocages, and bulk cut nanoparticles from the sodalite (SOD), body centered tetragonal (BCT), and wurtzite (WZ) ZnO polymorphs. Using suitable fits to interpolate and extrapolate these data allows us to assess the size-dependent energetic stabilities of each family. With increasing size our results indicate a progressive change in energetic stability from single-layered to multi-layered cage-like nanoclusters. For nanoparticles of around 2.6 nm diameter we identify a transitional region where multi-layered cages, SOD, and BCT nanostructures are very similar in energetic stability. This transition size also marks the size regime at which bottom-up nanoclusters give way to top-down bulk-cut nanoparticles. Eventually, a final crossover is found where the most stable WZ-ZnO polymorph begins to energetically dominate at N ∼ 2200. This size corresponds to an approximate nanoparticle diameter of 4.7 nm, in line with experiments reporting the observation of wurtzite crystallinity in isolated ligand-free ZnO nanoparticles of 4–5 nm size or larger.

---

Introduction

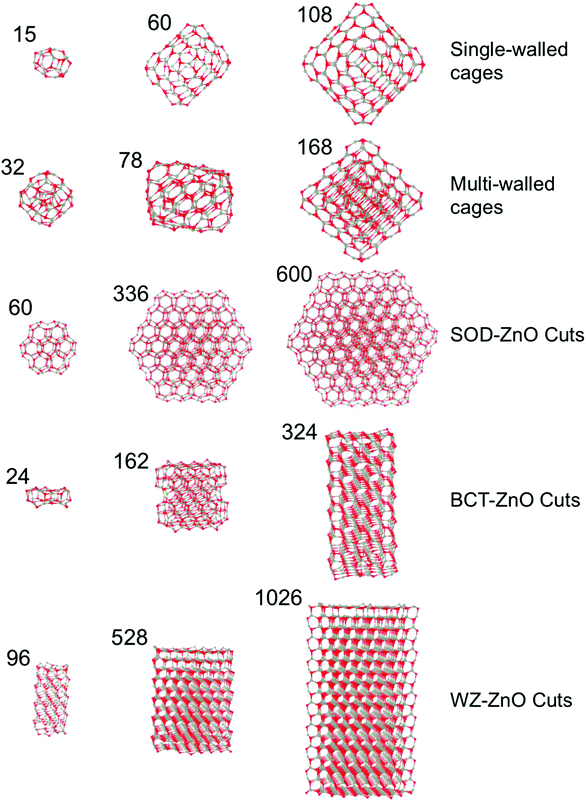
Zinc oxide (ZnO) has attracted much attention from both theoretical and experimental researchers largely due to its huge technological potential in fields such as optoelectronics and photocatalysis.^1,2 Although in such applications ZnO is very often used as a nanosized or nanostructured material, the underlying atomic ordering is almost always that of a stable bulk crystal polymorph; either wurtzite (WZ-ZnO) or zinc blende.^3,4 In this sense, the majority of experimentally fabricated nanoscale ZnO structures can be thought of as top-down (i.e. reduced size bulk-like) systems. Conversely, many theoretical studies and a few experimental studies of nano-ZnO start from monomeric ZnO or nano-ZnO “building blocks”, and investigate how the structures and properties of the growing nano-system vary in a bottom-up manner upon the progressive addition of the respective sub-units. Deposition of ZnO monomers on weakly interacting surfaces, for example, is theoretically predicted to lead to the growth of graphene-like nanoclusters (i.e. two-dimensional sheets formed mainly by tessellated Zn₃O₃ hexagonal rings).⁵ Other calculations have further indicated that very thin unsupported infinite films of ZnO energetically prefer to form a new non-bulk-like polymorph (layered-ZnO) formed of graphene-like layers.⁶ With increasing film thickness other polymorphs (such as the Body Centered Tetragonal phase – BCT-ZnO) are predicted to energetically compete with, and become more stable than, this layered phase, until eventually the bulk WZ-ZnO phase becomes most stable.^7,8 Particular top-down cuts of the WZ-ZnO crystal to form nanoparticles (NPs) and nanowires with high aspect ratios (e.g. long thin nanowires or flat wide NPs) are likewise predicted to be unstable to layer formation.^9,10 The thickness dependent transition between layered-ZnO and bulk-like ZnO thin films has been confirmed by detailed bottom-up surface science experiments studying the growth of ZnO on metal surfaces.^11,12

Bottom-up theoretical investigations of isolated low energy ZnO nanoclusters have also revealed the propensity of nanoscale ZnO to form graphene-like layers. Specifically, many studies report calculations confirming that the most stable structure of (ZnO)_N nanoclusters in the approximate size range 8 ≤ N ≤ 28 is cage-like.^13–21 These clusters can be considered to be formed from finite graphene-like sheets which also contain four-membered Zn₂O₂ rings to facilitate the necessary curvature to form closed single-layered cages. The preference for (ZnO)_N nanoclusters for 8 ≤ N ≤ 23 to exhibit cage-like isomers has further been confirmed by collaborative experimental–theoretical cluster beam studies.²² (ZnO)_N nanoclusters for 28 < N ≤ 108 are predicted to energetically favor either: (i) single-layered cages, or (ii) cages encapsulating smaller nanoclusters. Especially for the larger nanoclusters in this size range, where the interior nanocluster is itself a smaller cage, these species can be viewed as double-layered cages. Double-layered cages were first theoretically proposed as low energy cluster isomers for ZnS.^23,24 Cluster beam experiments finding anomalously high abundances of (ZnO)_N clusters with N = 34, 60, and 78 were also initially taken to be evidence of double-layered cages.²⁵ Although the most stable isomer of (ZnO)₃₄ does not appear to be a double-layered cage,²⁶ the 12@48 (ref. 16, 21, 27 and 28) and 18@60 (ref. 21) isomers—where we use the notation X@Y to indicate a (ZnO)_X+Y cluster constituted by a (ZnO)_X cage encapsulated within a (ZnO)_Y cage—have been shown to be very low energy cluster isomers. It is found that symmetry plays an important role in the stability of single- and double-layered cages. For example, the single-layered (ZnO)_N octahedral cages for N = 12, 48, 108 (T_h symmetry), N = 16, 36, 64, 100 (T_d symmetry), and N = 28 (T symmetry) are all candidate global minima.²¹ Similarly, double-layered cages which use these cages and maintain octahedral symmetry (e.g. N = 32 (4@28), 60 (12@48), 80 (16@64)) are also found to be very stable.²¹ The particularly high energetic stability of these symmetric species has led to them being proposed as building blocks for cluster-assembled ZnO bulk polymorphs.^28–32 Of such materials, sodalite (SOD-ZnO) based on the union of single-layered octahedral (ZnO)₁₂ cages is found to be particularly stable (only 0.15 eV per ZnO higher in energy than wurtzite).²⁹ Based on this stability, symmetric finite assemblies of (ZnO)₁₂ cages following the stacking pattern in SOD-ZnO, have also been proposed as alternative global minima structures for (ZnO)_N sizes N = 60, 78, 96.²⁷ For (ZnO)_N nanoclusters in the size range 108 < N ≤ 168 only double-layer and triple-layer cages have thus far been proposed as potential global minima. We note that the global minimum for the (ZnO)₁₆₈ nanocluster has been proposed to be a triple-layer 12@48@108 cage based on three octahedral nanoclusters.²¹

There have been few attempts to extrapolate from this non-bulk-like nanocluster size regime to WZ-ZnO bulk phase in order to estimate the cluster-to-bulk transition size. Based on comparing the energetic stabilities per ZnO unit of single-layered cages with respect to bulk-like clusters cut from the WZ-ZnO crystal, the cage-to-WZ-ZnO crossover size has been reported by Zhao et al. to be >26 units, and by Woodley et al. to be between 75 (ref. 33)–120 (ref. 34) ZnO units. As is noted in these studies, these estimates are rather approximate due the fact that that the cluster-to-bulk crossover will not actually be directly from single-layered cages to WZ-ZnO. Using the most extensive set of cage-like clusters thus far reported,²¹ extrapolating the cohesive energies per unit of the single-layered cages to infinite size results in a limiting “bulk” cohesive energy that is much lower than that of bulk WZ-ZnO.²¹ This clearly indicates that other more stable species are involved in filling the energy gap between single-layered cages and WZ-ZnO with increasing cluster size. From the discussion above, we know that, with increasing size, the stability of single-layered cages will be first superseded by multi-layered cages, and then perhaps by other cluster types at intermediate sizes, before bulk-like WZ-ZnO clusters become the most stable form of ZnO. Taking the energies of double- and triple-layered cages also into account when extrapolating to infinite size leads to a limiting “bulk” cohesive energy which is closer to, but still significantly lower than, that of WZ-ZnO.²¹ Even by selecting the few most stable “magic” clusters, containing a small set of single-, double-, and triple-layered cages, the extrapolated cohesive energy limit is still 0.187 eV per ZnO above of that of bulk WZ-ZnO.²¹ Tens of metastable bulk polymorphs have been calculated to lie in the energy range <0.19 eV per ZnO relative to WZ-ZnO.^8,29,35,36 The BCT-ZnO and SOD-ZnO low density polymorphs are of particular interest in this respect as they are both particularly low in energy with respect to their density³⁶ and have thus been studied with respect to being possible targets for stabilization under negative pressure conditions.^37–39 This strongly suggests that nanoclusters based on cuts from such phases will be become energetically competitive with layered cages with increasing nanocluster size, and may provide natural smooth crossover phases from cluster-to-bulk.

In this study we accurately evaluate the energetic stabilities of (ZnO)_N nanoclusters with N = 10–1026 using all electron, relativistic, density functional theory (DFT) based calculations. In this unprecedented size range, in addition to considering bottom-up generated single-, double, and triple-layered cages, we also take top-down cuts from three bulk polymorphs: SOD-ZnO, BCT-ZnO, and WZ-ZnO. By tracking the energetic stability of these species with size we are able to follow the gradual transition from non-bulk-like cage nanoclusters through metastable polymorphic cuts and eventually to bulk WZ-ZnO.

Methodology

All reported nanoclusters and nanoparticles were fully optimized with no symmetry contraints employing all electron, relativistic, density functional theory (DFT) based calculations using the FHI-AIMS code.⁴⁰ The electronic density was expanded using a “light-tier-1” basis of numerical atom-centered orbitals (NAO), approximately providing results of a similar or higher quality to those obtained with valence triple-zeta plus polarization Gaussian type orbitals.⁴¹ In the case of ZnO, recent work has established that the quality of this NAO basis set is even higher than that of the aug-cc-pVDZ,⁴² in line with systematic studies of these NAO basis sets.⁴³ The Perdew–Burke–Ernzerhof (PBE)⁴⁴ Generalized Gradient Approximation (GGA) functional was used throughout. Previous studies have confirmed the reliability of GGA functional respect to experimental data for structural, mechanical and energetic properties of ZnO in both bulk^42,45,46 and nanofilms.^8,12 GGA functionals have also been extensively confirmed in their treatment of structure and relative energetics of a wide range ZnO clusters¹⁷ and low density ZnO polymorphs.³⁵ In all calculations, scalar-relativistic effects were taken into account using the zero order regular approximation (ZORA).^47,48

Herein, we focus on five families of (ZnO)_N nanostructures of both a bottom-up type: (1) single-layered cages, and (2) multi-layered cages; and those derived from top-down cuts from the respective bulk polymorph: (3) SOD-ZnO, (4) BCT-ZnO, and (5) WZ-ZnO – see Fig. 1. We found that the structures of low energy single-layered (ZnO)_N cages for sizes N ≤ 60 could be derived using basin hopping global optimization approach⁴⁹ together with an interatomic potential parameterized for MgO but with ionic charges chosen to bias the energy landscape towards cages.^29,50 For larger single-layered and multi-layered nanoparticles we employed low energy (ZnO)_N structures from previous works.^21,28 For the (ZnO)_N nanoparticles of SOD-ZnO, we employed a previously reported stable bulk-cut with size N = 60 (ref. 27) and further made seven new larger cuts with N = 162–600. All these latter SOD-ZnO bulk-cuts were created maintaining the low energy symmetric (ZnO)₆₀ nanocluster as a core. For both BCT-ZnO and WZ-ZnO we used the Wulff construction to obtain initial geometries for the bulk cuts. Due to the similar hexagonal structure of WZ-ZnO and BCT-ZnO in both cases, the surface stability ordering of WZ-ZnO was employed to build up the Wulff-derived nanoparticles.⁵¹ We note that the (0001) polar facets of the WZ-ZnO nanoparticles formally induce a finite dipole over the nanoparticle. Calculations were thus carried out with both reconstructed (i.e. with facet ion vacancies to compensate the dipole) and clean facets. Both pristine and reconstructed polar facets were considered for the WZ-ZnO nanoparticles, as the energy differences between these two scenarios were minor. For BCT-ZnO, (ZnO)_N nanoparticles with up to N = 324 were created. We note that for (ZnS)_N nanoparticles of a similar size, bottom-up computational studies have predicted the emergence of the BCT structure.²⁴ For WZ-ZnO, the known most stable ZnO polymorph with increasing size, we extended our nanoparticle size range to N = 1026. A selection of (ZnO)_N nanoclusters from each of these five families can found in Fig. 1.

Fig. 1 Examples of different sized (ZnO)_N species from each of the five families of nanostructures considered, where the numbers relate to the number of ZnO units in the corresponding nanostructure. Grey and red spheres denote Zn and O atoms, respectively.

Results and discussion

Properties of nanoclusters evolve as a function of size. Following the spherical cluster approximation,⁵² where internal degrees of freedom of the cluster are ignored, one can show that the surface area to “bulk” ratio of a cluster is proportional to N^−1/3. It is found that many generic properties, G(N), of simple closed-packed clusters (e.g. total energies, ionisation energies, melting temperatures) can be approximately fitted by a scaling law of the following type:⁵¹

G(N) = G_bulk + a₁N^−1/3, (1)

where G_bulk is a characteristic constant value of the property in question for the corresponding bulk phase of the cluster. Taking into account that real clusters are comprised of bonded aggregates of atoms/ions, higher order terms (i.e. a₂(N^−1/3)², a₃(N^−1/3)³ …) can become more significant contributions to G(N).⁵³ For the case when G(N) is the total (free) energy of the cluster, for example, the second order term can be largely ascribed to compressive effects due to surface stress.^54,55

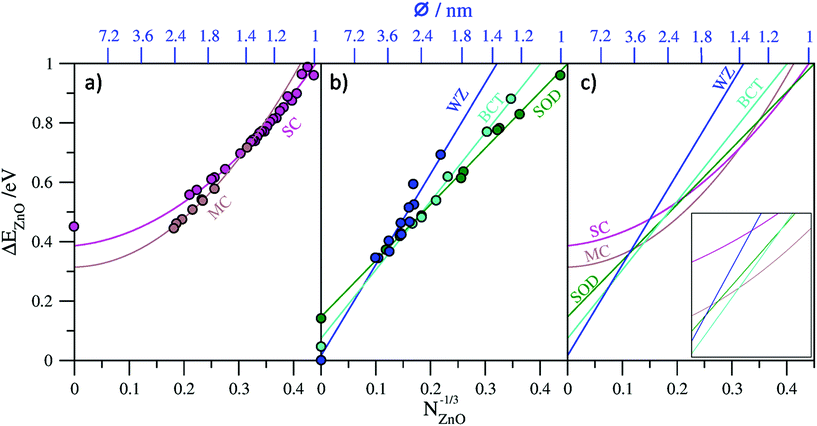
In Fig. 2a and b we plot our calculated total energies of a range of (ZnO)_N nanoclusters with respect to N^−1/3 together with lines fitted to the data. In all cases we use the energy per ZnO unit (eV per ZnO) with respect to the calculated total energy per unit of bulk WZ-ZnO as, obviously, obtained from the same computational setup as indicated below. For the top-down bulk-cut nanoclusters we found that a first order linear fit to the data could be made with corresponding coefficients of determination (R²) of 0.996 for SOD-ZnO, 0.993 for BCT-ZnO, and 0.918 for WZ-ZnO. As a further check we compared the energy corresponding to the extrapolated bulk limit of each fit (i.e. for N^−1/3 → 0) with the explicitly calculated energy of the respective bulk phase from a periodic calculation using exactly the same level of theory and code as used for the nanoclusters. The comparison between the extrapolated bulk energies and the explicitly calculated bulk energies (see Table 1) shows a very good match, with the differences between these two values being <0.03 eV per ZnO in all cases. We note that although the high R² values tend to indicate that these linear fits are formally “good”, as shown in Table 1, second order fits also give very similar R² values but can also give significantly different limiting energies. For WZ-ZnO and BCT-ZnO, for example, the bulk limiting energies from extrapolated second order fits are >0.125 eV per ZnO higher than the respective explicitly calculated bulk energies. This clearly shows that these fits are not trustworthy as guides to the trends in energetic stability for increasingly larger nanoclusters. For SOD-ZnO we find that both first and second order fits to the nanocluster data give exactly the same R² values and respectively extrapolate to slightly above (+0.017 eV per ZnO) and slightly below (−0.005 eV per ZnO) the explicitly calculated bulk energy of SOD-ZnO. Although either fit is physically acceptable, examining the second order fitting equation reveals that it is dominated by the linear first order term. Importantly, this implies that both fit lines are negligibly different over the size range where SOD-ZnO nanoclusters could be energetically competitive with the lowest energy nanoclusters, and thus does not affect our results.

Fig. 2 Plots of calculated relative energies of nanoclusters/nanoparticles and bulk phases with respect to N^−1/3 (lower x-axes) and approximate diameter (upper x-axes, see main text for details): (a) data for single-layered cages (SC) and multi-layered cages (MC) with corresponding second order fit lines and the calculated energy of an infinite single layer, (b) data for bulk-cut nanoparticles of SOD-ZnO (SOD), BCT-ZnO (BCT), and WZ-ZnO (WZ) phases with corresponding first order fit lines and the calculated energies of the respective bulk phases, (c) collated plot of fit lines for all five families of nanocluster considered.

Table 1 Limiting bulk energies per ZnO unit from extrapolated fits to the calculated size versus energy data are reported for first order fits (column 2) and second order fits (column 3). Note: all energies are given with respect to that for bulk WZ-ZnO. The R² values for each corresponding fit are given in parentheses. Relative energies for explicit calculations of bulk phases are reported in column 4. The differences in energy between the extrapolated values and the explicit bulk calculations are reported in column 5 with respect to the first and second order fits, respectively

Nanocluster type	Bulk limiting energy from extrapolated first order fit (eV per ZnO)	Bulk limiting energy from extrapolated second order fit (eV per ZnO)	Explicit calculation of bulk energy (eV per ZnO)	Energy differences (eV per ZnO)
WZ-ZnO cuts	0.016 (0.918)	0.155 (0.925)	0.00	+0.016/+0.155
BCT-ZnO cuts	0.074 (0.993)	0.174 (0.995)	0.046	−0.028/+0.128
SOD-ZnO cuts	0.146 (0.996)	0.124 (0.996)	0.129	+0.017/−0.005
Multi-walled cages	0.085 (0.992)	0.314 (0.999)	—	—/—
Single-walled cages	0.113 (0.979)	0.386 (0.987)	0.465	−0.352/−0.079

---

For the bottom-up generated single- and multi-layered nanoclusters, linear fits to the respective data also resulted in high R² values (see Table 1). In the case of the single-layered cages we can also take the infinite “bulk” limit to correspond to a flat, infinite in two dimensions, single layer of ZnO. Comparing the explicitly calculated energy of this layer with that obtained from the extrapolated limit of the linear fit results in a large mismatch (−0.352 eV per ZnO), showing that a linear fit is physically inappropriate. Conversely, a second order fit to the single-layered nanocluster energy data gives a very slightly improved R² value, but, more significantly, has an extrapolated infinite limiting energy that is relatively close (+0.079 eV per ZnO) to the calculated energy of a single ZnO layer. Considering that single-layered cages are, in a sense, only made from bonded networks of surface atoms, it is perhaps not surprising that higher order terms related to the surface stress contributions to the total energy are required for a physically improved fit.

For the multi-layered cages, unlike in the case of the single-layered cages, size increase does not imply a corresponding overall layer flattening, as, with growth, one retains more and more closed inner layers of ZnO, all concentric around a single point. As such, a limiting infinite onion-like cage is not amenable to calculation via periodic DFT calculations and we cannot provide an explicit calculation of the bulk limit in order to guide the physical appropriateness of our fit to the data. First and second order fits to the multi-layered cage data both give high R² values but yield very different extrapolated bulk limiting energies of 0.085 eV per ZnO and 0.314 eV per ZnO respectively with respect to WZ-ZnO. Double- and triple-layered cages are clearly energetically preferred over single-layered cages for the largest cage-like nanoclusters sizes we consider, which is understandable due to the attractive interlayer interactions between concentric cages. This strongly implies that the infinite bulk limit of multi-layered cages should be lower in energy than a single infinite layer; a constraint that is satisfied by both fits. We also note that the limiting infinite extrapolations of both fits also yield energies lower than that from the corresponding limit of the second order fit to the single-layer cage data (see Fig. 2a). The set of multi-layered cages we employ only contains a limited number of double- and triple-layered cages and thus does not sample cages with higher numbers of layers. Infinite limiting extrapolations to only these sub-classes of multi-layered cages is complicated by the fact that free-standing bilayers and trilayers of ZnO tend to relax to very weakly interacting planar layers^6,56 which do not capture the stronger distortion-inducing interactions between the layers in multi-layered cages.²⁸ However, a bulk ZnO polymorph with strongly interacting planar hexagonal layers, known as the 5–5 (ref. 57) or hexagonal^29,37 phase, hereafter referred to as hex-ZnO, has been shown computationally to be stable. The hex-ZnO phase can be thought of as a limit to which the outer layers of multi-layered particle approach with increasing size. Clearly, however, any such particle will always retain its growing concentric core of closed layers and thus will always be higher in energy than a perfect stacking of interacting planar layers as in hex-ZnO. Consistent with previous reports^8,29 herein we calculate the (bulk) hex-ZnO polymorph to be metastable with respect to WZ-ZnO by 0.14 eV per ZnO, which we thus take as a lower bound for the limiting energy for multi-layered cages. Following the above, the extrapolated infinite limiting energy of any fit to the data for multi-layered ZnO cages should ideally lay between 0.14–0.465 eV per ZnO. As the second order fit is most consistent with this criterion, we consider this fit in the remainder. We note that the set of multi-layered cages, although classed as a single family herein, is unlike the other families considered as it really corresponds to a range of cages of with different shapes and numbers of layers. As such, a higher order fit may be better able to account for this variability (e.g. as used to track the energetics of (TiO₂)_N nanoclusters³⁵) and yield an even more physically realistic extrapolated value. However, without more criteria to use as a guide, we use the second order fit.

In Fig. 2c we collate all fit lines for the five considered families of nanoclusters in order to provide an approximate guide to the evolution of nanocluster structure/polymorph and energetic stability with respect to size. We note that the nanocluster diameters with respect to N^−1/3 on the upper x-axes in Fig. 2a–c are approximate values which take the diameter of a sphere of N units of ZnO, where the volume occupied by a ZnO unit is taken to be that in bulk WZ-ZnO. Although only providing an approximate estimate of size, this measure is used as it is generally applicable to all nanocluster families. We note also that this approximation is clearly most accurate for the case of spherical WZ-ZnO nanoparticles. For the very smallest nanocluster sizes in the range 12 ≤ N ≤ 14 the fit line with the lowest energy appears to imply that the SOD-ZnO polymorphic phase is most stable. This, however, is rather misleading as it really is just a result of the high energetic stability of the N = 12 single-walled sodalite cage which was used in the fit for SOD-ZnO. For N ≥ 15 the fit line corresponding to the single-layered cages is found to persistently be the lowest in energy up to N = 37, where we find a stability crossover to multi-layered cages. We note that this crossover size corresponds quite well with the size of the first double-layered cage global minimum for N = 32 (i.e. 4@28). The fit lines predict that multi-layered cage nanoclusters are the most stable type of nanocluster up to a crossover to BCT-ZnO occurring at N = 364, where the nanocluster diameter is approximately 2.6 nm. In this sense the crossover represents a transition from aperiodic bottom-up nanoclusters to top-down bulk cuts from periodic crystal polymorphs. Interestingly, at this nanocluster size, the fit line for SOD-ZnO nanoclusters comes within 0.014 eV per ZnO of the point of crossover (see inset to Fig. 2c) indicating that SOD-ZnO nanoclusters are energetically competitive around this size. Due to the uncertainty involved in the fits, it could well be that SOD-ZnO nanoclusters in this size regime are the most energetically stable species, or at least potentially realizable metastable species. Previous work has indeed suggested that SOD-ZnO nanoclusters could become more stable that other types of clusters for specific sizes for N < 100.²⁷ For nanoparticle diameters in the approximate range 2.6–4.7 nm those based on cuts from the BCT-ZnO polymorph are predicted to be the most energetically stable. As noted above, the emergence of the BCT phase has also been predicted to occur in bottom-up modelling studies of ZnO nanofilms^7,8 and in moderately sized (ZnS)_N nanoparticles up to ∼4 nm diameter.²⁴ Experimentally, a reversible phase transition between the BCT-ZnO lattice and WZ-ZnO could be activated in ZnO(101̄0) surfaces,⁵⁸ further confirming the small energy difference between the two phases. Finally, our fits predict nanoparticles based on cuts from the bulk WZ-ZnO polymorph to be most energetically favored for nanoclusters with N > 2200 corresponding to nanoclusters with approximate diameters >4.7 nm. We note that the smallest isolated ligand-free ZnO nanoparticles reported to exhibit the wurtzite crystallographic structure are of typically 4–5 nm diameter,^59,60 consistent with our prediction.

Although our study is not exhaustive with respect to the nanostructure types considered, our selection is based on the most probable low energy structures and polymorphic phases likely to be encountered for nanoscale ZnO based on the current literature. Likewise, although our fits are necessarily based on sets of data points which are limited by current knowledge and computational constraints, our calculations represent the most comprehensively broad collection of DFT-optimised ZnO nanoclusters and nanoparticles yet reported. Moreover, considering that our collection includes all electron, relativistic, DFT calculations of nanoclusters with up to 2052 atoms, our work makes available an accurately calculated dataset for nanoscale ZnO up to an unprecedented size (the full set of calculated data is made available in the ESI†). On the basis of our data, and the fits thereof, our work thus provides the first attempt at a comprehensive description of the size-dependent structural and polymorphic evolution of low energy ZnO species from nanocluster to bulk.

Conclusions

We consider a comprehensive set of all-electron, relativistic, DFT based calculations of five families of ZnO nanoclusters: (A) single-layered nanocages, (B) multi-layered nanocages, (C) SOD-ZnO bulk-cuts, (D) BCT-ZnO bulk cuts, and (E) WZ-ZnO bulk-cuts. Using these data and explicit calculations of relevant bulk phases, we use appropriate fits and their extrapolations to estimate the size-dependent energetic stability of each nanocluster family. Our fits indicate a progressive change in energetic stability of the nanocluster families following the series A → B → (B/C/D) → D → E, where (B/C/D) indicates a region of transition (ø ∼ 2.6 nm) where multi-layered cages and bulk-cuts of both SOD-ZnO and BCT-ZnO are very similar in energetic stability. This transition size also marks the point at which bottom-up clusters give way to top-down bulk-cuts. Eventually, our results indicate a final crossover to cuts from the most stable WZ-ZnO polymorph will occur at about 2200 ZnO units corresponding to an approximate nanoparticle diameter of 4.7 nm, in line with previous experiments reporting wurtzite ZnO for nanoparticles of 4–6 nm size or bigger.^58,59

Acknowledgements

This research was supported by the Spanish MINECO/FEDER CTQ2015-64618-R grant and, in part, by Generalitat de Catalunya (grants 2014SGR97 and XRQTC) and by the NOMAD Center of Excellence project, which received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no 676580. O. L. G. is grateful to the Universitat de Barcelona for a predoctoral grant; and F. I. acknowledges additional support from the 2015 ICREA Academia Award for Excellence in University Research. F. V. thanks MINECO for postdoctoral Ramón y Cajal (RyC) research contract (RYC-2012-10129). Computational time at the Marenostrum supercomputer has been provided by the Barcelona Supercomputing Centre through grants from Red Española de Supercomputación and the COMPHOTOCAT project 2014112608 of the Partnership for Advanced Computing in Europe (PRACE).

References

1. A. Janotti and C. G. Van de Walle, Rep. Prog. Phys., 2009, 72, 126501.
2. C. Klingshirn, Phys. Status Solidi B, 2007, 244, 3027–3073.
3. X. Wang, J. Song and Z. L. Wang, J. Mater. Chem., 2007, 17, 711–720.
4. Z. L. Wang, J. Phys.: Condens. Matter, 2004, 16, R829–R858.
5. I. Demiroglu, S. M. Woodley, A. A. Sokol and S. T. Bromley, Nanoscale, 2014, 6, 14754–14765.
6. C. L. Freeman, F. Claeyssens, N. L. Allan and J. H. Harding, Phys. Rev. Lett., 2006, 96, 066102.
7. B. J. Morgan, Phys. Rev. B: Condens. Matter, 2009, 80, 174105.
8. I. Demiroglu and S. T. Bromley, Phys. Rev. Lett., 2013, 110, 245501.
9. L. Zhang and H. Huang, Appl. Phys. Lett., 2007, 90, 023115.
10. B. Wen and R. Melnik, Chem. Phys. Lett., 2008, 466, 84–87.
11. C. Tusche, H. L. Mayerheim and J. Kirschner, Phys. Rev. Lett., 2007, 99, 026102.
12. G. Weirrum, G. Barcaro, A. Fortunelli, F. Weber, R. Schennach, S. Surnev and F. Netzer, J. Phys. Chem. C, 2010, 114, 15432–15439.
13. E. C. Behrman, R. K. Foehrweiser, J. R. Myers, B. R. French and M. E. Zandler, Phys. Rev. A, 1994, 49, R1543.
14. J. M. Matxain, J. E. Fowler and J. M. Ugalde, Phys. Rev. A, 2000, 62, 053201.
15. A. C. Reber, S. N. Khanna, J. S. Hunjan and M. R. Beltran, Eur. Phys. J. D, 2007, 43, 221–224.
16. M. Zhao, Y. Xia, Z. Tan, X. Liu and L. Mei, Phys. Lett. A, 2007, 372, 39–43.
17. B. Wang, S. Nagase, J. J. Zhao and G. Wang, J. Phys. Chem. C, 2007, 111, 4956–4963.
18. A. A. Al Sunaidi, A. A. Sokol, C. R. A. Catlow and S. M. Woodley, J. Phys. Chem. C, 2008, 112, 18860–18875.
19. I. A. Sarsari, S. J. Hashemifar and H. Salamati, J. Phys.: Condens. Matter, 2012, 24, 505502.
20. G. Malloci, L. Chiodo, A. Rubio and A. Mattoni, J. Phys. Chem. C, 2012, 116, 8741–8746.
21. M. Chen, T. P. Straatsma, Z. Fang and D. Dixon, J. Phys. Chem. C, 2016, 120, 20400–20418.
22. J. Heinzelmann, A. Koop, S. Proch, G. F. Ganteför, R. Łazarski and M. Sierka, J. Phys. Chem. Lett., 2014, 5, 2642–2648.
23. E. Spano, S. Hamad and C. R. A. Catlow, J. Phys. Chem. B, 2003, 107, 10337–10340.
24. S. Hamad and C. R. A. Catlow, J. Cryst. Growth, 2006, 294, 2–8.
25. A. Dmytruk, I. Dmitruk, I. Blonskyy, R. Belosludov, Y. Kawazoe and A. Kasuya, Microelectron. J., 2009, 40, 218–220.
26. X. Wang, B. Wang, L. Tang, L. Sai and J. Zhao, Phys. Lett. A, 2010, 374, 850–853.
27. B. Wang, X. Wang and J. Zhao, J. Phys. Chem. C, 2010, 114, 5741–5744.
28. M. R. Farrow, J. Buckeridge, C. R. A. Catlow, A. J. Logsdail, D. O. Scanlon, A. A. Sokol and S. M. Woodley, Inorganics, 2014, 2, 248–263.
29. J. Carrasco, F. Illas and S. T. Bromley, Phys. Rev. Lett., 2007, 99, 235502.
30. Y. Yong, B. Song and P. He, J. Phys. Chem. C, 2011, 115, 6455–6461.
31. S. M. Woodley, M. B. Watkins, A. A. Sokol, S. A. Shevlin and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2009, 11, 3176–3185.
32. A. A. Sokol, M. R. Farrow, J. Buckeridge, A. J. Logsdail, C. R. A. Catlow, D. O. Scanlon and S. M. Woodley, Phys. Chem. Chem. Phys., 2014, 16, 21098–21105.
33. C. R. A. Catlow, S. T. Bromley, S. Hamad, M. Mora-Fonz, A. A. Sokol and S. M. Woodley, Phys. Chem. Chem. Phys., 2010, 12, 786–811.
34. C. R. A. Catlow, S. A. French, A. A. Sokol, A. A. Al-Sunaidi and S. M. Woodley, J. Comput. Chem., 2008, 29, 2234–2249.
35. I. Demiroglu, S. Tosoni, F. Illas and S. T. Bromley, Nanoscale, 2014, 6, 1181–1187.
36. M. A. Zwijnenburg, F. Illas and S. T. Bromley, Phys. Rev. Lett., 2010, 104, 175503.
37. W. Sangthong, J. Limtrakul, F. Illas and S. T. Bromley, Phys. Chem. Chem. Phys., 2010, 12, 8513–8520.
38. J. Wang, A. J. Kulkarni, M. Zhou, K. Sarasamak and S. Limpijumnong, Phys. Rev. Lett., 2006, 97, 105502.
39. D. Stradi, F. Illas and S. T. Bromley, Phys. Rev. Lett., 2010, 105, 045901.
40. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Phys. Commun., 2009, 180, 2175–2196.
41. O. Lamiel-Garcia, K. C. Ko, J. Y. Lee, S. T. Bromley and F. Illas, J. Chem. Theory Comput., 2017, 13, 1785–1793.
42. F. Viñes and F. Illas, J. Comput. Chem., 2017, 38, 523–529.
43. I. Y. Zhang, X. Ren, P. Rinke, V. Blum and M. Scheffler, New J. Phys., 2013, 15, 123033.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. M. Kalaya, H. H. Karta, S. Özdemir Karta and T. Çağın, J. Alloys Compd., 2009, 484, 431–438.
46. M. P. Molepo and D. P. Joubert, Phys. Rev. B: Condens. Matter, 2011, 84, 094110.
47. C. Chang, M. Pelissier and P. Durand, Phys. Scr., 1986, 34, 394–404.
48. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783.
49. D. J. Wales and J. P. K. Doye, J. Phys. Chem., 1997, 101, 5111–5116.
50. C. Roberts and R. L. Johnston, Phys. Chem. Chem. Phys., 2001, 3, 5024–5034.
51. A. Iglesias-Juez, F. Viñes, O. Lamiel-García, M. Fernández-García and F. Illas, J. Mater. Chem. A, 2015, 3, 8782–8792.
52. R. Johnston, Masters Series in Physics and Astronomy, in Atomic and Molecular Clusters, Taylor and Francis, London, 2002.
53. O. Lamiel-Garcia, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058.
54. A. S. Barnard and P. Zapol, Phys. Rev. B: Condens. Matter, 2004, 70, 235403.
55. A. S. Barnard and P. Zapol, J. Chem. Phys., 2004, 121, 4276.
56. I. Demiroglu and S. T. Bromley, J. Phys.: Condens. Matter, 2015, 28, 224007.
57. J. C. Schön and M. Jansen, Comput. Mater. Sci., 1995, 4, 43.
58. M.-R. He, R. Yu and J. Zhu, Angew. Chem., Int. Ed., 2012, 51, 7744.
59. D. Hapiuk, B. Masenelli, K. Masenelli-Varlot, D. Tainoff, O. Boisron, C. Albin and P. Mélinon, J. Phys. Chem. C, 2013, 117, 10220–10227.
60. Y. Liu, D. Wang, Q. Peng, D. Chu, X. Liu and Y. Li, Inorg. Chem., 2011, 50, 5841.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr02818k

---