Boron clusters with 46, 48, and 50 atoms: competition among the core–shell, bilayer and quasi-planar structures†
Abstract
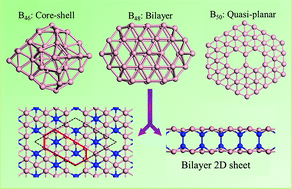
Using a genetic algorithm combined with density functional theory calculations, we perform a global search for the lowest-energy structures of Bn clusters with n = 46, 48, 50. Competition among different structural motifs including a hollow cage, core–shell, bilayer, and quasi-planar, is investigated. For B46, a core–shell B4@B42 structure resembling the larger Bn clusters with n ≥ 68 is found to compete with a quasi-planar structure with a central hexagonal hole. A quasi-planar configuration with two connected hexagonal holes is most favorable for B50. More interestingly, an unprecedented bilayer structure is unveiled at B48, which can be extended to a two-dimensional bilayer phase exhibiting appreciable stability. Our results suggest alternatives to the cage motif as lower-energy Bn cluster structures with n > 50.


 Please wait while we load your content...
Please wait while we load your content...