Mapping stress in polycrystals with sub-10 nm spatial resolution†
Abstract
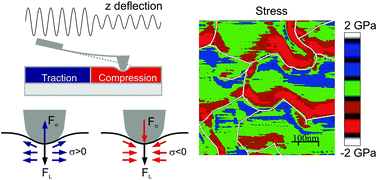
From aircraft to electronic devices, and even in Formula One cars, stress is the main cause of degraded material performance and mechanical failure in applications incorporating thin films and coatings. Over the last two decades, the scientific community has searched for the mechanisms responsible for stress generation in films, with no consensus in sight. The main difficulty is that most current models of stress generation, while atomistic in nature, are based on macroscopic measurements. Here, we demonstrate a novel method for mapping the stress at the surface of polycrystals with sub-10 nm spatial resolution. This method consists of transforming elastic modulus maps measured by atomic force microscopy techniques into stress maps via the local stress-stiffening effect. The validity of this approach is supported by finite element modeling simulations. Our study reveals a strongly heterogeneous distribution of intrinsic stress in polycrystalline Au films, with gradients as high as 100 MPa nm−1 near the grain boundaries. Consequently, our study discloses the limited capacity of macroscopic stress assessments and standard tests to discriminate among models, and the great potential of nanometer-scale stress mapping.


 Please wait while we load your content...
Please wait while we load your content...