Electron tomography analysis of 3D interfacial nanostructures appearing in annealed Si rich SiC films

Abstract

The optical and electrical properties of Si rich SiC (SRSC) solar cell absorber layers will strongly depend on interfacial layers between the Si and the SiC matrix and in this work, we analyze hitherto undiscovered interfacial layers. The SRSC thin films were deposited using a plasma-enhanced chemical vapor deposition (PECVD) technique and annealed in a nitrogen environment at 1100 °C. The thermal treatment leads to metastable SRSC films spinodally decomposed into a Si–SiC nanocomposite. After the thermal treatment, the coexistence of crystalline Si and SiC nanostructures was analysed by high resolution transmission electron microscopy (HRTEM) and electron diffraction. From the quantitative extraction of the different plasmon signals from electron energy-loss spectra, an additional structure, amorphous SiC (a-SiC) was found. Quantitative spectroscopic electron tomography was developed to obtain three dimensional (3D) plasmonic maps. In these 3D spectroscopic maps, the Si regions appear as network structures inside the SiC matrix where the a-SiC appears as an interfacial layer separating the matrix and Si network. The presence of the a-SiC interface can be explained in the framework of the nucleation and growth model.

---

1. Introduction

Insulating or semiconducting films containing Si nanoparticles (NPs), fabricated by thermal annealing from a Si rich matrix material have emerged as highly absorbing layers for third-generation solar cells.¹ The reason to use Si NPs is to achieve a band gap tunable absorber layer, where the band gap is controlled by quantum confinement effects related to the size of Si NPs.² Of several materials systems, Si rich SiO₂ (SRSO) and Si rich SiC (SRSC) absorber layers are the most studied systems. In order to improve the transport through the absorber film by hopping, the use of SRSC instead of SRSO films is motivated by the fact that the band gap of SiC is much lower than the one of SiO₂, which in turn facilitates carrier transport between two adjacent Si NPs in SRSC as compared to SRSO.^3,4 To understand the relationship between the absorber layer structure and optical properties, the size of the Si NPs was analyzed in SRSO films.^5–8

However, it has turned out that the interfacial properties of the Si NPs play a decisive role in determining the optical absorption and the optical activity of the Si NPs as concluded on both experimental and theoretical grounds.⁹ From atom probe tomography (APT) of SRSO films, a very thin compositionally distinct interfacial layer was observed between the Si NPs and the surrounding matrix.¹⁰ In principle, electron tomography could be used to understand such interfacial layers, since one has access to composition and structure by this method and can also address larger sample volumes than in APT. Whereas electron tomography has shown Si nanostructures in the SRSO films,^11,12 a direct three dimensional (3D) visualization of the interfacial structure between the precipitated NPs and their surrounding matrix is still lacking. This is due to the fact that the plasmon peaks of the amorphous matrix SiO_x and the interfacial layer SiO_y, that have different oxygen concentrations, would be at very similar energy and thus these layers could not be distinguished from plasmon spectra for SRSO films.¹³ The situation is different in the SRSC films, where the SiC matrix is crystalline and we can make use of distinct plasmons of different components in the SRSC system to analyze 3D interfacial layers.

In the plasmonic spectrum in the electron energy loss spectrum (EELS) in the TEM, of SRSC films, the Si, amorphous SiC (a-SiC), and crystalline SiC (3C-SiC) plasmon peaks have clearly distinct positions¹⁴ and can therefore be used to distinguish the presence of the different constituents of the materials systems. In addition, when the different parts of the system change their phase or crystallographic structure, this also leads to shifts in plasmon energy and makes such phase changes detectable.¹⁵ This makes plasmonic imaging a preferred tool to analyze these nanocrystalline absorber layers.

In order to obtain electron tomograms with high NP to matrix contrast, tilt series were acquired in the energy filtered TEM (EFTEM) mode in previous studies of the SRSO films, where each image in the series contains the signal of the Si NP plasmon.^11,12,17 However, the resulting tomograms do only show the Si NPs, but not the matrix structure and, a priori, the two structures do not have to be complementary. In order to obtain the complete picture of the absorber layer, one would like to acquire the entire plasmon spectrum at each image point and then, extract the plasmon images corresponding to the Si NPs and the matrix. In fact, Schamm et al. have acquired such spectrum image (SI) datasets and extracted the 2D distribution of Si NPs.¹⁸ To date, no electron tomography analysis has been performed where Si structures and matrix structures were quantitatively extracted from SIs.

In this work, we make use of and refine the EFTEM SI datasets to reveal the 3D distribution of all three Si, a-SiC and 3C-SiC in annealed SRSC films. The extraction of plasmon signals from EFTEM SI datasets was optimized by fitting the reference plasmon peaks to the low-loss region in EELS. The tomograms of Si, a-SiC and 3C-SiC sub-volumes have been reconstructed from the extracted plasmon images. Additional information about the morphology, the location of crystalline/amorphous nanostructures as well as their crystalline phases is obtained from bright field TEM (BFTEM) images, high resolution TEM (HRTEM) and electron diffraction. Molecular dynamic simulations have been carried out with the aim to understand the disordering of the atomic position at the interface between the crystalline Si (c-Si) and 3C-SiC NPs. Finally, the growth mechanism of the observed structures is discussed in the framework of spinodal decomposition and the nucleation and growth model.

2. Experimental details

2.1 Materials

Thin hydrogenated amorphous SRSC films were deposited by using plasma-enhanced chemical vapor deposition (PECVD). For the deposition, a mixture of silane and methane gases was used with flow rates of 10.2 and 91.8 sccm, respectively. The pressure in the reaction chamber was set to 1.4 mbar. The RF power density and frequency were 139 mW cm⁻² and 13.56 MHz, respectively. The films were deposited on 1 mm thick fused quartz substrates at a substrate temperature of 360 °C. The film thickness was 246 nm as determined by spectroscopic ellipsometry. This corresponds to a growth rate of 0.42 nm s⁻¹. Elastic Recoil Detection Analysis (ERDA) reveals that the composition of the SRSC film after 1 hour of annealing is Si_0.67C_0.33. Also oxygen (∼8%) was detected in the annealed films from the ERDA analysis. This may be due to the fact that the SRSC films were kept in the air atmosphere for two months before ERDA analysis.

For annealing purposes the sample was cut into smaller pieces with dimensions of 5 × 5 mm². Then annealing was performed in a crucible mounted on a heating stage fabricated by Linkam Scientific Instruments Ltd. During annealing the heating stage was purged with nitrogen with a flow rate of 60 ml min⁻¹. The gas purity was 99.997% and the measured oxygen content was 0.3 ppm. The samples were annealed at different times (15 and 60 minutes) at 1100 °C. For every anneal time a fresh sample was used. The heating and cooling rate was 168.63 °C min⁻¹.

2.2 Transmission electron microscopy

All TEM experiments were carried out on a FEI Tecnai F30ST equipped with a field emission gun operating at 300 keV (Schottky emitter, energy spread of 1.3 eV) and a Gatan Tridiem imaging spectrometer. The energy filtered zero-loss diffraction patterns were obtained using a selected area diffraction (SAD) aperture with a diameter of about 800 nm and an 8 eV energy slit. We found a sensitive increase of the signal-to-noise-ratio at this slit width as compared to wider energy selecting slits. The camera length was calibrated with the calculated lattice spacings of Si in the [111] zone axis, thereby minimizing the error of the camera calibration. Conventional TEM sample preparation techniques, including mechanical polishing and grazing incidence (6°, 5 kV) Ar-ion milling, were chosen to obtain samples in plane view geometry. The sample thickness for acquisition of images and tomography data is about 20–30 nm. The SIs in the EFTEM mode were acquired in the low-loss region of the EELS spectrum (from −4 eV to 40 eV) with a 2 eV energy slit and using 1 eV energy steps with a 7.6 mrad semi collection angle. The cut-off angle for scattering from a Si volume plasmon is 6.5 mrad,¹⁹ a 7.6 mrad semi-collection angle was chosen to avoid the peak broadening due to the single electron excitation. The zero-loss peak was used to calibrate the energy shift. The offline spectrum treatment includes Fourier log deconvolution to remove the plural scattering,²⁰ linear background subtraction, and non-negative least squares (NNLS) fitting²¹ in the low-loss region and extraction of plasmon images was performed in DigitalMicrograph® (DM). The linear background under the plasmon peak results most likely from the surface plasmons and Cherenkov losses. This background model is interpolated between 5 eV and 35 eV. The plasmon peaks were modelled as Gaussians.

2.3 Electron tomography

The tilt series was carried out using the SI technique in EFTEM. For the acquisition of each EFTEM SI in the tilt series, we used a 2 eV energy slit and 2 eV energy as steps, and then moved the energy slit from −4 eV to 40 eV. To minimize the missing wedge effect, a double tilt series was acquired using a Fischione model 2020 tomography sample holder. The tilt series were taken from ±60° with 3° increments. Before the tomographic reconstruction, the individual plasmon images for Si, a-SiC and 3C-SiC were extracted from each EFTEM SI data cube in the tilt series. The alignment and reconstruction of the image stack was carried out using the IMOD software package.^22,23 Most likely related to the low density of the sample (about 1 g cm⁻³ as compared to 2.3 g cm⁻³ and about 3 g cm⁻³ for Si and SiC respectively), we observe a slight shrinking of the sample with an increasing exposure dose during the pre-irradiation of the sample. Under the acquisition of the tilt series, the sample was stable. Other structural modifications are not observed. To prevent disturbances in the tomography reconstruction process coming from this irradiation damage, the sample was irradiated for 30 minutes before the data acquisition with an electron beam of about half micron. The sample thickness is about 20–30 nm. 3D Slicer software was used for the segmentation of the tomograms by volume rendering at a fixed threshold. In the reconstructed tomograms, the Si, 3C-SiC and a-SiC structures have a soft outline in about 1 nm range. The segmentation was performed by choosing a threshold intensity at which the soft outline was not included (Fig. S7†). A similar method was performed to segment the Si NPs in plasmon tomograms from SRSO films.¹¹ One or two pixels may overlap on the border between the three different segmented plasmon volumes when they are combined into one volume. This can be due to the error residue after tilt series alignment and the determination of the threshold intensity in the segmentation process. This overlap may bring a ±3% deviation on the volume fraction estimation when choosing different threshold intensities to perform the segmentations on each signal. Visualization of the 3-D images was carried out in the same software.

2.4 Molecular dynamics simulation

For the purpose of our molecular dynamics (MD) simulation study we made models of the interface at the {111} planes and models of embedded c-Si NPs in the 3C-SiC matrix. We considered the c-Si and 3C-SiC parts in both (100) and (110) directions, and the case of c-Si NPs in the 3C-SiC matrix, as detailed in Table 1. The simulated annealing of the models was carried out employing classical MD simulations, as implemented in the large scale atomic or molecular massively parallel simulation (LAMMPS) MD package,²⁴ using the Erhart and Albe parametrization of the SiC Tersoff potential.²⁵ The MD simulations were performed using the NPT ensemble, at the annealing temperature of the samples, 1373 K, and a pressure of 0 bar, during a period of 150 fs. The models were later cooled down for 50 fs by applying a damping force of 0.0005 eV ps Å⁻², allowing the volume of the models to relax, while keeping the pressure of the system at 0 bar, enforcing an energy and force convergence criterion of 10⁻¹⁰ eV and 10⁻¹⁴ eV Å⁻¹, respectively.

Table 1 Size of the Si and SiC parts, in nm, of the {111} interface models and the embedded Si NPs

Size in {001} direction		Size in {110} direction		Embedded Si NPs in SiC
Si	SiC	Si	SiC	Si	SiC
1.156	1.23	1.335	1.6	2.5	3.052

---

3. Results and discussion

3.1 Overview of the as-deposited and annealed SRSC films

The TEM images shown in Fig. 1a–c show the effect of annealing time on the formation of c-Si and 3C-SiC NPs. As can be seen in Fig. 1a, no crystalline NPs were observed in the as-deposited SRSC film, which indicates that the SRSC film is amorphous in the initial state. After 15 minutes of annealing, contrasting dark spots start appearing in the BFTEM image (Fig. 1b). These spots are the crystalline NPs precipitated from the SRSC film. The size of NPs ranges from 1.5 nm to 5 nm in diameter. After 1 hour of annealing, a large amount of bigger NPs are easily distinguishable as dark spots in the BFTEM image (Fig. 1c) with a diameter of 10–12 nm.

Fig. 1 Plane view BFTEM images and SAD patterns of as-deposited, 15 minute and 1 hour annealed SRSC films. BFTEM image of (a) the as-deposited SRSC film; (b) 15 minute annealed SRSC films; (c) 1 hour annealed SRSC films. The SAD patterns are displayed in (d) as-deposited, (e) 15 minute annealed SRSC films and (c) 1 hour annealed SRSC films. Five reflection rings marked by 1, 2, 3, 4 and 5 can be indexed by the lattice spacings of Si (111), 3C-SiC (111), Si (022), Si (113) and 3C-SiC (022), respectively.

In Fig. 1d, the diffused and broadened reflection rings were detected in the SAD pattern. This observation verifies that the crystallization of Si and SiC does not occur in the as-deposited SRSC film. The SAD pattern shown in Fig. 1e contains the reflection rings generated from both Si and 3C-SiC poly-crystalline NPs. This is expected since the cubic form of the 3C-SiC crystalline phase is more stable than the hexagonal form of the 6H-SiC crystalline phase at any temperature when the relative atomic concentration of Si to C is near 1 : 1.²⁶ The observation of 3C-SiC NPs in the annealed SRSC films was also reported in previous studies.¹⁴Fig. 1e indicates that the phase separation of Si and SiC starts after 15 minutes of annealing and continues by the crystallization of separated Si and SiC phases resulting in the coexistence of c-Si and 3C-SiC NPs during the first 15 minutes of annealing. From the SAD pattern acquired from the 1 hour annealed SRSC film, the reflection rings of c-Si and 3C-SiC contain many discrete spots, which indicate an increase in the size of poly-crystalline c-Si and 3C-SiC NPs after 1 hour of annealing. The volume fraction of c-Si (V_c-Si) as a function of annealing times was analyzed by Raman spectroscopy (Fig. S9†). A rapid increase of V_c-Si within the first half hour was observed. From 1 hour to 4 hours, V_c-Si slowly increases from 14% to 22%. Thus, the majority of Si–Si bonds are in the amorphous phase even after 4 hours of annealing at 1100 °C.

From the BFTEM images, the NP-like contrasts are clearly visible. However, the composition of these NPs is unknown from the BFTEM images. By analyzing the results obtained from the BFTEM images and SAD patterns, we can confirm that the phase separation of Si and SiC in the SRSC film occurs after the thermal treatment and the crystallization of each phase leads to the coexistence of c-Si and 3C-SiC NPs. The observation of the coexistence of c-Si and 3C-SiC NPs is in good agreement with previously reported results.¹⁴ The crystalline structure of the NPs is shown in the HRTEM images of c-Si and 3C-SiC NPs from the 15 minute (Fig. S1†) and 1 hour annealed SRSC films (Fig. S2†).

3.2 2D imaging Si network structure, 3C-SiC NPs and the interfacial structure from the EFTEM SI dataset

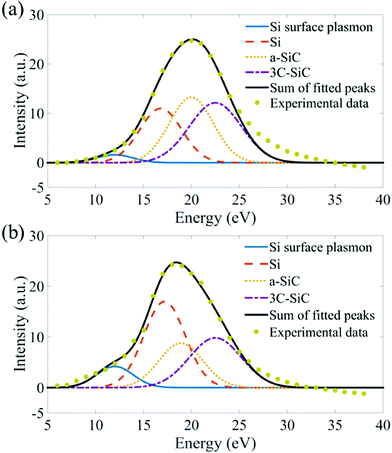
Though BFTEM and HRTEM images show good contrasts for c-Si NPs, the amorphous Si regions of the sample cannot be distinguished from the SiC matrix and the c-Si NP contrasts depend sensitively on their orientation. In order to assess the Si and SiC regions in the annealed SRSC films more quantitatively, we fitted plasmon peaks to the background subtracted spectra extracted from EFTEM SI images. The detailed discussion of the fitting procedure is specified in Fig. S3–S6.† The best result (Table 2) is obtained when four plasmon peaks, the Si surface plasmon peak (12 eV), the Si plasmon peak (17.2 eV), the a-SiC plasmon peak (20 eV) and the 3C-SiC plasmon peak (22.5 eV) are fitted to the experimental spectra (Fig. 2). In particular, the plasmon peak of a-SiC at 20 eV must be added as one of the plasmon peaks during the fitting so as to achieve the minimum of the fitting residues and maintain FWHM and positions of the other plasmon peaks that are physically meaningful.

Fig. 2 Reference plasmon spectra for pure Si, a-SiC, c-SiC and the fit of the reference spectra to the background subtracted low-loss region (in a range of 5–35 eV). The low-loss EELS spectra were constructed from the EFTEM SI dataset acquired from (a) 15-minute annealed and (b) 1-hour annealed SRSC films from the approximate same volumes.

Table 2 Fitting parameters of Si surface, Si, a-SiC and 3C-SiC plasmon peaks for 15 minute and 1 hour annealed samples at 1100°

	15 minute annealed		1 hour annealed
	Plasmon energy (eV)	FWHM (eV)	Plasmon energy (eV)	FWHM (eV)
Si surface	12	4.5 ± 0.3	12	4.5 ± 0.3
Si	17.2 ± 0.3	5.3 ± 0.3	17.2 ± 0.3	5.3 ± 0.3
a-SiC	20	5.1 ± 0.5	20	5.1 ± 0.5
3C-SiC	22.5	6.4 ± 0.6	22.5	6.4 ± 0.6

---

In the low-loss region, the center of the overall plasmon peak shifts from 20 eV for the 15-minute annealed film to 17.8 eV for the 1 hour annealed film. The related increases in the intensity of the fitted Si surface plasmon and Si plasmon peaks indicate a phase separation of Si when the annealing time is increased from 15 minutes to 1 hour. When the integrated area of the individual plasmon peaks is extracted from each pixel in the EFTEM SI images, the Si, a-SiC and 3C-SiC maps are obtained. From the as-deposited SRSC film, NP like contrasts were not observed from the extracted plasmon images (not shown). This indicates that the phase separation of Si and SiC from the SRSC film has not occurred during deposition.

In Fig. 3, the EFTEM images are shown that were obtained from the fitted plasmon peaks. After 15 minutes of annealing, Si and 3C-SiC structures appear with high contrasts in the respective plasmon images (in Fig. 3a and c). Thus, the phase separation of Si and SiC started in the first 15 minutes of annealing, which was equally verified by the SAD pattern (Fig. 1e).

Fig. 3 EFTEM images as generated from the fitted plasmon peaks: (a) and (d) Si plasmon images from 15 minute and 1 hour annealed SRSC films respectively; (b) and (e) a-SiC plasmon images from 15 minute and 1 hour annealed SRSC films respectively; (c) and (f) c-SiC plasmon images from 15 minute and 1 hour annealed SRSC films respectively. The scale bars are 20 nm.

After 1 hour of annealing, Si appears as a network like structure in Fig. 3d. In the 3C-SiC plasmon image (Fig. 3f) NP like structures were found. The small 3C-SiC NPs remain at about 5 nm in diameter, whereas the larger ones are found to be 12–15 nm in diameter. More interestingly, in the films annealed for 1 hour, we found that a-SiC (Fig. 3e) seems to appear at the interface between the Si network and 3C-SiC NPs. The 2D images do not provide high resolution information along the depth direction; possibly the Si network like structure consists of a high density of NPs. To study the 3D distribution of each phase, electron tomography was applied.

3.3 3D analysis on the sub-volumes of Si, a-SiC and 3C-SiC

Si, 3C-SiC and a-SiC tomograms were separately reconstructed from the extracted plasmon images by using the back-projection reconstruction method.²⁷ The segmentation was performed by choosing a threshold intensity whose contour is shown in Fig. S7.†Fig. 4a shows that Si has a network like morphology. A similar morphology of Si was also observed in annealed SRSO films.^{10,12,16,17,28} However, compared with the reported network like nanostructures in SRSO films, the observed Si network like structure in our case has two distinctive regions, a triple junction region (marked by a red dashed line in Fig. 4a and e) and thin connecting regions (marked by yellow dashed lines in Fig. 4a and e). The triple junction region of Si is surrounded by three 3C-SiC NPs (numbered by 1, 2, and 3 in red in Fig. 4b and f) and has a columnar like morphology along the Z direction. The width (in XY plane) of the thin connecting regions ranges from 1 nm to 3 nm with a very high surface-to-volume ratio, making the columnar like structures interconnected. The marked three 3C-SiC NPs shown in Fig. 4b and f are separated from each other and the thin connecting regions of Si are distributed as the boundary region between two 3C-SiC NPs.

Fig. 4 3D surface rendered of (a) Si network structure, (b) c-SiC NPs, (c) a-SiC interface and (d) the combined volume of (a), (b) and (c) of 1 hour annealed SRSC film. (e) is the tilted 3D view of (a). (f) is the tilted 3D view of (b). The scale bars are 10 nm. The volume size is X (60 nm) × Y (45 nm) × Z (20 nm).

Whereas the a-SiC plasmon peak was introduced to obtain a good fit to the low loss region, in fact, in the electron tomogram of the a-SiC plasmon, the a-SiC layer can be localized (Fig. 4c), and also it is observed that it appears systematically at the interface between 3C-SiC and Si NPs (Fig. 4d). The width of the a-SiC interfacial layer is 1–3 nm. The volume fraction of Si networks, 3C-SiC NPs and a-SiC interface is about 46 ± 3 vol%, 31 ± 3 vol% and 23 ± 2 vol%, respectively. Then, the overall concentration of the SRSC film as obtained from the tomograms is about Si_0.64C_0.36. This Si/C ratio matches well with the results obtained from the ERDA, where 67 at% of Si and 33 at% of C were measured.

The network like structure of Si is a typical morphology that can be found in thermally annealed SRSO films when the excess Si content is above 16 at%.^12,16 The formation mechanism of such a network like structure was explained by spinodal decomposition.^12,16 Seol et al. have presented the temporal evolution of the morphologies for spinodally decomposed phases in a binary system.²⁹ In the initial stage, the decomposition occurs homogeneously throughout the film and the excess element precipitates as well-separated particles distributed in 3D; then the particles become interconnected in the medium stage; finally, the excess phase results in an interconnected columnar morphology.²⁹ We thus conclude that the 1 hour annealed sample with its Si network formation is in the last phase of the spinodal decomposition process. In the short time annealed sample, dense Si NPs (Fig. 3a) are clearly observed. In the diffraction pattern (Fig. 1d), the diffused intensity from the amorphous structure is still present. Though, from the 2D images, it is difficult to distinguish the superposition of NPs in the image plane from NPs that are interconnected, it is clear that the 15 min annealed sample is either in the initial or the medium stage of the spinodal decomposition process. Yet, from the diffraction pattern of the 1 hour annealed SRSC film, a decrease in the amorphous ring intensity was observed as compared to the 15 min annealed sample (Fig. 1f). This indicates that the Si structure gets more crystallized with the continued spinodal decomposition process, i.e. after 1 hour of annealing.

3.4 Driving forces for the formation of the a-SiC interfacial layer

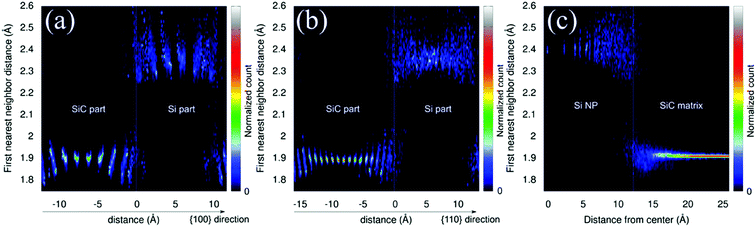
The observation of the a-SiC interfacial layer between the Si network structure and 3C-SiC NPs is the most intriguing finding from the electron tomography analysis. Though our observations are limited to two samples, certainly the following two physical magnitudes contribute to the explanation of the formation of the a-SiC interface layer in SRSC films: (1) the 19.7% mismatch of the c-Si and 3C-SiC crystals; (2) the presence of diffusion layers at the interface between Si and SiC.

Firstly, the formation of the disordered interface sandwiched by the bulk c-Si and 3C-SiC was observed by TEM.³⁰ Due to the 19.7% mismatch of lattice parameters between c-Si and 3C-SiC crystals, a high density of misfit dislocations of the SiC lattice planes was observed by TEM at the interface.³⁰ In order to understand the influence of strain on the atomic order at the Si/SiC interface, we carried out MD simulations. The results, displayed in Fig. 5, show the nearest neighbor distances and their variations close to the Si/SiC {111} interface with different numbers of unit cells along the {001} and {110} directions, as well as an interface for a Si NP surrounded by a SiC matrix. In the case of the planar interfaces (Fig. 5a and b), we observe an increase of the c-Si nearest neighbor distance variation up to about 5 Å away from the Si/SiC interface, note the larger distribution of nearest neighbor distances (y-axes) in this region. The nearest neighbor distance variations are slightly higher for Si than for SiC. The width of the interfacial disorder remains unchanged with increasing size of the Si and SiC parts in both {001} and {110} directions (Fig. S10(c) and (d))†. Once we insert a Si NP in the SiC matrix (Fig. 5c), the disorder in the Si gets smaller, showing crystallinity up to 5 Å from the center. A similar trend is observed for larger, ∼10 nm, Si and SiC NPs in SiC and Si matrixes, respectively (Fig. S10(e) and (f))†. Interestingly, the interfacial disorder observed from MD simulations, ∼1.1 nm, is in good agreement with the width of the a-SiC layer observed in the 3D analysis. This shows that the lattice mismatch between Si and SiC indeed contributes to an increased atomic disorder at the interface. It should also be noted that the Si part has a disordered zone which could lead to the amorphization of a part of the Si itself. This is in good agreement with Raman spectroscopy analysis in Fig. S9.†

Fig. 5 First nearest neighbour distance as a function of the distance from the interface in the model: (a) {111} interface with 12.3 Å SiC and 11.56 Å Si part along the {100} planes; (b) {111} interface with 16 Å SiC and 13.35 Å Si part along the {110} planes; and (c) 25 Å Si NP embedded in 30.52 Å SiC matrix.

Secondly, diffusion layers at the NP/matrix interface are predicted from the nucleation and growth model described by Thanh et al.³¹ The driving force for a particle to nucleate and grow from the surrounding matrix always consists of two parts: the decrease of the interfacial free energy and the solute concentration gradient at the interface.³² The concentration gradient at the interface as a function of the particle radius was modelled by Fick's first law of diffusion³¹ and thus this process creates a diffusion interface between the precipitated NP and the surrounding matrix such as we observe in the tomograms. Since the 3C-SiC is crystalline, the crystallites in this region are expected to be close to stoichiometric. In fact, from our EELS studies, we find that the concentration of Si in the a-SiC interface layer is intermediate between the Si network and the 3C-SiC regions (Fig. S8†). This non-stoichiometry, according to the phase diagram²⁶ can contribute to the formation of a metastable a-SiC interface layer. There is thus evidence that both, the spinodal decomposition model and the nucleation and growth model describe parts of the growth in the SRSC system. Both models seem to be needed for explaining the different structural evolutions and parameters in such nanostructured systems. This combination of both models has in fact been taken as a base for a generalized Gibb's approach, where the contradictions between the two models were removed.³³

4. Conclusions

In this article, a complete 3D characterization of the percolated Si and SiC nanostructures embedded in the SRSC film has been performed by using TEM-EELS related techniques. The 3D spectroscopic nanoscale study shows that decomposition processes in the SRSC generates a complex materials system. Our experimental findings can only be explained by supposing the presence of a-SiC in the SRSC materials system. In the reconstructed tomograms, we observed the formation of a Si network structure and could localize the a-SiC as a 1–3 nm thick interfacial layer between the 3C-SiC and the Si regions. Using 3D spectroscopic analysis in the TEM the different components of the complex, 3D system can be disentangled and thus, TEM can contribute to understand the structural evolution of these complex materials systems. This spectroscopic 3D TEM analysis can be extended to other materials systems and has thus the potential to reveal hidden structures appearing in crystallization and growth processes. The structural details found in the SRSC nanocomposite might be taken into account when the electronic structures and optical properties of such a nanocomposite are interpreted.

Acknowledgements

The authors acknowledge generous support from the EU founded FP7 project ‘SNAPSUN’ (grant agreement no 246310), the Swedish Research council (grant C0357901) and the Knut and Alice Wallenberg Stiftelse. We are also grateful for the help from Dr Daniel Primetzhofer for the ion beam analysis on SRSC films. Thanks for the Raman spectroscopy analysis performed by M. V. de Grunt.

Notes and references

1. G. Conibeer, M. Green, E.-C. Cho, D. Koenig, Y.-H. Cho, T. Fangsuwannarak, G. Scardera, E. Pink, Y. Huang, T. Puzzer, S. Huang, D. Song, C. Flynn, S. Park, X. Hao and D. Mansfield, Thin Solid Films, 2008, 516, 6748–6756.
2. M. a. Green, Prog. Photovolt: Res. Appl., 2001, 9, 123–135.
3. E. C. Cho, M. A. Green, G. Conibeer, D. Song, Y. H. Cho, G. Scardera, S. Huang, S. Park, X. J. Hao, Y. Huang and L. Van Dao, Adv. OptoElectron., 2007, 2007, 69578.
4. D. Song, E.-C. Cho, G. Conibeer, Y.-H. Cho, Y. Huang, S. Huang, C. Flynn and M. A. Green, J. Vac. Sci. Technol., B, 2007, 25, 1327–1335.
5. M. Van Sebille, R. A. Vasudevan, R. J. Lancee, R. A. C. M. M. Van Swaaij and M. Zeman, J. Phys. D: Appl. Phys., 2015, 48, 325302.
6. N.-M. Park, T.-S. Kim and S.-J. Park, Appl. Phys. Lett., 2001, 78, 2575–2577.
7. F. Iacona, G. Franzò and C. Spinella, J. Appl. Phys., 2000, 87, 1295.
8. G. Chang, F. Ma, D. Ma and K. Xu, Nanotechnology, 2010, 21, 465605.
9. D. Koenig, J. Rudd, M. A. Green and G. Conibeer, Sol. Energy Mater. Sol. Cells, 2009, 93, 753–758.
10. M. Roussel, E. Talbot, R. Pratibha Nalini, F. Gourbilleau and P. Pareige, Ultramicroscopy, 2013, 132, 290–294.
11. A. Yurtsever, M. Weyland and D. A. Muller, Appl. Phys. Lett., 2006, 89, 151920.
12. D. Friedrich, B. Schmidt, K. H. Heinig, B. Liedke, A. Muecklich, R. Huebner, D. Wolf, S. Koelling and T. Mikolajick, Appl. Phys. Lett., 2013, 103, 131911.
13. M. C. Cheynet and T. Epicier, Philos. Mag., 2004, 84, 1753–1771.
14. M. Kuenle, S. Janz, K. G. Nickel and O. Eibl, Phys. Status Solidi A, 2011, 208, 1885–1895.
15. M. Mitome, Y. Yamazaki, H. Takagi and T. Nakagiri, J. Appl. Phys., 1992, 72, 812–814.
16. B. Liedke, K.-H. Heinig, a. Mücklich and B. Schmidt, Appl. Phys. Lett., 2013, 103, 133106.
17. J. Laube, S. Gutsch, D. Wang, C. Kübel, M. Zacharias and D. Hiller, Appl. Phys. Lett., 2016, 108, 43106.
18. S. Schamm, C. Bonafos, H. Coffin, N. Cherkashin, M. Carrada, G. Ben Assayag, a. Claverie, M. Tencé and C. Colliex, Ultramicroscopy, 2008, 108, 346–357.
19. R. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, 2011.
20. P. J. Thomas and P. A. Midgley, Ultramicroscopy, 2001, 88, 187–194.
21. C. L. Lawson and R. J. Hanson, Solving least squares problems, 1995, vol. 15.
22. J. R. Kremer, D. N. Mastronarde and J. R. McIntosh, J. Struct. Biol., 1996, 116, 71–76.
23. D. N. Mastronarde, J. Struct. Biol., 1997, 120, 343–352.
24. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
25. P. Erhart, A. Klein and K. Albe, Phys. Rev. B, 2005, 72, 085213.
26. R. W. Olesinski and G. J. Abbaschian, Bull. Alloy Phase Diagrams, 1984, 5, 486–489.
27. S. W. Smith, The Scientist and Engineer's Guide to Digital Signal Processing, 1999.
28. T. Muller, K. H. Heinig, W. Moller, C. Bonafos, H. Coffin, N. Cherkashin, G. B. Assayag, S. Schamm, G. Zanchi, A. Claverie, M. Tence and C. Colliex, Appl. Phys. Lett., 2004, 85, 2373–2375.
29. D. J. Seol, S. Y. Hu, Y. L. Li, J. Shen, K. H. Oh and L. Q. Chen, Acta Mater., 2003, 51, 5173–5185.
30. F. J. Pacheco, A. M. Sanchez, S. I. Molina, D. Araujo, J. Devrajan, A. J. Steckl and R. Garcia, Thin Solid Films, 1999, 343, 305–308.
31. N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630.
32. Z. Guo and W. Sha, Mater. Trans., 2002, 43, 1273–1282.
33. J. W. P. Schmelzer and a. S. Abyzov, J. Eng. Thermophys., 2007, 16, 119–129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr00799j

---