Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Size and property bimodality in magnetic nanoparticle dispersions: single domain particles vs. strongly coupled nanoclusters†
E.
Wetterskog
 *a,
A.
Castro
b,
L.
Zeng
c,
S.
Petronis
d,
D.
Heinke
e,
E.
Olsson
c,
L.
Nilsson
bf,
N.
Gehrke
e and
P.
Svedlindh
a
*a,
A.
Castro
b,
L.
Zeng
c,
S.
Petronis
d,
D.
Heinke
e,
E.
Olsson
c,
L.
Nilsson
bf,
N.
Gehrke
e and
P.
Svedlindh
a
aSolid State Physics, Department of Engineering Sciences, Ångström Laboratory, Uppsala University, Sweden. E-mail: erik.wetterskog@angstrom.uu.se
bSOLVE Research and Consultancy AB, Lund, Sweden
cDepartment of Applied Physics, Chalmers University of Technology, Göteborg, Sweden
dSP Chemistry, Materials and Surfaces, SP Technical Research Institute of Sweden, Borås, Sweden
enanoPET Pharma GmbH, Berlin, Germany
fLund Centre for Field-Flow Fractionation, Department of Food Technology, Engineering and Nutrition, Lund University, Sweden
First published on 9th March 2017
Abstract
The widespread use of magnetic nanoparticles in the biotechnical sector puts new demands on fast and quantitative characterization techniques for nanoparticle dispersions. In this work, we report the use of asymmetric flow field-flow fractionation (AF4) and ferromagnetic resonance (FMR) to study the properties of a commercial magnetic nanoparticle dispersion. We demonstrate the effectiveness of both techniques when subjected to a dispersion with a bimodal size/magnetic property distribution: i.e., a small superparamagnetic fraction, and a larger blocked fraction of strongly coupled colloidal nanoclusters. We show that the oriented attachment of primary nanocrystals into colloidal nanoclusters drastically alters their static, dynamic, and magnetic resonance properties. Finally, we show how the FMR spectra are influenced by dynamical effects; agglomeration of the superparamagnetic fraction leads to reversible line-broadening; rotational alignment of the suspended nanoclusters results in shape-dependent resonance shifts. The AF4 and FMR measurements described herein are fast and simple, and therefore suitable for quality control procedures in commercial production of magnetic nanoparticles.
Introduction
Magnetic nanoparticles are used in a range of state-of-the-art applications in the area of biomedicine; as contrast agents in magnetic resonance imaging (MRI), and magnetic particle imaging (MPI); in magnetic hyperthermia, immune cell separation, and magnetic and magneto-optic biosensor assays.1–3 Optimization of these methods requires synthesis of particles with tailored properties, e.g. with respect to coercivity and magnetic relaxation properties,4,5 properties that vary strongly with primary particle size,6,7 shape,8 composition,9 and degree of clustering.10,11 The optimization of nanomaterials towards specific applications can therefore be particularly challenging using commercial (and often polydisperse) nanoparticle systems. In fact, only a few analytical methods are truly effective in resolving multimodal distributions in nanoparticle dispersions.12 Transmission Electron Microscopy (TEM) and Scanning Electron Microscopy (SEM) are used extensively but particle analyses are typically subject to sample preparation artefacts from drying.13,14 Arguably, only cryo-TEM techniques can provide an accurate view of the colloidal state of nanoparticle dispersions.15 Dynamic light scattering (DLS) is probably the most common technique used for characterization of particle size distributions in dispersions, but the biased response towards larger particles (∝d6) prevents the models to accurately describe samples with broad or multi-modal size distributions.14,16,17 Other options include the use of analytical ultra-centrifugation,18 and small angle scattering (SAS) using either neutrons or X-rays of fractionated dispersions,19 although the availability of these techniques are typically limited.In this study, we use asymmetric flow field-flow fractionation (AF4), ferromagnetic resonance (FMR) and AC- and DC-magnetomery to analyze a commercial magnetic nanoparticle system (nanoPET Pharma GmbH, FeraSpin). The system consists of a polydisperse mother batch (FeraSpin R) of magnetic nanoparticles with a wide size distribution,20 and the FeraSpin Series, comprising six from FeraSpin R fractioned components: FeraSpin XS, S, M, L, XL and XXL, where two (XS and L) were used in this work. We show that AF4 and FMR are effective in characterizing and classifying a nanoparticle dispersion as a bimodal, both with respect to its physical and magnetic properties. Although the magnetic material in each fraction consists of primary nanocrystals that are similar in size, they differ significantly with respect to the degree of clustering. We show that the strongly coupled colloidal nanoclusters exhibit magnetic properties, e.g. susceptibility, relaxation, and resonance properties, that are widely different than their isolated counterparts. Consequently, the non-fractioned sample exhibits three distinct ferromagnetic resonance fields, where two could be assigned to different populations of the bimodal size distribution. Immobilization/agglomeration of the suspended particles results in large changes of the FMR spectra due to dynamic line-broadening and resonance field shifts. The ability to quantitatively distinguish between mobile and immobilized/agglomerated particles suggests that FMR can be used as sensitive read-out method in several biosensing schemes.
Experimental section
Samples of FeraSpin R, XS and L were obtained from nanoPET and used as received at an iron concentration of 5.0, 5.0 and 5.1 mg mL−1, respectively. The iron concentration was determined photometrically by means of phenanthroline, employing iron standards for the calibration curve and iron oxide nanoparticle dispersions of known concentration as controls. The three dispersions have an orange-brown tint and the particles have a composition close to γ-Fe2O3 as determined by Mössbauer spectroscopy (not shown).Transmission electron microscopy (TEM)
A FEI Titan 80-300 TEM equipped with field emission gun and operated at 300 kV was used in this study. TEM specimens were prepared by drying a few drops of nanoparticle dispersion on holey carbon film coated Cu TEM grids. TEM bright field (BF) images of the particles were used to measure the size and aspect ratio of the nanoparticles and nanoclusters. The size of each particle is defined as the diameter of the circle that encloses the particle. In other words, the longest dimension of each particle is taken as the size of it. The aspect ratio of a particle is determined by the ratio between the major axis and minor axis of the ellipse that encloses the particle. Selected area electron diffraction (SAED) and dark field (DF) imaging were performed on individual nanoclusters in order to reveal the crystalline domain structures in the particles. Each DF image was formed by selecting a single diffraction spot using an objective aperture.Scanning electron microscopy (SEM)
SEM analysis of magnetic nanoparticles was performed using a Zeiss Supra 40VP system equipped with a field emission gun at 2–5 kV. FeraSpin L colloidal nanoclusters were prepared by electrostatic immobilisation of the nanoparticles on Si substrates, in order to prevent agglomeration of the particles during the drying process. The silicon substrates were first coated by a polyelectrolyte in order to provide a positive surface charge (opposite to the nanoclusters). The surface was then exposed to the nanoparticle dispersion for 1 min, rinsed in deionized water and spin-dried. High magnification (×400–600k) was used to image single nanoparticles and visualize their sub-structure and morphology. Lower magnification images (×150k) were used for particle size and shape analysis using the ImageJ software package.21Asymmetric flow field-flow fractionation (AF4)
The AF4 instrument (Eclipse 2 Separation System, Wyatt Technology, Dernbach, Germany) was connected to a MALS detector (Dawn Heleos II, Wyatt Technology) operating at a wavelength of 664 nm, a RI detector (Optilab T-Rex, Wyatt Technology) operating at 658 nm. An isocratic pump (Agilent 1100 G1311A, Agilent Technologies), with an in-line vacuum degasser and auto sampler, delivered the carrier flow and handled sample injection onto the AF4 channel. The AF4 channel (Wyatt Technology) had a tip-to-tip length of 17.4 cm, assembled with a 250 μm spacer and a regenerated cellulose ultrafiltration membrane with a 10 kDa cutoff (Merck Millipore, Billerica, MA, USA). The validation of the AF4 channel was performed with polystyrene nanoparticles of 60 nm of diameter (Thermo Scientific Cat. no. 3060A). The sample injection onto the channel was made at a flow rate of 0.20 mL min−1 for 1 min. The injected mass (mFe) was 10 μg for FeraSpin L and FeraSpin R and 30 μg for FeraSpin XS. The injected mass was optimized in order to ensure no overloading in the channel, by confirming that retention times were independent of several different injection amounts. The focusing time before elution was 1 min with a focusing flow of 2 mL min−1. An exponential decay cross-flow rate of 2 mL min−1 to 0.15 mL min−1 with half-life of 4 min was applied during elution. At the end of the decay, the cross-flow was held at 0.15 mL min−1 for 10 min allowing elution of the remaining material. Finally, the cross-flow was removed and the channel was flushed for 10 min before the next analysis. The detector flow was kept constant at 1 mL min−1 during analysis.The carrier liquid consisted of MilliQ water with 0.02 wt% NaN3 and 5 mM NaNO3. NaNO3 is used to reduce long-range electrostatic interactions during elution. Processing of the MALS data was made by the Astra software, version 6.1.2.84 (Wyatt Technology). The root square-mean diameter (Drms) was obtained from the light scattering data (MALS) by the Berry method,22 using a dn/dc value of 0.256 mL g−1.23
Dynamic light scattering (DLS)
The hydrodynamic diameter was determined using DLS Malvern Zetasizer Nano ZS (Malvern Instruments Ltd, Worcestershire, UK) using the viscosity and refractive index of the dispersant (H2O, μ = 0.8872 cP, n = 1.330). The temperature was set to 25 °C and the equilibration time to 60 s using a measurement angle of 173° (backscatter). The number of runs was set to 24, each run lasting 10 s. The measurements were done in triplicates. The data was processed using the cumulant and distribution analysis (general purpose model).Ferromagnetic resonance (FMR)
FMR was measured using a Bruker ELEXSYS E580 EPR spectrometer equipped with a standard X-band cavity. Measurements at cryogenic temperatures were performed using an Oxford ESR900 cryostat. The frequency of the microwave field was 9.78 GHz without the cryostat, and 9.47 GHz with the cryostat mounted. Thus, all measurements except the temperature series shown in Fig. 6a were measured at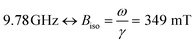 . Samples were mounted in (ID. Φ = 0.7 mm) quartz capillaries sealed in one end.
. Samples were mounted in (ID. Φ = 0.7 mm) quartz capillaries sealed in one end.
AC- and DC-magnetometry
Measurements were performed on a Quantum design MPMS-XL SQUID equipped with an RSO head. For the AC-measurements, an excitation field of BAC = 0.4 mT and frequencies of f = 0.17, 0.51, 1.7, 5.1, 17, 55, 170, 510, and 950 Hz were used. Liquid samples were mounted in cylindrical polymeric sample cups and filled with 30 μL dispersion (5 mg mL−1). The samples were weighed, and their volumes were determined assuming a density of 1.02 g mL−1. Freeze dried samples for AC-susceptibility measurements were prepared by dissolving 50 mM mannitol in the nanoparticle dispersions. Then, 30 μL of mannitol/nanoparticle dispersion was freeze-dried (directly in the cylindrical sample container). For the low-field DC-(±50 mT) and AC-magnetometry measurements we zeroed the field using the ultra-low field option, resulting in a background field of less than 1 μT. The dynamic scaling analysis was done setting the freezing temperatures to a value corresponding to the onset of dissipation, here 0.5 × max(χ′′(T)). The magnetic AC-moment was converted to dimensionless SI units (χ) assuming a density of 5 g cm−3 and a Fe/FexOy mass ratio of 0.7 (assuming γ-Fe2O3).Results and discussion
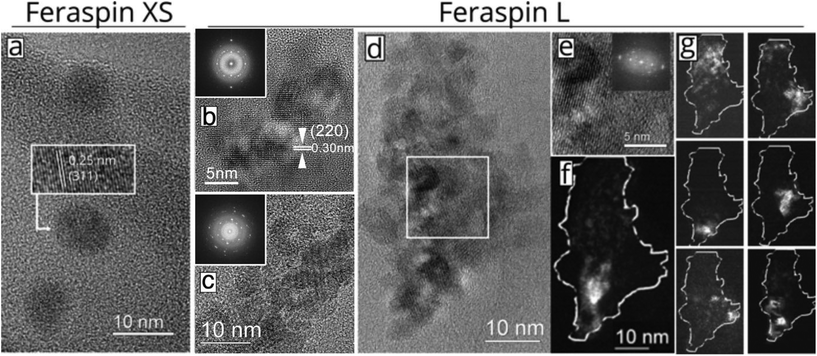
In this study, we compare experiments performed on three commercially available nanoparticle dispersions composed of carboxydextran-coated iron oxide particles in water. The starting material (FeraSpin R) is separated into increasingly larger fractions: FeraSpin XS-XXL. Out of the 6 fractions, two were used in this work (FeraSpin XS and FeraSpin L). Bright-field TEM images of the two fractions of FeraSpin R: FeraSpin XS and FeraSpin L are shown in Fig. 1a–d. The two fractions exhibit similar primary crystallite sizes but differ significantly with respect to the degree of clustering. FeraSpin XS appears to consist of small nanocrystals with an average size of ≈6 nm (σlog-normal = 0.26, see Fig. S1†). In most cases, the particles appear well separated (as shown in Fig. 1a), whereas they in some instances are found loosely aggregated (see Fig. S4†). We would like to point out that it is not possible to conclude from TEM alone whether these aggregates are also present in the dispersed state, but our fractionation study (vide infra) suggests that these are preparation artefacts caused by drying induced aggregation. High-resolution TEM (HRTEM) images (Fig. 1a) clearly show that the particles are nearly spherical and are crystalline enough to exhibit clear lattice fringes, as shown in the inset.In contrast, FeraSpin L consists of much larger, slightly elongated flake-like nanoclusters. We analyzed the shape and size of the nanoclusters using both SEM and TEM. In TEM, this is done by approximating their shapes with ellipses, taking the long semi-axis as the particle length and the ratio of the semi-axes. The lower resolution of SEM compared to TEM, is somewhat compensated by the large number of measurement points attainable through automatic segmentation of the images. In fact, both methods yield a value of ≈35 nm for the long axis of the FeraSpin L nanoclusters, whereas we find a slightly broader size distribution in the SEM analysis σlog-normal = 0.40 (TEM) vs. σlog-normal = 0.60 (SEM), see Fig. S1.† Similarly, TEM and SEM yield almost identical estimates of the nanoclusters mean aspect ratio: ≈1.40 (σlog-normal = 0.20, see Fig. S1†). Moreover, bright-field TEM images (Fig. 1b–d) show that the flake-like nanoclusters are composed of tightly packed nanocrystals with primary particle sizes comparable to FeraSpin XS. The nanocrystals are in direct physical contact and in many cases intergrown, as evidenced by common lattice fringes in neighbouring nanocrystals.
In fact, the HRTEM images and the corresponding FFT patterns (Fig. 1b–d) reveal that relatively large subdomains of the FeraSpin L nanoclusters exhibit crystallographic texture, possibly the result of an “oriented attachment” mechanism. In order to further investigate the intra-cluster particle orientation, we performed dark-field TEM (DFTEM) imaging. DFTEM images shown in Fig. 1f–g, suggest that the FeraSpin L nanoclusters indeed are composed of a large number of crystalline domains, although the average size of these domains supersede the size of the constituent nanocrystals. Epitaxial clusters of nanocrystals have in recent literature been referred to as e.g. monocrystalline “nanoflowers” (by the group of Gazeau),24 “colloidal nanoclusters” by the group of Yin,25,26 and “mesocrystals” by Cölfen.27,28
Asymmetric flow field-flow fractionation (AF4)
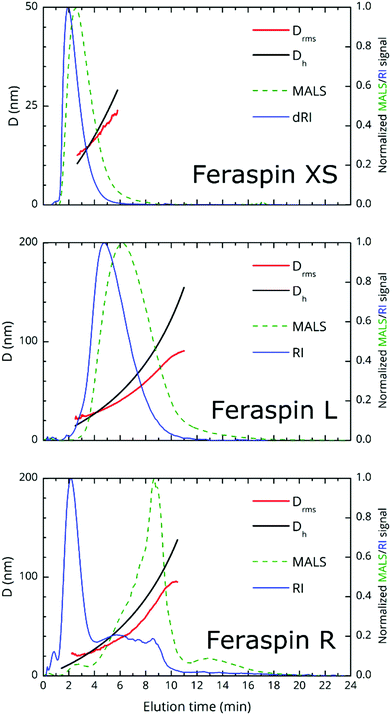
AF4 fractograms are shown in Fig. 2. AF4 is a sized-based separation technique which is chromatography-like but utilizes a channel, void of stationary phase, for separation of the sample in to narrowly distributed size fractions. The separation is based on the diffusion coefficient and, thus, the hydrodynamic diameter of the fractions can be determined from elution times via the Stokes–Einstein equation.29 Post-channel, a multiangle light scattering (MALS) detector is mounted for size determination as root mean-square diameter, Drms, equivalent to the diameter of gyration, in addition to a refractive index detector for concentration determination.The theoretical limit for the determination of Drms using the MALS detector is about 15 nm, since smaller particles are isotropic scatterers at the utilized wavelength (658 nm). From the fractograms, it is immediately obvious that FeraSpin XS and L have monomodal, but vastly different size distributions, whereas FeraSpin R, in some sense can be regarded as a mixture of the two, albeit with a slightly broader distribution of (larger) colloidal nanoclusters than in FeraSpin L. The data can be transformed into a differential weight fraction diagram, shown in Fig. S5,† with Drms cusp values of ≈13 and ≈33 nm for FeraSpin XS and L, respectively. The Drms of FeraSpin L is similar to the nanocluster size determined by SEM/TEM. For FeraSpin XS Drms > DNC ≈ 6 nm, indicating some aggregation of the primary nanocrystals.
Moreover, it is possible to determine the conformational ratio: Drms/Dh which can give information about the shape of the particles (see Fig. S5†). In general, although these ratios vary somewhat with the aging time of the particle dispersions (in particular FeraSpin XS, which aggregates slightly over time), we consequently find 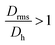 for the smallest fractions in each of the three samples. As a reference, a hard sphere with homogeneous mass distribution have
for the smallest fractions in each of the three samples. As a reference, a hard sphere with homogeneous mass distribution have 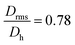 .
. 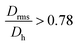 generally indicates elongated particles, whereas
generally indicates elongated particles, whereas 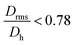 are found for e.g. swollen microgels.30 In particular, the most populous fraction of the FeraSpin L nanoclusters (≈20–40 nm) exhibits a conformational ratio of 1.2–0.83. This is indicative of an elongation of the nanoclusters, although the accuracy of the determination decreases near the resolution limit of the MALS detector. For particles, larger than 40 nm, the conformational ratio appears to converge towards
are found for e.g. swollen microgels.30 In particular, the most populous fraction of the FeraSpin L nanoclusters (≈20–40 nm) exhibits a conformational ratio of 1.2–0.83. This is indicative of an elongation of the nanoclusters, although the accuracy of the determination decreases near the resolution limit of the MALS detector. For particles, larger than 40 nm, the conformational ratio appears to converge towards 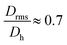 .
.
Comparing this analysis with the SEM analysis sorted into three size bins (<20 nm, 20–40 nm, >40 nm), see Fig. S3,† does not reveal any significant differences with respect to the particle aspect ratio, circularity or solidity with size. Admittedly, the SEM analysis is relatively poor for particles <20 nm; also, it should be noted that AF4, in contrast to SEM provides a measure of the colloidal (Dh or Drms) size and differences may reflect changes in structure of the capping agent. In summary, AF4/TEM/SEM concur that the largest population in FeraSpin L (≈20–40 nm) is slightly anisotropic, whereas AF4 suggests that the larger particles (≈40–60 nm) appear slightly micro-gelled, possibly the result of a solvent swollen dextran shell.
To conclude, we note that the major advantage of AF4 is that the fractionation eliminates many of the limitations of batch DLS measurements such as handling of multimodality/polydispersity through models and fitting procedures as well as obscuration of small particles caused by the presence of large particles. As a result, the sample size multimodality in FeraSpin R is obvious, simply by comparing the three relative refractive index signals (shown in the same plot, Fig. S6a†). This in stark contrast to conventional dynamic light-scattering (DLS), shown in Fig. S6b,† where the population of larger nanoclusters effectively shadows the smaller, but in terms of total volume equally large population of nanoparticles in the Dh = 10–20 nm range.
AC- and DC-magnetic properties
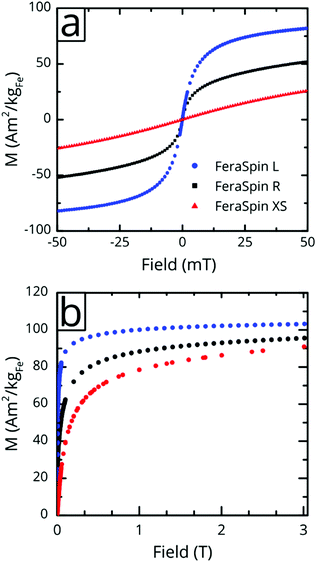
Fig. 3a shows the magnetization vs. low-field (±50 mT) curves for the three liquid nanoparticle dispersions. The particles are suspended during measurement, relax by Brownian rotation and consequently show no coercivity or remanent magnetization. The initial susceptibility of FeraSpin L is significantly larger than that of FeraSpin XS, suggesting that the apparent magnetic volume (Langevin size)31 of these particles differ greatly. Assuming that FeraSpin R is simply a mixture (linear combination) of FeraSpin XS and L yields a ratio of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
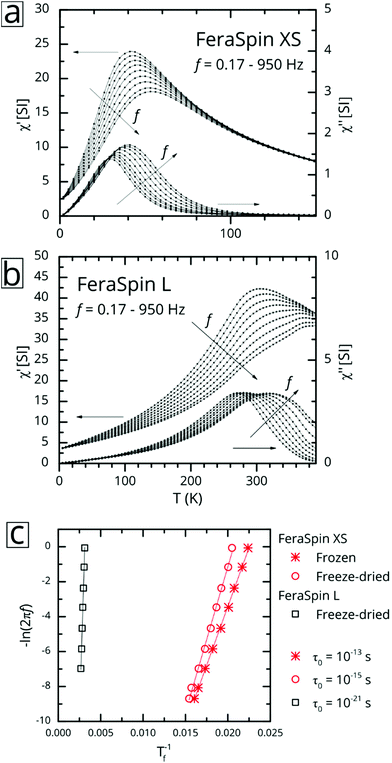
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 (see Fig. S9†), with very minor deviations near zero field. So, although it is clear from the fractograms (Fig. 2) that the size distribution of FeraSpin R has a slightly longer tail than FeraSpin L, its magnetization vs. field properties can very accurately be described as a mix of FeraSpin XS and L. Fig. 3b shows that also the high field properties differ significantly. Starting with the saturation magnetization, we find a slightly lower Ms(3 T) of FeraSpin XS (93 Am2 kgFe−1) compared to FeraSpin R and L (95 and 103 Am2 kgFe−1, respectively). The lower magnetization along with significantly larger high-field susceptibility (cf. slope in the range 1–3 T) provides an indirect evidence for surface spin-canting in FeraSpin XS. AC-susceptibility vs. temperature was performed on samples immobilized by freeze-drying in a sugar matrix (FeraSpin XS and L) allowing measurement up to 390 K, or by simply freezing the nanoparticle dispersion (FeraSpin XS). The freezing temperatures are typically defined as either the cusp temperature in the χ′(T) curves or the half max in the χ′′(T) curves. For FeraSpin XS these lie in the range Tf ≈ 45–65 K.
53 (see Fig. S9†), with very minor deviations near zero field. So, although it is clear from the fractograms (Fig. 2) that the size distribution of FeraSpin R has a slightly longer tail than FeraSpin L, its magnetization vs. field properties can very accurately be described as a mix of FeraSpin XS and L. Fig. 3b shows that also the high field properties differ significantly. Starting with the saturation magnetization, we find a slightly lower Ms(3 T) of FeraSpin XS (93 Am2 kgFe−1) compared to FeraSpin R and L (95 and 103 Am2 kgFe−1, respectively). The lower magnetization along with significantly larger high-field susceptibility (cf. slope in the range 1–3 T) provides an indirect evidence for surface spin-canting in FeraSpin XS. AC-susceptibility vs. temperature was performed on samples immobilized by freeze-drying in a sugar matrix (FeraSpin XS and L) allowing measurement up to 390 K, or by simply freezing the nanoparticle dispersion (FeraSpin XS). The freezing temperatures are typically defined as either the cusp temperature in the χ′(T) curves or the half max in the χ′′(T) curves. For FeraSpin XS these lie in the range Tf ≈ 45–65 K.
Fig. 4c shows a fit to an Arrhenius equation 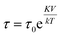 where K is an anisotropy constant, V is the particle volume, and τ0 is the microscopic attempt frequency. The fit yields a value of τ0 ≈ 10−15 s; the small value (τ0 ≪ 10−9–10−10 s) in combination with the frequency-dependent increase of the χ′′-cusps are indicators of magnetic (inter)particle interactions in the freeze-dried material. These interactions are slightly reduced but not eliminated (τ0 ≈ 10−13 s) in the frozen dispersion. Assuming that the particles are spherical with core diameter dc ≈ 6 nm, the Arrhenius approach yields K ≈ 1.6 × 105 J m−3, which is more than one order of magnitude larger than K reported for γ-Fe2O3 thin films (−0.46 × 104 J m−3).32 High K values have typically been reported for small particles, due to a significant contribution from surface anisotropy.7 In a second approach we consider the low-temperature part of the χ′(T) curve. The in-phase component χ′ of the AC susceptibility should approach a frequency independent value as the temperature approaches zero. This corresponds to the intra-potential well response of the particles moments χ⊥ (ref. 33)
where K is an anisotropy constant, V is the particle volume, and τ0 is the microscopic attempt frequency. The fit yields a value of τ0 ≈ 10−15 s; the small value (τ0 ≪ 10−9–10−10 s) in combination with the frequency-dependent increase of the χ′′-cusps are indicators of magnetic (inter)particle interactions in the freeze-dried material. These interactions are slightly reduced but not eliminated (τ0 ≈ 10−13 s) in the frozen dispersion. Assuming that the particles are spherical with core diameter dc ≈ 6 nm, the Arrhenius approach yields K ≈ 1.6 × 105 J m−3, which is more than one order of magnitude larger than K reported for γ-Fe2O3 thin films (−0.46 × 104 J m−3).32 High K values have typically been reported for small particles, due to a significant contribution from surface anisotropy.7 In a second approach we consider the low-temperature part of the χ′(T) curve. The in-phase component χ′ of the AC susceptibility should approach a frequency independent value as the temperature approaches zero. This corresponds to the intra-potential well response of the particles moments χ⊥ (ref. 33)
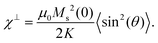 | (1) |
Here θ is the angle between the magnetic field and the (uniaxial) particle easy axis, and the value of 〈sin2(θ)〉 is averaged over the distribution of easy axis orientations. As a first approximation, it is reasonable to adopt a random distribution of easy axes, so that: 〈sin2(θ)〉 = 2/3. Although neither of these models take into account interparticle interactions, the intra potential-well approximation with Ms(0) ≈ 110 Am2 kgFe−1 gives a more reasonable value of K = 2.8(2) × 104 J m−3 for FeraSpin XS than the Arrhenius approach (see Table S1†), yet significantly larger (≈ × 7) than the reported K for γ-Fe2O3 (bulk).
In contrast, AC-susceptibility vs. temperature (5–390 K) measurements on freeze-dried FeraSpin L nanoclusters (Fig. 4b), show freezing temperatures in the range Tf ≈ 320–400 K. Fitting the freezing temperatures to the Arrhenius equation yields an unphysical value of τ0 ≈ 10−21 s, a clear sign of significant interactions, clearly invalidating the Arrhenius approach. The intra-potential well approximation using Ms(0) ≈ 120 Am2 kgFe−1, yields an effective anisotropy constant for FeraSpin L of K = 2.1(2) × 104 J m−3, smaller than for FeraSpin XS, but significantly larger than the bulk anisotropy of γ-Fe2O3. Thus, the FeraSpin L nanoclusters should be viewed as strongly coupled (collective) nanoclusters, with a significant anisotropy contribution originating either from surface or interfacial effects. The strong coupling results in a significant alteration of the magnetic relaxation times (Tf = 45 → 320 K). In fact, this large shift is impossible to explain based solely on dipolar interactions, i.e. by assuming particles with dc ≈ 6 nm in physical contact.34 In other words, although FeraSpin L is composed of fused nanocrystals of the same (apparent) primary size as FeraSpin XS, they exhibit a magnetic behaviour intermediate of the primary and secondary particle size of the colloidal nanoclusters. This is clear proof that (strong) exchange interactions between neighbouring surface spins, in addition to dipolar interactions, must be taken into account in order to accurately model the properties of colloidal clusters and nanoflowers.26
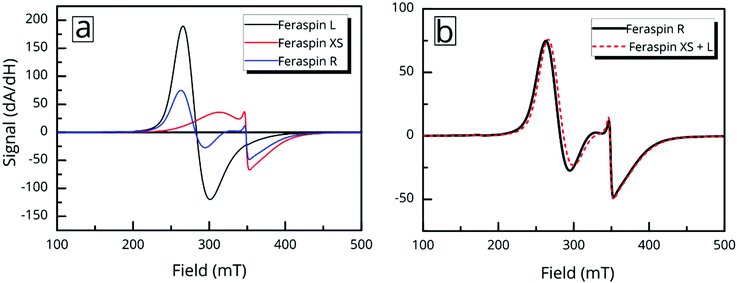
Ferromagnetic resonance (FMR) properties
Ferromagnetic resonance measurements were performed at the X-band, using aqueous dispersions mounted in quartz capillaries. Results from measurements on liquid samples (298 K) are shown in Fig. 5a. FeraSpin R exhibits a complex multi-component spectrum, that can be fitted to a sum of three Gaussian derivatives. This yields two broad lines with resonance field (Br) and full-with-half-maximum line-width (ΔBFWHM) of Br = 279 mT/ΔBFWHM = 41 mT, and Br = 333 mT/ΔBFWHM = 76 mT, respectively, in addition to a narrow line at Br = 350 mT/ΔBFWHM = 12 mT; the latter line coincides with the free electron resonance field: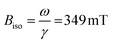 at X-band frequencies (ω = 2π × 9.78 × 109 rad s−1, γ = 1.76 × 1011 rad s−1 T−1). From the measurements of the fractioned samples (FeraSpin XS and L) it is clear that these resonances can be individually assigned to the large (Br = 279 mT) and small fractions (at Br = 333 mT, and at Br = 350 mT) of the bimodal distribution of FeraSpin R (see Fig. 5a). Although the AF4 analysis shows that FeraSpin R contains a slightly broader distribution of nanoclusters than FeraSpin L (see Fig. 2), we find that it is possible to fit the FeraSpin R spectra by a linear combination of FeraSpin XS and FeraSpin L with relatively good accuracy (see Fig. 5b). From the fits, we find ratios of 37
at X-band frequencies (ω = 2π × 9.78 × 109 rad s−1, γ = 1.76 × 1011 rad s−1 T−1). From the measurements of the fractioned samples (FeraSpin XS and L) it is clear that these resonances can be individually assigned to the large (Br = 279 mT) and small fractions (at Br = 333 mT, and at Br = 350 mT) of the bimodal distribution of FeraSpin R (see Fig. 5a). Although the AF4 analysis shows that FeraSpin R contains a slightly broader distribution of nanoclusters than FeraSpin L (see Fig. 2), we find that it is possible to fit the FeraSpin R spectra by a linear combination of FeraSpin XS and FeraSpin L with relatively good accuracy (see Fig. 5b). From the fits, we find ratios of 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 (R2 = 0.95) by mass in reasonable agreement with estimates from magnetometry (47
63 (R2 = 0.95) by mass in reasonable agreement with estimates from magnetometry (47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53, R2 = 0.999).
53, R2 = 0.999).
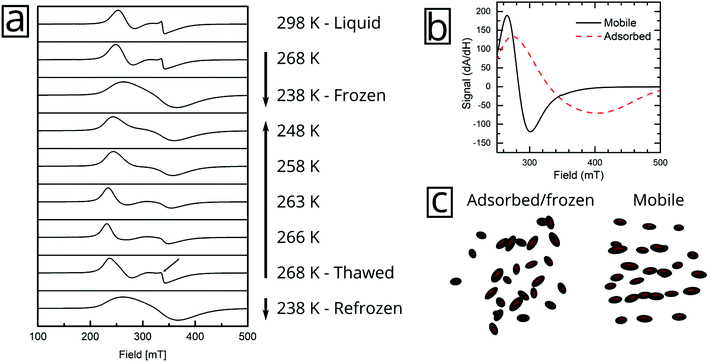
But the complex resonance signal of FeraSpin R is simply not the sum of several magnetic components; it is significantly influenced by interparticle interactions in the system, as well as the rotational degrees of freedom of the larger nanoclusters. This can be illustrated in two ways; freezing a FeraSpin R dispersion at 238 K eliminates the fine structure and the resonance signal collapses into one broad and slightly asymmetric mode (see Fig. 6a). Conversely, heating the frozen dispersion towards its melting point gradually recovers the three resonance lines, whereas the narrow line only reappears when the dispersion is completely thawed. Secondly, the fine structure can also be eliminated by absorbing the nanoparticle dispersion in cotton fibre (see Fig. S8†). Similar to the dispersed systems, the FMR signals are additive; the immobilized FeraSpin R particles can be nicely fitted to a linear combination of immobilized FeraSpin L and XS (see Fig. S8†).
Two-component spectra similar to that of FeraSpin XS have previously been observed for immobilized γ-Fe2O3 particles (d = 3.6 nm) mineralized in Listeria innocua cages. Two distinct resonances (broad and narrow) were attributed to a core–shell structure from the analysis of their temperature dependent linewidths.35–37 The narrow line was assigned to surface spins or very small particles. Noginova et al. found that the narrow line of a γ-Fe2O3 (d = 4.8 nm) ferrofluid gradually broadened upon increase of the concentration.38 In a sense, the line-broadening of the narrow component therefore provides a measure of interparticle interactions; here, the likely cause being ice segregation-induced agglomeration,39 in agreement with the AC susceptibility results. Additionally, the immobilization results in a slight shift and broadening of the second resonance line, from Br = 340 mT/ΔBFWHM = 76 mT to Br = 343 mT/ΔBFWHM = 96 mT.
The immobilization of FeraSpin L results in a much larger shift of the resonance line from Br = 283 mT to 330 mT (see Fig. 6b). Simply put, the FeraSpin L possesses a significant anisotropy, that allows the dispersed particles to (at least partially) rotate into the field, and thereby lower their magnetic energy. We would like to emphasize that this effect is not due to dipolar chaining of the colloidal nanoclusters,38 since we observe no changes in the resonance properties upon dilution of the dispersion (see Fig. S7†). At a first approximation, the resonance shift (ΔBr) due to the particle immobilization, can be qualitatively understood simply by considering the particle shape anisotropy. Under the assumption that the magnetization follows the field (θ = θH), results in the following resonance condition40
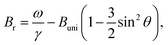 | (2) |
Nonetheless, it is clear that the dynamic fine structure allows FMR to swiftly, quantitively, and with good sensitivity differentiate between mobile and immobilized particles. These properties form the basis for many bio-sensing schemes,42 and suggests the use of FMR as a novel read-out method in magnetic biosensor assays. Also, since FMR spectra are in some sense fingerprints, sensitive to the physical properties (shape, anisotropy) but also to the colloidal state of any nanoparticle dispersion, we suggest its use as a tool for quality control, and monitoring in commercial production of magnetic nanoparticles.
Conclusions
Using a series of commercial nanoparticle dispersions, we have demonstrated a fast and quantitative assessment of particle size and property bimodality using AF4 and FMR: two sparsely used techniques in nanoparticle research. Although the particle fractions consist of primary nanocrystals similar in size, the oriented attachment of nanocrystals into tightly packed colloidal nanoclusters results in a material with drastically different magnetization, relaxation, and ferromagnetic resonance properties. When dispersed, the larger fraction of colloidal nanoclusters exhibit a resonance shift due to the alignment of the slightly anisotropic particles; a property which is likely to find use in a number of applications.Author contributions
E.W. conceived the study and designed the experiments. E.W and P.S. performed the magnetic characterization and analysis. A.C. and L.N. performed the DLS and AF4 experiments. L.Z. and E.O. acquired and analysed the TEM images. S.P acquired and analysed the SEM images. N.G. and D.H. synthesized and provided the materials. E.W. wrote the manuscript with input from all authors.Acknowledgements
This research was funded by the NANOMAG FP-7 project (Grant: FP7-NMP-604448). The authors would like to acknowledge Fikret Mamedov for his kind technical assistance with the EPR spectrometer. Daniel Hedlund is acknowledged for his assistance with the magnetometry measurements.Notes and references
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181 CrossRef CAS.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919–S2934 CrossRef CAS.
- S. H. Chung, A. Hoffmann, S. D. Bader, C. Liu, B. Kay, L. Makowski and L. Chen, Appl. Phys. Lett., 2004, 85, 2971–2973 CrossRef CAS.
- D. Eberbeck, F. Wiekhorst, S. Wagner and L. Trahms, Appl. Phys. Lett., 2011, 98, 2009–2012 CrossRef.
- N. A. Frey, S. Peng, K. Cheng and S. Sun, Chem. Soc. Rev., 2009, 38, 2532–2342 RSC.
- A. Lak, M. Kraken, F. Ludwig, A. Kornowski, D. Eberbeck, S. Sievers, F. J. Litterst, H. Weller and M. Schilling, Nanoscale, 2013, 5, 12286–12295 RSC.
- A. Demortière, P. Panissod, B. P. Pichon, G. Pourroy, D. Guillon, B. Donnio and S. Bégin-Colin, Nanoscale, 2011, 3, 225–232 RSC.
- G. Salazar-Alvarez, J. Qin, V. Šepelák, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. A. A. Macedo, M. Mikhaylova, M. Muhammed, M. D. Baró, J. Nogués, V. Sepelák, M. D. Baró and J. Nogués, J. Am. Chem. Soc., 2008, 130, 13234–13239 CrossRef CAS PubMed.
- E. Wetterskog, C.-W. Tai, J. Grins, L. Bergström and G. Salazar-Alvarez, ACS Nano, 2013, 7, 7132–7144 CrossRef CAS PubMed.
- D. F. Coral, P. Mendoza Zélis, M. Marciello, M. del P. Morales, A. Craievich, F. H. Sánchez and M. B. Fernández van Raap, Langmuir, 2016, 32, 1201–1213 CrossRef CAS PubMed.
- L. Lartigue, P. Hugounenq, D. Alloyeau, S. P. Clarke, M. Lévy, J.-C. Bacri, R. Bazzi, D. F. Brougham, C. Wilhelm and F. Gazeau, ACS Nano, 2012, 6, 10935–10949 CrossRef CAS PubMed.
- A. Lak, A. F. Thünemann, M. Schilling and F. Ludwig, J. Magn. Magn. Mater., 2015, 380, 140–143 CrossRef CAS.
- B. Michen, C. Geers, D. Vanhecke, C. Endes, B. Rothen-Rutishauser, S. Balog and A. Petri-Fink, Sci. Rep., 2015, 5, 9793 CrossRef CAS PubMed.
- R. F. Domingos, M. A. Baalousha, Y. Ju-nam, M. M. Reid, N. Tufenkji, J. R. Lead, G. G. Leppard and K. J. Wilkinson, Environ. Sci. Technol., 2009, 7277–7284 CrossRef CAS.
- K. Butter, P. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, J. Phys.: Condens. Matter, 2003, 15, S1451–S1470 CrossRef CAS.
- H. Hagendorfer, R. Kaegi, M. Parlinska, B. Sinnet, C. Ludwig and A. Ulrich, Anal. Chem., 2012, 84, 2678–2685 CrossRef CAS PubMed.
- M. Hassellöv, J. W. Readman, J. F. Ranville and K. Tiede, Ecotoxicology, 2008, 17, 344–361 CrossRef PubMed.
- J. Walter, K. Löhr, E. Karabudak, W. Reis, J. Mikhael, W. Peukert, W. Wohlleben and H. Cölfen, ACS Nano, 2014, 8, 8871–8886 CrossRef CAS PubMed.
- A. F. Thünemann, S. Rolf, P. Knappe and S. Weidner, Anal. Chem., 2009, 81, 296–301 CrossRef PubMed.
- F. Ludwig, T. Wawrzik, T. Yoshida, N. Gehrke, A. Briel, D. Eberbeck and M. Schilling, IEEE Trans. Magn., 2012, 48, 3780–3783 CrossRef.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- G. C. Berry, J. Chem. Phys., 1966, 44, 4550 CrossRef CAS.
- J. J. Ramsden and M. Mate, J. Chem. Soc., Faraday Trans., 1998, 94, 783–788 RSC.
- P. Hugounenq, M. Levy, D. Alloyeau, L. Lartigue, E. Dubois, V. Cabuil, C. Ricolleau, S. Roux, C. Wilhelm, F. Gazeau and R. Bazzi, J. Phys. Chem. C, 2012, 116, 15702–15712 CAS.
- Z. Lu and Y. Yin, Chem. Soc. Rev., 2012, 41, 6874–6887 RSC.
- A. Kostopoulou and A. Lappas, Nanotechnol. Rev., 2015, 4, 595–624 CAS.
- H. Cölfen and M. Antonietti, Angew. Chem., Int. Ed., 2005, 44, 5576–5591 CrossRef PubMed.
- M. Niederberger and H. Colfen, Phys. Chem. Chem. Phys., 2006, 8, 3271–3287 RSC.
- A. Håkansson, E. Magnusson, B. Bergenståhl and L. Nilsson, J. Chromatogr., A, 2012, 1253, 120–126 CrossRef PubMed.
- L. Nilsson, Food Hydrocolloids, 2013, 30, 1–11 CrossRef CAS.
- B. Luigjes, S. M. C. Woudenberg, R. de Groot, J. D. Meeldijk, H. M. Torres Galvis, K. P. de Jong, A. P. Philipse and B. H. Erné, J. Phys. Chem. C, 2011, 115, 14598–14605 CAS.
- B. Evans and D. L. Kohlstedt, Rock Physics & Phase Relations: A Handbook of Physical Constants, American Geophysical Union, Washington, D. C., 1995, vol. 3 Search PubMed.
- P. Svedlindh, T. Jonsson and J. L. García-Palacios, J. Magn. Magn. Mater., 1997, 169, 323–334 CrossRef CAS.
- M. S. Andersson, R. Mathieu, P. S. Normile, S. S. Lee, G. Singh, P. Nordblad and J. A. De Toro, Mater. Res. Express, 2016, 3, 45015 CrossRef.
- R. J. Usselman, M. T. Klem, S. E. Russek, M. Young, T. Douglas and R. B. Goldfarb, J. Appl. Phys., 2010, 107, 114703 CrossRef.
- R. J. Usselman, M. T. Klem, M. Allen, E. D. Walter, K. Gilmore, T. Douglas, M. Young, Y. Idzerda and D. J. Singel, J. Appl. Phys., 2005, 97, 10 CrossRef , M523.
- R. J. Usselman, S. E. Russek, M. T. Klem, M. A. Allen, T. Douglas, M. Young, Y. U. Idzerda and D. J. Singel, J. Appl. Phys., 2012, 112, 84701 CrossRef PubMed.
- N. Noginova, F. Chen, T. Weaver, E. P. Giannelis, A. B. Bourlinos and V. A. Atsarkin, J. Phys.: Condens. Matter, 2007, 19, 246208 CrossRef CAS PubMed.
- G. Kumaraswamy, B. Biswas and C. K. Choudhury, Faraday Discuss., 2016, 186, 61–76 RSC.
- F. Gazeau, J. C. Bacri, F. Gendron, R. Perzynski, Y. L. Raikher, V. I. Stepanov and E. Dubois, J. Magn. Magn. Mater., 1998, 186, 175–187 CrossRef CAS.
- J. A. Osborn, Phys. Rev., 1945, 67, 351–357 CrossRef.
- D. Issadore, Y. I. Park, H. Shao, C. Min, K. Lee, M. Liong, R. Weissleder and H. Lee, Lab Chip, 2014, 14, 2385–2397 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Size and aspect ratio determination, additional microscopy and magnetic characterization, and calculation of the effective demagnetization factor. See DOI: 10.1039/c7nr00023e |
| This journal is © The Royal Society of Chemistry 2017 |