Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The thermochemistry of long chain olefin isomers during hydroformylation†
Emilija
Kohls
 and
Matthias
Stein
and
Matthias
Stein
 *
*
Max Planck Institute for Dynamics of Complex Technical Systems, Sandtorstr. 1, 39106 Magdeburg, Germany. E-mail: matthias.stein@mpi-magdeburg.mpg.de
First published on 28th June 2017
Abstract
Rhodium-catalysed hydroformylation is the major industrial process to obtain aldehyde products from olefins. The isomerization of the olefin at the catalyst is the most prominent side reaction and lowers the overall yield of the process. We here investigate whether the olefin isomer distribution obtained from batch experiments using Rh(BiPhePhos) as a catalyst and n-decene as the olefin reaches the thermodynamic equilibrium and computational quantum chemical approaches are able to accurately reproduce the experimental olefin isomer distribution. The relative energies of cis/trans configurational and double bond positional isomers of long chain n-decene were calculated using Hartree–Fock, DFT and correlated ab initio methods. Results were compared to experimental data. Electron correlation was found to be critical for the description of cis-isomer relative energies. Dispersion corrections in the DFT calculations partially compensate for deficiencies and generally improve the agreement with experiment. Adding thermodynamic corrections suffers from the neglect of certain contributions to the entropy of flexible molecules. Accounting for the entropy of mixing of multiple conformers significantly reduces the deviation from experiment. The equilibrium distribution of long chain olefins is reasonably described by correlated QM and also some density functional methods. Computational thermochemistry has thus reached a state where it provides reliable parameters for complex reaction network models and process engineering.
Introduction
Hydroformylation or ‘oxo reaction’ refers to the transition metal (usually cobalt or rhodium) catalyzed conversion of alkenes to aldehydes. It represents one of the most important industrial processes in homogeneous catalysis with a volume of more than 10 million tons of oxo chemicals per year.1 The use of long chain olefins from sustainable sources in the hydroformylation reaction poses a challenge to the design of suitable solvents and also the continuous operation of semi-scale chemical plants.2Apart from the desired linear aldehyde product, double bond isomerization of the olefin coordinated to the catalyst occurs as a side reaction by which undesired branched aldehydes are being produced.3–6 This lowers the overall yield of the preferred main linear product. HRh(CO)(BiPhePhos) is an advanced hydroformylation (see Fig. 1) catalyst but also known to be very active in isomerization of the olefin double bond. By choice of appropriate conditions, the formation of undesired side products can be suppressed and thus an increase of yield or selectivity can be obtained.7
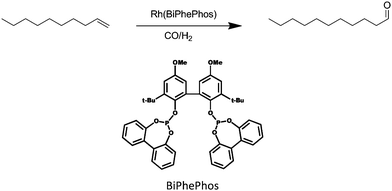 | ||
| Fig. 1 The hydroformylation reaction of 1-decene to the terminal undecanal as the desired product. Syngas (CO/H2) is used at 378 K, 20 bar in presence of a Rh(BiPhePhos) catalyst. | ||
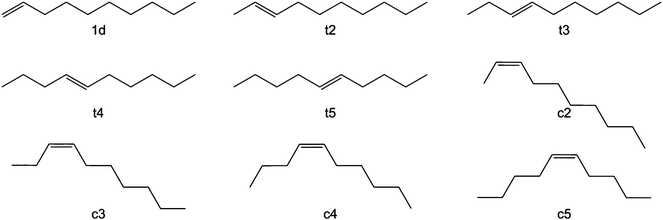
Long chain olefins from sustainable resources are a versatile alternative to substrates from petrochemicals.8,9 Their use poses challenges to an appropriate process design in terms of the solubility of substrates and the separation of products and catalyst.10,11 Recently, Jörke et al. have conducted an isothermal batch isomerization experiment using Rh(BiPhePhos)12 as catalyst and followed the concentration profiles of olefin isomers.13,14 1-Decene was used as the starting material and was isomerizing into all internal cis- and trans-decene isomers in presence of the catalyst and absence of syngas. This was assumed to be a stepwise process (Fig. 2). All n-decene positional isomers could be detected, assigned and quantified by gas chromatography. The time-resolved concentration profiles of each isomer were followed until no further changes in the concentration profiles were observed. The experimentally measured composition of isomers (Fig. 3) was used to deduce Gibbs free energy differences of internal n-decene isomers relative to the terminal 1-decene (values given in second column in Table 1).
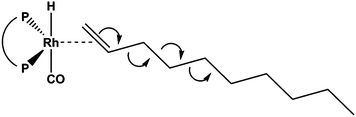 | ||
| Fig. 2 The olefin isomerization is the major side reaction to the hydroformylation. A Rh(BiPhePhos) catalyst in absence of syngas was used to investigate the 1-decene isomerization reaction. | ||
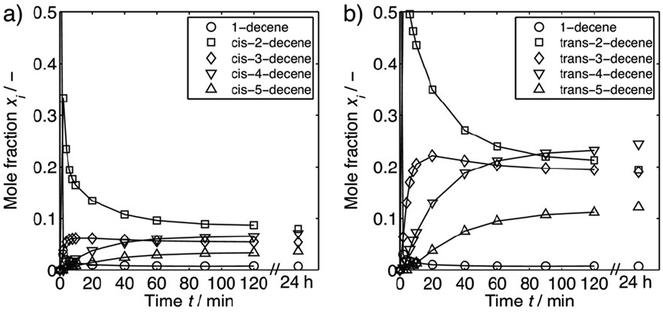 | ||
| Fig. 3 Experimentally measured equilibrium composition of all positional and geometrical linear decene isomers. (a) 1-Decene and internal cis-decene isomers; (b) 1-decene and internal trans-decene isomers. Reproduced with permission from the publisher from ref. 14. | ||
| Exp14 | HF | BP86 | BP86-D3 | B3LYP | B3LYP-D3 | M06-2X | B2PLYPa | B2PLYP | MP2 | LPNO-CCSDa | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Single point calculations at MP2/def2-TZVP optimized structures. | |||||||||||
| 1d | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00 | 0 | 0 |
| t2 | −10.07 | −9.44 | −13.94 | −11.66 | −12.46 | 10.51 | −9.80 | −10.48 | −11.11 | −10.65 | −9.22 |
| t3 | −9.98 | −9.06 | −13.35 | −10.84 | −12.01 | −9.90 | −8.91 | −10.12 | −11.28 | −10.75 | −8.31 |
| t4 | −10.75 | −9.40 | −13.98 | −11.41 | −12.56 | −10.37 | −9.33 | −10.46 | −11.63 | −11.24 | −9.17 |
| t5 | −8.56 | −9.40 | −13.96 | −11.39 | −12.54 | −10.34 | −9.48 | −10.46 | −11.62 | −11.28 | −9.09 |
| c2 | −7.28 | −2.27 | −8.64 | −7.68 | −6.57 | −5.84 | −4.93 | −5.40 | −6.48 | −5.83 | −4.75 |
| c3 | −5.99 | −1.27 | −7.47 | −6.68 | −5.52 | −5.01 | −3.53 | −4.66 | −6.18 | −5.92 | −3.86 |
| c4 | −6.87 | −1.62 | −8.02 | −7.59 | −5.97 | −5.72 | −3.83 | −5.02 | −7.02 | −7.00 | −4.41 |
| c5 | −4.78 | −1.62 | −8.07 | −7.66 | −6.00 | −5.82 | −4.26 | −5.57 | −7.77 | −7.12 | −4.43 |
| MUE | 2.73 | 2.89 | 1.33 | 1.69 | 0.91 | 1.51 | 1.07 | 1.30 | 1.07 | 1.51 | |
However, it could not finally be decided whether the final distribution of n-decene isomers was fully corresponding to the equilibrium distribution.
Computational aspects of modeling the hydroformylation process have mainly focused on mechanistic investigations (for recent reviews see ref. 15–17) and kinetics18 of the main reaction but not on the side reactions.
We here aim at a quantitative description of the distribution of positional and configurational n-decene isomers using quantum chemical (QC) thermochemistry.
Knowledge of thermochemical stability of chemical species is the key to industrial applications of structure-based calculations.19 Thermochemical predictions are of crucial importance for the design and control of industrial chemical processes. There are accurate composite approaches which include the Gn methodologies20 and the Wn theory.21,22 On the other hand, quantum chemical calculations, in particular Density Functional Theory (DFT), become increasingly important in chemical industry when determining thermochemical properties of larger systems. Insight gained at the molecular level and molecular industrial thermodynamics have recently been reviewed by Deglmann et al.19 They give an overview about current state-of-the-art applications of quantum chemical calculations to problems of engineering relevance. They use the calculation of chemical reaction thermodynamics as an example to demonstrate the accuracy of mostly DFT approaches. Nevertheless, Koglin and Meijer have very early shown that DFT methods are not sufficient to obtain a quantitatively correct description of n-hexane ggg and gtg conformers which needed to be carefully benchmarked against higher level calculations.23 There is large number of publications that demonstrate that B3LYP and other popular exchange–correlation functionals tend to have significantly larger errors for larger structures (in particular hydrocarbons).24–26 The failure is assigned to the inability of most functionals to describe long-range van der Waals effects and the neglect of medium-range electron correlation.27 The efforts to overcome these shortcomings resulted in the development of highly parameterized, dispersion-corrected, as well as double hybrid functionals. M05-2X functional performed satisfactorily for main-group thermochemistry and barrier heights due to its improved description of medium-range correlation.28,29 On the other hand, the increase in error with increasing system size for hydrocarbons using B3LYP, depended on the presence of particular structural and stereoelectronic features.29
The quantum thermochemistry of long-chain n-alkanes has received attention as model system for uncoupled internal rotations,30 one-dimensional hindered rotors31 and also to assess stereoelectronic effects32 and isodesmic bond separation energies.33 There is, however, much less work dedicated to the thermochemistry of olefins.
We here use DFT and higher correlated tools such as MP2 and coupled-cluster to calculate the distribution of highly flexible unbranched decene isomers and compare the results to those obtained from experiment. We also address the problem of scaling of vibrational frequencies, solvent effects, as well as the problem of entropic contributions and the related issue of consideration of multiple conformations.
Computational details
For all decene isomers several different levels of theory were tested: Hartree–Fock, Moller-Plesset second order perturbation theory (SCS-)MP2,34,35 coupled-cluster (DLPNO-CCSD36), as well as one representative from several classes of exchange–correlation DFT functionals: GGA functional BP86,37,38 hybrid meta GGA functional M06-2X,39 hybrid functional B3LYP37,40 and double hybrid functional B2PLYP.41 For the dispersion corrections to BP86 and B3LYP, D3 corrections according to Grimme42 were chosen. The molecules were optimized at every level of theory and then a frequency analysis was performed at the same level, except for the CCSD and the B2PLYP calculations which were single point calculations at the MP2/def2-TZVP geometries. A cc-pVTZ43,44 basis set for CCSD and a def2-TZVP45 basis sets was used in all calculations. Polarization functions are crucial to account for the small cis–trans energy differences.46 BP86 and MP2 calculations were done in the RI approximation.47 In the coupled cluster calculations the 10 lowest lying orbitals were frozen. Zero point vibrational energy (ZPVE) as well as enthalpic and entropic contributions at standard (298 K) and operating conditions (378 K) from the same level of theory were added using the rigid rotor/harmonic oscillator (RRHO) approximation. Solvent effects were probed by using an implicit continuum solvation model COSMO48 for ε = 2 and ε = 37 to model decane and dimethylformamide because the thermomorphic solvent used in the experiments is a mixture of both (ndecane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ndodecene
ndodecene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nDMF = 1
nDMF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4).14 All quantum chemical calculations were done with Turbomole 6.649 or Orca_v.3.0.1.50
4).14 All quantum chemical calculations were done with Turbomole 6.649 or Orca_v.3.0.1.50
For generating a library of conformers for each of the 9 isomers the stochastic Monte Carlo multiple minimum method (MCMM)51 was used in MacroModel 10.6.52 The maximum number of steps was set to 8000 and number of steps per rotatable bond to 2000. The energy window for saving the structures was set to 10 kJ mol−1. In order to determine the molecular mechanics force field best parameterized for the decene molecules we have also performed test calculations for different force fields and checked the quality of their stretch, bend and torsion parameters (not shown). We find that OPLS_200553 is the best parameterized for this case and it was used in the subsequent conformational search. Each generated conformer was re-optimized at B3LYP-D3/TZVP level of theory using Jaguar 8.6.54
Results and discussion
The thermodynamic equilibrium distribution of n-decene isomers after Rh-catalyzed isomerization
Jörke et al. used gas chromatographic separation to assign retention peaks of n-decene isomers after performing isomerization experiments catalysed by Rh(BiPhePhos) in the presence of inert nitrogen (N2) and absence of reactive gases (CO/H2) using commercially available decene isomers as standards. After 120 min of reaction time the GC-monitored concentration profiles of products remained constant with time and no change in concentrations up to 24 h was observed (see Fig. 3). This point was then assumed to have reached thermodynamic equilibrium. The experimentally observed n-decene isomer equilibrium composition at 378 K was subsequently used to estimate the Gibbs free energy differences using a standard mass action law. Non-ideal behaviour and activity coefficients would then cancel out in the relative equilibrium constants.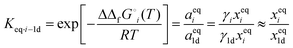 | (1) |
Physicochemical data for long chain n-olefins and kinetics regarding the isomerization side reaction are hardly available in the literature but required for a qualitative and quantitative understanding and control of the process.
The Benson group contribution method is an additive empirical approach to describe relative energies of molecules from functional group energy terms fitted to experiments. There are terms for sp3–sp2 carbon–carbon single bonds (one in 1-decene and two in other n-decene isomers), sp2–sp2 carbon–carbon double bonds, sp3–sp3 carbon–carbon single bonds and so one. The Benson group contribution method, however, cannot discriminate between subtle differences of structurally complex molecules such as 3- or 4-decene isomers and conformers. The Benson group contribution method gives a −4.9 kJ mol−1 energy difference between trans olefins and their cis isomers as a result of van der Waals repulsions which agrees well with 4.5 kJ mol−1 (1 kcal mol−1) which can be found in standard organic chemistry textbooks.55 These small energy differences point out the challenges to quantum chemical methods to accurately describe the thermodynamics and relative energies of long chain olefins.
The calculated relative energies (ΔE) are summarized in Table 1 and Fig. 5.
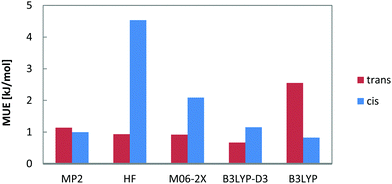 | ||
| Fig. 5 Performance of a subset of computational methods: mean unsigned errors for relative energies of all cis- and trans- n-decene isomers. Results for additional computational methods can be found in the ESI† (Table A). | ||
From Table 1 it becomes obvious that all computational methods (including DFT) give 1-decene to be the least stable isomer and the trans configurations to be lower in energy than their cis counterparts by 4–6.5 kJ mol−1. The experimentally determined energy differences between a cis isomer and its trans counterpart are below 4 kJ mol−1. This difference is best reproduced by the dispersion corrected functionals (BP86-D3 and B3LYP-D3). The mean unsigned error (MUE) decreases from 2.89 to 1.33 and from 1.69 to 0.91 kJ mol−1 for BP86(+D3) and B3LYP(+D3) respectively when dispersion corrections are added. This shows that dispersive corrections at least partially correct for the absence of long range dispersion in these density functionals.
From the DFs that were not corrected for vdW interactions, M06-2X with 54% of non-local, Hartree–Fock exchange performs best with a MUE of 1.51 kJ mol−1 followed by B3LYP and BP86. Since M06-2X was parameterized to account for the interpair but nonlocal electron correlations, it confirms that the medium range correlation is the missing part in the DFs for correctly describing hydrocarbon isomerization energies. The M06-2X functional, generated to overcome the correlation problem, is superior to B3LYP and other hybrid functionals but still does not provide complete correction of electron correlation. Song et al. conclude that local correlation needs to be incorporated and current exchange functionals are lacking this contribution.56 Double hybrid functionals such as B2PLYP were introduced to address the medium-range correlation issue and perform well for relative olefin double bond isomer energy differences (with a MUE of 1.30 kJ mol−1) and comparable to MP2 for single point calculations. Surprisingly, coupled cluster LPNO-CCSD calculations yield a larger deviation from experiment (1.51 kJ mol−1 on average) than MP2 (1.07 kJ mol−1) and this has to be assigned to the slower convergence with basis set size for these correlated wavefunction calculations which was also shown for the thermochemistry of the hydroformylation reaction.57
For the cis-configuration, all methods (except MP2 and B2PLYP) give cis-2-decene to be the most stable which agrees with the experimental findings. For trans-isomers, most of the methods predict either trans-2-decene or trans-4-decene (in agreement with experiment) to be the most stable one.
Hartree–Fock calculations perform well for the trans but not so for the cis isomers. This deficiency can be accounted for by inclusion of electron correlation (see MP2 values in Fig. 5). This level of treatment is necessary to correctly describe 1,4-alkyl–alkyl repulsive interactions in agreement with previous results for alkanes27 and relative stabilities of unbranched vs. branched alkene isomers.58Fig. 5 also shows that M06-2X with 54% of exact exchange exhibits larger error for the cis isomers than for the trans. This deficiency in cis stabilization arises from electron correlation and is not an exchange problem. The opposite is observed for B3LYP. It shows larger deviation for the trans isomers but this is significantly reduced by inclusion of dispersion interactions. MP2 is known to overestimate correlation effects in some chemical systems on the medium electron length scale but here we do not observe such an effect (spin-scaled MP2 yields identical results and therefore not given in Table 1).
It has to be noted that the experimental energy difference between some of the isomers is less than 1 kJ mol−1 and below the limits of computational accuracy. In several cases the difference in the calculated values is so minute that a couple of isomers can be considered to be isoenergetic and a strict energy ranking becomes impossible. According to experiment, the internal isomers (t5 and c5) are the least stable n-decene isomers. None of the computational methods, however, reproduce this finding from an electronic energy difference and thermal and entropic corrections to give Gibbs free energy differences must be accounted for (see below). Further, deviations from experimentally determined relative decene isomer stabilities may result from the neglect of solvent effects and the accessibility of multiple conformations for large, flexible long-chain molecules.33
Solvent effects on thermodynamic stability
Previous calculations were gas-phase calculations, but the experiments were performed in a solvent mixture of unpolar decane and polar DMF. We have considered the effect of both solvents on the relative energies of the n-decene isomers by incorporating an implicit solvent model (COSMO) with the respective dielectric constants. B3LYP was chosen as a representative method to assess the influence of solvent. The relative energies with and without solvent are given in Table 2 and deviations from experiment in Fig. 6.| B3LYP/def2-TZVP | ΔE (ε = 1) | ΔE (ε = 2) | ΔE (ε = 37) |
|---|---|---|---|
| 1d | 0 | 0 | 0 |
| t2 | −12.46 | −12.13 | −11.61 |
| t3 | −12.01 | −11.63 | −11.03 |
| t4 | −12.56 | −12.20 | −11.65 |
| t5 | −12.54 | −12.19 | −11.64 |
| c2 | −6.57 | −6.41 | −6.16 |
| c3 | −5.52 | −5.31 | −4.99 |
| c4 | −5.97 | −5.78 | −5.50 |
| c5 | −6.00 | −5.83 | −5.57 |
| MUE | 1.69 | 1.56 | 1.36 |
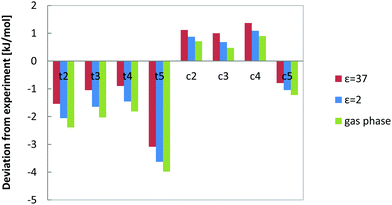 | ||
| Fig. 6 Solvent effects on calculated energy differences between 1-decene and the other n-decene isomers. The deviation of B3LYP results from experiment is given. | ||
Inclusion of solvent effects consistently lowers the energy differences between 1-decene and the other isomers and brings them closer to experiment. The effect of solvent stabilization, however, is small and below 1 kJ mol−1 in magnitude. All isomers are almost equally stabilized by the solvent effects which can be seen in Fig. 6.
The average deviation from experiment decreases from 1.69 to 1.56 in decane and to 1.36 kJ mol−1 in DMF in comparison to gas phase B3LYP data. The effect for a decane/DMF solvent system (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 w/w) will be intermediate. Since COSMO is an implicit solvent model specific solvent–solute interactions are not taken into account and the solution is ideal. We have previously estimated the non-ideality of a decane/DMF solvent system and their effect on the reaction enthalpy of the hydroformylation of dodecene.57 Significant activity αi and fugacity coefficients φi were needed to rationalize the equilibrium concentrations of reactants and products. For energy differences, however, these effects are assumed to cancel out.
20 w/w) will be intermediate. Since COSMO is an implicit solvent model specific solvent–solute interactions are not taken into account and the solution is ideal. We have previously estimated the non-ideality of a decane/DMF solvent system and their effect on the reaction enthalpy of the hydroformylation of dodecene.57 Significant activity αi and fugacity coefficients φi were needed to rationalize the equilibrium concentrations of reactants and products. For energy differences, however, these effects are assumed to cancel out.
Finite temperature thermochemistry
Although it is a common practice to compare quantum chemical electronic energies to experimental data, then zero point vibrational energies, thermal corrections and entropic contributions are usually neglected.When vibrational frequencies are obtained with sufficient accuracy, the calculated zero point vibrational energies (ZPVE) are also reliable. On the other hand Gibbs free energies i.e. entropies cannot be calculated with the same accuracy. This has its origins in approximating vibrations as being harmonic in nature. The vibrations that are most likely to have anharmonic character are the low-frequency vibrations which contribute most to the entropy. An error of 5% in a low frequency vibration causes an error of 15–30% in entropy.59 We here
(i) use empirical scaling factors from ref. 60 to partially compensate for anharmonic effects and deficiencies of the electronic structure calculation method; and
(ii) consider the accessibility of multiple conformers.
Frequency scaling
In order to examine the effect of frequency scaling on the calculated thermodynamic properties, we have used the vibrational scaling factors given in ref. 60 for BP86, B3LYP, M06-2X functionals as well as for MP2. For trans- and cis-5-decene the correct rotational symmetry number is used for calculating the entropy (symmetry number of two). The application of vibrational scaling factors does not reduce the MUE of Gibbs free energy differences from experiments (see Table 3). The effect is negligible for the thermodynamics of long chain olefins at 378 K. The calculated enthalpies and entropies are provided in the ESI† (Tables B1 and B2). The data for 298.15 K are given in the ESI† Table C.| Exp.14 | MP2a | B3LYPc | M06-2Xb | BP86d | |
|---|---|---|---|---|---|
| a λ = 0.9946. b λ = 0.9871. c λ = 1.0044. d λ = 1.0337. | |||||
| 1d | 0 | 0 | 0 | 0 | 0 |
| t2 | −10.07 | −12.05 (−12.04) | −16.22 (−16.23) | −16.62 (−16.61) | −18.74 (−18.79) |
| t3 | −9.98 | −11.40 (−11.40) | −15.43 (−15.43) | −14.60 (−14.58) | −17.66 (−17.69) |
| t4 | −10.75 | −12.55 (−12.54) | −12.65 (−12.64) | −17.36 (−17.35) | −13.96 (−13.98) |
| t5 | −8.56 | −10.46 (−10.45) | −11.31 (−11.31) | −9.05 (−9.04) | −12.95 (−12.96) |
| c2 | −7.28 | −9.37 (−9.37) | −12.53 (−12.53) | −13.59 (−13.59) | −16.47 (−16.51) |
| c3 | −5.99 | −9.59 (−9.59) | −8.03 (−8.02) | −8.58 (−8.57) | −10.62 (−10.64) |
| c4 | −6.87 | −9.60 (−9.60) | −10.35 (−10.34) | −8.37 (−8.36) | −12.61 (−12.63) |
| c5 | −4.78 | −8.16 (−8.16) | −6.75 (−6.74) | −2.62 (−2.62) | −8.81 (−8.81) |
| MUE | 2.36 (2.36) | 3.62 (3.62) | 3.85 (3.84) | 5.94 (5.97) | |
The entropy of mixing
At finite temperature, experimentally determined energy differences are ensemble-averages of a large number of conformers. QM reported energies are usually from single conformers only (in the best case the global minimum structure). The number of accessible conformers increases rapidly with the size and degree of flexibility of the molecule. Long-chain olefin compounds in liquid solution at elevated temperature are among the most flexible molecules and require an appropriate treatment of conformational equilibria.Enthalpies are in general less affected by the number of conformers which will be very close in energy (and thermodynamic corrections can be assumed to be identical for all conformers). Gibbs free energies, however, are much more affected by the presence of multiple conformers since they include entropic contributions. The difference in entropy between each conformer is negligible (ΔS for conformational change can be assumed to be zero; at most 2.8 J K−1 mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61), but the entropy of mixing multiple conformers is the critical contribution. So the total molar entropy, So, is the sum of entropies of each conformer plus a correction for the mixing term (ΔSmix) (eqn (2)):
61), but the entropy of mixing multiple conformers is the critical contribution. So the total molar entropy, So, is the sum of entropies of each conformer plus a correction for the mixing term (ΔSmix) (eqn (2)):
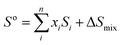 | (2) |
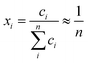 | (3) |
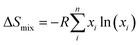 | (4) |
ΔSmix ≈ R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(n) ln(n) | (5) |
The importance of accounting for the entropy of mixing was pointed out amongst others by Block61et al. for small alcohols radicals. Guthrie62 describes in great detail the difficulties and approaches to properly account for entropy contributions for flexible molecules. Decene molecules are highly flexible with 8 rotatable bonds and the number of possible conformers that contribute to the energy at finite temperature is large. In the entropy of mixing, only distinguishable conformations have to be considered. Rotations about bonds to symmetrical groups (i.e. CH3, CF3, C(CH3)3) do not contribute to the number of conformers, while rotations about internal bonds or bonds to unsymmetrical terminal groups do.
We have conducted an exhaustive MCMM search to identify the number of possible conformers by torsional sampling. All obtained structures were subsequently re-optimized at the B3LYP-D3/TZVP level of theory. B3LYP-D3 was the method of choice for this analysis as it showed the best performance from the DFs in terms of energy and Gibbs free energy differences. After quantum-chemical re-optimization the number of conformers in an energy window of 2RT at: 298.15 K and 378 K (that is 5 kJ mol−1 and 6.3 kJ mol−1, respectively) were counted. The number of the conformers for each of the 9 positional and configurational isomers in an energy window of 6.3 kJ mol−1 is given in Table 4. The data for 298.15 K can be found in the ESI† (Table D).
| n | S (single conformer) | S corr | ΔG | Exp.14 | |
|---|---|---|---|---|---|
| 1d | 110 | 541.0 | 580.1 | 0.00 | 0.00 |
| t2 | 72 | 547.3 | 582.9 | −12.80 | −10.07 |
| t3 | 102 | 548.4 | 586.9 | −13.22 | −9.98 |
| t4 | 66 | 540.6 | 575.4 | −8.76 | −10.75 |
| t5 | 44 | 537.0 | 568.5 | −6.25 | −8.56 |
| c2 | 64 | 555.0 | 589.6 | −9.98 | −7.28 |
| c3 | 37 | 555.8 | 585.9 | −7.26 | −5.99 |
| c4 | 40 | 553.0 | 583.7 | −7.17 | −6.87 |
| c5 | 31 | 542.0 | 570.6 | −2.08 | −4.78 |
| MUE | 2.16 | ||||
Table 4 shows that consideration of entropy of mixing of conformers improves the agreement between calculated and observed values. It reduces the average deviation from experiment from 2.79 kJ mol−1 to 2.16 kJ mol−1 in terms of Gibbs free energy differences.
The optimized conformers in an energy window of 10 kJ mol−1 were used for performing a Boltzmann-weighted energy distribution. The mole fraction of the ith conformer of n conformers in equilibrium is weighted by its probability (eqn (6)):
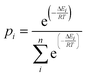 | (6) |
The Boltzmann-weighted energy for each isomer is then obtained:
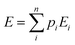 | (7) |
 th conformer. The results of the Boltzmann weighting are given in the ESI† in Table D1.
th conformer. The results of the Boltzmann weighting are given in the ESI† in Table D1.
For n-decene isomers, Boltzmann weighting did not improve the calculated relative energies (ΔE) compared to the single geometry calculations at the same level of theory (B3LYP-D3/TZVP) in Table 1.
This indicates that the very small energies of conformational change (often less than 0.1 kJ mol−1) are beyond the accuracy of current QM methods. Then, the calculated mole fractions of the conformers Boltzmann-weighted conformational energies do not reduce the deviation from experiment.
Conclusions
The thermochemistry of substrates, products and intermediates is a critical component to the design and control of chemical processes. The isomerization of 1-decene at the Rh(BiPhePhos) catalyst finally leads to a distribution of positional and configurational isomers at thermodynamic equilibrium. As can be seen from Fig. 3, isomerization of 1-decene first leads to a significant increase of formation of trans-2-decene and cis-2-decene to levels higher than their equilibrium composition. This can be explained by the steric demand of the BiPhePhos ligand (see Fig. 7). The isomerization to trans-2-decene is swift and possible despite the sterically demanding bisphenyl-bis-oxy rings of the ligand. cis-2-Decene formation is slower and requires some rearrangement of the olefin at the rhodium central metal atom. After a kinetically driven initial formation of 2-decenes, these react further to generate internal n-decene isomers. The olefin isomerization is a slow process and reaches its thermodynamic equilibrium after ∼90–100 min. It requires a sequential 1,2-hydrogen shift to then generate the next double bond positional isomer via a ‘chain walking’ mechanism. For n-decenes, the formation of internal olefins requires a re-arrangement of the alkyl chain due to the steric demand of the catalyst's ligand.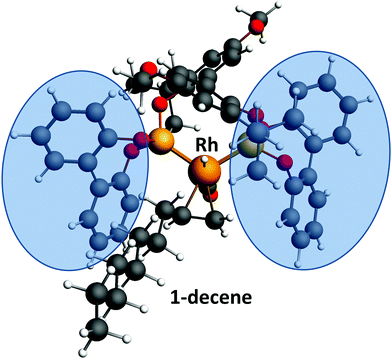 | ||
| Fig. 7 Calculated binding of 1-decene to a HRh(CO)(BiPhePhos) catalyst. The steric demand by the biphenylbisoxy ligand parts poses a steric restriction to coordination of internal n-decene isomers. | ||
The relative stabilities of n-decene isomers at thermodynamic equilibrium can qualitatively be reproduced by QM methods to rank trans- vs. cis-configurations lower in energy by about 4 kJ mol−1. The accuracy of the computational approaches to generate reliable thermodynamic data for industrial process engineering is not fully exploited yet and requires careful inspection.19 In previous studies for other alkane and alkene isomers27,58 DFT calculations were not able to reproduce the energetic ordering of the isomers. When comparing to experiment, the MUE for all methods is below 3 kJ mol−1. Comparison of the Hartree–Fock and correlated MP2 and CCSD methods establishes the importance of electron correlation in the description of the cis isomers, but less for the trans isomers. One possible explanation is the missing correlation in the description of 1,4-alkyl–alkyl repulsive interactions. According to our study, van der Waals interactions also play a critical role and empirically correcting them significantly improves the results for the DFs. The final relative thermodynamic stabilization of trans-4- versus trans-2-decene requires a careful inclusion of electron correlation from MP2 calculations (which is also included in the B2PLYP functional).
The molecular thermochemistry of long-chain olefins still poses a challenge to current computational approaches. The RRHO approximation introduces errors in the entropic part which questions the ability of standard simplifications to the state function Q to calculate thermodynamic properties with high accuracy. An agreement with experiment can be significantly improved by correcting for the entropy of mixing for flexible molecules. This benchmark of thermochemical data of long chain olefins will help to assign parameters required in the kinetic network model for the hydroformylation process.63,64
Acknowledgements
We thank the Max Planck Society for the Advancement of Science for financial support. This work is part of the Collaborative Research Center/Transregio 63 “Integrated Chemical Processes in Liquid Multiphase Systems” (subproject A4). Financial support by Deutsche Forschungsgemeinschaft (DFG) is gratefully acknowledged. Open Access funding provided by the Max Planck Society.References
- R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732 CrossRef CAS PubMed.
- T. Pogrzeba, D. Müller, T. Hamerla, E. Esche, N. Paul, G. N. Wozny and R. Schomäcker, Ind. Eng. Chem. Res., 2015, 54, 11953–11960 CrossRef CAS.
- A. Behr, D. Obst, C. Schulte and T. Schosser, J. Mol. Catal. A: Chem., 2003, 206, 179–184 CrossRef CAS.
- A. Behr, D. Obst and B. Turkowski, J. Mol. Catal. A: Chem., 2005, 226, 215–219 CrossRef CAS.
- C. Vogl, E. Paetzold, C. Fischer and U. Kragl, J. Mol. Catal. A: Chem., 2005, 232, 41–44 CrossRef CAS.
- B. Fell and H. Bahrmann, J. Mol. Catal., 1977, 2, 211–218 CrossRef CAS.
- E. Schafer, Y. Brunsch, G. Sadowski and A. Behr, Ind. Eng. Chem. Res., 2012, 51, 10296–10306 CrossRef.
- T. Vanbesien, E. Monflier and F. Hapiot, Eur. J. Lipid Sci. Technol., 2016, 118, 26–35 CrossRef CAS.
- C. De, R. Saha, S. K. Ghosh, A. Ghosh, K. Mukherjee, S. S. Bhattacharyya and B. Saha, Res. Chem. Intermed., 2013, 39, 3463–3474 CrossRef CAS.
- A. Behr, A. Westfechtel and J. P. Gomes, Chem. Eng. Technol., 2008, 31, 700–714 CrossRef CAS.
- A. Behr, G. Henze and R. Schomacker, Adv. Synth. Catal., 2006, 348, 1485–1495 CrossRef CAS.
- The systematic name of the ligand BiPhePhos is 6,6′-[(3,3′-di-tert-butyl-5,5′-dimethoxy-1,1′-biphenyl-2,2′-diyl)bis(oxy)]bis(dibenzo[d,f][1,3,2]dioxaphosphepin).
- A. Jörke, A. Seidel-Morgenstern and C. Hamel, Chem. Eng. J., 2015, 260, 513–523 CrossRef.
- A. Jörke, E. Kohls, S. Triemer, A. Seidel-Morgenstern, C. Hamel and M. Stein, Chem. Eng. Process., 2016, 102, 229–237 CrossRef.
- J. Jover and F. Maseras, in Computational Studies in Organometallic Chemistry, ed. S. A. Macgregor and O. Eisenstein, 2016, vol. 167, pp. 59–79 Search PubMed.
- T. Kegl, RSC Adv., 2015, 5, 4304–4327 RSC.
- G. Ujaque and F. Maseras, in Principles and Applications of Density Functional Theory in InorganicChemistry I, ed. N. Kaltsoyannis and J. E. McGrady, 2004, vol. 112, pp. 117–149 Search PubMed.
- L. E. Rush, P. G. Pringle and J. N. Harvey, Angew. Chem., Int. Ed., 2014, 53, 8672–8676 CrossRef CAS PubMed.
- P. Deglmann, A. Schäfer and C. Lennartz, Int. J. Quantum Chem., 2015, 115, 107–136 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 810–825 CrossRef CAS.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. Martin, M. Kallay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS PubMed.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856 CrossRef CAS.
- E. Koglin and R. J. Meier, Chem. Phys. Lett., 1999, 312, 284–290 CrossRef CAS.
- P. R. Schreiner, A. A. Fokin, R. A. Pascal and A. de Meijere, Org. Lett., 2006, 8, 3635–3638 CrossRef CAS PubMed.
- M. D. Wodrich, C. Corminboeuf and P. V. R. Schleyer, Org. Lett., 2006, 8, 3631–3634 CrossRef CAS PubMed.
- C. E. Check and T. M. Gilbert, J. Org. Chem., 2005, 70, 9828–9834 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed. Engl., 2006, 45, 4460–4464 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Org. Lett., 2006, 8, 5753–5755 CrossRef CAS PubMed.
- M. D. Wodrich, C. Corminboeuf, P. R. Schreiner, A. A. Fokin and P. V. R. Schleyer, Org. Lett., 2007, 9, 1851–1854 CrossRef CAS PubMed.
- P. Vansteenkiste, V. Van Speybroeck, G. B. Marin and M. Waroquier, J. Phys. Chem. A, 2003, 107, 3139–3145 CrossRef CAS.
- V. V. Speybroeck, P. Vansteenkiste, D. V. Neck and M. Waroquier, Chem. Phys. Lett., 2005, 402, 479–484 CrossRef.
- S. Grimme, Angew. Chem., Int. Ed., 2006, 45, 4460–4464 CrossRef CAS PubMed.
- S. Grimme, Org. Lett., 2010, 12, 4670–4673 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- S. R. Gandhi, M. A. Benzel, C. E. Dykstra and T. Fukunaga, J. Phys. Chem., 1982, 86, 3121–3126 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- TURBOMOLE V6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- G. Chang, W. C. Guida and W. C. Still, J. Am. Chem. Soc., 1989, 111, 4379–4386 CrossRef CAS.
- MacroModel, version 10.6. http://www.schrodinger.com/citations/41/11/1/(Schrödinger, New York, 2013).
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz and J. R. Maple, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed.
- Jaguar, version 8. 6, Schrödinger, LLC, New York, NY, 2014 Search PubMed.
- M. B. Smith and J. March, March's advanced organic chemistry: reactions, mechanisms, and structure, John Wiley & Sons, 2007 Search PubMed.
- J. W. Song, T. Tsuneda, T. Sato and K. Hirao, Org. Lett., 2010, 12, 1440–1443 CrossRef CAS PubMed.
- M. Lemberg, G. Sadowski, M. Gerlach, E. Kohls, M. Stein, C. Hamel and A. Seidel-Morgenstern, AIChE J., 2017 DOI:10.1002/aic.15782.
- P. S. Stewart, L. Rodriguez and D. H. Ess, J. Phys. Org. Chem., 2011, 24, 1222–1228 CrossRef CAS.
- A. L. East and L. Radom, J. Chem. Phys., 1997, 106, 6655–6674 CrossRef CAS.
- M. K. Kesharwani, B. Brauer and J. M. Martin, J. Phys. Chem. A, 2014, 119, 1701–1714 CrossRef PubMed.
- D. Block, D. Armstrong and A. Rauk, J. Phys. Chem. A, 1999, 103, 3562–3568 CrossRef CAS.
- J. P. Guthrie, J. Phys. Chem. A, 2001, 105, 8495–8499 CrossRef CAS.
- G. Kiedorf, D. M. Hoang, A. Müller, A. Jörke, J. Markert, H. Arellano-Garcia, A. Seidel-Morgenstern and C. Hamel, Chem. Eng. Sci., 2014, 115, 31–48 CrossRef CAS.
- B. Hentschel, G. Kiedorf, M. Gerlach, C. Hamel, A. Seidel-Morgenstern, H. Freund and K. Sundmacher, Ind. Eng. Chem. Res., 2015, 54, 1755–1765 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nj01396e |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2017 |