From molecules to dollars: integrating molecular design into thermo-economic process design using consistent thermodynamic modeling†
J.
Schilling
 a,
D.
Tillmanns
a,
D.
Tillmanns
 a,
M.
Lampe
a,
M.
Hopp
a,
M.
Lampe
a,
M.
Hopp
 b,
J.
Gross
b,
J.
Gross
 b and
A.
Bardow
b and
A.
Bardow
 *a
*a
aChair of Technical Thermodynamics, RWTH Aachen University, Germany. E-mail: andre.bardow@ltt.rwth-aachen.de
bInstitute of Thermodynamics and Thermal Process Engineering, Stuttgart University, Germany
First published on 9th June 2017
Abstract
The right molecules are often the key to overall process performance and economics of many energy and chemical conversion processes, such as, e.g., solvents for CO2 capture or working fluids for organic Rankine cycles. However, the process settings also impact the choices at the molecular level. Thus, ultimately, the process and the molecules have to be optimized simultaneously to obtain a thermo-economically optimal process. For a detailed design of the process and also the equipment, a thermodynamic model is required for both equilibrium and transport properties. We present an approach for the integrated thermo-economic design of the process, equipment and molecule on the basis of a comprehensive, thermodynamically consistent model of the molecule. For this purpose, we developed models for transport properties based on entropy-scaling of the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state. Thereby, a single model predicts both equilibrium and transport properties in our optimization-based approach for the integrated design of the process, equipment and molecule, the so-called 1-stage CoMT–CAMD approach. The predicted transport properties allow for the design and sizing of unit operations as degrees of freedom during the optimization. Computer-aided molecular design allows the design of novel molecules tailored to the specific process while considering safety and environmental issues. The presented approach is exemplified for the design of an organic Rankine cycle showing the merits of detailed sizing of heat exchangers with different heat transfer types and the rotating equipment as part of the optimization. Single-objective optimization is used to obtain a ranking of potential working fluids. The detailed trade-off between the total capital investment and the net power output of the ORC is studied using multi-objective optimization. Thus, the 1-stage CoMT–CAMD approach allows for efficient and holistic designs linking the molecular scale to economics.
Design, System, ApplicationThe design of molecules is usually not a goal by itself but should enable optimal performance at the process level. Here, we aim at the design of economically optimal molecules. Thus, we have to capture the impact of the molecular structure on process economics. To capture this impact, we integrate molecular design directly into thermo-economic design optimization. Thermo-economic design considers both the process and the employed equipment. The proposed integrated design allows us to quantify the trade- offs between molecular design, process settings and equipment sizing. We argue that the key to an efficient integrated design method is a thermodynamically consistent model for both equilibrium and transport properties. Here, we employ the physically based PC-SAFT equation of state. PC-SAFT has been extended beyond equilibrium properties to predict also viscosities and heat conductivities of fluids. We demonstrate the integrated thermo-economic design for an organic Rankine cycle to convert low-temperature heat into mechanical work. The design considers detailed correlations for sizing of the heat exchangers and the rotating equipment. The presented approach should be applicable to general problems for the integrated thermo-economic design of fluid molecules in energy and chemical engineering ranging, e.g., from refrigerants in heat pumps to solvents for CO2 absorption. |
1. Introduction
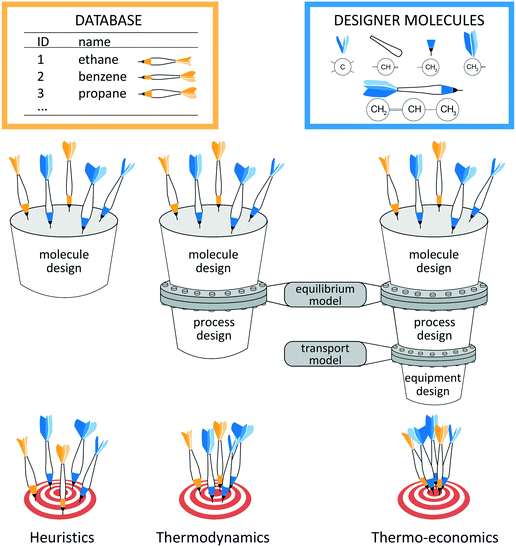
The key to energy and chemical conversion technologies is often the right choice of the molecules used as processing materials,1e.g., solvents2–6 and adsorption materials7,8 for CO2 capture or CO2/CH4 separation9 as well as methane storage,10 refrigerants,11,12 working fluids,13–17 conductor materials18 or polymers.19,20 Only the right molecule enables optimal and sustainable processes. However, choosing the right molecule is inherently complex as the choice of molecules depends directly on the design of the process itself. Thus, the process and molecule have to be designed simultaneously to obtain the optimal combination. In addition, the design has to reflect environmental restrictions and safety issues. However, the practically unlimited number of potential molecules renders the direct solution of the integrated design impossible in practice.2Systematic design approaches have therefore been proposed to select or even design the right molecule. These design approaches crucially depend on the employed selection criterion which should reflect the actual process performance. A general classification of the design approaches is schematically illustrated in Fig. 1 based on the employed selection criterion: heuristic, thermodynamic or thermo-economic criteria. The performance prediction is the basis to identify the optimal molecule. Thus, the quality of the performance prediction decides how reliable an approach is in finding the optimal molecules, i.e., hitting the target in Fig. 1.
Heuristic performance indicators allow separating the molecular design from the process design, since no information about the process is needed. The heuristics employed for molecule design merely rely on the physical properties of the molecule, e.g., boiling point or selectivity. The heuristic assessment of process performance requires experience which might be unreliable. An important heuristic method is the screening of existing molecule databases. A high-throughput screening approach is presented by Simon et al.10 Here, Monte Carlo simulations are used to identify adsorption materials for methane storage based on heuristic process indicators for storage capacity. Schwöbel et al.21 present a high-throughput screening approach for working fluid selection of ORCs based on a physical domain reduction and subsequent process simulations using COSMO-RS. Joos et al.7 present a multi-objective screening approach for selection of absorption materials for CO2 capture. Here, a post-Pareto search algorithm is used to select absorption materials considering heuristic performance indicators for selectivity and uptake. However, screening approaches are naturally limited to the considered databases. To design novel and promising molecules, systematic computer-aided molecular design (CAMD) approaches have been developed. Therein, group contribution (GC) approaches have been combined with heuristic performance indicators for a variety of problems, e.g., for refrigerants,12,22 solvents for metal degreasing and crystallization12 or for extraction–distillation processes.23 To circumvent the use of GC approaches that require measurement data for parameterization and group additivity, Scheffczyk et al.24 recently proposed an optimization-based CAMD approach for solvents of extraction processes using quantum mechanics-based predictions by COSMO-RS and heuristic process indicators. While heuristics are efficient, the process module information is missing leading to suboptimal results. For the case of adsorption materials, First et al.9 therefore only preselect a set of potential adsorption materials for CO2/CH4 separation using a heuristic screening approach. The preselected adsorption materials are then assessed in a subsequent thermo-economic process optimization to verify their performance. However, Kossack et al.25 show that different objective functions for preselection and process optimization can still lead to overall suboptimal solutions. These authors preselect an entrainer for extractive distillation based on the separation selectivity. However, the selected entrainer is undesirable in terms of economics.
To identify suitable selection criteria, targeting approaches have been developed aiming at the identification of favorable molecular properties, so-called targets. Targeting approaches commonly solve the design problem in two stages: in a first stage, favorable target properties are identified. Based on these targets, real molecules are designed in a second stage. Recent reviews recommend using process models for the identification of favorable target properties of the molecules to obtain an overall optimal solution.2,13,14,26 For this purpose, the molecular design has to be integrated into process design. The integration requires a thermodynamic model to capture all interactions between molecules and processes (see Fig. 1). If an equilibrium model is employed, a thermodynamic objective function can be used to assess the process performance (e.g., the thermal efficiency). However, by integrating CAMD into process design, discrete degrees of freedom are added to the process optimization. Therefore, the integrated design results in large-scale, challenging mixed integer nonlinear programming (MINLP) problems.27 A thermodynamic approach for the integrated design of Organic Rankine Cycles (ORC) and working fluid mixtures based on CAMD has been proposed by Papadopoulos et al.28 A tailored solution algorithm relaxes the feasibility constraints of one mixture component to design an optimal first component. Then, the identified optimal component is fixed to identify the corresponding optimal second component. The resulting optimal mixtures are shown to outperform proposed mixtures for ORCs from the literature.29 Targeting approaches have also been developed, e.g., for product design for metal degreasing based on property clustering techniques,30 solvent design based on group-contribution prediction31 or refrigerant design based on a cubic equation of state (EoS).11
In our previous work, we presented a targeting approach for integrated design of the process and solvent, the so-called continuous-molecular targeting (CoMT).3 Within this approach, the solvent is modelled using the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state.32 In a first stage, molecular targets are identified by relaxation of the pure component parameters representing the solvent in PC-SAFT. This relaxation transforms the integrated design problem into a nonlinear programming (NLP) problem. Due to this relaxation, the optimization results in a hypothetical optimal solvent, the target. In a second stage, the so-called structure mapping, real solvents are identified from a database using a Taylor approximation of the objective function to estimate the objective function values. The CoMT framework for database search has been applied to the integrated design of solvents for CO2 capture and storage3,5 and working fluids for ORCs.15 Lampe et al.33 extended the structure mapping of the CoMT framework by a CAMD formulation using a group contribution approach of PC-SAFT.34 Thereby, a mixed-integer quadratic programming (MIQP) problem is solved in the structure-mapping stage with the Taylor approximation as the objective function and the molecular structure of the working fluid as the degree of freedom. The resulting CoMT–CAMD approach allows designing novel molecules. Recently, we directly linked the CoMT framework3 to a CAMD formulation.35 This optimization-based approach, so-called 1-stage CoMT–CAMD, solves the resulting MINLP efficiently in one stage. The MINLP is solved using an outer-approximation algorithm extended by a relaxation strategy. Since an equilibrium thermodynamic model is employed, only thermodynamic objective functions, such as the power output of an ORC, can be considered. The 1-stage CoMT–CAMD approach has been exemplified by the integrated design of the process and pure working fluid of ORCs. Screening approaches can also be applied with a thermodynamic objective function if the computational effort can be reduced. Scheffczyk et al.36 present a high-throughput screening approach for more than 4600 solvents for extraction–distillation using a thermodynamic objective function and COSMO-RS. Pinch-based short-cut models of the process37,38 are used to reduce the high computational effort of such a screening approach.
However, the thermodynamically optimal molecule can differ from the thermo-economically optimal molecule.39 Thus, systematic approaches for thermo-economic optimization have been developed to obtain an overall optimal solution. A thermo-economic objective function requires the integration of equipment design into the process and molecular design to quantify the investment cost of the equipment. To size equipment, a model for the transport properties of the molecule is needed to capture all transport-related trade-offs (see Fig. 1).
The group around Adjiman, Galindo and Jackson pioneered in this area by presenting a thermo-economic approach for the integrated process and solvent design for physical CO2 absorption.40,41 Here, the search space is limited to the design of linear alkanes, which are modelled by the physically based statistical associating fluid theory for potentials of variable attractive range (SAFT-VR).42 The economics are predicted from the equipment sizes, which are estimated based on heuristic correlations for equipment sizing depending on operation conditions. Viscosity is predicted based on an empirical correlation for n-alkanes. They extended their approach in the work of Burger et al.4 using a hierarchical approach for the integrated thermo-economic design of the process and solvent for physical CO2 absorption. Within this approach, the equilibrium properties of the solvent are modelled using the SAFT-γ Mie equation of state.43,44 The design space of the solvent is extended beyond linear alkanes by groups for linear alkyl ethers. Recently, the same group proposed an optimization-based approach for the integrated design of absorption processes extending an outer-approximation formulation with a physically driven domain reduction.45 In this approach, infeasible process and molecular design regions are removed to ensure numerical robustness of the MINLP optimization. Zhou et al.46 present an integrated thermo-economic approach for solvent design of a Diels–Alder reaction using solvent descriptors determined from quantum chemical density functional theory calculations. Here, a reaction kinetics model is combined with a GC approach. Since no model for transport properties is considered, the equipment sizing for cost estimation is performed based on heuristic guidelines. Recently, the same authors47 proposed a hybrid stochastic–deterministic approach for the integrated thermo-economic design of the process and solvent exemplified for absorption–desorption. The economics are estimated using heuristic sizing models for absorption–desorption equipment.
Thus, the lack of a consistent model for transport properties has enforced equipment sizing based on empirical correlations and heuristics. Thereby, the detailed trade-offs between processes, equipment and molecules are neglected. The prediction of transport properties is less mature than that of equilibrium properties.48 However, recent progress enables predicting transport properties based on the PC-SAFT equation of state and entropy-scaling.49–51 Thereby, PC-SAFT yields a consistent model for both equilibrium and transport properties with a small set of physically based parameters.
In this work, the prediction of transport properties based on PC-SAFT and entropy-scaling is directly integrated into the 1-stage CoMT–CAMD design approach. Thereby, we enable the detailed sizing of the equipment within the design of the process and molecule yielding an overall optimal thermo-economic process. Herein, the PC-SAFT equation of state provides a thermodynamically consistent model for both equilibrium and transport properties. Thus, the design of the molecule, process and equipment is linked in a thermodynamically consistent way capturing all crucial interactions. A CAMD formulation allows designing molecules as degrees of freedom in the optimization. To ensure the design of a safe and environmentally benign process, additional safety and environmental limitations are considered. The 1-stage CoMT–CAMD approach enables identifying the thermo-economically optimal molecule and the corresponding optimal process in one single MINLP optimization.
The paper is structured as follows: in section 2, the framework of the 1-stage CoMT–CAMD approach for integrated thermo-economic design is presented. In section 3, the model of the organic Rankine cycle is presented, which is considered as a case study in this work. Designing an ORC process allows us to show detailed modelling of the process equipment during the integrated design of the process and molecule. Here, an axial turbine and heat exchangers for single-phase, evaporation and condensation heat transfer are modelled and sized during the optimization. The results are presented and validated in section 4. Conclusions are drawn in section 5.
2. Framework for thermo-economic optimization in molecular design
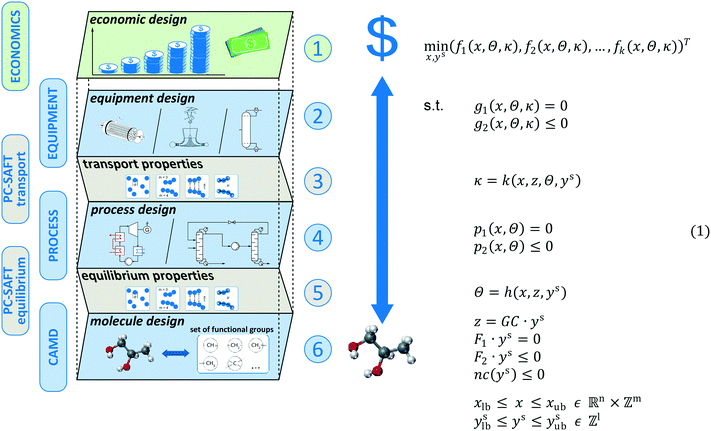
The proposed method aims at modelling the economic consequences of changing the molecular structure for energy and chemical conversion technologies. The model for thermo-economic optimization in molecular design can be decomposed into 6 levels (see Fig. 2): 1 main level, 3 design levels and 2 connector levels. The main level is the economic level (level 1). Here, the economics of the process are represented serving as assessment criteria. To estimate the total capital investment, the equipment has to be designed using detailed models for equipment sizing (level 2 – design). The detailed sizing of the equipment requires a model for the transport properties of the molecule (level 3 – connector). The equipment is sized according to the specifications from process design which requires a detailed model of the process (level 4 – design). To determine all states of the process, a model for the equilibrium properties of the molecule is required (level 5 – connector). In this work, both equilibrium and transport properties are modelled using the physically based PC-SAFT equation of state yielding a consistent model for both connector levels. To integrate the molecular design as a degree of freedom into the process design, a computer-aided molecular design formulation is used allowing the design of novel, promising molecules (level 6 – design). To capture all interactions between the economics, process, equipment, and molecule, simultaneous design of all levels is performed.Gani27 proposed a generic MINLP problem formulation for the integrated design of the process and molecule. The MINLP is originally formulated as single-objective optimization. In this work, we consider the generalized multi-objective optimization problem, which is given in problem (1) (Fig. 2). The model optimizes a set of thermo-economic objective functions (f1, f2,…, fk)T. These objectives depend on process and equipment variables x (e.g., pressure levels), equilibrium properties Θ (e.g., enthalpies) and transport properties κ (e.g., viscosities). The process and equipment models encompass equality constraints g1, p1 as well as inequality constraints g2, p2, respectively (see section 2.1). The equilibrium properties Θ and transport properties κ of the molecule are both calculated using the PC-SAFT equation of state.32 In PC-SAFT, a molecule is represented by a set of pure component parameters z (see section 2.2). A CAMD formulation is used to integrate the molecular design into the process design. Here, each molecule is characterized by the functional groups constituting its molecular structure. The integer vector ys contains the number of occurrences of a certain group of the molecule. To link PC-SAFT and the CAMD formulation, a group contribution (GC) approach is employed for calculating the PC-SAFT pure component parameters z from the molecular structure ys of the molecule. Structural feasibility of the molecular structure is ensured by additional equality F1·ys = 0 and inequality F2·ys ≤ 0 constraints.52,53 These constraints ensure a proper connectivity of the designed molecular structure, e.g., by the octet rule or additional bonding rules. Additionally, the molecular design is constrained by limitations on non-conventional properties nc (e.g., environmental or safety constraints), as presented in section 2.3.
The degrees of freedom of the full MINLP problem are the process and equipment variables x as well as the molecular structure of the molecule ys. The integrated thermo-economic design of the process and molecule is achieved by solving the MINLP given in problem (1). The optimization results in the optimal molecular structure and the corresponding optimal process and equipment. Integer-cuts54 can be used to obtain a ranking of optimal molecules allowing the consideration of further aspects, which are not covered by the optimization model. For a detailed description of the optimization strategy, see section 2.4.
2.1. Process and equipment models
The process and equipment models depend on three kinds of variables: process and equipment variables x (e.g., mass flow rates or pressure levels), equilibrium properties Θ (e.g., enthalpy or entropy) and transport properties κ (e.g., viscosity or thermal conductivity). Knowledge of the process allows determining the operating cost, while knowledge of the equipment determines the investment cost. Thus, any objective function can be considered for a detailed economic assessment of the process (e.g., specific investment cost or net present value). The general problem formulation also allows using a thermodynamic objective function (e.g., net power output for ORCs or energy demands for extraction–distillation). In this case, no detailed equipment sizing and, thus, no model for transport properties are required.The equality constraints are composed of process constraints p1(x, Θ) = 0 (e.g., mass balances or energy balances) and equipment constraints g1(x, Θ, κ) = 0 (e.g., heat transfer correlations). The inequality constraints consist of process constraints p2(x, Θ) ≤ 0 (e.g., pressure limits) and equipment constraints g2(x, Θ, κ) ≤ 0 (e.g., velocity limits in the heat exchangers). In general, structural degrees of freedom can additionally be regarded in the optimization considering different flowsheets of the process. In this work, only continuous process variables are considered.
2.2. Equilibrium and transport properties based on PC-SAFT and CAMD
To calculate the equilibrium and transport properties of the molecule, a thermodynamically consistent model is used: the perturbed-chain statistical associating fluid theory (PC-SAFT)32 including contributions for polar components.55,56 In PC-SAFT, each molecule is described by perturbed-chains of spherical segments. A set of typically 3 to 7 pure component parameters is required to represent a molecule. In this work, associative and quadrupolar molecules are excluded from the design space so that 4 pure component parameters are sufficient to characterize a molecule; two of them describe the geometry of the chains: the segment number m and the segment diameter σ. The van der Waals attraction is described by the segment dispersion energy ε/k and the dipole interaction by the dipole moment μ.To link PC-SAFT to the CAMD formulation, the homosegmented GC approach of PC-SAFT34 is used. With this GC approach, the pure component parameters can be calculated from the molecular structure ys of the molecule. The group contributions have been adjusted to measured vapor–liquid equilibria and liquid densities from a database.34 To calculate the pure component parameters from the molecular structure, the mixing rules of Vijande et al.57 are applied:
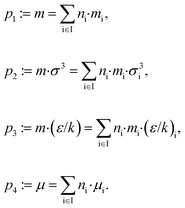 | (2) |
Here, ni denotes the number of functional groups of type i of the molecular structure represented by the vector ys = (n1, n2,…, nl)T. The contribution of group i is contained in the vector ẑi = (mi, σi, (ε/k)i, μi)T. Since a combination of the pure component parameters is used in the GC approach, this parameter combination is also used to define the vector z = (m, mσ3, mε/k, μ)T in problem (1).
PC-SAFT calculates both equilibrium and transport properties in every state of the process based on a consistent thermodynamic picture. The model is based on the residual Helmholtz energy. Thus, a reference property is needed to calculate absolute equilibrium properties Θ. Here, we use the heat capacity of the ideal gas cigp (T), which is calculated from the molecular structure using Joback's first-order GC approach.58 For a given pressure p and temperature T, absolute caloric properties such as the absolute enthalpy h can be calculated as the sum of a residual contribution (res) and an ideal contribution (id), which is based on an arbitrary reference temperature T0:
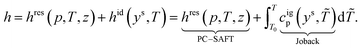 | (3) |
Besides the heat capacity of the ideal gas cigp, the molar mass M is also calculated from the molecular structure.
The calculation of transport properties κ from PC-SAFT is based on Rosenfeld's entropy-scaling.59,60 Therein, the transport properties of a molecule are found to be a monovariable function of the residual entropy sres. However, the function varies for different molecules. A GC approach for transport properties based on entropy-scaling and PC-SAFT is presented for viscosities η by Lötgering-Lin and Gross49 and for thermal conductivities λ by Hopp and Gross.50,51 In these approaches, the transport properties κ = (η, λ)T are defined as a product of a reduced transport property κ* = (η*, λ*)T and a reference transport property κref = (ηref, λref)T:
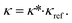 | (4) |
The reduced transport property κ* is described through a third-order polynomial depending on the residual entropy sres(T, p, z) calculated from PC-SAFT:
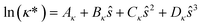 | (5) |
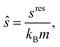 | (6) |
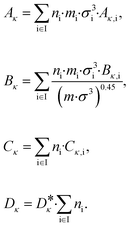 | (7) |
The vector ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) i = (Aκ,i, Bκ,i, Cκ,i)T contains the group contributions of group i. The scaling factor
i = (Aκ,i, Bκ,i, Cκ,i)T contains the group contributions of group i. The scaling factor 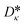 is a model constant and set to
is a model constant and set to 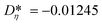 for viscosity and
for viscosity and 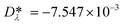 for thermal conductivity.
for thermal conductivity.
Lötgering-Lin and Gross49 use the Chapman–Enskog viscosity ηCE as reference viscosity ηref, which is related to the pure component parameters of PC-SAFT:
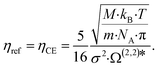 | (8) |
N A denotes the Avogadro constant and Ω(2,2)* indicates the reduced collision integral, which is calculated using an empirical approximation.61
As reference thermal conductivity λref, the Chapman–Enskog thermal conductivity λCE is insufficient, since it neglects vibrational degrees of freedom in regions of low densities. Thus, an additional contribution λvib is proposed by Hopp and Gross50 to cover the behavior of the gas phase. Thereby, the reference thermal conductivity is calculated as:
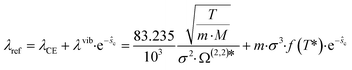 | (9) |
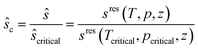 | (10) |
 | (11) |
The critical point (Tcritical, pcritical) is also calculated using PC-SAFT. With these GC approaches, PC-SAFT predicts the viscosity and thermal conductivity accurately from the molecular structure of the molecule for a given state. Compared to measurement data for n-hexane, the average errors are 5.5% for the viscosity and 5.2% for the thermal conductivity, showing the good accuracy of these approaches (see Fig. 3). In this work, a preliminary GC approach for the thermal conductivity is used.50 The extension of the full entropy-scaling approach for thermal conductivities51 to a GC approach is currently in progress.
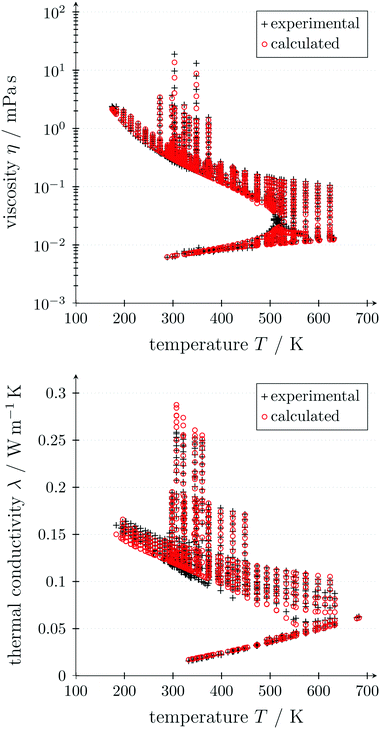 | ||
| Fig. 3 Predicted viscosities49 (top) and thermal conductivities50 (bottom) of n-hexane depending on temperature using GC PC-SAFT in comparison to measurement data. | ||
Hopp and Gross also work on an approach to predict the self-diffusion coefficients based on entropy-scaling and PC-SAFT.51 Diffusion is important to design processes in process engineering and would enhance the applicability of the thermo-economic 1-stage CoMT–CAMD approach to further types of processes.
In this work, GC approaches are used to predict the heat capacity of the ideal gas cigp, molar mass M, pure component parameters of PC-SAFT z, and the scaling factors for transport properties Aκ to Dκ. The groups considered within the presented approach are limited by the measurement data available to adjust the group contributions. To prevent extrapolation from the databases, a limitation of the molecular design space is regarded in the inequality constraints F2·ys ≤ 0 in problem (1). Thereby, a high accuracy is ensured.35 While large databases of experimental data exist for pure component parameters and viscosity, there is only scarce data for thermal conductivity. Thus, the employed groups are limited to the current state of the group contribution method for the thermal conductivity: –CH3, –CH2–, >CH– and >C< for branched alkanes, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 and
CH2 and ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– for 1-alkenes, Carom and CHarom for aromatics with alkyl side groups and –CH
CH– for 1-alkenes, Carom and CHarom for aromatics with alkyl side groups and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O for aldehydes. Additionally, methane CH4 and ethane C2H6 are defined as separated groups to increase the accuracy of these small molecules. Here, the heat capacity of the ideal gas is calculated using a molecule-specific correlation.62 Additional groups can easily be integrated into the approach, as soon as the GC approach for thermal conductivity is further developed.
O for aldehydes. Additionally, methane CH4 and ethane C2H6 are defined as separated groups to increase the accuracy of these small molecules. Here, the heat capacity of the ideal gas is calculated using a molecule-specific correlation.62 Additional groups can easily be integrated into the approach, as soon as the GC approach for thermal conductivity is further developed.
2.3. Non-conventional properties
To ensure the design of safe and environmentally benign processes, the molecular design space is constrained by limitations of non-conventional properties, i.e., flammability, auto-ignition temperature (AIT), toxicity, and the environmental properties global warming potential (GWP) as well as ozone depletion potential (ODP) (Table 1). The non-conventional properties are calculated from the molecular structure of the molecule using first-order GC approaches. A detailed description can be found in the ESI† (section S1).| Property | GC approach | Limitation | |
|---|---|---|---|
| Flammability | F-Number Γ | Kondo et al.63 | Γ < 0.8 (ref. 63) |
| AIT | Albahri and George64 | T max,process + 30 K ≤ AIT | |
| Toxicity | 96-h LC50 | Martin and Young65 | 96-h LC50 ≥ 10 mg l−1 (ref. 66) |
| Environmental impact | GWP | Hukkerikar et al.67 | GWP ≤ 150 (ref. 68) |
| ODP | Hukkerikar et al.67 | ODP = 0 | |
The limitations on GWP and OPD are implemented to demonstrate the general applicability of the consideration of environmental properties in the presented design approach. Since the considered groups have no significant environmental impact, both limitations have no influence on the optimization result of the current study. The limitations become relevant as soon as halogenated groups are added to the approach.
2.4. Optimization strategy
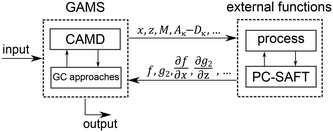
The 1-stage CoMT–CAMD approach enables single- and multi-objective optimization. The result of a single-objective optimization is one single optimal molecule and the corresponding optimal process. Integer-cuts54 are used to obtain a ranking of optimal molecules. Here, the MINLP is solved repeatedly, wherein integer-cuts constrain the feasible design space to exclude previous solutions. The result of a multi-objective optimization is a Pareto front, which can be calculated using multi-objective optimization strategies (e.g., normalized constraint method69 or epsilon-constraint method70).The optimization problem is solved using the software GAMS (version 24.6.1 (ref. 71)). However, the process model and PC-SAFT contain demanding iterative calculations for, e.g., boiling points. Thus, the process calculation and thermodynamic calculations of PC-SAFT are performed in external functions (Fig. 4). Here, GAMS forwards all molecule property parameters calculated from the molecular structure ys and all process variables x to the external functions. The molecule property parameters are the pure component parameters of PC-SAFT z, the parameters needed to calculate the heat capacity of the ideal gas cigp and the molar mass M as well as the coefficients to calculate the reduced transport properties (Aκ to Dκ). From the external functions, the objective function values f, the inequality constraints of the process p2 as well as equipment g2 and the first-order derivatives with respect to all parameters, which are forwarded to the external functions, are returned to the optimization problem in GAMS. This provides a black-box model to GAMS, which enables a very stable computation of the iterative calculations.
However, the external functions prevent the use of global MINLP solvers, since these still need explicit models today.72 Thus, the MINLP is solved using the local, deterministic MINLP solver DICOPT,73 which combines outer-approximation74 with a relaxation strategy. In DICOPT, series of nonlinear program (NLP) subproblems and mixed-integer linear program (MILP) master problems are solved. Initially, relaxation of problem (1) is solved to obtain a hypothetical optimal molecule, the so-called target. The relaxation problem is identical to the CoMT problem in the CoMT–CAMD approach.3 Afterwards, an optimal integer solution is identified using outer-approximation. As subsolvers, the NLP solver SNOPT75 and the MILP solver CPLEX76 are used.
3. Design of an organic Rankine cycle
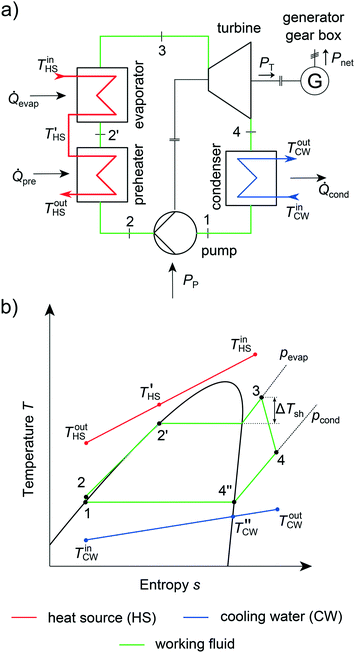
The integrated thermo-economic design of the equipment, process and molecule is a crucial challenge in the design of Organic Rankine Cycles (ORC) as recently reviewed by Linke et al.26 ORCs can be used to transform low-temperature heat stemming from renewable heat sources into electrical power.77 Renewable heat sources can be, e.g., solar heat,78 geothermal heat79 or biomass.80 Additionally, low-temperature waste heat from industry81 and automotive applications82 can be exploited. Due to the low exergy content of these heat sources, ORCs have to be tailored to the specific application to ensure an economic process.13 The operating principle of an ORC follows four steps (Fig. 5): firstly, the molecule, the so-called working fluid, is pumped to the upper pressure level pevap (1 → 2). Then, the working fluid is preheated, evaporated and optionally superheated exploiting the heat source (2 → 3). In a third step, the working fluid is expanded to the lower pressure level pcond in a turbine (3 → 4). A generator transforms the work of the turbine into electrical power. The working fluid is desuperheated and condensed to boiling liquid in the last step (4 → 1). In summary, an ORC encompasses three types of heat transfer (single phase, evaporation and condensation) and the design of several types of rotating equipment (turbine, pump, generator and gearbox). To exploit the renewable heat source in the most economical way, the process, equipment and working fluid have to be optimized simultaneously.In this work, the presented 1-stage CoMT–CAMD approach for integrated thermo-economic design of the process and molecule is applied to the design of an ORC for waste heat recovery. The general specifications of the case study are given in section 3.1. In section 3.2, the considered objective functions are described. The relevant assumptions for designing the heat exchangers and the rotating equipment are given in sections 3.3 and 3.4, respectively.
3.1. General specifications of the case study
In the case study, a subcritical, non-regenerated ORC is considered (Fig. 5). Industrial waste water is used as a heat source with a mass flow rate of ṁHS = 10 kg s−1 and an inlet temperature of TinHS = 150 °C (Table 2).83 The ORC is cooled using cooling water with a mass flow rate of ṁCW = 175 kg s−1 and an inlet temperature of TinCW = 15 °C. The heating is performed in two heat exchangers in series: a preheater for single-phase heat transfer to boiling liquid and an evaporator for evaporation and optional superheating. A detailed description of the thermodynamic model of the ORC process is given in the ESI† (section S2).| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Flow rate (heat source) | ṁ HS | 10 kg s−1 | Isentropic turbine efficiency | η T,is | 0.8 |
| Temperature (heat source) | T inHS | 150 °C | Isentropic pump efficiency | η P,is | 0.75 |
| Heat capacity (heat source) | c p,HS | 4.2 kJ kg−1 K−1 | Generator efficiency | η G | 0.98 |
| Flow rate (cooling water) | ṁ CW | 175 kg s−1 | Min. absolute pressure | p min | 1 bar |
| Temperature (cooling water) | T inCW | 15 °C | Min. reduced pressure | p redmin | 10−2 |
| Heat capacity (cooling water) | c p,CW | 4.2 kJ kg−1 K−1 | Max. absolute pressure | p max | 50 bar |
| Min. steam quality (turbine outlet) | φ min | 0.95 | Max. reduced pressure | p redmax | 0.8 |
| Max. segment number | n max | 25 |
The process degrees of freedom 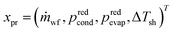 are the mass flow rate of the working fluid ṁwf, the reduced operating pressure levels of the condenser predcond and the evaporator predevap and the degree of superheating at the turbine inlet ΔTsh. Reduced pressures are defined as:
are the mass flow rate of the working fluid ṁwf, the reduced operating pressure levels of the condenser predcond and the evaporator predevap and the degree of superheating at the turbine inlet ΔTsh. Reduced pressures are defined as:
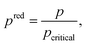 | (12) |
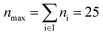 corresponding to 2648 structurally feasible molecular structures, which fulfill the CAMD constraints.
corresponding to 2648 structurally feasible molecular structures, which fulfill the CAMD constraints.
3.2. Objective function
For thermo-economic evaluation of a process, several objective functions can be used, e.g., specific investment cost or net present value. The specific investment costs SIC are defined as: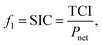 | (13) |
The total capital investment TCI is calculated as the sum of the purchased-equipment cost PECi multiplied by factors w for additional direct and indirect costs as:84
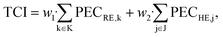 | (14) |
The net power output Pnet is calculated as:
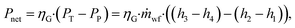 | (15) |
3.3. Purchased-equipment costs of the heat exchangers
The heat exchangers are modelled as shell and tube heat exchangers in counter-flow control without shell baffles. Hall et al.86 present a cost correlation for the purchased-equipment costs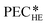 of shell and tube heat exchangers depending on the heat exchanger area AHE. The cost correlation is available for several material combinations of shell and tubes and already includes the installation costs. Since the organic working fluid of the process is not known during the design, the cost correlation for stainless steel for the shell and tubes is used to prevent corrosion. The cost correlation is defined as:
of shell and tube heat exchangers depending on the heat exchanger area AHE. The cost correlation is available for several material combinations of shell and tubes and already includes the installation costs. Since the organic working fluid of the process is not known during the design, the cost correlation for stainless steel for the shell and tubes is used to prevent corrosion. The cost correlation is defined as: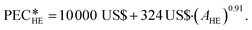 | (16) |
Originally, the cost correlation originates from 1982. The Chemical Engineering Plant Cost Index (CEPCI) is used to account for inflation and development of raw material prices. The CEPCI is relatively specific to the United States. However, the presented approach is independent of the cost models and conversion factors, which can be individually selected by the user for the designed application and its location. Using the CEPCI, the current PECHE is calculated as:
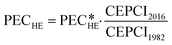 | (17) |
The heat exchanger area can be calculated as:
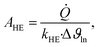 | (18) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) denotes the transferred heat flow, Δϑln indicates the logarithmic temperature difference in the heat exchanger88 and kHE represents the heat transmission coefficient. The heat transmission coefficient kHE is defined as:
denotes the transferred heat flow, Δϑln indicates the logarithmic temperature difference in the heat exchanger88 and kHE represents the heat transmission coefficient. The heat transmission coefficient kHE is defined as: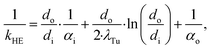 | (19) |
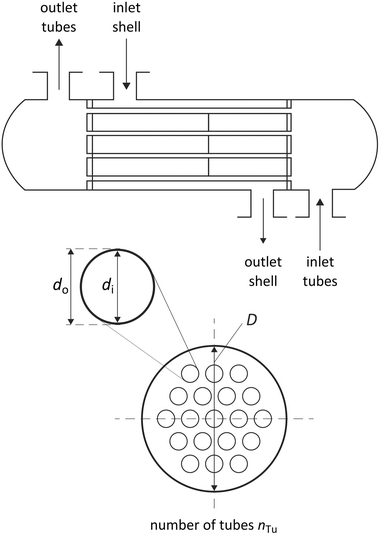 | ||
| Fig. 6 Degrees of freedom of the considered shell and tube heat exchangers in counter-flow control without shell baffles. | ||
The heat transmission coefficient kHE in eqn (19) depends on the inner and outer specific heat transfer coefficients αo and αi. The heat transfer coefficients are calculated for single phase, evaporation and condensation using specific heat transfer correlations (Table 3). Within these correlations, the heat transfer is described by dimensionless parameters such as Reynolds and Nusselt numbers, which strongly depend on the transport properties viscosity η and thermal conductivity λ. It is assumed that the working fluid is on the shell side and the water for heating and cooling is on the tube side. This configuration enables better cleaning of the heat exchangers. Since the heating and cooling medium is fixed to water, specific correlations for the properties of water are used.90 The heat transfer correlations for flow boiling in the evaporator and filmwise condensation in the condenser depend on the steam quality φ and, thus, represent the local heat transfer. Therefore, discretization of the steam quality φ is performed to calculate the heat exchanger areas for the evaporator and the condenser. The heat transfer for flow boiling additionally depends on the heat exchanger area itself enforcing an iterative calculation of the heat exchanger area. A detailed description of the correlations is given in the ESI† (section S3).
| Heat exchanger | Side | Type | Correlation | Features |
|---|---|---|---|---|
| Preheater | Shell | Single phase, forced convection | Gnielinski91 | |
| Tube | Single phase, forced convection | Gnielinski91 | ||
| Evaporator | Shell | Flow boiling | Gungor and Winterton92 | Discrete, iterative |
| Tube | Single phase, forced convection | Gnielinski91 | ||
| Condenser | Shell | Filmwise condensation | Numrich and Müller93 | Discrete |
| Tube | Single phase, forced convection | Gnielinski91 |
3.4. Purchased-equipment costs of the rotating equipment
The purchased-equipment costs PECRC of rotating equipment, i.e., pump, generator, gearbox and turbine, are calculated using the recent cost correlations from Astolfi et al.94 The proposed cost correlations are based on experience gained by the authors in the cooperation with manufacturers of ORC plants and turbines. The correlations are used to capture a detailed trade-off between the working fluid and purchased-equipment cost. However, inaccuracies can occur, since the correlations are used in an extended range of equipment sizes in comparison to the original reference. Since the cost correlations are provided in Euros, an exchange rate of k€→$ = 1.114 US$ per € (4th August 2016)95 is considered. The purchased-equipment cost of the pump PECRC,P is calculated based on the pump power input PP as: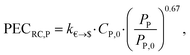 | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 € and PP,0 = 200 kW. The purchased-equipment cost of the generator PECRC,G is defined based on the net power output Pnet by:
000 € and PP,0 = 200 kW. The purchased-equipment cost of the generator PECRC,G is defined based on the net power output Pnet by: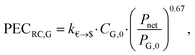 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 € and PG,0 = 5000 kW. The purchased-equipment costs of the gearbox PECRC,GB are regarded as 40% of the generator cost.94 The purchased-equipment cost of the turbine PECRC,T cannot be deduced from its power output PT, since the costs vary significantly for the same power output but different enthalpy drops, volume ratios and volume flow rates.94 Thus, Astolfi et al.94 proposed a cost correlation for axial turbines depending on the number of turbine stages nst and the last stage size parameter SP:
000 € and PG,0 = 5000 kW. The purchased-equipment costs of the gearbox PECRC,GB are regarded as 40% of the generator cost.94 The purchased-equipment cost of the turbine PECRC,T cannot be deduced from its power output PT, since the costs vary significantly for the same power output but different enthalpy drops, volume ratios and volume flow rates.94 Thus, Astolfi et al.94 proposed a cost correlation for axial turbines depending on the number of turbine stages nst and the last stage size parameter SP: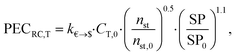 | (22) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230
230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 €, nst,0 = 2 and SP0 = 0.18 m. The size parameter SP is defined by:
000 €, nst,0 = 2 and SP0 = 0.18 m. The size parameter SP is defined by: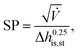 | (23) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) denotes the volume flow of the last stage and Δhis,st indicates the isentropic enthalpy drop of one stage. The size parameter SP is proportional to the stage diameter, which serves as a measure for the purchased-equipment costs. By using this detailed cost correlation, the number of turbine stages nst has to be considered as an additional integer degree of freedom within the optimization. As recommended by Astolfi et al.,94 two additional turbine design constraints are taken into account during the optimization: to avoid high Mach numbers and large blade heights, the maximal isentropic volume ratio of one stage Vratiois,st is limited to:
denotes the volume flow of the last stage and Δhis,st indicates the isentropic enthalpy drop of one stage. The size parameter SP is proportional to the stage diameter, which serves as a measure for the purchased-equipment costs. By using this detailed cost correlation, the number of turbine stages nst has to be considered as an additional integer degree of freedom within the optimization. As recommended by Astolfi et al.,94 two additional turbine design constraints are taken into account during the optimization: to avoid high Mach numbers and large blade heights, the maximal isentropic volume ratio of one stage Vratiois,st is limited to: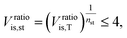 | (24) |
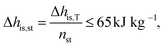 | (25) |
4. Results and discussion
The integrated thermo-economic design of the organic Rankine cycle is defined by 4 continuous process degrees of freedom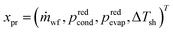 , 1 integer equipment degree of freedom xT = nst and 55 binary degrees of freedom describing the molecule in the CAMD formulation. A binary notation of the number of functional groups is used instead of an integer notation for an easy implementation of the integer-cuts.54 The 1-stage CoMT–CAMD approach is firstly applied to a single-objective optimization of the ORC using the specific investment cost SIC as the objective function in section 4.1. In section 4.2, the result of a multi-objective optimization is presented to demonstrate the trade-off between the total capital investment TCI and the net power output Pnet of the ORC. Finally, the results are validated in section 4.3.
, 1 integer equipment degree of freedom xT = nst and 55 binary degrees of freedom describing the molecule in the CAMD formulation. A binary notation of the number of functional groups is used instead of an integer notation for an easy implementation of the integer-cuts.54 The 1-stage CoMT–CAMD approach is firstly applied to a single-objective optimization of the ORC using the specific investment cost SIC as the objective function in section 4.1. In section 4.2, the result of a multi-objective optimization is presented to demonstrate the trade-off between the total capital investment TCI and the net power output Pnet of the ORC. Finally, the results are validated in section 4.3.
4.1. Results of single-objective optimization
The 1-stage CoMT–CAMD approach is applied to optimize the specific investment cost. Initially, the relaxed problem is solved in the so-called CoMT step leading to a value of SIC = 3058 US$ per kW. This target value could be achieved for a hypothetical working fluid. It serves as a lower bound on the objective function of all molecular structures captured by the 1-stage CoMT–CAMD approach. 1-stage CoMT–CAMD with integer-cuts is used to calculate a ranking of the top 10 real working fluids shown in Table 4. For this case study, the approach identifies mainly short-chained alkanes and alkenes. Benzenes and aldehydes are not identified.| Rank | Name | SIC (US$ per kW) | P net (kW) | TCI (106 US$) | Rank (real) |
|---|---|---|---|---|---|
| — | Target | 3058 | 434 | 1.33 | — |
| 1 | Propene | 3318 | 422 | 1.40 | 1 |
| 2 | Propane | 3476 | 393 | 1.37 | 2 |
| 3 | But-1-ene | 4646 | 328 | 1.52 | 3 |
| 4 | Isobutane | 4722 | 326 | 1.54 | 4 |
| 5 | n-Butane | 5040 | 324 | 1.63 | 5 |
| 6 | Neopentane | 6397 | 296 | 1.89 | 6 |
| 7 | 3-Methylbut-1-ene | 6741 | 276 | 1.86 | 7 |
| 8 | Pent-1-ene | 7241 | 262 | 1.90 | 8 |
| 9 | Pentane | 7781 | 251 | 1.95 | 10 |
| 10 | Isopentane | 7242 | 265 | 1.92 | 9 |
Propene is identified as the best working fluid with specific investment costs of SIC = 3318 US$ per kW. The objective function value is 8.5% higher than the target value. Propane shows a similar objective function value to that of propene (SIC = 3476 US$ per kW). For the 3rd rank, the predicted specific investment cost already increases significantly. The following working fluids are not competitive for this case study.
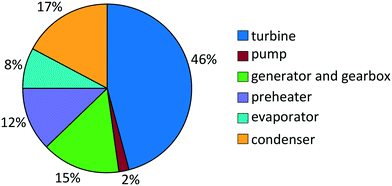
For propene, the turbine costs constitute the major part of the total purchased-equipment cost with a share of 46% (Fig. 7). About a third of the total purchased-equipment cost accounts for the heat exchangers. Here, the evaporator creates the smallest purchased-equipment cost with a share of 8%, although the transferred heat is similar to that of the preheater. This fact results from the benefited flow boiling heat transfer in the evaporator in comparison to the single-phase heat transfer in the preheater. As a result of the optimization, the optimal approach temperature is found to be ΔT = 8.4 K in the preheater and evaporator and ΔT = 9.1 K in the condenser. This approach temperature is a compromise between the low purchased-equipment cost of the heat exchanger, which decreases for high approach temperatures, and a high net power output.
By applying the 1-stage CoMT–CAMD approach without constraining the non-conventional properties (section 2.3), acetaldehyde is additionally identified in the top 10. However, acetaldehyde is excluded from the design space because of its low auto-ignition temperature of AIT = 140 °C.96 In this case study, the other non-conventional properties do not affect the result. However, all identified alkenes are classified as strongly flammable, which has to be considered in a subsequent assessment of the ranking.
In comparison to a thermo-economic design, Table 5 shows the top 5 working fluids identified by a thermodynamic design of the considered ORC using the net power output Pnet as an objective function. In this case, no trade-off between the objective function and the minimal approach temperature in the heat exchangers is reflected in the model, so the lower bound of the minimal approach temperature is set to ΔTlomin = 2 K.
| Rank | Name | P net/kW | SIC/US$ per kW | TCI/106 US$ |
|---|---|---|---|---|
| — | Target | 634 | 9227 | 5.85 |
| 1 | Propane | 589 | 6097 | 3.59 |
| 2 | Propene | 563 | 5934 | 3.34 |
| 3 | But-1-ene | 479 | 6659 | 3.19 |
| 4 | Isobutane | 489 | 6620 | 3.24 |
| 5 | Neopentane | 472 | 9436 | 4.46 |
The optimal net power output of the target is Pnet = 634 kW. The optimal real working fluid identified by 1-stage CoMT–CAMD is propane with a net power output of Pnet = 589 kW. The optimal thermo-economic process conditions for one working fluid differ from the optimal thermodynamic process conditions, since the trade-off between maximal net power output Pnet and minimal total capital investment TCI is considered within a thermo-economic optimization.
4.2. Results of multi-objective optimization
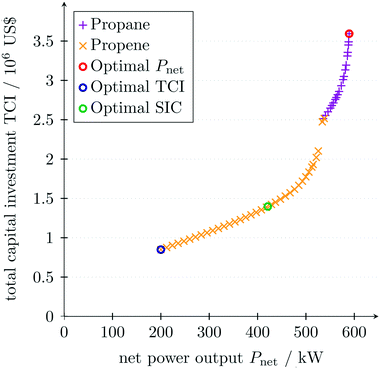
For better visualization of the trade-off between the net power output Pnet and the total capital investment TCI, a multi-objective optimization is performed using the normal constraint method.69 Since a local MINLP solver is used, the normal constraint method is repeated wherein the direction of movement of the normal constraint is changed. The resulting Pareto front is filtered according to Pareto dominance to increase the accuracy of the solution. To identify design trade-offs, non-aggregated objective functions should be chosen in multi-objective optimization, which do not comprise a trade-off itself.97 Thus, the net power output Pnet of the ORC is considered as one objective function and the total capital investment TCI as the other objective function. As for the single-objective optimization of the net power output, the lower bound of the minimal approach temperature is set to ΔTlomin = 2 K. Additionally, the lower bound of the net power output is set to Plonet = 200 kW to ensure the validity of the equipment design correlations for the given conditions. As seen in the single-objective optimization (Table 5), propane maximizes the net power output (Fig. 8). However, the total capital investment is high for a high net power output, since the low approach temperatures in the heat exchangers result in large heat exchanger areas. The strong increase of the total capital investment for high net power output can lead to misleading results if a thermodynamic objective function is solely considered in the integrated design of the process and molecule. Minimal total capital investment is achieved for minimal net power output using propene as a working fluid. The optimal working fluid changes at Pnet = 540 kW. In the range of net power outputs below Pnet ≤ 526 kW, the turbine can be operated with one turbine stage using propene as the working fluid. For higher net power output Pnet ≥ 526 kW, two turbine stages are necessary to satisfy the turbine constraints in eqn (24) and (25) resulting in a discontinuity in the Pareto front.In Fig. 8, the optimal specific investment cost is also marked. The optimal operating conditions and the optimal working fluid vary between the objective functions net power output Pnet, total capital investment TCI and specific investment cost SIC. Thus, the objective function has to be chosen deliberately in advance.
4.3. Validation
The thermo-economic evaluation of the ORC process is the key to a reliable selection of the working fluid. Accordingly, the results are validated with respect to three main aspects: firstly, the quality of the optimal solution and the computational effort are analyzed from a numerical point of view (section 4.3.1). Secondly, uncertainties of the thermodynamic model are investigated in section 4.3.2. Finally, the results of 1-stage CoMT–CAMD are compared to data from scientific publications and manufacturers to validate the employed cost models (section 4.3.3).The resulting real rank is used to validate the optimization result of 1-stage CoMT–CAMD which employed a non-global optimization algorithm. Still, the top 10 global optimal solutions are identified by the 1-stage CoMT–CAMD approach. The order is nearly correct (see the last column of Table 4). Thus, the local MINLP solver DICOPT provides a very good solution for the presented case study, but integer-cuts are necessary to find all good solutions.
The computational effort for the 1-stage CoMT–CAMD approach can be compared to the brute-force computations by the number of function evaluations of the process model: while an individual process optimization of all possible molecular structures requires 803![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209 function evaluations, only 9786 function evaluations are needed to calculate a ranking of 10 working fluids with 1-stage CoMT–CAMD, which corresponds to a saving of 98.8%. Thus, the 1-stage CoMT–CAMD approach is an accurate and efficient method for the integrated design of the molecule, process and equipment.
209 function evaluations, only 9786 function evaluations are needed to calculate a ranking of 10 working fluids with 1-stage CoMT–CAMD, which corresponds to a saving of 98.8%. Thus, the 1-stage CoMT–CAMD approach is an accurate and efficient method for the integrated design of the molecule, process and equipment.
| η | λ | c igp | T sat | h res | s res | c resp | v | |
|---|---|---|---|---|---|---|---|---|
| CV | 10% | 10% | 3% | 5% | 5% | 5% | 5% | 5% |
| Δ max | 27.9% | 31.1% | 9.2% | 17.8% | 13.2% | 14.2% | 15.3% | 15.6% |
| Δ min | −40.9% | −29.3% | −9.1% | −17.9% | −15.0% | −15.2% | −16.3% | −15.5% |
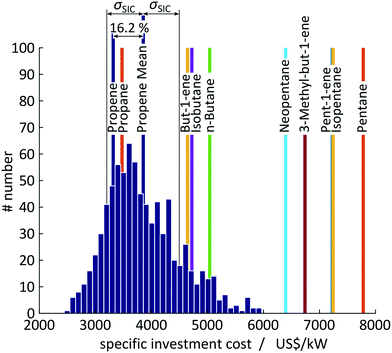
A test set of 1000 random samplings is used for the Monte Carlo simulations, of which finally 810 samplings converged to an optimal solution and are considered for the assessment. Overall, a mean value of SIC = 3854 US$ per kW with a standard deviation of σSIC = 648 US$ per kW (CV = 16.8%) is calculated for propene corresponding to an average deviation of 16.2% to the expected value of SIC = 3318 US$ per kW calculated in 1-stage CoMT–CAMD (see Fig. 9). The major source for the deviations in the objective function is uncertainties in the saturation temperature since they change the optimal pressure levels. For propene, pressure constraints are active in the optimum. Thus, any change in the saturation temperature forces the solution away from the optimal pressure levels. Thereby, the distribution is shifted to higher specific investment cost compared to the expected value calculated in 1-stage CoMT–CAMD. Thus, the authors expect a similar trend for working fluids with the same active set of constraints at the optimum identified by 1-stage CoMT–CAMD to that for propene. In contrast, a smaller shift is expected for working fluids without active constraints in the optimum. In the top 10 identified working fluids, only propane has the same active set of constraints as propene.
Within the standard deviation of σSIC = 648 US$ per kW, the two top working fluids, propane and propene, cannot be distinguished by 1-stage CoMT–CAMD. Propane and propene have very similar chemical structures and thus very similar performance in the process. In contrast, the candidates from rank 3 onwards give performance beyond the range of the standard deviations and thus can be clearly distinguished as inferior working fluids by our method. Thus, even based on the conservative uncertainties assumed by the authors, the presented 1-stage CoMT–CAMD approach can provide significant information on the real ranking of molecules.
Quoilin et al.14 compiled specific purchased-equipment costs of ORCs for waste heat recovery collected from ORC manufacturers and scientific publications, which are used as reference data. The specific purchased-equipment costs predicted for the top 10 working fluids show good agreement with the reference data (Fig. 10). In comparison to the reference data, we identify optimal working fluids in a range of low specific purchased-equipment costs showing the potential of the presented approach for thermo-economic optimization. Please note that the results are converted into Euros to allow for a better comparison with the reference data.
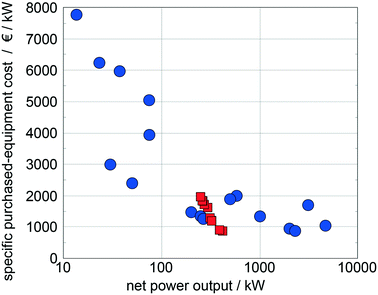 | ||
| Fig. 10 Comparison of the predicted specific purchased-equipment costs of the top 10 working fluids identified with the 1-stage CoMT–CAMD approach (squares) with specific purchased-equipment costs collected from ORC manufacturers and scientific publications14 (circles). | ||
Lemmens99 notes that the distribution of purchased-equipment costs commonly differs largely between estimated and real costs of the equipment. The purchased-equipment costs predicted by the 1-stage CoMT–CAMD approach (exemplified for propene in Fig. 11a) show good agreement with the cost distribution of the real ORC for waste heat recovery presented by Lemmens99 in Fig. 11b. However, the design of the real ORC differs from our design: a radial turbine, plate heat exchangers and an air cooling system are used. Considering lower purchased-equipment costs for plate heat exchangers and higher costs for an air cooling system, a sufficient accuracy of the cost distribution predicted by the 1-stage CoMT–CAMD approach is still expected. Since the aim of the presented approach is not a highly accurate prediction of the total capital investment of a process, but the thermo-economic comparison of different working fluids during the design of the process, the models considered in this work show good agreement with real ORC applications.
 | ||
| Fig. 11 Cost distribution of the purchased-equipment cost of (a) the predicted ORC for propene and (b) a real ORC.99 | ||
5. Conclusion
From molecules to dollars: in this work, we integrate molecular design into thermo-economic design of a process. For this purpose, a Computer-aided Molecular Design (CAMD) formulation is directly linked to models for process design and equipment sizing. In the resulting 1-stage CoMT–CAMD approach, the link is enabled by the physically based perturbed-chain associating fluid theory (PC-SAFT). PC-SAFT allows us to predict equilibrium as well as transport properties in a thermodynamically consistent way. The calculation of transport properties enables the detailed sizing of the equipment during the optimization. Heat exchangers are designed using detailed heat transfer models for single phase, evaporation and condensation. Thereby, the economic consequences of changing the molecule in the process are captured. To ensure safety and environmental protection, non-conventional properties of the molecule, e.g., flammability, toxicity or environmental properties, are considered. Thus, the approach enables a holistic design of the thermo-economically optimal molecule and the corresponding optimal process and equipment in one single MINLP optimization. Because of the efficient computation, the 1-stage CoMT–CAMD approach also allows multi-objective optimization to capture all process-related trade-offs.The presented 1-stage CoMT–CAMD approach is successfully applied to the integrated design of a subcritical organic Rankine cycle. This case study demonstrates the merits of detailed equipment models: sizing of heat exchangers considering the heat transfer for single phase, evaporation and condensation as well as the sizing of rotating equipment such as the turbine. The 1-stage CoMT–CAMD approach identifies the most promising working fluids, which minimize the specific investment costs of the ORC. It is shown that the integrated thermodynamic design of the process and molecule results in a combination of the optimal process and working fluid with high total capital investment showing the significance of an integrated thermo-economic design approach. A multi-objective optimization is used to more closely visualize the thermo-economic trade-off between the net power output and the total capital investment. We show that the predicted specific purchased-equipment cost and the cost sharing of the purchased-equipment cost show good accordance with real ORC applications. The 1-stage CoMT–CAMD approach can directly be applied to any process design which is sufficiently well described by the equation of state, e.g., to refrigerant design, solvent design or working fluid design.
Nomenclature
Latin symbols
| A | Area |
| A − D | Scaling factors of the Taylor polynomial |
| c | Velocity |
| c p | Heat capacity |
| CV | Coefficient of variation |
| d | Diameter |
| D | Diameter of the shell |
| f | Objective function |
| F 1/F2 | CAMD constraints |
| g 1/g2 | Equipment constraints |
| h | Enthalpy |
| k | Heat transmission coefficient |
| k B | Boltzmann constant |
| k €→$ | Exchange rate |
| m | Segment number |
| ṁ | Mass flow rate |
| M | Molar mass |
| n i | Number of functional group i |
| nc | Non-conventional fluid property constraints |
| N A | Avogadro's constant |
| p | Pressure |
| p 1/p2 | Process constraints |
| P | Power |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif)
| Heat flow |
| s | Entropy |
| SP | Size parameter |
| T | Temperature |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
| Volume flow |
| V ratio | Volume ratio |
| v | Molar volume |
| w 1/w2 | Correction factors for direct/indirect cost |
| x | Process degrees of freedom |
| y S | Molecular structure |
| z | Pure component parameters |
Greek symbols
| α | Heat transfer coefficient |
| Γ | F-number |
| Δ | Difference |
| ε/k | Segment dispersion energy |
| η | Efficiency |
| η | Viscosity |
| Θ | Equilibrium properties |
| ϑ | Temperature |
| κ | Transport properties |
| λ | Thermal conductivity |
| μ | Dipole moment |
| σ | Segment diameter |
| σ | Standard deviation |
| φ | Steam quality |
| Ω(2,2)* | Reduced collision integral |
Abbreviations
| AIT | Auto-ignition Temperature |
| CAMD | Computer-aided Molecular Design |
| CEPCI | Chemical Engineering Plant Cost Index |
| CoMT | Continuous-Molecular Targeting |
| DICOPT | Discrete and Continuous Optimizer |
| EoS | Equation of State |
| GC | Group Contribution |
| GWP | Global Warming Potential |
| MILP | Mixed-Integer Linear Program |
| MINLP | Mixed-Integer Nonlinear Program |
| MIQP | Mixed-Integer Quadratic Program |
| NLP | Nonlinear Program |
| ODP | Ozone Depletion Potential |
| ORC | Organic Rankine Cycle |
| PC-SAFT | Perturbed-Chain Statistical Associating Fluid Theory |
| PEC | Purchased-Equipment Cost |
| SIC | Specific Investment Cost |
| SNOPT | Sparse Nonlinear Optimizer |
| TCI | Total Capital Investment |
Subscript
| CE | Chapman–Enskog |
| cond | Condensation |
| critical | Critical state |
| CW | Cooling water |
| evap | Evaporation |
| G | Generator |
| HE | Heat exchangers |
| HS | Heat source |
| i | Inner |
| is | Isentropic |
| l | Liquid |
| lb | Lower bound |
| ln | Logarithmic |
| max | Maximal |
| min | Minimal |
| o | Outer |
| P | Pump |
| pr | Process |
| pre | Preheating |
| RE | Rotating equipment |
| ref | Reference |
| sh | Super heating |
| st | Stage |
| T | Turbine |
| Tu | Tubes |
| ub | Upper bound |
| wf | Working fluid |
| v | Vapor |
| 0 | Reference |
Superscript
| id | Ideal |
| ig | Ideal gas |
| in | Inlet |
| out | Outlet |
| red | Reduced |
| res | Residual |
| sat | Saturation |
| vib | Vibrational |
| * | Reduced |
Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (DFG) for funding this work (BA 2884/4-1 and GR 2948/2-1).References
- L. Zhang, D. K. Babi and R. Gani, New Vistas in Chemical Product and Process Design, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 557–582, DOI:10.1146/annurev-chembioeng-080615-034439
.
-
C. S. Adjiman, A. Galindo and G. Jackson, Molecules matter: the expanding envelope of process design, in Proceedings of the 8th International Conference on Foundations of Computer-Aided Process Design, ed. M. R. Eden, Elsevier, Amsterdam, 2014, pp. 55–64 Search PubMed
.
- A. Bardow, K. Steur and J. Gross, Continuous-Molecular Targeting for Integrated Solvent and Process Design, Ind. Eng. Chem. Res., 2010, 49, 2834–2840, DOI:10.1021/ie901281w
.
- J. Burger, V. Papaioannou, S. Gopinath, G. Jackson, A. Galindo and C. S. Adjiman, A hierarchical method to integrated solvent and process design of physical CO2 absorption using the SAFT-γ Mie approach, AIChE J., 2015, 61, 3249–3269, DOI:10.1002/aic.14838
.
- M. Stavrou, M. Lampe, A. Bardow and J. Gross, Continuous Molecular Targeting–Computer-Aided Molecular Design (CoMT–CAMD) for Simultaneous Process and Solvent Design for CO2 Capture, Ind. Eng. Chem. Res., 2014, 53, 18029–18041, DOI:10.1021/ie502924h
.
- A. I. Papadopoulos, S. Badr, A. Chremos, E. Forte, T. Zarogiannis, P. Seferlis, S. Papadokonstantakis, A. Galindo, G. Jackson and C. S. Adjiman, Computer-aided molecular design and selection of CO2 capture solvents based on thermodynamics, reactivity and sustainability, Mol. Syst. Des. Eng., 2016, 1, 313–334, 10.1039/c6me00049e
.
- L. Joos, K. Lejaeghere, J. M. Huck, V. van Speybroeck and B. Smit, Carbon capture turned upside down: High-temperature adsorption & low-temperature desorption (HALD), Energy Environ. Sci., 2015, 8, 2480–2491, 10.1039/C5EE01690H
.
- J. M. Huck, L.-C. Lin, A. H. Berger, M. N. Shahrak, R. L. Martin, A. S. Bhown, M. Haranczyk, K. Reuter and B. Smit, Evaluating different classes of porous materials for carbon capture, Energy Environ. Sci., 2014, 7, 4132–4146, 10.1039/C4EE02636E
.
- E. L. First, M. M. F. Hasan and C. A. Floudas, Discovery of novel zeolites for natural gas purification through combined material screening and process optimization, AIChE J., 2014, 60, 1767–1785, DOI:10.1002/aic.14441
.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, The materials genome in action: Identifying the performance limits for methane storage, Energy Environ. Sci., 2015, 8, 1190–1199, 10.1039/C4EE03515A
.
- D. Roskosch and B. Atakan, Reverse engineering of fluid selection for thermodynamic cycles with cubic equations of state, using a compression heat pump as example, Energy, 2015, 81, 202–212, DOI:10.1016/j.energy.2014.12.025
.
- A. P. Samudra and N. V. Sahinidis, Optimization-based framework for computer-aided molecular design, AIChE J., 2013, 59, 3686–3701, DOI:10.1002/aic.14112
.
- J. Bao and L. Zhao, A review of working fluid and expander selections for organic Rankine cycle, Renewable Sustainable Energy Rev., 2013, 24, 325–342, DOI:10.1016/j.rser.2013.03.040
.
- S. Quoilin, M. D. van Broek, S. Declaye, P. Dewallef and V. Lemort, Techno-economic survey of Organic Rankine Cycle (ORC) systems, Renewable Sustainable Energy Rev., 2013, 22, 168–186, DOI:10.1016/j.rser.2013.01.028
.
- M. Lampe, M. Stavrou, H. M. Bücker, J. Gross and A. Bardow, Simultaneous Optimization of Working Fluid and Process for Organic Rankine Cycles Using PC-SAFT, Ind. Eng. Chem. Res., 2014, 53, 8821–8830, DOI:10.1021/ie5006542
.
- A. I. Papadopoulos, M. Stijepovic and P. Linke, On the systematic design and selection of optimal working fluids for Organic Rankine Cycles, Appl. Therm. Eng., 2010, 30, 760–769, DOI:10.1016/j.applthermaleng.2009.12.006
.
- O. Palma-Flores, A. Flores-Tlacuahuac and G. Canseco-Melchor, Optimal molecular design of working fluids for sustainable low-temperature energy recovery, Comput. Chem. Eng., 2014, 72, 334–349, DOI:10.1016/j.compchemeng.2014.04.009
.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N. Duerloo, Y. Cui and E. J. Reed, Holistic computational structure screening of more than 12 000 candidates for solid lithium-ion conductor materials, Energy Environ. Sci., 2017, 10, 306–320, 10.1039/C6EE02697D
.
- R. Vaidyanathan and M. El-Halwagi, Computer-Aided Design of High Performance Polymers, J. Elastomers Plast., 1994, 26, 277–293, DOI:10.1177/009524439402600306
.
-
R. Gani, in Chemical product design: Toward a perspective through case studies, ed. K. M. Ng, Elsevier, Amsterdam, 1st edn, 2007, pp. 435–458 Search PubMed
.
- J. A. H. Schwöbel, M. Preißinger, D. Brüggemann and A. Klamt, High-Throughput Screening of Working Fluids for the Organic Rankine Cycle (ORC) Based on Conductor-like Screening Model for Realistic Solvation (COSMO-RS) and Thermodynamic Process Simulations, Ind. Eng. Chem. Res., 2017, 56, 788–798, DOI:10.1021/acs.iecr.6b03857
.
- N. V. Sahinidis, M. Tawarmalani and M. Yu, Design of alternative refrigerants via global optimization, AIChE J., 2003, 49, 1761–1775, DOI:10.1002/aic.690490714
.
- K. Kraemer, A. Harwardt, R. Bronneberg and W. Marquardt, Separation of butanol from acetone–butanol–ethanol fermentation by a hybrid extraction–distillation process, Comput. Chem. Eng., 2011, 35, 949–963, DOI:10.1016/j.compchemeng.2011.01.028
.
- J. Scheffczyk, L. Fleitmann, A. Schwarz, M. Lampe, A. Bardow and K. Leonhard, COSMO-CAMD: A framework for optimization-based computer-aided molecular design using COSMO-RS, Chem. Eng. Sci., 2017, 159, 84–92, DOI:10.1016/j.ces.2016.05.038
.
- S. Kossack, K. Kraemer, R. Gani and W. Marquardt, A systematic synthesis framework for extractive distillation processes, Chem. Eng. Res. Des., 2008, 86, 781–792, DOI:10.1016/j.cherd.2008.01.008
.
- P. Linke, A. Papadopoulos and P. Seferlis, Systematic Methods for Working Fluid Selection and the Design, Integration and Control of Organic Rankine Cycles—A Review, Energies, 2015, 8, 4755–4801, DOI:10.3390/en8064755
.
- R. Gani, Chemical product design: Challenges and opportunities, Comput. Chem. Eng., 2004, 28, 2441–2457, DOI:10.1016/j.compchemeng.2004.08.010
.
- A. I. Papadopoulos, M. Stijepovic, P. Linke, P. Seferlis and S. Voutetakis, Toward Optimum Working Fluid Mixtures for Organic Rankine Cycles using Molecular Design and Sensitivity Analysis, Ind. Eng. Chem. Res., 2013, 52, 12116–12133, DOI:10.1021/ie400968j
.
- P. Mavrou, A. I. Papadopoulos, M. Z. Stijepovic, P. Seferlis, P. Linke and S. Voutetakis, Novel and conventional working fluid mixtures for solar Rankine cycles: Performance assessment and multi-criteria selection, Appl. Therm. Eng., 2015, 75, 384–396, DOI:10.1016/j.applthermaleng.2014.10.077
.
- M. Eden, S. Jørgensen, R. Gani and M. El-Halwagi, A novel framework for simultaneous separation process and product design, Chem. Eng. Process., 2004, 43, 595–608, DOI:10.1016/j.cep.2003.03.002
.
- S. Bommareddy, N. G. Chemmangattuvalappil, C. C. Solvason and M. R. Eden, Simultaneous solution of process and molecular design problems using an algebraic approach, Comput. Chem. Eng., 2010, 34, 1481–1486, DOI:10.1016/j.compchemeng.2010.02.015
.
- J. Gross and G. Sadowski, Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules, Ind. Eng. Chem. Res., 2001, 40, 1244–1260, DOI:10.1021/ie0003887
.
- M. Lampe, M. Stavrou, J. Schilling, E. Sauer, J. Gross and A. Bardow, Computer-aided molecular design in the continuous-molecular targeting framework using group-contribution PC-SAFT, Comput. Chem. Eng., 2015, 81, 278–287, DOI:10.1016/j.compchemeng.2015.04.008
.
- E. Sauer, M. Stavrou and J. Gross, Comparison between a Homo- and a Heterosegmented Group Contribution Approach Based on the Perturbed-Chain Polar Statistical Associating Fluid Theory Equation of State, Ind. Eng. Chem. Res., 2014, 53, 14854–14864, DOI:10.1021/ie502203w
.
- J. Schilling, M. Lampe, J. Gross and A. Bardow, 1-stage CoMT-CAMD: An approach for integrated design of ORC process and working fluid using PC-SAFT, Chem. Eng. Sci., 2017, 159, 217–230, DOI:10.1016/j.ces.2016.04.048
.
- J. Scheffczyk, C. Redepenning, C. M. Jens, B. Winter, K. Leonhard, W. Marquardt and A. Bardow, Massive, automated solvent screening for minimum energy demand in hybrid extraction–distillation using COSMO-RS, Chem. Eng. Res. Des., 2016, 115, 433–442, DOI:10.1016/j.cherd.2016.09.029
.
- J. Bausa, R. V. Watzdorf and W. Marquardt, Shortcut methods for nonideal multicomponent distillation: I. Simple columns, AIChE J., 1998, 44, 2181–2198, DOI:10.1002/aic.690441008
.
- C. Redepenning, S. Recker and W. Marquardt, Pinch-based shortcut method for the conceptual design of isothermal extraction columns, AIChE J., 2017, 63, 1236–1245, DOI:10.1002/aic.15523
.
- S. Lecompte, S. Lemmens, H. Huisseune, M. van den Broek and M. de Paepe, Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery, Energies, 2015, 8, 2714–2741, DOI:10.3390/en8042714
.
- F. E. Pereira, E. Keskes, A. Galindo, G. Jackson and C. S. Adjiman, Integrated solvent and process design using a SAFT-VR thermodynamic description: High-pressure separation of carbon dioxide and methane, Comput. Chem. Eng., 2011, 35, 474–491, DOI:10.1016/j.compchemeng.2010.06.016
.
-
F. E. Pereira, E. Keskes, A. Galindo, G. Jackson and C. S. Adjiman, in Energy systems engineering, ed. E. S. Kikkinides, E. N. Pistikopoulos and M. C. Georgiadis, Wiley-VCH, Weinheim, 2008, pp. 231–248 Search PubMed
.
- A. Gil-Villegas, A. Galindo, P. J. Whitehead, S. J. Mills, G. Jackson and A. N. Burgess, Statistical associating fluid theory for chain molecules with attractive potentials of variable range, J. Chem. Phys., 1997, 106, 4168, DOI:10.1063/1.473101
.
- T. Lafitte, A. Apostolakou, C. Avendano, A. Galindo, C. S. Adjiman, E. A. Muller and G. Jackson, Accurate statistical associating fluid theory for chain molecules formed from Mie segments, J. Chem. Phys., 2013, 139, 154504, DOI:10.1063/1.4819786
.
- V. Papaioannou, T. Lafitte, C. Avendano, C. S. Adjiman, G. Jackson, E. A. Muller and A. Galindo, Group contribution methodology based on the statistical associating fluid theory for heteronuclear molecules formed from Mie segments, J. Chem. Phys., 2014, 140, 54107, DOI:10.1063/1.4851455
.
- S. Gopinath, G. Jackson, A. Galindo and C. S. Adjiman, Outer approximation algorithm with physical domain reduction for computer-aided molecular and separation process design, AIChE J., 2016, 62, 3484–3504, DOI:10.1002/aic.15411
.
- T. Zhou, K. McBride, X. Zhang, Z. Qi and K. Sundmacher, Integrated solvent and process design exemplified for a Diels-Alder reaction, AIChE J., 2015, 61, 147–158, DOI:10.1002/aic.14630
.
- T. Zhou, Y. Zhou and K. Sundmacher, A hybrid stochastic–deterministic optimization approach for integrated solvent and process design, Chem. Eng. Sci., 2017, 159, 207–216, DOI:10.1016/j.ces.2016.03.011
.
- E. Hendriks, G. M. Kontogeorgis, R. Dohrn, J.-C. de Hemptinne, I. G. Economou, L. F. Žilnik and V. Vesovic, Industrial Requirements for Thermodynamics and Transport Properties, Ind. Eng. Chem. Res., 2010, 49, 11131–11141, DOI:10.1021/ie101231b
.
- O. Lötgering-Lin and J. Gross, Group Contribution Method for Viscosities Based on Entropy Scaling Using the Perturbed-Chain Polar Statistical Associating Fluid Theory, Ind. Eng. Chem. Res., 2015, 54, 7942–7952, DOI:10.1021/acs.iecr.5b01698
.
- M. Hopp and J. Gross, Group-contribution method for thermal conductivity using PC-SAFT and entropy scaling, in Proceedings of 14th International Conference on Properties and Phase Equilibria for Product and Process Design 2016, ed. M. E. Macedo and J. N. C. Lopes, University of Porto and University of Lisboa, 2016 Search PubMed.
- M. Hopp and J. Gross, Thermal Conductivity of Real Substances from Excess Entropy Scaling Using PCP-SAFT, Ind. Eng. Chem. Res., 2017, 56, 4527–4538, DOI:10.1021/acs.iecr.6b04289
.
-
H. Struebing, PhD thesis, Imperial College London, 2011 Search PubMed
.
-
H. Struebing, C. S. Adjiman and A. Galindo, Optimal solvent design for reactions using computer-aided molecular design, available at: http://www.minlp.org/library/problem/mod/index.php?lib=MINLP&i=180&pi=-137, accessed 9 November 2015 Search PubMed
.
- I. E. Grossmann and Z. Kravanja, Mixed-integer nonlinear programming techniques for process systems engineering, Comput. Chem. Eng., 1995, 19, 189–204, DOI:10.1016/0098-1354(95)87036-9
.
- J. Gross, An equation-of-state contribution for polar components: Quadrupolar molecules, AIChE J., 2005, 51, 2556–2568, DOI:10.1002/aic.10502
.
- J. Gross and J. Vrabec, An equation-of-state contribution for polar components: Dipolar molecules, AIChE J., 2006, 52, 1194–1204, DOI:10.1002/aic.10683
.
- J. Vijande, M. M. Piñeiro, D. Bessières, H. Saint-Guirons and J. L. Legido, Description of PVT behaviour of hydrofluoroethers using the PC-SAFT EOS, Phys. Chem. Chem. Phys., 2004, 6, 766–770, 10.1039/b312223a
.
- K. G. Joback and R. C. Reid, Estimation of pure-component properties from group-contributions, Chem. Eng. Commun., 1987, 57, 233–243, DOI:10.1080/00986448708960487
.
- Y. Rosenfeld, Relation between the transport coefficients and the internal entropy of simple systems, Phys. Rev. A, 1977, 15, 2545–2549, DOI:10.1103/PhysRevA.15.2545
.
- Y. Rosenfeld, A quasi-universal scaling law for atomic transport in simple fluids, J. Phys.: Condens. Matter, 1999, 11, 5415–5427 CrossRef CAS
.
- P. D. Neufeld, Empirical Equations to Calculate 16 of the Transport Collision Integrals Ω(l, s), J. Chem. Phys., 1972, 57, 1100–1102, DOI:10.1063/1.1678363
.
-
B. E. Poling, J. M. Prausnitz and J. P. O'connell, The properties of gases and liquids, McGraw-Hill, New York, 5th edn, 2001 Search PubMed
.
- S. Kondo, Y. Urano, K. Tokuhashi, A. Takahashi and K. Tanaka, Prediction of flammability of gases by using F-number analysis, J. Hazard. Mater., 2001, 82, 113–128, DOI:10.1016/S0304-3894(00)00358-7
.
- T. A. Albahri and R. S. George, Artificial Neural Network Investigation of the Structural Group Contribution Method for Predicting Pure Components Auto Ignition Temperature, Ind. Eng. Chem. Res., 2003, 42, 5708–5714, DOI:10.1021/ie0300373
.
- T. M. Martin and D. M. Young, Prediction of the Acute Toxicity (96-h LC 50) of Organic Compounds to the Fathead Minnow (Pimephales promelas) Using a Group Contribution Method, Chem. Res. Toxicol., 2001, 14, 1378–1385, DOI:10.1021/tx0155045
.
- Globally harmonized system of classification and labelling of chemicals (GHS), United Nations, New York, 4th edn, 2011 Search PubMed.
- A. S. Hukkerikar, S. Kalakul, B. Sarup, D. M. Young, G. Sin and R. Gani, Estimation of environment-related properties of chemicals for design of sustainable processes: development of group-contribution+ (GC+) property models and uncertainty analysis, J. Chem. Inf. Model., 2012, 52, 2823–2839, DOI:10.1021/ci300350r
.
-
Guidance for Mobile Air Conditioning (MAC) Sectors. Guidance: F gas and ozone regulations, available at: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/394838/fgas-mac3-key-obligations.pdf, accessed 6 August 2016 Search PubMed
.
- A. Messac, A. Ismail-Yahaya and C. A. Mattson, The Normalized Normal Constraint Method for Generating the Pareto Frontier, Struct. Multidiscipl. Optim., 2003, 25, 86–98, DOI:10.1007/s00158-002-0276-1
.
- Y. Y. Haimes, L. S. Lasdon and D. A. Wismer, On a Bicriterion Formulation of the Problems of Integrated System Identification and System Optimization, IEEE Trans. Syst. Man Cybern. Syst., 1971, 1, 296–297 Search PubMed
.
-
R. E. Rosenthal, GAMS - A User's Guide, GAMS Release 24.6.1, Washington, DC, USA, 2016, available at: http://www.gams.com/help/topic/gams.doc/userguides/GAMSUsersGuide.pdf Search PubMed
.
- M. D. Stuber, J. K. Scott and P. I. Barton, Convex and concave relaxations of implicit functions, Optim. Methods Softw., 2014, 30, 424–460, DOI:10.1080/10556788.2014.924514
.
- G. R. Kocis and I. E. Grossmann, Computational experience with DICOPT solving MINLP problems in process systems engineering, Comput. Chem. Eng., 1989, 13, 307–315, DOI:10.1016/0098-1354(89)85008-2
.
- M. A. Duran and I. E. Grossmann, An outer-approximation algorithm for a class of mixed-integer nonlinear programs, Math. Program., 1986, 36, 307–339, DOI:10.1007/BF02592064
.
- P. E. Gill, W. Murray and M. A. Saunders, SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization, SIAM J. Optim., 2002, 12, 979–1006, DOI:10.1137/S1052623499350013
.
-
IBM Corporation, IBM ILOG CPLEX Optimization Studio, Version 12.6 Search PubMed
.
- P. Colonna, E. Casati, C. Trapp, T. Mathijssen, J. Larjola, T. Turunen-Saaresti and A. Uusitalo, Organic Rankine Cycle Power Systems: From the Concept to Current Technology, Applications, and an Outlook to the Future, J. Eng. Gas Turbines Power, 2015, 137, 100801, DOI:10.1115/1.4029884
.
- B. F. Tchanche, G. Papadakis, G. Lambrinos and A. Frangoudakis, Fluid selection for a low-temperature solar organic Rankine cycle, Appl. Therm. Eng., 2009, 29, 2468–2476, DOI:10.1016/j.applthermaleng.2008.12.025
.
- F. Heberle and D. Brüggemann, Exergy based fluid selection for a geothermal Organic Rankine Cycle for combined heat and power generation, Appl. Therm. Eng., 2010, 30, 1326–1332, DOI:10.1016/j.applthermaleng.2010.02.012
.
- U. Drescher and D. Brüggemann, Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants, Appl. Therm. Eng., 2007, 27, 223–228, DOI:10.1016/j.applthermaleng.2006.04.024
.
- Z. Q. Wang, N. J. Zhou, J. Guo and X. Y. Wang, Fluid selection and parametric optimization of organic Rankine cycle using low temperature waste heat, Energy, 2012, 40, 107–115, DOI:10.1016/j.energy.2012.02.022
.
- E. H. Wang, H. G. Zhang, B. Y. Fan, M. G. Ouyang, Y. Zhao and Q. H. Mu, Study of working fluid selection of organic Rankine cycle (ORC) for engine waste heat recovery, Energy, 2011, 36, 3406–3418, DOI:10.1016/j.energy.2011.03.041
.
- F. Heberle and D. Brüggemann, Thermo-economic analysis of zeotropic mixtures and pure working fluids in Organic Rankine Cycles for waste heat recovery, in Proceedings of the 3rd International Seminar on ORC Power Systems ASME-ORC 2015, ed. V. Lemort, S. Quoilin, M. De Paepe and M. van den Broek, University of Liège and Ghent University, 2015, pp. 152–161 Search PubMed.
-
A. Bejan, G. Tsatsaronis and M. J. Moran, Thermal design and optimization, Wiley, New York, 1996 Search PubMed
.
- L. Pierobon, T.-V. Nguyen, U. Larsen, F. Haglind and B. Elmegaard, Multi-objective optimization of organic Rankine cycles for waste heat recovery: Application in an offshore platform, Energy, 2013, 58, 538–549, DOI:10.1016/j.energy.2013.05.039
.
- S. G. Hall, S. Ahmad and R. Smith, Capital cost targets for heat exchanger networks comprising mixed materials of construction, pressure ratings and exchanger types, Comput. Chem. Eng., 1990, 14, 319–335, DOI:10.1016/0098-1354(90)87069-2
.
-
Chemical Engineering, Chemical Engineering Plant Cost Index, available at: www.chemengonline.com, accessed 17 May 2017 Search PubMed
.
-
W. Roetzel and B. Spang, C1 Thermal Design of Heat Exchangers, in VDI Heat Atlas, ed. The Association of German Engineers (VDI), Springer Berlin
Heidelberg, Berlin, Heidelberg, 2010, pp. 31–66 Search PubMed
.
-
G. Kirchner, O1 Hints on the Construction of Heat Exchangers, in VDI Heat Atlas, ed. The Association of German Engineers (VDI), Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 1523–1552 Search PubMed
.
-
M. Kleiber, R. Joh and R. Span, D3 Properties of Pure Fluid Substances, in VDI Heat Atlas, ed. The Association of German Engineers (VDI), Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 301–418 Search PubMed
.
- V. Gnielinski, New equations for heat and mass transfer in the turbulent flow in pipes and channels, NASA STI/Recon Technical Report A, 1975, pp. 8–16 Search PubMed.
- K. E. Gungor and R. Winterton, A general correlation for flow boiling in tubes and annuli, Int. J. Heat Mass Transfer, 1986, 29, 351–358, DOI:10.1016/0017-9310(86)90205-X
.
-
R. Numrich and J. Müller, J1 Filmwise Condensation of Pure Vapors, in VDI Heat Atlas, ed. The Association of German Engineers (VDI), Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 903–918 Search PubMed
.
- M. Astolfi, M. C. Romano, P. Bombarda and E. Macchi, Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium–low temperature geothermal sources – Part B: Techno-economic optimization, Energy, 2014, 66, 435–446, DOI:10.1016/j.energy.2013.11.057
.
- finanzen.net GmbH, Dollar exchange rate, available at: http://www.finanzen.net/devisen/dollarkurs, accessed 4 August 2016 Search PubMed
.
- Chemical Safety Sheets: Working safely with hazardous chemicals, Kluwer Academic Publishers, Dordrecht, Netherlands, Norwell, MA, U.S.A, 1991 Search PubMed.
- M. Hennen, S. Postels, P. Voll, M. Lampe and A. Bardow, Multi-objective synthesis of energy systems: Efficient identification of design trade-offs, Comput. Chem. Eng., 2017, 97, 283–293, DOI:10.1016/j.compchemeng.2016.10.010
.
-
G. E. P. Box and N. R. Draper, Empirical model-building and response surfaces, Wiley, New York, 1987 Search PubMed
.
- S. Lemmens, A perspective on costs and cost estimation techniques for Organic Rankine Cycle systems, in Proceedings of the 3rd International Seminar on ORC Power Systems ASME-ORC 2015, ed. V. Lemort, S. Quoilin, M. De Paepe and M. van den Broek, University of Liège and Ghent University, 2015, pp. 181–190 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed description of the non-conventional properties of the molecules, the thermodynamic model of the considered case study and the calculation of the heat transfer coefficients. See DOI: 10.1039/c7me00026j |
| This journal is © The Royal Society of Chemistry 2017 |