Ligand-induced conformational preorganization of loops of c-MYC G-quadruplex DNA and its implications in structure-specific drug design†
Abstract
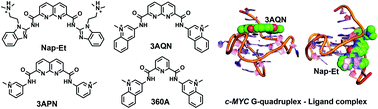
Stabilization of a G-quadruplex (G4) DNA structure in the proto-oncogene c-MYC using small molecule ligands has emerged as an attractive strategy for the development of anticancer therapeutics. To understand the subtle structural changes in the G4 structure upon ligand binding, molecular dynamics (MD) simulations of c-MYC G4 DNA were carried out in a complex with six different potent ligands: 3AQN, 6AQN, 3APN, 360A, Nap-Et, and Nap-Pr. The results show that the ligands 3AQN, 6AQN, 3APN, and 360A stabilize the G4 structure by making stacking interactions with the top quartet. On the other hand, Nap-Et and Nap-Pr bind at the groove of the G4 structure. These groove binding ligands make crucial H-bond contacts with the guanines and electrostatic interactions with the phosphate backbone. Two-dimensional dynamic correlation maps unraveled the ligand-induced correlated motions between the guanines in the quartet and a di-nucleotide present in the propeller loop-2 of the G4 structure. Cluster analysis and ONIOM calculations revealed the structural dynamics in the loop of the quadruplex upon ligand binding. Overall, the results from the present study suggest that engineering specific contacts with the propeller loop can be an efficient way to design c-MYC G4-specific ligands.


 Please wait while we load your content...
Please wait while we load your content...