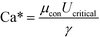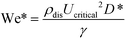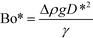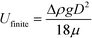Throughput enhancement of parallel step emulsifier devices by shear-free and efficient nozzle clearance†
Elad
Stolovicki‡
 *a,
Roy
Ziblat‡
*a and
David A.
Weitz
*a,
Roy
Ziblat‡
*a and
David A.
Weitz
 *ab
*ab
aSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA. E-mail: stolovicki@seas.harvard.edu; rziblat@seas.harvard.edu; weitz@seas.harvard.edu
bDepartment of Physics, Harvard University, Cambridge, MA 02138, USA
First published on 21st November 2017
Abstract
Step emulsification is an attractive method for production of monodisperse drops. Its main advantage is the ability to parallelize many step emulsifier nozzles to achieve high production rates. However, step emulsification is sensitive to any obstructions at the nozzle exit. At high production rates, drops can accumulate at nozzle exits, disturb the formation of subsequent drops and impair monodispersity. As a result, parallelized step emulsifier devices typically do not work at maximum productivity. Here a design is introduced that parallelizes hundreds of step emulsifier nozzles, and effectively removes drops from the nozzle exits. The drop clearance is achieved by an open collecting channel, and is aided by buoyancy. Importantly, this clearance method avoids the use of a continuous phase flow for drop clearance and hence no shear is applied on the forming drops. The method works well for a wide range of drops, sizing from 30 to 1000 μm at production rates of 0.03 and 10 L per hour and achieved by 400 and 120 parallelized nozzles respectively.
Introduction
An emulsion is a mixture of immiscible liquids and is commonly found in various disciplines such as food,1 chemistry,2,3 and pharmaceuticals.4 The use of the drops of an emulsion as miniature test tubes expands the utility of emulsions to basic research, diagnostics, biology,2,5–7 medicine,8,9 and biotechnology.10,11 Using emulsions with a well-defined drop size can increase the signal-to-noise ratio and improve the predictability and standardization of assays. Emulsification techniques such as mixers, colloid mills, high pressure homogenizers, and sonicators apply high shear forces to break larger emulsion drops into smaller ones.12,13 These high shear methods yield rather poly-disperse emulsion drops with a coefficient of variation (CV) of the diameter of typically 40%.14 The emulsification process is energetically inefficient and more than 95% of the energy invested is converted into heat.15,16 Furthermore, heat or shear sensitive materials can be damaged by these emulsification processes.17 To overcome the limitation of the high shear devices, direct emulsification methods have been developed such as membrane emulsification18 and microfluidic drop makers.12 In membrane emulsification, the dispersed phase is extruded through micro pores into the continuous phase.19,20 The continuous phase must be flowing, thereby applying shear that breaks the drops off the membrane. A membrane with round micro pores typically produces drops with a CV of diameter of 10%.21 Many microfluidic emulsifiers are shear-based devices where the flow of the fluids is used to decrease the drop size; these include T-junctions and co-flow or flow focusing devices.22–25 A single device can produce drops at rates up to 12 KHz26 and with an excellent diameter CV of less than 3%;27 however, since drop size strongly depends on flow rates of both the dispersed and continuous phases the total throughput is as low as 0.1 mL per hour.26 Moreover, it is challenging to robustly operate multiple drop makers in parallel. A second class of microfluidic emulsifiers rely on channel geometry to determine the drops size.25,28 In this case there is a step in the channel height and the difference in Laplace pressure as the drop forms when the dispersed phase enters the large channel at the step leads to the formation of drop of well-defined size.12,29–32 The drop sizes are independent of the flow rate of the dispersed phase, as long as it is significantly slower than the drop formation time at the step, leading to much slower production rates.12,15,28,30,31,33–44 However, step-emulsification devices are relatively easy to parallelize; examples include microchannel (MC) devices,12,30 through-hole arrays,36 asymmetric straight-through arrays,38 Edge based droplet generation (EDGE) devices,41,42 millipede devices,43,45 and step emulsification devices.46 Since drop formation is driven only by interfacial tension forces, without shear forces, drop size is independent of the flow rates of both the dispersed and the continuous phases.30,47,48 Flow of the continuous phase is not required for drop formation; nevertheless it is often used to remove the drops from the nozzles enabling formation of the next drops. Crowding of drops near the nozzle is problematic because it prevents the continuous phase from entering the nozzles and pinching off the drops.30 The drop accumulation also increases the interaction between the new forming drop, the device surfaces, and the existing drops, and can cause drops to coalesce. Drop accretion at the nozzle can also result in the broadening of drop size distribution, and is, in fact, a major bottleneck of the step emulsification devices.29,49 Flowing the continuous phase to remove the drops from the nozzle can apply shear forces on the drops, increasing their polydispersity and limiting the throughput. A design of the step emulsification device that overcomes this limitation and efficiently removes the drops from the nozzles without the use of shear would increase the production rate, without compromising drop monodispersity.In this paper, we introduce a method to increase drop production in parallel step-emulsifiers, by preventing drop accumulation at the nozzle exits, while preserving monodispersity. We show that the used design, aided by buoyancy, is an efficient method to clear nozzle exits without applying shear on the forming drops. The volcano emulsifier is a microfluidic device with parallel step emulsification nozzles, which produce monodisperse drops with diameter between 30 μm to 1000 μm with CVs ranging between 3% and 5%. We demonstrate high throughput of mono dispersed drops, producing up to 10 liters per hour of dispersed phase.
Results
The volcano device made from polydimethylsiloxane (PDMS) is used here for producing water in oil emulsions. The water flows through the device inlet, and split into 135 step-emulsifier nozzles with rectangular cross section of 135 × 700 μm. Each nozzle produces ∼570 μm size drops. The device is submerged in a quiescent oil reservoir. Buoyancy force aids the transfer of the formed water drops away from the nozzle exists area. The formed drops accumulate at the top of the reservoir, since the oil is denser than water. The schematics of a volcano device (pink) submerged in the oil reservoir (yellow) and produced water drops (blue) are shown in Fig. 1.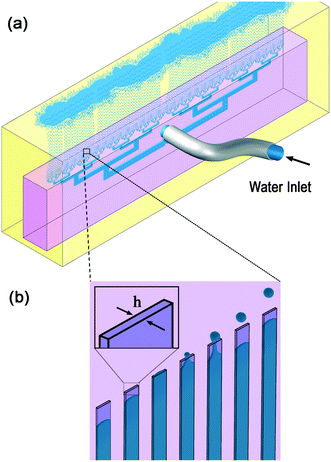 | ||
| Fig. 1 Schematics of experimental setup: a) a PDMS volcano device (pink) is submerged in oil (yellow), the continuous phase, with the nozzles pointing upwards. Water (blue), the dispersed phase, is pumped through the device and forms monodisperse drops. The drops rise to the top of the continuous phase reservoir. b) Enhancement of the nozzle area, with schematics of the propagating aqueous phase through the nozzle, left to right, followed by drop formation at the nozzle exits, and rising. The diameter of the drops is proportional to h, the nozzle height. Example of an operating device is available in Video SV1.† | ||
The drop size is almost independent of flow rate over an extended range. For flow rates between 12 to 70 mL min−1 the average drop diameter is 567 ± 6 μm. The drops are monodisperse with CV < 3%. At flow rates below 12 mL min−1 the average drop diameter begins to decrease and is 538 μm with a CV of 5%. At flow rates above 70 mL min−1, average drop size increase to 592 μm and the CV increase to 16%, as can be seen in Fig. 2. Due to the weak dependence of drop size on flow rate in the first regime, between 12–70 mL min−1, flow variations at each nozzle do not translate into significant drop size variations. It is this feature that enables all 135 nozzles to produce droplets of the same size.
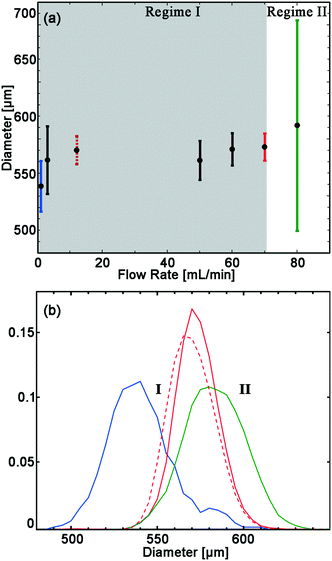 | ||
| Fig. 2 Drop diameter as a function of flow rate, for a device with 135 nozzles of 135 μm height. a) The average (black circle) and standard deviation (error bars) of drop diameter. Two regimes are observed; I. all nozzles are dripping, indicated with gray background. II. Part of the nozzles are jetting leading to a wider distribution (>16% CV), and formation of larger drops, in addition to drops with 579 μm diameter. b) Probability density function (PDF) of drop diameter at flows of: 0.5 (blue), 12 (dashed red), 70 (red) and 80 (green) mL min−1. The colors of error bars in (a) match colors of PDF in (b). The extended PDF of all measurements available in Fig. S1 and Table S1.† | ||
A nozzle of a step emulsifier can operate in either dripping or jetting mode. The transition from dripping to jetting occurs at a critical flow velocity. In the dripping mode, the instability that leads to drop breakup occurs inside the nozzle, and drops are monodisperse. In the first regime, where the flow rate is lower than 70 mL min−1, all nozzles are in dripping. At flow rate of 80 mL min−1 most nozzles are in dripping mode and produce monodisperse drops with an average diameter of 579 μm and CV of 4%. However, a few of the nozzles are in the jetting mode, producing drops with much larger diameter of 1455 μm. These large drops are <1% of the total drops yet account for ∼12% of the total drop volume. In this case, an increase in flow rate from 70 to 80 mL min−1 does not increase the production rate of the ∼579 μm-diameter drops, as shown in Fig. S1 and Table S1.† The maximum production rate for a volcano device is determined by the maximum flow rate where none of the nozzles transition from the dripping to the jetting mode. Hence, 70 mL min−1 is the maximum production rate for this device.
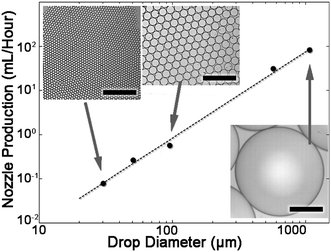
Next, the maximum production rates of monodisperse drops are determined for devices with nozzle heights ranging between 6–260 μm. The average nozzle maximal flow rates are calculated by dividing the maximal device production rate with the number of nozzles. The maximum flow rate is dependent on the drop diameter by a power law 2, as shown in Fig. 3. Therefore, a linear relation is found between the maximum production rate and the drop area (Fig. S2†). The device properties and results are summarized in Table S2.†
Previous studies have found that the step emulsification process is governed by surface tension.31,33,34,49 To characterize the transition from dripping to jetting, a comparison is made between the surface tension, viscous, inertia, and gravity forces at the critical velocity. The comparison is made by dimensionless numbers including the capillary, Weber, and Bond numbers all determined at the critical velocity:
The critical capillary number, Ca*, is the ratio between the viscous forces and the surface tension forces, at the critical velocity:
The critical Weber number, We*, is the ratio between the inertial forces and the surface tension forces, at the critical velocity:
The critical Bond number is the ratio between the gravitational forces and the surface tension forces:
In previous findings, the critical capillary numbers were found to be at least two orders of magnitude larger than the critical Weber and Bond numbers.15,31,33,47,49,50
In contrast, for some of the experiments here the critical Weber and Bond numbers are significantly larger than the capillary number. Their values are: Ca* ∼ 10−2, We* ∼ 10−1–10−2 and Bo* ∼ 10−3–1. Therefore, it is unclear if the capillary number alone determines the transition from dripping to jetting in the experiments here. Nevertheless, the drops produced are monodisperse. The critical Ca*, We* and Bo* values are presented in Table S3.†
The diameter of the drops is proportional to the nozzle height in a step-emulsifier. For the maximum production flow rates, the proportionality between nozzle height and drop diameter is 4.12 (Fig. S3†).
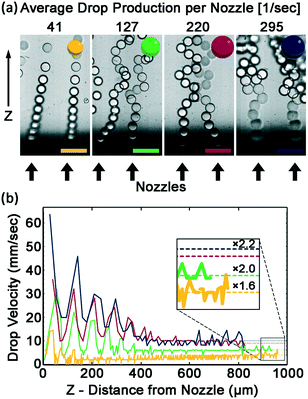
Drops accumulating at the nozzle exit can increase the resistance for the flow of the continuous phase into the nozzle, can impair drop breakup, and can decrease drop monodispersity. Therefore, efficient removal of the drops from the nozzle outlet is imperative to achieve high production rates while maintaining low CV. To measure the efficiency of drops clearing the nozzle exits, nozzle clearance is captured by imaging with a fast camera at varying flow rates, for a device with 20 μm height nozzles. To quantify the efficiency of drop removal, the velocity of the drop is determined from the movies as a function of the distance from the nozzle. Two regions of velocity are observed. In the first region, near the nozzle, drop velocity is governed by the production rate. In the second region far from the nozzle, drop velocity reaches a plateau. The flow pattern of the drops is dictated by the flow rate of the dispersed phase. At low flow rate, the drop velocity and the space between drops both increase with distance from the nozzle. At higher drop production rate, the drops remain in contact with one another. The contact between the drops causes the newly formed drop to push and accelerate the previously created drops causing their speed to oscillate at the drop production frequency. These oscillations decay into a steady velocity after 5–6 cycles, as can be seen in Fig. 4b. The velocity of a drop near the nozzle is larger than the velocity far from the nozzle, resulting in a broadening of the column of drops. The broadening increases with drop production rate. Nevertheless, even at the maximum flow rate the nozzle exits are relatively free to form additional drops, and each newly formed drop is in contact with only a single former drop, as shown in Fig. 4a.
The hydrodynamic interactions between the rising drops lead to effective drag reduction.51–57 Thus the plateau velocity is 3 to 5 times faster than the finite velocity of a single sphere, as calculated by Stokes law:58
A simplified way of characterizing the flow of a cluster of drops is to assume that the cluster behaves as a single drop that has a larger effective diameter. The effective diameter of this drop is calculated using the Stokes equation with the plateau velocity of the cluster. The effective diameters are 1.6 to 2.2 larger than a single drop, as shown in Fig. 4. Videos are available in Videos SV2–SV5.†
Conclusions
Step emulsification is an attractive technique to produce a high quantity of monodisperse emulsion drops. However, when parallelizing step emulsifiers, drops can accumulate and jam the nozzle area. The drop build-up limits the production rate. The volcano is designed to overcome this problem. The drop clearance method is buoyancy-aided and helps each nozzle to function at the highest stable production rates, determined by the dripping to jetting transition. This method enables production of up to 10 L per hour of monodisperse drops by a 75 × 50 × 5 mm3 size device, as demonstrated here (Video SV6†).The maximum production rate varies as a power law in drop diameter with an exponent of 2. In addition, the maximum production rate is not limited to very small values of the Weber and Bond number compared to the capillary, instead, in some instances, the Weber or Bond numbers dominate. Currently there is no model to account for this behavior.
Parallelization of step emulsifiers is robust because of the weak dependence of drop size on flow rate. Therefore, flow variations at each nozzle do not translate into significant variation in drop size; moreover, monodisperse drops can also be obtained by unsteady flow of the dispersed phase. The volcano devices can, therefore, be operated by manual injection of the dispersed phase, for example using a syringe (Videos SV7†). Therefore, there is no requirement for precision pumps or expensive gas regulators for preparing a monodispersed emulsion.
Emulsification operation can be further standardized by converting the volcano emulsifier into a pipettor tip. With the tip volcano, the nozzles are fabricated into the wall of the tip. The dispersed phase is pushed via the nozzles, and drops are made in the continuous phase tube. Alternatively, the dispersed phase can be pulled into a tip prefilled with continuous phase, forming the drops inside the tip. The tip volcano can take advantage of existing pipettor technology like multi-well and robots for parallelizing and automation of the encapsulation assay (Videos SV8†).
The volcano design will be useful for applications that demand large scale production of monodispersed drops. Alternatively, the volcano can be used to encapsulate small volumes of chemical or biological samples into drops within seconds, which would otherwise spoil or decay.
Methods
Device preparation
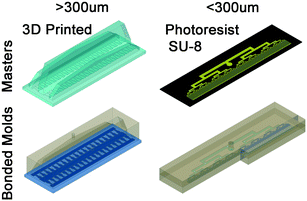
The emulsification devices are cast from polydimethylsiloxane (PDMS, SYLGARD® 184, Dow Corning, USA) on a molding master. The molding masters are designed using computer aided design (CAD) software (AutoCad 2015, Autodesk, CA, USA). The size of drops that are formed by step emulsification is dictated by nozzle height. Here we study high throughput production of drops with diameter ranging from 30 μm to 1000 μm. To achieve the wide range of diameter, two methods are used for fabricating the required molding masters. Masters for drops with diameter smaller than 300 μm are made with lithography of spin-coated silicon wafer with SU-8 photoresist (Microchem, USA).61 For drops larger than 300 μm, the masters are 3D printed using Objet 30 (Objet Geometries Ltd., Billerica, MA, USA). The required dimensions for distribution channels for producing liters per hour of emulsion are millimeters to centimeters in scale. 3D printers are advantageous in fabricating channels from sub-millimeter to centimeters scales. The process for producing a 3D mold master is cheap and requires only designing and sending to print. Notably, some chemical interaction between the freshly 3D-printed molding master and the PDMS prevent the curing of the PDMS. To prevent the curing issues, the 3D-printed masters are baked overnight at 90 °C before their first PDMS casting. Once the PDMS is cured, the devices are peeled off from the master and tubing holes are punched. The devices are then exposed to oxygen plasma and bonded to a glass slide or a second PDMS slab, as shown in Fig. 5. Proper surface treatment of the nozzles outlet is critical for high production rates. The devices are surface treated prior to experiment with 2% v/v trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich, USA) in HFE 7500 (Novec Engineered Fluid, 3M, USA) to increase the hydrophobicity of the PDMS.Emulsification experiments
High purity water (Milli-Q, USA) is used as the dispersed phase. In the large drop production experiments, food color (McCormick & Co., USA) is added to the water. The continuous phase in the experiments is HFE 7500 supplemented with 1% w/w fluoro-surfactant (008-FluoroSurfactant, RAN Biotechnologies, MA, USA). The dispersed phase is injected into the device using syringe pumps, PHD 2000 (Harvard Apparatus, MA, USA).Experimental setup
Two different setups are used for the visualization and measurement of the emulsion drops. For the small drops experiment, homemade horizontal microscope is used. The microscope is composed of ×2 long distance objective (M plan Apo, Mitutoyo, Japan) and a tube lens (Proximity series, Infinity, USA). Images are capture with Phantom High-Speed camera (V 7.3, Vision Research, NJ, USA). The total magnification of the microscope is 2 μm per pixel. The large drop imaging is done with a macro lens (Macro X10, Computar, Japan) connected to video camera (XCD-V60 SONY, Japan). Images are acquired using Matlab Imaq toolbox (Matlab 2015b, Mathworks, MA). The setup magnification is 22.4 μm per pixel. The high production rate of drops causes a challenge for visualizing a single layer of drops, which is required for automated size quantification. To overcome this problem, a clear slanting bottom sleeve is submerged into the continuous phase tank. The drops rising from the drop maker nozzles to the slanting bottom slide upward along the slope, as illustrated in Fig. S4 and Movie SV9–SV12.†Image analysis
Homemade Image analysis software is used (Matlab 2015b, Mathworks, MA) for automatic extraction of drop diameter, as shown in Fig. S5.† The side view movies of the drop making are used to study the drop's evacuation process of the nozzle exists area. The buoyancy rates of the formed drops are extracted from the movies using ImageJ (NIH, USA).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (DMR-1708729) and by the Harvard Materials Research Science and Engineering Center (DMR-1420570). This work was performed in part at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Infrastructure Network (NNIN), which is supported by the National Science Foundation under NSF award no. ECS-0335765. CNS is part of Harvard University. We are grateful for the support of Human Frontiers Science Program, Long Term Fellowship. We thank Lakshminarayanan Mahadevan, Michael P. Brenner and Shmuel Rubinstein for fruitful discussions, James Weaver and Alex Meckes for their help with 3D printing, Matthew G. Zahanzinger and Zsolt J. Terdik for their useful editorial help.References
- T. Nakashima, M. Shimizu and M. Kukizaki, Particle control of emulsion by membrane emulsification and its applications, Adv. Drug Delivery Rev., 2000, 45(1), 47–56 CrossRef CAS PubMed.
- H. Song, D. L. Chen and R. F. Ismagilov, Reactions in Droplets in Microfluidic Channels, Angew. Chem., Int. Ed., 2006, 45(44), 7336–7356 CrossRef CAS PubMed.
- A. B. Theberge, et al., Microdroplets in Microfluidics: An Evolving Platform for Discoveries in Chemistry and Biology, Angew. Chem., Int. Ed., 2010, 49(34), 5846–5868 CrossRef CAS PubMed.
- J. Renukuntla, et al., Approaches for Enhancing Oral Bioavailability of Peptides and Proteins, Int. J. Pharm., 2013, 447(0), 75–93 CrossRef CAS PubMed.
- A. Rotem, et al., Single-cell ChIP-seq reveals cell subpopulations defined by chromatin state, Nat. Biotechnol., 2015, 33(11), 1165–1172 CrossRef CAS PubMed.
- J. Lederberg, A Simple Method For Isolating Individual Microbes, J. Bacteriol., 1954, 68(2), 258–259 CAS.
- G. J. V. Nossal and J. Lederberg, Antibody Production by Single Cells, Nature, 1958, 181(4620), 1419–1420 CrossRef CAS PubMed.
- B. G. Chung, et al., Microfluidic fabrication of microengineered hydrogels and their application in tissue engineering, Lab Chip, 2012, 12(1), 45–59 RSC.
- T. M. S. Chang, Semipermeable Microcapsules, Science, 1964, 146(3643), 524–525 CAS.
- B. Rotman, Measurement Of Activity Of Single Molecules Of B-D-Galactosidase, Proc. Natl. Acad. Sci. U. S. A., 1961, 47(12), 1981–1991 CrossRef CAS.
- E. Mastrobattista, et al., High-Throughput Screening of Enzyme Libraries: In Vitro Evolution of a β-Galactosidase by Fluorescence-Activated Sorting of Double Emulsions, Chem. Biol., 2005, 12(12), 1291–1300 CrossRef CAS PubMed.
- T. Kawakatsu, Y. Kikuchi and M. Nakajima, Regular-sized cell creation in microchannel emulsification by visual microprocessing method, J. Am. Oil Chem. Soc., 1997, 74(3), 317–321 CrossRef CAS.
- G. Vladisavljević, I. Kobayashi and M. Nakajima, Production of uniform droplets using membrane, microchannel and microfluidic emulsification devices, Microfluid. Nanofluid., 2012, 13(1), 151–178 CrossRef.
- M. Saito, et al., Comparison of stability of bovine serum albumin-stabilized emulsions prepared by microchannel emulsification and homogenization, Food Hydrocolloids, 2006, 20(7), 1020–1028 CrossRef CAS.
- S. Sahin and K. Schroen, Partitioned EDGE devices for high throughput production of monodisperse emulsion droplets with two distinct sizes, Lab Chip, 2015, 15(11), 2486–2495 RSC.
- D. J. McClements, Food Emulsions: Principles, Practices, and Techniques, CRC Press, 3rd edn, 2015 Search PubMed.
- C. Charcosset, I. Limayem and H. Fessi, The membrane emulsification process—a review, J. Chem. Technol. Biotechnol., 2004, 79(3), 209–218 CrossRef CAS.
- T. Nakashima and M. Shimizu, Preparation of monodispersed O/W emulsion by porous glass membrane, Kagaku Kogaku Ronbunshu, 1993, 19(6), 984–990 CrossRef CAS.
- G. T. Vladisavljević, S. Tesch and H. Schubert, Preparation of water-in-oil emulsions using microporous polypropylene hollow fibers: influence of some operating parameters on droplet size distribution, Chem. Eng. Process.: Process Intesif., 2002, 41(3), 231–238 CrossRef.
- T. Nakashima, M. Shimizu and M. Kukizaki, Preparation of monodispersed O/W emulsion by porous glass membrane, Key Eng. Mater., 1992, 61–62, 513–516 CrossRef.
- S. Omi, et al., Synthesis of polymeric microspheres employing SPG emulsification technique, J. Appl. Polym. Sci., 1994, 51(1), 1–11 CrossRef CAS.
- V. V. Steijn, et al., Block-and-break generation of microdroplets with fixed volume, Biomicrofluidics, 2013, 7(2), 024108 CrossRef PubMed.
- T. Thorsen, et al., Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device, Phys. Rev. Lett., 2001, 86(18), 4163–4166 CrossRef CAS PubMed.
- D. R. Link, et al., Geometrically mediated breakup of drops in microfluidic devices, Phys. Rev. Lett., 2004, 92(5), 054503 CrossRef CAS PubMed.
- J. K. Nunes, et al., Dripping and jetting in microfluidic multiphase flows applied to particle and fiber synthesis, J. Phys. D: Appl. Phys., 2013, 46(11), 114002 CrossRef PubMed.
- L. Yobas, et al., High-performance flow-focusing geometry for spontaneous generation of monodispersed droplets, Lab Chip, 2006, 6(8), 1073–1079 RSC.
- Z. Nie, et al., Emulsification in a microfluidic flow-focusing device: effect of the viscosities of the liquids, Microfluid. Nanofluid., 2008, 5(5), 585–594 CrossRef CAS.
- S. Sahin, et al., Microfluidic EDGE emulsification: the importance of interface interactions on droplet formation and pressure stability, Sci. Rep., 2016, 6, 26407 CrossRef CAS PubMed.
- I. Kobayashi, et al., Large microchannel emulsification device for mass producing uniformly sized droplets on a liter per hour scale, Green Processes Synth., 2012, 1(4), 353–362 CAS.
- S. Sugiura, et al., Preparation of Monodispersed Solid Lipid Microspheres Using a Microchannel Emulsification Technique, J. Colloid Interface Sci., 2000, 227(1), 95–103 CrossRef CAS PubMed.
- S. Sugiura, et al., Interfacial Tension Driven Monodispersed Droplet Formation from Microfabricated Channel Array, Langmuir, 2001, 17(18), 5562–5566 CrossRef CAS.
- I. Chakraborty, et al., Microfluidic step-emulsification in axisymmetric geometry, Lab Chip, 2017, 17(21), 3609–3620 RSC.
- I. Kobayashi, S. Mukataka and M. Nakajima, Production of Monodisperse Oil-in-Water Emulsions Using a Large Silicon Straight-Through Microchannel Plate, Ind. Eng. Chem. Res., 2005, 44(15), 5852–5856 CrossRef CAS.
- M. Rayner, et al., Using the Surface Evolver to model droplet formation processes in membrane emulsification, J. Colloid Interface Sci., 2004, 279(1), 175–185 CrossRef CAS PubMed.
- I. Kobayashi, et al., Preparation of micron-scale monodisperse oil-in-water microspheres by microchannel emulsification, J. Am. Oil Chem. Soc., 2001, 78(8), 797–802 CrossRef CAS.
- I. Kobayashi, M. Nakajima and S. Mukataka, Preparation characteristics of oil-in-water emulsions using differently charged surfactants in straight-through microchannel emulsification, Colloids Surf., A, 2003, 229(1), 33–41 CrossRef CAS.
- S. Sugiura, M. Nakajima and M. Seki, Prediction of droplet diameter for microchannel emulsification: prediction model for complicated microchannel geometries, Ind. Eng. Chem. Res., 2004, 43(26), 8233–8238 CrossRef CAS.
- I. Kobayashi, et al., Production of monodisperse water-in-oil emulsions consisting of highly uniform droplets using asymmetric straight-through microchannel arrays, Microfluid. Nanofluid., 2008, 7(1), 107–119 CrossRef.
- I. Kobayashi, et al., Straight-through microchannel devices for generating monodisperse emulsion droplets several microns in size, Microfluid. Nanofluid., 2008, 4(3), 167–177 CrossRef.
- I. Kobayashi, et al., Generation of uniform drops via through-hole arrays micromachined in stainless-steel plates, Microfluid. Nanofluid., 2008, 5(5), 677–687 CrossRef CAS.
- K. van Dijke, et al., Parallelized edge-based droplet generation (EDGE) devices, Lab Chip, 2009, 9(19), 2824–2830 RSC.
- K. C. van Dijke, et al., EDGE emulsification for food-grade dispersions, J. Food Eng., 2010, 97(3), 348–354 CrossRef CAS.
- E. Amstad, et al., Robust scalable high throughput production of monodisperse drops, Lab Chip, 2016, 16(21), 4163–4172 RSC.
- F. Dutka, A. S. Opalski and P. Garstecki, Nano-liter droplet libraries from a pipette: step emulsificator that stabilizes droplet volume against variation in flow rate, Lab Chip, 2016, 16(11), 2044–2049 RSC.
- A. Ofner, et al., High-Throughput Step Emulsification for the Production of Functional Materials Using a Glass Microfluidic Device, Macromol. Chem. Phys., 2017, 218(2), 1600472 CrossRef.
- R. Dangla, et al., The physical mechanisms of step emulsification, J. Phys. D: Appl. Phys., 2013, 46(11), 114003 CrossRef.
- S. Sugiura, et al., Characterization of Spontaneous Transformation-Based Droplet Formation during Microchannel Emulsification, J. Phys. Chem. B, 2002, 106(36), 9405–9409 CrossRef CAS.
- I. Kobayashi, et al., Large microchannel emulsification device for producing monodisperse fine droplets, Procedia Food Sci., 2011, 1, 109–115 CrossRef CAS.
- N. Mittal, et al., Dynamics of step-emulsification: From a single to a collection of emulsion droplet generators, Phys. Fluids, 2014, 26(8), 082109 CrossRef.
- G. T. Vladisavljević, I. Kobayashi and M. Nakajima, Effect of dispersed phase viscosity on maximum droplet generation frequency in microchannel emulsification using asymmetric straight-through channels, Microfluid. Nanofluid., 2011, 10(6), 1199–1209 CrossRef.
- B. R. Morton, G. Taylor and J. S. Turner, Turbulent Gravitational Convection from Maintained and Instantaneous Sources, Proc. R. Soc. London, Ser. A, 1956, 234(1196), 1–23 CrossRef.
- J. Happel and R. Pfeffer, The motion of two spheres following each other in a viscous fluid, AIChE J., 1960, 6(1), 129–133 CrossRef CAS.
- V. G. Levich, Physicochemical hydrodynamics, Prentice-Hall, Englewood Cliffs, N.J., 1962 Search PubMed.
- B. Gal-Or and S. Waslo, Hydrodynamics of an ensemble of drops (or bubbles) in the presence or absence of surfactants, Chem. Eng. Sci., 1968, 23(12), 1431–1446 CrossRef CAS.
- R. Clift, J. R. Grace and M. E. Weber, Bubbles, Drops, and Particles, Academic Press, 1978 Search PubMed.
- B. Metzger, M. Nicolas and É. Guazzelli, Falling clouds of particles in viscous fluids, J. Fluid Mech., 2007, 580, 283 CrossRef CAS.
- M. Roper, et al., Dispersal of fungal spores on a cooperatively generated wind, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(41), 17474–17479 CrossRef CAS PubMed.
- J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer, Netherlands, 1983 Search PubMed.
- V. G. Levich and V. S. Krylov, Surface-Tension-Driven Phenomena, Annu. Rev. Fluid Mech., 1969, 1(1), 293–316 CrossRef.
- H. A. Stone and L. G. Leal, The effects of surfactants on drop deformation and breakup, J. Fluid Mech., 1990, 220, 161–186 CrossRef CAS.
- D. Qin, Y. Xia and G. M. Whitesides, Rapid prototyping of complex structures with feature sizes larger than 20 μm, Adv. Mater., 1996, 8(11), 917–919 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7lc01037k |
| ‡ Equal contributors. |
| This journal is © The Royal Society of Chemistry 2018 |