Full-angle tomographic phase microscopy of flowing quasi-spherical cells†
Massimiliano M.
Villone
a,
Pasquale
Memmolo
 bc,
Francesco
Merola
b,
Martina
Mugnano
b,
Lisa
Miccio
b,
Pier Luca
Maffettone
bc,
Francesco
Merola
b,
Martina
Mugnano
b,
Lisa
Miccio
b,
Pier Luca
Maffettone
 ab and
Pietro
Ferraro
ab and
Pietro
Ferraro
 *b
*b
aDipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, University of Naples “Federico II”, Piazzale Tecchio 80, 80125 Napoli, Italy
bNational Research Council of Italy, Institute of Applied Sciences and Intelligent Systems “E. Caianiello”, Via Campi Flegrei 34, Pozzuoli, Naples, Italy. E-mail: pietro.ferraro@cnr.it
cNational Research Council of Italy, Institute for Microelectronics and Microsystems, Via Pietro Castellino 111, Naples, Italy
First published on 31st October 2017
Abstract
We report a reliable full-angle tomographic phase microscopy (FA-TPM) method for flowing quasi-spherical cells along microfluidic channels. This method lies in a completely passive optical system, i.e. mechanical scanning or multi-direction probing of the sample is avoided. It exploits the engineered rolling of cells while they are flowing along a microfluidic channel. Here we demonstrate significant progress with respect to the state of the art of in-flow TPM by showing a general extension to cells having almost spherical shapes while they are flowing in suspension. In fact, the adopted strategy allows the accurate retrieval of rotation angles through a theoretical model of the cells' rotation in a dynamic microfluidic flow by matching it with phase-contrast images resulting from holographic reconstructions. So far, the proposed method is the first and the only one that permits to get in-flow TPM by probing the cells with full-angle, achieving accurate 3D refractive index mapping and the simplest optical setup, simultaneously. Proof of concept experiments were performed successfully on human breast adenocarcinoma MCF-7 cells, opening the way for the full characterization of circulating tumor cells (CTCs) in the new paradigm of liquid biopsy.
Introduction
Three-dimensional (3D) label-free and high-throughput single-cell analysis in continuous flow is one of the most challenging targets for the whole characterization of biological samples at lab-on-a-chip scale.1–9 In the past decade, the most promising approach proposed to address this aim was tomographic phase microscopy (TPM).10–18 TPM exploits quantitative phase imaging techniques4,19–25 to map the 3D refractive index (RI) of cells by adopting beam deflection, direct mechanical rotation or holographic optical tweezers to probe the sample along a number of controlled directions. Despite the efforts to improve the TPM process by reducing the computational cost13,14 or providing smart and powerful learning methods to build tomographic reconstructions,15 very few approaches are capable of performing in-flow tomography at the single cell level.12,16 Recently, in-flow cyto-tomography has been demonstrated,17 thus achieving full 3D label-free characterization in continuous flow of red blood cells (RBCs) and diatom algae. A computational method was adopted for recovering 3D orientations of the cells while they were flowing. In practice, this cyto-TPM technique works by exploiting the rotation of cells while they are flowing along a microfluidic channel; it is possible to obtain in-line phase-contrast tomography of such cells if smart strategies for wavefront analysis are adopted. In fact, a priori knowledge of the 3D position and orientation of rotating cells is no longer needed because this information can be completely retrieved through digital holography wavefront numerical analysis. However, in ref. 17 the retrieval of angles was based mainly on the assumption of a significant asymmetric shape of these cells.17,26,27 This aspect was a clear limitation in the case of cells having an almost spherical morphology. Here, in order to overcome these limitations, we have conceived and implemented a robust and general framework of rolling angle recovery in tomographic reconstructions, allowing full angle TPM (FA-TPM) of quasi-spherical cells. In the literature, the rotational dynamics of particles has received great attention since the early 20th century, when the first theoretical predictions for spheres28 and ellipsoids29 suspended in Newtonian liquids were derived. Since then, many experimental and numerical contributions have appeared on this theme, some of which, even very recently, specifically focus on the rotation of particles, both of spherical30 and non-spherical shapes,31 in microfluidics. A wide range of literature also exists dealing with the dynamics of particles suspended in non-Newtonian media (see, for example, ref. 32 and the references therein). The proposed computational method of FA-TPM is able to provide full 3D tracking and orientation of cells in continuous flow. FA-TPM of quasi-spherical cells is based on two main steps: (i) theoretical modeling of how cells rotate in the microfluidic flow, which is able to provide the simulated rolling conditions, and (ii) calculation of the cells' rolling angles, starting from the experimental phase-contrast reconstructions, by means of the above-mentioned theoretical model. We demonstrate the results of the proof of concept experiments by applying FA-TPM to circulating metastatic breast carcinoma MCF-7 and normal human mammary epithelial MCF-10A cells in microfluidic flow. Moreover, we extend the analysis to circulating MCF-7 clusters by simultaneously mapping the RI structures of all cells in the cluster. The proposed approach could open a realistic route for the detection and sorting of circulating tumor cells (CTCs) in the peripheral blood flow.33–37Materials and methods
Preparation of samples
Human breast adenocarcinoma MCF-7 and normal human mammary epithelial MCF-10A cells were chosen for 3D quantitative characterization by TPM. MCF-7 cells were cultured in RPMI 1640 (Sigma Aldrich) supplemented with 10% fetal bovine serum, 2 mM L-glutamine and 100 U ml−1 penicillin, 100 μg ml−1 streptomycin. MCF-10A cells were cultured in mammary epithelial cell growth medium (MEGM SingleQuots, Lonza Clonetics) at 37 °C in a CO2 atmosphere. Subsequently, they were harvested from the Petri dish by incubation with a 0.05% trypsin–EDTA solution (Sigma, St. Louis, MO) for 5 min. The cells were then centrifuged for 5 min at 1500 rpm, resuspended in complete medium and injected into the microfluidic channel.In-flow quantitative phase imaging
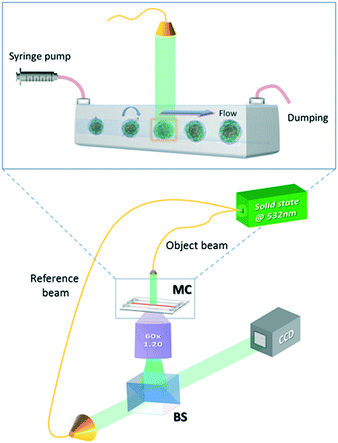
The experimental apparatus used to acquire the holographic sequences of cells is a microfluidic holographic microscope working in a transmission configuration.17 It is composed of a Mach-Zehnder interferometer equipped with a 400 mW fiber-coupled laser at 532 nm, whose main beam is directed at an objective microscope (water-immersion 60×, NA 1.20 (MO), by Olympus), allowing bright-field imaging of the cells. The reference beam is recombined with the first one by a beam splitter generating interference fringe patterns (the digital holograms) of the samples that are recorded by a 2048 × 2048 CCD camera (USB 3.0 u-eye, from IDS) recording at 75 fps in full frame. This set-up is depicted in Fig. 1. The sample is injected into a microchannel using a syringe and capillary tubes furnished by Microfluidic Chip Shop. The channel is made of PMMA polymer and has dimensions of 1000 μm × 200 μm (width × height). At the bottom, the cover lid is 140 μm thick, allowing the use of an immersion objective. While the cells are rolling in the channel, holograms are acquired, ensuring that a full 360 degree view of the sample is observed.17 By estimating the number of cells accomplishing a complete rotation (360 degrees) in the field of view, we could in principle observe about 40–50 rolling cells per minute. However, by enhancing the frame rate of the camera and/or the number (concentration) of the flowing cells, the throughput may increase. In our experiments, small confinement and low flow rate ensure a tumbling condition with no deformation of the sample.17 The resulting voxel resolution is ∼360 nm per side. Tomographic reconstructions are limited by the minimum detectable angle of rotation, that is, ∼1° for this optical arrangement.17Finally, we performed quantitative phase-contrast reconstructions of the entire sequence of recorded holograms and implemented a new computational algorithm, described in the next section, to retrieve the 3D orientation of all imaged rolling cells to be used as input for the filtered back-projection tomographic reconstruction algorithm.
Numerical simulations
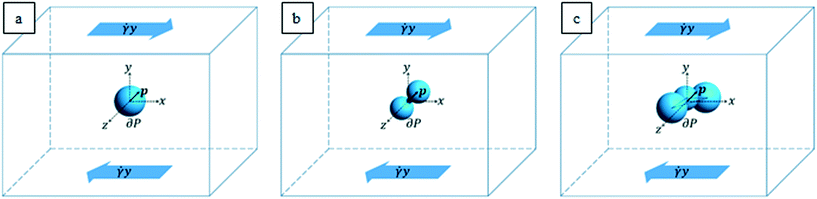
The characteristic lengths of the cells and cell clusters are within 1/10 of the microfluidic device height (equal to 200 μm, as reported above) and the suspended objects are transported by the suspending medium around the middle of the channel height. These geometric and flow conditions are such that the flow field that the particles “feel” can be locally approximated to a shear flow. In order to mimic the actual shapes of the cells and cell clusters arising from the experiments, we considered an ellipsoidal particle (see Fig. 2a), an aggregate of two spheres connected by a neck (see Fig. 2b), and a cluster of three partially interpenetrating spheres (see Fig. 2c) suspended in a Newtonian liquid subjected to unbounded shear flow. A Cartesian system of coordinates is centered at the cell/aggregate center of volume, with the x-, y-, and z-axes oriented as the flow, gradient, and vorticity directions, respectively. Far from the particle, we imposed the unperturbed velocity field u∞ = (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) y,0,0), with
y,0,0), with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) as the shear rate. The particle orientation is described by the unit vector p, which identifies the direction of the major axis of the particle in the cases depicted in Fig. 2a and b and the normal to the plane formed by the centers of the three spheres in the case depicted in Fig. 2c.
as the shear rate. The particle orientation is described by the unit vector p, which identifies the direction of the major axis of the particle in the cases depicted in Fig. 2a and b and the normal to the plane formed by the centers of the three spheres in the case depicted in Fig. 2c.
It is worth remarking that as the in-flow cell clusters are seen to have their longest dimension almost oriented along the vorticity (where the experimental device is 5 times longer than its height), the hypothesis of negligible confinement still holds for aggregates. From the values of the experimental parameters, we make a preliminary estimation of the Reynolds number Re = ρvD/η, with ρ as the suspending liquid density, v as the flow characteristic velocity, D as the particle characteristic length, and η as the suspending liquid viscosity. Since such estimation yields a value in the order of 10–3, in the system, inertial forces can be considered negligible with respect to viscous ones; thus we can model the fluid motion through the mass and momentum balance equations in the Stokes formulation, which reads as follows:
| ∇·u = 0 | (1) |
| −∇p + η∇2u = 0 | (2) |
For what concerns the boundary conditions, far from the particle we apply the unperturbed shear flow velocity u∞ (see above), whereas on the particle boundary ∂P(t), the rigid-body motion condition is imposed in the form
| u = ω × r | (3) |
The hydrodynamic torque acting on the particle also needs to be specified. Since inertia is neglected, the particle is torque free, i.e., the total torque T on the spherical surface is zero. In mathematical language
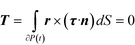 | (4) |
The fact that inertia is neglected implies that no initial condition for the velocity field u needs to be specified. The initial orientation of the particle can be chosen by assigning p(t = 0) = p0.
The solution of eqn (1) and (2) with the boundary conditions of eqn (3) and (4) enables to compute the time evolution of the u- and p-fields and of the angular velocity ω, which, in turn, allows to compute the particle orientation dynamics p(t). Such data can then be compared with the experimental cell/cluster orientation. For the solution of the equations presented above, the finite element method is used. The fluid domain is discretized through a mesh of quadratic tetrahedra. On the particle boundary, the mesh aligns with the tetrahedral element faces (quadratic triangles). During the simulations, the elements of the volume mesh progressively deform due to the particle rotation.
Any time the “quality” of the mesh elements in the domain becomes unacceptable, a re-meshing is performed, as technically detailed in ref. 38. At every time step of the simulation, once the angular velocity ω is computed, the orientation of the particle is updated by using the quaternion formalism.39 The open-source software Gmsh is used for the design of the computational domain and discretization through a mesh made of quadratic tetrahedra. Moreover, the numerical solution of the mathematical model of the system, given by eqn (1)–(4), is calculated through a non-commercial finite element numerical code written in Fortran.
Results and discussion
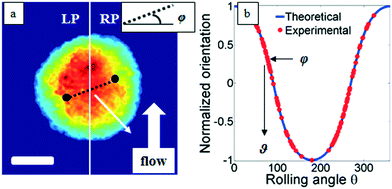
Classical TPM approaches are based on a perfect knowledge of multiple sample observation directions, which are typically controlled by high precision opto-mechanical and/or opto-electronic devices, limiting the maximum viewing range up to 180 degrees.10,13,14 In ref. 17, two full 360 degree sample observation methods have been proposed for RBCs and diatoms in continuous flow. However, these approaches are limited to classes of rolling cells having suitable properties, such as homogeneous RI distribution or mirror phase symmetry. Here, we implement a general framework to detect the full 3D pose of cells by exploiting the periodicity of the non-spherical shape features of any sequence of quantitative phase map (QPM) reconstructions of rolling cells. To this aim, we take inspiration from the 3D pose estimation framework, which is referred to as the estimation of the location of body parts and how they are connected in an image or a video sequence.40 To this aim, a theoretical model of the cell rotation in a microfluidic flow is implemented, where the cells' transversal orientation dynamics is recovered as a function of rolling angles, as described in the previous section (see Numerical simulations). Therefore, we used the theoretical behavior of the cell rotation as our gold method to recover the experimental rolling angles, i.e. by fitting this curve with the estimated transversal orientations of the cells in the QPMs. In particular, the locations of the two centroids of the body parts of one cell, corresponding to the left and right parts of the corresponding QPM, are calculated, and the angle formed between the segments joining the centroids and the orthogonal axis with respect to the flow direction represents the estimation of the transverse orientation (see Fig. 3a). Repeating this process for the same cell in all QPMs, an experimental transversal orientation dynamics is obtained and fitted with the theoretical one to calculate the rolling angles. An example of this last step is reported in Fig. 3 for a single MCF-7 metastatic breast carcinoma cell.In particular, Fig. 3b highlights how to use the recovered transversal orientation of the imaged cell in Fig. 3a, named φ, to calculate the corresponding rolling angle ϑ. Actually, we investigated two experimental situations in which tomographic reconstructions of single rolling cells as well as a rolling cluster of cells are obtained. In fact, the proposed FA-TPM method can be easily adapted to recover the rolling angles of a cluster of cells in flow. Considering a number of cells N in a cluster, the 3D pose of the cluster can be calculated by identifying the centroids of each cell and calculating the orientation of the N-sided polygon obtained connecting these centroids. In Fig. 4a, we report the 3D RI reconstruction of the central slice of the single MCF-7 cell reported in Fig. 3, while a different representation of the tomogram, highlighting three ranges of the RI, i.e. 1.334–1.355 (blue), 1.355–1.375 (green) and 1.375–1.400 (red), is shown in Fig. 4b. This last representation aims to identify the membrane region as well as the cell nucleus which is typically characterized by the highest RI values. Moreover, Fig. 4(c) and (d) report the central slice and the three-level tomogram of an MCF-10A cell, used as the healthy cell control in terms of tomographic signatures. Finally, in Fig. 5 we demonstrate the FA-TPM method for clusters of two and three MCF-7 cells. Notice that, also in this case, the experimental transverse orientations of the entire clusters perfectly fit the theoretical cell's transversal orientation dynamics calculated by the simulations (see Fig. 5a and d).
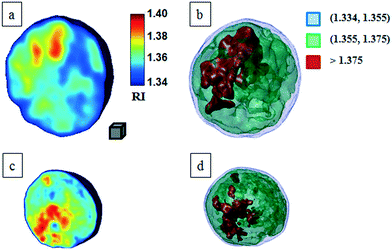 | ||
| Fig. 4 FA-TPM images for single quasi-spherical cells. (a and c) Tomographic reconstruction of the central slices of MCF-7 and MCF-10A, respectively; (b and d) alternative representations of the tomograms by using three RI ranges as thresholds. The gray cube, with a volume equal to 10 μm3, is used as the 3D scale bar for the tomograms. In movie S1,† the entire FA-TPM process is reported for the case of the single MCF-7 cell. | ||
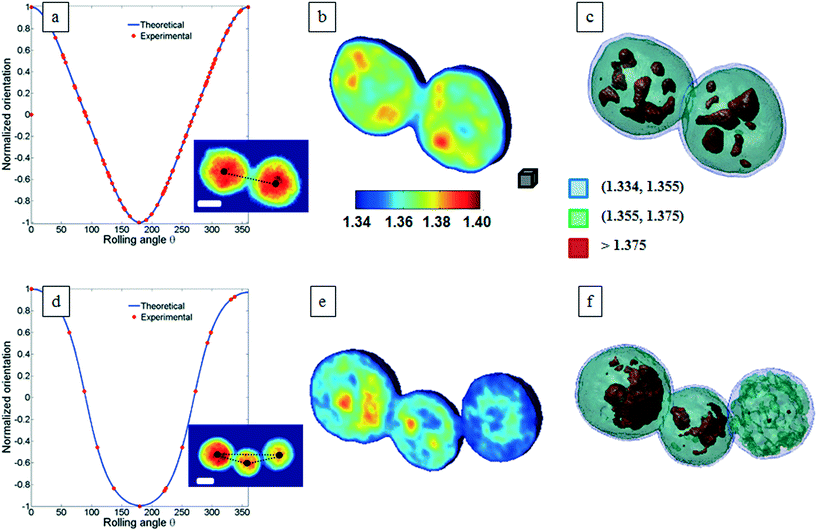 | ||
| Fig. 5 FA-TPM images for clusters of MCF-7 cells. (a and d) The theoretical curves of the normalized cluster orientations vs. the rolling angles are fitted with the estimated cluster orientations and the corresponding central slices of the tomographic reconstructions are obtained and shown in (b and e) for the cases of two and three MCF-7 cells per cluster, respectively. QPMs of the two- and three-cell clusters are reported as subfigures in (a) and (d), respectively. The black dots identify the centroid of each cell and their connection describes a 3D polygon that is used to calculate the orientation of the cluster. (c and f) report the representations of the tomograms by using the same RI ranges used in Fig. 4b. Movie S2 and S3† report the entire FA-TPM process for the two- and three-cell clusters, respectively. The white scale bars in the inset figures of (a) and (d) are 10 μm. The gray cube in (b), with a volume equal to 10 μm3, is used as the 3D scale bar for the tomograms. | ||
The central slices in Fig. 5b and e show different RI density distributions; thus the representations in Fig. 5c and f report on the fragmentation of the higher RI regions. In particular, the cell at the right of Fig. 5f shows a very small region of RI > 1.375. Definitely, all the information contained in the tomographic reconstructions can be used for cancer diagnosis. Typically, pathologists examine the tissue structure and cellular morphometry, including the cell's size and the nucleus distribution, to ascertain the diagnosis. In the case of tomographic reconstructions, one can calculate all morphometric features of cells, thus helping in the objectivity of the diagnosis.
For this motivation, we evaluated the main biophysical characteristics of the analyzed cells, i.e. the cellular volume and the average RI. Notice that the nucleus size could also be retrieved by tomographic reconstruction by detecting the higher density regions of the cell, i.e. the higher RI distributions. However, a perfect knowledge of the RI range of the nucleus is necessary for its identification. Cellular volumes and average RIs for all cells in Fig. 4 and 5 are reported in Table 1. All results reported in Fig. 3–5 are obtained by using the functions and scripts of the image processing and 3D visualization toolboxes in the MATLAB language. In particular, the 3D renders are obtained by extracting the isosurface data from the tomographic reconstructions (MATLAB function “isosurface”).
| Cell. vol. (μm3) | Avg. RI | |
|---|---|---|
| Single MCF-10A | 871.1 | 1.361 |
| Single MCF-7 | 4849.5 | 1.365 |
| Two MCF-7 cluster (L) | 6071.7 | 1.369 |
| Two MCF-7 cluster (R) | 6203.1 | 1.368 |
| Three MCF-7 cluster (L) | 4989.5 | 1.364 |
| Three MCF-7 cluster (C) | 2787.9 | 1.366 |
| Three MCF-7 cluster (R) | 3790.5 | 1.357 |
They are in agreement with the values reported in the literature.41,42 As expected, the cell at the right of Fig. 5f has the lower RI.
Conclusions
We propose for the first time an approach for achieving a full-angle tomography of flowing cells by a very simple optical set-up, FA-TPM. This method is robust; in fact, we demonstrate for the first time, to the best of our knowledge, that single cells as well as clusters of circulating human breast adenocarcinoma MCF-7 cells can be fully characterized in microfluidic flow by using the proposed FA-TPM algorithm. Despite the incredible effort of the entire scientific community in the field of liquid biopsy for CTC identification, many issues, mainly regarding the detection and the complete characterization of CTCs, remain unknown. Here, we prove that the proposed framework is highly suitable for the analysis of circulating cells, opening the way for the enrichment and identification of CTCs by this new label-free method.Author contributions
M. M. Villone and P. Memmolo contributed equally to this work.Conflicts of interest
There are no conflicts to declare.References
- A. K. S. Lau, H. C. Shum, K. K. Y. Wong and K. K. Tsia, Lab Chip, 2016, 16, 1743–1756 RSC.
- J.-L. Wu, Y.-Q. Xu, J.-J. Xu, X.-M. Wei, A. C. S. Chan, A. H. L. Tang, A. K. S. Lau, B. M. F. Chung, H. C. Shum, E. Y. Lam, K. K. Y. Wong and K. K. Tsia, Light: Sci. Appl., 2017, 6, e16196 CrossRef CAS.
- R. A. Kellogg, R. Gómez-Sjöberg, A. A. Leyrat and S. Tay, Nat. Protoc., 2014, 9, 1713–1726 CrossRef CAS PubMed.
- Y. Cotte, F. Toy, P. Jourdain, N. Pavillon, D. Boss, P. Magistretti, P. Marquet and C. Depeursinge, Nat. Photonics, 2013, 7, 113–117 CrossRef CAS.
- F. Merola, P. Memmolo, L. Miccio, V. Bianco, M. Paturzo and P. Ferraro, Proc. IEEE, 2015, 103(2), 192–204 CrossRef CAS.
- Y. C. Seow, S. P. Lim, B. C. Khoo and H. P. Lee, Sens. Actuators, B, 2010, 147(2), 607–611 CrossRef CAS.
- H. L. Liu, Y. Shi, L. Liang, L. Li, S. S. Guo, L. Yin and Y. Yang, Lab Chip, 2017, 17, 1280–1286 RSC.
- L. Liang, Y. F. Zuo, W. Wu, X. Q. Zhu and Y. Yang, Lab Chip, 2016, 16, 3007–3014 RSC.
- W. Z. Song, X. M. Zhang, A. Q. Liu, C. S. Lim, P. H. Yap and H. M. M. Hosseini, Appl. Phys. Lett., 2006, 89(20), 203901 CrossRef.
- W. Choi, C. Fang-Yen, K. Badizadegan, S. Oh, N. Lue, R. R. Dasari and M. S. Feld, Nat. Methods, 2007, 4, 717–719 CrossRef CAS PubMed.
- T. Kim, R. Zhou, M. Mir, S. D. Babacan, P. S. Carney, L. L. Goddard and G. Popescu, Nat. Photonics, 2014, 8, 256–263 CrossRef CAS.
- N. C. Pegard and J. Fleischer, Lab Chip, 2014, 14, 4447–4450 RSC.
- K. Kim, K. S. Kim, H. Park, J. C. Ye and Y. K. Park, Opt. Express, 2013, 21, 32269–32278 Search PubMed.
- G. Dardikman, M. Habaza, L. Waller and N. T. Shaked, Opt. Express, 2016, 24, 11839–11854 CrossRef CAS PubMed.
- U. S. Kamilov, I. N. Papadopoulos, M. H. Shoreh, A. Goy, C. Vonesch, M. Unser and D. Psaltis, Optica, 2015, 2, 517–522 CAS.
- S. O. Isikmana, W. Bisharaa, S. Mavandadia, F. W. Yua, S. Fenga, R. Laua and A. Ozcan, PNAS, 2011, 108(18), 7296–7301 CrossRef PubMed.
- F. Merola, P. Memmolo, L. Miccio, R. Savoia, M. Mugnano, A. Fontana, G. D'Ippolito, A. Sardo, A. Iolascon, A. Gambale and P. Ferraro, Light: Sci. Appl., 2017, 6, e16241 CrossRef CAS.
- R. Horstmeyer, J. Chung, X. Ou, G. Zheng and C. Yang, Optica, 2016, 3, 827–835 CAS.
- E. Cuche, F. Bevilacqua and C. Depeursinge, Opt. Lett., 1999, 24, 291–293 CrossRef CAS PubMed.
- P. Ferraro, A. Wax and Z. Zalevsky, Coherent Light Microscopy, Series in Surface Sciences, Springer, vol. 46, 2011 Search PubMed.
- G. Popescu, Quantitative phase imaging of cells and tissues, McGraw-Hill, New York, 2011 Search PubMed.
- M. K. Kim, SPIE Rev., 2010, 1, 018005 Search PubMed.
- F. Merola, L. Miccio, P. Memmolo, G. Di Caprio, A. Galli, R. Puglisi, D. Balduzzi, G. Coppola, P. A. Netti and P. Ferraro, Lab Chip, 2013, 13, 4512–4516 RSC.
- W. Bishara, H. Zhu and A. Ozcan, Opt. Express, 2010, 18, 27499–27510 CrossRef CAS PubMed.
- X. Ou, R. Horstmeyer, C. Yang and G. Zheng, Opt. Lett., 2013, 38, 4845–4848 CrossRef PubMed.
- L. Miccio, P. Memmolo, F. Merola, P. A. Netti and P. Ferraro, Nat. Commun., 2015, 6, 6502 CrossRef CAS PubMed.
- P. Memmolo, F. Merola, L. Miccio, M. Mugnano and P. Ferraro, J. Biomed. Opt., 2016, 21(12), 121509 Search PubMed.
- A. Einstein, Ann. Phys., 1906, 19, 289–306 CrossRef CAS.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 CrossRef.
- J. Suo, E. E. Edwards, A. Anilkumar, T. Sulchek, D. P. Giddens and S. N. Thomas, R. Soc. Open Sci., 2016, 3, 160298 CrossRef PubMed.
- M. M. Villone, G. D'Avino, M. A. Hulsen and P. L. Maffettone, Phys. Rev. E, 2015, 92, 062303 CrossRef CAS PubMed.
- G. D'Avino and P. L. Maffettone, J. Non-Newtonian Fluid Mech., 2015, 215, 80–104 CrossRef.
- C. Alix-Panabières and K. Pantel, Nat. Rev. Cancer, 2014, 14(9), 623–631 CrossRef PubMed.
- M. Cristofanilli, G. T. Budd, M. J. Ellis, A. Stopeck, J. Matera, M. C. Miller, J. M. Rueben, G. Doyle, W. J. Allard, L. W. Terstappen and D. F. Hayes, N. Engl. J. Med., 2004, 351, 781–791 CrossRef CAS PubMed.
- E. S. Lianidou and A. Markou, Clin. Chem. Lab. Med., 2011, 49(10), 1579–1590 CrossRef CAS PubMed.
- H. Esmaeilsabzali, T. V. Beischlag, M. E. Cox, A. M. Parameswaran and E. J. Park, Biotechnol. Adv., 2013, 31, 1063–1084 CrossRef CAS PubMed.
- A. Bardelli and K. Pantel, Cancer Cell, 2017, 31, 172–179 CrossRef CAS PubMed.
- H. H. Hu, N. A. Patankar and M. Zhu, J. Comput. Phys., 2001, 169(2), 427–462 CrossRef CAS.
- D. C. Rapaport, The Art of Molecular Dynamics Simulation, Cambridge University Press, New York, 1995 Search PubMed.
- N. Sarafianosa, B. Boteanub, B. Ionescub and I. A. Kakadiaris, Comput. Vis. Image Underst., 2016, 152, 1–20 CrossRef.
- A. Geltmeier, B. Rinner, D. Bade, K. Meditz, R. Witt, U. Bicker, C. Bludszuweit-Philipp and P. Maier, PLoS One, 2015, 10(8), e0134999 Search PubMed.
- M. Habaza, M. Kirschbaum, C. Guernth-Marschner, G. Dardikman, I. Barnea, R. Korenstein, C. Duschl and N. T. Shaked, Adv. Sci., 2017, 4, 1600205 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7lc00943g |
| This journal is © The Royal Society of Chemistry 2018 |