Open Access Article
Open Access ArticleMicrofluidic magnetic bead conveyor belt†
Stijn
van Pelt
 a,
Arjan
Frijns
b and
Jaap
den Toonder
*ac
a,
Arjan
Frijns
b and
Jaap
den Toonder
*ac
aMicrosystems, Department of Mechanical Engineering, Eindhoven University of Technology, The Netherlands. E-mail: s.v.pelt@tue.nl
bEnergy Technology, Department of Mechanical Engineering, Eindhoven University of Technology, The Netherlands. E-mail: a.j.h.frijns@tue.nl
cInstitute for Complex Molecular Systems (ICMS), Eindhoven University of Technology, The Netherlands. E-mail: j.m.j.d.toonder@tue.nl
First published on 6th October 2017
Abstract
Magnetic beads play an important role in the miniaturization of clinical diagnostics systems. In lab-on-chip platforms, beads can be made to link to a target species and can then be used for the manipulation and detection of this species. Current bead actuation systems utilize complex on-chip coil systems that offer low field strengths and little versatility. We demonstrate a novel system based on an external rotating magnetic field and on-chip soft-magnetic structures to focus the field locally. These structures were designed and optimized using finite element simulations in order to create a number of local flux density maxima. These maxima, to which the magnetic beads are attracted, move over the chip surface in a continuous way together with the rotation of the external field, resulting in a mechanism similar to that of a conveyor belt. A prototype was fabricated using PDMS molding techniques mixed with iron powder for the magnetic structures. In the subsequent experiments, a quadrupole electromagnet was used to create the rotating external field. We observed that beads formed agglomerates that rolled over the chip surface, just above the magnetic structures. Field rotation frequencies between 0.1–50 Hz were tested resulting in magnetic bead speeds of over 1 mm s−1 for the highest frequency. With this, we have shown that our novel concept works, combining a simple design and simple operation with a powerful and versatile method for bead actuation. This makes it a promising method for further research and utilization in lab-on-chip systems.
1 Introduction
Magnetic beads play an important role in the miniaturization of clinical diagnostics systems. In lab-on-chip platforms, beads can be made to link to a target species and can then be used for the manipulation and/or detection of this target. Current manipulation techniques include for example: target immobilization, mixing, separation and transport.1–4Some of these techniques rely on an external magnetic field. These use large permanent magnets or coils to manipulate beads in a microfluidic environment.2,5,6 However, this makes it difficult to create high field gradients which are required to create a force on a paramagnetic bead.7 Another disadvantage is the difficulty to address and distinguish between several different magnetic functions within one chip.
Local control on the micro-scale can be achieved by using integrated micro-coils with a typical diameter in the order of 10–100 μm.8,9 Due to their small size and close proximity to the microfluidic channel, the field gradient is relatively large. Drawbacks of this approach are a more complex chip-design and a lower field strength because this is limited by the current through the micro-coils. The current induces Joule heating which can be a biocompatibility issue.10
To create both a large field strength and a large field gradient, the two methods can be combined. A macroscopic magnetic field can be used to generate a strong field that magnetizes the beads. A microscopic field can then be used to create a local field gradient that determines the location and direction of the force on the beads. The local field can be created using micro-coils but a more simple solution is to use soft-magnetic structures. When placed in an external field, they focus the field lines and thus increase the local field strength and field gradient. By careful design of these soft-magnetic structures, local bead manipulation is possible by controlling the external field.11–14
Making a paramagnetic bead move in different directions is difficult because in general it is only possible to apply attractive forces with a magnet.7 The bead will move toward the magnet and stop when it hits the surface. To keep the bead moving, one needs to move the magnet. Several examples of this method exist, but they rely on large moving magnets5,15,16.
Alternatively, multiple micro-coils can be used in a stepping stone fashion where the beads “jump” from coil to coil. This however, requires a complex coil design and current control scheme.8,17 By smart use of anisotropy effects in soft-magnetic structures, a similar stepping stone behavior can be achieved with a rotating external field.18–20 A problem with this non-continuous method is that the beads have to “jump” across gaps. The length of this gap is critical. When the gap is too large, the beads will not move. When it is too small, the speed is limited and there can be crosstalk between adjacent structures.
We demonstrate a novel continuous bead actuation method that uses an array of carefully designed soft-magnetic structures. The beads are attracted toward the local field gradient maximum of each soft-magnetic structure. By rotating the external field, this maximum moves along the channel wall, pulling the beads along, similar to a conveyor belt. Because we use a rotating field, we also expect to see rotating chains of beads due to a magnetic torque acting on the chains.21 When this happens in close proximity to a solid surface and with a force that pushes the chains toward the wall, the bead chains will start to roll across the surface.22–24 These two mechanisms can work in tandem to offer a very simple, robust and reversible actuation method. The main advantages with respect to existing methods are that no moving magnets and no discrete control scheme are required while keeping the fabrication very simple. At the same time, the method is bio-orthogonal, using a purely magnetic signal, there is no heating and no electrical field that could cause ionization.
In this work, both numerical and experimental techniques were used to verify the actuation method. First, finite element simulations were used to find the critical geometrical parameters and to optimize them. We then proceeded with the fabrication of a prototype using PDMS molding techniques. We experimentally tested the actuation method in a setup with a rotating field. Here, bead agglomerates reached speeds of over 1 mm s−1 while rolling over the solid surface. This is a promising result which opens up the way to a range of new ideas, as discussed in the final part of this paper.
2 Theory
2.1 Concept
Our magnetic bead actuation method uses an external rotating field in combination with local soft-magnetic structures. Using careful design of these structures, the magnitude and direction of the forces on a super-paramagnetic bead can be tuned. In Fig. 1 a schematic representation is given of the magnetic mushroom-shaped structures that were used in this work.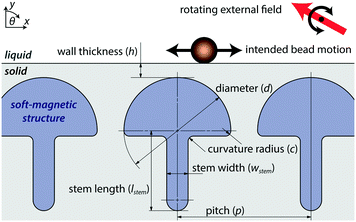 | ||
| Fig. 1 Schematic of an array of soft-magnetic mushroom-shaped structures underneath a solid wall. It shows the different parameters that were changed in the simulations to optimize the geometry. | ||
The soft-magnetic structures have high magnetic permeability and low hysteresis. These allow a uniform external field to be focussed locally. To generate a force on a super-paramagnetic bead, a flux density gradient must be present. The force vector scales linearly with ∇B2 where B is the magnetic flux density.3 This means that magnetic beads will be attracted to the north and south poles of each individual structure.
When the external field is aligned with the stem of the mushroom (θ = 0°), the north and south poles will be the top of the hat and the end of the stem of the mushroom structure. When the external field is orthogonal to the stem (θ = 90°), the sides of the hat will be the north and south pole. When the field is rotating, one of the poles will travel over the circumference of the mushroom hat. This means that the point of attraction for magnetic beads will also move over the hat. Because the bead movement is restricted by the solid surface, the effective point of attraction will travel over this surface in a straight line. With multiple mushroom structures in an row, the point of attraction will move from structure to structure in a continuous way. This gives rise to a behavior similar to a conveyor belt or to peristaltic motion.
When the stem of the mushroom is made very long, it makes the structure shape anisotropic. This means it has a preferred magnetization direction. Similarly, when multiple structures are placed next to each other, this makes the total geometry shape anisotropic. By tuning the stem length to the array length, the total shape-anisotropy can be controlled.
2.2 Actuation mechanisms
When placed in an external field, the force Fb,m on a single magnetic bead may be calculated with:8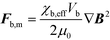 | (1) |
Here, the bead is modeled as a point-dipole with a magnetization depending on the local flux density B, the bead volume Vb and its effective susceptibility χb,eff, μ0 is the permeability of free space with a value of μ0 = 4π × 10−7 NA−2. The effective susceptibility depends on the specific magnetic bead that is used and should be determined experimentally, for instance using a vibrating sample magnetometer (VSM). Independent of the exact beads that will be used, the force scales with ∇B2. This means a field gradient must be present and the bead will be attracted toward the location of highest flux density.
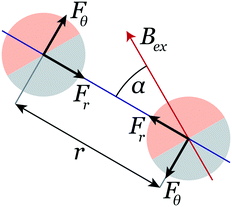
A spherical super-paramagnetic bead has no shape-anisotropy and thus the external rotating field will not impose a torque upon a single bead. However, on clusters consisting of 2 beads or more, a magnetic torque can be present. Consider, for example the case when 2 beads are placed in an external field B in close proximity to each other. These beads will have a force acting between them:21
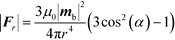 | (2) |
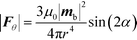 | (3) |
Here, Fr and Fθ are the radial and tangential force on a bead respectively (see Fig. 2 for definitions), mb is the magnetic moment of a bead, r is the distance between the beads and α the angle the external field makes with the line connecting the two beads. In our situation, the external field is relatively mild, so there is no magnetic saturation and the magnetization mb can be calculated with:
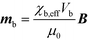 | (4) |
Because the force on both beads will be equal, but in opposing direction, the net force will be zero. However a non-zero torque T will still remain that tends to align the beads with the external field, which equals:
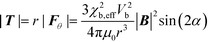 | (5) |
This means that the torque on an agglomerate will scale with B2. Therefore, the final geometry optimization strategy was to maximize B2 to get maximum torque and ∇B2 for the maximum force.
2.3 Parameter optimization
The goal was to have a high yet constant bead velocity along the wall. Therefore, the geometry was optimized for the maximum translational and rotational motion that was equal for all field orientations. As the force and torque depend on ∇B2 and B2, we used the finite element method to simulate the magnetic field. For this, we used the “Magnetic Field, No Currents” module in Comsol Multiphysics 5.2 which solves for the magnetic scalar potential. From this, the local B and H fields can be obtained in order to predict magnetic bead behavior. 2D Simulations were performed to optimize the in-plane geometry. 3D Simulations were performed to investigate the out-of-plane behavior and to confirm the validity of the simplifications in the 2D case. Because no significant differences between the 2D and 3D simulations were found, we will focus on the 2D simulation results in this work. The flux density B was prescribed on all external boundaries with: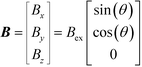 | (6) |
Here Bex is the external flux density magnitude and θ is the angle of the field rotation in the xy-plane. The magnetic scalar potential was prescribed in a single point to act as a zero point reference. The non-magnetic materials were modeled with a relative permeability of μr = 1. Because relatively low field strengths were used, magnetic saturation was not taken in account and a linear relation between the B and H field was used:
| B = μ0μrH | (7) |
Here, H is the magnetic field. At the locations of interest, the cell size was 1 μm, for more detail, see Fig. 10 in the appendix.
The motion of magnetic beads in the calculated magnetic field can be simulated explicitly, by placing the beads in the computational domain shown in Fig. 1 and modeling the net force on the beads by integrating the magnetic traction (computed using the Maxwell stress tensor) on the bead surface, according to the method introduced by Kang et al.25 However this approach is computationally expensive, and for the purpose of this research, a good estimation will already be sufficient. Therefore we limited ourselves to estimating the forces and torques on the particles by calculating B2 and ∇B2.
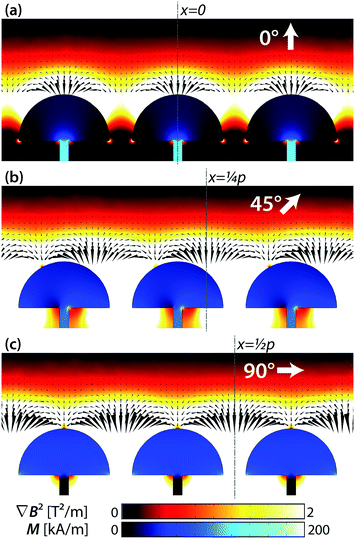
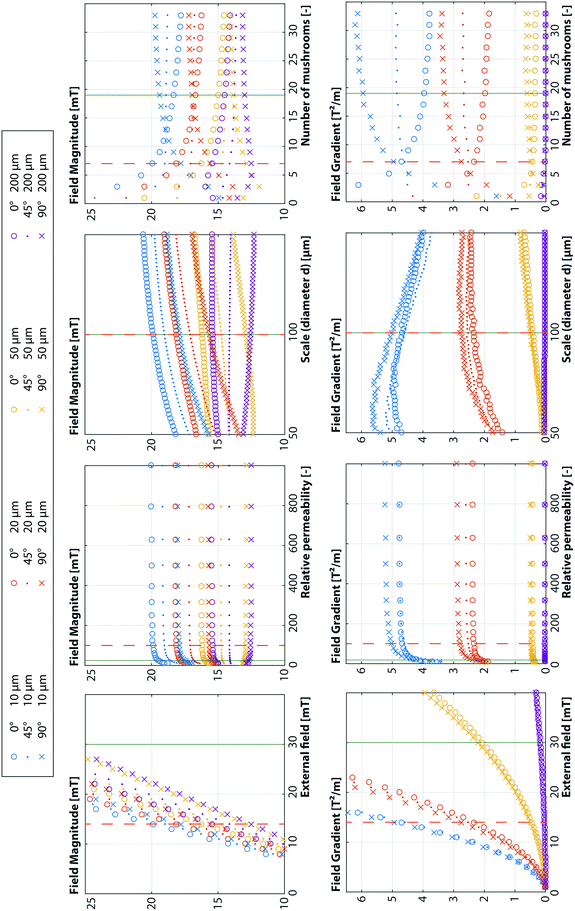
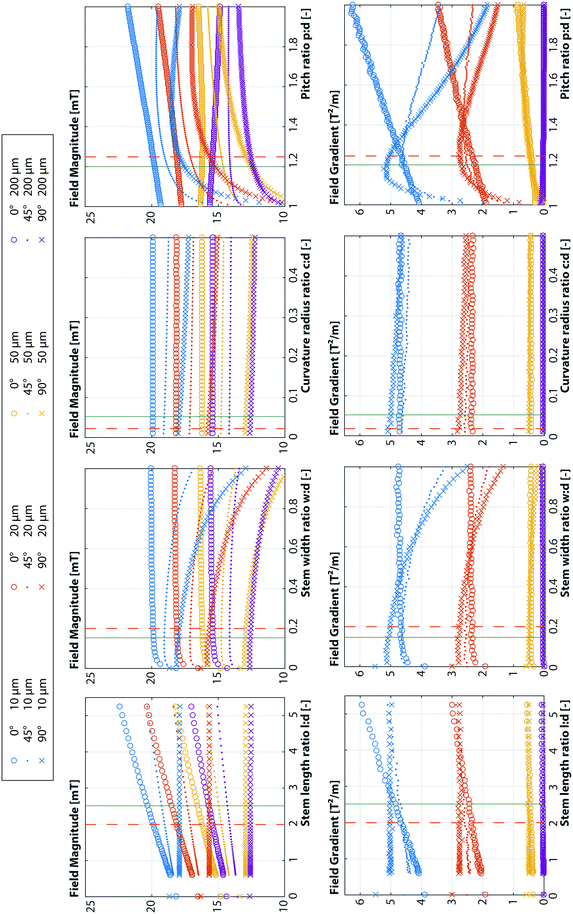
All the different geometrical parameters were changed independently to see influence they had on the B and ∇B2 parameters. As a reference, we used an external field of |B| = 14 mT and a relative permeability for the magnetic structures of μr = 100.26 The reference geometry had diameter d = 100 μm, number of mushroom structures n = 7, stem length l = 200 μm, stem width w = 10 μm, curvature radius c = 2 μm and pitch p = 125 μm. The wall thickness h (see Fig. 1 for definitions) was varied by investigating the parameters at different proximities ranging from 5–200 μm. Also, 3 different external field orientations were investigated: θ = 0°, 45° and 90°. The results of one such simulation can be seen in Fig. 3.
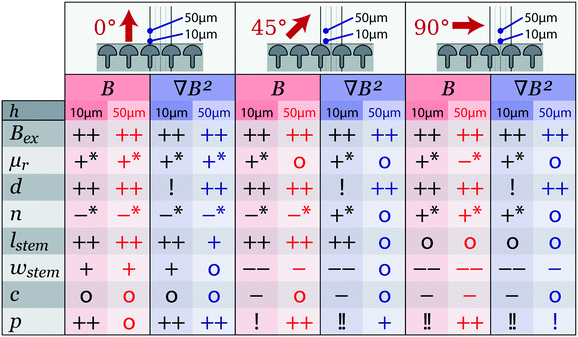
A qualitative overview of the influence of the different parameters on B and ∇B2 is given in Table 1. More detailed simulation results on which this qualitative overview is based, can be found in the appendix (Fig. 11 and 12).
Looking at the influence of the different parameters, we can see that increasing the external field strength Bex has a positive influence on both B and ∇B2 for all field orientations θ and proximities h, therefore, it should be as high as possible. Increasing the relative permeability μr only has an influence up until 200. For both B and ∇B2 the influence is positive, except at proximities of h ≥ 50 μm for non-zero field orientations. The scale, represented by the mushroom structure diameter d, has a strong positive correlation with both B and ∇B2, except for the ∇B2 parameter at close proximities which shows an optimal scale. It must be noted here that the proximities were not scaled together with the mushroom diameter. It does appear though, that for a certain scale d there exists an optimum proximity or wall thickness. Increasing the number of mushroom structures n has a positive influence for θ = 90° but a negative influence for θ = 0°. The influence of the stem length lstem and to slightly lesser extent the stem width wstem has exactly the opposite behavior. This makes these three parameters ideal to tune the force and torque on beads for different field orientations. The curvature c has very little influence for most situations. The pitch p has a positive correlation for a few field orientation/proximity situations, but it also shows an optimum for many other situations. The optimum appears to lie at a p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d ratio between 1.1–1.3.
d ratio between 1.1–1.3.
The final geometry was chosen based on these simulation results and the fabrication limitations. The latter put restrictions on the minimum feature size that could be used as is discussed in the next section. These parameters were different from the reference values that were used in the simulations. The final parameter values that were used for fabrication as well as the simulation reference values can be found in the detailed simulation results in the appendix.
3 Materials and experimental setup
3.1 Chip fabrication
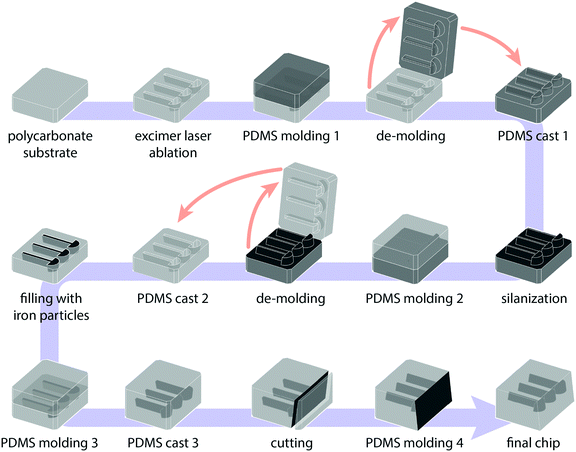
Soft-lithography of PDMS mixed with iron particles was used for making the chips with soft-magnetic structures that were used in the experiments. For fabrication of the soft-magnetic structures, usually electroplated ferromagnetic materials like iron and nickel are used because of their high magnetic permeability. However, electroplating requires a current carrying layer during the fabrication process which complicates the design. Additionally, it can be difficult to obtain a homogeneous thickness with this method.14 Therefore, we used soft-lithography which is a simpler method where magnetic particles are molded after mixing them with a polymer resin.27,28A schematic representation of the fabrication steps is given in Fig. 4. The first step was to make the mold using excimer laser ablation in a 750 μm thick polycarbonate substrate (Sabic Lexan™ film). An Optec Micromaster KrF laser operating at 247 nm was used for the ablation. The laser has a top-hat profile that can be shaped using a mask. To create the mushroom structures, a rectangular mask was used for the stem and a semicircular mask for the hat. The depth of the structures was set to approximately 50 μm.
After cleaning the polycarbonate mold with isopropanol, it was used for PDMS molding. The PDMS resin (Sylgard 184) and curing agent were mixed in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio using a Thinky Are-250 mixer. After degassing, it was poured over the polycarbonate mold and degassed again in a vacuum desiccator. After an overnight bake at 65 °C, the crosslinked PDMS was peeled off the mold manually using tweezers. This molding step was used as an additional cleaning step. After 3 repetitions, both the cast and the mold were free from ablation debris.
1 ratio using a Thinky Are-250 mixer. After degassing, it was poured over the polycarbonate mold and degassed again in a vacuum desiccator. After an overnight bake at 65 °C, the crosslinked PDMS was peeled off the mold manually using tweezers. This molding step was used as an additional cleaning step. After 3 repetitions, both the cast and the mold were free from ablation debris.
Because the PDMS cast was going to be used as a mold for the next step, it had to be silanized to prevent cross-linking between the cast and mold and to decrease friction during the release step.29 The surface of the PDMS cast was first activated using a corona discharge (Tantec SpotTEC). Next 100 μl of 1H,1H,2H,2H-perfluorodecyltriethoxysilane was mixed with 1 ml of alcohol and applied on the activated PDMS surface. After 5 minutes, it was rinsed in alcohol and baked at 65 °C for 1 hour.
The silanized PDMS cast was now ready to be used as a mold. The same procedure as mentioned before was used for the PDMS mixing, de-gassing, pouring, baking and de-molding. The new PDMS cast had the same geometry as the original polycarbonate mold with hollow mushroom structures.
Next, an abundance of carbonyl iron particles was mixed with a small drop of pre-mixed PDMS resin. The resulting paste-like substance was applied over the mushroom structures in the PDMS cast. The cast with the iron particles was then placed in a vacuum desiccator to ensure that the iron particles moved into the mushroom-shaped cavities and no air-bubbles remained. Then a razorblade edge was pulled over the cast to get rid of excess iron particles. The cast was then baked for 15 minutes at 65 °C to fixate the iron particles. Then an additional amount of PDMS resin (without Fe particles) was poured over the cast to fully cover the mushroom structures. After another overnight bake, the new PDMS cross-linked with the cast to form a single piece of PDMS with included magnetic structures.
Using a custom made mechanical guiding system and a razorblade, the PDMS chips were cut from the cast. This was done under a stereo-microscope for better accuracy. The final cut had to be made very close to the mushroom structures to minimize the wall thickness. For this, the guide was used to set the angle between the blade and the horizontal to approximately 70°. This angle was used to make observation from above with a microscope more convenient. If the wall would be straight, it would be fully orthogonal to the microscope's plane of focus and its surface would be unobservable. With the concave side-wall, the wall surface could be observed while focussing on the beads' plane of motion. Because the mushroom structures were also slightly concave due to the ablation process, the wall thickness was roughly constant over the height of the mushroom structures.
The roughness that resulted from the cut was in the order of the bead size: 1–5 μm. To reduce it, a drop of PDMS resin was placed onto the surface which was then placed onto a polycarbonate substrate. It was pressed down to minimize the thickness of the additional layer. After baking, the chips were released with tweezers, resulting in an optically clear surface.
The final geometry that was used in the experiment is as follows. With our fabrication method, a wall thickness of 20 μm was obtained. Using the parameter optimization from the simulations, the optimal mushroom diameter for this wall thickness was 100 μm with a pitch of 120 μm. The minimum stem width that resulted in a correctly molded structure was 15 μm. Stem lengths were varied between 100–300 μm. For the experiments described in this work, a geometry was used with stem width 15 μm and stem length 250 μm. The iron powder has a relative permeability of around 20.30 The number of mushroom structures n was 19. The total length of the mushroom array was therefore 2.3 mm. All the used values are also depicted in the simulation results in the appendix. A photo of the finished chip can be seen in Fig. 5(b).
3.2 Setup and experimental protocol
In the experiments, an existing octopole setup31 (see Fig. 5(a)) was used to create the external rotating magnetic field. This was done by controlling the current through the coils. Because the rotation was in the horizontal plane, only 4 poles were required. The rotational frequency f was varied between 0.1–50 Hz. The flux density of a single pole was varied between 1.4–14 mT. This resulted in a maximum flux density of 30 mT in the central area when opposite poles were working in tandem. Super-paramagnetic beads with a diameter of 2.8 μm (Dynabeads M-270 carboxylic acid) were suspended in water inside a circular container that also held the chip with the magnetic structures. The beads were suspended in de-ionized water with a concentration of 2 × 108 ml−1. This concentration was fairly high in order to quickly get formation of agglomerates. Bead movement was observed using an optical microscope and a camera that recorded at a 640 × 480 resolution in grayscale at a framerate of 30 Hz.In the experiment, after injecting the suspended beads into the container, the field was turned on and aligned with the mushroom stems. This caused the beads to form up into chains aligned with the external field. Beads that were within approximately 500 μm of the mushroom structures were attracted toward these structures. After 1 minute at t0, the field rotation was turned on and the actual experiment was started.
4 Results and discussion
4.1 Experiment observations
In the experiments, different rotational frequencies were tested. Frames from the captured videos can be found in Fig. 6. The actual videos from the experiments can be found in the ESI.† Typically, during an experiment, free floating beads formed up into chains that rotated in phase with the external field. Beads on the chip surface formed agglomerates of different shapes and sizes. These agglomerates also followed the rotation of the external field which caused them to roll over the chip surface. The rotation and horizontal motion would stop immediately when the field rotation was turned off. Also, when the rotation was reversed, the agglomerates would likewise reverse their rotation and direction of motion. | ||
| Fig. 6 Captured video frames from an experiment, the external field is turned on at t = 0 s, rotating at 10 Hz. Agglomerates form and start to roll over the surface, the yellow contour shows the position of 3 agglomerates in the first frame (a). The movement of these agglomerates can be seen in the subsequent frames (b–e). The complete video files can be found in the ESI.† | ||
At low frequencies (≤0.5 Hz), sometimes rolling agglomerates were observed to make a small jump. This occurred both in the forward and in the backward direction. At higher frequencies, this was not observed. At higher frequencies (≥10 Hz), large agglomerates created vortices that dragged along smaller agglomerates, especially at the start of the experiment when many agglomerates were present. The agglomerates frequently changed shape by splitting up into smaller agglomerates or recombining into larger ones.
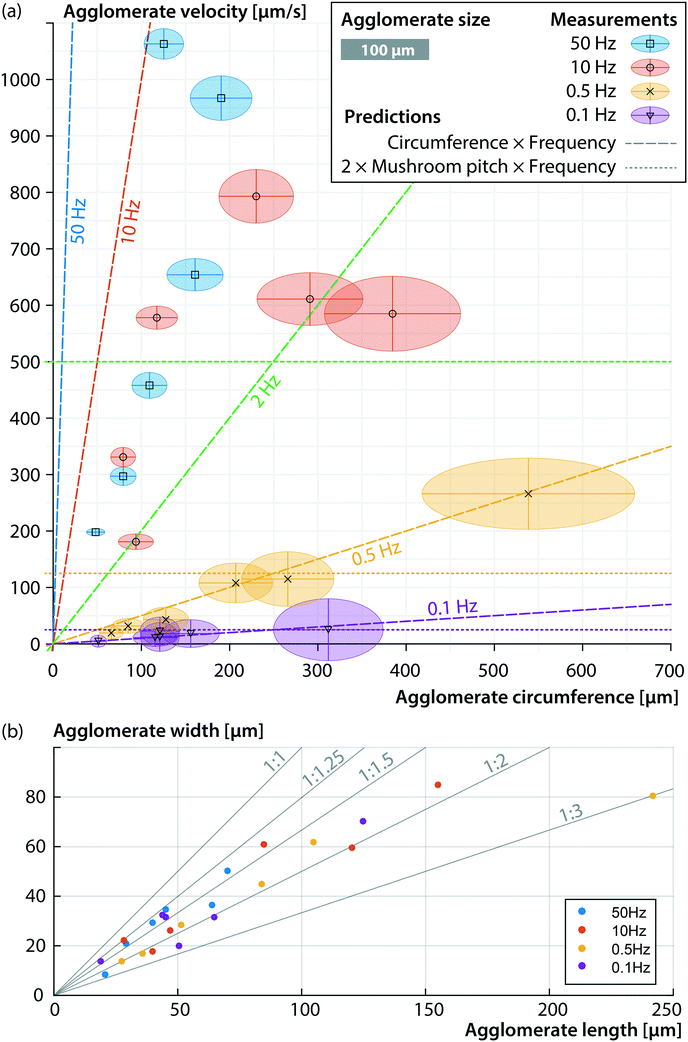
In order to quantify the bead transportation characteristics, the apparent agglomerate circumference was compared to the lateral motion. Using the recorded video frames, two points in time were chosen from which the agglomerate position, length and width were manually obtained. Care was taken to select a time interval over which there was a significant and uninterrupted motion of the agglomerate. The velocity was then calculated by dividing the lateral movement by the time difference. The circumference of the agglomerate Ca was obtained using a Ramanujan approximation of the circumference of an ellipse:
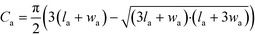 | (8) |
The values for la and wa were obtained from the average agglomerate length and width over the two points in time. The agglomerates ranged in diameter between 20–240 μm. Smaller agglomerates were observed, but they did not move long distances. Instead they tended to stick to the substrate surface or they merged with other agglomerates.
As can be seen in Fig. 7, the agglomerates moved faster at higher frequencies, reaching speeds of up to 1 mm s−1 at 50 Hz. In this case, the total length of the array which was 2.3 mm was covered in approximately 2.1 s. We predicted 2 different mechanisms by which the beads could be moved over the surface (see section 2). The first one was the field gradient causing a force on a dipole (eqn (1)). For each half field rotation, the point of attraction would move from one mushroom structure to the next. Therefore, the agglomerate would move over the chip surface with a velocity of 2 times the mushroom structure pitch times the field rotation frequency: vx = 2 pf. This effect is independent of agglomerate size, as long as the viscous drag on the agglomerates is sufficiently low, which we assume here. The prediction of this mechanism is depicted in Fig. 7 by the horizontal lines at 25, 125 and 500 μm s−1 for 0.1, 0.5 and 2 Hz respectively. The predictions for higher frequencies fall outside the graph. Only a few cases are close to this prediction and only for the lower frequencies of ≤0.5 Hz.
The maximum velocity of a bead due to the magnetic gradient can be calculated by comparing the magnetic force (eqn (1)) to the drag force using Stoke's law for a sphere moving through a fluid:
| Fb,d = 6πηrbvb | (9) |
Here, Fb,d is the drag force on a bead, η is the dynamic viscosity of the surrounding liquid (equal to 10−3 Pa s for water at room temperature), rb is the bead radius and vb is the bead velocity. From our simulations, we can estimate that ∇B2 = 2 T2 m−1 in close proximity to the wall. For spherical beads with a 2.8 μm diameter, the volume is Vb = 4/3πr3 = 11.5 μm. In previous work,32 the effective susceptibility of similar beads was measured to be χb,eff = 1.52. After plugging in all values we get a maximum magnetic force of 13.9 × 10−12 N resulting in a maximum velocity of 0.5 mm s−1. Because we observed bead velocities up to 1 mm s−1 and because our predicted velocity for a field rotation of 0.5 Hz does not match, another mechanism must play a role.
The second mechanism was that the rotating field would impose a torque on the agglomerates, causing them to roll over the chip surface. If this torque is large enough, the agglomerate rotational frequency will be the same as that of the external field. In this case the lateral velocity should be equal to the agglomerate circumference times the frequency of rotation: vx = Caf. These predictions have also been plotted in Fig. 7 and it can be clearly seen that for f = 0.1 Hz and f = 0.5 Hz, almost all the experimental results coincide with this prediction. From this, it can be concluded that for frequencies of ≤0.5 Hz, the agglomerates rotated at the same frequency as the external field. For higher frequencies of 10 Hz and above, even though it was not directly observed due to limitations in the camera frame rate, the results suggest that the agglomerates rotated at a lower frequency than the external field.
Looking at the length to width ratio of the agglomerates in Fig. 7(b), it can be seen that they all fall within 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.25 and 1
1.25 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. In order to understand why the agglomerates had this range of aspect ratio and why they could follow the rotational frequency of the external field only up to 0.5 Hz, additional simulations on the agglomerate torque were performed, the results of which are discussed subsection 4.2.
3. In order to understand why the agglomerates had this range of aspect ratio and why they could follow the rotational frequency of the external field only up to 0.5 Hz, additional simulations on the agglomerate torque were performed, the results of which are discussed subsection 4.2.
It should be noted, that not all beads were always mobile. Some beads stopped and started moving again several times. After 1 minute, a layer of immobilized beads could be seen on the surface. The beads could be removed by rinsing the surface after the experiment. It is unclear whether this is a magnetic or chemical effect. It could be the case that the beads adhere well to PDMS surface of the chip. Alternatively, the local magnetic field could be such that it only attracts the beads at certain locations, effectively trapping them. Possible causes for this effect could be the roughness of the fabricated magnetic structures or the influence of the beads on the local magnetic field which was not implemented in the simulations. However, we do not believe that this is the case because we observe a uniform layer of immobile beads. If it was indeed a chemical effect, a way to solve this would be to coat the PDMS surface with a bead-repelling material. The beads themselves have a dispersive coating, so the same coating potentially could be used on the chip surface. Another solution might be to use non-spherical beads. If for instance ellipsoidal beads are used, the individual beads will be subject to a torque due to their shape-anisotropy, which makes them less likely to become immobile.
4.2 Agglomerate torque
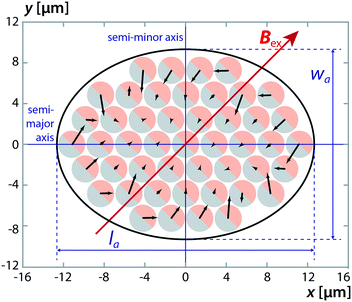
The resulting torque on an agglomerate from dipole interactions can be calculated using eqn (2), (3) and (4). This was done by prescribing a roughly elliptical shape with a hexagonal packing structure for the agglomerates. For spherical beads with a 2.8 μm diameter, the volume is Vb = 4/3πr3 = 11.5 μm. In previous work,32 the effective susceptibility of similar beads was measured to be χb,eff = 1.52. Using a flux density of |B| = 30 mT which was the maximum for our setup, eqn (4) then yields a magnetic moment of mb = 4.17 × 10–13 Am2 for each bead. We then calculated the interaction between each possible bead-to-bead combination. Summing up all interactions, gave the total force on each bead Fb. Fig. 8 gives the result of such a calculation. The total torque with respect to the agglomerate center Ta was calculated by summation over all the beads.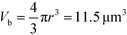 | (10) |
Here rb,c is position vector of the bead with respect to the agglomerate center and Fb is the total force acting on the bead due to dipole interaction.
In Fig. 8 it can be seen that the particles in the outermost layer have a large resulting force compared to the inner particles. This is because there is an r−4 dependency (see eqn (2) and (3)) so only the neighbouring beads have a significant influence. Beads that are surrounded by 6 neighbours are pulled in all directions equally because of symmetry. But beads on the edge of the agglomerate are not in a symmetrical position. This behavior can be compared to the surface tension of drop and an additional effect is that it keeps the agglomerate together in a stable way.
For circular agglomerates with a hexagonal packing structure, the resulting torque was zero. However, for elliptical shapes, the torque was non-zero, this shows that a shape-anisotropy is required to generate a torque. This explains why no moving circular agglomerates were observed in the experiments. The maximum torque is reached when the misalignment between the external field and the long axis is 45° and the long axis of the agglomerate will tend to align with the external field. Because the torque increases with misalignment, a stable rotation can be obtained if the external field is rotated at sufficiently low rotation frequency. At increasing frequency, an increase in viscous torque will be balanced by an increased phase-lag between the agglomerate main axis and the external field orientation. When the phase-lag becomes greater than 45°, the agglomerate will no longer be able to rotate at the same frequency as the magnetic field.
In order to estimate this maximum rotational frequency, the total viscous torque on different agglomerates was estimated. For this, the agglomerates were modeled as a single stable shape, not taking in account the shape of individual beads and their interactions. This was done using finite element simulations, performed with the laminar flow module in Comsol Multiphysics 5.2. A hemispherical domain was used with a symmetry boundary on the plane of rotation. The agglomerate was modeled as an elliptical disc with thickness equal to the bead diameter. The edge was rounded with a curvature radius equal to the bead radius. The rotation of the agglomerate was modeled by prescribing the velocity on the agglomerate surface.
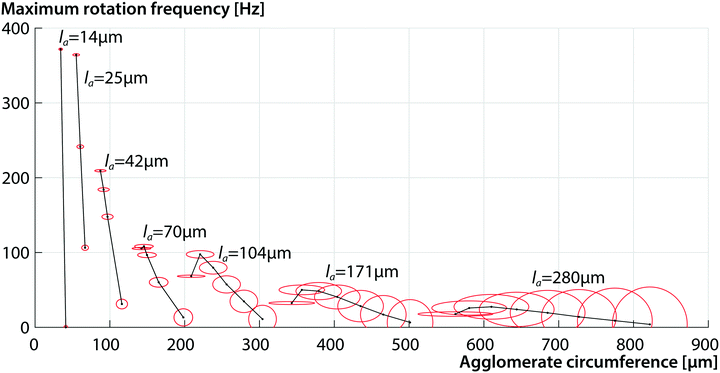
The resulting total shear stress on the agglomerate surface was then used to calculate the total torque acting on the agglomerate due to viscous forces. This resulting torque scales linearly with the rotational frequency. Using this, the rotational frequency can be found, at which the viscous torque equals the maximum magnetic torque for a given agglomerate. Results for this maximum frequency are plotted in Fig. 9. It must be noted here that this maximum frequency is only a rough estimate where we assume that the agglomerate is stable. For the study of agglomerate formation, stability and break-up, centrifugal forces, bead-to-bead friction, bead-to-bead magnetic forces and viscous forces on individual beads should be taken in account.
Agglomerates with smaller length are able to follow the rotation of the external field up to higher frequencies. For an agglomerate with given length la, the closer it approaches a circular shape, the slower it will be able to rotate. One reason is the reduction of shape-anisotropy and hence the reduction in magnetic torque. But also the viscous torque increases as the surface area increases. For larger agglomerates, there exists an optimum length-to-width ratio around 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Higher length-to-width ratios will result in a lower maximum rotational frequency.
3. Higher length-to-width ratios will result in a lower maximum rotational frequency.
These results compare well to the experiments. The most observed agglomerate aspect ratio was slightly lower than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, but this could be a stability effect which was not taken in account in our simulations. The agglomerate shape in the experiments was not a perfect elliptical disc. At high frequencies, the viscous shear forces might be high enough to deform or even break apart the agglomerate. Also the presence of a nearby wall would increase the viscous torque but this was not included in this analysis. Looking at the maximum rotational frequency versus the agglomerate size, it can be seen that smaller agglomerates could follow the external field rotation up to higher frequencies than the larger agglomerates. This is most clearly seen in our experiments performed at 10 Hz and to a smaller extent at 50 Hz. (see Fig. 7) The predicted maximum frequencies are higher than the experimentally observed frequencies, but again, this is probably due to the increased viscous effects from the wall that were not taken into account in the calculations. Additionally, at higher frequencies, the magnetic field strength will reduce in our experimental setup as it takes a finite amount of time for the poles to magnetize in response to the current. This will cause the magnetic torque to be overestimated for high frequencies. Still, we see a good qualitative agreement between the experiments and calculations.
3, but this could be a stability effect which was not taken in account in our simulations. The agglomerate shape in the experiments was not a perfect elliptical disc. At high frequencies, the viscous shear forces might be high enough to deform or even break apart the agglomerate. Also the presence of a nearby wall would increase the viscous torque but this was not included in this analysis. Looking at the maximum rotational frequency versus the agglomerate size, it can be seen that smaller agglomerates could follow the external field rotation up to higher frequencies than the larger agglomerates. This is most clearly seen in our experiments performed at 10 Hz and to a smaller extent at 50 Hz. (see Fig. 7) The predicted maximum frequencies are higher than the experimentally observed frequencies, but again, this is probably due to the increased viscous effects from the wall that were not taken into account in the calculations. Additionally, at higher frequencies, the magnetic field strength will reduce in our experimental setup as it takes a finite amount of time for the poles to magnetize in response to the current. This will cause the magnetic torque to be overestimated for high frequencies. Still, we see a good qualitative agreement between the experiments and calculations.
4.3 Outlook
In this work, we have shown the basic operating principle of how an external rotating field can be used in conjunction with local soft-magnetic structures to linearly actuate magnetic beads. We believe that this method can be used in many lab-on-chip applications. When functionalized magnetic beads are used, they can be used as carriers for biological molecules. Our method can then be used to arrange transport between different sites that provide for instance injection, mixing, reactions, detection and selection. This can be done without the need for fluidic pumps.In our case, an array length of 2.3 mm was used, but in our setup, lengths up to 5 mm are possible and multiple arrays can be stacked or placed side-by-side. Also a larger setup is possible. The mechanism can easily be used on curved walls or serpentine channels to cover a larger area. Also channels that form loops or traps are possible. Additionally, a mixing chamber could be envisioned with rotating agglomerates in order to counteract long diffusion times. This could also work using non-functionalized beads where the beads are used as a pump to drive the fluid.
For our experiments, we used a rather complex octopole setup. However, to create a rotating magnetic field, a permanent magnet and a rotor suffice. This makes the method feasible to be used outside of a laboratory environment, adding to the applicability of the method.
5 Conclusions
We have shown a new method for the actuation of agglomerates of magnetic beads in a microfluidic environment, using an external rotating field. By careful design of magnetic structures just below the surface of a microfluidic chip, the local magnetic field will show a motion that can be used to move magnetic beads similar to a conveyer belt. We have parameterized the structures in order to find the optimal geometry using finite element simulations. Our experiments correspond well with these simulations. Two regimes of operation were observed, at low (≤0.5 Hz) frequencies, the agglomerates rotate at the same frequency as the external field and they roll over the surface without slip. At higher frequencies (≥10 Hz), the agglomerate rotation was slower than the external field, most probably due to viscous effects and interactions with the wall. Still, transport velocities up to 1 mm s−1 were observed over a distance of 2.3 mm. With this we have shown that the concept works and could be a potential candidate for application in lab-on-chip applications. Furthermore, we believe that our concept could be expanded upon. Using smart design of the geometry, functions like mixing or target selection could be possible using similar magnetic structures and a rotating field.Appendix
A Simulation mesh
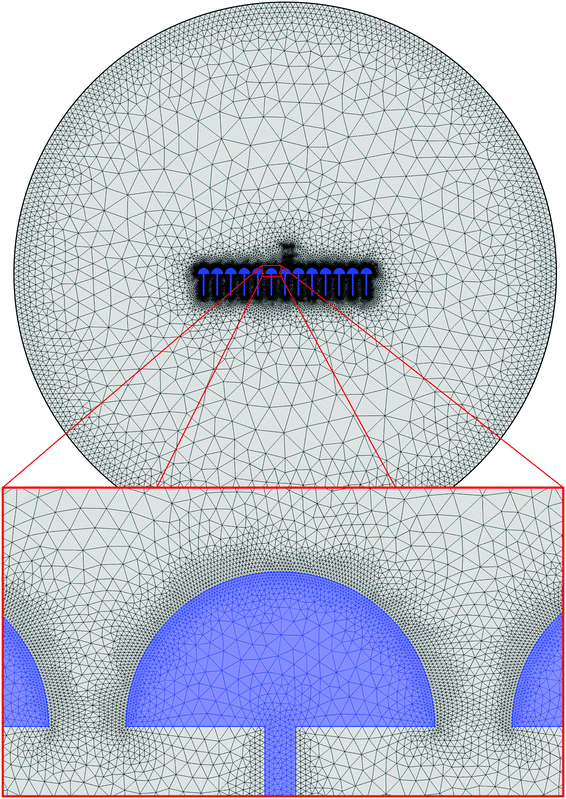 | ||
| Fig. 10 Overview of the mesh that was used in the 2D simulations for a 13 mushroom array with mushroom hat diameter d = 100 μm, the smallest element size was 1 μm. | ||
B Simulation results
Conflicts of interest
There are no conflicts to declare.References
- A. van Reenen, A. M. de Jong, J. M. J. den Toonder and M. W. J. Prins, Integrated lab-on-chip biosensing systems based on magnetic particle actuation a comprehensive review, Lab Chip, 2014, 14(12), 1966 RSC.
- K. S. Kim, J.-K. Park, K. S. Kim and J.-K. Park, Magnetic force-based multiplexed immunoassay using superparamagnetic nanoparticles in microfluidic channel, Lab Chip, 2005, 5(6), 657–664 RSC.
- M. A. M. Gijs, Magnetic bead handling on-chip: new opportunities for analytical applications, Microfluid. Nanofluid., 2004, 1(1), 22–40 CAS.
- N. Pamme, Magnetism and microfluidics, Lab Chip, 2006, 6(1), 24–38 RSC.
- E. Kurtoğlu, A. Bilgin, M. Şeşen, B. Mısırlıoğlu, M. Yıldız, H. Funda, Y. Acar and A. Koşar, Ferrofluid actuation with varying magnetic fields for micropumping applications, Microfluid. Nanofluid., 2012, 13(4), 683–694 CrossRef.
- B. Verbruggen, T. Tóth, M. Cornaglia, R. Puers, M. A. M. Gijs and J. Lammertyn, Separation of magnetic microparticles in segmented flow using asymmetric splitting regimes, Microfluid. Nanofluid., 2014, 18(1), 91–102 CrossRef.
- R. S. M. Rikken, R. J. M. Nolte, J. C. Maan, J. C. M. Van Hest, D. A. Wilson and P. C. M. Christianen, Manipulation of micro-and nanostructure motion with magnetic fields, Soft Matter, 2014, 10(9), 1295–1308 RSC.
- F. T. Abu-Nimeh and F. M. Salem, An integrated open-cavity system for magnetic bead manipulation, IEEE Trans. Biomed. Circuits Syst., 2013, 7(1), 31–42 CrossRef CAS PubMed.
- R. Fulcrand, A. Bancaud, C. Escriba, Q. He, S. Charlot, A. Boukabache and A.-M. Gué, On chip magnetic actuator for batch-mode dynamic manipulation of magnetic particles in compact lab-on-chip, Sens. Actuators, B, 2011, 160(1), 1520–1528 CrossRef CAS.
- S. H. Song, H. Lyn Lee, Y. H. Min and H. I. Jung, Electromagnetic microfluidic cell labeling device using on-chip microelectromagnet and multi-layered channels, Sens. Actuators, B, 2009, 141(1), 210–216 CrossRef CAS.
- S. van Pelt, R. Derks, M. Matteucci, M. F. Hansen and A. Dietzel, Flow-orthogonal bead oscillation in a microfluidic chip with a magnetic anisotropic flux-guide array, 2011, pp. 353–359 Search PubMed.
- D. W. Inglis, R. Riehn, J. C. Sturm and R. H. Austin, Microfluidic high gradient magnetic cell separation, J. Appl. Phys., 2006, 99(8), 99–102 CrossRef.
- Y. Moser, T. Lehnert and M. A. M. Gijs, Quadrupolar magnetic actuation of superparamagnetic particles for enhanced microfluidic perfusion, Appl. Phys. Lett., 2009, 94(92), 22505–24104 CrossRef.
- E. Koch, J.-W. Thies and A. Dietzel, Periodic convection of superparamagnetic beads within a microfluidic channel by interlocked, electroplated structures activated by a static field, Microelectron. Eng., 2016, 158, 46–51 CrossRef.
- Z. Long, A. M. Shetty, M. J. Solomon and R. G. Larson, Fundamentals of magnet-actuated droplet manipulation on an open hydrophobic surface, Lab Chip, 2009, 9(11), 1567–1575 RSC.
- T. Ohashi, H. Kuyama, N. Hanafusa and Y. Togawa, A simple device using magnetic transportation for droplet-based PCR, Biomed. Microdevices, 2007, 9(5), 695–702 CrossRef CAS PubMed.
- R. Wirix-Speetjens, W. Fyen, J. De Boeck and G. Borghs, Enhanced magnetic particle transport by integration of a magnetic flux guide: Experimental verification of simulated behavior, J. Appl. Phys., 2006, 99(8), 99–102 CrossRef.
- M. Donolato, P. Vavassori, M. Gobbi, M. Deryabina, M. F. Hansen, V. Metlushko, B. Ilic, M. Cantoni, D. Petti, S. Brivio and R. Bertacco, On-Chip Manipulation of Protein-Coated Magnetic Beads via Domain-Wall Conduits, Adv. Mater., 2010, 22(24), 2706–2710 CrossRef CAS PubMed.
- A. Torti, V. Mondiali, A. Cattoni, M. Donolato, E. Albisetti, A. M. Haghiri-Gosnet, P. Vavassori and R. Bertacco, Single particle demultiplexer based on domain wall conduits, Appl. Phys. Lett., 2012, 101(14), 142405 Search PubMed.
- K. Gunnarsson, P. E. Roy, S. Felton, J. Pihl, P. Svedlindh, S. Berner, H. Lidbaum and S. Oscarsson, Programmable Motion and Separation of Single Magnetic Particles on Patterned Magnetic Surfaces, Adv. Mater., 2005, 17(14), 1730–1734 CrossRef CAS.
- I. Petousis, E. Homburg, R. Derks and A. Dietzel, Transient behaviour of magnetic micro-bead chains rotating in a fluid by external fields, Lab Chip, 2007, 7(12), 1746 RSC.
- M. Karle, J. Wöhrle, J. Miwa, N. Paust, G. Roth, R. Zengerle and F. Von Stetten, Controlled counter-flow motion of magnetic bead chains rolling along microchannels, Microfluid. Nanofluid., 2011, 10(4), 935–939 CrossRef CAS.
- C. Peng Lee, H. Y. Tsai and M. F. Lai, Rotary transportation of magnetic nanoparticle chains on magnetic thin film array, Appl. Phys. Lett., 2012, 100(26), 264102 CrossRef.
- C. E. Sing, L. Schmid, M. F. Schneider, T. Franke and A. Alexander-Katz, Controlled surface-induced flows from the motion of self-assembled colloidal walkers, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(2), 535–540 CrossRef CAS PubMed.
- T. G. Kang, M. A. Hulsen, J. M. J. den Toonder, P. D. Anderson and H. E. H. Meijer, A direct simulation method for flows with suspended paramagnetic particles, J. Comput. Phys., 2008, 227(9), 4441–4458 CrossRef.
- E. C. Snelling, Soft Ferrites: Properties and Applications, Butterworth, London, 1989 Search PubMed.
- R. Zhou, Q. Yang, F. Bai, J. A. Werner, H. Shi, Y. Ma and C. Wang, Fabrication and integration of microscale permanent magnets for particle separation in microfluidics, Microfluid. Nanofluid., 2016, 20(7), 110 CrossRef.
- S. De Pedro, V. J. Cadarso, X. Muñoz-Berbel, J. A. Plaza, J. Sort, J. Brugger, S. Büttgenbach and A. Llobera, PDMS-based, magnetically actuated variable optical attenuators obtained by soft lithography and inkjet printing technologies, Sens. Actuators, A, 2014, 215, 30–35 CrossRef CAS.
- J. R. Anderson, D. T. Chiu, R. J. Jackman, O. Chemiavskaya, J. C. McDonald, H. Wu, S. H. Whitesides and G. M. Whitesides, Fabrication of topologically complex three-dimensional microfluidic systems in PDMS by rapid prototyping, Anal. Chem., 2000, 72(14), 3158–3164 CrossRef CAS PubMed.
- A. J. F. Bombard, I. Joekes, M. R. Alcântara and M. Knobel, Magnetic susceptibility and saturation magnetization of some carbonyl iron powders used in magnetorheological fluids, Mater. Sci. Forum, 2003, 416-418(1), 753–758 CrossRef CAS.
- Y. Gao, M. A. Hulsen, T. G. Kang and J. M. J. den Toonder, Numerical and experimental study of a rotating magnetic particle chain in a viscous fluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(4), 041503 CrossRef CAS PubMed.
- R. J. S. Derks, A. Dietzel, R. Wimberger-Friedl and M. W. J. Prins, Magnetic bead manipulation in a sub-microliter fluid volume applicable for biosensing, Microfluid. Nanofluid., 2007, 3(2), 141–149 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7lc00718c |
| This journal is © The Royal Society of Chemistry 2017 |