Custom 3D printer and resin for 18 μm × 20 μm microfluidic flow channels†
Abstract
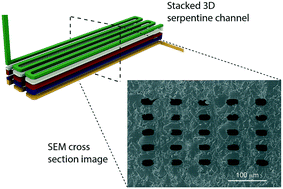
While there is great interest in 3D printing for microfluidic device fabrication, to-date the achieved feature sizes have not been in the truly microfluidic regime (<100 μm). In this paper we demonstrate that a custom digital light processor stereolithographic (DLP-SLA) 3D printer and a specifically-designed, low cost, custom resin can readily achieve flow channel cross sections as small as 18 μm × 20 μm. Our 3D printer has a projected image plane resolution of 7.6 μm and uses a 385 nm LED, which dramatically increases the available selection of UV absorbers for resin formulation compared to 3D printers with 405 nm LEDs. Beginning with 20 candidate absorbers, we demonstrate the evaluation criteria and process flow required to develop a high-resolution resin. In doing so, we introduce a new mathematical model for characterizing the resin optical penetration depth based only on measurement of the absorber's molar absorptivity. Our final resin formulation uses 2-nitrophenyl phenyl sulfide (NPS) as the UV absorber. We also develop a novel channel narrowing technique that, together with the new resin and 3D printer resolution, enables small flow channel fabrication. We demonstrate the efficacy of our approach by fabricating 3D serpentine flow channels 41 mm long in a volume of only 0.12 mm3, and by printing high aspect ratio flow channels <25 μm wide and 3 mm tall. These results indicate that 3D printing is finally positioned to challenge the pre-eminence of methods such as soft lithography for microfluidic device prototyping and fabrication.


 Please wait while we load your content...
Please wait while we load your content...