Droplet trapping and fast acoustic release in a multi-height device with steady-state flow†
Abstract
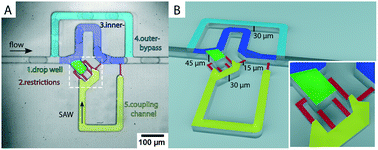
We demonstrate a novel multilayer polydimethylsiloxane (PDMS) device for selective storage and release of single emulsion droplets. Drops are captured in a microchannel cavity and can be released on-demand through a triggered surface acoustic wave pulse. The surface acoustic wave (SAW) is excited by a tapered interdigital transducer (TIDT) deposited on a piezoelectric lithium niobate (LiNbO3) substrate and inverts the pressure difference across the cavity trap to push a drop out of the trap and back into the main flow channel. Droplet capture and release does not require a flow rate change, flow interruption, flow inversion or valve action and can be achieved in as fast as 20 ms. This allows both on-demand droplet capture for analysis and monitoring over arbitrary time scales, and continuous device operation with a high droplet rate of 620 drops per s. We hence decouple long-term droplet interrogation from other operations on the chip. This will ease integration with other microfluidic droplet operations and functional components.


 Please wait while we load your content...
Please wait while we load your content...