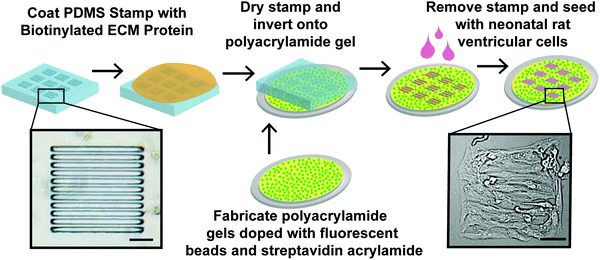
Engineering micromyocardium to delineate cellular and extracellular regulation of myocardial tissue contractility†
Nethika R.
Ariyasinghe
a,
Caitlin H.
Reck
a,
Alyssa A.
Viscio
a,
Andrew P.
Petersen
a,
Davi M.
Lyra-Leite
a,
Nathan
Cho
a and
Megan L.
McCain
 *ab
*ab
aLaboratory for Living Systems Engineering, Department of Biomedical Engineering, USC Viterbi School of Engineering, University of Southern California, 1042 Downey Way, DRB 140, Los Angeles, CA 90089, USA. E-mail: mlmccain@usc.edu; Tel: +1 213-821-0791
bDepartment of Stem Cell Biology and Regenerative Medicine, Keck School of Medicine of USC, University of Southern California, Los Angeles, CA 90033, USA
First published on 12th July 2017
Abstract
Cardiovascular diseases are a leading cause of death, in part due to limitations of existing models of the myocardium. Myocardium consists of aligned, contractile cardiac myocytes interspersed with fibroblasts that synthesize extracellular matrix (ECM). The cellular demographics and biochemical and mechanical properties of the ECM remodel in many different cardiac diseases. However, the impact of diverse cellular and extracellular remodeling on the contractile output of the myocardium are poorly understood. To address this, we micropatterned 13 kPa and 90 kPa polyacrylamide gels with aligned squares of fibronectin (FN) or laminin (LN). We seeded gels with two concentrations of primary neonatal rat ventricular myocytes, which naturally contain fibroblasts. Cells assembled into aligned “μMyocardia” with fibroblast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) myocyte ratios dependent on initial seeding concentration. Using traction force microscopy (TFM), we found that the peak systolic longitudinal cross-sectional force was similar across conditions, but the peak systolic work was significantly lower on 90 kPa gels. This indicates that ECM elasticity dominates over ECM ligand and cell demographics in regulating contractile output. Because our platform provides independent control over cell–cell and cell–matrix interactions, it has many applications for cardiac disease modeling.
myocyte ratios dependent on initial seeding concentration. Using traction force microscopy (TFM), we found that the peak systolic longitudinal cross-sectional force was similar across conditions, but the peak systolic work was significantly lower on 90 kPa gels. This indicates that ECM elasticity dominates over ECM ligand and cell demographics in regulating contractile output. Because our platform provides independent control over cell–cell and cell–matrix interactions, it has many applications for cardiac disease modeling.
Insight, innovation, integrationThe myocardium consists of aligned cardiac myocytes interspersed with fibroblasts that synthesize the extracellular matrix (ECM), a protein network with defined biochemical and mechanical properties. In many cardiac pathologies, it is challenging to pinpoint the precise cellular and extracellular factors that underlie declines in contractility due to their coordinated and coupled remodeling. To overcome this, we engineered aligned, micro-scale tissues comprised of cardiac myocytes and fibroblasts on hydrogels with tunable elasticity, modular composition, and an integrated contractility assay. Our engineered μMyocardia demonstrate that peak systolic work, a correlate to stroke work, is regulated primarily by ECM elasticity, but is independent of ECM ligand and cell demographics. This highly-tunable, engineered model of myocardium with quantitative functional outputs offers many benefits over existing platforms. |
Introduction
Cardiovascular diseases are the leading cause of death in the United States.1 Furthermore, cardiotoxicity is a common reason for market withdrawal of drugs.2 These issues occur partially because existing model systems cannot accurately recapitulate the complexity of native myocardium, provide quantitative functional data, and/or achieve reasonable scalability for medium- to high-throughput disease modeling and drug screening. Myocardium consists of highly aligned cardiac myocytes and fibroblasts surrounded by a compliant extracellular matrix (ECM) basement membrane that comprises mostly fibronectin (FN) and laminin (LN). Importantly, dynamic remodeling of both ECM composition and its mechanical properties, especially elasticity, have been observed throughout cardiac development and disease,3–6 suggesting they play a prominent role in the physiology of the myocardium. However, animal models are not effective for controllably identifying how distinct changes to the ECM impact cardiac function. Animal models are also expensive to maintain, are challenging to scale, and have limited relevance to humans.7 Alternatively, in vitro models are less expensive and more scalable. This approach usually entails culturing cardiac myocytes on highly-simplified surfaces, such as culture dishes uniformly coated with ECM protein, that poorly recapitulate the architecture of native myocardium. Furthermore, standard outputs of these models include morphology, viability, cell beating, and electrophysiology,8,9 which are relatively indirect metrics of cardiac function compared to contractility.Recently, tissue engineering has been leveraged to develop more sophisticated in vitro models that mimic key features of native myocardium and integrate built-in assays for quantifying contractility. For example, stresses generated by single and paired cardiac myocytes have been measured with traction force microscopy (TFM) by culturing cells on FN-micropatterned hydrogels.10–13 The advantage of this approach is that both cell shape and the ECM are relatively tunable. However, these one- and two-cell myocyte constructs lack the diverse cell demographics and cell–cell interactions seen in native myocardium. Aligned, multi-cellular cardiac tissues have been engineered on FN-micropatterned PDMS14–16 or micromolded gelatin hydrogels17 pre-cut into mm-scale cantilevers parallel to the orientation of the patterning. After tissue formation, these cantilevers can be peeled up to measure stresses generated by the tissue based on cantilever curvature.15,18,19 However, because the cantilevers must be manually released, this assay is relatively low-throughput. Three-dimensional cardiac tissues have been generated by encapsulating cells in ECM hydrogels within fabricated molds.20,21 These constructs are likely closer representations of the cell–cell interactions seen in native myocardium, but the architecture of these constructs is difficult to control and measuring contractility is cumbersome. These tissues also require relatively large quantities of cells, which increases cost and limits scalability. Thus, there is a need for a biomimetic myocardial contractility platform that offers tunability over the ECM and improved scalability compared to current methods.
To address the limitations of existing models of the myocardium, we engineered a medium-throughput platform that outputs contractile forces generated by aligned cardiac myocyte and fibroblast tissues engineered on ECM substrates with tunable mechanical and biochemical properties. To achieve this, we microcontact printed 200 μm-sided squares of arrayed 15 μm-wide lines of FN or LN onto polyacrylamide gels with elastic moduli tuned to mimic healthy (13 kPa) or fibrotic (90 kPa) myocardium.22 We seeded gels with two different densities of neonatal rat ventricular cardiac myocytes, which naturally contain cardiac fibroblasts. The cardiac myocytes and fibroblasts self-assembled into aligned patches of tissue, which we refer to as μMyocardia, with distinct fibroblast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) myocyte ratios based on cell seeding density. Next, we used TFM to quantify peak systolic displacement, cross-sectional force, and work generated by μMyocardia as a function of ECM elasticity, ECM ligand, and cell demographics. Our results indicate that peak systolic longitudinal cross-sectional force was relatively independent of ECM elasticity, ECM ligand, or cell demographics. However, peak systolic longitudinal displacement and work were significantly lower on more rigid gels. Thus, ECM elasticity appears to be the most dominant factor regulating contractile output. Because this platform offers independent control over ECM ligand, ECM elasticity, and cell demographics, it can be used to engineer customized μMyocardia that mimic unique aspects of healthy and diseased myocardium. This platform is also relatively scalable compared to existing in vitro contractility assays and thus can be extended to screening drug toxicity and/or efficacy.
myocyte ratios based on cell seeding density. Next, we used TFM to quantify peak systolic displacement, cross-sectional force, and work generated by μMyocardia as a function of ECM elasticity, ECM ligand, and cell demographics. Our results indicate that peak systolic longitudinal cross-sectional force was relatively independent of ECM elasticity, ECM ligand, or cell demographics. However, peak systolic longitudinal displacement and work were significantly lower on more rigid gels. Thus, ECM elasticity appears to be the most dominant factor regulating contractile output. Because this platform offers independent control over ECM ligand, ECM elasticity, and cell demographics, it can be used to engineer customized μMyocardia that mimic unique aspects of healthy and diseased myocardium. This platform is also relatively scalable compared to existing in vitro contractility assays and thus can be extended to screening drug toxicity and/or efficacy.
Results
Engineering μMyocardia
Myocardium is densely-packed with aligned cardiac myocytes that are supported by fibroblasts23 and a compliant basement membrane consisting primarily of FN and LN.24 Our goal was to engineer the minimum functioning unit of myocardium, which we call μMyocardium, with independent control over ECM ligand and elastic modulus and an integrated assay for measuring contractility. Previously, we used TFM to measure contractile stresses generated by single and paired cardiac myocytes cultured on micropatterned polyacrylamide gels.11,12 Here, we expanded this approach to multi-cellular tissues (Fig. 1) by fabricating PDMS stamps with arrays of 200 μm-sided squares. Each square contains 15 μm-wide, 5 μm-deep lines separated by 2 μm-wide gaps, which is a miniaturized version of a previous pattern.14,16 Next, we used these stamps to microcontact print biotinylated FN or LN onto 13 kPa and 90 kPa streptavidin-doped polyacrylamide gels to mimic the elasticity of healthy and fibrotic myocardium,22 respectively. With this approach, we can mimic the alignment of native myocardium while independently controlling the biochemical and mechanical properties of the ECM.Cellular architecture of μMyocardia
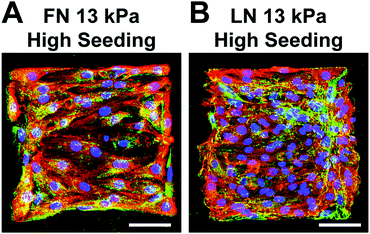
Next, we seeded our micropatterned gels with primary neonatal rat ventricular myocytes, which naturally contain a low percentage of fibroblasts that are not completely separated during the harvest process. To determine the optimal seeding density for creating aligned, confluent μMyocardia, we seeded constructs with either 5.5 × 104 cells per cm2 or 1.1 × 105 cells per cm2, referred to as low and high seeding density, respectively. After four days in culture, we stained μMyocardia for nuclei, actin, and sarcomeric α-actinin (Fig. 2A), counted the overall number of nuclei per μMyocardium, and counted the number of nuclei not located within sarcomeric α-actinin-positive cells, which we classified as fibroblasts. As expected, low density μMyocardia had a lower overall number of cells (Fig. 2B). Furthermore, high density μMyocardia had approximately twice as many myocytes compared to low density μMyocardia. This is expected because myocytes are post-mitotic and therefore final myocyte density should be comparable to initial myocyte seeding density. Conversely, low density μMyocardia had approximately twice as many fibroblasts compared to high density μMyocardia (Fig. 2B). This is likely because fibroblasts in both conditions proliferated until they were contact-inhibited, which would occur earlier in high density μMyocardia. For both low and high density μMyocardia, cell density and demographics were independent of ECM elasticity and ECM ligand (Fig. 2B), indicating that these factors did not differentially impact cell adhesion, proliferation, or survival.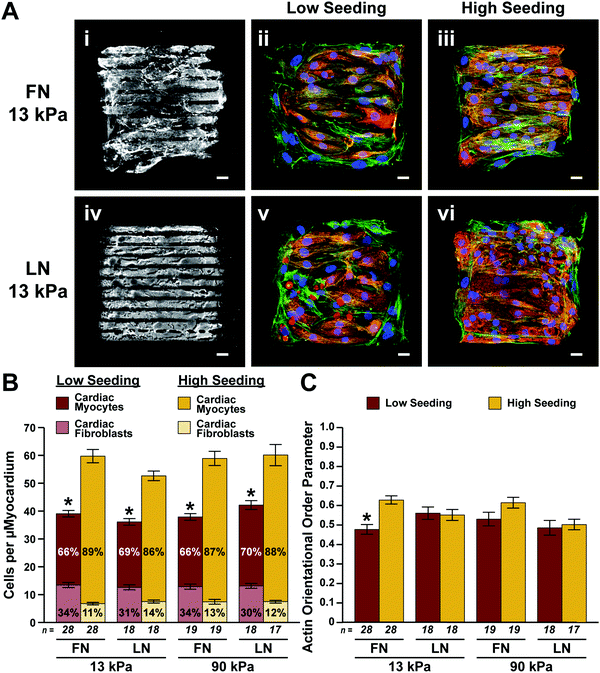 | ||
| Fig. 2 Cell demographics and actin alignment in engineered μMyocardia. (A) Representative images of micropatterned ECM proteins (i and iv) and μMyocardia engineered using low (ii and v) and high (iii and vi) seeding densities on FN- and LN-patterned 13 kPa gels. Scale bars, 20 μm; blue, nuclei; red, sarcomeric α-actinin; green, actin. (B) Total number of cells per μMyocardium (mean ± standard error of the mean; *p < 0.05 for the total cell number and number of fibroblasts compared to high seeding density for the same ECM elasticity and ligand, ANOVA followed by Tukey's test for multiple comparisons). (C) Average actin orientational order parameter for each condition (mean ± standard error of the mean; *p < 0.05 compared to high seeding density for the same ECM elasticity and ligand, Kruskal–Wallis followed by the Bonferroni method for multiple comparisons). Details of statistical analyses are located in Tables S1–S4 (ESI†). | ||
Because native myocardium is highly aligned, we next determined if our engineered μMyocardia mimicked this hallmark architectural feature by calculating the orientational order parameter of actin fibers15,19 in multiple μMyocardia for each condition. As shown in Fig. 2C, the average actin orientational order parameter for all the conditions was 0.4–0.7, which is a relatively high level of alignment consistent with values seen previously in aligned tissues.25,26 We found no statistical differences in alignment between the conditions, except for low density and high density μMyocardia patterned with FN on 13 kPa gels, suggesting that ECM ligand and elasticity do not considerably impact cytoskeletal alignment.
Quantifying contractile parameters in engineered μMyocardia
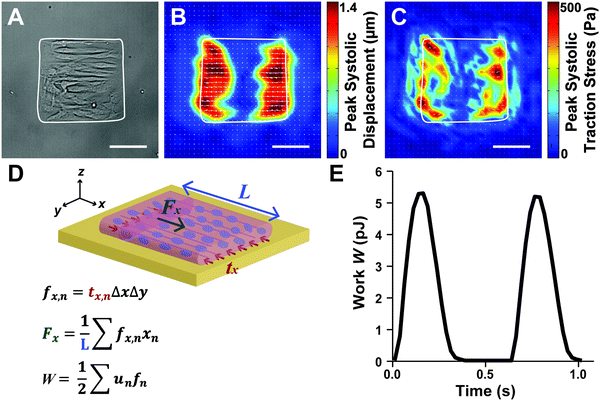
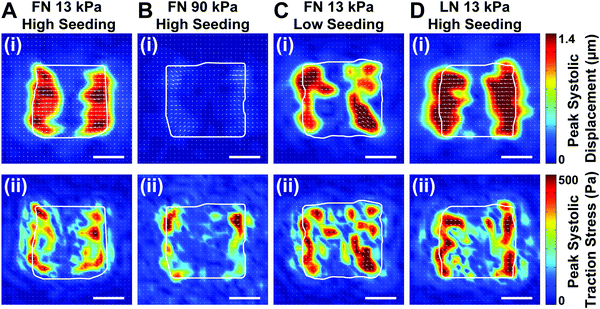
Because the essential function of myocardium is to contract and pump blood, contractility is a desirable output for an in vitro model of the myocardium. To facilitate contractility measurements, we cultured μMyocardia on polyacrylamide gels doped with fluorescent beads for TFM analysis. After four days in culture, we electrically stimulated μMyocardia at 2 Hz, inducing tissues to contract and deform the gel. For each μMyocardium, we recorded bead movement and calculated longitudinal (ux,n) and lateral (uy,n) displacement vectors and longitudinal (tx,n) and lateral (ty,n) traction stress vectors at discretized locations for each contraction (Fig. 3A–C), taking into account the elastic modulus of each gel. We then calculated the longitudinal cross-sectional force (Fx) and work (W) over two contractions (Fig. 3D and E). As shown in the representative heatmaps in Fig. 4, displacement and traction stress vectors at peak systole relative to diastole were predominantly oriented parallel to the long axis of the tissue, which is expected based on their alignment. Similar to other studies,11,12 displacement vectors were significantly smaller on the more rigid gels (Fig. 4A and B). We also observed that vector maps were similar in magnitude, but more uniform and symmetrical for the high seeding density compared to the low seeding density (Fig. 4A and C), which is likely due to greater myocyte confluence in the high seeding condition. Qualitatively, there were no apparent differences in displacement or traction stress vector maps based on ECM ligand (Fig. 4A and D).To characterize the spatial distribution of force transmission from μMyocardia to the ECM, we next summed and normalized the magnitudes of peak systolic longitudinal displacement vectors at each x-position for each μMyocardium. As shown in Fig. 5, for all conditions, the average spatial distribution of longitudinal displacement vectors was similar, with displacement concentrated at the longitudinal edges of the tissues. Conversely, in the center of the tissue, minimal amounts of displacement were detected. Thus, in all conditions, μMyocardia consistently transmitted force predominantly at the longitudinal boundaries of the tissue.
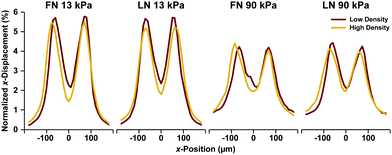 | ||
| Fig. 5 Spatial distributions of x-displacement vectors in μMyocardia. For each condition, the normalized x-displacement was calculated at each x-position for all μMyocardia, averaged, and plotted. | ||
Comparing contractile output of μMyocardia
Next, we calculated time to peak systole, peak systolic longitudinal displacement, and peak systolic Fx for multiple μMyocardia for each condition. As shown in Fig. 6A, time to peak systole was similar for all conditions. As suggested by the displacement maps (Fig. 4), peak systolic longitudinal displacement was significantly lower on 90 kPa gels compared to 13 kPa gels (Fig. 6B). However, this parameter was not regulated by ECM ligand or cell density. Interestingly, peak systolic Fx was similar across all conditions, except for low density LN 13 kPa differing from high density LN 13 kPa and low density FN 13 kPa (Fig. 6C). Thus, μMyocardia had relatively consistent force production, independent of ECM elasticity, ECM ligand, or cell demographics. For all conditions, peak systolic displacement and cross-sectional force in the longitudinal direction were higher than these values in the lateral direction, as expected due to the uniaxial alignment of the μMyocardia (Fig. S1, ESI†). Thus, peak systolic Fx generated by μMyocardia is relatively conserved, regardless of ECM ligand, ECM elastic modulus, and cell seeding density.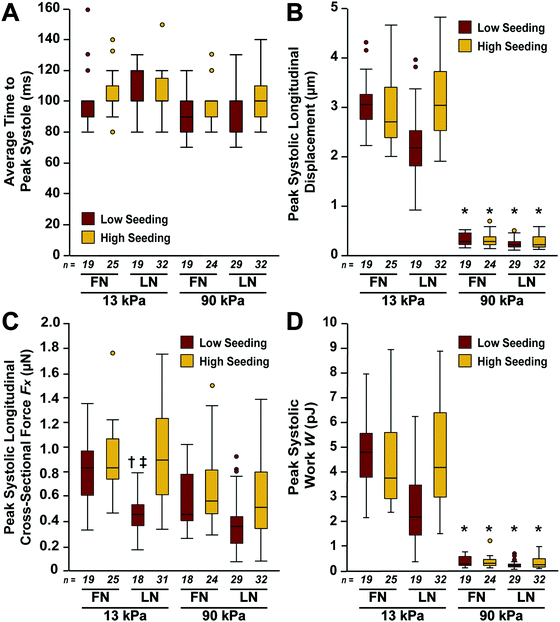 | ||
| Fig. 6 Average longitudinal contractile parameters for μMyocardia. Time to peak systole (A), peak systolic longitudinal displacement (B), peak systolic longitudinal cross-sectional force Fx (C), and peak systolic work W (D) for each condition (*p < 0.05 compared to 13 kPa, same ECM ligand, same seeding density; †p < 0.05 compared to FN, 13 kPa, low seeding density; ‡p < 0.05 compared to LN, 13 kPa, high seeding density; Kruskal–Wallis followed by the Bonferroni method for multiple comparisons). Details of statistical analyses are located in Tables S5–S8 (ESI†). | ||
With each contraction cycle, left ventricular myocardium must both shorten and generate stress to eject blood into the aorta. Stroke work is defined as the amount of work needed for this process and is calculated by multiplying stroke volume times aortic pressure, or calculating the area of a pressure–volume loop over one contraction cycle.27 In our system, peak systolic W is analogous to stroke work because it considers both displacement and stress from diastole to systole. Peak systolic W was independent of both ECM ligand and seeding density (Fig. 6D). Thus, μMyocardia generated equivalent levels of work, independent of the number of cardiac myocytes. However, peak systolic W was significantly higher for μMyocardia on 13 kPa gels compared to those on 90 kPa gels (Fig. 6D). Thus, peak systolic W generated by μMyocardia was inversely regulated by ECM elastic modulus, but was independent of both ECM ligand and cell seeding density for the tested ranges.
Identifying non-patterned ECM molecules
Although we micropatterned pure solutions of FN or LN onto gels, ECM molecules are also synthesized by cells and are present in the media due to our use of serum. Thus, we next investigated if LN was present in FN-patterned tissue and vice versa by immunostaining for the ECM molecule that is the counterpart to the micropatterning. As shown in Fig. 7, we detected LN and FN fibers in FN- and LN-patterned tissues, respectively. The LN and FN immunosignals were primarily localized with fibroblasts instead of myocytes, which is expected. Thus, μMyocardia synthesized detectable amounts of ECM molecules beyond those initially micropatterned on the surface, which potentially diminished the effects of the distinct ECM ligands patterned on the gel.Discussion
To address some of the limitations of existing in vivo and in vitro models of myocardium, we engineered a μMyocardium platform that offers independent control over ECM elasticity, ECM ligand, and cell demographics, as well as an integrated contractility assay. Our results indicate that the amount of peak systolic W generated by μMyocardia is regulated by ECM elasticity, but not ECM ligand or the number of myocytes. These results are important for understanding how distinct cellular and extracellular parameters independently impact the contractile output of myocardium. Furthermore, our platform is relatively scalable and therefore can be used for a variety of applications related to disease modeling and drug screening.Myocardium is powered by cardiac myocytes that are highly aligned and densely packed with myofibrils,24 which maximizes force generation parallel to the long axis of the tissue.15,28,29 To mimic this critical architectural feature, we used photolithography, soft lithography, and microcontact printing to micropattern arrayed lines of biotinylated FN or LN onto streptavidin-doped polyacrylamide gels. Although this approach has previously been used for FN,11–13 our results show that it is also compatible with LN. On both 13 kPa and 90 kPa gels, micropatterned FN and LN successfully induced cells to self-assemble into aligned tissues. However, in many pathological settings, such as the border zone surrounding a myocardial infarction,30 myocytes lose their hallmark alignment. Because ECM patterning can be manipulated simply by altering photomask design, our platform can be easily tuned to engineer cardiac disease models with physiologically-relevant architectural features. Fine-tuning tissue architecture could also reveal further insight into relationships between myocyte shape, alignment, and contractility to complement previous studies in single cells10,12 and multicellular, mm-scale tissues.15,19,29 Furthermore, in this study, we only tested FN and LN individually. However, the basement membrane of healthy myocardium contains both ligands in defined concentrations and ratios, which are often altered in many pathological settings.3,5,6 The biochemical characteristics of physiological and pathological ECM could easily be mimicked in our platform by mixing and customizing the concentration of FN and LN in the stamping solution. Thus, our approach enables users to independently dictate tissue alignment, ECM elasticity, and ECM composition, which is highly beneficial for cardiac disease modeling.
Cardiac myocytes occupy the most volume in myocardium (75%) but comprise only 30–40% of the myocardium in terms of cell numbers. Fibroblasts comprise the majority of the remaining cells.23 Fibroblasts play mostly a supportive role in the myocardium by synthesizing, depositing, and degrading the ECM.4 In many pathological settings, such as after a myocardial infarction, the number of fibroblasts at and/or near the affected area increases due to myocyte necrosis and fibroblast proliferation.23 Because we utilized primary neonatal rat ventricular myocytes in this study, we naturally had a small percentage of fibroblasts present in our engineered μMyocardia. Since fibroblasts are proliferative, and myocytes are not, the number and ratio of these two cell types was ultimately regulated by the initial cell seeding density. Specifically, our high seeding density μMyocardia had 10–15% fibroblasts and low seeding density μMyocardia had 30–35% fibroblasts. These fibroblast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) myocyte ratios are lower than both healthy and diseased myocardium, but it is challenging to form tissues that maintain electrical coupling between cardiac myocytes in 2-D culture if 60–70% of the tissue is fibroblasts. This inability to truly replicate the 3-D architecture and cell positioning of native myocardium is one limitation of our in vitro system. However, our results still have important implications for understanding the impact of fibroblasts on myocytes. For example, we found that the initial cell seeding density, and thus the number of cardiac myocytes, had relatively minimal impact on the contractile parameters that we measured. This could have a variety of explanations, as detailed below.
myocyte ratios are lower than both healthy and diseased myocardium, but it is challenging to form tissues that maintain electrical coupling between cardiac myocytes in 2-D culture if 60–70% of the tissue is fibroblasts. This inability to truly replicate the 3-D architecture and cell positioning of native myocardium is one limitation of our in vitro system. However, our results still have important implications for understanding the impact of fibroblasts on myocytes. For example, we found that the initial cell seeding density, and thus the number of cardiac myocytes, had relatively minimal impact on the contractile parameters that we measured. This could have a variety of explanations, as detailed below.
One potential explanation for the independence of contractile output on the number of myocytes is that fibroblasts had a beneficial effect on the cardiac myocytes. As described above, we found that the fibroblast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) myocyte ratio was higher in the tissues seeded at low density. Previous studies have shown that increasing the fibroblast
myocyte ratio was higher in the tissues seeded at low density. Previous studies have shown that increasing the fibroblast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) myocyte ratio improves cardiac myocyte morphology and electrical31 and contractile32 phenotype in a variety of engineered tissue systems. This could be because fibroblasts secrete ECM molecules, which provide additional mechanical and structural support to cardiac myocytes. Evidence also suggests that fibroblasts can form functional cell–cell junctions with cardiac myocytes33,34 and therefore likely affect cardiac myocytes in many ways beyond ECM synthesis and remodeling. Together, our results combined with these previous studies indicate that fibroblasts likely do play an important role in maintaining and promoting the structural and functional phenotype of cardiac myocytes in vitro and should not be perceived only as a “contamination” of primary cultures. These hypotheses can be explored in future studies by more deliberately altering μMyocardia cellular composition. Our results also suggest that fibroblasts could potentially enhance the functionality and/or maturity of stem cell-derived cardiac myocytes. Currently, stem cell-derived cardiac myocytes are typically differentiated, purified, and maintained in monoculture.35,36 However, previous studies have shown that co-culturing stem cell-derived cardiac myocytes with fibroblasts has a beneficial effect on the adhesion and functionality of the myocytes,37–39 which is in-line with our current results. Collectively, our study provides further evidence that fibroblasts are important components to include in both healthy and diseased cardiac tissue models.
myocyte ratio improves cardiac myocyte morphology and electrical31 and contractile32 phenotype in a variety of engineered tissue systems. This could be because fibroblasts secrete ECM molecules, which provide additional mechanical and structural support to cardiac myocytes. Evidence also suggests that fibroblasts can form functional cell–cell junctions with cardiac myocytes33,34 and therefore likely affect cardiac myocytes in many ways beyond ECM synthesis and remodeling. Together, our results combined with these previous studies indicate that fibroblasts likely do play an important role in maintaining and promoting the structural and functional phenotype of cardiac myocytes in vitro and should not be perceived only as a “contamination” of primary cultures. These hypotheses can be explored in future studies by more deliberately altering μMyocardia cellular composition. Our results also suggest that fibroblasts could potentially enhance the functionality and/or maturity of stem cell-derived cardiac myocytes. Currently, stem cell-derived cardiac myocytes are typically differentiated, purified, and maintained in monoculture.35,36 However, previous studies have shown that co-culturing stem cell-derived cardiac myocytes with fibroblasts has a beneficial effect on the adhesion and functionality of the myocytes,37–39 which is in-line with our current results. Collectively, our study provides further evidence that fibroblasts are important components to include in both healthy and diseased cardiac tissue models.
Our previous studies in pairs of cardiac myocytes showed that, at the cell–cell interface, myocytes predominantly release their focal adhesions and form cohesive cell–cell junctions.11,13 Thus, at the cell–cell interface, minimal stresses are transmitted to the ECM, which are the only stresses that we can measure using TFM. However, we can safely assume that stresses transmitted at cell–matrix adhesions are appropriately balanced by stresses transmitted to cell–cell adhesions due to the need for forces to balance.11,40 Due to this feature, we previously observed that traction stresses generated by a single myocyte and a pair of myocytes is relatively equivalent, if the cell(s) occupy the same surface area and are arranged linearly.11,12 Thus, the surface area of tissue adhesion dominates the amount of stress transmitted to the ECM compared to the actual number of myocytes. In our μMyocardia, we similarly observed that traction stresses were concentrated at the longitudinal ends of the tissues over a relatively consistent surface area, suggesting that cell–cell adhesions were dominant over cell–matrix adhesions in the interior of the tissue. Furthermore, we observed that contractile parameters were independent of the number of myocytes. Together, our observations in μMyocardia further support the idea that, up to a certain point, the geometry and surface area of the tissue, rather than the overall number of myocytes, dominates the amount of contractile stress transmitted to the ECM, given that ECM elasticity is kept constant. Overall, our data spanning from single myocyte to myocyte pair to multi-cellular μMyocardium further demonstrate that the myocardium functions as a mechanical syncytium, where myocytes form robust cell–cell adhesions that seamlessly transmit force across the tissue.
The ECM is a network of proteins and molecules that have both structural and non-structural functions. Myocardial ECM is dominated by Type I collagen fibers, which serve largely structural and stabilizing roles.6 The basement membrane that directly surrounds myocytes and links myocytes to collagen fibers consists primarily of the glycoproteins FN and LN,24 which are adhesive ligands for integrin receptors.41,42 Concurrent remodeling of both ECM composition and elastic modulus have been reported in many disease settings.3 For example, many cardiac diseases are associated with fibrosis and/or scar tissue formation,4 which alters ECM composition,5,43 including elevated expression of FN,44,45 and increases the elastic modulus of the tissue beyond 50 kPa.22 With in vivo models, it is challenging, if not impossible, to truly de-couple ECM composition and elasticity to identify the structural and functional impact of these parameters. With our in vitro approach, we independently controlled ECM elasticity and ECM ligand such that we could quantify how these two parameters alter the contractile output of myocardium. Our results indicate that ECM elasticity has a greater functional impact on μMyocardia compared to ECM ligand. One explanation for this result is that, although FN and LN are ligands for distinct integrin receptors,42 the engagement of different integrin receptors had minimal impact on contractility. A second explanation is that, because myocytes and predominantly fibroblasts secrete FN and LN, ultimately both ligands were present in our constructs, regardless of the identity of the original micropatterned ligand. For example, our immunostained tissues do show evidence of cell-generated FN in LN-patterned tissues, and vice versa. Thirdly, our use of serum in the media could have confounded our results because serum contains many ECM molecules. However, polyacrylamide gels are non-fouling surfaces, which is the reason for using biotin–streptavidin linkages to adhere micropatterned FN and LN to the surface. As a result, cells did not adhere to any regions of the gel not subjected to micropatterning, suggesting that ECM molecules from the serum did not deposit on the surface of the gel. However, we cannot exclude any interactions between soluble ECM molecules in the serum with the micropatterned ECM molecules or with the cells themselves. Thus, ECM synthesis by the cells and the presence of ECM molecules in the serum could potentially have masked any differences due to FN versus LN.
Our results indicate that, in μMyocardia, peak systolic displacement and W were lower on 90 kPa gels compared to 13 kPa gels, but Fx was preserved. Interestingly, we observed slightly different trends in single and paired cardiac myocytes: peak systolic displacement and various metrics for peak systolic force were lower on 90 kPa gels compared to 13 kPa gels, but peak systolic work was preserved.11,12 Thus, in all cases, peak systolic displacement was lowest on the more rigid gels. However, in μMyocardia, the difference in displacement between 13 kPa and 90 kPa gels was much greater compared to this difference in single cells and cell pairs. This ultimately led to a smaller difference in the traction stress and Fx generated on 13 kPa and 90 kPa gels, as this value is dependent on both gel elasticity and displacement. Consequently, peak systolic work in μMyocardia was also much lower on the 90 kPa gels compared to 13 kPa gels, as this is a function of both displacement and traction stress. Thus, relationships between displacement, force, and work do not perfectly scale from single cell to cell pair to multi-cellular tissue. One key difference between μMyocardia and single and paired myocytes is the presence of fibroblasts, which could potentially add greater resistance to contraction in μMyocardia. Another important consideration is that we did not measure changes in diastolic parameters in our μMyocardia, as all measurements reflect changes from diastole to systole. There could be differences in baseline diastolic displacement, force, and/or work that are important for understanding how the parameters we tested potentially contribute to diseases such as diastolic heart failure.46 These measurements are an important topic for follow-up studies.
Many limitations of our study are inherent to in vitro systems. For example, we used polyacrylamide gels functionalized with ECM proteins such that we could independently modulate mechanical and biochemical properties of the ECM. However, these gels are highly synthetic and limit the ability of cells to interact with and remodel the ECM, which is an important process in native myocardium. Ideally, we would use hydrogels consisting purely of our ECM molecule of interest, but this is cost-prohibitive. Another limitation is that we only tested FN and LN, but the basal lamina in native myocardium has many other molecules, such as Collagen IV.24 However, our biotin–streptavidin approach should be compatible with testing other ECM molecules and combinations of ECM molecules in future studies. Future studies could also investigate lower elastic moduli, such as 1 kPa,11 to establish how modulating ECM elasticity and composition impacts contractility in more of a developmental context.47,48
Another limitation is that our constructs are two-dimensional. However, three-dimensional constructs require large quantities of cells and are less scalable, so although we compromise physiological relevance, our two-dimensional approach offers many practical advantages. Furthermore, μMyocardia remain planar throughout the experimental measurements, require minimal user intervention, and are not endpoint experiments. Thus, our μMyocardia are well-suited to be enclosed in a fluidic device to create a “Myocardium on a Chip” platform that could be used for extended drug testing or coupling with other “Organs on Chip” platforms.14,49 Our platform is also relatively versatile and should be compatible with measuring contractile parameters in other types of muscle cells, such as vascular or bronchial smooth muscle.
Our study is also limited by the use of neonatal rat cardiac myocytes, which are non-human. For future studies, we plan to use this same platform with human induced pluripotent stem cell (hiPSC)-derived cardiac myocytes sourced from wildtype patients and patients with inherited cardiomyopathies, similar to previous studies.16,50,51 By combining our μMyocardia platform with hiPSC-derived cardiac myocytes, we can build robust, human-relevant, patient-specific platforms to study inherited cardiomyopathies, identify novel therapeutic targets, and screen drugs with quantitative functional outputs. Importantly, because our platform offers control over the ECM, we can also determine how diverse forms of ECM remodeling potentially synergize with genetic mutations in inherited diseases. For example, merosin-deficient congenital muscular dystrophy is an inherited striated muscle myopathy caused by a mutation in the LAMA2 gene, which encodes for the LN-α2 chain.52 Our platform would be especially powerful for elucidating intracellular and extracellular mechanisms of this disease because we could independently tune the LN composition of the ECM for both wildtype and LAMA2-deficient hiPSC-derived cardiac myocytes.
In summary, we have fabricated a scalable platform for engineering and interrogating customizable μMyocardia, which has revealed novel insight into how remodeling of the ECM and cellular composition impact the contractile function of myocardium. Our platform has many applications for functional disease modeling and drug screening, especially when combined with hiPSC-derived cardiac myocytes.
Methods
Photolithography and soft lithography
A photolithographic chromium mask containing 200 μm × 200 μm squares of 15 μm wide lines separated by 2 μm-wide gaps (referred to as 15 × 2) was designed in AutoCAD (Autodesk Inc.), similar to previous publications.14,53 We chose 200 μm × 200 μm-sized square tissues because these dimensions were the maximum size that was visible in the field of view of our inverted fluorescent microscope with a 20× objective, which was essential for resolving fluorescent beads for TFM measurements.Silicon wafers were fabricated in a Class 100 Cleanroom using standard photolithography protocols.54 Briefly, cleaned silicon wafers were spin coated with hexamethyldisilazane and then SU-8 2005 negative photoresist (MicroChem). The wafers were exposed to UV light through the chromium photomask using a mask aligner. The non-cross-linked portions of the wafers were removed by submerging the wafers in propylene glycol monomethyl ether acetate. Last, the wafers were silanized overnight in a desiccator with a drop of trichloro (1H,1H,2H,2H-perfluorooctyl) silane. PDMS stamps were created by mixing the base and curing agents of Sylgard 184 (Dow Corning) at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio and then pouring this mixture over the wafer in a Petri dish. The PDMS was degassed, cured at 65 °C for four hours, and peeled off the wafer and cut into square stamps.
1 mass ratio and then pouring this mixture over the wafer in a Petri dish. The PDMS was degassed, cured at 65 °C for four hours, and peeled off the wafer and cut into square stamps.
Biotinylation of extracellular matrix proteins
FN was biotinylated similar to previously published protocols.11,12 Briefly, 200 μg mL−1 of biotinylated FN dissolved in sodium carbonate was incubated overnight with Sulfo-NHS-LC-Biotin (Pierce) in a 100 mM sodium carbonate solution and then dialyzed for 4 hours in phosphate buffered saline (PBS). LN was biotinylated by dialyzing laminin dissolved in Tris–HCl and sodium chloride for four hours in a 100 mM sodium carbonate solution. LN was then incubated overnight with Sulfo-NHS-LC-Biotin (Pierce) in a 100 mM sodium carbonate solution and dialyzed for four hours in PBS.Fabrication of micropatterned polyacrylamide gels
Glass coverslips were chemically activated using previously published methods by immersing the coverslips in 0.5% APTES in 95% ethanol, followed by 70% glutaraldehyde in water.11,12 Polyacrylamide gels with 13 kPa and 90 kPa elastic moduli were fabricated similar to previously published methods. 40% acrylamide and 2% N,N-methylenebisacrylamide solutions were mixed in a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio for 13 kPa gels and a 1
4 ratio for 13 kPa gels and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for 90 kPa gels. For 13 kPa gels, 240 μL of the acrylamide/bis mixture was combined with 190.1 μL of water. For 90 kPa gels, 360 μL of the acrylamide/bis mixture was combined with 70.1 μL of water. Each of these mixtures was combined with 60 μL PBS, 0.9 μL tetramethylethylenediamine, and 3 μL ammonium persulfate. For traction force microscopy (TFM) measurements, 6 μL fluorescent microbeads were added to the gel solution. For samples used for immunostaining, an extra 6 μL of water was added to the gel solution. Streptavidin-acrylamide was mixed with the complete gel solution using a volume ratio of 1
1 ratio for 90 kPa gels. For 13 kPa gels, 240 μL of the acrylamide/bis mixture was combined with 190.1 μL of water. For 90 kPa gels, 360 μL of the acrylamide/bis mixture was combined with 70.1 μL of water. Each of these mixtures was combined with 60 μL PBS, 0.9 μL tetramethylethylenediamine, and 3 μL ammonium persulfate. For traction force microscopy (TFM) measurements, 6 μL fluorescent microbeads were added to the gel solution. For samples used for immunostaining, an extra 6 μL of water was added to the gel solution. Streptavidin-acrylamide was mixed with the complete gel solution using a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. 15 μL of the resulting solution was pipetted onto chemically activated 25 mm coverslips and covered with 18 mm coverslips. The coverslips were left at room temperature for approximately half an hour until the gel cured, at which point the top 18 mm coverslips were removed using a razor blade.
5. 15 μL of the resulting solution was pipetted onto chemically activated 25 mm coverslips and covered with 18 mm coverslips. The coverslips were left at room temperature for approximately half an hour until the gel cured, at which point the top 18 mm coverslips were removed using a razor blade.
To microcontact print the gels, PDMS stamps were sonicated, dried, coated with biotinylated FN or LN, and incubated for at least one hour at room temperature. The polyacrylamide gels were placed in a 37 °C incubator for approximately ten minutes to remove excess moisture from the gel surface, taking care not to over-dry the gels. Then, the stamps were dried using compressed air and inverted onto the gels such that the patterned side of the stamp was in contact with the gel. Patterned gels were stored in PBS at 4 °C until cell seeding.
Harvest and culture of neonatal rat ventricular myocytes
Two-day old Sprague-Dawley rats were euthanized using a protocol approved by the University of Southern California Institutional Animal Care and Use Committee, similar to previous protocols.10–12,15,19 Ventricular tissue was isolated from rats, incubated in a 1 mg mL−1 trypsin solution for 11–13 hours at 4 °C, and vigorously pipetted in four serial solutions of 1 mg mL−1 collagenase to dissociate the tissue into a single cell suspension. The cells were strained and preplated twice to reduce non-myocyte cell populations. The purified cell solution was seeded onto the micropatterned gels in six-well plates, at a concentration of 5.5 × 104 cells per cm2 or 1.1 × 105 cells per cm2 per gel. Cells were maintained in M199 media supplemented with 10 mM HEPES, 0.1 mM MEM nonessential amino acids, 20 mM glucose, 2 mM L-glutamine, 1.5 μM vitamin B-12, 50 U mL−1 penicillin, and 10% heat-inactivated fetal bovine serum (FBS) for two days. At this point, FBS was reduced to 2% and media was exchanged every other day.Immunostaining
After four days of culture, tissues were fixed in 4% paraformaldehyde and permeabilized with 0.2% Triton X-100. After rinsing samples in PBS, samples were incubated with monoclonal mouse anti-sarcomeric α-actinin (Sigma, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) primary antibody and rabbit anti-FN primary antibody (Sigma, 1
200) primary antibody and rabbit anti-FN primary antibody (Sigma, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) or rabbit anti-LN primary antibody (Sigma, 1
200) or rabbit anti-LN primary antibody (Sigma, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) for one hour at room temperature. The samples were rinsed with PBS and then incubated with Alexa Fluor 546 goat anti-mouse secondary antibody (Life Technologies, 1
200) for one hour at room temperature. The samples were rinsed with PBS and then incubated with Alexa Fluor 546 goat anti-mouse secondary antibody (Life Technologies, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), 4′,6-diamidino-2-phenylindole (DAPI, 1
200), 4′,6-diamidino-2-phenylindole (DAPI, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), Alexa Fluor 488 Phalloidin (Life Technologies, 1
200), Alexa Fluor 488 Phalloidin (Life Technologies, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), and Alexa Fluor 633 goat anti-rabbit secondary antibody (Life Technologies, 1
200), and Alexa Fluor 633 goat anti-rabbit secondary antibody (Life Technologies, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) for one hour at room temperature. The samples were rinsed in PBS again and then mounted onto glass slides using ProLong Gold Antifade (Life Technologies).
200) for one hour at room temperature. The samples were rinsed in PBS again and then mounted onto glass slides using ProLong Gold Antifade (Life Technologies).
Quantifying cell density and cytoskeletal alignment
Stained tissues were imaged using a 20× objective on a Nikon Ti inverted fluorescence microscope and an Andor Zyla scientific CMOS camera. A cell counter program in ImageJ was used to count the number of nuclei per μMyocardia for multiple μMyocardia taken from at least two different harvests for each condition tested. Actin alignment was determined using previously-described custom MATLAB software created based on a fingerprint detection algorithm.15 Briefly, images were converted to binary and skeleton images. Vectors pointing in the direction of actin fibers were assigned and the maximal eigenvalue of all the vectors was defined as the orientational order parameter, which ranges from zero (for completely isotropic systems) to one (for completely anisotropic systems).Quantifying contractile parameters with traction force microscopy
Coverslips containing μMyocardia were incubated in Tyrode's solution (1.8 mM CaCl2, 5 mM glucose, 5 mM HEPES, 1 mM MgCl2, 5.4 mM KCl, 135 mM NaCl, 0.33 mM NaH2PO4, pH 7.4) and placed in an incubation chamber set at 37 °C on a Nikon Ti inverted fluorescence microscope. Tissues were electrically stimulated with a field electrode at 13 V and 2 Hz. The pacing frequency was chosen as 2 Hz because most tissues had spontaneous beat rates greater than 1 Hz, but could not be consistently captured at 3 Hz. Thus, 2 Hz was the pacing rate with the most consistent success. A brightfield image of each tissue was taken in order to measure tissue length, and then three-second videos were captured with a 20× objective and Andor Zyla scientific CMOS camera at 100 frames per s.Videos were cropped using ImageJ so that each video started at diastole and comprised exactly two contractions. In MATLAB, fluorescent bead videos were used to calculate longitudinal (x-direction) and lateral (y-direction) displacement vectors, ux,n and uy,n, respectively, discretized to a grid with n field elements. The dimensions of each field element were 10.4 μm in the x-direction (Δx) and 10.4 μm in the y-direction (Δy). Displacement was calculated as the average magnitude of the three highest displacement vectors for the first and second contractions. Longitudinal (tx,n) and lateral (ty,n) traction stress vector fields were determined using Fourier transform traction cytometry, as described in previous publications.10,55 Longitudinal force vectors at each field element (fx,n) were calculated by multiplying the traction stress vectors (tx,n) at each field element n by the surface area of the field element (ΔxΔy):
| fx,n = tx,nΔxΔy | (1) |
| fy,n = ty,nΔxΔy | (2) |
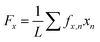 | (3) |
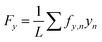 | (4) |
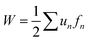 | (5) |
Statistical analysis
All measurements were tested for normality using the Lilliefors Test in MATLAB. Normally distributed data was analyzed using one-way, two-tailed ANOVA and Tukey's test for multiple comparisons in MATLAB with α = 0.05. Data that was not normally distributed was analyzed using a two-tailed Kruskal–Wallis test, and then Bonferroni's method to test multiple comparisons in MATLAB with α = 0.05. The statistical power was calculated using a post hoc F-test and the “ANOVA: fixed effects, omnibus, one-way” option on G*Power.56 The statistical test for each condition is noted in the figure legend, with additional analyses included in the Supplementary Tables (ESI†).Author contributions
N. R. A. designed and conducted all experiments, analyzed data, and wrote the manuscript. C. H. R., A. A. V., and A. P. P. assisted in data analysis. D. M. L., N. C., and A. P. P. assisted with the cell harvest. M. L. M. designed experiments and wrote the manuscript. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project was supported by the USC Viterbi School of Engineering, the American Heart Association Scientist Development Grant 16SDG29950005, The Saban Research Institute Team Science Grant, USC Women in Science and Engineering, and the USC Graduate School (Provost Fellowship to N. R. A. and N. C., Annenberg Fellowship to D. M. L., and Rose Hills Fellowship to A. P. P.). We acknowledge the W. M. Keck Foundation Photonics Center Cleanroom for photolithography equipment and facilities.References
- D. Mozaffarian, E. J. Benjamin, A. S. Go, D. K. Arnett, M. J. Blaha, M. Cushman, S. R. Das, S. de Ferranti, J. P. Després, H. J. Fullerton, V. J. Howard, M. D. Huffman, C. R. Isasi, M. C. Jiménez, S. E. Judd, B. M. Kissela, J. H. Lichtman, L. D. Lisabeth, S. Liu, R. H. Mackey, D. J. Magid, D. K. McGuire, E. R. Mohler, C. S. Moy, P. Muntner, M. E. Mussolino, K. Nasir, R. W. Neumar, G. Nichol, L. Palaniappan, D. K. Pandey, M. J. Reeves, C. J. Rodriguez, W. Rosamond, P. D. Sorlie, J. Stein, A. Towfighi, T. N. Turan, S. S. Virani, D. Woo, R. W. Yeh, M. B. Turner, W. G. Members, A. H. A. S. Committee and S. S. Subcommittee, Circulation, 2016, 133, e38–e360 CrossRef PubMed.
- N. Ferri, P. Siegl, A. Corsini, J. Herrmann, A. Lerman and R. Benghozi, Pharmacol. Ther., 2013, 138, 470–484 CrossRef CAS PubMed.
- M. L. McCain and K. K. Parker, Pfluegers Arch., 2011, 462, 89–104 CrossRef CAS PubMed.
- D. Fan, A. Takawale, J. Lee and Z. Kassiri, Fibrog. Tissue Repair, 2012, 5, 15 CrossRef CAS PubMed.
- K. E. Sullivan, K. P. Quinn, K. M. Tang, I. Georgakoudi and L. D. Black, Stem Cell Res. Ther., 2014, 5, 14 CrossRef PubMed.
- S. Jane-Lise, S. Corda, C. Chassagne and L. Rappaport, Heart Failure Rev., 2000, 5, 239–250 CrossRef CAS PubMed.
- V. G. Desai, E. H. Herman, C. L. Moland, W. S. Branham, S. M. Lewis, K. J. Davis, N. I. George, T. Lee, S. Kerr and J. C. Fuscoe, Toxicol. Appl. Pharmacol., 2013, 266, 109–121 CrossRef CAS PubMed.
- R. T. Dorr, K. A. Bozak, N. G. Shipp, M. Hendrix, D. S. Alberts and F. Ahmann, Cancer Res., 1988, 48, 5222–5227 CAS.
- V. Shirhatti, M. George, R. Chenery and G. Krishna, Toxicol. Appl. Pharmacol., 1986, 84, 173–191 CrossRef CAS PubMed.
- P. L. Kuo, H. Lee, M. A. Bray, N. A. Geisse, Y. T. Huang, W. J. Adams, S. P. Sheehy and K. K. Parker, Am. J. Pathol., 2012, 181, 2030–2037 CrossRef CAS PubMed.
- M. L. McCain, H. Lee, Y. Aratyn-Schaus, A. G. Kleber and K. K. Parker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9881–9886 CrossRef CAS PubMed.
- M. L. McCain, H. Yuan, F. S. Pasqualini, P. H. Campbell and K. K. Parker, Am. J. Physiol.: Heart Circ. Physiol., 2014, 306, H1525–H1539 CrossRef CAS PubMed.
- Y. Aratyn-Schaus, F. S. Pasqualini, H. Yuan, M. L. McCain, G. J. Ye, S. P. Sheehy, P. H. Campbell and K. K. Parker, J. Cell Biol., 2016, 212, 389–397 CrossRef CAS PubMed.
- A. Agarwal, J. A. Goss, A. Cho, M. L. McCain and K. K. Parker, Lab Chip, 2013, 13, 3599–3608 RSC.
- A. Grosberg, P. W. Alford, M. L. McCain and K. K. Parker, Lab Chip, 2011, 11, 4165–4173 RSC.
- G. Wang, M. L. McCain, L. Yang, A. He, F. S. Pasqualini, A. Agarwal, H. Yuan, D. Jiang, D. Zhang, L. Zangi, J. Geva, A. E. Roberts, Q. Ma, J. Ding, J. Chen, D. Z. Wang, K. Li, J. Wang, R. J. Wanders, W. Kulik, F. M. Vaz, M. A. Laflamme, C. E. Murry, K. R. Chien, R. I. Kelley, G. M. Church, K. K. Parker and W. T. Pu, Nat. Med., 2014, 20, 616–623 CrossRef CAS PubMed.
- M. L. McCain, A. Agarwal, H. W. Nesmith, A. P. Nesmith and K. K. Parker, Biomaterials, 2014, 35, 5462–5471 CrossRef CAS PubMed.
- P. W. Alford, A. W. Feinberg, S. P. Sheehy and K. K. Parker, Biomaterials, 2010, 31, 3613–3621 CrossRef CAS PubMed.
- A. W. Feinberg, P. W. Alford, H. Jin, C. M. Ripplinger, A. A. Werdich, S. P. Sheehy, A. Grosberg and K. K. Parker, Biomaterials, 2012, 33, 5732–5741 CrossRef CAS PubMed.
- W. Bian, C. P. Jackman and N. Bursac, Biofabrication, 2014, 6, 024109 CrossRef CAS PubMed.
- T. Boudou, W. R. Legant, A. Mu, M. A. Borochin, N. Thavandiran, M. Radisic, P. W. Zandstra, J. A. Epstein, K. B. Margulies and C. S. Chen, Tissue Eng., Part A, 2012, 18, 910–919 CrossRef CAS PubMed.
- M. F. Berry, A. J. Engler, Y. J. Woo, T. J. Pirolli, L. T. Bish, V. Jayasankar, K. J. Morine, T. J. Gardner, D. E. Discher and H. L. Sweeney, Am. J. Physiol.: Heart Circ. Physiol., 2006, 290, H2196–H2203 CrossRef CAS PubMed.
- P. Camelliti, T. K. Borg and P. Kohl, Cardiovasc. Res., 2005, 65, 40–51 CrossRef CAS PubMed.
- C. A. Walker and F. G. Spinale, J. Thorac. Cardiovasc. Surg., 1999, 118, 375–382 CrossRef CAS PubMed.
- A. Agarwal, Y. Farouz, A. P. Nesmith, L. F. Deravi, M. L. McCain and K. K. Parker, Adv. Funct. Mater., 2013, 23, 3738–3746 CrossRef CAS PubMed.
- M. L. McCain, S. P. Sheehy, A. Grosberg, J. A. Goss and K. K. Parker, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9770–9775 CrossRef CAS PubMed.
- W. Schramm, J. Clin. Monit. Comput., 2010, 24, 213–217 CrossRef PubMed.
- A. W. Feinberg, P. W. Alford, H. Jin, C. M. Ripplinger, A. A. Werdich, S. P. Sheehy, A. Grosberg and K. K. Parker, Biomaterials, 2012, 33, 5732–5741 CrossRef CAS PubMed.
- M. B. Knight, N. K. Drew, L. A. McCarthy and A. Grosberg, Biophys. J., 2016, 110, 1615–1624 CrossRef CAS PubMed.
- T. Matsushita, M. Oyamada, K. Fujimoto, Y. Yasuda, S. Masuda, Y. Wada, T. Oka and T. Takamatsu, Circ. Res., 1999, 85, 1046–1055 CrossRef CAS PubMed.
- B. R. Desroches, P. Zhang, B. R. Choi, M. E. King, A. E. Maldonado, W. Li, A. Rago, G. Liu, N. Nath, K. M. Hartmann, B. Yang, G. Koren, J. R. Morgan and U. Mende, Am. J. Physiol.: Heart Circ. Physiol., 2012, 302, H2031–H2042 CrossRef CAS PubMed.
- H. Saini, A. Navaei, A. Van Putten and M. Nikkhah, Adv. Healthcare Mater., 2015, 4, 1961–1971 CrossRef CAS PubMed.
- G. Gaudesius, M. Miragoli, S. P. Thomas and S. Rohr, Circ. Res., 2003, 93, 421–428 CrossRef CAS PubMed.
- P. Kohl and R. G. Gourdie, J. Mol. Cell. Cardiol., 2014, 70C, 37–46 CrossRef PubMed.
- P. W. Burridge, E. Matsa, P. Shukla, Z. C. Lin, J. M. Churko, A. D. Ebert, F. Lan, S. Diecke, B. Huber, N. M. Mordwinkin, J. R. Plews, O. J. Abilez, B. Cui, J. D. Gold and J. C. Wu, Nat. Methods, 2014, 11, 855–860 CrossRef CAS PubMed.
- X. Lian, J. Zhang, S. M. Azarin, K. Zhu, L. B. Hazeltine, X. Bao, C. Hsiao, T. J. Kamp and S. P. Palecek, Nat. Protoc., 2013, 8, 162–175 CrossRef CAS PubMed.
- I. C. Parrag, P. W. Zandstra and K. A. Woodhouse, Biotechnol. Bioeng., 2012, 109, 813–822 CrossRef CAS PubMed.
- K. Pfannkuche, S. Neuss, F. Pillekamp, L. P. Frenzel, W. Attia, T. Hannes, J. Salber, M. Hoss, M. Zenke, B. K. Fleischmann, J. Hescheler and T. Saric, Stem Cells Dev., 2010, 19, 1589–1599 CrossRef CAS PubMed.
- J. Xi, M. Khalil, D. Spitkovsky, T. Hannes, K. Pfannkuche, W. Bloch, T. Saric, K. Brockmeier, J. Hescheler and F. Pillekamp, Stem Cells Dev., 2011, 20, 821–830 CrossRef PubMed.
- V. Maruthamuthu, B. Sabass, U. S. Schwarz and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4708–4713 CrossRef CAS PubMed.
- M. Rienks, A. P. Papageorgiou, N. G. Frangogiannis and S. Heymans, Circ. Res., 2014, 114, 872–888 CrossRef CAS PubMed.
- R. S. Ross and T. K. Borg, Circ. Res., 2001, 88, 1112–1119 CrossRef CAS PubMed.
- P. Oliviero, C. Chassagne, N. Salichon, A. Corbier, G. Hamon, F. Marotte, D. Charlemagne, L. Rappaport and J. L. Samuel, Cardiovasc. Res., 2000, 46, 346–355 CrossRef CAS PubMed.
- J. L. Samuel, A. Barrieux, S. Dufour, I. Dubus, F. Contard, V. Koteliansky, F. Farhadian, F. Marotte, J. P. Thiery and L. Rappaport, J. Clin. Invest., 1991, 88, 1737–1746 CrossRef CAS PubMed.
- M. M. Ulrich, A. M. Janssen, M. J. Daemen, L. Rappaport, J. L. Samuel, F. Contard, J. F. Smits and J. P. Cleutjens, J. Mol. Cell. Cardiol., 1997, 29, 2533–2543 CrossRef CAS PubMed.
- G. P. Aurigemma, M. R. Zile and W. H. Gaasch, Circulation, 2006, 113, 296–304 CrossRef PubMed.
- A. J. Engler, C. Carag-Krieger, C. P. Johnson, M. Raab, H. Y. Tang, D. W. Speicher, J. W. Sanger, J. M. Sanger and D. E. Discher, J. Cell Sci., 2008, 121, 3794–3802 CrossRef CAS PubMed.
- S. Majkut, T. Idema, J. Swift, C. Krieger, A. Liu and D. E. Discher, Curr. Biol., 2013, 23, 2434–2439 CrossRef CAS PubMed.
- S. N. Bhatia and D. E. Ingber, Nat. Biotechnol., 2014, 32, 760–772 CrossRef CAS PubMed.
- J. T. Hinson, A. Chopra, N. Nafissi, W. J. Polacheck, C. C. Benson, S. Swist, J. Gorham, L. Yang, S. Schafer, C. C. Sheng, A. Haghighi, J. Homsy, N. Hubner, G. Church, S. A. Cook, W. A. Linke, C. S. Chen, J. G. Seidman and C. E. Seidman, Science, 2015, 349, 982–986 CrossRef CAS PubMed.
- C. S. Young, M. R. Hicks, N. V. Ermolova, H. Nakano, M. Jan, S. Younesi, S. Karumbayaram, C. Kumagai-Cresse, D. Wang, J. A. Zack, D. B. Kohn, A. Nakano, S. F. Nelson, M. C. Miceli, M. J. Spencer and A. D. Pyle, Cell stem cell, 2016, 18, 533–540 CrossRef CAS PubMed.
- M. Durbeej, Curr. Top. Membr., 2015, 76, 31–60 Search PubMed.
- G. Wang, M. L. McCain, L. Yang, A. He, F. S. Pasqualini, A. Agarwal, H. Yuan, D. Jiang, D. Zhang, L. Zangi, J. Geva, A. E. Roberts, Q. Ma, J. Ding, J. Chen, D. Z. Wang, K. Li, J. Wang, R. J. Wanders, W. Kulik, F. M. Vaz, M. A. Laflamme, C. E. Murry, K. R. Chien, R. I. Kelley, G. M. Church, K. K. Parker and W. T. Pu, Nat. Med., 2014, 20, 616–623 CrossRef CAS PubMed.
- D. Qin, Y. Xia and G. M. Whitesides, Nat. Protoc., 2010, 5, 491–502 CrossRef CAS PubMed.
- J. P. Butler, I. M. Tolic-Norrelykke, B. Fabry and J. J. Fredberg, Am. J. Physiol.: Cell Physiol., 2002, 282, C595–C605 CrossRef CAS PubMed.
- F. Faul, E. Erdfelder, A. G. Lang and A. Buchner, Behav. Res. Methods, 2007, 39, 175–191 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ib00081b |
| This journal is © The Royal Society of Chemistry 2017 |