A new selective route towards benzoic acid and derivatives from biomass-derived coumalic acid†
Abstract
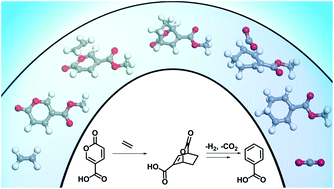
The selective production of aromatics from bio-based sources is an area of interest to expand the potential for greener alternatives to petroleum-derived chemicals. A scalable, efficient route to produce bio-based benzoates is demonstrated by carrying out heterogeneous catalytic reactions in non-toxic bio-based solvents at 180 °C obtaining yields of up to 100 mol%. This approach extends the 2-pyrone (coumalic acid/methyl coumalate) Diels–Alder platform by utilizing a bioavailable co-reactant ethylene. A detailed investigation using a combination of kinetic experiments, DFT calculations, and multi-dimensional NMR was carried out to determine the detailed reaction network, and the corresponding activation energies for critical steps. Additionally, a series of experiments were conducted to maximize the yields by comparing different solvents, for both coumalic acid and methyl coumalate. Our results show that the choice of solvent was a significant factor when coumalic acid was the reactant (yields 71–92 mol%), while methyl coumalate was only minimally affected by the solvent (yields 95–100 mol%). Interestingly, the reaction network and kinetic analysis showed that the Diels–Alder reactions were not significantly different between coumalic acid and methyl coumalate, with the rate limiting step for both being decarboxylation with an activation barrier of 141 kJ mol−1 compared to 77 kJ mol−1 for the formation of the bicyclic adduct. Finally, the reaction cascade was found to be highly susceptible to by-product formation when as little as 5 vol% water was present in the solvent, which demonstrates that the absence of water is essential for high yielding benzoate production.
- This article is part of the themed collection: 2017 Green Chemistry Hot Articles


 Please wait while we load your content...
Please wait while we load your content...