Probing the interplay between geometric and electronic structure in a two-dimensional K–TCNQ charge transfer network

Abstract

Scanning tunnelling microscopy (STM), low energy electron diffraction (LEED), ultraviolet and soft X-ray photoelectron spectroscopy (UPS and SXPS) have been used to characterise the formation of a coadsorption phase of TCNQ and K on Ag(111), while the normal incident X-ray standing waves (NIXSW) technique has been used to obtain quantitative structural information. STM and LEED show that an ordered incommensurate phase is formed in which the K atoms are surrounded by four TCNQ molecules in a ‘windmill’ motif, characteristic of other metal/TCNQ phases, in which the nominal TCNQ : K stoichiometry is 1 : 1. UPS and SXPS data indicate the TCNQ is in a negatively-charged state. NIXSW results show that the carbon core of the TCNQ is essentially planar at a height above the Ag(111) surface closely similar to that found without coadsorbed K. In the presence of TCNQ the height of the K ions above the surface is significantly larger than on clean Ag(111), and the ions occupy sites above ‘holes’ in the TCNQ network. NIXSW data also show that the N atoms in the molecules must occupy sites with at least two different heights above the surface, which can be reconciled by a tilt or twist of the TCNQ molecules, broadly similar to the geometry that occurs in bulk TCNQ/K crystals.

---

Introduction

The use of thin molecular films in organic electronic devices (OEDs) has attracted a significant amount of interest in recent years, offering a low-cost, transparent, flexible and light-weight alternative to typical inorganic semiconductor devices.^1,2 Although these devices have already seen some commercial success, further optimisation is required to meet the demands of current electronic applications. The performance of OEDs is highly dependent on the interfacial energy-level alignment, particularly between the metallic electrodes and the active organic material, as this defines the height of the barrier for the transport of charge carriers.^3,4 Consequently, the overall efficiency of a device can be improved by optimising the energy-level alignment across this metal–organic interface. One common approach to achieve this is to add interfacial layers designed to tune the local electrostatic dipole and thus the relative energy of the frontier molecular orbitals with respect to the electrode Fermi level. In the case of organic photovoltaic devices, ultra-thin films of materials with high electron affinity can be used as a hole-extraction layer to raise the work function of the metal electrode and reduce the barrier for charge transport across the metal–organic interface.^5–8 This hole-extraction layer should be as thin as possible, as a thicker layer may itself hinder charge transfer across the interface, and ideally would also allow the work function shift to be tuned to allow the hole-extraction layer to be optimised for the particular electrode and active material in the device.⁵ Recently, charge-transfer networks, consisting of small molecular electron acceptors and donors, have also been identified as promising candidates for use as hole-extraction layers.^9–12 These charge-transfer networks offer the advantage of tuneable electronic properties through synthetic chemical modification of the electron donors and acceptors.^11,12 Furthermore, such charge-transfer networks form ordered layers through supramolecular self-assembly, which is an effective method for fabricating nanoscale structures.¹³ It has also been suggested that through this approach, tuneable hole-extraction layers that have a thickness of only a single molecular layer (thus minimising the hindrance on charge carrier transport across the interface) could be a realistic possibility.¹² One example of this is the two-dimensional (2D) networks that are formed between the strong electron acceptor molecule tetracyanoquinodimethane (TCNQ) and alkali metals.^11,12

Scanning tunnelling microscopy (STM) studies show that TCNQ molecules co-adsorbed with alkali metals assemble into stable and well-defined metal–organic structures. Structures observed for Cs–TCNQ networks on Ag(100)¹¹ and for Li–TCNQ and Na–TCNQ networks on Au(111)^14,15 are all characterised by a common ‘windmill’ motif in which a central alkali metal ion is bound to four TCNQ molecules. Density functional theory (DFT) calculations performed for the Cs–TCNQ/Ag(100) system indicate that the alkali metal ions play a dual role, both directing the self-assembly of the molecules through ionic bonding and having a significant impact on the electronic properties of the surface.^11,12 The high electron affinity of TCNQ molecules means that they become charged on metallic substrates, and the combination of the charged molecules and their image charges in the metallic substrate creates relatively strong dipole moments perpendicular to the surface. The mutual repulsion of these dipoles might be expected to suppress self-assembly, but the addition of metallic adatoms^16–18 – in particular alkali adatoms^11,14,15 – produces strong dipoles of opposite polarity, stabilising the metal–organic networks, and also reducing the work function increase caused by the negatively charged TCNQ molecules in isolation. One surprising feature of the network structure predicted by DFT calculations is that despite the alkali ions occupying ‘pores’ or ‘holes’ in the molecular assembly that are large enough to comfortably accommodate them in a coplanar bonding arrangement, they occupy sites above the molecular plane.¹² This effect has been rationalised as being due to the larger positive dipole moment that arises from the increased height of the alkali metal ion above the surface, which stabilises the negative molecular dipoles more effectively.¹² The DFT calculations therefore predict a rather interesting result indicating a close relationship between the height of the alkali metal ion above the substrate, and the electronic properties of the surface.

So far there have been no experimental quantitative structural studies of this phenomenon, although our recent structural investigation of TCNQ on Ag(111) has shown clear evidence for the stabilising effect of Ag adatoms in the molecular self-assembly.¹⁹ Here, we report on a significant extension of this work to investigate the structure formed by coadsorption of TCNQ and potassium (K) on Ag(111), using a combination of techniques to probe the interplay between the adsorption structure and the electronic properties of the surface. STM and low energy electron diffraction (LEED) were used to determine the molecular ordering, to obtain precise surface unit mesh dimensions and to ascertain whether the molecular overlayer is commensurate with respect to the underlying substrate. Soft X-ray and ultraviolet photoelectron spectroscopy (SXPS, UPS) provided complementary information on the composition and chemical and electronic properties of the surface. Most significantly, we have also used the normal incident X-ray standing wave technique (NIXSW), to obtain quantitative structural information, and specifically to determine the height of the constituent atoms within the alkali-molecule network above the underlying surface.

Methods

All characterisation experiments in this work were conducted at room-temperature under ultra-high vacuum (UHV) conditions. STM measurements were performed in an UHV system at the University of Warwick and NIXSW, SXPS and UPS experiments were performed in the UHV end-station installed on beamline I09 of the Diamond Light Source storage ring. This beamline is equipped with both a crystal monochromator to provide the ‘hard’ X-rays needed to perform the NIXSW experiments and a grazing incidence plane grating monochromator providing soft X-rays to perform high-resolution SXPS. LEED patterns were recorded both at Warwick and at Diamond, providing a cross-reference for the preparation of comparable samples in both UHV chambers. Low current LEED optics were used in both UHV systems (Warwick: Omicron SPECTALEED, I09: OCI BDL800IR-MCP LEED) to avoid beam damage to the molecular overlayer. LEED pattern simulations were obtained using LEEDpat software.²⁰ A single crystal Ag(111) substrate (cutting precision of 0.1°) was prepared in situ using cycles of sputtering with 1 keV Ar⁺ ions for 30 minutes followed by annealing to ∼500 °C for another 30 minutes. The sample temperature was measured indirectly by a thermocouple in contact with the sample plate onto which the crystal was mounted. STM images were recorded at ambient temperature in constant current mode using electrochemically etched polycrystalline tungsten tips. All STM images were plane corrected and flattened using the open source image-processing software Gwyddion.²¹

The NIXSW technique^22,23 exploits the X-ray standing wave formed by the interference of incident and scattered X-rays at a Bragg condition. The strong backscattering out of the crystal leads to a finite extinction length of the X-rays and consequently to the strong reflectivity existing in a finite range of incident X-ray energies. Within this range the standing wave, which has a periodicity in intensity equal to that of the scattering planes, shifts in phase relative to the scattering planes in a systematic fashion. Monitoring the X-ray absorption at atoms immersed in the standing wave (within or above the crystal) through this photon energy range thus provides a profile characteristic of the height of the absorbing atoms above the scattering planes. In the present case, X-ray absorption at the C and N atoms of TCNQ, as well as the co-adsorbed K atoms, was monitored, whilst sweeping the photon energy through the (111) Bragg condition at near-normal incidence to the surface, by measuring the intensity of the C 1s, N 1s and K 2p photoelectron spectra collected using a VG Scienta EW4000 HAXPES hemispherical electron analyser (angular acceptance range ± 30°) mounted at 90° to the incident photon beam. The NIXSW absorption profiles were corrected for non-dipolar effects in the angular distribution of the photoemission, values for the backward-forward asymmetry parameter Q (ref. 24) were obtained from theory-based computations of the angular distribution parameters.²⁵ UP spectra were recorded using a monochromated He-I_α source (hν = 21.23 eV), work functions were determined using a sample bias of −8.00 V in order to measure the secondary electron cut-off.

TCNQ powder (98% pure; Sigma Aldrich) was triply purified by thermal gradient sublimation and thoroughly degassed before being deposited onto the Ag(111) substrate from an organic molecular beam deposition source at an operating temperature of 400 K. K was deposited via resistive heating of an SAES alkali metal dispenser using a current of 6.3 A. The K–TCNQ networks were prepared in situ by first depositing a nominally saturated single layer (defined here as ∼1 monolayer (ML)) of TCNQ onto Ag(111) and post annealing the substrate to 550 K to yield a sub-monolayer adsorption phase.¹⁹ K was then deposited onto this layer before annealing the sample to 470 K.

Results

STM, LEED and photoemission characterisation

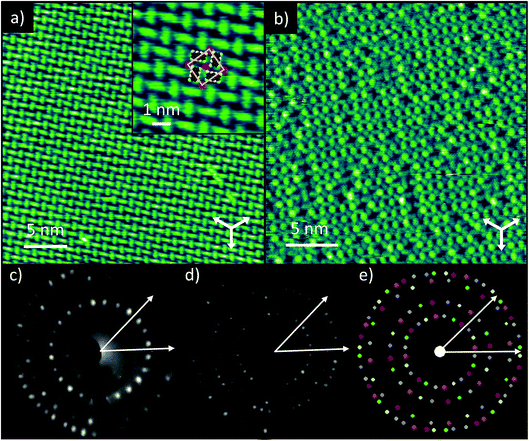
STM of TCNQ co-deposited with K on Ag(111) shows the formation of large ordered domains, with bright, oblong protrusions identified as TCNQ molecules (Fig. 1a). The molecules assemble into windmill-like structures, consisting of four TCNQ molecules spiralling around a central point. This ‘windmill’ motif is common for TCNQ on surfaces and is usually brought about by the presence of metal adatoms, either from the underlying substrate¹⁹ or co-deposited along with the molecules.^{11,14,15,17,18} This packing also bears a strong resemblance to the bulk crystal structure of K–TCNQ in which layers of TCNQ molecules arrange in similar four-fold coordinated windmill structures in layers on either side of a plane of K⁺ ions (see ESI, Fig. S1†).²⁶ This suggests that on Ag(111) the TCNQ molecules form two-dimensional networks with the codeposited K atoms via ionic interactions with their cyano groups. This possibility is supported by STM images taken at larger negative voltage biases which show bright circular protrusions at the centre of the windmills; these we interpret as the locations of the K atoms (Fig. 1b). This interpretation is consistent with that of previous STM studies of Na–TCNQ networks on Au(111)¹⁵ and Cs–TCNQ networks on Ag(100),¹¹ which show similar bright protrusions. The K–TCNQ coadsorption phase is described by a unit mesh containing two TCNQ molecules and two alkali metal atoms with vectors of length a = (13.7 ± 0.4) Å and b = (13.0 ± 0.4) Å, having an included angle of (88 ± 2)°; the vector a is offset by (9 ± 2)° from the substrate 〈110〉 directions. Fig. 1e shows the simulated LEED pattern obtained using this unit mesh (fine-tuned within the error ranges of the STM measurements). As the overlayer mesh does not share the three-fold rotational and 〈211〉 mirror symmetries of the substrate there are 6 symmetrically equivalent domains of the overlayer, and the simulated pattern shows the beams from each domain in a different colour. The experimental LEED patterns (Fig. 1c and d) are in excellent agreement with the simulated pattern, confirming, by a technique not susceptible to instrumental drift or calibration errors, the accuracy of the STM-derived unit mesh. The LEED patterns also indicate that this overlayer phase is incommensurate with respect to the substrate as simulations of the closest commensurate structure yield a distinctly different simulated LEED pattern (see ESI, Fig. S2†).

Fig. 1 TCNQ co-deposited with K on Ag(111). (a) Representative STM image showing an ordered domain of TCNQ molecules arranged into windmill-like structures (V_samp = 0.1 V, I = 175 pA, white arrows indicate the substrate 〈110〉 directions). Inset: expanded region of the image with superimposed scaled molecular models and K atoms and the overlayer unit mesh indicated. (b) STM image showing alternative contrast with bright protrusions, interpreted to be K atoms, visible between the TCNQ molecules (V_samp = −1.5 V, I = 300 pA, white arrows indicate the substrate 〈110〉 directions). (c) LEED pattern recorded at a kinetic energy of 14.5 eV with two substrate 〈211〉 directions shown as white arrows. (d) LEED pattern recorded at a kinetic energy of 23.5 eV with two substrate 〈211〉 directions shown as white arrows. (e) Simulated LEED pattern derived from the STM measured unit mesh with beams originating from the six distinct domains coloured separately and two substrate 〈211〉 directions shown as white arrows.

The STM images indicate that the ordered phase can accommodate one K atom per TCNQ molecule, but the images recorded at larger bias voltages appear to show that there is a significant concentration of K atom vacancies. Stoichiometry estimates based on the measured K 2p and C 1s photoemission intensities (corrected for the difference in photoemission cross-sections) also indicate that there were fewer K atoms than TCNQ molecules on the samples measured with NIXSW. STM images showed the same ordering when the surface was prepared using a lower K exposure, albeit with an increased concentration of vacancies (see ESI, Fig. S3†), which indicates that this ordered phase of TCNQ, which can accommodate up to 1 K per TCNQ molecule, is favourable for a range of K : TCNQ stoichiometric ratios. Similar structures have been reported for Na–TCNQ and Li–TCNQ networks on Au(111)^14,15 although on the Ag(100) surface, Cs–TCNQ networks with a smaller stoichiometric ratio of 1 : 4, are found to form.¹¹

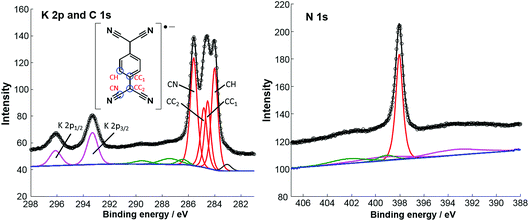
Fig. 2 shows high-resolution SXP spectra recorded from the ordered surface phase. The C 1s spectrum clearly shows at least three distinct peaks, which have been fitted with four components (Table 1), corresponding to the four chemically inequivalent C species in TCNQ (see the inset of the K 2p and C 1s spectrum). In previous reports, C 1s XPS has been used to deduce the charge state of TCNQ, with the relative binding energies and overall lineshape of the spectrum being characteristically different when TCNQ is negatively charged compared to when it is neutral.^14,27 Based on this interpretation it has previously been shown that TCNQ accepts electrons from the Ag(111) substrate, becoming negatively charged.^14,19 This is reinforced by UPS work function measurements, measured both here and in a previous study,¹⁴ that show an increase of 0.4 eV when TCNQ is deposited on clean Ag(111) (data not shown). This is consistent with the molecules being negatively charged; a neutral molecule would be expected to decrease the work function via the ‘push-back’ effect.³ Here, upon the addition of K, the overall line shape of the C 1s spectrum remains the same, albeit with a small shift of ∼0.2 eV in the binding energies compared to TCNQ alone,¹⁹ indicating that the TCNQ molecules retain their negative charge. The value of the N 1s binding energy of 398.1 eV is also in good agreement with other systems in which TCNQ is believed to be negatively charged.^14,27,28 The K 2p SXPS shows binding energies of 293.3 eV and 296.1 eV for the K 2p_3/2 and K 2p_1/2 components respectively, which are consistent with typical binding energies for K⁺ in ionic systems.²⁹ This is a negative shift of 1.2 eV from K deposited alone on Ag(111) which gives binding energies of 294.5 eV and 297.3 eV for these two components and is more consistent with the binding energies of elemental K.³⁰ These values can be reconciled with the charge state of K, DFT calculations predicting a relatively small charge of 0.16–0.24e for K on Ag(111)³¹ whereas for K–TCNQ networks on Ag(100), similar to those presented here, the alkali metal is predicted to completely donate its valence electron.¹² The implication is that K interacts ionically in the networks with TCNQ on the Ag(111) surface. The measured work function of the surface shows a 0.5 eV decrease from that of TCNQ/Ag(111) with a net 0.1 eV decrease relative to clean Ag(111) (data not shown). This is consistent with K becoming positively charged on the surface and also illustrates how the addition of an alkali metal can be used to tune the surface work function.

Table 1 XPS measured binding energies of the main C 1s, N 1s and K 2p peaks

Component	CH	CC1	CC2	CN	K 2p3/2	K 2p1/2	N
Binding energy/eV	284.0	284.5	284.8	285.6	293.3	296.1	398.1

---

Fig. 2 Soft X-ray photoelectron spectra of the K–TCNQ windmill phase on Ag(111). The K 2p/C 1s spectrum was recorded with a photon energy of 435 eV, with measured intensity (black circles) and the sum of fitted components (black line) comprising a background (blue), four main C 1s components (red), shakeup features (green), a beam damage feature (grey) and a single split K 2p component (magenta). The N 1s spectrum was recorded with a photon energy of 550 eV, with measured intensity (black circles), and the sum of fitted components (black line) comprising of a linear background (blue), one main component (red), two N shakeup features (green) and two Ag 3d plasmon features (magenta).

NIXSW and structural models

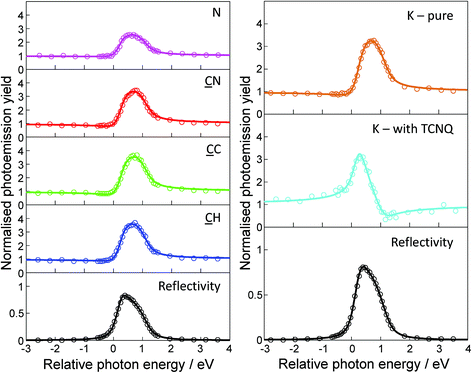
As described in the Methods section, the NIXSW technique offers the ability to determine the height of X-ray absorbing atoms above the scattering planes of the chosen Bragg reflection. So, by using normal incidence to the surface, the (111) scattering planes are parallel to the surface, and the measured height is relative to the outermost atomic layer of the surface providing that there is no significant relaxation of the outermost substrate layers. For the specific case of fcc(111) surfaces these surface relaxations are known to be extremely small (<∼0.02 Å) at the clean surface, while such relaxations of all surfaces are generally reduced in the presence of adsorbates. By using core level photoemission to monitor the absorption we can not only identify the atomic species of the absorber through its photoelectron binding energy, but also distinguish absorption at atoms of the same elemental species in chemically distinct sites through the chemical shifts in these binding energies.

Measured NIXSW absorption profiles can be uniquely fitted by two structural parameters known as the coherent position, P, and the coherent fraction, f (Fig. 3). If the absorbing atoms occupy a single well-defined site, the value of P is a direct measure of the atom’s height relative to the nearest bulk-extended scattering plane (in units of the interplanar spacing). In this simple case, f is essentially an order parameter which is equal to unity in a system with perfect static and dynamic order, although in practice values of ≥0.80 are typical for absorbers occupying a single site. However, the interpretation of NIXSW results becomes significantly more complex when the value of f is much lower, as this can generally not be attributed to disorder and almost certainly indicates that the atomic species occupies two or more distinctly different heights. For example, in the extreme case of two sites that are equally occupied and separated by exactly half of the scattering plane spacing, the value of f is zero, and the measured P is meaningless, despite the system being highly ordered. This effect proves to be important in interpreting aspects of the data from the present system.

Fig. 3 Sample set of NIXSW photoemission yield curves obtained using the [111] reflection for C, N, and K in the K–TCNQ coadsorption phase, in addition to pure K on Ag(111). Photon energies are quoted relative to the Bragg energy of 2.630 keV. Least square fits (solid lines) to the photoemission yields (circles) were obtained to extract the coherent fractions and coherent positions.

Table 2 shows the results of NIXSW measurements recorded for the K–TCNQ coadsorption phase, for pure K on Ag(111), and for the pure TCNQ phase measured by us on Ag(111).¹⁹ The values of P have been converted to layer spacings in Å units, shown as D₍₁₁₁₎, adding one bulk layer spacing where appropriate to ensure one has physically plausible interatomic distances. The reported values of the coherent fractions have been adjusted to account for non-linearity in the electron analyser (as described in detail in the ESI†). For the K–TCNQ network, the NIXSW at all three chemically-distinct C atoms yields high coherent fractions (>0.8), indicating that the molecules occupy a single well-defined height above the surface. The corresponding coherent positions show the molecules adopt a relatively flat conformation ∼2.8 Å above the surface, with the peripheral nitrile C atoms only slightly lower (<0.1 Å) than the central C ring. In contrast to this, the N NIXSW yields a low coherent fraction of 0.37, clearly indicating that the N atoms must occupy two or more different heights above the surface. In this case the N coherent position of 2.79 Å, which is a weighted average of the different contributing heights, is almost identical to the height of the C atoms. This indicates that the two or more different N atom heights must be distributed relatively evenly about the height of the carbon backbone of the molecule. The C and N NIXSW measurements for the K–TCNQ networks therefore show very similar behaviour to that of TCNQ deposited alone on the Ag(111) surface, with the coherent positions and fractions of the two systems being closely related. For TCNQ on Ag(111) without coadsorbed K, the results of our combined DFT and NIXSW study show that the low N coherent fraction can be rationalised by the inclusion of Ag adatoms within the molecular adsorption structure; this results in some N atoms bonding to nearby adatoms, leading to their associated CN bonds pointing up out of the surface, whereas the other N atoms – located further from the Ag adatoms – bond to the underlying surface Ag atoms, causing their associated CN bonds to point down towards the substrate.¹⁹ This creates two different N heights and results in a reduction in the N coherent fraction.

Table 2 NIXSW fitting parameters for the K–TCNQ phase, TCNQ on Ag(111)¹⁹ and K on Ag(111). Separate fitting parameters were obtained for the different C 1s photoemission components as defined in Fig. 2 (due to lower resolution at the photon energies required for NIXSW, components CC₁ and CC₂ were fitted together in a single component here). The coherent position D₍₁₁₁₎ is given as D₍₁₁₁₎ = (P + 1)d₁₁₁ where P is the fractional coherent position and d₁₁₁ is the spacing of the [111] lattice planes (2.359 Å)

	K–TCNQ		TCNQ only^19		K only
	f	D (111)/Å	f	D (111)/Å	f	D (111)/Å
K	0.71(8)	3.56(3)	—	—	0.74(8)	2.81(1)
CH	0.90(10)	2.85(1)	0.86(9)	2.86(2)	—	—
CC	0.90(10)	2.79(1)	0.89(10)	2.78(2)	—	—
CN	0.82(9)	2.79(1)	0.80(9)	2.76(2)	—	—
N	0.37(4)	2.79(5)	0.35(4)	2.75(3)	—	—

---

In the case of the K–TCNQ network, the closely similar N NIXSW parameters are more difficult to rationalise. The windmill structure of four TCNQ molecules coordinated to a single K ion is somewhat similar to the structure formed by TCNQ molecules and Ag adatoms in the absence of adsorbed K, but the 1 : 1 K to TCNQ stoichiometry of the K–TCNQ network means that every CN group should be in close proximity to a K ion. One might therefore expect that all of the N atoms would bond to K ions in a similar way and thus that all the N atoms would have the same height above the surface. One possible solution to this dilemma may lie in the fact that the STM images (Fig. 1b) indicate that there is a significant concentration of K vacancies, at which N atoms would only be able to bond to the lower Ag atoms of the substrate. However, an estimate of the concentration of these vacancies in the NIXSW experiments can be obtained from the relative intensities of the XPS peaks from the K atoms and the TCNQ atomic components, which indicate a K vacancy concentration of ∼20%. In this case, even if the height difference of the N atoms at the vacancies and the K bonding sites was exactly half the spacing of the [111] planes (i.e. a height difference of 1.18 Å), the coherent fraction would only be reduced to 0.6. A smaller or larger height difference would lead to an even higher coherent fraction. The presence of these vacancies is thus insufficient to account for the much lower measured N coherent fraction. We return to this problem below.

The coherent fractions for the K atoms, both alone and coadsorbed with TCNQ, are high, indicating that they occupy a single well-defined height above the surface in each phase. In the absence of TCNQ, the coherent position of the K atoms corresponds to a height of 2.81 Å above the surface, in excellent agreement with the results of a previous quantitative LEED structure determination of K on Ag(111).³² In the K–TCNQ networks, the K ions occupy sites significantly higher (3.56 Å) above the surface. Presumably this greater height is because the K ions are lying on top of the molecular layer rather than interacting directly with the underlying Ag substrate, and indeed they lie 0.77 Å above the C backbone of the molecules. This qualitative conclusion is consistent with the findings of an earlier DFT study of TCNQ/alkali coadsorption phases on the Ag(100) surface.¹² As remarked in the introduction, on the (100) surface the alkali ions are expected to occupy sites significantly above the ‘holes’ in the TCNQ network,¹² despite the fact that simple consideration of atoms sizes would indicate that they could ‘fall through’ these holes to bond directly to the substrate. For the present coadsorption system on Ag(111), in which the pores in the molecular layer are smaller than those calculated on the Ag(100) surface, it is interesting to establish if the height of the K ions may be reconcilable with simple considerations of the expected N–K interaction distance.

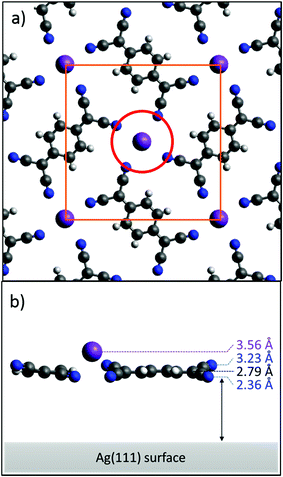
Fig. 4a shows a model of the K–TCNQ phase on Ag(111) that is consistent with the STM and LEED results. The molecules in this model are assumed to lie flat and coplanar, consistent with the NIXSW results for the C atoms. Here the K ions lie above a pore in the molecular layer that is 5.23 Å in diameter (red circle in Fig. 4a). The bulk crystal structure of K–TCNQ has K–N interatomic distances of 2.93 Å,²⁶ which corresponds almost exactly to the sum of the K⁺ ionic radius (1.37 Å)³³ and the N van der Waals radius (1.55 Å).³⁴ If the same interatomic distance occurs in an adsorbed K–TCNQ monolayer, a pore with a diameter of 5.84 Å or larger would be required to accommodate the K ion in a site coplanar with the molecules. As the pore size in the K–TCNQ coadsorption phase (5.23 Å) is smaller than this, the K ions occupying this pore site should lie 1.30 Å above the molecules, a value significantly greater than the measured height difference of 0.77 Å. However, this simple model assumes that all of the N atoms are at the same height above the surface, which is inconsistent with the measured low N coherent fraction of 0.37. If this low coherent fraction is attributed to the influence of two equally occupied N sites at different heights – the simplest multi-site model – a height difference of 0.87 Å is required to reduce the coherent fraction from 0.89, the largest possible value expected for an absorbing atom when accounting for vibrations, to the observed value of 0.37. In this model the measured N coherent position (2.79 Å) corresponds to the average height of the two sites, so half of the N atoms must have a height of 2.36 Å whereas the others are 3.23 Å above the surface. The high coherent fraction of the K ions rules out the possibility of multiple K adsorption heights, excluding for example the possibility of two different fourfold coordination sites surrounded by ‘all-up’ or ‘all-down’ N atoms. Instead, both N heights must be present surrounding each K site. In this situation, there are two possibilities: either pairs of N atoms opposite each other around the K coordination site have the same height, or adjacent pairs of N atoms around this site have the same height. In the former case the height of the upper pairs of N atoms determines the height of the K ions, which would be forced up to 4.53 Å, much higher than the experimentally measured value. By contrast, if adjacent pairs of N atoms surrounding the K atoms have different heights, the K ions could lie closer to the surface. While not strictly necessary, this type of N height pairing would be satisfied if the TCNQ molecules were tilted with respect to the surface by rotation about the long molecular axis; this phenomenon has been reported for other small, nominally planar, molecules on metal surfaces.^35–37 Interestingly, in the bulk crystal structure of K–TCNQ (in which TCNQ arranges into similar windmill structures around out of plane K⁺ ions – see Fig. S1†), the molecules are tilted about the long molecular axis in just this fashion, with a tilt angle of between 8.9–15.8° depending on whether the crystal is in its high or low temperature structural phase.²⁶ A height difference for the two inequivalent N sites of 0.87 Å on the surface (the maximum value estimated above to be required to match the measured coherent fraction on Ag(111)) would require a tilt of 11.5°. This tilt would also lower the predicted coherent fractions of the C atoms in the molecule, but to a lesser extent, with expected values of 0.71, 0.89 and 0.71 for the CH, CC and CN coherent fractions, respectively. The experimental values for CC and CN are consistent with this model, but the measured coherent fraction for the CH component is significantly higher than predicted for this model, indicating that the central carbon ring does lie more closely parallel to the surface. A solution to this inconsistency is provided if the peripheral CN groups are twisted with respect to the central ring, rather than the full planar molecule being tilted. This twist model is depicted in Fig. 4b. Other studies have found that TCNQ can lose its planarity upon becoming negatively charged, leading to the peripheral C atoms becoming sp³ hybridised and the central ring aromatising.^18,38–40 This gives the molecule improved flexibility and allows TCNQ to bend and distort from a planar geometry, so such a twist in the molecule is certainly plausible. It should be noted, however, that whilst the twist model can satisfy all of the experimental results, other factors, such as the influence of K vacancies described above, may also contribute to the low coherent fraction of N; the actual difference in height of the inequivalent N atoms surrounding occupied K sites that is required to account for the low coherent fraction may therefore be lower than the suggested 0.87 Å, thereby reducing the required twist or tilt angle.

Fig. 4 (a) Top view of the K–TCNQ adsorbed phase. The orange square depicts the unit mesh with sides 13.4 Å in length. The red circle cuts through the centre of the four N atoms surrounding a K ion and has a diameter of 5.23 Å. (b) Side-on view of the proposed ‘twist’ model with the heights of the K ion, N atoms and the centre of the molecule highlighted.

Conclusions

In summary, we have shown using STM and LEED that the codeposition of TCNQ and K on the Ag(111) surface leads to the formation of an incommensurate ‘windmill’ phase with a nominal K : TCNQ stoichiometry of 1 : 1. SXPS and UPS data indicate that the TCNQ molecules are negatively charged on the surface, with the K atoms acting as positive counterions. NIXSW measurements indicate that the TCNQ molecules adsorb in a relatively flat geometry with K ions lying above the molecular plane. However, a low measured coherent fraction for the N atoms clearly shows that the N atoms occupy two or more different heights above the surface. The simplest model that appears to be compatible with all of these experimental results has the central TCNQ ring almost exactly parallel to the surface, with the peripheral moieties twisted such that out of the four CN groups coordinating to each K ion, one adjacent pair points up and the other pair points down, in a similar manner to the geometry found in the bulk crystal structure of K–TCNQ. As yet, this is the only quantitative structural study of any TCNQ/alkali coadsorption phase and it would certainly be of considerable interest to establish the generality of the structural implications we have observed.

Acknowledgements

G. C. and D. A. W. acknowledge financial support from the EU through the ERC Grant “VISUAL-MS”.

References

1. S. R. Forrest, Nature, 2004, 428, 911–918.
2. P. Peumans, A. Yakimov and S. R. Forrest, J. Appl. Phys., 2003, 93, 3693–3723.
3. S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472.
4. H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625.
5. S. Lattante, Electronics, 2014, 3, 132.
6. I. Hancox, L. A. Rochford, D. Clare, M. Walker, J. J. Mudd, P. Sullivan, S. Schumann, C. F. McConville and T. S. Jones, J. Phys. Chem. C, 2013, 117, 49–57.
7. N. Koch, S. Duhm, J. P. Rabe, A. Vollmer and R. L. Johnson, Phys. Rev. Lett., 2005, 95, 237601.
8. M. Kröger, S. Hamwi, J. Meyer, T. Riedl, W. Kowalsky and A. Kahn, Appl. Phys. Lett., 2009, 95, 123301.
9. G. Bae, H. Jung, N. Park, J. Park, S. Hong and W. Park, Appl. Phys. Lett., 2012, 100, 183102.
10. E. L. Hanson, J. Guo, N. Koch, J. Schwartz and S. L. Bernasek, J. Am. Chem. Soc., 2005, 127, 10058–10062.
11. N. Abdurakhmanova, A. Floris, T.-C. Tseng, A. Comisso, S. Stepanow, A. De Vita and K. Kern, Nat. Commun., 2012, 3, 940.
12. A. Floris, A. Comisso and A. De Vita, ACS Nano, 2013, 7, 8059–8065.
13. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671–679.
14. C. Wackerlin, C. Iacovita, D. Chylarecka, P. Fesser, T. A. Jung and N. Ballav, Chem. Commun., 2011, 47, 9146–9148.
15. T. R. Umbach, I. Fernández-Torrente, M. Ruby, F. Schulz, C. Lotze, R. Rurali, M. Persson, J. I. Pascual and K. J. Franke, New J. Phys., 2013, 15, 083048.
16. M. N. Faraggi, N. Jiang, N. Gonzalez-Lakunza, A. Langner, S. Stepanow, K. Kern and A. Arnau, J. Phys. Chem. C, 2012, 116, 24558–24565.
17. T.-C. Tseng, N. Abdurakhmanova, S. Stepanow and K. Kern, J. Phys. Chem. C, 2011, 115, 10211–10217.
18. S. Barja, D. Stradi, B. Borca, M. Garnica, C. Díaz, J. Rodriguez-García, M. Alcamí, A. Vázquez de Parga, F. Martín and R. Miranda, J. Phys.: Condens. Matter, 2013, 25, 484007.
19. P. J. Blowey, S. Velari, L. A. Rochford, D. A. Duncan, D. A. Warr, T.-L. Lee, A. De Vita, G. Costantini and D. P. Woodruff, to be published.
20. K. E. Hermann and M. A. Van Hove, LEEDpat, 2014, http://www.fhi-berlin.mpg.de/KHsoftware/LEEDpat/index.html.
21. D. Nečas and P. Klapetek, Cent. Eur. J. Phys., 2012, 10, 181–188.
22. D. P. Woodruff, Prog. Surf. Sci., 1998, 57, 1–60.
23. D. P. Woodruff, Rep. Prog. Phys., 2005, 68, 743.
24. C. J. Fisher, R. Ithin, R. G. Jones, G. J. Jackson, D. P. Woodruff and B. C. C. Cowie, J. Phys.: Condens. Matter, 1998, 10, L623.
25. M. B. Trzhaskovskaya, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2001, 77, 97–159.
26. M. Konno, T. Ishii and Y. Saito, Acta Crystallogr., Sect. B: Struct. Sci., 1977, 33, 763–770.
27. R. Precht, R. Hausbrand and W. Jaegermann, Phys. Chem. Chem. Phys., 2015, 17, 6588–6596.
28. R. Precht, S. Stolz, E. Mankel, T. Mayer, W. Jaegermann and R. Hausbrand, Phys. Chem. Chem. Phys., 2016, 18, 3056–3064.
29. W. E. Morgan, J. R. Van Wazer and W. J. Stec, J. Am. Chem. Soc., 1973, 95, 751–755.
30. L. G. Petersson and S. E. Karlsson, Phys. Scr., 1977, 16, 425.
31. K. Doll, Phys. Rev. B: Condens. Matter, 2002, 66, 155421.
32. G. S. Leatherman, R. D. Diehl, P. Kaukasoina and M. Lindroos, Phys. Rev. B: Condens. Matter, 1996, 53, 10254–10260.
33. R. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767.
34. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
35. L. Duy, A. Maral, K. Adam and S. R. Talat, J. Phys.: Condens. Matter, 2012, 24, 222001.
36. W. Liu, A. Tkatchenko and M. Scheffler, Acc. Chem. Res., 2014, 47, 3369–3377.
37. X. Stammer, K. Tonigold, A. Bashir, D. Kafer, O. Shekhah, C. Hulsbusch, M. Kind, A. Groß and C. Woll, Phys. Chem. Chem. Phys., 2010, 12, 6445–6454.
38. B. Milián, R. Pou-Amérigo, R. Viruela and E. Ortí, J. Mol. Struct.: THEOCHEM, 2004, 709, 97–102.
39. D. Stradi, B. Borca, S. Barja, M. Garnica, C. Diaz, J. M. Rodriguez-Garcia, M. Alcami, A. L. Vazquez de Parga, R. Miranda and F. Martin, RSC Adv., 2016, 6, 15071–15079.
40. L. Romaner, G. Heimel, J.-L. Brédas, A. Gerlach, F. Schreiber, R. L. Johnson, J. Zegenhagen, S. Duhm, N. Koch and E. Zojer, Phys. Rev. Lett., 2007, 99, 256801.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7fd00093f

‡ Present address: School of Chemistry, University of Birmingham, Birmingham, B15 2TT, UK.

---