Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reversible ultralow-voltage liquid–liquid electrowetting without a dielectric layer†
Nico E. A.
Cousens
and
Anthony R. J.
Kucernak
*
Department of Chemistry, Imperial College London, London, SW7 2AZ, UK. E-mail: Anthony@imperial.ac.uk
First published on 19th January 2017
Abstract
Electrowetting-on-dielectric devices typically have operating voltages of 10–20 V. A reduction in the operating voltage could greatly reduce the energy consumption of these devices. Herein, fully reversible one-electrolyte electrowetting of a droplet on a solid metal surface is reported for the first time. A reversible change of 29° for an 800 mV step is achieved. The effects of surface roughness, electrolyte composition, electrolyte concentration and droplet composition are investigated. It was found that there is a dramatic dependence of the reversibility and hysteresis of the system on these parameters, contrary to theoretical predictions. When a 3-chloro-1-propanol droplet is used, a system with no hysteresis and a 40° change in angle are obtained.
Introduction
Electrowetting is a phenomenon by which the wettability of a surface is manipulated with an electric field. Electrowetting on dielectric (EWOD), pioneered by Berge in 1996, has come to be the dominant method of electrowetting and currently has a use in a wide range of technologies including liquid lenses, low power displays and microfluidics.1,2 However, a minimum of 10–20 volts is required to operate these devices, although some recent progress has been made in trying to reduce these operating voltages.3–6 For this reason it is of interest to develop electrowetting systems with much lower operating voltages (<1 V), on the basis that energy consumption scales with the square of the voltage.‡ The method of electrowetting that we are concerned with in this paper can be traced back to experiments performed by Frumkin during the 1930s.7 These experiments, which we have reproduced for the benefit of comparison with new results, involved an oil droplet on a mercury electrode surrounded by an electrolyte solution. Upon stepping the potential away from the point of zero charge (PZC), the electrochemical double layer restructures, lowering the energy of the mercury|electrolyte interface. This in turn changes the balance of the interfacial forces and the droplet changes shape (contracts). The change in contact angle is described by the following equation:2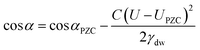 | (1) |
The capacitance of the electrochemical double layer in a Frumkin system is usually tens of microfarads per square centimeter, in comparison to hundreds of nanofarads per square centimeter for a simple dielectric capacitor with a micron thick dielectric layer. As a result, 10 to 100 times greater voltages are needed to induce observable changes in the contact angle for EWOD systems compared to the Frumkin system.
There is, however, a limitation of the Frumkin system. Frumkin’s experiments were performed on mercury, and he reported that although the wettability of other metals (such as silver) was also affected by the potential, the wettability was not reversible.7 Furthermore, there are very few reports in the literature of reversible electrowetting on unmodified metal surfaces. Beni and Hackwood have reported that a reversible potential-dependent wetting can be seen on gold if the gold surface is kept free of dust particles, although they did not quantify the reversibility or show the contact angle dependence on the potential.8,9 Other electrowetting systems also exist, such as those of Sondag-Huethorst and Fokkink, and of Gorman et al.6,10 This first system involves the reversible oxidation of surface adsorbed ferrocene-terminated thiols, wherein reduced and oxidised surfaces have differing wettabilities. The second system involves the potential controlled reversible adsorption of an organothiol monolayer onto a gold electrode, again allowing two different surface wettabilities to be accessed. Nonetheless, these systems operate on different principles to the Frumkin system in that they rely on electrochemical modification of surface adsorbed functional groups to induce a change in the wettability.
The only system similar to that of Frumkin to have been studied in detail on solid surfaces is the system that one of us has previously studied.11 This system concerns the electrowetting of an oil droplet surrounded by water, but with electrolyte in both the aqueous and oil phases. In this instance the droplet|aqueous phase interface is what is known as an interface between two immiscible electrolyte solutions (ITIES), which is expected to enhance the electrowetting behavior of the system.12–14 Experimental results with this system did indeed show a reversible electrowetting response on a solid (gold) electrode, albeit with some hysteresis.
The question remains as to why a process supposedly driven by charging of the electrochemical double layer has only been studied in detail on mercury and not on other (solid) metals. If such a system was found to work on solid surfaces, this would provide an electrowetting system that would operate at much lower voltages, and potentially reduce the power consumption of portable electrowetting devices. Hence in this paper we have looked at the effect of surface roughness on the electrowetting response, utilising ultra-flat gold electrodes prepared through template stripping and comparing them to sputtered gold surfaces. Template stripping is a recently developed technique for the preparation of surfaces with near-atomic roughness.15,16 It involves the use of a very smooth surface, such as mica or glass, onto which a metal is deposited by either evaporation or sputtering. The thin layer of deposited metal is then fixed to a support using an adhesive and removed from the template. The newly exposed metal surface has a similar roughness to the template and is smoother than can typically be produced through polishing. It does not have the large grain boundary defects seen on thermally annealed surfaces.
Methods
Template stripped gold surfaces were prepared by sputtering a 100 nm layer of gold onto 2 cm × 7.5 cm pre-cleaned glass microscope slides, followed by bonding onto a secondary substrate and removal of the initial glass surface (see ESI†).17 Sputtered gold surfaces were prepared by sputtering 100 nm of gold onto pre-cleaned glass with a 20 nm titanium interlayer. The gold template stripped surfaces reported herein had an RMS roughness of 4.5 Å over 80 × 80 μm2 compared with 40.3 Å for the sputtered surfaces over the same area (see ESI Fig. S1† for the AFM image).The experimental configuration used for obtaining the liquid–liquid experimental measurements is illustrated in Fig. 1. For electrowetting on mercury, the working electrode consisted of a pool of mercury with a height of 1 cm in a 2 cm × 2 cm × 5 cm glass cuvette composed of optical flat glass. Above the mercury pool were placed a saturated calomel reference electrode (SCE) and platinum counter electrode. The cell had a PTFE lid to allow degassing of the electrolyte. For electrowetting on gold, the gold working electrode (sputtered gold or template stripped gold) was mounted in a horizontal PTFE holder designed to sit inside a 5 cm × 5 cm × 5 cm glass cuvette. Also mounted in the holder was an Ag/AgCl wire used as the reference electrode and a gold counter electrode.
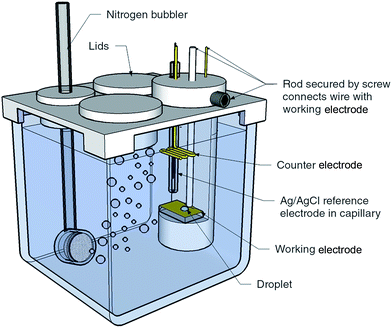 | ||
| Fig. 1 Experimental cell and configuration used to obtain the liquid–liquid electrowetting measurements. The size of the glass cuvette is 5 cm × 5 cm × 5 cm. | ||
LiCl, NaCl and KCl were purchased from Sigma-Aldrich, used as received (greater than 99% purity), and dissolved in ultrapure water (Millipore Milli-Q, 18.2 MΩ cm). A droplet (DCE or 3-chloro-1-propanol, purchased from Sigma-Aldrich and used as received, greater than 98% purity) was placed onto the working electrode using a micropipette with plasticiser free Gilson tips. The droplet was approximately 0.5 μL and 0.5–1 mm wide. Triple distilled 99.999% ACS mercury was used to replicate the Frumkin experiment. The organic phases were pre-equilibrated with water, and the aqueous phases were pre-equilibrated with the organic liquid.
A Gamry Reference 600 potentiostat was used to control the applied potential. The potential was varied in 100 mV steps with 10 s gaps between the steps. There was no electrochemical pretreatment of the electrode and all scans began at the open circuit potential. The potentiostat simultaneously gave an indication of the background currents, which were consistently low within the potential range measured (within ±20 μA cm−2), to ensure that no significant faradaic reactions were occurring. Experiments were completed within 15 min of submerging the electrode. The ambient temperature was 22 ± 2 °C.
All the electrowetting responses shown are characteristic for the described conditions, although some small variation between repeat experiments was commonly observed due to the unpredictable nature of the pinning process. As the potential of the working electrode was varied, photographs of the droplet (640 × 480 pixels) were automatically taken with a CCD camera (from a Phillips SPC900NC webcam) through a video zoom microscope (Edmund Optics Infinity K2/S Long Distance Video Lens) at 20× magnification. The contact angles for each potential were subsequently computed using Fta32 2.0 contact angle software (First Ten Ångstroms). At least five points at the droplet|aqueous phase interface were used to calculate the contact angle. The interfacial energy of the liquid|liquid interfaces was measured using the pendant drop method. The density of the liquids was measured using a pycnometer, with an internal volume of 10 ml (Cole-Parmer).
Results and discussion
Although electrowetting on mercury was first performed by Frumkin in the 1930s, and again by Ivošević and Žutić in 1998, similar results are reported here, with an emphasis on the lack of contact angle hysteresis shown by the system, to enable direct comparison with the electrowetting on solid metal surfaces.7,18Fig. 2 shows the electrowetting response for a droplet of dichloroethane (DCE) on the surface of a mercury electrode. The droplet was surrounded by an aqueous phase of 0.10 mol dm−3 LiCl. The electrode potential was cycled from 0 mV to −100 mV.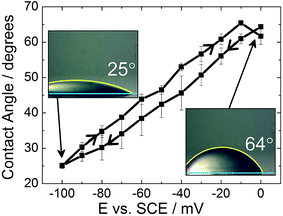 | ||
| Fig. 2 Electrowetting response for a dichloroethane droplet on mercury surrounded by 0.10 mol dm−3 LiCl. | ||
As the potential increases, in 10 mV steps, the droplet contact angle increases as also reported by Frumkin. The potential was not increased above 0 mV due to the onset of faradaic processes (i.e. formation of Hg2Cl2), while at potentials more negative than −100 mV the droplet contact angle was too small to be measured accurately. There were also issues with the droplet sliding out of view on the mercury surface as the potential was stepped. It can be seen that the difference in contact angle between the forward and reverse scans is very small (less than 5°). Therefore there is very little hysteresis between the forward and reverse scans. Furthermore, the time response was less than the frame rate of the camera (30 frames per second).
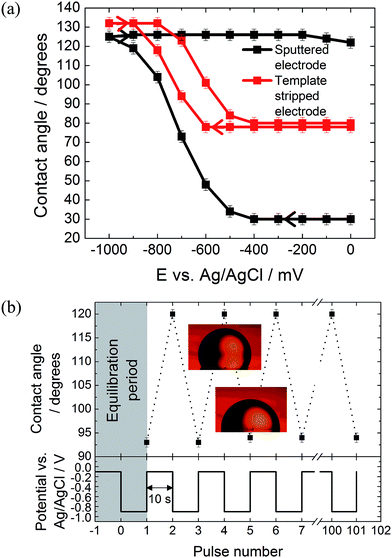
The effect of the surface roughness on the electrowetting can be seen in Fig. 3(a). The electrowetting responses shown are for a droplet of pure DCE on either a sputtered or template stripped gold surface, surrounded by a 0.10 mol dm−3 LiCl solution. As seen for the mercury surfaces, the contact angle changes with the potential, with a larger contact angle seen at potentials more negative than the PZC (measured to be −400 ± 50 mV versus Ag/AgCl in 0.10 mol dm−3 LiCl electrolyte). This is in agreement with the theoretical predictions outlined in the introduction, however, the authors are not aware of any other reports in the literature of a reversible electrowetting response on plain solid metal surfaces using a similar experimental set up. Indeed, the response is very repeatable, and no degradation of the contact angle response was seen over the course of 100 potential steps, alternating between −100 mV and −900 mV versus Ag/AgCl, Fig. 3(b).
No electrowetting response was seen at positive potentials (the potential was stepped even up to +1600 mV) and the contact angle ‘saturates’ at around −900 mV. This of course disagrees with theoretical predictions suggesting that there should be a parabolic electrowetting response around the PZC with the contact angles eventually attaining 180° (dewetting of the droplet). This result was also reported for ITIES electrowetting, although no explanation as to why was given.11 At potentials more positive than the PZC, anion adsorption occurs, and this process may hinder the electrowetting process.
Comparing the two gold surfaces, it can be seen that the minimum contact angle for the template stripped gold, when compared with the sputtered gold, is higher. This is because the surface of the freshly exposed gold is not coated with a thin layer of organic compounds adsorbed from the atmosphere.19 These organics make the surface more hydrophobic, explaining the difference in the minimum contact angle. Aside from the differing contact angles, there is substantially less contact angle hysteresis with the template stripped gold as the potential is stepped from −1000 mV to 0 mV and back again. With the sputtered gold surface there is a gap of over 400 mV between the forward and reverse scans, while this gap drops to less than 150 mV for the template stripped surface. Furthermore, the difference between the initial and final contact angles is also larger with the sputtered gold surface, meaning a larger range of contact angles is accessible.
It is assumed that this variation in the electrowetting response is due to the different surface roughnesses, where the lower roughness of the template stripped surface provides less resistance to droplet shape change which reduces contact angle hysteresis. Therefore, template stripped gold electrodes were used for all subsequent experiments reported here. The effect of electrolyte composition on the electrowetting response was tested. In comparison to 0.10 mol dm−3 solutions of LiCl, 0.10 mol dm−3 solutions of NaCl, MgCl2, NH4Cl and NaF showed no reversible electrowetting response. The results with NaCl are typical for such a lack of reversible response – although the contact angle changes as the potential is decreased, it does not return to its initial value when the potential is returned to 100 mV. Other than the LiCl solution, only a KCl solution provided a reversible, yet very heavily pinned, response (ESI Fig. S2†).
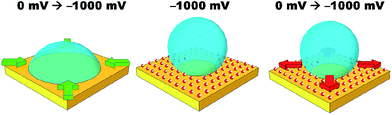
Simple salt electrolytes at similar concentrations show similar differential capacitance curves.20 Therefore, lower capacitance cannot be used to explain the lack of an electrowetting response for these electrolytes. The authors propose that the extreme pinning must be the result of a change in the wettability of the surface upon cycling the potential. For instance, as a potential is applied, water molecules or cations/anions become strongly adsorbed to the gold surface. Then as the potential is relaxed, the water/cations/anions remain strongly adsorbed to the gold surface preventing the oil from spreading back across the surface, as illustrated in Fig. 4. Especially for anions/cations, the high free energy for transfer of the ions into the DCE phase would explain their “reluctance” to desorb. Indeed, a similar effect has been seen for electrowetting on dielectric systems in which the electrode material is barium titanate, a piezoelectric material.21 In this case, bistable electrowetting is possible because of charge trapping in the barium titanate, which leads to compensating charges on the surface of the dielectric. It is suggested that these charges contribute to strong pinning. Different electrolytes may affect the adsorption of water or a similar process. This hypothesis is loosely supported by a growing body of evidence for the differences in interfacial structure in alkali metal salt solutions.22–24 Alternatively, as lithium salts have an enhanced solubility in organic solvents, as the organic droplet spreads back across the surface it may be able to incorporate (dissolve) the lithium ions adsorbed to the surface.25 As the other salts are less soluble in organic solvents, the system is more heavily pinned. Solution densities and liquid|liquid interfacial energies were also measured. It was found that the variations in these properties were less than one percent, and are therefore unlikely to contribute to the observed effects. Clearly, this effect is poorly understood and efforts to better understand and explain it are currently underway.
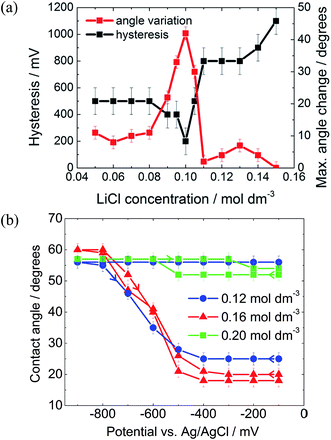
As described by the Gouy–Chapman theory, the capacitance of the metal|electrolyte interface increases with electrolyte concentration.20 Therefore, it might be expected that increasing the electrolyte concentration would increase the electrowetting response. In fact, as seen in Fig. 5(a), this is true only up to a certain threshold concentration, after which the maximum attainable change in contact angle decreases dramatically and pinning simultaneously increases.
The initial reduction in hysteresis can be explained by the argument just given; however, it is not clear as to why pinning should then increase at high salt concentrations. Clearly a different phenomenon is responsible for this result. We again postulate that there must be a change in the wettability of the gold surface that is not undone when the potential is relaxed to the PZC (Fig. 4). It seems that this change is more profound at high salt concentrations, perhaps due to changes in the double layer structure.
Finally, the effect of the droplet composition on the electrowetting response was investigated. It was found that very hydrophobic liquids, which are highly immiscible with water, were very strongly pinned (similar behavior to NaCl with a DCE droplet, ESI Fig. S2†). These included cyclohexane and the perfluorinated solvent FC40. Partially water miscible solvents such as butyl acetate (water solubility: 10 g dm−3) and nitrobenzene (1.9 g dm−3) were less pinned, while n-butanol (73 g dm−3) had a response close to that of DCE, which itself has a water solubility of 8.7 g dm−3.26
Again, based on the theoretical explanation of electrowetting, the droplet composition should not have a critical effect on the electrowetting response. The droplet|aqueous phase interfacial energy controls how much the contact angle changes for a given voltage step; however, it should not prevent electrowetting from occurring. So why are some droplets composed of some oils heavily pinned while others are not? The results would seem to agree with the hypothesis presented above: that a strong adsorption of water to the gold surface prevents droplets from spreading back across the surface. The more water miscible (more hydrophilic) solvents, such as DCE and n-butanol, are able to spread across the hydrophilic surface, while hydrophobic solvents such as FC40 and cyclohexane cannot. Alternatively, the partially water-miscible solvents, which constitute a significant fraction of the aqueous phase, may localise at the gold surface, facilitating spreading of the droplet. Significant intermixing of the two phases will also bring the relative permittivities of the two phases closer to each other, similarly blurring the discontinuity at the three-phase contact line.27 Furthermore as the two phases become more similar (density and viscosity) due to the partially miscible nature of the liquid–liquid system, it would be expected that the amplitude of the capillary waves at the interface would increase. Large amplitude capillary waves may then be important for overcoming local pinning at the solid–liquid–liquid three phase line.
To test this idea, a solvent with a very low aqueous phase|oil surface energy was investigated. It was found that 3-chloro-1-propanol, although completely miscible with pure water, was salted out by dilute salt solutions, forming a biphasic system. The liquid|liquid surface energy of pure DCE with water is 28.7 mJ m−2 compared to 6.0 ± 0.5 mJ m−2 for 3-chloro-1-propanol in contact with aqueous 0.16 mol dm−3 LiCl.28
The 3-chloro-1-propanol electrowetting response can be seen in Fig. 5(b). At a LiCl concentration of 0.16 mol dm−3, there was no hysteresis in the electrowetting response at negative potentials over a contact angle range of over 40°. Nonetheless, the reversibility of the response still depends emphatically on the LiCl concentration, as was the case with a DCE droplet, Fig. 5a. At 0.12 mol dm−3 LiCl, the droplet is completely pinned, while at 0.20 mol dm−3 LiCl the droplet barely changes shape. However, due to the mild acidity of 3-chloro-1-propanol, there is a background low faradaic current due to H+ reduction at potentials below −500 mV versus Ag/AgCl. The addition of NaOH delays the onset of this reductive process by 800 mV, suggesting that the reaction is indeed H+ reduction rather than reduction of the 3-chloro-1-propanol (ESI Fig. S2†).
Furthermore, although pinned, the 3-chloro-1-propanol system shows an electrowetting response positive of the PZC (in a region where no faradaic processes occur). This was not seen with any other solvents, suggesting that 3-chloro-1-propanol is particularly conducive to electrowetting.
Conclusions
The electrowetting experiments of Frumkin involving oil droplets on mercury have been repeated. It was shown that there is very little contact angle hysteresis between the applied potential and contact angle. Using a similar experimental geometry, a reversible electrowetting response was investigated on gold for the first time. It was found that the roughness of the gold had a substantial effect on the contact angle hysteresis. Smooth template stripped surfaces showed a significantly better performance than sputtered surfaces. Unexpectedly, it was found that the nature of the electrolyte solution surrounding the dichloroethane droplet was critical to the contact angle response. By simply changing the ionic species of the electrolyte, the reversibility of the electrowetting response could be stopped outright. LiCl was found to be the best electrolyte for electrowetting, although the concentration of the LiCl also played a crucial role in the reversibility, with the reversibility increasing up to a critical LiCl concentration beyond which the reversibility would rapidly decrease. Furthermore, the nature of the droplet itself (with no added electrolyte and therefore not affected by the low potentials) also determines whether the response is reversible or not, with less hydrophobic droplets being more reversible. We suggest that one or all of these factors (effect of the electrolyte ions, concentration, electrode surface roughness and droplet composition) may explain why low hysteresis electrowetting on solid surfaces has not been reported previously. Droplets of 3-chloro-1-propanol, which is more than 20% miscible in LiCl solution, showed no contact angle hysteresis and therefore replicate the electrowetting on mercury surfaces but with a solid electrode. However, due to the acidity of the 3-chloro-1-propanol, faradaic processes occur at the same time as electrowetting.Many questions remain about the origins of contact angle saturation at large potentials and the absence of electrowetting at positive electrode potentials. It is also hoped that a solvent with high aqueous miscibility could be found, with similar electrowetting properties to 3-chloro-1-propanol yet without background faradaic reactions. It is hoped that a deeper understanding of the phenomena reported herein will enable the design of an ultra-low voltage electrowetting system with a similar performance to that of EWOD systems in the near future.
Acknowledgements
The authors wish to thank the UK Engineering and Physical Sciences Research Council for PhD funding for NC and for support under grant EP/L02098X/1.Notes and references
- M. Vallet, B. Berge and L. Vovelle, Polymer, 1996, 37, 2465–2470 CrossRef CAS
.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS
.
- S. Berry, J. Kedzierski and B. Abedian, J. Colloid Interface Sci., 2006, 303, 517 CrossRef CAS PubMed
.
- M. Khodayari, J. Carballo and N. B. Crane, Mater. Lett., 2012, 69, 96–99 CrossRef CAS
.
- B. Raj, N. R. Smith, L. Christy, M. Dhindsa and J. Heikenfeld, Composite dielectrics and surfactants for low voltage electrowetting devices, 17th Biennial University/Government/Industry Micro/Nano Symposium, Piscataway, NJ, USA, 2008, pp. 187–190 Search PubMed.
- C. B. Gorman, H. A. Biebuyck and G. M. Whitesides, Langmuir, 1995, 11, 2242–2246 CrossRef CAS
.
- A. N. Frumkin, B. Kabanow and M. Nekrasow, Phys. Z. Sowjetunion, 1932, 1, 255–284 CAS
.
- G. Beni and S. Hackwood, Appl. Phys. Lett., 1980, 38, 207–209 CrossRef
.
- G. Beni, S. Hackwood and J. L. Jackel, Appl. Phys. Lett., 1982, 40, 912–914 CrossRef CAS
.
- J. A. M. Sondag-Huethorst and L. G. J. Fokkink, Langmuir, 1994, 10, 4380–4387 CrossRef CAS
.
- A. A. Kornyshev, A. R. Kucernak, M. Marinescu, C. W. Monroe, A. E. S. Sleightholme and M. Urbakh, J. Phys. Chem. C, 2010, 114, 14885–14890 CAS
.
- C. W. Monroe, L. I. Daikhin, M. Urbakh and A. A. Kornyshev, J. Phys.: Condens. Matter, 2006, 18, 2837–2869 CrossRef CAS
.
- C. W. Monroe, L. I. Daikhin, M. Urbakh and A. A. Kornyshev, Phys. Rev. Lett., 2006, 97, 136102 CrossRef PubMed
.
- C. W. Monroe, M. Urbakh and A. A. Kornyshev, J. Electrochem. Soc., 2009, 156, P21–P28 CrossRef CAS
.
- N. Vogel, J. Zieleniecki and I. Koeper, Nanoscale, 2012, 4, 3820–3832 RSC
.
- M. Hegner, P. Wagner and G. Semenza, Surf. Sci., 1993, 291, 39–46 CrossRef CAS
.
- L. Chai and J. Klein, Langmuir, 2007, 23, 7777–7783 CrossRef CAS PubMed
.
- N. Ivošević and V. Žutić, Langmuir, 1998, 14, 231–234 CrossRef
.
- K. W. Bewig and W. A. Zisman, J. Phys. Chem., 1965, 69, 4238–4242 CrossRef CAS
.
-
A. J. Bard and L. Faulkner, Electrochemical Methods, Fundamentals and Applications, John Wiley and Sons, Oxford, 2nd edn, 2001 Search PubMed
.
- M. K. Kilaru, J. Heikenfeld, G. Lin and J. E. Mark, Appl. Phys. Lett., 2007, 90, 212906 CrossRef
.
- M. Bostrom, W. Kunz and B. W. Ninham, Langmuir, 2005, 21, 2619–2623 CrossRef CAS PubMed
.
- D. Horinek, A. Herz, L. Vrbka, F. Sedlmeier and S. Mamatkulov, Chem. Phys. Lett., 2009, 479, 173–183 CrossRef CAS
.
- F. Bresme, E. Chacon, P. Tarazona and A. Wynveen, J. Chem. Phys., 2012, 137, 114706 CrossRef PubMed
.
- Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, USA, 2006 Search PubMed.
- Knovel Critical Tables, Knovel, New York, 2nd edn, 2008 Search PubMed.
- P. Wang and A. Anderko, Fluid Phase Equilib., 2001, 186, 103–122 CrossRef CAS
.
- A. Trojánek, A. Lhotský, V Mareček and Z. Samec, J. Electroanal. Chem., 2004, 565, 243–250 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7fd00016b |
| ‡ In principle, much of the capacitative energy stored in the system may be recovered if one steps back to the initial potential, although this complicates the design of the electronics used to drive the system and is not performed in real operational systems. |
| This journal is © The Royal Society of Chemistry 2017 |