Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical and numerical analysis of nano-actuators based on grafted polyelectrolytes in an electric field
N. V.
Brilliantov
 *a,
Yu. A.
Budkov
bc and
C.
Seidel
d
*a,
Yu. A.
Budkov
bc and
C.
Seidel
d
aDepartment of Mathematics, University of Leicester, Leicester LE1 7RH, UK. E-mail: nb144@le.ac.uk; Tel: +44 116 252 2521
bNational Research University Higher School of Economics, Department of Applied Mathematics, Moscow, Russia
cG. A. Krestov Institute of Solution Chemistry, Russian Academy of Sciences, Akademicheskaya St. 1, 153045 Ivanovo, Russia. E-mail: urabudkov@rambler.ru
dMax Planck Institute of Colloids and Interfaces, Science Park Golm, D-14424 Potsdam, Germany. E-mail: seidel@mpikg.mpg.de
First published on 3rd February 2017
Abstract
We analyze, theoretically and by means of molecular dynamics (MD) simulations, the generation of mechanical force by a polyelectrolyte (PE) chain grafted to a plane and exposed to an external electric field; the free end of the chain is linked to a deformable target body. Varying the field, one can alter the length of the non-adsorbed (bulk) part of the chain and hence the deformation of the target body and the arising force. We focus on the impact of added salt on the magnitude of the generated force, which is especially important for applications. In particular, we develop a simple variational theory for the double layer formed near electrodes to compute the electric field acting on the bulk part of the chain. Our theoretical predictions agree well with the MD simulations. Next, we study the effectiveness of possible PE-based nano-vices, comprised of two clenching planes connected by PEs exposed to an external electric field. We analyze a novel phenomenon – two-dimensional diffusion of a nano-particle, clenched between two planes, and introduce a quantitative criterion for clenching efficiency, the clenching coefficient. It is defined as a logarithm of the ratio of the diffusion coefficients of a free and clenched particle. Using first a microscopic counterpart of the Coulomb friction model, and then a novel microscopic model based on surface phonons, with the vibration direction normal to the surface, we calculate the clenching coefficient as a function of the external electric field. Our results demonstrate a dramatic decrease of the diffusion coefficient of a clenched nano-particle for the range of parameters relevant for applications; this proves the effectiveness of the PE-based nano-vices.
1 Introduction
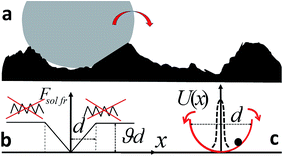
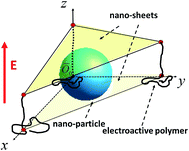
In future nano-technology which will manipulate nano-objects, such as viruses, small bacteria, cell organelles, vesicles, colloidal particles, etc., nano-actuators will play an important role. In particular, it is expected that special devices that can keep a nano-object fixed will be highly needed. Indeed, thermal fluctuations, which are hardly visible in our macroscopic world, become dominant in the nano-world, where interactions between a nano-object and the molecules of the surrounding medium cannot be ignored. In contrast to the macroscopic world where one needs to apply a force to make a body move, due to the presence of friction, in the nano-world one needs to apply a force to prevent a particle’s motion. This occurs due to perpetual molecular fluctuations which cause Brownian motion. Hence it is highly desirable to have a device that can fix and release nano-size objects, subjected to an external signal. We will call these devices “nano-vices” or “nano-nippers”. For biological applications and nano-medicine it is also desirable that such devices will be able to operate in aqueous solutions, including solutions with dissolved salt. Recently, carbon nano-tube nano-tweezers operated by an electric field have been proposed and tested experimentally.1 These, however, have a serious limitation: the effectiveness of such nano-tweezers is questionable for aqueous solutions, especially in the presence of salt, which makes the solution conductive.1 Another limitation of such devices is a relatively narrow range of operating distances, which implies that the carbon nano-tube nano-tweezers can be exploited to operate nano-objects of a particular size, determined by the respective size of the carbon nano-tube. Another set of devices, designed to keep nano-objects fixed, are optical tweezers.2 These, however, require specific optical properties of an immobilized particle, which limits possible applications of the optical tweezers. Here we propose an alternative approach for a controllable nano-device that can immobilize a nano-size object. Namely, we propose an application of electro-active polymers (polyelectrolytes) as a working body of nano-actuators; polyelectrolytes can change their dimension in response to an external electric field and generate a mechanical force to keep a nano-object immobile.In short, such nano-devices are comprised of two parallel planes (nano-sheets, e.g. carbon nano-sheets3) and a few charged polyelectrolyte (PE) chains, which are linked to the planes. If the voltage is applied to one (or two) nano-sheets, it gives rise to an electric field between them that changes the PEs conformation, since PEs are attracted to the oppositely charged plane. The change of the PEs dimension will cause a change in distance between the planes. Hence if a nano-sized object is placed between the two planes it will be squeezed and kept immobilized. Varying the voltage, one can either release the particle or fix it stronger, see Fig. 1. The fixation strength may be quantified by the resulting diffusion coefficient of the clenched particle; it is expected that the latter quantity becomes smaller by orders of magnitude. Therefore two related problems are to be addressed: (i) generation of a mechanical force by electro-active polymers in a response to an external electric field and (ii) the immobilization efficiency of a nano-size object by the nano-vices.
In our previous studies we analyzed salt-free solutions4–6 and showed the possibility to clench a nano-size object using electroactive polymers in electric field. For possible applications, however, the presence of additional salt ions is essential, especially for biotechnological or nano-medical applications. This makes the problem significantly more complicated, since the salt ions cause a screening of the applied electric field, noticeably affecting the efficiency of the nano-device. Moreover, the space distribution of the salt ions will depend on the conformation of the chain (i.e. on the length of its adsorbed part) making the problem still more involved. Hence, one of the main goals of the present study is to confirm that the nano-vices can operate in the presence of salt and estimate the impact of salt on its efficiency. In order to describe the electric field in the presence of salt ions near the charged surface, one can use the well-known Poisson–Boltzmann (PB) equation.7,8
Although numerous theoretical models of the electric double layer based on the PB equation and its various modifications have been developed,9–14 the presence of a charged PE chain within the electric double layer makes the direct application of these theories problematic. To avoid the difficulties associated with the use of the PB equation, we formulate here a simple variational model, which can be successfully applied to find the distribution of the salt ions in the presence of a PE chain, provided the electric field of the charged surfaces is not small.
Obviously, the fixation of a nano-size object in a nano-vice manifests a dramatic decrease of the diffusion of the clenched object, owing to the increasing friction between the planes of the nano-vices and the nano-particle, when the latter becomes squeezed. We propose a new criteria of clenching effectiveness, based on the degree of the diffusion suppression of a clenched object. Hence the effectiveness of nano-vices is determined by the magnitude of the friction force (tangential to the nano-vice planes) which arises in response to the increasing normal load on the clenched particle. In our previous study we have exploited a mesoscopic model of friction force between a nano-particle and clenching planes,15 with a phenomenological friction coefficient which lacks microscopic derivation. In the present study we develop a novel microscopic model of solid friction based on surface acoustic phonons. In contrast to existing microscopic theories of solid friction, associated with the energy dissipation due to phonons, the new model demonstrates an explicit dependence of the friction force on the normal load, which is crucial for the analysis of the nano-vice efficiency. Our theoretical analysis of the generated force is accompanied by numerical simulations.
The rest of the article is organized as follows. In Section 2 we consider the dependence of the chain conformation on the applied electric field. In Section 3 we analyze the diffusion of a nano-particle squeezed by the two planes and estimate the effectiveness of clenching. In Section 4 we discuss our results and Section 5 summarizes our findings.
2 Generation of mechanical force by electro-active polymers in an electric field
2.1 Theory
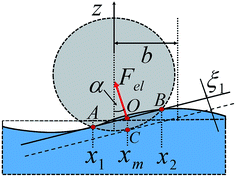
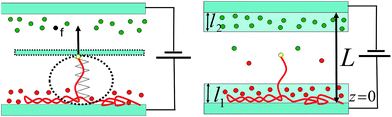
To compute the force generated by electro-active polymers in response to an external electric field we will analyze a simplified one-chain model. Here the external field E is the field associated with the surface charge of the bottom and upper electrodes. In this model it is assumed that a charged polymer (polyelectrolyte) is linked by one of its ends to one (bottom) plane, charged with the opposite sign, and by the other end to a deformable (target) body, see Fig. 2, left panel†. The increase of the electric field, that is, the increase of the surface charge of the bottom plane, will lead to an increased adsorption of the chain on the surface, which implies a decrease of the length of the bulk part of the chain. This will cause the deformation of the target body, and hence the generation of the mechanical force acting on the end of the chain. To find the equilibrium conformation of the chain and the force acting on its end, we compute the total free energy of the system, comprising the PE chain, microions (salt ions and counterions) and the deformable target body. Minimizing the free energy we will find the length of the bulk part of the chain and the force, generated by the chain.We performed molecular dynamics (MD) simulations for the range of electric fields, salt concentrations and chain lengths which may be relevant for applications. For these system parameters we have observed that the charge distribution in the cell has three different zones. Two zones are located near the surfaces of the charged planes and correspond to the adsorption layers of the electrodes. The third zone corresponds to the bulk part of the cell. While the charge density is relatively large in the near-electrodes zones, the corresponding charge density in the bulk zone is rather small. These results are consistent with our previous findings for the salt-free case,4–6,15 where all counterions of the PE chain were accumulated at one, oppositely charged electrode, leaving the bulk part of the chain unscreened. This resulted in the renormalization of the external field owing to the additional surface charge at the electrode due to the adsorbed counterions.
These observations motivate us to apply the following simple model of charge distribution for the case when the additional salt ions are present. We assume that there are two near-surface layers of thickness l1 (near the bottom plane) and l2 (near the top plane) where the most of the ions are located. Since l1 and l2 are of the order of an ion size, we additionally assume that the charge density in these layers is constant, both in vertical and lateral directions. If the height of the cell is L, then in the third zone of thickness, L − l1 − l2, the charge density is relatively small. In this zone, there is a renormalized electric field Er, which is the sum of the initial (bare) electric field E and the additional electric field due to the adsorbed ions at both electrodes. Both values l1 and l2 are variational parameters, which will be obtained self-consistently from the minimization of the system free energy.
Let the PE chain be comprised of N0 charged monomers of charge qe (e is the elementary charge) and size b and let Ns be the number of the chain monomers adsorbed on the bottom surface. Then N = N0 − Ns is the number of monomers that belong to the bulk part of the chain. Let N0 chain’s counterions carry the charge −qe and let N+ = N− = Nion be the total number of positive and negative salt ions. Some of the salt ions are adsorbed on the electrodes and we denote N(i)± and N(i)0 the numbers of positive and negative ions and counterions adsorbed on ith electrode, where i = 1, 2 is the electrode number; we attribute i = 1 to the positively charged bottom electrode and i = 2 to the negatively charged upper electrode (see Fig. 2). Using the shorthand notation {N(i)} = N(1)+, N(2)+, N(1)−, N(2)−, N(1)0, N(2)0, for the set of these variables, we write the total free energy of the system in the following form
| Ftot(N,{N(i)}) = Fp(N,{N(i)}) + Fion({N(i)}) | (1) |
| Fion({N(i)±}) = F(id)ion({N(i)}) + F(el)ion({N(i)}), | (2) |
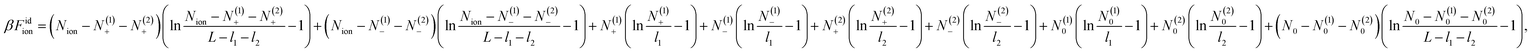 | (3) |
and skip unimportant constants. Here a = ±, 0 and Λa is the respective thermal wavelength of the ions. Here ρa(r) are the densities of the ions, that read N(1)±,0/l1S for the bottom layer, N(2)±,0/l2S for the upper layer and (Nion − N(1)± − N(2)±)/(L − l1 − l2)S and (N0 − N(1)0 − N(2)0)/(L − l1 − l2)S, for the middle zone; S is the electrode area.
The electrostatic part of the free energy associated with ions may be expressed in terms of the difference of the energy of the electric field17 for the case in the presence of the ions and for the case in their absence,
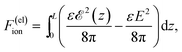 | (4) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z) is the electric field in the presence of the ions, E is the external field and ε is the dielectric permittivity of the solvent. For the assumed uniform charge distribution within the adsorption layers, one can easily find the field
(z) is the electric field in the presence of the ions, E is the external field and ε is the dielectric permittivity of the solvent. For the assumed uniform charge distribution within the adsorption layers, one can easily find the field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z) (e.g. using the Gauss law):
(z) (e.g. using the Gauss law):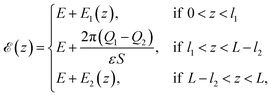 | (5) |
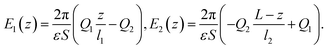 | (6) |
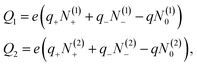 | (7) |
Substituting eqn (5) into (4) we obtain
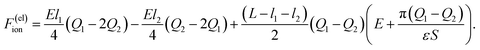 | (8) |
Turn now to the free energy of the PE chain in the field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z). Following ref. 4 and 5 we assume that the bulk part of the chain is fully stretched and that one can neglect the interaction between the adsorbed and bulk parts of the chain‡. Then one can write,
(z). Following ref. 4 and 5 we assume that the bulk part of the chain is fully stretched and that one can neglect the interaction between the adsorbed and bulk parts of the chain‡. Then one can write,
| Fp = Uspring + Fbulk + Fsurf. | (9) |
The elastic properties of the target body are modeled by a non-linear spring with the elastic energy,
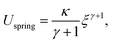 | (10) |
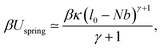 | (11) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z) in the bulk part of the system. The former part reads for the fully stretched chain
(z) in the bulk part of the system. The former part reads for the fully stretched chainwhere the zi = bi is the z-coordinate of ith monomer (see ref. 4 and 5 for the detail), while the latter one may be written as
where we introduce the renormalized field
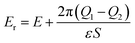 , which corresponds to the field
, which corresponds to the field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z), eqn (5), in the middle zone (that is, in the bulk part of the system, apart from the surface layers). This field is almost uniform, and φr(z) = −Erz is the renormalized potential. This term is the same as for the salt-free case,4,5 with the field E substituted by the field Er. Hence one can write,
(z), eqn (5), in the middle zone (that is, in the bulk part of the system, apart from the surface layers). This field is almost uniform, and φr(z) = −Erz is the renormalized potential. This term is the same as for the salt-free case,4,5 with the field E substituted by the field Er. Hence one can write,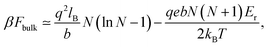 | (12) |
The free energy of the adsorbed part of the polyelectrolyte chain takes the form
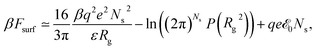 | (13) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0 =
0 = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0(b/2),
0(b/2), ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z) is given by eqn (5) and Ns = N0 − N is the number of adsorbed monomers. The first term in the r.h.s. of eqn (13) is the electrostatic energy of the adsorbed part of the PE chain which we estimate as the energy of a homogeneously charged flat disc of total charge qeNs and radius Rg, corresponding to the gyration radius of the adsorbed part.4,5 The second term is related to the configurational entropy of the ideal polymer chain on a plane with the distribution function of the square of the gyration radius P(Rg2) and the third term accounts for the interaction of the adsorbed part of the chain with the field
(z) is given by eqn (5) and Ns = N0 − N is the number of adsorbed monomers. The first term in the r.h.s. of eqn (13) is the electrostatic energy of the adsorbed part of the PE chain which we estimate as the energy of a homogeneously charged flat disc of total charge qeNs and radius Rg, corresponding to the gyration radius of the adsorbed part.4,5 The second term is related to the configurational entropy of the ideal polymer chain on a plane with the distribution function of the square of the gyration radius P(Rg2) and the third term accounts for the interaction of the adsorbed part of the chain with the field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (z), within the adsorption layer at the bottom surface. The distribution function of the gyration radius P(Rg2) is available in the literature for three,18 two5 and d-dimensional cases.19 Due to the repulsion between the chain segments, which is practically not screened (the adsorbed ions of the same charge do not screen the adsorbed chain monomers) the surface part of the chain is stretched. Hence one needs to use P(Rg2) for the case when Rg2 ≫ b2Ns,5,18,19
(z), within the adsorption layer at the bottom surface. The distribution function of the gyration radius P(Rg2) is available in the literature for three,18 two5 and d-dimensional cases.19 Due to the repulsion between the chain segments, which is practically not screened (the adsorbed ions of the same charge do not screen the adsorbed chain monomers) the surface part of the chain is stretched. Hence one needs to use P(Rg2) for the case when Rg2 ≫ b2Ns,5,18,19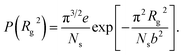 | (14) |
Furthermore, minimizing the part of the free energy in eqn (13) with respect to the radius of gyration Rg, one can obtain the free energy of the adsorbed part of the chain,
βFsurf ≃ p(q2![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) B)2/3Ns − Ns B)2/3Ns − Ns![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2π + ln 2π + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ns, Ns, | (15) |
We consider the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, i.e., when q+ = −q− = 1. Moreover, we assume that q = −1. Thus, minimizing the total free energy, eqn (1), with respect to the adsorption layer thicknesses li and numbers of adsorbed particle N(i)a, where a = ±, 0 and i = 1, 2, we arrive at the following system of coupled equations in the limit L ≫ li
1 electrolyte, i.e., when q+ = −q− = 1. Moreover, we assume that q = −1. Thus, minimizing the total free energy, eqn (1), with respect to the adsorption layer thicknesses li and numbers of adsorbed particle N(i)a, where a = ±, 0 and i = 1, 2, we arrive at the following system of coupled equations in the limit L ≫ li
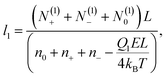 | (16) |
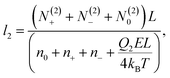 | (17) |
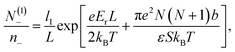 | (18) |
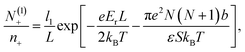 | (19) |
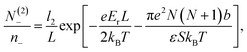 | (20) |
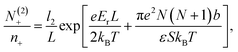 | (21) |
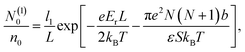 | (22) |
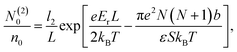 | (23) |
The above system of eight equations for eight unknowns, li, N(i)0 and N(i)± for i = 1, 2 may be further simplified if the electric field is not small, so that βeEb ∼ 1. In this case the size of the surface layers will be mainly determined by the electrostatic field E and will not be noticeably affected by the presence of counterions, which destroy the symmetry. Hence we expect that l1 ≈ l2 = l in this case. For the same reason the following approximations are expected to be valid, N(1)− ≈ N(2)+ = N1, N(2)− ≈ N(1)+ = N2, N(1)0 ≪ N0, and N(2)0 ≈ N0. This also follows from the straightforward analysis of the above set of equations. As a result, the basic eqn (18)–(21) may be significantly simplified, yielding
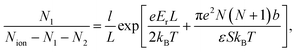 | (24) |
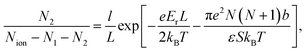 | (25) |
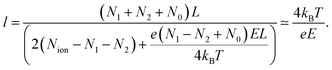 | (26) |
Minimization of the total free energy with respect to the number of desorbed (bulk) monomers N yields
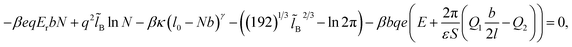 | (27) |
![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) B = lB/b, is introduced.
B = lB/b, is introduced.
The system of coupled eqn (24)–(27) allows the calculation of the number of desorbed monomers N as a function of the applied electric field E and the number of salt ions Nion in the cell. Using N one can also find the generated force, f = −∂Uspring/∂r, exploiting the relation
| f = κ(l0 − Nb)γ. | (28) |
Note that the above analysis based on eqn (16)–(23), or (24)–(26) and (27) allows to find all quantities that determine the actual electric field in the system and hence find the potential difference between the electrodes U. In this way we have one-to-one correspondence between the external field E and U. For simplicity we use below the variable E.
2.2 MD simulations
To confirm the predictions of our theory we performed MD simulations. The setup was similar to that reported in ref. 4–6. Namely, we consider a freely jointed bead-spring chain. All N0 = 80 beads, except the one bound to the plane at z = 0, carry one (negative) elementary charge q = −1. N0 monovalent free counterions and Nion positive ions with charge q+ = 1 and Nion negative ions with q− = −1, make the system electroneutral. We assume an implicit good solvent,20 that is, we assume that the solvent is a structureless dielectric medium with a dielectric permittivity ε, and that all particles suffer short-ranged, purely repulsive interactions, described by a shifted Lennard-Jones potential.21,22 Neighboring beads along the chain are connected by the standard FENE potential.21,22 The bond length at zero force is b ≃ σLJ where σLJ is the Lennard-Jones parameter.21,22 All particles except the anchor one interact with a short-ranged repulsive potential with the grafting plane at z = 0 and upper plane at z = Lz. The simulation box has the following parameters: its lateral dimension is Lx × Ly × = 50b × 50b and the box height is Lz = L = 40b.The charged particles interact with each other and the external field with an unscreened Coulomb potential, quantified by the Bjerrum length. We set lB = σLJ and use a Langevin thermostat23 to hold the temperature kBT/εLJ = 1, where εLJ is the Lennard-Jones energy parameter. More simulation details are also given in ref. 21 and 22. The free end of the chain is linked to a deformable target body, modeled by a Hertzian spring, eqn (11) and (28) with γ = 3/2 and the elastic constant ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) = βκb3/2 = 1. It has been shown recently the Hertzian force may be used to model “core” interactions between nano-particles.24 For simplicity, we assume that the anchor of a spring is fixed and aligned in the direction of the applied field.
= βκb3/2 = 1. It has been shown recently the Hertzian force may be used to model “core” interactions between nano-particles.24 For simplicity, we assume that the anchor of a spring is fixed and aligned in the direction of the applied field.
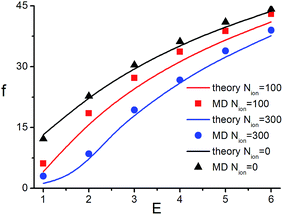
We consider three different systems, with Nion = 0, which corresponds to the salt-free system, with Nion = 100, which corresponds to the solution with a salt concentration ns = 4.6 × 10−4 M, and with Nion = 300, which corresponds to ns = 1.38 × 10−3 M, and we explore bare fields Ẽ = βeEb ≥ 1. We have observed that for these fields adsorbed layers with a thickness of about one microion size are formed, leaving the bulk of the system practically salt-free.
In Fig. 3 we compare the predictions of our theory with the results of the MD simulations. As one can see from the figure, the increase of salt concentration in the cell leads to a decrease of the mechanical force. As also seen in the figure, the theoretical model is in a good agreement with the simulation results for the studied range of electric fields. The accuracy of the theory worsens, however, for smaller fields, Ẽ < 1, where the theory underestimates the force. This is probably related to the fact that for small electric fields the concept of well defined adsorption layers is no more justified.25
3 Diffusivity of a nano-particle between two planes: analysis of clenching efficiency
3.1 Definition of clenching efficiency and classification of friction models
As we have already mentioned, the mechanics of the nano-world has an astonishing principle: to keep a body immobilized, one needs to apply a force. This happens due to permanent thermal fluctuations that give rise to a continuous Brownian motion of a particle. The intensity of the Brownian motion may be quantified by its diffusion coefficient D. If the particle is clenched between two planes, as it is considered in our model of nano-vices, the friction forces between the planes and the particle, hinders its diffusivity. Obviously, the smaller the resulting diffusion coefficient D, the more efficient the actuator. Ideally, one wishes to completely suppress D, which is not, strictly speaking, possible; nevertheless, D may be reduced up to a desired order.To quantify the clenching efficiency of nano-vices we introduce the clenching coefficient χcl, defined as a natural logarithm of the ratio of the diffusion coefficient D0 of a free particle and that of a clenched particle D,
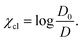 | (29) |
The surrounding fluid, acts on a particle twofold – first, with a random force ψ(t), and second the particle suffers a viscous force −γvV directed against its velocity V, where γv is the friction coefficient. In thermal equilibrium there exists a relation, the so-called “fluctuation–dissipation theorem”, which relates the time correlation function of the random force ψ(t) and the friction coefficient γv:
| 〈ψi(t)ψj(t′)〉 = 2kBTγvδijδ(t − t′) i, j = x, y, z. | (30) |
The action of the surrounding fluid is dubbed as “viscous friction” and the friction coefficient may be related to the radius of the nano-particle Rp = l0/2 and the fluid viscosity η by the Stokes law, γv = 6πηRp.16
The friction force that acts between the electrode surfaces and the particle is called “dry friction” or “solid friction”; we designate it as Fsol.fr.. Then the Langevin equation of motion for a nano-particle of mass m reads,
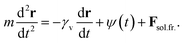 | (31) |
The dry friction force is well known for macroscopic bodies, where it is described by a Coulomb friction model, Fsol.fr. = −μFNV/|V|, with the dry friction coefficient μ and the normal force FN.26 Using the above Langevin equation, the Brownian motion under the action of the Coulomb friction force27 and the combination of the Coulomb and viscous friction force28,29 has been studied. Still, a first-principle molecular model of solid friction on nano-scales is presently lacking.30,§
Here we will consider two microscopic models of solid friction which we will call “athermal” and “thermal” models. In the athermal model it is assumed that the friction force plays only a passive role of hindering the relative motion of two contacting surfaces. It is determined by the “quenched” roughness of the surfaces and is characterized by the static friction force¶, which does not depend on the relative velocity of the surfaces, as the Coulomb friction force.26 This model is applicable for surfaces with a high roughness, when the amplitude of the thermal fluctuations of a surface (normal to the plane) is much smaller than the characteristic size of the surface asperities, see Fig. 4; the viscous friction, proportional to the velocity is significantly smaller than the static friction and we will neglect it for this model.
The thermal model corresponds to the dynamic roughness of very smooth (molecularly smooth) surfaces, which arises due to surface phonons, transversal to the plane, see Fig. 6. The example of such surfaces are the surfaces of mono-crystals or carbon nano-sheets with a small density of surface defects. We also assume that one can neglect static friction as for the case of incommensurate periodic surfaces at a contact.34,36 The dynamic roughness, determined by the propagation and decay of the transversal to the plane surface phonons, gives rise to a fluctuating tangential random force that can cause a spontaneous two-dimensional Brownian motion; this mechanism of Brownian motion may be efficient only for nano-particles, with a size smaller or comparable to the surface phonons’ wavelengths. According to the fluctuation–dissipation theorem, similar to eqn (30), the fluctuating force of the thermal model is accompanied by the resistance force proportional to the particle velocity and directed against the velocity.
Below we consider separately thermal and athermal models of solid friction. We wish to stress however that we analyze the diffusion of a squeezed nano-particle only between the planes, that is, we do not consider a possibility of the particle leaving the device; the latter may produce a potential well itself for the particle.
3.2 Athermal model of surface friction: quenched roughness
The microscopic derivation of the friction force for the athermal model is very complicated. Hence we use here a Cundall–Strack-like model,37 which is a microscopic version of the Coulomb friction model. The Cundall–Strack (CS) model has been applied to describe the tangential friction between colloidal particles.38 The derivation of the diffusion coefficient for the athermal CS model has been done in our recent study;15 here we briefly sketch this approach.In our CS-like model it is assumed that the solid friction force, acting against an external force, is equal to the force of a harmonic spring, −ϑΔ, where Δ = (r − r0) and r0 is the initial position of a body before the external force started to act. When the displacement from the initial position reaches some quantity d, the spring breaks and the body remains displaced by Δ = d in the direction of the acting force, see Fig. 4b. After this displacement to the new position takes place, the resistance force acts with respect to the new (shifted) initial position. Hence the body moves by jerks, which are not visible for macroscopic bodies, since the jerks occur on the microscopic scale d. The maximal force in this model is ϑd, while the average force is equal to 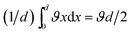 . On the macroscopic scale, L ≫ d, the body moves smoothly with the average resistance force equal to Fsol.fr. = μFN = ϑd/2, hence we obtain, ϑ = 2μFN/d.
. On the macroscopic scale, L ≫ d, the body moves smoothly with the average resistance force equal to Fsol.fr. = μFN = ϑd/2, hence we obtain, ϑ = 2μFN/d.
When the displacement from an initial position is smaller than d, the restoring harmonic force may be written as the gradient of the restoring potential, Fsol.fr. = −∇U with U = μFN(r − r0)2/d. Substituting this expression for Fsol.fr. into eqn (31) we obtain the Langevin equation for a particle in a potential U. Therefore, in the athermal CS-like model of solid friction we have the following physical picture of a particle diffusion: it performs a thermal motion within a potential well U, centered at its initial position. If, subjected to a random force, the particle moves away from the center, further than d, then it arrives at a new potential well, centered at the distance d away from the initial well. In this way a jerk from the position r0 to a new position r0 + d takes place. After k such jerks the position of the particle will be r0 + d0 + d1 +…dk, where |di| = d and 〈di·dj〉 = d2δij, since all these jerks are uncorrelated. If the average time between successive jerks is equal, τ, it is straightforward to show that the diffusion coefficient reads D = d2/4τ.15
Hence to compute the diffusion coefficient one needs to know τ. This may be found, using the Langevin eqn (31) with the potential U. We assume that the viscous force is large, so that the inertial effects may be neglected. Then the x-component of the overdamped Langevin equation takes the form,39
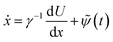 | (32) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (t)
(t)![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (t′)〉 = 2D0δ(t − t′), where D0 = kB/γ is the diffusion coefficient of a non-constrained particle and U(x) = μFNx2/d; we also choose r0 = 0.
(t′)〉 = 2D0δ(t − t′), where D0 = kB/γ is the diffusion coefficient of a non-constrained particle and U(x) = μFNx2/d; we also choose r0 = 0.
The above Langevin equation allows us to write an equation for the average time, T(x), needed for a particle, initially located at point x within the potential well, to reach the point x = ±d, where the particle releases from the well and a jerk takes place. This equation, which is called “mean first-passage time” equation39,40 reads,
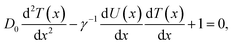 | (33) |
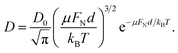 | (34) |
From eqn (34) one finds the clenching coefficient for the athermal model of solid friction between the particle and the electrodes:
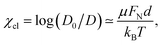 | (35) |
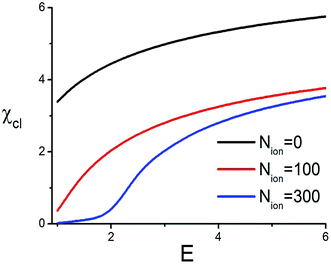
As it may be seen from eqn (35), the clenching coefficient linearly increases with the increasing normal force FN. The latter quantity is determined by the applied electric field, as has been discussed in the previous section. Using μ = 0.2, motivated by the friction coefficients between polymer surfaces (e.g. μ = 0.5 for polystyrene–polystyrene, μ = 0.15–0.25 for nylon–nylon, etc.), and taking into account that the friction force acts on the top and bottom part of a clenched particle, which duplicates the friction force, we calculate χcl as a function of the electric field, see Fig. 5.
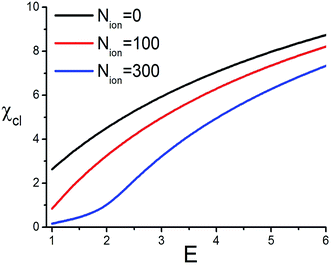 | ||
| Fig. 5 The dependencies of the clenching coefficient for the athermal CS model of solid friction, eqn (35), on the applied electric field, Ẽ = eEb/kBT, for different concentrations of salt. The model parameters are μ = 0.2 and d = b, while the other parameters are the same as in Fig. 3. The magnitude of the normal force FN is taken from the MD simulations. | ||
3.3 Thermal model of surface friction: dynamical roughness due to surface phonons
In this subsection we develop a theory of dynamical surface roughness caused by the transversal surface phonons, with the displacement direction normal to the surface. The current height of the surface at a point r and time t is determined by the amplitude and phase of the surface phonons at this point, see Fig. 6. We assume that only acoustic long-wavelength phonons are important for this friction mechanism and neglect high-frequency optical phonons. We also assume that the wave-length of the acoustic phonons λ is much larger than the particle size, λ ≫ Rp.Note that the crucial role of phonons in energy dissipation for solid friction for molecular smooth surfaces was recognized long ago. The independent oscillator model, also known as Prandtl–Tomlinson model is the most simple model of surface friction due to the damped oscillation of atoms, already suggested in 1928.35,36 In this model, two solids slide with respect to each other, so that all atoms of the lower solid are immobile and present a periodic potential to the atoms of the upper solid. Only the surface atoms of the upper solid are movable; they are connected to the bulk part of the upper solid via springs that mimic the chemical bonds. These atoms, however, are unconnected to each other or any other oscillators. Due to the presence of the periodic potential, the relative lateral motion of the two solids leads to the vertical vibrations of the surface atoms; these independent dumped oscillations dissipate energy||. In the one-dimensional Frenkel–Kontorova model and in its two-dimensional generalizations the moving surface atoms are interconnected by springs,34,36,41,42 while in the Frenkel–Kontorova–Tomlinson models (see e.g.ref. 35, 36 and 43) the moving surface atoms are connected not only between themselves but also to the upper part of the solid. Similar features have composite oscillators and hybrid models (see e.g.ref. 36 and 44). In these models the phonon modes are excited by the periodic potential as the two solids slide on each other and the energy of the directed motion transforms into the energy of the phonon modes, giving rise to a microscopic dissipation mechanism. In some models phenomenological damping constants are ascribed to the connecting springs, while other models use the microscopic elastic constants of the solid material, so that the viscous damping coefficient is determined by the parameters of the periodic potential and phonon dispersion.36,41 Most of the above models are essentially phenomenological ones. A first-principles model of phonon dissipation has been developed for solid friction for adsorbed monolayers;31–33,36 however, a given periodic potential between surfaces was assumed.
Unfortunately, none of the above theories may be directly applied for the case of interest to describe solid friction of a nano-particle and analyze the efficiency of nano-vices. The reason for this is two-fold: (i) the above models mostly deal with infinite flat surfaces, or clusters of surface atoms, while we need to consider friction for a particle of a limited size, but with an essential volume dimension, like e.g. a colloidal particle. (ii) The periodic inter-surface potential that causes the coupling between the lateral motion of the surfaces and vibration modes (phonons) is considered as a given one. No relations between the parameters of this potential and the normal load are available. Hence for the case of dynamical roughness, that yields the velocity-dependent friction, it is not possible to exploit these models to analyze the dependence of the solid friction and diffusion of a nano-particle, on the normal load, generated by nano-vices.
In contrast, the novel model of solid friction developed here, naturally relates the tangential force acting on a nano-particle to the amplitude and phase of the transversal to the plane surface phonons. The dependence of the lateral force on the normal load naturally appears in the new theory. In what follows we give a detailed derivation of the microscopic solid friction force for the case of the thermal model. Since we neglect the atomic scale corrugation of the surface, which entails static friction, our model provides an estimate for the low boundary of the solid friction force due to the thermal fluctuations only.
Note that the rigorous approach requires the derivation of the theory in two steps – firstly, one needs to construct a classical Hamiltonian and, secondly, to perform second quantization in terms of creation and annihilation phonon operators. This program is rather ambitious and we leave it for future studies. Here we perform a classical analysis.
Consider a bottom plane, located at z = 0 and a nano-particle, which we model by a sphere of radius Rp. If the particle is not deformed, and the plane is not disturbed by the surface phonons, the z-coordinate of its center is located at z0 = Rp. If the particle is squeezed, so that z0 < Rp, we define its deformation as ξ = Rp − z0. Then the Hertzian elastic force Fel,0, in the absence of the phonons (marked by the index 0) is equal to:45
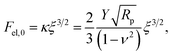 | (36) |
We will model the surface acoustic phonons as transversal harmonic waves:
z(r,t) = Ak![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(k·r − ωkt − bk)e−t/τph, cos(k·r − ωkt − bk)e−t/τph, | (37) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−t/τph.
e−t/τph.
We will address here the case of small amplitudes, Rp ≫ Ak, and small deformation of the nano-particle and analyze the deformation and the elastic force in the presence of the surface phonons. For small Ak, one has a linear regime, so that the impact of each phonon may be inspected separately. Consider a phonon with the wave-vector k parallel to the axis x, where λk ∼ k−1 ≫ Rp; Fig. 6 sketches the corresponding geometry. The problem may be analyzed as a usual Hertzian contact problem,45 but with an inclined plane due to the surface phonon. The boundary between two surfaces may be approximated by the plane AB and the elastic force Fel is applied at the center O of a circular contact zone (see e.g.ref. 45). The deformation ξ1 may be found from the simple geometry as ξ1 = lOC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, where lOC is the length of the vertical segment OC and α is the angle between the direction of the elastic force, perpendicular to the contact plane, AB, and the z-axis. The length lOC follows again from the simple geometry, see Fig. 6:
α, where lOC is the length of the vertical segment OC and α is the angle between the direction of the elastic force, perpendicular to the contact plane, AB, and the z-axis. The length lOC follows again from the simple geometry, see Fig. 6:
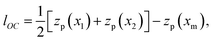 | (38) |
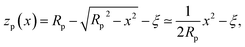 | (39) |
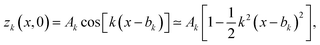 | (40) |
| zk(x) = zp(x). | (41) |
Using the above equations we find the following result, keeping only leading-order terms in k:
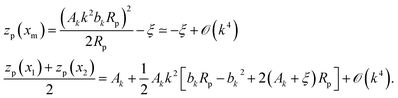 | (42) |
From the simple geometry it also follows:
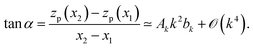 | (43) |
For small amplitudes Ak the angle α is also small, so that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α ≃ α and
α ≃ α and
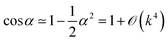 | (44) |
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α ≃ Akk2bk + α ≃ Akk2bk + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (k4). (k4). | (45) |
Using the above equations we obtain for the deformation ξ1:
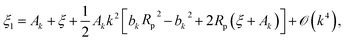 | (46) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α:
α:Fx = −κAkk2bk(Ak + ξ)3/2 + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (k4). (k4). | (47) |
Since the direction of the axis x was chosen along an arbitrary wave-vector k, eqn (47) provides a lateral force acting on the nano-particle due to a surface phonon that is characterized by its wave-vector k, amplitude Ak and the phase shift bk. It may be also written as
Fk ≃ −κ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) Akk2bk(Ak + ξ)3/2, Akk2bk(Ak + ξ)3/2, | (48) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k is a unit vector in the direction of k. To obtain the total lateral force one needs to sum over all wave-vectors k and average with an appropriate statistical weight over all possible values of Ak and bk††. We assume that the classical Boltzmann–Gibbs distribution P({Ak,bk}),
= k/k is a unit vector in the direction of k. To obtain the total lateral force one needs to sum over all wave-vectors k and average with an appropriate statistical weight over all possible values of Ak and bk††. We assume that the classical Boltzmann–Gibbs distribution P({Ak,bk}),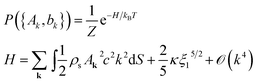 | (49) |
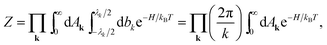 | (50) |
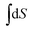 in the above equation denotes integration over the surface of the bottom plane with the total area S.
in the above equation denotes integration over the surface of the bottom plane with the total area S.
All directions of k have equal probability, therefore the average total lateral force due to the solid friction is zero. For the thermal model considered here, the general fluctuation–dissipation theorem is valid. According to this theorem, the thermal force of molecular origin, which acts on a particle, may be represented as a sum of two components, a stochastic one, which the average is zero, and a regular one, that depends on the particle velocity V, that is,46
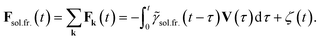 | (51) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sol.fr.(t) may be expressed in terms of the time-correlation function of the stochastic component,
sol.fr.(t) may be expressed in terms of the time-correlation function of the stochastic component,〈ζ(t′)·ζ(t)〉 = 2kBT![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sol.fr.(t − t′), 〈ζ(t)〉 = 0, sol.fr.(t − t′), 〈ζ(t)〉 = 0, | (52) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sol.fr.(t − t′) = 4γsol.fr.δ(t − t′). Then the memory function may be substituted by the friction coefficient which reads,
sol.fr.(t − t′) = 4γsol.fr.δ(t − t′). Then the memory function may be substituted by the friction coefficient which reads,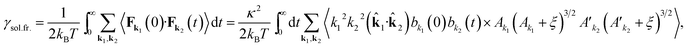 | (53) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−t/τph, as it follows from eqn (37), for the model of decaying phonons and the averaging is to be performed with the distribution P({Ak,bk}) given by eqn (49). Since all directions
e−t/τph, as it follows from eqn (37), for the model of decaying phonons and the averaging is to be performed with the distribution P({Ak,bk}) given by eqn (49). Since all directions ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) are equivalent we conclude that we need to use (
are equivalent we conclude that we need to use (![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) 1·
1·![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) 2) = δ
2) = δ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) 1,
1,![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) 2 in the above equation. If we also assume that the thermal amplitudes of the phonons are small, so that Ak ≪ ξ, we obtain,
2 in the above equation. If we also assume that the thermal amplitudes of the phonons are small, so that Ak ≪ ξ, we obtain,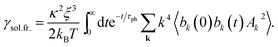 | (54) |
Using the distribution (49) one can write:
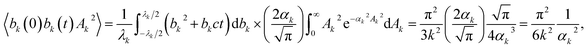 | (55) |
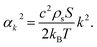 | (56) |
Substituting eqn (55) and (56) into (54) and integrating over t we obtain,
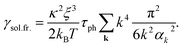 | (57) |
To perform the summation over all possible wave-vectors k of the acoustic surface phonons, we follow the standard procedure: (i) we change the summation to the integration, using the factor (S/4π2) which accounts for the density of phonons and (ii) we integrate up to the maximal wave-vector kD = ωD/c, corresponding to the Debye frequency ωD:47
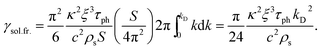 | (58) |
The Debye frequency ωD (ref. 47) can be estimated from the relation, see e.g.ref. 47:
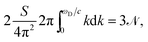 | (59) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the total number of atoms (molecules) at the surface (3
is the total number of atoms (molecules) at the surface (3![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the number of the degrees of freedom of surface atoms, which can perform lateral and tangential to the surface vibrations); the factor of two in the left hand side of the above equation takes into account the fact that for each wave-vector k one has two (sinusoidal and cosinusoidal) modes. Taking into account that the normal force squeezing the particle is FN = Fel,0 = κξ3/2 and using ρs = m0
is the number of the degrees of freedom of surface atoms, which can perform lateral and tangential to the surface vibrations); the factor of two in the left hand side of the above equation takes into account the fact that for each wave-vector k one has two (sinusoidal and cosinusoidal) modes. Taking into account that the normal force squeezing the particle is FN = Fel,0 = κξ3/2 and using ρs = m0![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) /S, where m0 is a mass of a surface atom (molecule), we finally arrive at the following expression for the friction coefficient,
/S, where m0 is a mass of a surface atom (molecule), we finally arrive at the following expression for the friction coefficient,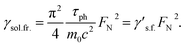 | (60) |
For further estimates we take the following values: c = 104 m s−1, m0 = 2 × 10−26 kg, which are respectively the characteristic speed of sound in solids (we use its bulk value) and the characteristic atomic mass (we use the mass of a carbon atom). To estimate the value of τph we take into account that in a bulk of a crystal the characteristic scattering length of phonons is about ten lattice units;47 with the above speed of sound it yields the value of τph ∼ 10−11 s.
We wish to stress that this coefficient corresponds to the thermal friction model and characterizes the lateral resistance force F⊥ = −γsol.fr.V acting against the velocity of a particle V. It has a different nature than that of the Coulomb friction force, which is athermal and does not depends on a particle velocity.
The diffusion coefficient may be found now from the Langevin eqn (31),
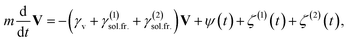 | (61) |
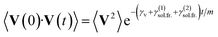 | (62) |
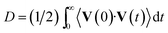 :
: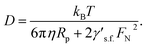 | (63) |
The clenching coefficient in this case reads,
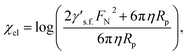 | (64) |
 | ||
| Fig. 7 The dependencies of the clenching coefficient for the thermal model of solid friction, eqn (64), on the applied electric field, Ẽ = eEb/kBT, for different concentrations of salt. The model parameters are Rp = l0/2 = 10b, c = 104 m s−1, m0 = 2 × 10−26 kg and τph = 10−11 s. For the fluid viscosity η we use the water viscosity at T = 300 K. The other parameters are the same as in Fig. 3. The magnitude of the normal force FN is taken from the MD simulations. | ||
4 Results and discussion
As one can see from Fig. 3, our theory for the mechanical force, generated by a PE in an electric field, linked to a deformable target body agrees fairly well with MD simulations if the field is not small, Ẽ = βeEb > 1, but loses its accuracy for smaller fields for high salt concentrations. The main reason for this is that the concept of a localized surface layer, with a size l much smaller than the size of the cell L, l ≪ L, is not adequate. For small fields, one has l ∼ L for our setup, so that the idealization of an unscreened bulk part of the chain, located in the renormalized uniform electric field is not any more realistic. This idealization, however, may be applicable for longer chains, in cells with larger L, so that the approximation l ≪ L remains valid.Nevertheless, one can expect that small fields are not of much relevance for possible applications, since the force generated by the nano-vices should be strong enough to keep a nano-size object fixed. Hence the limitations of our theory for small fields are not very important.
As it follows from Fig. 5 the mechanical force generated in the studied setup is large enough to significantly reduce the diffusion coefficient of a nano-particle, which is quantified by the clenching coefficient χcl. One can also notice that the presence of salt noticeably reduces the efficiency of clenching, since the salt ions diminish the effective field and hence reduce the generated force.
Comparing Fig. 5 and 7 one can notice that the athermal model demonstrates a much larger clenching coefficient which has a much steeper dependence on the electric field E as compared to that of the thermal model. Certainly, this is not surprising, since the athermal model corresponds to a rough surface on the electrodes, while the thermal model – to the smooth one. Such surface properties of the electrodes are to be taken into account in the engineering implications of nano-actuators, based on PEs in electric field.
5 Conclusions
We have studied, theoretically and by means of molecular dynamics (MD) simulations, the working principle of nano-actuators based on electroactive polymers (polyelectrolytes) in an electric field. In particular, we consider polyelectrolyte (PE) based nano-vices, that may clench and unclench nano-size objects. The nano-vices can be comprised of two parallel planes linked by PEs in an electric field. The dimension of PEs depends on the applied field, so that one can regulate the distance between the planes by varying the applied field. Hence, if a nano-particle is placed between the planes, the applied field may cause the squeezing of the particle; this significantly reduces its mobility, due to the increasing solid friction between the particle and the clenching planes. The squeezing force FN acting on the particle depends on the properties of the surrounding medium, PE properties and the applied field. We develop a theory that quantifies this force as the function of the field and salt concentration. To obtain a quantitative theory we elaborate a simple variational approach, where the distribution of microions inside the cell and the conformation of the PE chain are treated in a self-consistent manner.Next, we analyze the efficiency of PE-based nano-vices. Namely, we explore the degree of immobilization of a particle, introducing the clenching coefficient χcl as the logarithm of the ratio of the diffusion coefficients D0 of a free (unclenched) particle and D of a clenched one. The larger the χcl, the more efficient the nano-device. To compute the diffusion coefficient D of a clenched particle, we study the Brownian motion of a nano-particle squeezed between two planes, under an action of a random force from the surrounding fluid and solid friction forces from the clenching planes. We analyze two models of solid friction – an athermal model, which is applicable for rough surfaces, and a thermal model, which refers to smooth surfaces. In the former case we apply a Cundall–Strack-like model and in the latter one we develop a novel model of solid friction based on surface transversal acoustic phonons. In contrast to the previous models of surface friction, where the phonon dissipation mechanism is assumed, the new model allows one to find an explicit dependence of the friction force on the normal load, which is of primary importance for the analysis of the efficiency of nano-devices.
We observed that while for the athermal model the clenching coefficient depends linearly on the squeezing force FN, its dependence on FN in the thermal model is significantly weaker as it has a logarithmic dependence.
The results of our study may be used for the practical implementation of PE based nano-actuators.
References
- P. Kim and C. Lieber, Science, 1999, 286, 2148–2150 CrossRef CAS PubMed.
- P. MacDonald, et al. , Science, 2002, 296, 1101–1103 CrossRef PubMed.
- J. N. Coleman, et al. , Science, 2002, 331, 568–571 CrossRef PubMed.
- N. V. Brilliantov and C. Seidel, Europhys. Lett., 2012, 97, 28006 CrossRef.
- C. Seidel, Y. A. Budkov and N. V. Brilliantov, J. Nanoeng. Nanosyst., 2013, 227, 142–149 Search PubMed.
- N. V. Brilliantov, Y. A. Budkov and C. Seidel, Phys. Rev. E, 2016, 93, 032505 CrossRef CAS PubMed.
- D. Ben-Yaakov, D. Andelman, D. Harries and R. Podgornik, J. Phys.: Condens. Matter, 2009, 21, 424106 CrossRef PubMed.
- A. Naji, M. Kanduc, J. Forsman and R. Podgornik, J. Chem. Phys., 2013, 139, 150901 CrossRef PubMed.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 109, 046102 CrossRef PubMed.
- A. A. Kornyshev and R. Qiao, J. Phys. Chem. C, 2015, 118, 18285 Search PubMed.
- A. C. Maggs and R. Podgornik, Soft Matter, 2016, 12, 1219 RSC.
- Y. A. Budkov, A. L. Kolesnikov and M. G. Kiselev, Europhys. Lett., 2015, 111, 28002 CrossRef.
- Y. A. Budkov, A. L. Kolesnikov and M. G. Kiselev, J. Chem. Phys., 2016, 114, 184703 CrossRef PubMed.
- N. V. Brilliantov, Y. A. Budkov and C. Seidel, Philos. Trans. R. Soc., A, 2016, 374, 20160143 CrossRef PubMed.
- P. Atkins and J. D. Paulo, Physical Chemistry, Oxford University Press, Oxford, 8th edn, 2006 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Electrodynamics of Continuous Media, Elsevier, Amsterdam, 1960 Search PubMed.
- M. Fixman, J. Chem. Phys., 1962, 36, 306–310 CrossRef CAS.
- Y. A. Budkov and A. L. Kolesnikov, J. Stat. Mech.: Theory Exp., 2016, 2016, 103211 CrossRef.
- B. Roux and T. Simonson, Biophys. Chem., 1999, 78, 1–20 CrossRef CAS PubMed.
- F. S. Csajka and C. Seidel, Macromolecules, 2000, 33, 2728–2739 CrossRef CAS.
- N. A. Kumar and C. Seidel, Macromolecules, 2005, 38, 9341–9350 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic press, San Diego, 2nd edn, 2002 Search PubMed.
- K. Saitoh, A. Bodrova, H. Hayakawa and N. V. Brilliantov, Phys. Rev. Lett., 2010, 105, 238001 CrossRef PubMed.
- R. R. Netz, Eur. Phys. J. E, 2001, 5, 557–574 CrossRef CAS.
- B. N. J. Persson, Sliding Friction: Physical Principles and Applications, Springer, Berlin, 2nd edn, 2010 Search PubMed.
- H. Hayakawa, Phys. D, 2005, 205, 48–56 CrossRef.
- Y. Chen, A. Baule, H. Touchette and W. Just, Phys. Rev. E, 2013, 88, 052103 CrossRef PubMed.
- Y. Chen and W. Just, Phys. Rev. E, 2014, 89, 022103 CrossRef PubMed.
- B. Bhushann, Philos. Trans. R. Soc., A, 2008, 366, 1351–1381 CrossRef PubMed.
- M. Cieplak, E. D. Smith and M. O. Robbins, Science, 1994, 265, 1209–1212 CAS.
- E. D. Smith, M. O. Robbins and M. Cieplak, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8252–8260 CrossRef CAS.
- J. B. Sokoloff, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 760–765 CrossRef.
- A. Vanossi, N. Manini, M. Urbakh, S. Zapperi and E. Tosatti, Rev. Mod. Phys., 2013, 85, 529–552 CrossRef CAS.
- V. L. Popov, The Prandtl–Tomlinson Model for Dry Friction in Contact Mechanics and Friction, Springer, Berlin, Heidelberg, 2010 Search PubMed.
- J. Krim, Adv. Phys., 2012, 61, 155–323 CrossRef CAS.
- P. A. Cundall and O. D. L. Strack, Geotechnique, 1979, 29, 47–65 CrossRef.
- V. Becker and H. Briesen, Phys. Rev. E, 2008, 78, 061404 CrossRef PubMed.
- C. W. Gardiner, Handbook of Stochastic Methods, Springer, Berlin, 2nd edn, 1985 Search PubMed.
- S. Redner, A Guide to First-Passage Processes, Cambridge University Press, Cambridge, 2001 Search PubMed.
- J. Norell, A. Fasolino and A. de Wijn, Phys. Rev. E, 2016, 94, 023001 CrossRef PubMed.
- N. Manini, O. M. Braun, E. Tosatti, R. Guerra and A. Vanossi, J. Phys.: Condens. Matter, 2016, 28, 293001 CrossRef CAS PubMed.
- T. Gyalog and H. Thomas, Europhys. Lett., 1997, 37, 195–200 CrossRef CAS.
- Z. Xu and P. Huang, Wear, 2007, 262, 972–977 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Oxford University Press, Oxford, 1965 Search PubMed.
- H. Mori, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston, 1976 Search PubMed.
Footnotes |
| † In the one-chain model, this mimics the action of the upper plane of the device. |
| ‡ The deviations from the stretched conformation are not large and my be accounted by the regular approach developed in ref. 6 and 15, where the interaction between the bulk and adsorbed parts has been also taken into account and was proven to be small. Here we use the simplified theory of the completely stretched chain and neglect interactions between the bulk and adsorbed parts. |
| § Here we mean the lack of a first-principle theory of solid friction between a nano-particle under a load and a solid surface. There exists, however, first-principle31–34 and molecular-level phenomenological theories, e.g.ref. 34–36, of solid friction for adsorbed monolayers, see the discussion below. |
| ¶ Here we neglect, for simplicity, the difference between the static and sliding friction force; the latter is generally smaller.26,34 |
| || Although this dissipation mechanism is classified usually as a phononic one, see e.g. a review, ref. 36, the dissipation takes place in dumped oscillations of independent oscillators rather than in collective modes. |
| ** Note that it has already been shown that the Hertz law, eqn (36), is applicable for nano-particles of about 500–1000 atoms.24 |
| †† We assume that the total force may be written as the sum over all k, Ak and bk, that is, we assume that the superposition of the deformation forces Fk is applicable. It is expected that in the regime of linear deformations and small values of ξ and Ak this approximation is reasonable. |
| This journal is © The Royal Society of Chemistry 2017 |

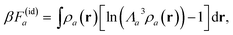
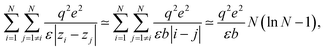
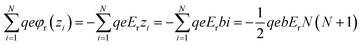
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif)