Selective hydrogenation of CO on Fe₃S₄{111}: a computational study

Abstract

Fischer–Tropsch (FT) synthesis has been a recursive method to form valuable molecules from syngas. Metal surfaces have been extensively studied as FT catalysts; among them, iron presents several phases under reaction conditions, oxides and carbides, as active sites for the FT and reverse water gas shift reaction. We present CO reduction on an iron sulfide phase with spinel structure, Fe₃S₄, also considering the pathways where C–O dissociates leaving CH_x species on the surface, which may feed longer aliphatic chains via the FT process. We analysed the thermodynamic and kinetic availability of each step leading to O and OH species co-adsorbed on the surface as well as the formation of H₂O from the hydrogenation of the alcohol group in the molecule. This detailed analysis led to energy profiles on both active sites of the surface, and we conclude that this Fe₃S₄ surface is highly selective towards the formation of methanol, in full agreement with experimental results. These findings point out that the C–C bond formation on greigite takes place through a hydroxycarbene FT mechanism.

---

Introduction

Fischer–Tropsch (FT) synthesis has been the subject of intense investigation for many decades as it gives access to industrially important chemicals from simple inorganic molecules (CO and H₂).^1–3 It is considered one of the most attractive routes to convert syngas into liquid fuels and chemicals, which consists of mainly paraffins and olefins, and low levels of oxygenates including alcohols, aldehydes, ketones and acids.⁴ Traditionally, four types of chain growth mechanisms have been proposed: the carbene mechanism,⁵ the hydoxycarbene mechanism,⁶ the CO-insertion mechanism,⁷ and the CH₂-insertion mechanism.⁸

The mechanism for methanol synthesis on metal catalysts has been extensively investigated with both experimental^9–11 and theoretical methods,^11–13 in part because it is considered to be an important alternative fuel for future transportation needs, either for methanol fuel cells or for the on-board generation of H₂ for proton-exchange membrane fuel cells.^14,15 Comparing the formation enthalpies of methanol and methane, fully reduced compounds, it is obvious that the latter is thermodynamically more favourable and therefore should hinder the formation of methanol. Methane is generated through the C–O bond fission, which may take place in adsorbed intermediate species (CH_xO and CH_xOH) somewhere along the CO hydrogenation pathway.^13,16 Indeed, minor CH_x species have been detected in methanol decomposition on metal surfaces, particularly at high pressures,¹⁷ while they may desorb rather than react under ultra-high vacuum conditions.¹⁸ Among the catalysts containing metals, iron-based catalysts have considerable merits due to their potential activity for the water–gas shift (WGS) reaction as well as their high FT activity and low cost.^3,19 The catalytic performance of these catalysts have been examined drawing the conclusion that several carbide and oxide phases are present under working conditions, among them Fe₃O₄.^20–25

A sulfide isomorphic to Fe₃O₄, greigite, has recently showed low turnover to electro-reduce CO₂ to small molecules, methanol among them.²⁶ However, the presence of S on FT catalysts has been considered as a poison, which raises the queries of the actual mechanism and the role of sulfur in the sulfide catalysts. In this work, we account for the lack of CH₄ in the experimental analysis and provide evidence of the selectivity of Fe₃S₄ between hydrogenation pathways from CO to CH₃OH and CH_x on the surface, for this is crucial to complete and understand the intricate reaction networks that can be intercrossed at any stage of the reaction.

Computational details

Periodic plane-wave DFT calculations were performed using the Vienna ab initio simulation package (VASP),^27,28 the Perdew–Wang 91 functional²⁹ within the spin interpolation formula of Vosko et al.,³⁰ and a kinetic energy of 600 eV to expand the plane-waves of the Kohn–Sham valence states.³¹ The inner electrons were represented by the projector-augmented wave (PAW) pseudopotentials considering also non-spherical contributions from the gradient corrections.³² All the calculations include the long-range dispersion correction approach by Grimme,³³ which is an improvement on pure DFT when considering large polarizable atoms.^34–39 We have used the global scaling factor parameter optimized for PBE, (s₆ = 0.75). The optimisation thresholds were 10⁻⁵ eV and 0.03 eV Å⁻¹ for the electronic and ionic relaxation, respectively. The Brillouin zone was sampled by a Γ-centred k-point mesh generated through a Monkhorst–Pack grid of 5 × 5 × 1 k-points, which ensures electronic and ionic convergence.⁴⁰ In order to improve the convergence of the Brillouin-zone integrations, partial occupancies were determined using the tetrahedron method with Blöch corrections smearing with a set width for all calculations of 0.02 eV.

The greigite unit cell consists of eight Fe₃S₄ subunits with a cubic lattice parameter of ∼9.8 Å (ref. 41 and 42) which is close to the calculated parameter resulting from the cell optimization (9.671 Å). The inverse thio-spinel arrangement is reflected by the formula AB₂S₄, where there are two possible locations for the Fe ions: tetrahedral sites (A), filled by Fe³⁺ ions, and octahedral sites (B), where both Fe³⁺ and Fe²⁺ ions co-exist.^43–49 The initial magnetic moment of the slab was described by a high spin distribution in both types of Fe with antiparallel orientation as reported previously,^50,51 which results in a ferromagnetic material.^{43,44,46–48,52–54} For an accurate treatment of the electron correlation in the localized d-Fe orbital, we have used the U approximation^55,56 (U_eff = 1 eV),^49,54,57 which improves the description of localized states in this type of systems where standard LDA and GGA functionals fail.⁵⁸ The orbital spin-splitting in the valence region results in localized outermost 3d-electrons and in ordered magnetism^45,59,60 in good agreement with experimental evidence.^50,51 We have prepared the Fe₃S₄{111} surface as a slab model by cutting the bulk structure with the METADISE code,⁶¹ which considers periodicity in the plane direction and provides the atomic layer stacking resulting in non-dipolar reconstructions.⁶² The slab contains 56 atoms (24 Fe and 32 S) per unit cell exposing an area of 81.0 Ų and a thickness of sufficient size to relax the two uppermost layers (four Fe₃S₄ units), keeping the bulk structure frozen at the bottom. We added a vacuum width of 12 Å between periodic slabs, big enough to avoid interaction between periodic images. The molecules in the gas phase were relaxed in an asymmetric box of 15 × 16 × 17 ų.

We employed the improved dimer method (IDM), to find the transition states.^63,64 We defined the adsorption energy as the difference between the isolated species and the combined system. The activation energy (E_A) of a certain step is the energy required to surmount the potential barrier characteristic of the transition state. We have defined this energy barrier as the difference between the initial state and transition state energy for the forward process. The reaction energy (E_R) of each step is calculated as the total energy difference between the final state (product(s)) and the initial state (reactant(s)).

Results and discussion

Greigite (Fe₃S₄) is an inverse spinel-structured material whose particles produced in hydrothermal synthesis expose {001} and {111} surfaces.²⁶ We focused on the active {111} surface and, due to the presence of non-equivalent Fe ions, it has two distinct terminations depending on the relative Fe_A position with respect to the uppermost sulfur layer. The most stable termination contains two adsorption sites, Fe_A and Fe_B, originally occupying tetrahedral and octahedral bulk positions.⁶⁵ The top S layer has a bulk-like structure consisting of rows along the [0−11] direction with rhombohedral packing.

We have explored the adsorption of reactants and products on Fe₃S₄{111}. While CO adsorbs on Fe_A and Fe_B with a binding energy of −0.68 and −1.07 eV respectively, the adsorption of CH₃OH is 20% weaker and CH₄ does not chemisorb. Hence, all the CH₄ molecules produced from the CO reduction will desorb from the surface leading to an overall exothermic process driven by the production of H₂O. The co-adsorption of CO and four H ad-atoms is also higher in energy than adsorbed CH₃OH (ΔE = 0.6 eV), indicating a favourable process.

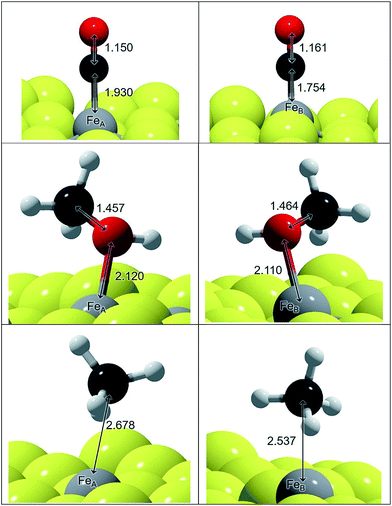
We have represented the optimised structures of CO and CH₃OH in Fig. 1 and displayed the C–O and Fe–C distances. The C–O distances in the adsorbed states on Fe_A and Fe_B are 1–2% longer than in isolated CO and CH₃OH molecules respectively. The molecules are placed practically on top of the metal sites at a distance according to their binding energy: the distances on Fe_A are longer than on Fe_B, indicating a weaker bond. The elongation of the C–O bond is also reflected in the ν_C–O stretching mode, which changes by ∼100 and ∼50 cm⁻¹ for CO and CH₃OH respectively compared to the gas phase molecules.

Fig. 1 Schematic representation of CO, CH₃OH and CH₄ on Fe_A and Fe_B sites of Fe₃S₄{111}. Inset distances are in Å. Colour scheme: light-grey is Fe, yellow is S, red is O, white is H and dark-grey is C.

While the redox property of the surface determines the capacity to transfer electrons to the adsorbates, the acid–base character controls the gain and loss of hydrogens and therefore the yields of hydrogenation products. We have explored the co-adsorption and reaction of CO and H ad-atoms on the Fe₃S₄{111} surface leading to competition between hydrogenation and C–O fission.

The adsorption of these species on transition metal surfaces has been previously investigated leading to a wide range of data. Using a similar methodology to the one we employed here, CO adsorption is reported between −0.23 and −3.21 eV (corresponding to Cu and Pd respectively),¹³ while on oxides such as Fe₃O₄{111} the adsorption energies are −1.09 and −1.94 eV on Fe_A and Fe_B respectively,⁶⁶ which are stronger than on the sulfide counterpart. These reports also indicated a C–O stretching red-shift, in agreement with our calculations, except that on pure metals it is considerably lower (∼1900 cm⁻¹).¹² Methanol adsorbs on top of fcc metals with an ideal surface releasing ∼0.5 eV, while methoxy was found to be unstable on Pt{111}.^67,68 On Fe₃O₄{111}, the adsorption of CH₃OH is weaker than of CO, which is similar to what we found on the thio-spinel, Fe₃S₄{111}, where the E_B difference between CH₃OH and CO is ∼0.1 eV.¹⁷ This is due to the fact that Fe₃O₄ is reluctant to modify its electronic structure while the sulfide has a milder ionic character.⁵⁰

Adsorption of H_xCOH and H_xCO surface species (x = 0–3)

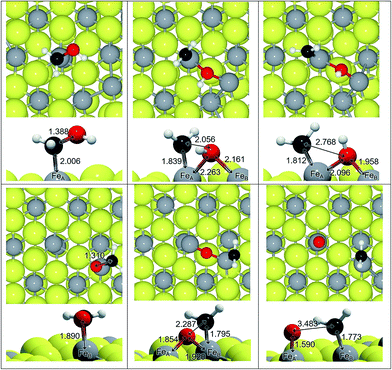
We have adsorbed the species involved in the generation of CH₃OH and characterised the most stable configurations (see Table 1). We found progressive changes between the different species along the reduction process: (i) the C–O distance increases by 0.3 Å, which on average is only 0.06 Å shorter in H_xCO than in the H_xCOH species (∼1.392 Å), (ii) the Fe–C distance also increases by >1 Å, and (iii) the C–O stretching vibrational mode shifts by ∼1000 cm⁻¹. All these changes are related to the change in carbon orbital hybridisation from sp¹ to sp³. It is noticed that the saturation of the C by hydrogens makes the molecule bind to the surface through the O(H). This implies charge transfer from the surface and makes the distances and frequencies lay slightly out from the trend line, as in the case of H₂CO (q = −0.5e) and more drastically in the Fe–C distance for the methoxy bonded through the oxygen (q = −0.35e). The relative stability of the intermediates is expressed in Table 1 by the energy difference between the intermediate in question, and the CO with the corresponding number of hydrogens on the Fe₃S₄{111} surface. It shows that although the formation of CH₃OH is thermodynamically favourable, there are less favourable intermediates making the process less likely, especially on Fe_A.

Table 1 Relative energies (ΔE), distances (d) and C–O stretching vibrational modes (ν_C–O) of the different CH_xOH and CH_xO intermediates on Fe_A and Fe_B sites of the Fe₃S₄{111} surface. The energies are relative to adsorbed CO, taking into account the corresponding number of H ad-atoms

Label	Adsorbate	Site	ΔE (eV)	d C–O (Å)	d Fe–C (Å)	ν C–O (cm^−1)
a1	CO	FeA	0.00	1.157	1.864	2049
a2	HCO		0.55	1.201	1.940	1747
a3	HCOH		0.79	1.319	1.822	1273
a4	H2CO		1.30	1.443	2.006	895
a5	H2COH		0.20	1.388	2.006	1131
a6	H3CO		0.01	1.446	3.550	962
a7	H3COH		−0.55	1.457	3.132	962
b1	CO	FeB	0.00	1.163	1.749	2026
b2	HCO		0.63	1.178	1.763	1940
b3	HCOH		0.89	1.330	1.781	1265
b4	H2CO		0.07	1.131	2.054	1288
b5	H2COH		0.55	1.396	1.997	1119
b6	H3CO		−0.16	1.406	3.017	1085
b7	H3COH		−0.57	1.464	2.981	944

---

Although the CH₃OH formation from CO is still a matter of discussion, it is well documented on fcc metals. Cu showed good catalytic performance to reduce CO though most of the reaction intermediates (those in Table 1) adsorb weakly or endothermically.⁶⁹ This is not the case for heavier metals, of which the general trend is that adsorption weakens in line with the C-orbitals hybridisation,¹³i.e. the greater hybridisation the weaker the adsorption. The geometrical changes taking place on the different species, such as the increase in bond length and red-shift of the C–O stretching vibrational mode, are also common features.¹²

Dissociation of H_xCOH and H_xCO species (x = 0–3)

We have studied the C–O scission of each intermediate species lying on Fe_A and Fe_B taking into account that the products may be displaced to a nearby Fe site; for instance, the C–O splitting of H₂COH adsorbed on Fe_A, leads to CH₂ remaining on Fe_A while OH binds both Fe_A and Fe_B, see Fig. 2. Once the C–O bond is completely dissociated, the CH_x species lie an average of 0.4 Å closer to Fe than before dissociation. This short distance is also a consequence of the electrophilic character of the co-adsorbed O and OH groups, which withdraw electrons from nearby atoms; a co-adsorbed O ad-atom makes the Fe–C distance 0.09 Å shorter than a co-adsorbed hydroxyl on Fe_A, while it remains practically invariable on Fe_B (Δd_Fe–C = 0.01 Å).

Fig. 2 Top and side views of C–O dissociation on the Fe₃S₄{111} surface: H₂COH on Fe_A and H₂CO on Fe_B. Reactants are on the right, the transition states are in the centre and the products are on the left. Colour scheme: light-grey is Fe, yellow is S, red is O, white is H and dark-grey is C. All distances in Å.

Table 2 summarises the activation and reaction energies for the direct C–O scission. On Fe_A sites, the reaction energy (E_R) related to C–O bond breaking is (i) endothermic (E_R > 1 eV) for a2, a3 and a5 species, (ii) slightly endothermic (0 < E_R > 1 eV) for methoxy (a6), and (iii) exothermic (E_R < 0 eV) for formaldehyde (a4) and methanol (a7). Nevertheless, the high energy barriers indicate that the process is kinetically hindered and the C–O scission is unlikely; the lowest E_A is for H₂CO but still above 1 eV. The electronic and geometrical differences between sites make Fe_B behave differently: the process is endothermic for all the intermediates and E_R is lower than 1 eV only for H₃COH, while all the energy barriers are well above 1.5 eV.

Table 2 Activation (E_A) and reaction (E_R) energies for breaking the surface species C–O bond on Fe_A and Fe_B sites of the Fe₃S₄{111} surface

Label	Site	Reactants → products	E A (eV)	E R (eV)
R1	FeA	HCO → CH + O	3.91	2.08
R2		HCOH → CH + OH	2.79	1.56
R3		H2CO → CH2 + O	1.27	−0.55
R4		H2COH → CH2 + OH	1.84	1.50
R5		H3CO → CH3 + O	2.46	0.48
R6		H3COH → CH3 + OH	1.87	−0.19
R7	FeB	HCO → CH + O	4.34	3.48
R8		HCOH → CH + OH	1.72	1.69
R9		H2CO → CH2 + O	2.97	2.56
R10		H2COH → CH2 + OH	2.17	1.02
R11		H3CO → CH3 + O	2.52	1.72
R12		H3COH → CH3 + OH	2.32	0.69

---

The energy data in Table 2 shows that breaking the C–O bond is unfavourable under mild conditions. Although the activation and reaction energies have been found to be much smaller on pure metallic systems such as Pd{111},¹³ they follow a similar trend, showing the C–O splitting to be more favourable on HCOH and H₂COH intermediates.

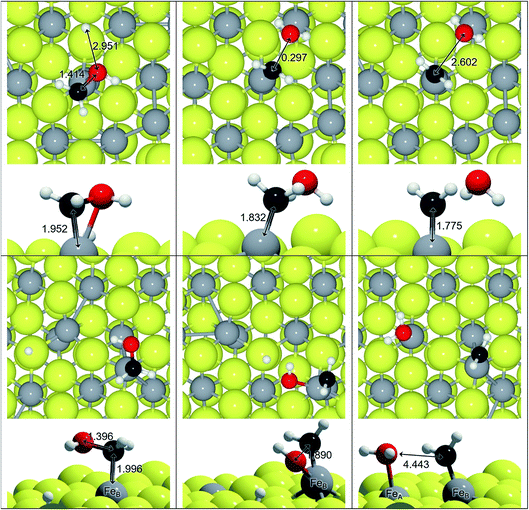
We have explored an alternative mechanism for C–O bond breaking driven by H₂O generation, which is schematically represented in Fig. 3. Table 3 contains the activation and reaction energies for that process on Fe_A and Fe_B, respectively. The energy trends show decreasing values as the number of hydrogens in the molecule is increased, i.e. the C-orbital hybridisation changes from sp¹ to sp³. In spite of this, the process is endothermic and kinetically unfavourable.

Fig. 3 Top and side views of H₂O driven C–O dissociation on the Fe₃S₄{111} surface: H₂COH on Fe_A and on Fe_B sites. Reactants are on the right, transition states are in the centre and products are on the left. Colour scheme: light-grey is Fe, yellow is S, red is O, white is H and dark-grey is C. All distances in Å.

Table 3 Activation (E_A) and reaction (E_R) energies for the reaction H_xCOH → H_xC + H₂O on Fe_A and Fe_B sites of the Fe₃S₄{111} surface

	Site	Reactants → products	E A (eV)	E R (eV)
R13	FeA	HCOH + H → CH + H2O	1.71	0.77
R14		H2COH + H → CH2 + H2O	0.93	0.72
R15		H3COH + H → CH3 + H2O	1.75	−0.22
R16	FeB	HCOH + H → CH + H2O	2.46	2.06
R17		H2COH + H → CH2 + H2O	1.75	0.63
R18		H3COH + H → CH3 + H2O	1.98	−0.15

---

Among the different reaction mechanisms explored, only R3 and R6 are exothermic. Despite this, they are kinetically disabled and therefore the presence of CH_x groups should be very scarce on Fe₃S₄{111}. Fig. 4 shows the energy profile for the reduction of CO to methanol (black lines) and the different paths studied describing the C–O dissociations for the direct and H₂O driven pathways (red and blue lines, respectively). Most of these pathways are hindered by the high energy barrier, however, we noticed that for H_xCO(H) species with x > 2, the dissociation of the C–O bond requires the same or less energy than some steps undertaken during the CO reduction. Therefore, if the system has enough energy to overcome the barrier of producing H_xCO(H) intermediates, the C–O dissociation is accessible and some pathways become competitive, e.g. R4, R6, R11, R12, R14, R15, R17 and R18.

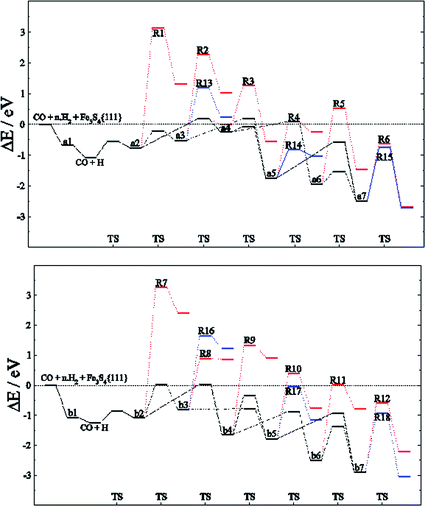Fig. 4 Energy profile for the reduction mechanism of CO to CH₃OH (black line) on Fe_A (top) and Fe_B (bottom) sites of Fe₃S₄{111} considering the direct scission of C–OH_x bond (red line) and its dissociation assisted by an H ad-atom leading to H₂O (blue line). Intermediates and C–O dissociation reactions are labelled according to Tables 1–3.

The reaction network for CH₃OH formation on Fe_A may take place through H_xCO and H_xCOH intermediates; nonetheless, the path for the formation of a6 from a4 requires more energy to overcome the transition energy than that leading to a5. However, R14 is more kinetically feasible leading to CH_x + H₂O, although the process is thermodynamically unfavourable. Thus, a5 (H₂COH) is crucial for the production of methanol, the desorption of which is >1 eV below the H₃C–OH scission energy barriers. On the other hand, the C–O dissociations on Fe_B have a higher energy barrier: the stabilisation of b4 means that both H₃CO and H₃COH will be formed, the latter desorbing from the catalyst prior to dissociation. These results are in full agreement with the fact that CH₄ molecules were not detected during the experiments using gas-chromatography and ¹H-NMR techniques.²⁶

Conclusions

We have studied systematically the competitive reactions of CO hydrogenation and C–O dissociation on both adsorption sites, Fe_A and Fe_B, of Fe₃S₄{111}. All the calculations were performed using DFT+U, including the long-range dispersion forces. We found a correlation of the C–O bond strength with the C orbital hybridization according to the bond distances and vibrational analysis, which is similar to the trends reported on metals and metal oxides. The examination of relative energies between the reactants and intermediates showed that although the reactions leading to the formation of methanol and methane are thermodynamically favorable, driven by the high energy of the H₂ molecules (and the formation of H₂O), it is necessary to overcome a reaction barrier. There are intermediates of higher energy, HCOH and H₂CO, that determine the formation of products, especially on Fe_A. The lower energy reaction pathway leads exclusively to methanol through HCOH on Fe_A while both the HCOH and H₂CO intermediates are of competing stability in the reaction mechanism on Fe_B. Thus, the C–O scission is generally an endothermic or kinetically disabled process under mild conditions on Fe₃S₄{111}; for this reason, this surface presents a selective CO reduction towards a low level of oxygenated molecules while iron oxides may lead to totally reduced molecules.

Acknowledgements

We acknowledge the Engineering & Physical Sciences Research Council (grant EP/K035355/1 and EP/K035355/2) for funding. This work made use of the ARCHER facilities, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, funded by the Office of Science and Technology through EPSRC's High End Computing Programme and provided via our membership of the HPC Materials Chemistry Consortium (EPSRC EP/L000202). The authors also acknowledge the use of the UCL Legion High Performance Computing Facility and the Advanced Research Computing @ Cardiff (ARCCA) at Cardiff University, and associated support services, in the completion of this work. All data created during this research is openly available from the University of Cardiff Research Portal at http://doi.org/10.17035/d.2016.0011347963.

References

1. C. K. Rofer-DePoorter, Chem. Rev., 1981, 81, 447–474.
2. J. J. C. Geerlings, J. H. Wilson, G. J. Kramer, H. P. C. E. Kuipers, A. Hoek and H. M. Huisman, Appl. Catal., A, 1999, 186, 27–40.
3. M. E. Dry, Catal. Today, 2002, 71, 227–241.
4. A. Y. Khodakov, W. Chu and P. Fongarland, Chem. Rev., 2007, 107, 1692–1744.
5. F. Fischer and H. Tropsch, Ber. Dtsch. Chem. Ges., 1926, 59, 830–831.
6. J. T. Kummer and P. H. Emmett, J. Am. Chem. Soc., 1953, 75, 5177–5183.
7. A. Y. Krylova, Solid Fuel Chem., 2014, 48, 22–35.
8. P. M. Maitlis, R. Quyoum, H. C. Long and M. L. Turner, Appl. Catal., A, 1999, 186, 363–374.
9. I. A. Fisher and A. T. Bell, J. Catal., 1997, 172, 222–237.
10. J. Nerlov and I. Chorkendorff, J. Catal., 1999, 181, 271–279.
11. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893.
12. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
13. R. García-Muelas, Q. Li and N. López, ACS Catal., 2015, 5, 1027–1036.
14. A. K. Avcı, Z. İ. Önsan and D. L. Trimm, Top. Catal., 2003, 22, 359–367.
15. D. R. Palo, R. A. Dagle and J. D. Holladay, Chem. Rev., 2007, 107, 3992–4021.
16. S. Lin, J. Ma, X. Ye, D. Xie and H. Guo, J. Phys. Chem. C, 2013, 117, 14667–14676.
17. M. Baumer, J. Libuda, K. M. Neyman, N. Rosch, G. Rupprechter and H.-J. Freund, Phys. Chem. Chem. Phys., 2007, 9, 3541–3558.
18. S. K. Desai, M. Neurock and K. Kourtakis, J. Phys. Chem. B, 2002, 106, 2559–2568.
19. D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097.
20. M. D. Shroff, D. S. Kalakkad, K. E. Coulter, S. D. Kohler, M. S. Harrington, N. B. Jackson, A. G. Sault and A. K. Datye, J. Catal., 1995, 156, 185–207.
21. R. J. O'Brien, L. Xu, R. L. Spicer and B. H. Davis, Energy Fuels, 1996, 10, 921–926.
22. Q.-L. Hao, F.-X. Liu, H. Wang, J. Chang, C.-H. Zhang, L. Bai, H.-W. Xiang, Y.-W. Li, F. Yi and B.-F. Xu, J. Mol. Catal. A: Chem., 2007, 261, 104–111.
23. M. Ding, Y. Yang, J. Xu, Z. Tao, H. Wang, H. Wang, H. Xiang and Y. Li, Appl. Catal., A, 2008, 345, 176–184.
24. M. Luo, H. Hamdeh and B. H. Davis, Catal. Today, 2009, 140, 127–134.
25. L. A. Cano, M. V. Cagnoli, J. F. Bengoa, A. M. Alvarez and S. G. Marchetti, J. Catal., 2011, 278, 310–320.
26. A. Roldan, N. Hollingsworth, A. Roffey, H. U. Islam, J. B. Goodall, C. R. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. de Leeuw, Chem. Commun., 2015, 51, 7501–7504.
27. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
28. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
29. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
30. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
31. N. D. Mermin, Phys. Rev., 1965, 137, 1441–1443.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
33. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
34. S. Irrera, A. Roldan, G. Portalone and N. H. De Leeuw, J. Phys. Chem. C, 2013, 117, 3949–3957.
35. N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Chem. Phys., 2013, 139, 124708.
36. S. S. Tafreshi, A. Roldan, N. Y. Dzade and N. H. de Leeuw, Surf. Sci., 2014, 622, 1–8.
37. S. Haider, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2013, 118, 1958–1967.
38. N. Dzade, A. Roldan and N. de Leeuw, Minerals, 2014, 4, 89–115.
39. F. Zhang, J. D. Gale, B. P. Uberuaga, C. R. Stanek and N. A. Marks, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054112–054117.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
41. J. M. D. Coey, M. R. Spender and A. H. Morrish, Solid State Commun., 1970, 8, 1605–1608.
42. M. R. Spender, J. M. D. Coey and A. H. Morrish, Can. J. Phys., 1972, 50, 2313–2326.
43. D. J. Vaughan and J. A. Tossell, Phys. Chem. Miner., 1983, 9, 253–262.
44. D. J. Vaughan and J. A. Tossell, Am. Mineral., 1981, 66, 1250–1253.
45. D. J. Vaughan and J. R. Craig, Am. Mineral., 1985, 70, 1036–1043.
46. K. K. Surerus, M. C. Kennedy, H. Beinert and E. Munck, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 9846–9850.
47. M. J. Dekkers, H. F. Passier and M. A. A. Schoonen, Geophys. J. Int., 2000, 141, 809–819.
48. M. J. Dekkers and M. A. A. Schoonen, Geophys. J. Int., 1996, 126, 360–368.
49. L. Chang, B. D. Rainford, J. R. Stewart, C. Ritter, A. P. Roberts, Y. Tang and Q. W. Chen, J. Geophys. Res.: Solid Earth, 2009, 114, 1–10.
50. A. Roldan, D. Santos-Carballal and N. H. de Leeuw, J. Chem. Phys., 2013, 138, 204712–204716.
51. D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195106.
52. D. J. Vaughan and M. S. Ridout, J. Inorg. Nucl. Chem., 1971, 33, 741–746.
53. M. Braga, S. K. Lie, C. A. Taft and W. A. Lester, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 10837–10851.
54. L. Chang, A. P. Roberts, Y. Tang, B. D. Rainford, A. R. Muxworthy and Q. Chen, J. Geophys. Res., 2008, 113, 1–16.
55. V. I. Anisimov, M. A. Korotin, J. Zaanen and O. K. Andersen, Phys. Rev. Lett., 1992, 68, 345–348.
56. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
57. A. J. Devey, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195126–195133.
58. I. D. R. Moreira, F. Illas and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102–155116.
59. D. J. Vaughan and J. A. Tossell, Am. Mineral., 1981, 66, 1250–1253.
60. D. Rickard and G. W. Luther, Chem. Rev., 2007, 107, 514–562.
61. G. W. Watson, E. T. Kelsey, N. H. deLeeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438.
62. P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984.
63. G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022.
64. A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101–224115.
65. A. Roldan and N. H. de Leeuw, Proc. R. Soc. London, Ser. A, 2016, 472.
66. G. S. Parkinson, Surf. Sci. Rep., 2016, 71, 272–365.
67. B. A. Sexton, Surf. Sci., 1981, 102, 271–281.
68. E. M. Karp, T. L. Silbaugh, M. C. Crowe and C. T. Campbell, J. Am. Chem. Soc., 2012, 134, 20388–20395.
69. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Norskov, Energy Environ. Sci., 2010, 3, 1311–1315.

---