Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Aqueous singlet oxygen reaction kinetics of furfuryl alcohol: effect of temperature, pH, and salt content†
Elena
Appiani‡
a,
Rachele
Ossola‡
a,
Douglas E.
Latch
b,
Paul R.
Erickson
*a and
Kristopher
McNeill
 *a
*a
aInstitute of Biogeochemistry and Pollutant Dynamics (IBP), Department of Environmental Systems Science, ETH Zurich, 8092 Zurich, Switzerland. E-mail: paul.erickson@env.ethz.ch; kris.mcneill@env.ethz.ch
bDepartment of Chemistry, Seattle University, Seattle, Washington 98122, USA
First published on 14th February 2017
Abstract
The rate constant for the reaction between furfuryl alcohol (FFA) and singlet oxygen (1O2) in aqueous solution was measured as a function of temperature, pH and salt content employing both steady-state photolysis (β value determination) and time-resolved singlet oxygen phosphorescence methods. The latter provided more precise and reproducible data. The reaction rate constant, krxn,FFA, had a relatively small temperature dependence, no pH dependence and showed a small increase in the presence of high salt concentrations (+19% with 1 M NaCl). A critical review of the available literature suggested that the widely used value of 1.2 × 108 M−1 s−1 is likely overestimated. Therefore, we recommend the use of 1.00 × 108 M−1 s−1 for reactions performed in low ionic strength aqueous solutions (freshwater) at 22 °C. Furthermore, corrections are provided that should be applied when working at higher or lower temperatures, and/or at high salt concentrations (seawater).
Environmental impactSinglet oxygen is a short-lived oxidant formed in sunlit surface waters and is important to the fate of anthropogenic and naturally occurring organic compounds. Due to its short lifetime, the use of molecular probes to quantify its steady-state concentration are needed. Furfuryl alcohol has become the most widely used probe molecule for singlet oxygen studies. This work greatly improves the utility of furfuryl alcohol as a singlet oxygen probe by assessing the reaction rate constant under a wide variety of environmentally relevant conditions. |
Introduction
Singlet oxygen (1O2, O2 (1Δg)), the first electronic excited state of dioxygen, is widely studied due to its importance in both biological and environmental systems. In the context of aquatic photochemistry, 1O2 was first recognized as a potentially important species in sunlit surface waters by Zepp in 1977.1 Singlet oxygen is a selective electrophile, reacting primarily with anilines, electron-rich phenols, S-containing compounds, furans and other electron-rich heterocycles.2–4 It is worth noting that five naturally occurring amino acids (histidine, tryptophan, tyrosine, methionine, cysteine) fall into these categories.5–7 Singlet oxygen has been shown to be the main oxidant for histidine photodegradation in natural waters, accounting for essentially 100% of its sunlight-mediated degradation.5 Singlet oxygen is also involved in the environmental degradation of proteins, viruses and biomolecules, making it an important species in carbon cycling.6–12 In addition, 1O2 contributes to the photodegradation of well-known micropollutants such as the fungicide propiconazole13 and antibiotics belonging to the sulfonamide group.14 It has also been found to be the primary reactive species responsible for cimetidine15 and bacitracin A16 photochemical decomposition.From Zepp's initial report of 1O2 in surface waters onward, the study of 1O2 in environmental systems has relied heavily on the use of 1O2-reactive molecular probe molecules. In 1984, Haag et al. proposed the use of furfuryl alcohol (FFA) and since that time it has become the standard probe molecule for 1O2.18 There are several reasons for FFA's ascendancy. Nardello et al. outlined several criteria for an ideal 1O2 probe:17 (1) it must be water soluble; (2) it must react selectively and with high rate constants with 1O2; (3) it should not absorb light at the working wavelength(s); (4) it should not quench 1O2 or sensitizer triplets physically; (5) it must form stable products; and, (6) it should be indefinitely stable under dark conditions. FFA meets all of these requirements. In addition, it is commercially available, inexpensive, and has excellent chromatographic properties.
Critical to its use as a probe molecule is FFA's bimolecular reaction rate constant with 1O2, krxn,FFA. Most workers in the field of environmental chemistry use the value reported by Haag et al. in 1984 of 1.2 × 108 M−1 s−1,18 which was determined indirectly through O2 consumption in photoirradiated aqueous solutions containing Rose Bengal. Our group and a few others have used 0.83 × 108 M−1 s−1, a value that is 30% lower, which was based on direct observation of 1O2 quenching by FFA in D2O by time-resolved phosphorescence.15 Over the past few years, it has become clear to us that there are reasons to be suspicious of both of these values. For instance, careful reading of the initial report of Haag et al. reveals that they did not measure 1.2 × 108 M−1 s−1; rather, they determined a value of 1.09 × 108 M−1 s−1 at 22 °C and averaged it with the previously reported rate constant of 1.4 × 108 M−1 s−1 measured at 37 °C by Sluyterman.18,19 The time-resolved phosphorescence-based value that we determined was based on the assumption that FFA was not significantly consumed during the brief laser irradiation period, which we now believe to likely be incorrect. The shortcomings of these previous measurements will be discussed in more detail below, but suffice it to say that there was good motivation to re-evaluate the FFA-1O2 rate constant.
In addition to re-measuring the rate constant for FFA and 1O2, we felt it was also important to undertake an evaluation of the effects of temperature, pH and salt concentration on krxn,FFA. It is valuable to understand these effects not only because of the natural variability of surface waters (e.g., freshwater vs. seawater), but also because of the fact that mechanistic or in situ investigations may require, for example, a wide range of temperatures and pH values.
In the present study, we used two different methods for the determination of the rate constant of 1O2 and FFA. In the first method, we followed the initial rate of FFA consumption in the presence of 1O2 at various FFA concentrations. The initial rate saturates at sufficiently high FFA concentrations and the half-saturation concentration of FFA (the beta value, β) can be directly related to krxn,FFA. This is similar to the method of Haag et al., but following FFA instead of O2 consumption. We reasoned that this would be a more direct measure of the bimolecular reaction rate constant, as there might be other reactions that consume O2 besides that of FFA with 1O2. In the second method, we followed the kinetics of 1O2 relaxation in the presence of increasing concentrations of FFA by time-resolved phosphorescence laser spectroscopy. These experiments were performed in H2O, which was deemed better than previous measurements in D2O, as it is unknown whether there is a solvent isotope effect on krxn,FFA. This latter method proved to be highly precise and reproducible and was therefore used further to determine the temperature, pH, and salt concentration dependence of krxn,FFA.
Materials and methods
Materials
Perinaphthenone (PN), sodium bromide, guanidinium chloride, lithium chloride and sodium phosphate dibasic were purchased from Sigma Aldrich. Furfuryl alcohol (FFA) was obtained from Merck, and purified by distillation prior to use. Sodium bicarbonate, sodium chloride and magnesium dichloride hexahydrate were also purchased from Merck. Potassium dihydrogen phosphate, magnesium sulfate heptahydrate, calcium dichloride dehydrate, sodium perchlorate monohydrate and potassium chloride were from Fluka. D2O was obtained from Armar. All solvents used for the analysis were of HPLC grade. All aqueous solutions were prepared in ultrapure water (resistivity > 18 MΩ, Barnstead Nanopure Diamond System). N2 (99.999%) and O2 (99.9995%) were purchased from CarbaGas.Steady-state photolysis experiments
| −d[FFA]/dt = krxn,FFA[1O2]ss[FFA], | (1) |
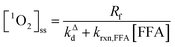 | (2) |
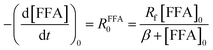 | (3) |
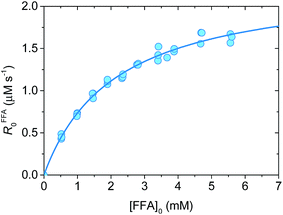
Fig. 1 shows a plot of RFFA0vs. [FFA]0. The curve is an example of saturation kinetics, and as such is characterized by two parameters: Rf and β. The formation rate (Rf, [M s−1]) represents the asymptote of the curve, and is thus the maximum FFA degradation rate (Rf = RFFA0 = RFFA0,max when [FFA]0 ≫ β). The half-saturation constant β [M] corresponds to the FFA concentration that gives RFFA0 = 1/2 × Rf. β is the parameter of interest in this study, since it can be used to derive krxn,FFAviaeqn (4).
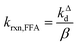 | (4) |
Time-resolved singlet oxygen phosphorescence experiments
 | (5) |
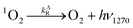 | (6) |
 | (7) |
 | (8) |
By integration of the kinetic rate law, it is possible to demonstrate that the 1O2 concentration will follow a growth and decay profile as described by eqn (9).27
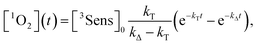 | (9) |
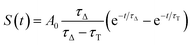 | (10) |
| kΔ = kΔd + krxn,FFA[FFA] | (11) |
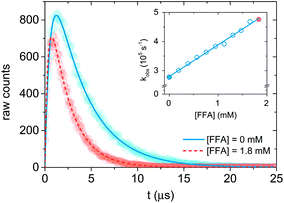 | ||
| Fig. 2 Singlet oxygen formation and decay profiles in the presence of 0 mM (blue) and 1.8 mM (red) FFA recorded with 75 μM PN in MilliQ water for 10 s. The circles represent the experimental points, and the lines are the curve fits performed with Origin (eqn (12)). For data analysis, decay portions were fit to a monoexponential function (eqn (10)). The insert is the Stern–Volmer plot obtained with the experimental data. The points associated with the signal in the main plot are highlighted in blue and red. | ||
Therefore, a plot of kΔvs. [FFA] provides krxn,FFA from the slope of the regression line (Stern–Volmer plot, insert in Fig. 2),31 while the intercept yields the solvent deactivation rate constant kΔd (experimental values in the ESI†).
Time-resolved 1O2 phosphorescence experiments. The experimental setup used for 1O2 phosphorescence measurements was based on a previously published design.22 For our experiment, excitation pulses were generated by converting the primary 795 nm output of a regeneratively amplified laser (Solstice, Spectra-Physics, Darmstadt, Germany, pulse width < 100 fs, 1 kHz repetition rate) with a TOPAS optical parametric amplifier (Light Conversion, Vilnius, Lithuania) to 365 nm. A cuvette containing the sample solution was housed in a cuvette holder (Thor labs CVH100) with an integrated lens/fiber optic mount. Samples were excited with a collimated beam (spot size approx. 7 mm) set to a power of 50–70 mW. Singlet oxygen phosphorescence was monitored 90° to the excitation, and the emitted photons were first passed through a 1270 ± 5 nm bandpass filter, and collected with a lens focused onto a 1 mm i.d. optical fiber which terminates into a fiber mount attached to the window of a near-IR PMT (Hamamatsu, model H10330-45). The PMT output was sent to a preamplifier (PAM 103-P PicoQuant) and then on to a multichannel scaler (TimeHarp 260Nano, PicoQuant) for integrated photon counting. Singlet oxygen phosphorescence was collected in one of two ways. First, photon counts were integrated until approximately 600 counts were reached at the signal maximum (see Fig. 2 for an indication of the relative signal to noise achieved at 600 counts), after which the measurements were manually stopped. Second, photon counts were integrated for 10 s. Both methods provided adequate signal for reliable data fitting, and no significant differences could be seen between them. Transient data were exported to Origin for fitting and analysis.
Temperature variation experiments. A 1-cm pathlength flow-through cuvette was connected via Tygon tubing to a three-necked flask (250 mL) containing a solution of PN (200 mL, 75 μM PN, pH 6.8 phosphate-buffered, I = 10 mM corrected with NaCl). The flask, which acted as a reservoir, was placed in a stirred, temperature-controlled water bath. A peristaltic pump ensured good mixing and continuous circulation through the system. The solution was continuously circulated from the reservoir to the cuvette, and then back to the reservoir at a flow rate of approximately 2.5 mL s−1. The PN solution was first equilibrated at the desired temperature, then the reservoir was purged with O2 for approx. 5 min. An aliquot of FFA stock (400 μL, 0.1 M FFA in water) was added to the PN solution, and after 3 min of equilibration, a sample (150 μL) was removed for HPLC analysis to determine the actual FFA concentration. The FFA addition and data collection procedure was repeated 10 times, until a total FFA stock volume of 4 mL (10 × 400 μL) was added. Data were collected at seven different temperatures: 5, 10, 25, 30, 35, 40, and 45 °C.
pH effect and salt effect (concentration and type) experiments. The measurements were performed using a flow-to-waste setup. This experimental arrangement is identical to the flow-through setup except that the solution in the cuvette is flushed to a waste beaker during irradiation to avoid buildup of degradation products. A 1-cm flow-through cuvette was connected via Tygon tubing to a reservoir filled with PN solution (ca. 500 mL, 75 μM). For each pH variation experiment, the pH was adjusted to the desired value with NaOH 1 M or HCl 1 M. In NaCl concentration experiments, PN solutions were prepared in pH 6.8 phosphate buffer (10 mM), and the salt concentration was increased by addition of NaCl. Similarly, salt effect experiments were performed in pH 6.8 phosphate-buffered PN solutions at 2 M total salt concentration. For each experiment, the solution was stirred, purged with O2, and circulated in the system for 5 min prior to analysis using a peristaltic pump. FFA (neat, 5 μL) was added to the solution, and after 2 min of equilibration, an aliquot (150 μL) was withdrawn for HPLC analysis. The FFA addition and data collection procedure was repeated 10 times, until a total FFA stock volume of 50 μL (10 × 5 μL) was added. The FFA concentration was later determined by HPLC analysis. This experiment was repeated at ten pH values, from 3 to 12, and at 6 different NaCl concentrations in the interval 0.01–1 M. The salt effect was tested on 2 M solutions of NaCl, NaBr, NaI, NaClO4, LiCl, MgCl2 and guanidinium chloride (GnCl). A duplicate measurement was also recorded using artificial seawater prepared according to Brujewicz.32
| S(t) = C × e−t/τΔ | (12) |
Eqn (12) is a simplified form of eqn (10) that holds when only the decay portion of the singlet oxygen signal is taken into account, i.e., for t > 2.5 μs. Prior to 2.5 μs PN is still forming 1O2, thus the signal cannot be treated as a simple monoexponential decay. The reciprocal of the lifetime, kobs = 1/τΔ, was plotted against the [FFA] determined by HPLC analysis. The bimolecular rate constant krxn,FFA was obtained as the slope of the regression line (eqn (11)). Using data obtained from the temperature variation experiments, Arrhenius and Eyring plots were constructed in order to extract the activation parameters of the reaction, namely energy of activation (Ea), preexponential factor (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A), enthalpy of activation (ΔH‡) and entropy of activation (ΔS‡).
A), enthalpy of activation (ΔH‡) and entropy of activation (ΔS‡).
Results and discussion
Temperature dependence
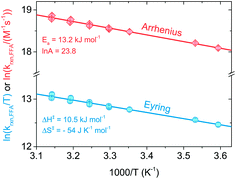
The temperature dependence of krxn,FFA was assessed over a 40 °C range (T = 5–45 °C) with both steady-state and time-resolved methods. Activation parameters determined from both Arrhenius and Eyring analyses are summarized in Table 1. As a general observation, the two methods provide comparable and consistent results. However, the time-resolved data were more reproducible and precise: lower experimental variability was observed with the time-resolved method across all of the experiments performed in this study. Therefore, the following sections will focus primarily on the time-resolved data.| Method | T range (°C) | Arrhenius parameters | Eyring parameters | Reference | ||
|---|---|---|---|---|---|---|
| E a (kJ mol−1) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
ΔH‡ (kJ mol−1) | ΔS‡ (J K−1 mol−1) | |||
| a Converted from the Arrhenius parameters using the following relationships (T = 298 K): Ea = ΔH‡ + RT; A = ekBT/h × e(ΔS‡/R).34 | ||||||
| β value FFA consumption | 5–45 | 18 ± 2 | 26 ± 1 | 16 ± 2 | −(40 ± 8) | This work |
| Time-resolved phosphorescence | 5–45 | 13.2 ± 0.5 | 23.8 ± 0.2 | 10.5 ± 0.5 | −(54 ± 2) | This work |
| β value O2 consumption | 15–45 | 22.7 | 27.8 | 20.2a | −22a | Gottfried and Kimel (1991)33 |
| β value FFA consumption | 0–23 | 19.9 | 26.9 | 17.6 | −28.8 | Gassmann (1984)38 |
Fig. 3 shows Arrhenius (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krxn,FFAvs. 1/T) and Eyring (ln(krxn,FFA/T) vs. 1/T) plots used to determine the activation parameters for the time-resolved phosphorescence data. A linear regression of the former provided Ea = (13.2 ± 0.5) kJ mol−1 and ln
krxn,FFAvs. 1/T) and Eyring (ln(krxn,FFA/T) vs. 1/T) plots used to determine the activation parameters for the time-resolved phosphorescence data. A linear regression of the former provided Ea = (13.2 ± 0.5) kJ mol−1 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = 23.8 ± 0.2, while the Eyring analysis gave ΔH‡ = (10.5 ± 0.5) kJ mol−1 and ΔS‡ = −(54 ± 2) J K−1 mol−1. The steady-state photolysis method (β determination, Fig. S2†) gave a higher ΔH‡ ((16 ± 3) kJ mol−1) and less negative ΔS‡ (−(40 ± 8) J K−1 mol−1), with higher uncertainty in both values than found with time-resolved phosphorescence.
A = 23.8 ± 0.2, while the Eyring analysis gave ΔH‡ = (10.5 ± 0.5) kJ mol−1 and ΔS‡ = −(54 ± 2) J K−1 mol−1. The steady-state photolysis method (β determination, Fig. S2†) gave a higher ΔH‡ ((16 ± 3) kJ mol−1) and less negative ΔS‡ (−(40 ± 8) J K−1 mol−1), with higher uncertainty in both values than found with time-resolved phosphorescence.
Activation parameters for the reaction of FFA with 1O2 were previously determined by Gottfried and Kimel using a porphyrin sensitizer and a Clark electrode apparatus for measuring dissolved oxygen (entry 6 in Table 2).33 Their reported values, when converted to enthalpy and entropy of activation (Ea = ΔH‡ + RT; A = ekBT/h × e(ΔS‡/R)),34 are ΔH‡ = 20.2 kJ mol−1 and ΔS‡ = −22 J K−1 mol−1, which are generally consistent with those determined here. We favor the values found in the present study as there was more precision in the individual measurements and the temperature dependence was determined over a greater temperature range (40 vs. 30 °C range).
| Entry | k rxn,FFA (108 M−1 s−1) | T (°C) | k rxn,FFA (108 M−1 s−1) | Sensitizerb | Solvent | pH | Method | Reference |
|---|---|---|---|---|---|---|---|---|
| a Calculated with eqn (14). b Sensitizer abbreviations: PF = proflavine, RB = Rose Bengal, PS-RB = polystyrene-bound RB, TPPS4 = meso-tetraphenylporphyrin tetrasulfonate, Hpd = hematoporphyrin derivative, PN = perinaphthenone. c Measured. d Reported. e The error is the standard deviation calculated from the two reported values. f The error is the standard deviation calculated from the determinations performed at the different pH values. g The rate constant was also determined in D2O and no solvent isotope effect was found (kH/kD = 1.00 ± 0.06). | ||||||||
| 1 | 1.4 | 37 | 1.30 | PF | H2O | 3–9 | O2 consumption (Warburg manometer) | Sluyterman (1961)19 |
| 2 | 1.1 | 9 | 0.79 | PS-RB | H2O | — | FFA consumption | Gassmann (1984)38 |
| 3 | 1.09 ± 0.09c | 22 | 1.00 | RB | H2O | 7 (?) | O2 consumption (Clark electrode) | Haag (1984)18 |
| 1.2d | ||||||||
| 4 | 0.93 ± 0.15e | 22 | 1.00 | Hpd | 15 mM NaCl, H2O | 7.4 (?) | O2 consumption (Clark electrode) | Murasecco (1985)51 |
| 5 | 1.2 | — | — | RB | H2O | 7–11.5 | O2 consumption (Clark electrode) | Scully and Hoigné (1987)39 |
| 6 | 1.4 | 25 (15–45) | 1.06 | TPPS4 | H2O | 6.6–7.6 | O2 consumption (Clark electrode) | Gottfried and Kimel (1991)33 |
| 7 | 0.83 | 23 ± 2 | — | RB | D2O | 7.5 | Time-resolved 1O2 phosphorescence | Latch (2003)15 |
| 8 | 0.94 ± 0.01f | 19–20 (5–45) | 0.95–0.97 | PN | H2Og | 3–12 | Time-resolved 1O2 phosphorescence | This work |
| 9 | 1.0 ± 0.6 | 26 (5–45) | 1.08 | PN | H2O | 4–10 | FFA consumption | This work |
It is worth noting that the enthalpy of activation determined in this study, while low, is still significantly higher than found for other furans reacting with 1O2. For example, Gorman et al. reported ΔH‡ of (0.0 ± 0.4) kcal mol−1 for the reaction of 1O2 with both furan and dimethylfuran in toluene solvent.35 Near-zero and even negative ΔH‡ values have led to the conclusion that 1O2 forms an exciplex prior to reaction. We speculate that the solvent (water) is likely the key difference giving the distinctly higher ΔH‡ value measured here. Temperature-dependent changes in aqueous diffusion rate constants, which are due to the relatively steep viscosity–temperature relationship for water, lead to apparent activation energies of 12–20 kJ mol−1 (5–200 °C).36,37 This has been interpreted as the activation energy associated with the diffusion of solutes in water.36
In summary, despite the relatively small enthalpy of activation, a temperature dependence on krxn,FFA does exist and should be considered when performing photolysis experiments. This might be important when temperature is likely to vary or be high, for example during the course of long photolysis experiments or when high light intensities are employed. As shown in Fig. S1,† in our photoreactor, the solution temperature can increase up to 10 °C if not controlled. Using the results in Table 1 one can calculate a reaction rate enhancement of about 20% when heating the solution from 24 °C to 34 °C (from 1.04 to 1.24 × 108 M−1 s−1). Therefore, as a good practice, one should record the temperature trend during the experiment, and then calculate the value of krxn,FFA to be used in the data analysis. The rate constant at an arbitrary temperature can be calculated using eqn (13), obtained from the linear regression of the experimental points.
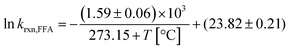 | (13) |
In the range of common laboratory and photoreactor temperatures (T = 20–40 °C), it is perfectly adequate (<0.6% error) to use the simple linear eqn (14).
| krxn,FFA = (1.00 ± 0.04) × 108 M−1 s−1 + [(2.1 ± 0.3) × 106 M−1 s−1 °C−1] × (T − 22 °C); 20 < T < 40 °C | (14) |
This equation gives a nice rule-of-thumb that krxn,FFA is 1.00 × 108 M−1 s−1 at 22 °C and changes 2% for every degree Celsius.
pH dependence
The rate constant krxn,FFA was also studied as function of pH in the range of 3–12 using both steady-state and time-resolved methods.Our measurements are summarized in Fig. 4 and S3.† Data from the time-resolved phosphorescence method showed no pH dependence from pH 3 to 12, giving kavgrxn,FFA = (9.4 ± 0.1) × 107 M−1 s−1 (T = 19–20 °C) (Fig. 4). Measurements made between pH 4 and 10 by the steady-state method show qualitatively the same results, albeit with a much larger (ca. +20%) variation in the measured rate constants (Fig. S3†). The absence of a pH dependence fits the fact that neither 1O2 nor FFA have pKa values in this range. Variations in 1O2 reaction rate constants that depend on pH are usually associated with a change in protonation state of the substrate. For example, rate constants for phenols are typically 2 orders of magnitude smaller than those of phenolates.2,39,40 Histidine and histamine also have speciation-dependent reaction rate constants.41
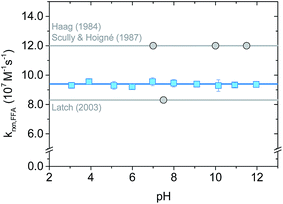 | ||
| Fig. 4 pH dependence on krxn,FFA studied with time-resolved singlet oxygen phosphorescence at 19–20 °C (lab temperature). The error bars indicate the standard deviation of the linear regression performed on the Stern–Volmer plot for each experiment. The blue solid line is the average value across the whole pH range; the grey lines show Haag18 (most used) and Latch15 (most recent) values. | ||
The absence of a pH dependence is also in agreement with previous literature findings. Sluyterman (entry 1 in Table 2) reported a constant oxygenation rate constant for furfuryl alcohol in the pH range 3–9.19 Similarly, Scully and Hoigné (entry 5 in Table 2) observed constant krxn,FFA values at pH 7, 10 and 11.5.39 By contrast, Gottfried and Kimel (entry 6 in Table 2) measured a 60% increase in the reaction rate constant when lowering the pH from 7.6 to 6.6. In light of the results reported here, we believe that the Gottfried and Kimel result is simply the outlier of the group, and that there is no pH dependence in krxn,FFA.
Dependence on salt content
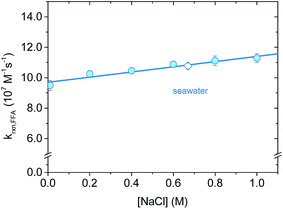
Salt concentration dependence was assessed with time-resolved 1O2 phosphorescence using NaCl solutions in the ionic strength range I = 0.01–1 M. This range includes all major natural water types, from surface waters (I = 1–5 mM) to ground water (I = 10–20 mM) and seawater (I = 670 mM).42,43 Even though the chemical nature of the ionic components can vary greatly, we focused on sodium chloride because of its abundance in a typical high-salinity environment. In a representative seawater sample (salinity 3.5%) Cl− represents 95% of the total anions content, while Na+ accounts for 86% of the total cations (by mole percent).44,45As reported in Fig. 5, krxn,FFA increases slightly with [NaCl], corresponding to a reaction rate constant enhancement of +13.4% for artificial seawater (I = 0.67 M) and +19% obtained with 1 M NaCl (I = 1.0 M). We explored two possible explanations for this increase. The first is that the ionic strength of the medium might influence the kinetics. The second is that there is a salt effect similar to what has been observed for Diels–Alder reactions, which have been interpreted in terms of the hydrophobic effect.46,47 Both of these hypotheses are testable by examining the influence of different salt compositions on the kinetics. In the first case, the kinetics should be the same for two solutions of the same ionic strength regardless of the identity of the ions involved. In the second case, the reaction should be accelerated by “salting out” ions (e.g., LiCl) and decelerated by “salting in” ions (e.g. guanidinium chloride, GnCl), as proposed by Breslow.46 This is the result of water–ion interactions: small, hard ions strongly bind to water, increasing the cavitation energy and therefore favoring aggregate formation between hydrophobic molecules (i.e., formation of activated complexes). On the other hand, big, soft ions loosely interact with water, decreasing the cavitation energy. It has also been suggested that “salting-in” ions disrupt hydrophobic aggregation by enhancing the water solubility of organic molecules through direct interactions.48
Table 3 lists rate constants determined in the presence of various ions (at 2 M), and clearly demonstrates that neither of the above explanations is satisfactory. The rate constants change with different salt compositions, arguing against a simple ionic strength effect. Furthermore, the rate constants do not follow the order predicted by the hydrophobic effect hypothesis. For example, LiCl and GnCl are expected to be opposite end members, but instead show almost identical rate constants. We noted that krxn,FFA increases with the anion radius, but shows a less defined trend with respect to the cation size.
| Salt (2 M) | k rxn,FFA (108 M−1 s−1) | k saltrxn,FFA/kbufferrxn,FFA | r cation (pm) | r anion (pm) |
|---|---|---|---|---|
| Reference:a crystal radius from Shannon.49b Calculated ionic radius from Marcus.50 | ||||
| NaCl | 1.27 ± 0.05 | 1.34 | 113a | 167a |
| NaBr | 1.28 ± 0.04 | 1.35 | 113a | 182a |
| NaClO4 | 1.41 ± 0.04 | 1.49 | 113a | 226a |
| MgCl2 | 1.1 ± 0.1 | 1.18 | 86a | 167a |
| LiCl | 1.05 ± 0.02 | 1.11 | 90a | 167a |
| GnCl | 1.02 ± 0.02 | 1.07 | 210b | 167a |
Whatever the origin of the salt effect, for aquatic systems where sodium and chloride ions are dominant, it is important to note that there is an empirical linear relationship between molar concentration of NaCl and the rate constant at 20 °C (eqn (15)).
| k20 °Crxn,FFA = (9.7 ± 0.1) × 107 M−1 s−1 + (1.7 ± 0.2) × 107 M−2 s−1 × [NaCl] | (15) |
Comparison with previous studies
Table 2 summarizes the available literature on 1O2 reaction rate constants with FFA in water. Note that for entry 3, both the widely used value of 1.2 × 108 M−1 s−1 is given, as well as the value actually measured by Haag et al. of (1.09 ± 0.09) × 108 M−1 s−1. The latter value was calculated from the reported β value of (2.3 ± 0.2) × 10−3 M, using eqn (4), while the former value was arrived at by Haag et al. by averaging the measured value (at 22 °C) with the previously measured value of Sluyterman (at 37 °C) (entry 1).In general, the most common experimental technique employed until the 1990s consists of measuring the loss of ground state oxygen under pseudo first-order conditions (i.e., high FFA concentrations) and then relating it to the loss of FFA assuming a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio. This has been done with both pressure (entry 1) and amperometric measurements (entries 3–6). Once the ground state oxygen depletion kinetics are known, it is possible to calculate krxn,FFA using the β value method. The only time-resolved determination that we are aware of was performed in 2003 (entry 7). However, due to the poor response time of the available Ge-based detector, the measurement could only be performed in D2O, where the singlet oxygen lifetime is 14 times longer than in H2O.26
1 stoichiometric ratio. This has been done with both pressure (entry 1) and amperometric measurements (entries 3–6). Once the ground state oxygen depletion kinetics are known, it is possible to calculate krxn,FFA using the β value method. The only time-resolved determination that we are aware of was performed in 2003 (entry 7). However, due to the poor response time of the available Ge-based detector, the measurement could only be performed in D2O, where the singlet oxygen lifetime is 14 times longer than in H2O.26
As far as the values are concerned, O2 consumption-based rate constants are generally higher than what was measured in the current work. For example, Sluyterman obtained krxn,FFA = 1.4 × 108 M−1 s−1, while on the basis of eqn (14) one would expect krxn = 1.30 × 108 M−1 s−1 at 37 °C. Similarly, Haag found krxn,FFA = 1.09 × 108 M−1 s−1 at 22 °C, while we would predict it to be 9% lower. A general difference between the previous studies and ours is the choice of the sensitizer. While in the past Rose Bengal (RB) was the most commonly employed sensitizer, we decided to use perinaphthenone (PN) instead, the main reason being the pH-dependent sensitization properties of RB.52 PN is a convenient sensitizer to use because of its UV-A absorption (λmax = 365 nm), pH independent speciation and high singlet oxygen quantum yields in a variety of solvents (i.e., ΦΔ = 0.95 in water).53–56 Indeed, because of these features PN is acknowledged as a reference compound for (photochemically generated) singlet oxygen quantum yield determinations.54 As a further point, the very low triplet energy of PN helps to ensure that no processes other than singlet oxygen production take place from oxygen quenching of PN triplet excited state, whereas for other sensitizers oxygen quenching can also generate superoxide anions (as a result of electron transfer).57–64
The use of RB as a sensitizer might be problematic with respect to unwanted side reactions. Though not conclusive, several literature sources point toward the non-innocent role of a superoxide radical anion pathway in oxygen quenching of RB triplets. For instance, Srinivasan et al.59 used superoxide dismutase to detect O2−˙ generated during constant steady-state irradiation of aqueous RB solution, obtaining a yield as high as 23% for superoxide radical anion formation. A similar result was observed by Lee and Rodgers, who used benzoquinone to trap O2−˙ generated upon laser flash photolysis of RB solutions (ΦO2−˙ = 0.20).60 However, Lambert and Kochevar recently questioned these findings,65 providing experimental evidence of the inefficiency of superoxide radical anion formation in aqueous environments (ΦO2−˙ < 0.01). Regardless of the mechanism, photobleaching is commonly observed for RB and other dyes. It has been shown that in the presence of oxygen and low concentration of dye ([dye] < 10 μM), sensitizer degradation follows first order kinetics, with the rate determining step being the attack of ground state oxygen on the excited triplet state (D–O mechanism).66 Thus, several pieces of evidence suggest that RB sensitized photolysis experiments can be biased by other oxygen-consuming processes.
Regarding the krxn,FFA value reported by Latch (entry 7), a reanalysis of the data revealed that the experimental design may have led to an artificially low krxn,FFA value. In their experiment, they measured krxn,FFA by additive spiking of an FFA stock into a single sensitizer solution which was repeatedly irradiated. In some instances this is a reasonable method, however one must consider that FFA may be consumed to a significant extent during the measurement. For slow reactions, or short irradiation times, the change in quencher concentration will be small, and may be neglected. We now make the case that FFA consumption should have been taken into account in the previous krxn,FFA determination experiments. With the sensitizer concentration and laser power levels employed in the present work, about 10% of the starting FFA was consumed in a roughly 4 mL sample during the 6–10 s of signal acquisition. Fig. 6 shows that when FFA consumption is taken into account, the regression line based on the “spiked” FFA concentrations is less steep, resulting in artificially low quenching rate constants. To illustrate, for the same [FFA]0 and kobs values, krxn,FFA increases from 8.3 to 9.7 × 107 M−1 s−1 when adjusting from 0% to 20% loss of FFA starting concentration. We think that this might explain the discrepancy between the Latch value and the one reported here.
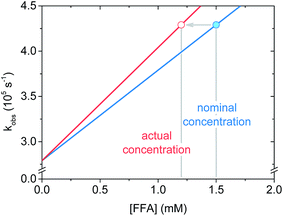 | ||
| Fig. 6 Schematic graph showing the effect of furfuryl alcohol degradation on the apparent slope of the fitted line (i.e. the rate constant) in a Stern–Volmer plot. | ||
Conclusions
The reaction rate constant for the reaction of furfuryl alcohol with singlet oxygen in water was investigated as a function of temperature, pH, and salt content using both steady-state (β value) and time-resolved methods. Temperature was the main factor influencing krxn,FFA, while the reaction was shown to be pH independent. A small increase in krxn,FFA was observed at relatively high ionic strengths, using both NaCl and artificial seawater. In low ionic strength solutions (below 50–100 mM) the effect was negligible. In measuring krxn, time-resolved singlet oxygen phosphorescence was shown to be a superior method compared to the classical one based on β value determination due to its higher precision and reproducibility.We discourage the use of the well-known 1.2 × 108 M−1 s−1 value of Haag et al., both because it may be an overestimate due to Rose Bengal-induced side reactions and because the actual value measured in that study was 1.09 × 108 M−1 s−1. This implies that the past values are most likely underestimated by 10–20%, depending on the solution temperature and ionic strength, as well as the assumptions in the calculation of [1O2]ss (i.e., whether FFA quenching is considered or not; more details in the ESI†). Likewise, the use of the 8.3 × 107 M−1 s−1 value reported by Latch et al. should be discontinued due to experimental conditions that likely led to the underreporting of the true reactivity of FFA with 1O2.
For future studies using FFA as a 1O2 probe molecule, we recommend the following:
(1) Monitor the temperature of the sample during the photolysis experiment;
(2) Use the temperature-adjusted krxn,FFA value (see eqn (13) and (14));
(3) Apply a salt content correction if working at elevated salt concentrations (e.g. in seawater; see eqn (15)).
Acknowledgements
This work was financially supported by a grant from the Swiss National Science Foundation (Project numbers CRSI22_127568). We thank Annika Linkhorst and Prof. Charles Sharpless (Univ. of Mary Washington) for conducting preliminary experiments and helpful discussions.References
- R. G. Zepp, N. L. Wolfe, G. L. Baughman and R. C. Hollis, Nature, 1977, 267(5610), 421–423 CrossRef CAS.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, in Environmental Organic Chemistry, John Wiley & Sons, Inc., 2002, pp. 655–686 Search PubMed.
- E. L. Clennan and A. Pace, Tetrahedron, 2005, 61(28), 6665–6691 CrossRef CAS.
- H. H. Wasserman, Ann. N. Y. Acad. Sci., 1970, 171(1), 108–120 CrossRef CAS.
- A. L. Boreen, B. L. Edhlund, J. B. Cotner and K. McNeill, Environ. Sci. Technol., 2008, 42(15), 5492–5498 CrossRef CAS PubMed.
- R. A. Lundeen, E. M.-L. Janssen, C. Chu and K. McNeill, Chimia, 2014, 68(11), 812–817 CrossRef CAS PubMed.
- M. J. Davies, Photochem. Photobiol. Sci., 2004, 3(1), 17–25 CAS.
- T. Kohn, M. Grandbois, K. McNeill and K. L. Nelson, Environ. Sci. Technol., 2007, 41(13), 4626–4632 CrossRef CAS PubMed.
- K. Rule Wigginton, L. Menin, J. P. Montoya and T. Kohn, Environ. Sci. Technol., 2010, 44(14), 5437–5443 CrossRef CAS PubMed.
- T. Sigstam, G. Gannon, M. Cascella, B. M. Pecson, K. R. Wigginton and T. Kohn, Appl. Environ. Microbiol., 2013, 79(11), 3455–3467 CrossRef CAS PubMed.
- G. Bentivenga, C. Bonini, M. D'Auria and A. J. De Bona, Photochem. Photobiol., 1999, 128(1–3), 139–143 CrossRef CAS.
- C. Bonini, M. D'Auria, G. Mauriello, D. Viggiano and F. J. Zimbardi, Photochem. Photobiol., 1998, 118(2), 107–110 CrossRef CAS.
- M. E. Karpuzcu, A. J. McCabe and W. A. Arnold, Environ. Sci.: Processes Impacts, 2016, 18(2), 237–245 CAS.
- A. L. Boreen, W. A. Arnold and K. McNeill, Environ. Sci. Technol., 2004, 38(14), 3933–3940 CrossRef CAS PubMed.
- D. E. Latch, B. L. Stender, J. L. Packer, W. A. Arnold and K. McNeill, Environ. Sci. Technol., 2003, 37(15), 3342–3350 CrossRef CAS PubMed.
- R. A. Lundeen, C. Chu, M. Sander and K. McNeill, Environ. Sci. Technol., 2016, 50(16), 8586–8595 CrossRef CAS PubMed.
- V. Nardello, N. Azaroual, I. Cervoise, G. Vermeersch and J.-M. Aubry, Tetrahedron, 1996, 52(6), 2031–2046 CrossRef CAS.
- W. R. Haag, J. Hoigné, E. Gassman and A. Braun, Chemosphere, 1984, 13(5), 631–640 CrossRef CAS.
- L. A. A. Sluyterman, Recl. Trav. Chim. Pays-Bas, 1961, 80(9), 989 CrossRef CAS.
- J. H. Espenson, in Chemical Kinetics and Reaction Mechanisms, McGraw-Hill, New York, 1995, pp. 70–100 Search PubMed.
- M. Rougée and R. V. Bensasson, C. R. Seances Acad. Sci., Ser. 2, 1986, 302(20), 1223 Search PubMed.
- A. Jiménez-Banzo, X. Ragàs, P. Kapusta and S. Nonell, Photochem. Photobiol. Sci., 2008, 7(9), 1003–1010 Search PubMed.
- S. Nonell and C. Flors, in Singlet Oxygen: Applications in Biosciences and Nanosciences, 2016, vol. 2, pp. 7–26 Search PubMed.
- P. R. Ogilby, Chem. Soc. Rev., 2010, 39(8), 3181–3209 RSC.
- H. Wu, Q. Song, G. Ran, X. Lu and B. Xu, TrAC, Trends Anal. Chem., 2011, 30(1), 133–141 CrossRef CAS.
- F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1995, 24(2), 663–677 CrossRef CAS.
- S. Nonell and S. E. Braslavsky, Methods Enzymol., 2000, 319, 37–49 CAS.
- J. Baier, T. Fuß, C. Pöllmann, C. Wiesmann, K. Pindl, R. Engl, D. Baumer, M. Maier, M. Landthaler and W. J. Bäumler, J. Photochem. Photobiol., B, 2007, 87(3), 163–173 CrossRef CAS PubMed.
- A. M. Braun, H. Dahn, E. Gassmann, I. Gerothanassis, L. Jakob, J. Kateva, C. G. Martinez and E. Oliveros, Photochem. Photobiol., 1999, 70(6), 868–874 CAS.
- P. Di Mascio, M. H. G. Medeiros, H. Sies, S. Bertolotti, S. E. Braslavsky, D. PilóVeloso, B. H. L. N. Sales, E. Magalhães, R. Braz-Filho and E. J. H. Bechara, J. Photochem. Photobiol., B, 1997, 38(2), 169–173 CrossRef.
- B. Valeur, in Molecular Fluorescence, Wiley-VCH Verlag GmbH, 2001, pp. 72–124 Search PubMed.
- H. U. Sverdrup, M. W. Johnson and R. H. Fleming, The Oceans: their physics, chemistry, and general biology, Prentice-Hall, New York, 1942 Search PubMed.
- V. Gottfried and S. J. Kimel, J. Photochem. Photobiol., B, 1991, 8(4), 419–430 CrossRef CAS.
- T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, New York, 3rd edn, 1987 Search PubMed.
- A. A. Gorman, G. Lovering and M. A. J. Rodgers, J. Am. Chem. Soc., 1979, 101(11), 3050–3055 CrossRef CAS.
- A. J. Elliot, D. R. McCracken, G. V. Buxton and N. D. Wood, J. Chem. Soc., Faraday Trans., 1990, 86(9), 1539–1547 RSC.
- K. Krynicki, C. D. Green and D. W. Sawyer, Faraday Discuss. Chem. Soc., 1978, 66(0), 199–208 RSC.
- E. Gassmann, Die Quantenausbeute der Singulettsauerstoff-sensibilisierung in heterogener Phase, EPFL, 1984 Search PubMed.
- F. E. Scully and J. Hoigné, Chemosphere, 1987, 16(4), 681–694 CrossRef CAS.
- C. Li and M. Z. Hoffman, J. Phys. Chem. A, 2000, 104(25), 5998–6002 CrossRef CAS.
- C. Chu, R. A. Lundeen, C. K. Remucal, M. Sander and K. McNeill, Environ. Sci. Technol., 2015, 49(9), 5511–5519 CrossRef CAS PubMed.
- D. Hillel, Salinity management for sustainable irrigation: integrating science, environment, and economics; 20842, The World Bank, 2000, pp. 1–102 Search PubMed.
- R. E. Zeebe and D. Wolf-Gladrow, CO2 in Seawater: Equilibrium, Kinetics, Isotopes, Elsevier, 2001 Search PubMed.
- D. R. Kestel, I. W. Duedall, D. N. Connors and R. M. Pytkowicz, Assoc. Sci. Limnol. Oceanogr., 1967, 12(1), 176–179 CrossRef.
- M. E. Q. Pilson, An introduction to the chemistry of the sea, Cambridge University Press, Cambridge, 2nd edn, 2013 Search PubMed.
- R. Breslow, Acc. Chem. Res., 1991, 24(6), 159–164 CrossRef CAS.
- A. Kumar, Chem. Rev., 2001, 101(1), 1–20 CrossRef CAS PubMed.
- R. Breslow and T. Guo, Proc. Natl. Acad. Sci., 1990, 87(1), 167–169 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767 CrossRef.
- Y. Marcus, J. Chem. Thermodyn., 2012, 48, 70–74 CrossRef CAS.
- P. Murasecco, E. Oliveros, A. M. Braun and P. Monnier, Photobiochem. Photobiophys., 1985, 9(3), 193–201 CAS.
- V. R. Batistela, D. S. Pellosi, F. D. de Souza, W. F. da Costa, S. M. de Oliveira Santin, V. R. de Souza, W. Caetano, H. P. M. de Oliveira, I. S. Scarminio and N. Hioka, Spectrochim. Acta, Part A, 2011, 79(5), 889–897 CrossRef CAS PubMed.
- M. C. Daza, M. Doerr, S. Salzmann, C. M. Marian and W. Thiel, Phys. Chem. Chem. Phys., 2009, 11(11), 1688–1696 RSC.
- M. Segado and M. Reguero, Phys. Chem. Chem. Phys., 2011, 13(9), 4138–4148 RSC.
- C. N. Sanramé, R. H. Rossi and G. A. de Argüello, Photochem. Photobiol., 1998, 68(4), 474–480 Search PubMed.
- R. Schmidt, C. Tanielian, R. Dunsbach and C. Wolff, J. Photochem. Photobiol., A, 1994, 79(1), 11–17 CrossRef CAS.
- J. P. Tardivo, A. Del Giglio, C. S. de Oliveira, D. S. Gabrielli, H. C. Junqueira, D. B. Tada, D. Severino, R. de Fátima Turchiello and M. S. Baptista, Photodiagn. Photodyn. Ther., 2005, 2(3), 175–191 CrossRef CAS PubMed.
- S. C. Núñez and A. S. G., Photochem. Photobiol. Sci., 2014, 13(3) Search PubMed.
- V. S. Srinivasan, D. Podolski, N. J. Westrick and D. C. Neckers, J. Am. Chem. Soc., 1978, 100(20), 6513–6515 CrossRef CAS.
- P. C. Lee and M. A. Rodgers, Photochem. Photobiol., 1987, 45(1), 79–86 CrossRef CAS PubMed.
- E. Ben-Hur, A. Carmichael, P. Riesz and I. Rosenthal, Int. J. Radiat. Biol. Relat. Stud. Phys., Chem. Med., 1985, 48(5), 837–846 CrossRef CAS.
- W. M. Draper and D. G. Crosby, J. Agric. Food Chem., 1983, 31(4), 734–737 CrossRef CAS.
- C. E. Diaz-Uribe, M. C. Daza, F. Martínez, E. A. Páez-Mozo, C. L. B. Guedes and E. Di Mauro, J. Photochem. Photobiol., A, 2010, 215(2–3), 172–178 CrossRef CAS.
- M.-T. Maurette, E. Oliveros, P. P. Infelta, K. Ramsteiner and A. M. Braun, Helv. Chim. Acta, 1983, 66(2), 722–733 CrossRef CAS.
- C. R. Lambert and I. E. Kochevar, J. Am. Chem. Soc., 1996, 118(13), 3297–3298 CrossRef CAS.
- W. W. Wilson and J. R. Heitz, J. Agric. Food Chem., 1984, 32(3), 615–617 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6em00646a |
| ‡ These authors contributed equally to this work and are listed alphabetically. |
| This journal is © The Royal Society of Chemistry 2017 |