Open Access Article
Open Access ArticleAtmospheric oxidation of halogenated aromatics: comparative analysis of reaction mechanisms and reaction kinetics
Goran
Kovacevic
 and
Aleksandar
Sabljic
and
Aleksandar
Sabljic
 *
*
Rudjer Boskovic Institute, Division of Physical Chemistry, POB 180, HR-10002 Zagreb, Republic of Croatia. E-mail: sabljic@irb.hr; Fax: +385-1-468-0245; Tel: +385-1-456-1089
First published on 1st December 2016
Abstract
Atmospheric transport is the major route for global distribution of semi-volatile compounds such as halogenated aromatics as well as their major exposure route for humans. Their major atmospheric removal process is oxidation by hydroxyl radicals. There is very little information on the reaction mechanism or reaction-path dynamics of atmospheric degradation of halogenated benzenes. Furthermore, the measured reaction rate constants are missing for the range of environmentally relevant temperatures, i.e. 230–330 K. A series of recent theoretical studies have provided those valuable missing information for fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene. Their comparative analysis has provided additional and more general insight into the mechanism of those important tropospheric degradation processes as well as into the mobility, transport and atmospheric fate of halogenated aromatic systems. It was demonstrated for the first time that the addition of hydroxyl radicals to monohalogenated as well as to perhalogenated benzenes proceeds indirectly, via a prereaction complex and its formation and dynamics have been characterized including the respective transition-state. However, in fluorobenzene and chlorobenzene reactions hydroxyl radical hydrogen is pointing approximately to the center of the aromatic ring while in the case of hexafluorobenzene and hexachlorobenzene, unexpectedly, the oxygen is directed towards the center of the aromatic ring. The reliable rate constants are now available for all environmentally relevant temperatures for the tropospheric oxidation of fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene while pentachlorophenol, a well-known organic micropollutant, seems to be a major stable product of tropospheric oxidation of hexachlorobenzene. Their calculated tropospheric lifetimes show that fluorobenzene and chlorobenzene are easily removed from the atmosphere and do not have long-range transport potential while hexafluorobenzene seems to be a potential POP chemical and hexachlorobenzene is clearly a typical persistent organic pollutant.
Environmental impactA study on the atmospheric fate and degradation of semi-volatile halogenated aromatics is of high environmental relevance as well as of broad interest for several areas of environmental research such as atmospheric chemistry, environmental modeling, degradation/transformation of chemicals, secondary pollution, etc. The atmospheric transport is the major route for their global distribution as well as a major exposure route to humans. The major atmospheric removal process of halogenated aromatics is their oxidation by hydroxyl radicals. This comparative study will provide additional and more general insight into the mechanism of this important tropospheric process as well as into the mobility, transport and atmospheric fate of halogenated aromatic systems. The reported results will also be important for modeling their environmental behavior and fate. |
1. Introduction
A large amount of volatile and semivolatile organic chemicals (108 tons) are released annually into the atmosphere from a variety of anthropogenic sources.1 The primary removal route of anthropogenic pollutants from the atmosphere is their oxidation by various oxidizing species present in the atmosphere.2,3 The most effective atmospheric degradation process is oxidation by hydroxyl radicals4–7 due to their high reactivity as well as their significant and constant tropospheric concentration, i.e. 9.7 × 105 radicals cm−3.8 It is of interest to note here that oxidation by hydroxyl radicals is also important for (bio)degradation of organic pollutants in aquatic and terrestrial systems.9–12 Other oxidation species that effectively contribute to the removal of anthropogenic pollutants from the atmosphere are ozone (O3), the nitrate radical (NO3) and halogen atoms. However, NO3 radicals only reach sufficient concentration and reactivity during the night13 whereas ozone molecules show significant reactivity only with unsaturated compounds, i.e. alkenes and polyenes. Consequently, these two oxidation species contribute less to the global oxidizing capacity of the atmosphere.Today, the databases of evaluated kinetic data for the gas-phase reactions of hydroxyl (OH) radicals with various organic compounds contain about 800 recommended reaction rate constants,2,14–16 primarily derived from laboratory studies performed during the last four decades. In the last couple of years, the annual rate of collection and evaluation of those reaction rates is such that it allows for the addition of 10–20 new organic compounds per year. At the same time, the rate constants for the reaction of NO3 radicals with organic pollutants are available for only about 260 compounds,2,17,18 and there are even less data for the reactions of ozone with alkenes or polyenes, i.e. for about 170 compounds.19–22 However, the number of commercial chemicals that are produced in significant quantities, and/or are in everyday use, is at least two orders of magnitude larger, i.e. up to 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 commercial chemicals.23
000 commercial chemicals.23
Since the experimental data on tropospheric degradation rates of commercial chemicals are available only for about 1% of those substances and because this information is critical for a reliable evaluation of their mobility, long-range transport, and environmental fate as well as their possible adverse effects or exposure on humans and the environment (i.e. for the environmental risk assessment of commercial chemicals), a large number of quantitative models have been developed since the early eighties for estimating the gas-phase (tropospheric) degradation rates of organic chemicals in oxidation reactions with OH or NO3 radicals and ozone.5–7,9,13,16,18,21,22,24,25 The early models were based either on the fragment contribution method24,25 or on simple correlations with spectroscopic data26–28 or some physico-chemical properties.29,30 The most popular model, even today, is the Atkinson's group contribution method,25 which is implemented by the US EPA into the EPIWIN Suite of models31 as the AOPWIN module and which is regularly used to routinely estimate the tropospheric degradation rates and half-lives of organic compounds.
During the last twenty years the emphasis of modeling research has shifted towards the development of complex statistical multivariate quantitative models based on a large number of topological, structural, geometric and/or electronic properties (descriptors) primarily calculated by various quantum-chemical methods.7,9,16,18,21,22,32–38 The majority of these statistical models claims a high level of accuracy in predicting tropospheric degradation rates of organic chemicals by the respective oxidation species and may be useful in estimating degradation rates of commercial chemicals for which no such data are available. Unfortunately, those statistical multivariate models provide no information regarding either the reaction mechanism and reaction-path dynamics of these important atmospheric processes or about the temperature dependence of the reaction rates, despite claims to the contrary in some of those studies. At best, those modeling studies can only support results on the reaction mechanism or reaction-path dynamics obtained by experimental or theoretical studies.
A tremendous development of computational technology, hardware and software during the last two decades has enabled the accurate and efficient calculation of the energy profiles and reaction-path dynamics of gas-phase reactions with various tropospheric oxidation species. Since the mid-nineties, literally hundreds of theoretical studies have been published6,7,9 on the detailed reaction mechanisms of the oxidation of organic chemicals by OH radicals, NO3 radicals, ozone, halogen atoms or other reactive species present in the troposphere. Today, those studies are routinely performed by a large number of research groups around the globe. One of the early major achievements made by theoretical studies was to reveal that, contrary to the generally accepted opinion,39–44 the hydrogen abstraction by OH radicals proceeds by an indirect mechanism, i.e. through the formation of a pre-reaction complex.45–48 Concomitantly, analogous theoretical studies have been performed for almost all types of aliphatic compounds, such as alkanes and alkenes,39,49–51 halogenated alkanes and alkenes,40,45,52–55 terpenes,56–58 alcohols,59,60 ethers,61,62 carbonyl compounds,47,63–65 organic acids66,67 and esters.68,69 These studies have revealed the detailed reaction mechanisms, the reaction-path dynamics and the reaction rates for tropospheric degradation of aliphatic chemicals. On the contrary, the number of studies in which the OH radical reacts or interacts with aromatic systems is quite limited. The detailed investigations on reaction mechanisms, reaction-path dynamics and reaction kinetics are available mainly for benzene and some of its monosubstituted derivatives, i.e. benzene,70–74 toluene,75–77 phenol,78 fluorobenzene,79 chlorobenzene80,81 or naphthalene.82 There are several reasons for such a small number of theoretical studies on aromatic compounds but the major ones are: (i) their significant size and exceptionally complex reaction mechanisms, which involve several reaction channels with a large number of intermediates as well as the primary and secondary products, and (ii) the use of advanced theoretical methods that are not of a routine nature and require experienced researchers to obtain meaningful results.
In our earlier studies on fluorobenzene79 and chlorobenzene81 various levels of quantum-chemical theory and kinetic theory have been evaluated in order to reveal the approach that most satisfactorily reproduces the experimental reaction rates and unusual temperature dependence for their oxidation by hydroxyl radicals. It was demonstrated that MP2 and G3 methods provide valuable information on the reaction mechanism of hydroxyl radical addition to simple haloaromatic systems and the corresponding thermodynamic data. Those results coupled with the RRKM (Rice–Ramsperger–Kassel–Marcus) kinetic theory have successfully reproduced the measured reaction rates and unusual temperature dependence for the oxidation of fluorobenzene79 and chlorobenzene.81 Recently, the same approach was also successfully applied to obtain valuable information on the reaction mechanism and reaction-path dynamics for atmospheric oxidation of perhalogenated benzenes,83,84 one of them being hexachlorobenzene, a model persistent organic pollutant (POP) from the original list of the twelve major POPs listed under the Stockholm Convention.85,86 In this study, a comparative analysis will be made on the reaction mechanisms, thermodynamic data, calculated reaction rates and their temperature dependence as well as on the potential stable products of the atmospheric oxidation of halogenated benzenes by OH radicals. A particular emphasis will be given to the effect of anharmonicity and a two-dimensional particle-in-the-box approximation on the reaction dynamics and kinetics. This way we hope to gain additional and more general insight into the mechanism of those important tropospheric degradation processes as well as into the mobility, transport and atmospheric fate of halogenated aromatic systems.
2. Computational framework
The optimized geometries of all stationary points and corresponding frequencies were calculated using either MP2/6-31+G(d,p) for oxidation of fluorobenzene and chlorobenzene or the MP2/6-311G(d,p) method for oxidation of hexafluorobenzene and hexachlorobenzene while the unrestricted wavefunction was used for all radical species. IRC calculations have confirmed the connection between the transition state and minima in each reaction pathway and for all reaction steps. Geometry, frequency and IRC calculations were conducted using the GAMESS program.87 Single point energies were calculated by the G3 method88,89 on all optimized stationary points using the Gaussian program package.90The prereaction complexes were optimized with a very tight gradient cutoff (10−7 Ha bohr−1) and a projection Hessian matrix was used in normal mode calculations to remove translational and rotational contaminants.91 Their normal modes were examined and those describing dissociation of the prereaction complexes were determined.
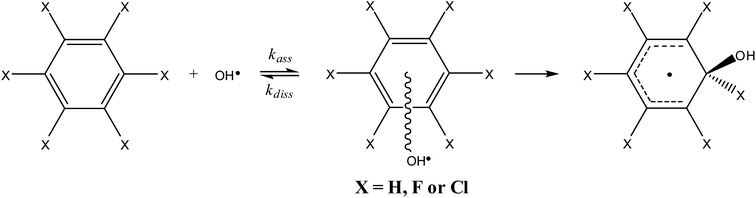
The MP2/6-31+G(d,p) or MP2/6-311G(d,p) optimized geometries and G3 energies were used for calculating the rate constants and frequencies were scaled by 0.941 before using them in the thermodynamic and density of states calculations. However, the normal modes that describe internal rotation of the hydroxyl group were treated explicitly as internal rotors. Furthermore, the relative translation of the hydroxyl radical with respect to halogenated benzenes in the prereaction complexes was treated as a two-dimensional particle-in-the-box potential.79,81,83,84 Reaction between the hydroxyl radical and individual halogenated benzene is divided into two steps (eqn (1)). The first step is the association of reactants and formation of a prereaction complex and the corresponding rate constants were calculated by combining the statistical thermodynamics calculations using the Thermo program from the MULTIWELL program package92–94 and RRKM method95,96 in the high pressure limiting regime. The second step is rearrangement of the prereaction complex into the adduct and its efficiency is modeled using the exact Gillespie stochastic method.
A separate density of states calculation was performed for the prereaction complex treating the relative translation of the OH radical over halogenated benzenes as the particle-in-the-box. The particle-in-a-box approximation is implemented in the Densum program of MULTIWELL program package. It was applied in the density of states calculation for the prereaction complex by selecting an appropriate option for the relative translation of the OH radical over halogenated benzenes.
 | (1) |
A more detailed description of computational methods and procedures can be found in the original studies.79,81,83,84
3. Comparative analysis and discussion
3.1. Formation and properties of prereaction complexes
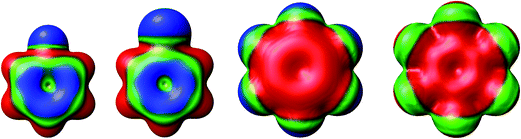
The reaction path for the addition of hydroxyl radicals to halogenated benzenes proceeds via a prereaction complex as shown in Fig. 1 for hexafluorobenzene. The prereaction complexes are strongly bound species and their binding energies for mono- and per-fluorinated or chlorinated benzenes range from 3 to 6.6 kcal mol−1. In the prereaction complexes, the hydroxyl radical is almost perpendicular to the benzene ring (Fig. 2). In monohalogenated benzenes, fluorobenzene and chlorobenzene, the hydrogen atom is pointing approximately to the center of the aromatic ring79,81 while for perhalogenated benzenes, hexafluorobenzene and hexachlorobenzene, an oxygen atom is pointing approximately to the center of the aromatic ring.83,84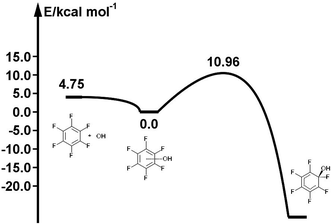 | ||
| Fig. 1 Schematic energy path for the addition of hydroxyl radicals to hexafluorbenzene. The values obtained by the G3 method are enthalpies at room temperature (298.15 K) relative to the prereaction complex in kcal mol−1. Reprinted from ref. 83 with the permission of Croatian Chemical Society according to CC BY license (https://creativecommons.org/licenses/by/4.0/). | ||
The separations between hydroxyl radical hydrogen and the center of the aromatic ring are 2.35 and 2.44 Å, respectively, for fluorobenzene and chlorobenzene while the separations between hydroxyl radical oxygen and the aromatic ring are somewhat larger for hexafluorobenzene and hexachlorobenzene, i.e. 2.76 and 2.89 Å, respectively. The higher stabilization energies of prereaction complexes with perhalogenated benzenes (4.75 or 6.6 kcal mol−1) seem to be a consequence of electrostatic interaction between the partially negatively charged oxygen atom and a positive electrostatic potential of the aromatic ring due to the strong electron withdrawing effect of six halogen atoms (Fig. 3).97 An analogous complex was published also for hexafluorobenzene and hydrogen fluoride.98 In the case of monohalogenated benzenes, the lower stabilization energies of prereaction complexes (2.98 or 2.99 kcal mol−1) are a result of electrostatic interaction between the partially positively charged hydrogen atom and a negative electrostatic potential of the aromatic ring (Fig. 3).97
The formation of prereaction complexes proceeds across loose transition states79,81,83,84,95,96 which are favorable for the formation of prereaction complexes since those transition states reduce the dissociation rate of prereaction complexes (eqn (1)). The loose transition states seem to be analogous to the outer transition state suggested for the addition of the hydroxyl radical to ethylene.99 Each prereaction complex has several low vibrational frequencies (35–90 cm−1) corresponding to the relative motions of the OH radical and halogenated benzene which are critical for the oxidation of halogenated benzenes. One degree of freedom corresponds to receding of the hydroxyl radical from the corresponding halogenated benzene while two degrees of freedom correspond to the nearly free movement of the hydroxyl radical across the plain of the aromatic ring. By the last two motions, the hydroxyl radical can approach all aromatic carbons and interact with them. The normal mode which corresponds to the receding motion of the hydroxyl radical is responsible for the dissociation of the prereaction complex.
3.2. Rearrangement of prereaction complexes into the “hot” adducts
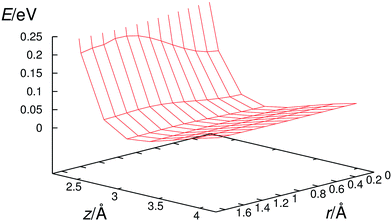
In the prereaction complexes, the hydroxyl radical is almost perpendicular to the aromatic ring and points approximately to the center of the aromatic ring. It has a flat potential energy surface (Fig. 4) which makes possible the large amplitude motions of the hydroxyl radical. For example, in the case of a hexachlorobenzene prereaction complex the change in its potential energy is only 8 meV (0.185 kcal mol−1) while the OH radical slides from the center of the ring to one of the carbon atoms which compares favorably with the room temperature thermal energy of about 25 meV (0.577 kcal mol−1). These large amplitude motions enable the hydroxyl radical to approach all carbon atoms in the benzene ring and interact with them.Once the hydroxyl radical approaches one of the carbon atoms in halogenated benzenes, it starts to change its orientation from perpendicular to parallel with respect to the benzene ring. At the same time, the oxygen atom and a specific carbon atom start to attract each other and, consequently, the carbon atom at the reaction center moves from the aromatic ring plain toward the oxygen atom. The range of displacements of such carbon atoms from planarity is between 0.2 and 0.4 Å for tested halogenated benzenes. All these processes result in a significant increase in the potential energy of the reacting system and the transition state is formed at that stage (Fig. 5). In the transition state, the hydroxyl radical is approximately parallel to the aromatic ring. The oxygen atom is located directly above the interacting carbon atom while the hydrogen atom is pointing towards the ring center. The separation between hydroxyl radical oxygen and reacting carbons is almost identical, i.e. 1.96–1.97 Å, for all ten transition states of fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene oxidation by the hydroxyl radical. The C–O bond formation and concurrent relaxation of the aromatic ring lower the energy of the reacting molecular system and it slides into a deep well producing a “hot” adduct with a large amount of excess energy (20–40 kcal mol−1). The detailed reaction pathway dynamics, from the prereaction complexes to the formation of adducts, for chlorobenzene and hexachlorobenzene are shown in the video files published as freely accessible supplement material in the source publications (http://dx.doi.org/10.1016/j.chemosphere.2013.04.041 and http://dx.doi.org/10.1016/j.chemosphere.2016.06.026).81,84
3.3. Reaction thermodynamics
All oxidation reactions of halogenated benzenes by hydroxyl radicals are highly exothermic and have reaction enthalpies from −14.5 to −32.8 kcal mol−1 (Table 1) and, at its first step, produce “hot” adducts with large amounts of excess energy. However, all those reactions also have high reaction barriers which range from 5.2 up to 7.3 kcal mol−1 (Table 1) and consequently the rearrangement of prereaction complexes into “hot” adducts seems to be kinetically driven. Unfortunately, there is no simple correlation between calculated reaction barriers and measured reaction rates although the slowest reaction for hexachlorobenzene also has the highest reaction barrier. Thus, it is fair to conclude that the rate control for the oxidation reactions of halogenated benzenes by the hydroxyl radical is most probably an intricate interplay between the depth of the prereaction complex well, i.e. the amount to excess energy present in the prereaction complex, and the height of the reaction barrier for the individual reaction.| Properties | C6H5F | C6H5Cl | C6F6 | C6Cl6 |
|---|---|---|---|---|
| Prereaction complex binding energy (kcal mol−1) | 2.98 | 2.99 | 4.75 | 6.59 |
| Reaction barrier (kcal mol−1) | 5.21 | 4.69 | 6.21 | 7.30 |
| Reaction enthalpy (kcal mol−1) | 14.49–20.61 | 14.90–17.76 | 32.78 | 24.58 |
| Rate constant × 1013 (298 K) | 7.90 | 6.02 | 1.52 | 0.28 |
3.4. Reaction rates and atmospheric lifetimes
There is an exceptional correspondence between the calculated and measured rate constants for all four oxidation reactions of halogenated benzenes by hydroxyl radicals79,81,83,84 (Table 2) and it holds for the whole temperature range of available measured data. Thus, for the first time, reliable rate constants are available for the whole range of environmentally relevant temperatures for atmospheric degradation of important halogenated benzenes, i.e. fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene. Furthermore, the unusual and different temperature trends were nicely reproduced for all four oxidation reactions of halogenated benzenes by hydroxyl radicals, i.e. no or very weak temperature dependence for fluorobenzene and chlorobenzene, weak but significant positive temperature dependence for hexafluorobenzene and positive, nonlinear temperature dependence for hexachlorobenzene.| T/K | k calc × 1013 | T/K | k exp × 1013 |
|---|---|---|---|
| a Ref. 100. b Ref. 101. c Ref. 80. d Ref. 102. e Ref. 103. f Estimated in ref. 103. | |||
| Fluorobenzene | |||
| 230–310 | 9.46–7.60 | 230–310 | 6.90 ± 1.38 |
| 295 | 7.76 | 296 | 7.9 ± 2.2b |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Chlorobenzene | |||
| 230–300 | 7.98–3.15 | 230–300 | 7.7 ± 3.1 |
| 300 | 3.15 | 299 | 5.83–6.17c |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Hexafluorobenzene | |||
| 330 | 0.81 | 327 | 2.15 ± 0.12 |
| 290–300 | 0.60–0.64 | 294 | 1.52 ± 0.09 |
| 270–280 | 0.46–0.52 | 275 | 1.36 ± 0.08 |
| 260 | 0.42 | 260 | 1.09 ± 0.06 |
| 240–250 | 0.27–0.33 | 244 | 0.79 ± 0.04 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Hexachlorobenzene | |||
| 380 | 2.10 | 386 | 2.45 ± 0.07 |
| 360 | 1.30 | 367 | 1.75 ± 0.05 |
| 340 | 1.07 | 347 | 1.05 ± 0.03 |
| 300 | 0.31 | 298 | 0.20–0.38f |
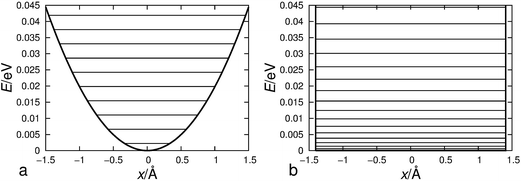
However, in order to obtain such a good correspondence between the calculated and measured rate constants, it was necessary to introduce two critical approximations in the procedure for calculating reaction rate constants. First of all, we had to apply a two-dimensional particle-in-the-box approximation to correctly describe the relative translation of the hydroxyl radical with respect to individual halobenzene in the prereaction complex since the harmonic oscillator approximation poorly describes this low frequency motion which has a very flat potential as shown for hexachlorobenzene in Fig. 4. In order to demonstrate even more clearly the poor performance of harmonic oscillator approximation in describing this translational motion, we have plotted in Fig. 6 the 2D potential energy of harmonic oscillator vs. two-dimensional particle-in-the-box approximation for the translation of the hydroxyl radical over hexachlorobenzene. Even a brief inspection of Fig. 6 clearly shows that the particle-in-the-box approximation provides far more adequate description of flat potential presented in Fig. 4. It should be also indicated here that, besides the major difference in the shape of those two potential curves, there is a large difference in the zero point energies, 2.28 (0.053) vs. 0.153 (0.0035) meV (kcal mol−1), as well as in the density of states. Thus, the particle-in-the-box approximation facilitates the rearrangement of prereaction complexes into adducts and significantly increases all reaction rates, up to several orders of magnitude for hexachlorobenzene (Table 3).
| Correction factors | C6H5F | C6H5Cl | C6F6 | C6Cl6 |
|---|---|---|---|---|
| a na – not applied. | ||||
| Two-dimensional particle-in-the-box approximation (cm3 per molecule per s) | 29.6 | 1.80 | 22.0 | 749 |
| Lowering of the reaction barrier and prereaction complex well (cm3 per molecule per s) | 23.7 | 12.8 | 12.1 | na |
| Energy correction (kcal mol−1) | 0.7 | 1.07 | 0.7 | None |
| Rate constant × 1013 (300 K) | 7.70 | 3.15 | 0.64 | 0.31 |
For reactions of fluorobenzene, chlorobenzene and hexafluorobenzene, it was also necessary to adjust the level of the reaction barrier and prereaction complex well in order to reproduce the measured reaction rate constants. This correction facilitates the formation of prereaction complexes as well as the rearrangement of prereaction complexes into adducts. However, although this correction also has a significant effect on reaction rates, its magnitude is relatively constant and about an order of magnitude for all three reactions (Table 3). It should be noted that the energy correction applied for those three oxidation reactions is smaller or equal to the uncertainty (1.07 kcal mol−1) in G3 results obtained for a representative set of 376 test molecules.88 Furthermore, by energy corrections of reaction barriers and prereaction complex wells, the whole potential energy profiles between them have been shifted and, thus, the energy gaps between those two most important stationary points were unaltered.
The high quality of calculated reaction rate constants for the whole range of environmentally relevant temperatures79,81,83,84 enabled the calculation of accurate tropospheric lifetimes for fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene. Their tropospheric lifetimes were calculated by
| τ = 1/(kcalc × [OH]) | (2) |
| Properties | C6H5F | C6H5Cl | C6F6 | C6Cl6 |
|---|---|---|---|---|
| Rate constant × 1013 (277 K) | 7.94 | 3.947 | 0.502 | 0.229 |
| Tropospheric lifetime (days) | 15 | 30 | 237 | 522 |
The calculated tropospheric lifetimes of fluorobenzene and chlorobenzene show that those chemicals are relatively easily removed from the atmosphere and do not have potential for a long-range transport. For hexafluorobenzene the calculated tropospheric lifetime is 237 days which indicates its status as a potential POP chemical. Finally, the calculated tropospheric lifetime of hexachlorobenzene is 522 days which supports its status of a classical POP chemical as well as its observed long-range transport.105,106 Namely, today hexachlorobenzene is regularly detected all over the world in the air, soil, water, sediment, biota and human tissue samples including the remote areas.105–108 Furthermore, in the recent study it was detected in 99.9% of human serum samples of the US population.109
3.5. Stable oxidation products of halogenated benzenes
There is little or no information on the reaction products of hydroxyl radical addition to halogenated benzenes and in particular for perhalogenated derivatives, hexafluorobenzene and hexachlorobenzene. The reaction with O2 has been identified as the main reaction channel in the troposphere for aromatic adducts (X–C6H5–OH, X = H, CH3, OH, etc.)74,110,111 and major stable products are phenols.110,112–114 Glowacki et al.73 examined the product formation channels for hydroxyl radical addition to benzene. It was found out that phenol and HO2 are formed predominantly by direct ipso-hydrogen abstraction by O2 from the HO–benzene adduct. Their high yield (55%) was in agreement with the recent experimental results.112,113,115For fluorobenzene, the yield of 4-fluorophenol was 10% following the reaction of the hydroxyl radical and fluorobenzene while the yield of 2-fluorophenol or 3-fluorophenol was below the detection limits (>3%).101 Consequently, we have calculated the reaction barriers for the elimination of fluorine atom from an ipso-adduct, product phenol, as well as for the elimination of hydrogen atom from the para-adduct, product 4-fluorophenol.79 The G3 reaction barrier for elimination of fluorine atom was 22.4 kcal mol−1 but, since the excess energy of the “hot” ipso-adduct was 27.6 kcal mol−1, this reaction channel seems to be feasible. However, since the ipso-adduct is only a minor primary product, this reaction channel may contribute only a small fraction of total phenols. The G3 reaction barrier for elimination of hydrogen atom was similar, i.e. 23.8 kcal mol−1 while the excess energy of the “hot” para-adduct was 19.7 kcal mol−1 and this reaction channel may be feasible too. Since the para-adduct is a major primary product, it seems that the direct elimination of hydrogen atom also contributes to the formation of 4-fluorophenol. It was also evaluated for chlorobenzene80 and bromobenzene116 that phenol can be produced by the direct elimination of halogen atoms from their ipso-adducts.
By analogy to the tropospheric oxidation of monosubstituted benzenes, it may be assumed for perhalogenated derivatives that the major ring-retaining product will be pentafluorophenol or pentachlorophenol, produced by direct elimination of halogen atoms from the respective adduct (eqn (3)).
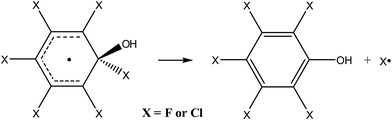 | (3) |
In order to prove that this process is thermodynamically and kinetically feasible, the transition state was optimized for the direct elimination of chlorine atom from the “hot” hexachlorobenzene adduct. The optimized geometry shows that the separation between the quaternary carbon atom and the leaving chlorine in the transition state is 3.31 Å and that the reaction barrier for the direct elimination of chlorine atom and formation of pentachlorophenol is quite low, only 4.1 kcal mol−1.84 Since the excess energy of the “hot” hexachlorobenzene adduct is huge with respect to this reaction barrier, i.e. 32 kcal mol−1, the above results unambiguously demonstrate that the formation of pentachlorophenol is thermodynamically and kinetically feasible and that it should proceed easily. An analogous product, i.e. pentafluorophenol, was also recently postulated for the reaction of the hydroxyl radical with hexafluorobenzene83 since for its “hot” adduct excess energy is also more than 30 kcal mol−1.
Since the tropospheric concentration of hexachlorobenzene is fairly constant and uniform,117,118 the atmospheric production of pentachlorophenol seems to be a global phenomenon that will proceed at a constant pace for a long time due to the steady-state concentration of atmospheric hexachlorobenzene. Once produced, pentachlorophenol, due to its lower hydrophobicity, will be transported by the wet or dry deposition into the Earth's aquatic and solid systems since both compartments have a much higher affinity for pentachlorophenol than the air. Those results reveal that the troposphere may be an undisclosed global secondary source of pentachlorophenol relevant for all environmental compartments as well as a new exciting research area.
4. Conclusions
Direct and detailed insight was obtained into the complete reaction mechanism and reaction dynamics of OH radical addition to four halogenated benzenes, i.e. fluorobenzene, chlorobenzene, hexafluorobenzene and hexachlorobenzene. The presented studies have shown for the first time that the addition of OH radicals to all halogenated benzenes proceeds via a prereaction complex. The structure and reaction dynamics of prereaction complexes of monohalogenated benzenes are substantially different from those of perhalogenated benzenes. Namely, in the prereaction complexes of fluorobenzene and chlorobenzene hydrogen atoms of hydroxyl radicals are pointing approximately to the center of the aromatic ring while in the case of hexafluorobenzene and hexachlorobenzene the oxygen atom is unexpectedly directed towards the center of the aromatic ring. The substantial structural difference in the prereaction complexes is a consequence of a positive electrostatic potential of the aromatic ring in hexafluorobenzene and hexachlorobenzene due to the strong electron withdrawing effect of six halogen atoms. All oxidations of halogenated benzenes by hydroxyl radicals are highly exothermic and produce “hot” adducts with large amounts of excess energy. It was also demonstrated that pentachlorophenol, a well-known organic micropollutant, may be a major stable product of tropospheric oxidation of hexachlorobenzene and that atmosphere seems to be its hidden global secondary source. The reliable rate constants are now determined for the whole range of environmentally relevant temperatures (230–330 K) for the oxidation of fluorobenzene, chlorobenzene hexafluorobenzene and hexachlorobenzene by hydroxyl radicals and calculated rate constants are in excellent agreement with available experimental data. However, for such a good correspondence between the calculated and experimental results it was necessary to use two-dimensional particle-in-the-box approximation for the translation of the hydroxyl radical in prereaction complexes. Furthermore, it is now also possible to calculate the reliable tropospheric lifetimes of those halogenated benzenes for the whole range of environmentally relevant temperatures. The calculated tropospheric lifetimes clearly show that fluorobenzene and chlorobenzene are relatively easily removed from the atmosphere and do not have potential for a long-range transport while hexafluorobenzene with a calculated tropospheric lifetime of 237 days indicates its status as a potential POP chemical and the calculated tropospheric lifetime of hexachlorobenzene, i.e. 522 days, supports its status of a classical persistent organic pollutant.Acknowledgements
This work has been supported by the Croatian Ministry of Science, Education and Sport, under Project No. 098-0982915-2944.References
- T. E. Graedel, D. T. Hawkins and L. D. Claxton, Atmospheric Chemical Compounds: Sources, Occurrence, and Bioassay, Academic Press, Orlando, FL, 1986 Search PubMed.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Evaluated kinetic and photochemical data for atmospheric chemistry: volume II – gas phase reactions of organic species, Atmos. Chem. Phys., 2006, 6, 3625–4055, DOI:10.5194/acp-6-3625-2006.
- R. A. Cox, Evaluation of laboratory kinetics and photochemical data for atmospheric chemistry applications, Chem. Soc. Rev., 2012, 41, 6231–6246, 10.1039/c2cs35092k.
- R. Atkinson, Gas-Phase Tropospheric Chemistry of Organic Compounds, Journal of Physical and Chemical Reference Data Monograph No. 2, American Chemical Society: Washington, DC and American Institute of Physics, Woodbury, NY, 1994 Search PubMed.
- H. Guesten, Z. Medven, S. Sekusak and A. Sabljic, Predicting tropospheric degradation of chemicals: From estimation to computation, SAR QSAR Environ. Res., 1995, 4, 197–209, DOI:10.1080/10629369508032980.
- L. Vereecken and J. S. Francisco, Theoretical studies of atmospheric reaction mechanisms in the troposphere, Chem. Soc. Rev., 2012, 41, 6259–6293, 10.1039/c2cs35070j.
- L. Vereecken, D. R. Glowacki and M. J. Pilling, Theoretical Chemical Kinetics in Tropospheric Chemistry: Methodologies and Applications, Chem. Rev., 2015, 115, 4063–4114, DOI:10.1021/cr500488p.
- R. G. Prinn, R. F. Weiss, B. R. Miller, J. Huang, F. N. Alyea, D. M. Cunnold, P. J. Fraser, H. E. Hartley and P. G. Simmonds, Atmospheric trends and lifetime of CH3CCL3 and global OH concentrations, Science, 1995, 269, 187–192, DOI:10.1126/science.269.5221.187.
- A. Sabljic and W. Peijnenburg, Modeling lifetime and degradability of organic compounds in air, soil, and water systems, Pure Appl. Chem., 2001, 73, 1331–1348, DOI:10.1351/pac200173081331.
- I. Stefanic, I. Ljubic, M. Bonifacic, A. Sabljic, K.-D. Asmus and D. A. Armstrong, A surprisingly complex aqueous chemistry of the simplest amino acid. A pulse radiolysis and theoretical study on H/D kinetic isotope effects in the reaction of glycine anions with hydroxyl radicals, Phys. Chem. Chem. Phys., 2009, 11, 2256–2267, 10.1039/b816353g.
- C. Rucker and K. Kummerer, Modeling and predicting aquatic aerobic biodegradation – a review from a user's perspective, Green Chem., 2012, 14, 857–887, 10.1039/c2gc16267a.
- A. Sabljic and Y. Nakagawa, Biodegradation and quantitative structure–activity relationship (QSAR), in Non-first order degradation and time-dependent sorption of organic chemicals in soil, ed. W. Chen, A. Sabljic, S. A. Cryer and R. S. Kookana, ACS Symposium Series e-Book, American Chemical Society, Washington DC, 2014, vol. 1174, p. 57 Search PubMed.
- S. S. Brown and J. Stutz, Nighttime radical observations and chemistry, Chem. Soc. Rev., 2012, 41, 6405–6447, 10.1039/c2cs35181a.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Evaluated kinetic and photochemical data for atmospheric chemistry: volume I – gas phase reactions of Ox, HOx, NOx and SOx species, Atmos. Chem. Phys., 2004, 4, 1461–1738, DOI:10.5194/acp-4-1461-2004.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi, J. Troe and T. J. Wallington, Evaluated kinetic and photochemical data for atmospheric chemistry: volume IV – gas phase reactions of organic halogen species, Atmos. Chem. Phys., 2008, 8, 4141–4496, DOI:10.5194/acp-8-4141-2008.
- Y. Wang, J. Chen, X. Li, B. Wang, X. Cai and L. Huang, Predicting rate constants of hydroxyl radical reactions with organic pollutants: algorithm, validation, applicability domain, and mechanistic interpretation, Atmos. Environ., 2009, 43, 1131–1135, DOI:10.1016/j.atmosenv.2008.11.012.
- R. Atkinson, Kinetics and mechanisms of the gas-phase reactions of the NO3 radical with organic compounds, J. Phys. Chem. Ref. Data, 1991, 20, 459–507 CrossRef CAS.
- M. Schindler, A QSAR for the prediction of rate constants for the reaction of VOCs with nitrate radicals, Chemosphere, 2016, 154, 23–33, DOI:10.1016/j.chemosphere.2016.03.096.
- R. Atkinson and W. P. L. Carter, Kinetics and mechanisms of the gas-phase reactions of ozone with organic-compounds under atmospheric conditions, Chem. Rev., 1984, 84, 437–470, DOI:10.1021/cr00063a002.
- R. Atkinson, Gas-phase tropospheric chemistry of volatile organic compounds. 1. Alkanes and alkenes, J. Phys. Chem. Ref. Data, 1997, 26, 215–290 CrossRef CAS.
- M. H. Fatemi, Prediction of ozone tropospheric degradation rate constant of organic compounds by using artificial neural networks, Anal. Chim. Acta, 2006, 556, 355–363, DOI:10.1016/j.aca.2005.09.033.
- X. Li, W. Zhao, J. Li, J. Jiang, J. Chen and J. Chen, Development of a model for predicting reaction rate constants of organic chemicals with ozone at different temperatures, Chemosphere, 2013, 92, 1029–1034, DOI:10.1016/j.chemosphere.2013.03.040.
- ECHA, 2016, Information on Chemicals, accessed on September 19, 2016, https://echa.europa.eu/information-on-chemicals.
- R. Atkinson, A structure–activity relationship for the estimation of rate constants for the gas-phase reactions of OH radicals with organic compounds, Int. J. Chem. Kinet., 1987, 19, 799–828 CrossRef CAS.
- E. S. C. Kwok and R. Atkinson, Estimation of hydroxyl radical reaction-rate constants for gas-phase organic-compounds using a structure–reactivity relationship – an update, Atmos. Environ., 1995, 29, 1685–1695, DOI:10.1016/1352-2310(95)00069-B.
- H. Guesten, L. Klasinc and D. Maric, Prediction of the abiotic degradability of organic compounds in the troposphere, J. Atmos. Chem., 1984, 2, 83–93 CrossRef CAS.
- H. Parlar, D. Kotzias, M. Herrmann and A. Zsolnay, Relationship between the OH radical rate constants of organic compounds in gaseous phase and their chemical shifts in 1H and 13C-NMR spectroscopy, Chemosphere, 1986, 15, 971–980 CrossRef CAS.
- A. Sabljic and H. Guesten, Predicting the night time NO3 radical reactivity in the troposphere, Atmos. Environ., 1990, 24, 73–78 CrossRef.
- J. Heicklen, The correlation for rate coefficients for H-atom abstraction by HO radicals with C–H bond dissociation enthalpies, Int. J. Chem. Kinet., 1981, 13, 651–665 CrossRef CAS.
- G. S. Jolly, G. Paraskevopoulos and D. L. Singleton, Rates of OH radical reactions. XII. The reactions of OH with c-C3H6, c-C5H10, and c-C7H14. Correlation of hydroxyl rate constants with bond dissociation energies, Int. J. Chem. Kinet., 1985, 17, 1–10 CrossRef CAS.
- US EPA, 2010, EPI Suit™, https://www.epa.gov/tsca-screening-tools/download-epi-suitetm-estimation-program-interface-v411, accessed on September 29, 2016.
- Z. Medven, H. Guesten and A. Sabljic, Comparative QSAR study on hydroxyl radical reactivity with unsaturated hydrocarbons. PLS versus MLR, J. Chemom., 1996, 10, 135–147 CrossRef CAS.
- W. M. Meylan and P. H. Howard, A review of quantitative structure–activity relationship methods for the prediction of atmospheric oxidation of organic chemicals, Environ. Toxicol. Chem., 2003, 22, 1724–1732 CrossRef CAS PubMed.
- P. Gramatica, P. Pilutti and E. Papa, Predicting the NO3 radical tropospheric degradability of organic pollutants by theoretical molecular descriptors, Atmos. Environ., 2003, 37, 3115–3124, DOI:10.1016/s1352-2310(03)00293-0.
- P. Gramatica, P. Pilutti and E. Papa, A tool for the assessment of VOC degradability by tropospheric oxidants starting from chemical structure, Atmos. Environ., 2004, 38, 6167–6175, DOI:10.1016/j.atmosenv.2004.07.026.
- J. Kerdouci, B. Picquet-Varrault and J.-F. Doussin, Prediction of rate constants for gas-phase reactions of nitrate radical with organic compounds: a new structure–activity relationship, ChemPhysChem, 2010, 11, 3909–3920, DOI:10.1002/cphc.201000673.
- S. Gupta, N. Basant, D. Mohan and K. P. Singh, Inter-moieties reactivity correlations: an approach to estimate the reactivity endpoints of major atmospheric reactants towards organic chemicals, RSC Adv., 2016, 6, 50297–50305, 10.1039/c6ra06805g.
- C. Li, X. H. Yang, X. H. Li, J. W. Chen and X. L. Qiao, Development of a model for predicting hydroxyl radical reaction rate constants of organic chemicals at different temperatures, Chemosphere, 2014, 95, 613–618, DOI:10.1016/j.chemosphere.2013.10.020.
- V. S. Melissas and D. G. Truhlar, Interpolated variational transition-state theory and semiclassical tunneling calculations of the rate-constant of the reaction OH + C2H6 at 200–3000 K, J. Phys. Chem., 1994, 94, 875–886 CrossRef.
- Y. J. Fu, W. Lewisbevan and J. Tirrell, An ab initio investigation of the reaction of trifluoromethane with the hydroxyl radical, J. Phys. Chem., 1995, 99, 630–633 CrossRef CAS.
- J. S. Francisco, An examination of substitution effects on the reaction of OH radicals with HXCO (where X = H, F, and Cl), J. Chem. Phys., 1992, 96, 7597–7602 CrossRef CAS.
- J. S. Francisco, Reaction of OH radicals with CH3C(O)H and CF3C(O)H, J. Chem. Soc., Faraday Trans., 1992, 88, 1943–1947, 10.1039/ft9928801943.
- M.-T. Rayez, J.-C. Rayez, T. Berces and G. Lendvay, Theoretical-study of the reactions of OH radicals with substituted acetaldehydes, J. Phys. Chem., 1993, 97, 5570–5576, DOI:10.1021/j100123a019.
- A. Bottoni, G. Poggi and S. S. Emmi, An ab initio study of H-abstraction in halogen-substituted methanes by the OH radical, J. Mol. Struct.: THEOCHEM, 1993, 279, 299–309 CrossRef.
- S. Sekusak, K. R. Liedl, B. M. Rode and A. Sabljic, Reaction-path dynamics of hydroxyl radical reactions with ethane and haloethanes, J. Phys. Chem. A, 1997, 101, 4245–4253 CrossRef CAS.
- S. Sekusak and A. Sabljic, The role of complexes in hydrogen abstraction from haloethanes by hydroxyl radical. A case of guided reactions, Chem. Phys. Lett., 1997, 272, 353–360 CrossRef CAS.
- J. R. Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, On the importance of prereactive complexes in molecule-radical reactions: hydrogen abstraction from aldehydes by OH, J. Am. Chem. Soc., 2001, 123, 2018–2024, DOI:10.1021/ja003372g.
- A. Galano, J. R. Alvarez-Idaboy, M. E. Ruiz-Santoyo and A. Vivier-Bunge, Rate coefficient and mechanism of the gas phase OH hydrogen abstraction reaction from formic acid: a quantum mechanical approach, J. Phys. Chem. A, 2002, 106, 9520–9528, DOI:10.1021/jp020297i.
- Z. J. Li, P. Nguyen, M. F. de Leon, J. H. Wang, K. L. Han and G. Z. He, Experimental and theoretical study of reaction of OH with 1,3-butadiene, J. Phys. Chem. A, 2006, 110, 2698–2708 CrossRef CAS PubMed.
- J. P. Senosiain, S. J. Klippenstein and J. A. Miller, Reaction of ethylene with hydroxyl radicals: a theoretical study, J. Phys. Chem. A, 2006, 110, 6960–6970 CrossRef CAS PubMed.
- E. W. Wilson, W. A. Hamilton, H. R. Kennington, B. Evans, N. W. Scott and W. B. DeMore, Measurement and estimation of rate constants for the reactions of hydroxyl radical with several alkanes and cycloalkanes, J. Phys. Chem. A, 2006, 110, 3593–3604 CrossRef CAS PubMed.
- J. M. Martell and R. J. Boyd, Ab-initio studies of reactions of hydroxyl radicals with fluorinated ethanes, J. Phys. Chem., 1995, 99, 13402–13411 CrossRef CAS.
- S. Sekusak, H. Guesten and A. Sabljic, An ab initio investigation of transition-states and reactivity of chloroethane with OH radical, J. Chem. Phys., 1995, 102, 7504–7518 CrossRef CAS.
- S. Sekusak, H. Guesten and A. Sabljic, An ab initio study on reactivity of fluoroethane with hydroxyl radical: Application of G2 theory, J. Phys. Chem., 1996, 100, 6212–6224, DOI:10.1021/jp952819i.
- S. Sekusak, K. R. Liedl and A. Sabljic, Reactivity and regioselectivity of hydroxyl radical addition to halogenated ethenes, J. Phys. Chem. A, 1998, 102, 1583–1594 CrossRef CAS.
- J. Peeters, L. Vereecken and G. Fantechi, The detailed mechanism of the OH-initiated atmospheric oxidation of alpha-pinene: a theoretical study, Phys. Chem. Chem. Phys., 2001, 3, 5489–5504 RSC.
- J. R. Wells, Gas-phase chemistry of alpha-terpineol with ozone and OH radical: rate constants and products, Environ. Sci. Technol., 2005, 39, 6937–6943 CrossRef CAS PubMed.
- L. Vereecken and J. Peeters, A theoretical study of the OH-initiated gas-phase oxidation mechanism of beta-pinene (C10H16): first generation products, Phys. Chem. Chem. Phys., 2012, 14, 3802–3815, 10.1039/c2cp23711c.
- F. Cavalli, I. Barnes and K. H. Becker, FT-IR kinetic and product study of the OH radical-initiated oxidation of 1-pentanol, Environ. Sci. Technol., 2000, 34, 4111–4116 CrossRef CAS.
- F. Reisen, S. M. Aschmann, R. Atkinson and J. Arey, Hydroxyaldehyde products from hydroxyl radical reactions of Z-3-hexen-1-ol and 2-methyl-3-buten-2-ol quantified by SPME and API-MS, Environ. Sci. Technol., 2003, 37, 4664–4671 CrossRef CAS PubMed.
- J. Espinosa-Garcia, Ab initio and variational transition-state theory study of the CF3CF2OCH3 plus OH reaction using integrated methods: mechanism and kinetics, J. Phys. Chem. A, 2003, 107, 1618–1626 CrossRef CAS.
- A. Galano, J. R. Alvarez-Idaboy and M. Francisco-Marquez, Mechanism and Branching Ratios of Hydroxy Ethers + ˙OH Gas phase Reactions: Relevance of H Bond Interactions, J. Phys. Chem. A, 2010, 114, 7525–7536, DOI:10.1021/jp103575f.
- G. Fantechi, L. Vereecken and J. Peeters, The OH-initiated atmospheric oxidation of pinonaldehyde: Detailed theoretical study and mechanism construction, Phys. Chem. Chem. Phys., 2002, 4, 5795–5805 RSC.
- J. P. Le Crane, E. Villenave, M. D. Hurley, T. J. Wallington and J. C. Ball, Atmospheric chemistry of propionaldehyde: kinetics and mechanisms of reactions with OH radicals and Cl atoms, UV spectrum, and self-reaction kinetics of CH3CH2C(O)O−2 radicals at 298 K, J. Phys. Chem. A, 2005, 109, 11837–11850 CrossRef CAS PubMed.
- F. Caralp, W. Forst, E. Henon, A. Bergeat and F. Bohr, Tunneling in the reaction of acetone with OH, Phys. Chem. Chem. Phys., 2006, 8, 1072–1078, 10.1039/b515118j.
- F. De Smedt, X. V. Bui, T. L. Nguyen, J. Peeters and L. Vereecken, Theoretical and experimental study of the product branching in the reaction of acetic acid with OH radicals, J. Phys. Chem. A, 2005, 109, 2401–2409 CrossRef CAS PubMed.
- D. Vimal and P. S. Stevens, Experimental and theoretical studies of the kinetics of the reactions of OH radicals with acetic acid, acetic acid-d(3) and acetic acid-d(4) at low pressure, J. Phys. Chem. A, 2006, 110, 11509–11516 CrossRef CAS PubMed.
- L. Yang, J. Liu and Z. Li, Theoretical studies of the reaction of hydroxyl radical with methyl acetate, J. Phys. Chem. A, 2008, 112, 6364–6372, DOI:10.1021/jp800986d.
- S. Jorgensen, V. F. Andersen, E. J. K. Nilsson, O. J. Nielsen and M. S. Johnson, Theoretical study of the gas phase reaction of methyl acetate with the hydroxyl radical: Structures, mechanisms, rates and temperature dependencies, Chem. Phys. Lett., 2010, 490, 116–122, DOI:10.1016/j.cplett.2010.03.031.
- I. V. Tokmakov and M. C. Lin, Kinetics and mechanism of the OH + C6H6 reaction: a detailed analysis with first-principles calculation, J. Phys. Chem. A, 2002, 106, 11309–11326 CrossRef CAS.
- C. Chen, J. W. Bozelli and J. T. Farrel, Thermochemical properties, pathway, and kinetic analysis on the reactions of benzene with OH: an elementary reaction mechanism, J. Phys. Chem. A, 2004, 108, 4632–4652 CrossRef CAS.
- S. Raoult, M. T. Rayez, J. C. Rayez and R. Lesclaux, Gas phase oxidation of benzene: kinetics, thermochemistry and mechanism of initial steps, Phys. Chem. Chem. Phys., 2004, 6, 2245, 10.1039/b315953a.
- D. R. Glowacki, L. Wang and M. J. Pilling, Evidence of formation of bicyclic species in the early stages of atmospheric benzene oxidation, J. Phys. Chem. A, 2009, 113, 5385–5396, DOI:10.1021/jp9001466.
- S. Olivella, A. Sole and J. M. Bofill, Theoretical mechanistic study of the oxidative degradation of benzene in the troposphere: reaction of benzene–HO radical adduct with O2, J. Chem. Theory Comput., 2009, 5, 1607–1623, DOI:10.1021/ct900082g.
- V. H. Uc, I. García-Cruz, A. Hernández-Laguna and A. Vivier-Bunge, New channels in the reaction mechanism of the atmospheric oxidation of toluene, J. Phys. Chem. A, 2000, 104, 7847–7855, DOI:10.1021/jp0627751.
- I. Suh, D. Zhang, R. Zhang, L. Molina and M. J. Molina, Theoretical study of OH addition reaction to toluene, Chem. Phys. Lett., 2002, 364, 454–462 CrossRef CAS.
- R. R. Wu, S. S. Pan, Y. Li and L. M. Wang, Atmospheric Oxidation Mechanism of Toluene, J. Phys. Chem. A, 2014, 118, 4533–4547, DOI:10.1021/jp500077f.
- M. J. Lundqvist and L. A. Eriksson, Hydroxyl radical reactions with phenol as a model for generation of biologically reactive tyrosyl radicals, J. Phys. Chem. B, 2000, 104, 848–855, DOI:10.1021/jp993011r.
- G. Kovacevic and A. Sabljic, Theoretical study on the mechanism and kinetics of addition of hydroxyl radicals to fluorobenzene, J. Comput. Chem., 2013, 34(8), 646–655, DOI:10.1002/jcc.23175.
- M. G. Bryukov, V. D. Knyazev, W. M. Gehling and B. Dellinger, Kinetics of the gas-phase reaction of OH with chlorobenzene, J. Phys. Chem. A, 2009, 113, 10452–10459, DOI:10.1021/jp9049186.
- G. Kovacevic and A. Sabljic, A. Mechanisms and reaction-path dynamics of hydroxyl radical reactions with aromatic hydrocarbons: the case of chlorobenzene, Chemosphere, 2013, 92(7), 851–856, DOI:10.1016/j.chemosphere.2013.04.041.
- Z. J. Zhang, L. Lin and L. M. Wang, Atmospheric oxidation mechanism of naphthalene initiated by OH radical. A theoretical study, Phys. Chem. Chem. Phys., 2012, 14, 2645–2650, 10.1039/c2cp23271e.
- G. Kovacevic and A. Sabljic, Tropospheric degradation of perfluorinated aromatics: a case of hexafluorobenzene, Croat. Chem. Acta, 2015, 88(4), 547–552, DOI:10.5562/cca2823.
- G. Kovacevic and A. Sabljic, Atmospheric oxidation of hexachlorobenzene: new global source of pentachlorophenol, Chemosphere, 2016, 159, 488–495, DOI:10.1016/j.chemosphere.2016.06.026.
- F. Wania and D. Mackay, Tracking the distribution of persistent organic pollutants, Environ. Sci. Technol., 1996, 30(9), 390A–396A CrossRef CAS PubMed.
- A. Sabljic, QSAR models for estimating properties of persistent organic pollutants required in evaluation of their environmental fate and risk, Chemosphere, 2001, 43(3), 363–375, DOI:10.1016/s0045-6535(00)00084-9.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. J. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General atomic and molecular electronic structure system, J. Comput. Chem., 1992, 14(11), 1347–1363, DOI:10.1002/jcc.540141112.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, Gaussian-3 (G3) theory for molecules containing first and second-row atoms, J. Chem. Phys., 1998, 109(18), 7764–7776, DOI:10.1063/1.477422.
- L. A. Curtiss, P. C. Redfern, K. Raghavachari, V. Rassolov and J. A. Pople, Gaussian-3 theory using reduced Møller–Plesset order, J. Chem. Phys., 1999, 110(10), 4703–4709, DOI:10.1063/1.478385.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- W. H. Miller, N. C. Handy and J. E. Adams, Reaction path Hamiltonian for polyatomic molecules, J. Chem. Phys., 1980, 72(1), 99–112, DOI:10.1063/1.438959.
- J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell computer program suite, Int. J. Chem. Kinet., 2001, 33(4), 232–245, DOI:10.1002/kin.1017.
- J. R. Barker and N. F. Ortiz, Multiple-well, multiple-path unimolecular reaction systems. II. 2-methylhexyl free radicals, Int. J. Chem. Kinet., 2001, 33(4), 246–261 CrossRef CAS.
- J. R. Barker, N. F. Ortiz, J. M. Preses, L. L. Lohr, A. Maranzana and P. J. Stimac, MultiWell-2.08 Software, University of Michigan, Ann Arbor, MI, 2007, http://aoss.engin.umich.edu/multiwell/ Search PubMed.
- A. Fernandez-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Truhlar, Modeling the kinetics of bimolecular reactions, Chem. Rev., 2006, 106(11), 4518–4584, DOI:10.1021/cr050205w.
- W. Forst, Unimolecular Reactions, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- S. E. Wheeler and K. N. Houk, Through-Space Effects of Substituents Dominate Molecular Electrostatic Potentials of Substituted Arenes, J. Chem. Theory Comput., 2009, 5(9), 2301–2312, DOI:10.1021/ct900344g.
- B. K. Mishra and N. Sathyamurthy, van der Waals complexes of small molecules with benzenoid rings: influence of multipole moments on their mutual orientation, J. Phys. Chem. A, 2007, 111(11), 2139–2147, DOI:10.1021/jp065584r.
- E. E. Greenwald, S. W. North, Y. Georgievskii and S. J. Klippenstein, A two transition state model for radical-molecule reactions: a case study of the addition of OH to C2H4, J. Phys. Chem. A, 2005, 109(27), 6031–6044, DOI:10.1021/jp058041a.
- R. Atkinson, Kinetics and Mechanisms of the Gas-phase Reactions of the Hydroxyl Radical with organic compounds, Journal of Physical and Chemical Reference Data Monograph No. 1, American Chemical Society: Washington, DC and American Institute of Physics, Woodbury, NY, 1989 Search PubMed.
- M. P. Sulbaek Andersen, O. J. Nielsen, M. D. Hurley and T. J. Wallington, Kinetics and mechanism of the gas-phase reaction of Cl atoms and OH radicals with fluorobenzene at 296 K, J. Phys. Chem. A, 2002, 106, 7779–7787, DOI:10.1021/jp025725z.
- A. McIlroy and F. P. Tully, Kinetic-study of OH reaction with perfluoropropene and perfluorobenzene, J. Phys. Chem., 1993, 97, 610–614, DOI:10.1021/j100105a013.
- W. W. Brubaker and R. A. Hites, OH reaction kinetics of gas-phase α- and γ-hexachlorocyclohexane and hexachlorobenzene, Environ. Sci. Technol., 1998, 32(6), 766–769, DOI:10.1021/es970650b.
- M. J. Prather and C. M. Spivakovsky, Tropospheric OH and the lifetimes of hydrochlorofluorocarbons, J. Geophys. Res., 1990, 95(D11), 18723–18729, DOI:10.1029/jd095id11p18723.
- J. L. Barber, A. J. Sweetman, D. van Wijk and K. C. Jones, Hexachlorobenzene in the global environment: emissions, levels, distribution, trends and processes, Sci. Total Environ., 2005, 349(1–3), 1–44, DOI:10.1016/j.scitotenv.2005.03.014.
- S.-D. Choi and F. Wania, On the reversibility of environmental contamination with persistent organic pollutants, Environ. Sci. Technol., 2011, 45(20), 8834–8841, DOI:10.1021/es2017544.
- C. J. Galban-Malagon, N. Berrojalbiz, R. Gioia and J. Dachs, The “degradative” and “biological” pumps controls on the atmospheric deposition and sequestration of hexachlorocyclohexanes and hexachlorobenzene in the North Atlantic and Arctic Oceans, Environ. Sci. Technol., 2013, 47(13), 7195–7203, DOI:10.1021/es4011256.
- C. Galban-Malagon, A. Cabrerizo, G. Caballero and J. Dachs, Atmospheric occurrence and deposition of hexachlorobenzene and hexachlorocyclohexanes in the Southern Ocean and Antarctic Peninsula, Atmos. Environ., 2013, 80, 41–49, DOI:10.1016/j.atmosenv.2013.07.061.
- D. G. Patterson, L. Y. Wong, W. E. Turner, S. P. Caudill, E. S. Dipietro, P. C. McClure, T. P. Cash, J. D. Osterloh, J. L. Pirkle, E. J. Sampson and L. L. Needham, Levels in the US population of those persistent organic pollutants (2003–2004) included in the Stockholm Convention or in other long-range transboundary air pollution agreements, Environ. Sci. Technol., 2009, 43(4), 1211–1218, DOI:10.1021/es801966w.
- J. G. Calvert, R. Atkinson, K. H. Becker, R. M. Kamens, J. H. Seinfeld, T. J. Wallington and G. Yarwood, The Mechanisms of Atmospheric Oxidation of Aromatic Hydrocarbons, Oxford University Press, Oxford, UK, 2002 Search PubMed.
- R. Koch, R. Knispel, M. Elend, M. Siese and C. Zetzsch, Consecutive reactions of aromatic-OH adducts with NO, NO2 and O2: benzene, naphthalene, toluene, m- and p-xylene, hexamethylbenzene, phenol, m-cresol and aniline, Atmos. Chem. Phys., 2007, 7, 2057–2071 CrossRef CAS.
- R. Volkamer, B. Klotz, I. Barnes, T. Imamura, K. Wirtz, N. Washida, K. H. Becker and U. Platt, OH-initiated oxidation of benzene – part I. Phenol formation under atmospheric conditions, Phys. Chem. Chem. Phys., 2002, 4(9), 1598–1610, 10.1039/b108747a.
- T. Berndt and O. Böge, Formation of phenol and carbonyls from the atmospheric reaction of OH radicals with benzene, Phys. Chem. Chem. Phys., 2006, 8(10), 1205–1214, 10.1039/b514148f.
- J. Noda, R. Volkamer and M. J. Molina, Dealkylation of alkylbenzenes: a significant pathway in the toluene, o-, m-, p-xylene plus OH reaction, J. Phys. Chem. A, 2009, 113(35), 9658–9666, DOI:10.1021/jp901529k.
- B. Klotz, R. Volkamer, M. D. Hurley, M. P. S. Andersen, O. J. Nielsen, I. Barnes, T. Imamura, K. Wirtz, K.-H. Becker, U. Platt, T. J. Wallington and N. Washida, OH-initiated oxidation of benzene – part II. Influence of elevated NOx concentrations, Phys. Chem. Chem. Phys., 2002, 4, 4399–4411, 10.1039/b204398j.
- Y. Nakano, M. Kawasaki, D. A. Ponomarev, M. D. Hurley and T. J. Wallington, Kinetics and mechanism of the gas phase reaction of Cl atoms and OH radicals with bromobenzene, Chem. Phys. Lett., 2002, 353(1–2), 77–83, DOI:10.1016/s0009-2614(01)01499-3.
- G. Wang, Y. L. Lu, J. Y. Han, W. Luo, Y. J. Shi, T. Y. Wang and Y. M. Sun, Hexachlorobenzene sources, levels and human exposure in the environment of China, Environ. Int., 2010, 36(1), 122–130, DOI:10.1016/j.envint.2009.08.005.
- R. E. Bailey, Global hexachlorobenzene emissions, Chemosphere, 2001, 43(2), 167–182, DOI:10.1016/s0045-6535(00)00186-7.
| This journal is © The Royal Society of Chemistry 2017 |