Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A lung-inspired approach to scalable and robust fuel cell design†
P.
Trogadas‡
 ab,
J. I. S.
Cho‡
ab,
J. I. S.
Cho‡
 ab,
T. P.
Neville
ab,
T. P.
Neville
 ab,
J.
Marquis§
c,
B.
Wu
ab,
J.
Marquis§
c,
B.
Wu
 d,
D. J. L.
Brett
b and
M.-O.
Coppens
d,
D. J. L.
Brett
b and
M.-O.
Coppens
 *a
*a
aEPSRC “Frontier Engineering” Centre for Nature Inspired Engineering & Department of Chemical Engineering, University College London, London, WC1E 7JE, UK. E-mail: m.coppens@ucl.ac.uk
bElectrochemical Innovation Lab, Department of Chemical Engineering, University College London, London, WC1E 7JE, UK
cDepartment of Chemical and Biological Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
dDepartment of Mechanical Engineering, Imperial College London, London, SW7 2AZ, UK
First published on 25th October 2017
Abstract
A lung-inspired approach is employed to overcome reactant homogeneity issues in polymer electrolyte fuel cells. The fractal geometry of the lung is used as the model to design flow-fields of different branching generations, resulting in uniform reactant distribution across the electrodes and minimum entropy production of the whole system. 3D printed, lung-inspired flow field based PEFCs with N = 4 generations outperform the conventional serpentine flow field designs at 50% and 75% RH, exhibiting a ∼20% and ∼30% increase in performance (at current densities higher than 0.8 A cm−2) and maximum power density, respectively. In terms of pressure drop, fractal flow-fields with N = 3 and 4 generations demonstrate ∼75% and ∼50% lower values than conventional serpentine flow-field design for all RH tested, reducing the power requirements for pressurization and recirculation of the reactants. The positive effect of uniform reactant distribution is pronounced under extended current-hold measurements, where lung-inspired flow field based PEFCs with N = 4 generations exhibit the lowest voltage decay (∼5 mV h−1). The enhanced fuel cell performance and low pressure drop values of fractal flow field design are preserved at large scale (25 cm2), in which the excessive pressure drop of a large-scale serpentine flow field renders its use prohibitive.
Broader contextFlow-field design is crucial to fuel cell performance, since non-uniform transport of species to and from the membrane-electrode assembly results in significant power losses. The long channels of conventional, serpentine flow fields cause large pressure drops between inlets and outlets, thus large parasitic energy losses and low fuel cell performance. This issue is exacerbated for small, portable fuel cells, where the power required for fluid transport should be minimal. To ensure uniform distribution of reactants across the electrode and a low pressure drop, we use a nature-inspired design that is rooted in thermodynamic and mechanical fundamentals, rather than biomimicry in a narrow sense. Inspiration is derived from the structure of the human lung, which ensures uniform gas distribution via an optimized fractal structure linking bronchi to alveoli, and realizing a remarkable combination of minimal entropy production, low pressure drop, and scale-invariant operation. Our 3D-printed, conducting flow-field plates maintain these unique characteristics of the lung, resulting in improved fuel cell performance over conventional serpentine flow-field based fuel cells. Uniformity in reactant distribution and minimal pressure drop are retained during scale-up, demonstrating the robustness of the proposed nature-inspired approach across length scales. |
1. Introduction
Polymer electrolyte fuel cells (PEFCs) have tremendous potential as an energy technology with zero emissions at point of use.1 The rapid start-up time, low weight and high efficiency make PEFCs particularly attractive for portable and automotive applications.2 However, there remain challenges to broader commercialization of this technology, including high electrocatalyst cost, durability issues and performance limitations associated with unoptimized flow-field designs. For example, poor flow-field design can lead to channels becoming clogged with liquid water and non-uniform reactant distribution.3,4 Such mass transport issues can lead to the accumulation of excess water in the pores of the gas diffusion layer (GDL)5 and reactant starvation, which, in turn, can lead to corrosion of carbonaceous support material,6 electrocatalyst sintering and facile membrane degradation,5 all of which are detrimental to fuel cell longevity. Reactions of bulk and crossover gases at each electrode7 result in the formation of harmful radicals,8 which significantly hinder the oxygen reduction kinetics and oxygen/air transport through the polymer electrolyte.9Thus far, there have been two prevalent strategies reported in the literature to overcome the uneven reactant distribution issue in PEFCs. The first approach is based on empirical alteration of the channel configurations (such as channel path length,10 land width,11,12 and land/channel ratio13,14), whereas the second approach imitates the apparent structure of biological organisms.15–19 The consensus to the first strategy is that the utilization of flow-fields with wider rib spacing, narrower and shorter channels and path length improves reactant distribution.10,11,14 However, these modifications tend to result in lower membrane hydration and membrane conductivity,13 a higher pressure drop20 as well as ineffective water and heat management.10
These drawbacks to the first strategy have led to the exploration of an alternative route, taking “inspiration” from biological systems. The term “inspiration” is purposely enclosed within parentheses, since all reports to date imitate the apparent structure of a natural fluid distribution system (such as leaves, lungs, veins, etc.) without being fundamentally grounded in the underlying physical phenomena.15–19 Lack of a formal mathematical description and a methodology to inform the design of such flow-fields leads to difficulties in reproducing those designs, optimizing their channel geometries and scaling them up.
Here, a more systematic nature-inspired approach21–23 is used to design (Fig. 1A) and evaluate against conventional serpentine flow-field based PEFCs, the performance of PEFCs with flow fields guided by the structure of a lung. This approach is based on the mechanistic understanding of the structure of the respiratory organ, applied in the context of fuel cell technology. In the following sections, the utilization of this approach for engineering lung-inspired flow fields is presented step-by-step, followed by experimental validation.
2. Lung-inspired flow field design and experimental validation
2.1 Theoretical background
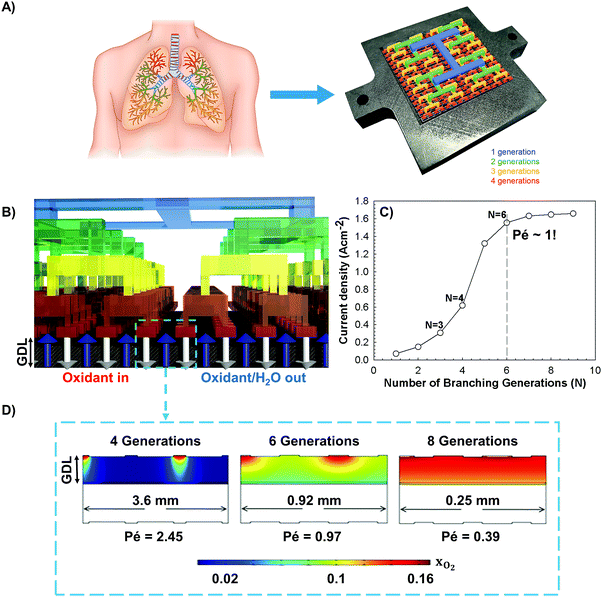
The major role of the flow-field in a PEFC is to achieve effective reactant distribution across the catalyst layer, perform water and heat management, as well as transfer of electrical current between individual cell components in a fuel cell stack.1 The lung serves a purpose in nature that is similar in several aspects: air is drawn from the atmosphere and transported through its fractal architecture into the bloodstream to oxygenate the blood cells. Its fractal geometry obeys Murray's law, which states that the cube of the diameter of the parent vessel is equal to the sum of the cubes of the diameters of the daughter vessels at each level of bifurcation, hereby leading to minimal mechanical energy losses.24 The repeatedly branching fractal structure of the lung ensures uniform distribution of oxygen throughout the given volume.25–27 The upper generations (∼14–16) of branches (bronchi) are proportioned so as to optimally slow down the gas flow from the bronchial (convection driven flow) to the acinar airways (diffusion driven flow; ∼7–9 lower generations), resulting in constant entropy production in both regions and, thus, in minimal global entropy production over the entire structure.28,29 Hence, the condition for thermodynamic optimality is directly associated with the pressure drop in the lung, which must be the same across every branch, according to:25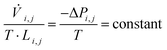 | (1) |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) i,j and ΔPi,j are the individual gas flow rate and pressure drop for each branch, respectively, Li,j is the associated Onsager coefficient25 (which depends on the length and radius of each branch), and T is the temperature.25 Using this criterion for each branch, the self-similar architecture of the lung preserves thermodynamic optimality, irrespective of scale.
i,j and ΔPi,j are the individual gas flow rate and pressure drop for each branch, respectively, Li,j is the associated Onsager coefficient25 (which depends on the length and radius of each branch), and T is the temperature.25 Using this criterion for each branch, the self-similar architecture of the lung preserves thermodynamic optimality, irrespective of scale.
Another important characteristic of the fractal structure of the lung is the harmonization of convection and diffusion driven flow between bronchial and acinar airways.30 This feature prompts the following question: why should an optimal design decrease the flow in the bronchial airways, and aim to achieve this through the minimum number of bifurcations? The answer lies in the Péclet number, Pé, which is the ratio of convective to diffusive transport rate.27 For Pé numbers larger than 1 (Pé > 1), transport by convection is faster than transport by diffusion, resulting in significant oxygen concentration gradients and, thus, suboptimal oxygen transport to acini. Reduction of the flow via a minimum number of bifurcations is optimal, since the “units” needed to build N bifurcations grow exponentially with N.30 Thus, a Pé number close to 1 after N bifurcations is not only necessary for efficient transport, but also sufficient.30
2.2 Modeling
The above-mentioned characteristics of the lung serve as a guide towards the proposed design of new fractal flow fields for PEFCs. A theoretical model was developed that includes the distribution of reactants and liquid water transport (Section S1, ESI†), and simulations were conducted to determine the number of generations required to achieve uniform reactant distribution and minimal entropy production. The modeling domain consists of the fractal flow fields, gas diffusion layers (GDL), and membrane electrode assembly (Fig. 1B and Fig. S1, ESI†). The model considers the variation of branching generations on fuel cell performance, ensuring that the number of inlets and outlets modeled remains constant for any given number of fractal generations. The thickness of the GDL, catalyst layer and polymer electrolyte membrane remains constant, regardless of the number of fractal generations. However, the size of the modeling domain, along with the size of the inlets, outlets, and land area changes with each additional fractal generation (Fig. S2, ESI†). The main modeling assumptions and governing equations for these comprehensive multiscale simulations are available in ESI† (Section S1).Numerical simulations carried out with COMSOL v5, reveal that the ideal number of generations for minimum entropy production lies between N = 5 and 7 (Fig. 1D) for a flow field plate with surface area of 10 cm2. For lower numbers of generations (N = 1–4), the spacing between adjacent distributor inlets is larger than the thickness of the GDL and the flow leaving the final generation is convection driven (Pé > 1; Fig. 1D). Beyond this (N = 5–7), as oxidant moves through successive generations with decreasing diameter, the convection driven flow becomes similar in magnitude to the diffusion driven flow at the exits (Pé ∼ 1; Fig. 1D). At higher generations (N ≥ 8), the spacing between adjacent inlets becomes very small (∼100 μm) and the flow leaving the outlets of the final generation is diffusion driven (Pé < 1; Fig. 1D). At present, it is very difficult to construct fractal flow-fields with such high numbers of generations, since it leads to geometric constraints: prototypes would require 50 μm feature sizes, without any available space for a fluid outlet network and land area in between.
Fortunately, however, a larger N might be unnecessary. Indeed, the effect of uniform reactant distribution across the electrode is evident around N = 6 in Fig. 1C and Fig. S3 (ESI†). As the number of generations is increasing, reactant concentrations throughout the catalyst layer begin to rise and homogenize (Fig. 1C and Fig. S3, ESI†). Between N = 5 and 7, where the convective flux matches the diffusive flux (Pé ∼ 1), fluids are uniformly distributed, which is a precursor to enhanced fuel cell performance due to a full areal usage of the catalyst below (Fig. 1C). Above N = 7, fuel cell performance reaches a plateau, demonstrating that the incorporation of additional branching generations is no longer beneficial.
Thus, fractal, lung-inspired scaling with an optimal number of branching levels and channel dimensions following Murray's law leads to the ideal, uniform boundary conditions for the catalyst layer, ultimately resulting in exceptional current densities that maximize catalyst utilization.
2.3 From theory to practice
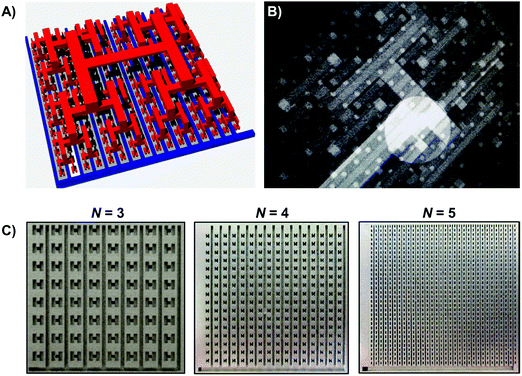
The promising modeling results emphasized the need to engineer lung-inspired, fractal flow-fields and evaluate their performance under fuel cell operating conditions. Three-dimensional (3D) fractal flow-fields with multiple generations have not previously been validated experimentally, due to complications associated with the manufacturing of objects with a controlled 3D internal structure; conventional fabrication methods, such as machining or stamping, are limited to two-dimensional structures.These limitations can be circumvented through the exploitation of 3D printing via Direct Metal Laser Sintering (DMLS), which is used to create 3D objects from successive layers of sintered stainless steel.31,32 Three flow-fields with N = 3, 4 and 5 were fabricated and assembled in PEFCs and their performance compared against conventional, serpentine flow-field based PEFCs. Details of the experimental procedure are available in the ESI† (Section S2).
Fig. 2 illustrates the 3D network of the interdigitated inlet and outlet fractal branches, as well as the final generation of the inlet and outlet channels for the three different prototypes (a video based on X-ray tomography of a flow-field with N = 5 is available in ESI†). The final generation of H-shaped branches of the N = 3 and N = 4 flow-fields were left open to create additional contact area between the gas channel and the GDL. However, due to fabrication limitations, only the tips of the fifth-generation H-shaped branches were open to the GDL for the N = 5 prototype.
Prior to experimental testing, X-ray radiography (Zeiss Xradia Versa 520, Zeiss USA) was used to inspect the flow-field channels for structural defects and blockages caused by various process parameters, such as laser energy density, layer thickness, and hatch distance.33 The outlet aperture of the N = 5 flow field is the smallest at 200 × 300 μm; with a resolution of 33 × 33 μm, large blockages of the outlets would be observable. Radiographs reveal that the internal structure of the flow-field is well defined and defect-free, especially in the early branching generations, allowing for uniform gas distribution (Fig. 2B).
2.4 Experimental validation
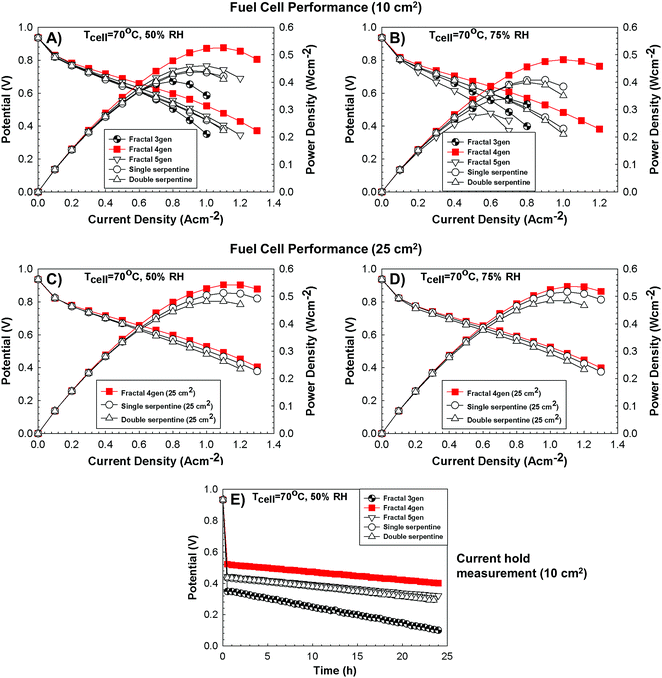
The engineered, fractal flow fields are gold-plated prior to any fuel cell polarization measurement to minimize their corrosion under fuel cell operation (Section S2.3, ESI†). These flow fields are then assembled in the cathode of a PEFC (a conventional double serpentine flow field is mounted on the anode, where there are no notable transport limitations) and high-frequency resistance measurements (Fig. S12–14, ESI†) are conducted to ensure that membrane hydration is similar for fractal and serpentine flow field based PEFCs under operating conditions. Optimal fuel cell performance is attained at 50% RH for all flow-fields, as it appears to provide near flood-free PEFC operating conditions with small ohmic losses (Fig. 3A).34,35 The “N = 3 design” (fractal with three generations of branching) exhibits the worst performance due to the large spacing between adjacent outlets,36 which, in turn, leads to insufficient oxygen concentration on the electrode surface and, hence, sluggish kinetics.5 On the contrary, the N = 4 design demonstrates a ∼20% increase in performance (at current densities higher than 0.8 A cm−2) and ∼25% increase in maximum power density compared to serpentine-based PEFCs, due to the enhanced uniformity in reactant distribution across the catalyst layer.A similar trend in performance of fractal and serpentine flow field based PEFCs is observed at higher humidity levels (75% RH). PEFC performance is slightly lower, despite better membrane hydration, due to the presence of more liquid water in the system37 that impedes effective gas diffusion (Fig. 3B). Nevertheless, the N = 4 design exhibits a ∼20% increase in performance (at current densities higher than 0.8 A cm−2) and ∼30% increase in maximum power density compared to conventional serpentine based PEFCs.
However, under all experimental conditions tested, fractal flow-field based PEFCs with N = 5 demonstrate lower performance than expected. Although it is thermodynamically favorable to operate the PEFC at this state (minimum entropy production of the system),25 the performance results indicate that operation at Pé > 1 under high humidity conditions requires methods for the efficient removal of liquid water to avoid flooding.
The above statement is verified by fuel cell performance measurements at fully humidified conditions (Fig. S4, ESI†). At 100% RH, additional generation of water vapor (after complete membrane hydration) supersaturates the PEFC, resulting in water condensation in the electrode and flow-field channels, increasing the mass transport resistance. This is evident by the lower performance (∼10%) of the N = 4 design compared to serpentine based PEFCs (Fig. S4, ESI†). Fractal flow-field based PEFCs with N = 5 could not be tested due to excess flooding; the gas flow rate from individual fractal channels is insufficient to effectively remove liquid water.
Fractal and serpentine flow-field based PEFCs were also subjected to a 24 h current hold experiment to further evaluate the effect of reactant distribution across the electrode. The positive effect of uniform reactant distribution on fuel cell performance is evident (Fig. 3E). Fractal flow-fields with N = 4 exhibit the lowest voltage decay (∼5 mV h−1) compared to the serpentine flow-field design (∼6.2 mV h−1). Assuming that the initial catalyst loading is uniform, the increased voltage decay rate of the serpentine flow field based PEFCs shows that uneven reactant distribution leads to higher particle agglomeration and carbon support loss across the channel.38 The highest voltage decay rate (∼11 mV h−1) is observed for fractal flow-fields with N = 3, in which the insufficient reactant concentration may have caused local reactant deprivation and cell reversal.5
In terms of pressure drop (Fig. S6–S8, ESI†), fractal flow-fields with N = 3 and 4 exhibit the lowest values (respectively ∼75% and ∼50% lower than conventional serpentine flow-field design for all RH tested) reducing the power requirements for pressurization and recirculation of the reactants.39 On the contrary, fractal flow-fields with N = 5 exhibit a similar pressure drop to serpentine flow-field designs due to the constricted air flow through smaller hydraulic diameters of the inlet and outlet channels.40,41
3. Unique characteristic of the proposed nature-inspired approach: scalability
To sum up, the obtained experimental results show that the proposed nature-inspired approach can be successfully used to resolve uneven reactant distribution issues in PEFCs. The defining characteristic of the fractal approach, though, is scalability, which is an important feature in nature. This characteristic makes the proposed nature-inspired approach stand out among other, bio-mimetic techniques reported in the literature, even though advancements in 3D printing technology via DMLS are required to mass produce large fractal flow fields with a high number of generations.Fractal flow-fields can bridge multiple length scales by adding further generations, while preserving the building units and microscopic function of the system.21,42 Larger, 3D printed fractal flow-fields (25 cm2 surface area) with N = 4 are compared to conventional, serpentine flow-field based PEFCs. Performance results (Fig. 3C, D and Fig. S5, ESI†) show that fractal and serpentine flow-field based PEFCs have similar polarization curves, which is attributed to the significantly higher pressure drop (∼25 kPa) of large serpentine flow fields compared to fractal flow-fields (Fig. S9–S11, ESI†). The increased mass flow rate enhances the overall reaction rate and greatly reduces the resident water in the serpentine channels, resulting in a more uniform reactant distribution across the electrode and thus, improved performance.43 On the contrary, large fractal flow-fields with N = 4 have minimal pressure drop (<2 kPa) under all RH conditions tested, revealing their difficulty to purge the produced liquid water from the fuel cell at the same pace as the serpentine flow-fields. Hence, to further improve the design of these fractal flow-fields, it is required to implement different outlet channel designs to remove the unreacted gas and product water, while operating the PEFC at a Péclet number close to unity. The combination of these two design parameters will achieve maximum fuel cell efficiency from uniform entropy production and minimal parasitic loss, leading to a maximum power density.
4. Conclusions
In conclusion, this article introduces a nature-inspired engineering methodology, which is utilized step-by-step to solve the uneven reactant distribution issue in PEFCs. 3D printed, lung-inspired fractal flow-fields with N = 4 generations outperform the serpentine flow fields at high current densities (at 50% and 75% RH) due to more uniform reactant distribution across the catalyst layer. At higher humidity levels (100% RH), though, the performance of N = 5 fractal flow fields significantly deteriorates; the reduced air flow rate within the fractal flow fields hampers effective gas diffusion within the porous medium, resulting in insufficient convective liquid water removal. Even though modeling results suggest that a N = 5 design delivers optimum PEFC performance, in practice, the utilization of a fractal flow-field above N = 4 is not currently feasible. The identification of the shortcomings of fractal flow-fields pertaining to water management provides a rationale for design improvements, mainly on the land and outlet channels. The closely intertwined nature of these two factors emphasizes the need to implement alternative outlet channel geometry or engineered water removal strategies to alleviate flooding and parasitic loss, especially at higher generations. A critical comparison of different cathode flow-field designs is presented in Table 1.| Flow field design | Advantages | Disadvantages |
|---|---|---|
| Serpentine |
• Efficient water removal
• Designed for small active area |
• High pressure drop
• Water build-up in bends • Highly uneven reactant distribution due to reactant depletion along channels |
| Multiple serpentine |
• Moderate water removal
• Designed for large active area |
• Moderate pressure drop
• Uneven reactant distribution • Elevated susceptibility to flooding with increased number of channels |
| Interdigitated | • Efficient water removal |
• Highest pressure drop of all flow-field designs
• Possible damage to electrode from excess convective force • Uneven reactant distribution • Difficult to scale |
| Lung-inspired |
• Low pressure drop
• Uniform reactant distribution for low and high temperature fuel cells • Higher electrocatalyst stability than serpentine • Easily scalable |
• More susceptible to flooding than serpentine at high RH |
The uniform gas distribution across the catalyst layer is preserved when these fractal flow fields are scaled-up (25 cm2 surface area). The fuel cell performance of the large-scale fractal flow field remains almost unchanged on a per area basis, compared to its smaller active area counterpart. On the contrary, larger, conventional serpentine flow fields (25 cm2 surface area) exhibit improved relative performance over 10 cm2 ones due to an order-of-magnitude higher pressure drop than that of a fractal flow field, resulting in faster overall reaction rates and better liquid water removal. However, such excessive pressure drop renders the use of a large-scale serpentine flow field prohibitive, thus favoring the fractal flow field. Implementation of effective water removal mechanisms should circumvent remaining problems of high-generation fractal flow fields.
Current water management strategies44–46 for commercial flow fields cannot be easily employed into these engineered fractal flow fields, since they require the installation of a porous carbon plate to wick out the generated liquid water. Hence, additional theoretical and experimental studies are needed to design new water removal mechanisms and integrate these with the fractal flow fields. To fully assess the effect of channel geometries on water removal, a 3D model should be developed. Despite its high computational demands, such a model will be able to fully simulate flooding at high RH conditions. These modeling results, in combination with experimental neutron radiography measurements, will provide valuable information towards the development of a water management strategy for fractal flow fields.
However, at present, typical operating conditions of PEFCs in practice are much lower than 100% RH.47 Commercial PEFCs utilize air without humidification to pre-empt flooding in the cathode.47 These operating conditions favor the utilization of the proposed fractal flow fields, due to their excellent performance at low and mid humidity levels, which is superior to commercial flow fields.
Finally, the proposed nature-inspired approach is not limited to PEFCs, but should lead to performance improvements in other electrochemical systems as well. Redox flow batteries, electrolyzers and different types of fuel cells (alkaline, high temperature, direct methanol, etc.) could thus benefit from the proposed nature-inspired approach, as flooding is mitigated in these systems.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge the financial support from an EPSRC “Frontier Engineering” Award (EP/K038656/1) and a UCL Faculty of Engineering Sciences Dean's Scholarship for Jason I. S. Cho. They thank Dr Paul Shearing and the EPSRC Centre for Grid Scale Energy Storage (EP/L014289/1) for access to X-ray tomography equipment.References
- J. Larminie, Fuel Cell Systems Explained, Wiley & Sons, Chichester, West Sussex, 2nd edn, 2003 Search PubMed.
- R. T. White, F. P. Orfino, M. E. Hannach, O. Luo, M. Dutta, A. P. Young and E. Kjeang, J. Electrochem. Soc., 2016, 163, F1337–F1343 CrossRef CAS.
- S. Ge and C.-Y. Wang, J. Electrochem. Soc., 2007, 154, B998–B1005 CrossRef CAS.
- Z. Tayarani-Yoosefabadi, D. Harvey, J. Bellerive and E. Kjeang, J. Power Sources, 2016, 303, 208–221 CrossRef CAS.
- A. Taniguchi, T. Akita, K. Yasuda and Y. Miyazaki, J. Power Sources, 2004, 130, 42–49 CrossRef CAS.
- P. Trogadas, T. F. Fuller and P. Strasser, Carbon, 2014, 75, 5–42 CrossRef CAS.
- V. O. Mittal, H. R. Kunz and J. M. Fenton, J. Electrochem. Soc., 2007, 154, B652–B656 CrossRef CAS.
- P. Trogadas, J. Parrondo and V. Ramani, Chem. Commun., 2011, 47, 11549–11551 RSC.
- T. Okada, Y. Ayato, H. Satou, M. Yuasa and I. Sekine, J. Phys. Chem. B, 2001, 105, 6980–6986 CrossRef CAS.
- S. Shimpalee, S. Greenway and J. W. Van Zee, J. Power Sources, 2006, 160, 398–406 CrossRef CAS.
- A. P. Manso, F. F. Marzo, J. Barranco, X. Garikano and M. Garmendia Mujika, Int. J. Hydrogen Energy, 2012, 37, 15256–15287 CrossRef CAS.
- P. Wawdee, S. Limtrakul, T. Vatanatham and M. W. Fowler, Int. J. Hydrogen Energy, 2015, 40, 3739–3748 CrossRef CAS.
- D. H. Ahmed and H. J. Sung, J. Power Sources, 2006, 162, 327–339 CrossRef CAS.
- S.-W. Cha, R. O’Hayre, S. J. Lee, Y. Saito and F. B. Prinz, J. Electrochem. Soc., 2004, 151, A1856–A1864 CrossRef CAS.
- N. Guo, M. C. Leu and U. O. Koylu, Int. J. Hydrogen Energy, 2014, 39, 21185–21195 CrossRef CAS.
- J. P. Kloess, X. Wang, J. Liu, Z. Shi and L. Guessous, J. Power Sources, 2009, 188, 132–140 CrossRef CAS.
- R. Roshandel, F. Arbabi and G. K. Moghaddam, Renewable Energy, 2012, 41, 86–95 CrossRef CAS.
- B. Ramos-Alvarado, A. Hernandez-Guerrero, F. Elizalde-Blancas and M. W. Ellis, Int. J. Hydrogen Energy, 2011, 36, 12965–12976 CrossRef CAS.
- K. Tüber, A. Oedegaard, M. Hermann and C. Hebling, J. Power Sources, 2004, 131, 175–181 CrossRef.
- S. Shimpalee and J. W. Van Zee, Int. J. Hydrogen Energy, 2007, 32, 842–856 CrossRef CAS.
- P. Trogadas, M. M. Nigra and M.-O. Coppens, New J. Chem., 2016, 40, 4016–4026 RSC.
- M. M. Lynch, J. Liu, M. Nigra and M.-O. Coppens, Langmuir, 2016, 32, 9604–9610 CrossRef CAS PubMed.
- M.-O. Coppens, Curr. Opin. Chem. Eng., 2012, 1, 281–289 CrossRef CAS.
- C. D. Murray, Proc. Natl. Acad. Sci. U. S. A., 1926, 12, 207–214 CrossRef CAS.
- S. Gheorghiu, S. Kjelstrup, P. Pfeifer and M.-O. Coppens, in Fractals in Biology and Medicine, ed. G. A. Losa, D. Merlini, T. F. Nonnenmacher and E. R. Weibel, Birkhäuser Basel, Basel, 2005, pp. 31–42 DOI:10.1007/3-7643-7412-8_3.
- B. Mauroy, M. Filoche, E. R. Weibel and B. Sapoval, Nature, 2004, 427, 633–636 CrossRef CAS PubMed.
- B. Sapoval, M. Filoche and E. R. Weibel, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10411–10416 CrossRef CAS PubMed.
- S. Kjelstrup, M.-O. Coppens, J. G. Pharoah and P. Pfeifer, Energy Fuels, 2010, 24, 5097–5108 CrossRef CAS.
- P. Trogadas, V. Ramani, P. Strasser, T. F. Fuller and M.-O. Coppens, Angew. Chem., Int. Ed., 2016, 55, 122–148 CrossRef CAS PubMed.
- C. Hou, S. Gheorghiu, M.-O. Coppens, V. H. Huxley and P. Pfeifer, in Fractals in Biology and Medicine, ed. G. A. Losa, D. Merlini, T. F. Nonnenmacher and E. R. Weibel, Birkhäuser Basel, Basel, 2005, pp. 17–30 DOI:10.1007/3-7643-7412-8_2.
- J. C. Ruiz-Morales, A. Tarancon, J. Canales-Vazquez, J. Mendez-Ramos, L. Hernandez-Afonso, P. Acosta-Mora, J. R. Marin Rueda and R. Fernandez-Gonzalez, Energy Environ. Sci., 2017, 10, 846–859 CAS.
- R. L. Truby and J. A. Lewis, Nature, 2016, 540, 371–378 CrossRef CAS PubMed.
- S. Seyed Farid Seyed, G. Samira, M. Mehdi, Y. Hooman, M. Hendrik Simon Cornelis, K. Nahrizul Adib and O. Noor Azuan Abu, Sci. Technol. Adv. Mater., 2015, 16, 033502 CrossRef PubMed.
- J. R. Atkins, S. C. Savett and S. E. Creager, J. Power Sources, 2004, 128, 201–207 CrossRef CAS.
- T. F. Fuller and J. Newman, J. Electrochem. Soc., 1992, 139, 1332–1337 CrossRef CAS.
- J. Marquis, PhD thesis, Rensselaer Polytechnic Institute, Troy, NY, 2013 Search PubMed.
- I. S. Hussaini and C.-Y. Wang, J. Power Sources, 2009, 187, 444–451 CrossRef CAS.
- J. Chen, J. B. Siegel, T. Matsuura and A. G. Stefanopoulou, J. Electrochem. Soc., 2011, 158, B1164–B1174 CrossRef CAS.
- H. Kahraman and M. F. Orhan, Energy Convers. Manage., 2017, 133, 363–384 CrossRef CAS.
- D.-H. Chang and S.-Y. Wu, Int. J. Hydrogen Energy, 2015, 40, 11659–11667 CrossRef CAS.
- M. Mortazavi and K. Tajiri, Renewable Sustainable Energy Rev., 2015, 45, 296–317 CrossRef CAS.
- M.-O. Coppens, Ind. Eng. Chem. Res., 2005, 44, 5011–5019 CrossRef CAS.
- A. B. LaConti, M. Hamdan and R. C. McDonald, in Handbook of Fuel Cells: Fundamentals, Technology, and Applications, ed. W. Vielstich, H. A. Gasteiger and A. Lamm, John Wiley & Sons, New York, 2003, vol. 3, pp. 647–662 Search PubMed.
- T. Fabian, R. O’Hayre, S. Litster, F. B. Prinz and J. G. Santiago, J. Power Sources, 2010, 195, 3640–3644 CrossRef CAS.
- S. Litster, C. R. Buie, T. Fabian, J. K. Eaton and J. G. Santiago, J. Electrochem. Soc., 2007, 154, B1049–B1058 CrossRef CAS.
- J. S. Yi, J. D. Yang and C. King, AIChE J., 2004, 50, 2594–2603 CrossRef CAS.
- T. Yoshida and K. Kojima, Electrochem. Soc. Interface, 2015, 24, 45–49 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee02161e |
| ‡ Both authors contributed equally. |
| § Current address: Momentive Performance Materials, Waterford, NY 12188, USA. |
| This journal is © The Royal Society of Chemistry 2018 |