Trackable galvanostatic history in phase separation based electrodes for lithium-ion batteries: a mosaic sub-grouping intercalation model†
Abstract
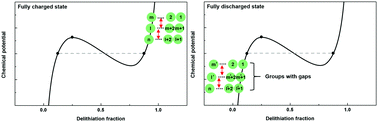
An in-depth understanding of electrode reactions is essential to achieve a breakthrough in lithium-ion battery technology, the new ‘engine’ for electric vehicles. Recent studies have continued to reveal unexpected electrode behaviors, providing a more refined view of the operating mechanisms of electrodes from the atomistic to particle level and offering new perspectives to design better battery systems. Herein, it is observed for the first time that the history of applied current densities is memorized in electrode materials that operate via a two-phase reaction and systematically induces a transient galvanostatic profile variation of the electrode. These unforeseen profile changes can be explained by a new proposed intercalation model in which active particle sub-groupings are intermittently generated with a non-uniform chemical potential distribution at the end of charge or discharge. The types of active particle groupings are determined by the current density of the prior charge or discharge, resulting in distinct signatures in the electrochemical profile in the subsequent galvanostatic process. Our proposed intercalation model affords a more comprehensive view of the behavior of electrodes containing many-body particles by elucidating the effect of the applied current densities.
- This article is part of the themed collection: 2017 Energy and Environmental Science HOT articles


 Please wait while we load your content...
Please wait while we load your content...