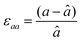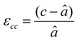Enhanced oxygen exchange of perovskite oxide surfaces through strain-driven chemical stabilization†
Bonjae
Koo‡
a,
Hyunguk
Kwon‡
 b,
YeonJu
Kim
a,
Han Gil
Seo
a,
Jeong Woo
Han
b,
YeonJu
Kim
a,
Han Gil
Seo
a,
Jeong Woo
Han
 *b and
WooChul
Jung
*b and
WooChul
Jung
 *a
*a
aDepartment of Materials Science and Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Republic of Korea. E-mail: wcjung@kaist.ac.kr
bDepartment of Chemical Engineering, University of Seoul, Seoul, Republic of Korea. E-mail: jwhan@uos.ac.kr
First published on 27th September 2017
Abstract
Surface cation segregation and phase separation, of strontium in particular, have been suggested to be the key reason behind the chemical instability of perovskite oxide surfaces and the corresponding performance degradation of solid oxide electrochemical cell electrodes. However, there is no well-established solution for effectively suppressing Sr-related surface instabilities. Here, we control the degree of Sr-excess at the surface of SrTi0.5Fe0.5O3−δ thin films, a model mixed conducting perovskite O2-electrode, through lattice strain, which significantly improves the electrode surface reactivity. Combined theoretical and experimental analyses reveal that Sr cations are intrinsically under a compressive state in the SrTi0.5Fe0.5O3−δ lattice and that the Sr–O bonds are weakened by the local pressure around the Sr cation, which is the key origin of surface Sr enrichment. Based on these findings, we successfully demonstrate that when a large-sized isovalent dopant is added, Sr-excess can be remarkably alleviated, improving the chemical stability of the resulting perovskite O2-electrodes.
Broader contextSolid oxide electrochemical cells (SOCs) provide environmentally friendly energy storage/conversion that can store energy in the form of chemical fuels (electrolysis mode) or convert the fuels into electricity (fuel-cell mode) with high efficiency. A key challenge hindering SOC development is severe degradation of the perovskite oxide electrode, primarily due to its chemically unstable surface at high operating temperatures (>600 °C). Here, concurrent studies of lattice strain, surface composition, and surface reactivity of a model perovskite electrode reveal a key driving force of surface chemical inhomogeneity, often called cation segregation. An in-depth understanding of this phenomenon is expected to provide a practical solution for effectively improving the durability of SOC electrodes. |
As a carbon-neutral, sustainable future energy technology, solid oxide electrochemical cells (SOCs) have attracted considerable attention because of their high conversion efficiencies, even in the absence of expensive precious metal catalysts.1,2 SOCs are a general class of electrochemical devices using a solid oxide electrolyte, which include both solid oxide fuel cells (SOFCs) for electricity generation from oxidizing fuels and solid oxide electrolysis cells (SOECs) for the conversion of steam and carbon dioxide into hydrogen and carbon monoxide via electricity. A key step in the SOC energy-conversion processes is the oxygen reduction/evolution reaction (ORR/OER) at O2-electrodes (i.e., the cathode in SOFCs and the anode in SOECs), in which the rapid exchange of oxygen at the electrode surface is critical for facilitating the overall reaction rate.
Perovskite oxides (chemical formula: ABO3), such as (La,Sr)(Co,Fe)O3, (Ba,Sr)(Co,Fe)O3 and Sr(Fe,Ti,Ni)O3, have widely been used for SOC O2-electrode materials given their high electronic and ionic conductivities and favorable catalytic activity for electrode reactions.3–9 However, the chemical instability of their surfaces, particularly at elevated temperatures (>500 °C), leads to severe degradation of the electrode performance over time. Surface cation segregation and phase separation have recently been suggested as the key reason for the instability of perovskite surfaces. Upon annealing in an oxidizing atmosphere, A-site cation segregation (Sr in particular) near the surface of perovskite oxides has been observed and studied.5,10–17 Nevertheless, the underlying mechanism for this phenomenon is not completely understood. Therefore, it is unclear how to effectively inhibit the behavior and secure the stability of SOC O2-electrodes.
It was recently reported that surface Sr enrichment and the resulting formation of SrOx-like precipitates can be controlled by lattice strain. For example, Yildiz et al. observed changes in surface composition under lattice strain in La0.8Sr0.2CoO3 and La0.7Sr0.3MnO3 epitaxial thin films.18,19 Basu et al. reported a similar result in that the Sr concentration increases on the surface of tensile-strained La1−xSrxCo0.2Fe0.8O3 films.20 We have also proposed that mechanical strain can be a key factor for surface SrOx precipitation in SrTi1−xFexO3 thin film electrodes.21,22 These results elucidate the mechanism to a certain extent, but have yet to provide an ultimate solution to prevent electrode degradation which can be readily applied to real devices.
This study investigates the influence of the Sr–O bond strength in a strained perovskite lattice on surface Sr-excess. Considering dense thin films of SrTi0.5Fe0.5O3−δ (STF) as a model system, which is representative of a mixed ionic electronic conducting (MIEC) perovskite oxide electrode, we control the lattice strain of STF films by epitaxially growing them onto single-crystal substrates with different lattice parameters, and monitor how the surface composition and oxygen exchange kinetics change accordingly. STF is a model system suitable for this study due to the excellent phase stability and simplicity of its composition. Despite there being a large number of oxygen vacancies, this material system maintains a disordered cubic structure over a wide range of temperatures, gas atmospheres and compositions, except with 100% Fe.23 Furthermore, Sr in an STF lattice, a neutral constituent and not an aliovalent dopant with an effectively negative charge, can allow us to focus on the elastic effects of strain, neglecting the effects of electrostatic interactions between the cations at the A-site.16 Here, we found that tensile strain inhibits surface Sr enrichment significantly and enhances the surface oxygen exchange rate, whereas large amounts of excess Sr were observed on the surfaces of compressed films. DFT calculations showed that local compressive states around the Sr atoms in a SrTiO3-type perovskite lattice weakened the Sr–O bond strength, which in turn promoted Sr-excess. We conclusively demonstrated that the compressive strain could be sufficiently alleviated by introducing a large-sized isovalent dopant, suggesting a new strategy for improving the chemical stability of perovskite O2-electrodes for high-performance SOCs.
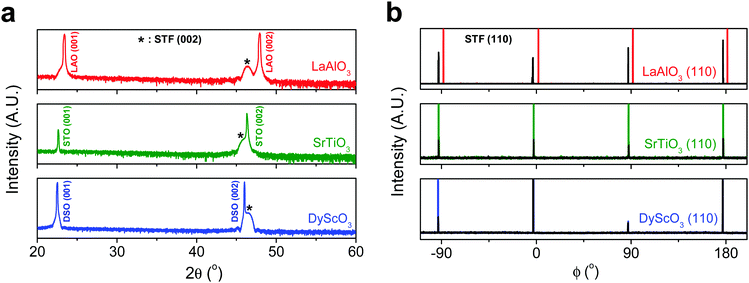
First, we fabricated strain-controlled STF thin films by pulsed laser deposition (PLD) on three single-crystal substrates (i.e., LaAlO3(001), SrTiO3(001) and DyScO3(110), which are referred to as LAO, STO and DSO, respectively), and measured their surface compositions and oxygen exchange rates by angle-resolved X-ray photoelectron spectroscopy (AR-XPS) and electrical conductivity relaxation (ECR), respectively. Transmission electron microscopy (TEM) and atomic force microscopy (AFM) confirmed that the epitaxial films with a thickness of 25 nm and smooth surfaces (i.e., surface roughness < 1 nm) were grown (Fig. S1, S2 and Table S1, ESI†). The misfit strain of each film for both in-plane and out-of-plane directions was calculated by high-resolution X-ray diffraction (HR-XRD), as shown in Fig. 1. The resulting films have larger relaxed unit cell volumes than those in bulk samples, likely due to oxygen deficiency in the PLD films.24 Accordingly, the values of the relaxed lattice parameter (â) of each film, as a reference, were calculated by combining the interplanar distance of the (002) and (110) peaks with a Poisson ratio of 0.232,25 and the levels of both in-plane and out-of-plane strain were then defined by their deviations from â, as reported by Shao-Horn et al.26 The STF thin films on LAO and STO substrates are compressed in-plane and dilated in the direction normal to the film surface (i.e., in-plane strain (εaa) of −3.04% and −1.48%, respectively). On the other hand, the film on DSO shows tensile strain along the in-plane direction (i.e., εaa of +0.61%) (see Table 1). This is also supported by the average interatomic distance of the three films measured by scanning transmission electron microscopy (STEM) (Fig. S1, ESI†). The absolute misfit strain of the STF films is remarkably high. For example, the in-plane strain of −3.04% in the film on LAO roughly corresponds to a mechanical stress of ∼7.13 GPa, given a biaxial modulus of 233 GPa of SrTiO3.27
| Substrate | Strained in-plane lattice parameter a (Å) | Strained out-of-plane lattice parameter c (Å) | Relaxed film lattice parameteraâ (Å) | In-plane strain (%) | Out-of-plane strain (%) |
|---|---|---|---|---|---|
a
â was calculated using 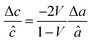 , assuming â = ĉ and ν = 0.23225 for STF. , assuming â = ĉ and ν = 0.23225 for STF.
|
|||||
| LaAlO3 (3.790 Å) | 3.800 | 3.992 | 3.920 ± 0.006 | −3.04 ± 0.14 | 1.86 ± 0.24 |
| SrTiO3 (3.905 Å) | 3.851 | 3.944 | 3.909 ± 0.006 | −1.48 ± 0.15 | 0.89 ± 0.22 |
| DyScO3 (3.948 Å) | 3.942 | 3.904 | 3.918 ± 0.006 | 0.61 ± 0.15 | −0.36 ± 0.22 |
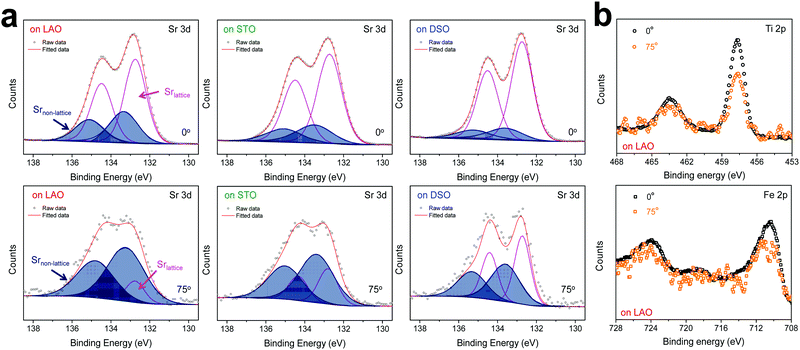
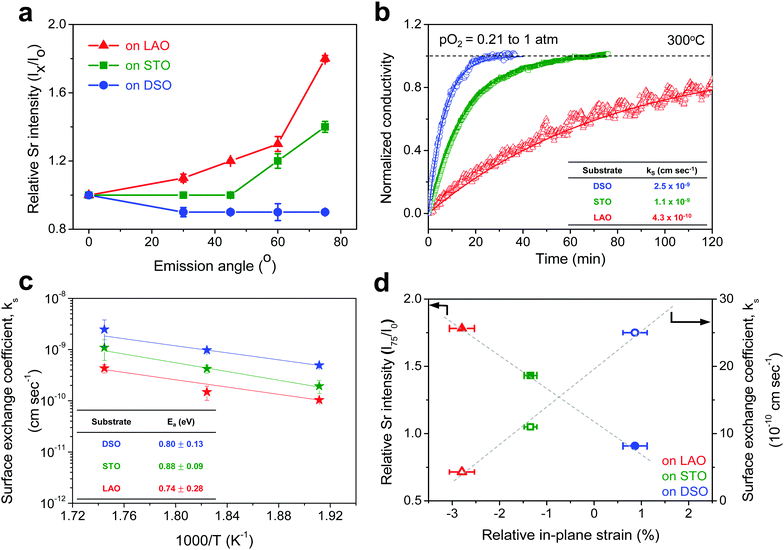
The chemical composition of each film was analyzed at different depths from the surface via AR-XPS, focusing on the effects of lattice strain on surface Sr enrichment. Fig. 2 presents the photoelectron spectra of each constituent cation in STF films at emission angles of 0° and 75°. Because a higher emission angle is more surface sensitive (e.g., corresponding to average depths of ∼10 nm and ∼2.5 nm for 0° and 75°, respectively), it is clear that the Sr 3d peak is markedly different at the surface (=75°) compared to its signature from the bulk (=0°) of the material (Fig. 2a). On the other hand, in contrast to the Sr 3d peak, the Fe and Ti 2p spectra remain largely the same, regardless of the depth from the surface, as shown in Fig. 2b. In fact, the Sr 3d spectra were fitted well using two sets of spin–orbit doublets with an energy separation of ∼1.8 eV and an area ratio of 1.5. The main Sr 3d doublet corresponds to Sr in the bulk lattice, whereas the other doublet with the higher binding energy originates from the surface Sr species.10,11 The surface Sr peaks are dominant for a compressive strained film. In contrast, the main bulk peaks prevail for the film stretched in-plane.
For more quantitative analysis, the relative Sr enrichment with respect to the B-site cation content was calculated by fitting the XPS spectra of each constituent cation measured at different emission angles. To eliminate technical difficulties in the XPS analysis, I0([Sr/(Ti + Fe)]0°) and Ix([Sr/(Ti + Fe)]x°) were used to refer to the ratio of the A-site cation content to the B-site cation content measured at detection angles of 0° (more bulk sensitive) and X° (more surface sensitive as X° increases), respectively. The Ix/I0 ratio was then evaluated to represent the relative Sr surface enrichment. As shown in Fig. 3a, the relative Sr intensity (Ix/I0) increases sharply with increasing emission angle, particularly for the compressed film on LAO, confirming the appreciable degree of Sr-excess at the surface of the STF thin film. On the other hand, the Sr intensity decreases with decreasing compressive strain. As a result, the in-plane stretched film on DSO shows a negligible degree of Sr-excess at the surface. In contrast, no surface enrichment in the relative Fe content, which is defined by Ix/I0([Fe/(Ti + Fe)x°]/[Fe/(Ti + Fe)0°]) at various emission angles, is found, confirming that the surface chemical inhomogeneity results mainly from the Sr redistribution, not Fe or Ti (Fig. S3, ESI†). Note that the bulk composition of STF films was also analyzed by inductively coupled plasma mass spectroscopy (ICP-MS), showing good agreement with that in the target materials (see Table S2, ESI†).
Fig. 3b presents the relaxation profiles of STF films, showing the transient behavior of the conductivity with a step change in the pO2 of the surrounding gas. Because the thickness of the STF films is below the critical thickness,28 the relaxation profile reflects the kinetics of the surface exchange reaction, rather than the bulk diffusion of oxygen. Therefore, the surface oxygen exchange coefficient (ks) can be calculated using eqn (1) as follows:
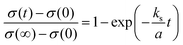 | (1) |
Overall, more tensile strain tends to decrease the levels of Sr-excess and simultaneously enhance ks (Fig. 3d). Previously, we observed a significant reduction in the area-specific resistance (ASR) of the STF thin film electrodes by chemically etching the Sr-enriched layer, showing that the SrOx-related species at the STF surfaces serves as a passivation barrier for oxygen exchange.21,22 Considering these results, the inhibited Sr enrichment by tensile strain is thought to enhance the surface exchange kinetics. Two factors need to be mentioned here. First, this observation is direct evidence supporting the hypothesis we have proposed in previous studies; mechanical strain is a relevant driving force for Sr-rich phases at the STF surfaces.21,22 The atomistic scale mechanism for strain-driven Sr-excess will be discussed in greater detail below. Second, these results suggest that perovskite surfaces can be stabilized chemically by strain-engineering. Lattice strain influences many material properties, such as electrical conductivity, electronic structure, and defect concentration.29–31 Several studies have recently reported the strain-driven changes in chemical composition or the oxygen exchange of perovskite surfaces.18–20,26,32,33 For example, Fleig et al. reported that the tensile strain accelerated the tracer surface exchange coefficients in (La,Sr)CoO3 thin films.32 Shao-Horn et al. showed that the tensile-strained LaCoO3 electrode exhibited a decrease in charge transfer resistance compared to the compressive one.33 Yildiz et al. examined the effects of lattice strain on the surface electronic and chemical states of La0.8Sr0.2CoO3 and La0.7Sr0.3MnO3 thin films.18,19 To the best of the authors’ knowledge, however, there have been no concurrent studies on the lattice strain, surface chemical composition, and surface reactivity of a mixed conducting perovskite oxide.
From the point of view of defect chemistry, Sr enrichment and the resulting formation of SrO at the perovskite oxide surfaces can be understood as the result of partial Schottky defect formation reaction. In order to form SrO on the surface, Sr and O in the oxide lattice must be pulled out one by one to the surface, as shown in eqn (2).
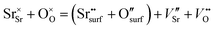 | (2) |
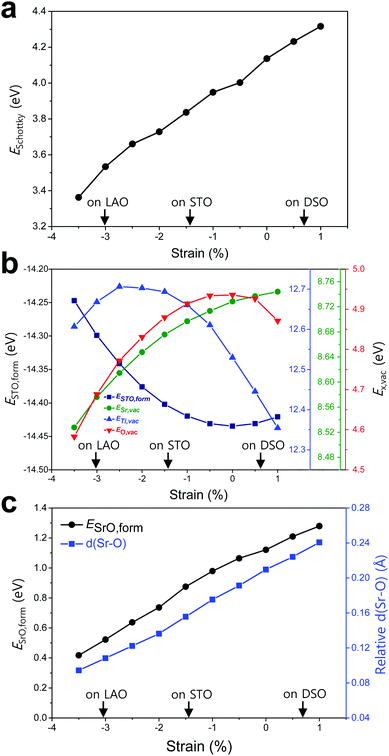
To elucidate the origin of the surface Sr-excess, we additionally carried out DFT calculations on two elemental thermodynamic steps: “the removal of Sr from the crystal lattice” and “the formation of a product phase on the surface,” as explained by Feng et al.34 First, the stability of the Sr atom according to biaxial strain was investigated by calculating the vacancy formation energy of Sr (ESr,vac). Here, we used STO bulk to emphasize that a driving force of Sr enrichment would be generally applied to the various types of STO-based perovskites. In addition, by using the STO bulk model instead of STF, the complexity of configurations at the B-site caused by Fe doping can be removed. Indeed, it turns out that our main reasoning can also be applied to STF as well as STO (Fig. S5, ESI†). Fig. 4b shows that ESr,vac decreases under compressive strain due to the weakened Sr–O bond strength, which explains the experimentally observed Sr enrichment at the compressive strained surface in Fig. 3d. Meanwhile, an interesting tendency of ESr,vac was found in the range of tensile strain. ESr,vac continues to increase rather than decrease with increasing tensile strain. To investigate this behavior in detail, the bond length between the nearest Sr and O was calculated according to the biaxial strain (Fig. S6, ESI†). When a cubic STO perovskite is biaxially strained, the equivalent twelve Sr–O bonds are differentiated into two types (bond A and bond B in Fig. S6a, ESI†). Although all Sr–O bond lengths are no longer identical under the applied strain, the two types of bond lengths increase nonetheless when applying biaxial tensile strain (Fig. S6b, ESI†). In the strain-free equilibrium state, the Sr–O bond length is shorter than the optimal Sr–O bond length in the most stable state within the bulk lattice where ESr,vac would be the highest. Owing to the shorter bond length in the strain-free state compared to that in the tensile-strained state, expansion of perovskite oxide increases ESr,vac (at least up to the tensile strain of ∼1%) while making the Sr atoms more stable. This indicates that Sr atoms are intrinsically in a compressive state in the STO bulk lattice. Accordingly, we concluded that the thermodynamic instability of Sr in the bulk lattice as identified in this calculation can cause the strain-driven enrichment phenomenon, thus explaining our experimental observations.
To further understand the structural characteristics of STO perovskite and confirm the validity of our argument that Sr atoms are instrinsically under a local compressive state, we also calculated the formation energy of STO perovskite (ESTO,form) and the vacancy formation energies of its constituent elements (ETi,vac and EO,vac). As can be seen in Fig. 4b, ESTO,form always increased once the STO perovskite deviated from the zero strain state, due to the weakened bond strengths (Sr–O and/or Ti–O) within the STO perovskite. Since oxygen is bonded with both A-site cations (Sr) and B-site cations (Ti), the dependence of EO,vac on the strain is similar to that of ESTO,form, both of which have a critical point at zero strain but with the opposite sign of the quadratic curve. On the other hand, ESr,vac and ETi,vac show apparently different behaviors compared with EO,vac (Fig. 4b). This reveals that in unstrained STO perovskite, the large Sr atom is under a local compressive state whereas the small Ti atom is under a local tensile state. Although Sr–O and Ti–O may not be in the most stable state individually, they are in an optimal balance at zero strain, thereby stabilizing the overall STO perovskite.
Next, the tendency to form the Sr-rich secondary phase on the surface was also evaluated. Since a SrOx-like insulating phase has been detected experimentally through previous in situ STM/STS analysis and is proposed as one of the major product phases formed by Sr-excess,21,22 the formation energy of an SrO monolayer on the perovskite surface (ESrO,form) was calculated in this work (Fig. S7, ESI†). Fig. 4c shows that the SrO monolayer is more difficult to form on the STF surface with increasing biaxial strain, which is in good agreement with both the experimental and computational observations in Fig. 3d and 4a, respectively. To analyse this result, the Sr–O distances between the bulk SrO with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the SrO monolayer formed on the surface were compared. The details for measuring the distances are described in Fig. S8 (ESI†). As shown in Fig. 4c, the average Sr–O distance of the SrO monolayer is longer than that of the bulk SrO, suggesting that the SrO monolayer formed on the STF surface is somewhat stretched. Therefore, a high ESrO,form is observed at the tensile-strained surface to retain its original bulk structure on the STF surface. As a result, the unfavorable SrO formation would have a synergetic effect to lower the Sr enrichment at tensile-strained surfaces in combination with reduced Sr accumulation.
m and the SrO monolayer formed on the surface were compared. The details for measuring the distances are described in Fig. S8 (ESI†). As shown in Fig. 4c, the average Sr–O distance of the SrO monolayer is longer than that of the bulk SrO, suggesting that the SrO monolayer formed on the STF surface is somewhat stretched. Therefore, a high ESrO,form is observed at the tensile-strained surface to retain its original bulk structure on the STF surface. As a result, the unfavorable SrO formation would have a synergetic effect to lower the Sr enrichment at tensile-strained surfaces in combination with reduced Sr accumulation.
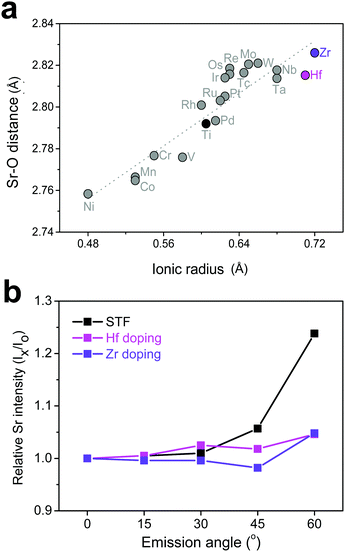
Based on the discussion so far, it was found that surface Sr-excess can be suppressed by intentionally adjusting the bond strength (or length) between Sr and O in a perovskite lattice. Because it is practically impossible to apply direct pressure to the electrodes in operation, an attempt was made to replace the B-site cation with isovalent cations with different sizes, which may relax the compressive strain within the lattice. To explore the appropriate candidate of the dopant cation, the bond length between Sr and O in a bulk Sr(Ti0.25M0.25Fe0.50)O3 perovskite (M = transition metal with a formal charge of 4+ and a coordination number of 6) was calculated. Fig. 5a shows the greater increase in the Sr–O bond length by replacing Ti with a larger cation, such as Hf and Zr, and the strength is thus reinforced. Subsequent AR-XPS analysis confirmed that Hf and Zr doping actually suppresses Sr enrichment on the surface. As shown in Fig. 5b, the Sr relative intensity with the emission angle confirmed that the Sr intensity in Hf- and Zr-doped STF films remains constant and unchanged, even if it is near the surface. Considering that this experiment was carried out using thick polycrystalline thin films with little lattice strain applied through the substrate, it is clear that isovalent B-site doping is a useful method for preventing surface cation segregation, and this method can be easily applicable to real SOC O2-electrodes. Recently, Yildiz et al. have shown that surface modification with less reducible cations, such as Hf and Zr, can improve the surface chemical and electrochemical stability of La0.8Sr0.2CoO3.35 They explained that these cations lower the concentration of surface oxygen vacancies that are positively charged and reduce the electrostatic attraction of negatively charged Sr dopants (SrLa′) towards the surface. In this study, it is believed that the importance of electrostatic interaction is much weaker in comparison with their case because Sr itself, which is a host rather than an isovalent dopant, is enriched. Therefore, we think that this study proposes a new directional approach that explains a similar surface cation segregation phenomenon in terms of elastic interaction: the local coordinate states around the Sr cation determine the surface stability of Sr-containing perovskite oxides.
This study investigated the lattice strain-driven changes in the surface chemical composition and oxygen exchange kinetics of epitaxial thin films of SrTi0.5Fe0.5O3−δ, as a representative mixed conducting perovskite O2-electrode, focusing on surface Sr-excess. The tensile strain in the in-plane direction considerably inhibits enrichment and facilitates the surface reaction rate. DFT calculations showed that the relatively weak bond strength induced by the compressed Sr–O bond in the perovskite lattice drives the increased surface Sr component. Based on these observations, we conclude that the extent of deviation from the optimal A–O bond strength in the most stable state of the A-site cation is the main driving force for surface segregation in ABO3-type perovskite oxides. Consequently, we offer isovalent doping as an effective way to establish the chemical stability of perovskite oxide surfaces, thereby enhancing the electrode performance in solid oxide electrochemical cells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the Samsung Research Funding Center for Future Technology (G01150336). The authors also acknowledge S.-S. Ha and D. Y. Noh of Gwangju Institute of Science and technology (GIST) for their assistance with XRD analysis.Notes and references
- C. Graves, S. D. Ebbesen, S. H. Jensen, S. B. Simonsen and M. B. Mogensen, Nat. Mater., 2015, 14, 239–244 CrossRef CAS PubMed.
- J. T. S. Irvine, D. Neagu, M. C. Verbraeken, C. Chatzichristodoulou, C. Graves and M. B. Mogensen, Nat. Energy, 2016, 1, 1–13 Search PubMed.
- Y. Ohno, S. Nagata and H. Sato, Solid State Ionics, 1981, 3–4, 439–442 CrossRef CAS.
- W. Jung and H. L. Tuller, Adv. Energy Mater., 2011, 1, 1184–1191 CrossRef CAS.
- G. M. Rupp, T. Téllez, J. Druce, A. Limbeck, T. Ishihara, J. Kilner and J. Fleig, J. Mater. Chem. A, 2015, 3, 22759–22769 CAS.
- E. P. Murray, M. J. Sever and S. A. Barnett, Solid State Ionics, 2002, 148, 27–34 CrossRef.
- Z. Shao and S. M. Haile, Nature, 2004, 431, 170–173 CrossRef CAS PubMed.
- Y. Chen, W. Zhou, D. Ding, M. Liu, F. Ciucci, M. Tade and Z. Shao, Adv. Energy Mater., 2015, 5, 1500537 CrossRef.
- G. Yang, W. Zhou, M. Liu and Z. Shao, ACS Appl. Mater. Interfaces, 2016, 8, 35308–35314 CAS.
- Z. Cai, M. Kubicek, J. Fleig and B. Yildiz, Chem. Mater., 2012, 24, 1116–1127 CrossRef CAS.
- E. J. Crumlin, E. Mutoro, Z. Liu, M. E. Grass, M. D. Biegalski, Y.-L. Lee, D. Morgan, H. M. Christen, H. Bluhm and Y. Shao-Horn, Energy Environ. Sci., 2012, 5, 6081–6088 CAS.
- J. Druce, T. Ishihara and J. A. Kilner, Solid State Ionics, 2014, 262, 893–896 CrossRef CAS.
- M. Kubicek, A. Limbeck, T. Frömling, H. Hutter and J. Fleig, J. Electrochem. Soc., 2011, 158(6), B727–B734 CrossRef CAS.
- H. Wang, K. J. Yakal-Kremski, T. Yeh, G. M. Rupp, A. Limbeck, J. Fleig and S. A. Barnett, J. Electrochem. Soc., 2016, 163(6), F581–F585 CrossRef CAS.
- A.-K. Huber, M. Falk, M. Rohnke, B. Luerßen, L. Gregoratti, M. Amati and J. Janek, Phys. Chem. Chem. Phys., 2012, 14, 751–758 RSC.
- W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, J. Am. Chem. Soc., 2013, 135, 7909–7925 CrossRef CAS PubMed.
- H. Kwon, W. Lee and J. W. Han, RSC Adv., 2016, 6, 69782–69789 RSC.
- Z. Cai, Y. Kuru, J. W. Han, Y. Chen and B. Yildiz, J. Am. Chem. Soc., 2011, 133, 17696–17704 CrossRef CAS PubMed.
- H. Jalili, J. W. Han, Y. Kuru, Z. Cai and B. Yildiz, J. Phys. Chem. Lett., 2011, 2, 801–807 CrossRef CAS.
- Y. Yu, K. F. Ludwig, J. C. Woicik, S. Gopalan, U. B. Pal, T. C. Kaspar and S. N. Basu, ACS Appl. Mater. Interfaces, 2016, 8, 26704–26711 CAS.
- W. Jung and H. L. Tuller, Energy Environ. Sci., 2012, 5, 5370–5378 CAS.
- Y. Chen, W. Jung, Z. Cai, J. J. Kim, H. L. Tuller and B. Yildiz, Energy Environ. Sci., 2012, 5, 7979–7988 CAS.
- A. Rothschild, W. Menesklou, H. L. Tuller and E. Ivers-Tiffée, Chem. Mater., 2006, 18, 3651–3659 CrossRef CAS.
- Y. Davila, A. Petitmangin, C. Hebert, J. Perriere and W. Seiler, Appl. Surf. Sci., 2011, 257, 5354–5357 CrossRef CAS.
- H. Ledbetter, M. Lei and S. Kim, Phase Transitions, 1990, 23, 61–70 CrossRef CAS.
- G. Jose la O’, S.-J. Ahn, E. Crumlin, Y. Orikasa, M. D. Biegalski, H. M. Christen and Y. Shao-Horn, Angew. Chem., Int. Ed., 2010, 49, 5344–5347 CrossRef PubMed.
- S. Piskunov, E. Heifets, R. I. Eglitis and G. Borstel, Comput. Mater. Sci., 2004, 29, 165–178 CrossRef CAS.
- R. Merkel and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874–3894 CrossRef PubMed.
- C. Solís, M. D. Rossell, G. Garcia, G. Van Tendeloo and J. Santiso, Adv. Funct. Mater., 2008, 18, 785–793 CrossRef.
- A. D. Rata, A. Herklotz, K. Nenkov, L. Schultz and K. Dörr, Phys. Rev. Lett., 2008, 100, 076401 CrossRef CAS PubMed.
- A. Kushima, S. Yip and B. Yildiz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115435 CrossRef.
- M. Kubicek, Z. Cai, W. Ma, B. Yildiz, H. Hutter and J. Fleig, ACS Nano, 2013, 7(4), 3276–3286 CrossRef CAS PubMed.
- K. A. Stoerzinger, W. S. Choi, H. Jeen, H. N. Lee and Y. Shao-Horn, J. Phys. Chem. Lett., 2015, 6, 487–492 CrossRef CAS PubMed.
- Z. Feng, W. T. Hong, D. D. Fong, Y.-L. Lee, Y. Yacoby, D. Morgan and Y. Shao-Horn, Acc. Chem. Res., 2016, 49, 966–973 CrossRef CAS PubMed.
- N. Tsvetkov, Q. Lu, L. Sun, E. J. Crumlin and B. Yildiz, Nat. Mater., 2016, 15, 1010–1016 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental methods and supplementary data. See DOI: 10.1039/c7ee00770a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |