Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparison of the Ca2+ complexing properties of isosaccharinate and gluconate – is gluconate a reliable structural and functional model of isosaccharinate?†
C.
Dudás
a,
B.
Kutus
a,
É.
Böszörményi
a,
G.
Peintler
b,
Z.
Kele
c,
I.
Pálinkó
 d and
P.
Sipos
d and
P.
Sipos
 *a
*a
aDepartment of Inorganic and Analytical Chemistry, University of Szeged, Dóm tér 7, Szeged, H-6720, Hungary. E-mail: sipos@chem.u-szeged.hu; Fax: +36 62 544 340; Tel: +36 62 544 054
bDepartment of Physical Chemistry and Material Science, University of Szeged, Aradi vértanúk tere 1, Szeged, H-6720, Hungary
cDepartment of Medical Chemistry, University of Szeged, Dóm tér 8, H-6720, Hungary
dDepartment of Organic Chemistry, University of Szeged, Dóm tér 8, H-6720, Hungary
First published on 18th September 2017
Abstract
The calcium complexation and acid–base properties of α-D-isosaccharinate (Isa−) in neutral and in (hyper)alkaline solutions have been investigated via potentiometric titrations, multinuclear NMR, ESI-MS and quantum chemical calculations. Isa− is the primary alkaline degradation product of cellulose, and may be present in radioactive waste repositories and therefore, it could contribute to the mobilization of radioactive nuclei. Because of its limited availability, D-gluconate (Gluc−) is commonly used as a structural and functional model of Isa−. Therefore, the thermodynamic and structural data obtained for Isa− were compared with those of Gluc−. The formation constants of the CaIsa+ and CaGluc+ complexes present in neutral solutions are practically identical, but the binding sites are in different positions and the CaIsa20 solution species cannot be detected. The stepwise formation constant of the CaIsaH−10 complex (forming in alkaline medium) is somewhat larger than that of CaGlucH−10, which is in line with the observation that IsaH−12− is a stronger base than GlucH−12−. The most striking difference is that, unlike Gluc−, Isa− does not form polynuclear complexes with Ca2+. The structural reason for this is that the alcoholate groups on C2 and C3 adjacent to the carboxylate moiety on Gluc− are able to simultaneously bind Ca2+, making the formation of polynuclear Ca-complexes possible. On Isa−, only the alcoholate on C2 is involved, while the other one on C6 is not (supposedly for steric reasons). In conclusion, during the interactions of Gluc− and Isa− with Ca2+, differences rather than similarities prevail.
Introduction
Recently, it has been shown via using a variety of thermodynamic and structural experimental means that in (hyper)alkaline solutions containing Ca2+ and various sugar carboxylates (L− = D-gluconate, Gluc− and D-heptagluconate, Hglu−), bi- and trinuclear Ca2+-sugar-carboxylate complexes with surprisingly high stability were formed.1,2 As a consequence, in solutions with pH > 12, Ca2+ will be present predominantly in the form of Ca2LH−30 and Ca3L2H−40. Additionally, the formation of mononuclear CaLH−10 with lower stability was also detected and it is noticeable that all of the complexes formed are neutral.Organic ligands containing –OH and –COO− donor groups (i.e., sugar carboxylates) are known to form stable binary solution complexes with various metal ions (e.g., alkaline earth and transition metals,1–11 lanthanides,12–15 actinides,16–26etc.), and their complexing ability is more pronounced under (hyper)alkaline conditions than under neutral conditions, due to the binding of the metal ion to the alcoholate group(s).1,2,5,9,10,13,14,16,19,21,24 In an even more complex system, where polyhydroxy carboxylate-, Ca2+ and further three- or four valent cations (e.g., radionuclides) were present, the formation of heteropolynuclear complexes with remarkably high stability was observed in some cases.21,23,27–30
Hyperalkaline conditions prevail in Ca2+-containing cementitious environments foreseen in some repository concepts for disposal of nuclear waste. One of the disposal options widely considered for low- and intermediate level waste (L/ILW) involves the stabilization of waste with cement or cementitious materials. Furthermore, cement-based materials will be widely used as construction materials. The pH of cement pore water (CPW) varies between 8 < pH < 13.3 depending on the composition of cement and brine as well as the solid to brine ratio, etc.31,32 (generally, the pH in a model CPW is usually set to 13.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23). If CPW is in contact with various calcium silicates, the total concentration of Ca2+ ([Ca2+]T; hereafter [X]T denotes the total concentration, while [X] stands for the equilibrium concentration of species X) changes between 2 × 10−3 M and 2 × 10−2 M,31 while the pH can reach 13 in close-to-saturated NaCl solutions.31 In contrast, in MgCl2-dominated brines, Ca2+ concentrations could be several orders of magnitude higher.32
23). If CPW is in contact with various calcium silicates, the total concentration of Ca2+ ([Ca2+]T; hereafter [X]T denotes the total concentration, while [X] stands for the equilibrium concentration of species X) changes between 2 × 10−3 M and 2 × 10−2 M,31 while the pH can reach 13 in close-to-saturated NaCl solutions.31 In contrast, in MgCl2-dominated brines, Ca2+ concentrations could be several orders of magnitude higher.32
Under alkaline conditions, the degradation of organic macromolecules (mainly cellulose) yields various low-molecular-weight carboxylates and hydroxycarboxylates. Among them, α-D-isosaccharinate and its epimeric form, β-D-isosaccharinate are formed in the largest quantities.33 In the literature, significantly more attention has been paid to the aqueous chemistry of α-D-isosaccharinate (Isa− hereafter),34–36 than to its epimeric form, as the former is claimed to be a stronger complexant33,37 than the latter. In the CPW of L/ILW repositories, the maximum concentration of Isa− can be as high as 0.1 M.38 Another relevant organic compound in cementitious environments is Gluc−, which is released from the solid matrix itself being one of the most frequently used cement additives (plasticizer) used during the processing of concrete.39 The concentration range for Gluc− in CPW is considered to be 10−5–10−2 M in numerous studies.23 Therefore, the complexation of radionuclides with Gluc− and in particular with Isa− may increase their solubility and/or decrease their sorption on cement, and can be regarded as a relevant factor contributing to the mobilization of these metal ions from an underground L/ILW repository to the environment.
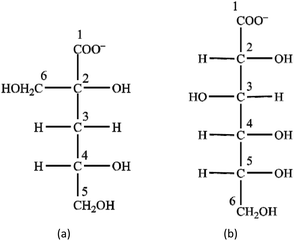
Gluc− is often considered8,23,39,40 as a readily available functional analogue and model compound of α-Isa− (see Scheme 1); the latter is not only expensive, when commercially acquired, but also challenging to prepare in sufficiently pure form.5,7,41 Assuming the structural similarity, the formation of the neutral CaLH−10 complex (at lower [Ca2+]T) with a stability constant identical to L− = Gluc− and Isa− can be suggested.
In the current publication, the assumed similarity of Isa− and Gluc− is scrutinized. For this, we compare the acid–base properties, the Ca2+-binding abilities (both under neutral and alkaline conditions) and the structure of the Ca(II)-complexes of the two sugar carboxylates.
Experimental
Reagents and solutions
Calcium chloride stock solution was prepared by dissolving CaCl2·2H2O (Sigma-Aldrich, ≥99% purity) in water, and the exact concentration of Ca2+ was determined by titration with EDTA. Sodium hydroxide stock solution was prepared by diluting a carbonate-free concentrated NaOH solution,42 and standardized against HCl. The ionic strength was adjusted to 1 M with sodium chloride (Molar Chemicals, a.r. grade) in each sample. All reagents were dissolved in Milli-Q Millipore water.Calcium α-D-isosaccharinate, Ca(Isa)2 was prepared according to the method of Whistler and BeMiller.41 The original procedure was slightly modified as follows: 220 g of lactose monohydrate (Sigma-Aldrich, ≥99% purity) and 60 g of Ca(OH)2 were dissolved in 2 liters of boiled water, and stirred for 3 days at room temperature. After this time, the mixture was boiled for 8 hours. The hot solution was filtered, and the volume of the filtrate was reduced to about 400 mL by evaporating the solvent. The mixture was filtered, and the crude product was recrystallized from water. The success of the synthesis was proven by X-ray diffractometry as well as 1H and 13C NMR spectroscopy.
Sodium α-D-isosaccharinate, NaIsa stock solution was prepared as follows: 10 g of Ca(Isa)2 was stirred with an appropriate amount of the hydrogen form of Amberlite® IR120 ion-exchange resin (Sigma-Aldrich) in about 40 mL water for several hours. The mixture was filtered through a 0.45 μm hydrophilic PTFE membrane filter (VWR). The α-D-isosaccharinic acid, HIsa solution obtained was standardized against NaOH by adjusting the pH to about 8. The pH of the solution was monitored with a calibrated pH-sensitive glass electrode (SenTix® 62 by WTW).
NMR experiments
1H and 13C NMR spectra were recorded on a Bruker Avance DRX 500 MHz NMR spectrometer equipped with a 5 mm inverse broadband probe head furnished with z-oriented magnetic field gradient capability. The magnetic field was stabilized by locking it to the 2D signal of the solvent prior to the measurements. The sample temperature was set to (25 ± 1) °C during the measurements at constant temperature and to 0–50 °C during the temperature-dependent measurement. For the individual samples, 64 and 256 scans were acquired to record 1H NMR and 13C NMR spectra, respectively. Each highly alkaline solution was placed into a PTFE liner, and the liner was placed into an external quartz tube containing D2O. In this way D2O was not mixed with the H2O solvent and therefore the results presented here refer to pH values.For the determination of the deprotonation constant of the alcoholic OH group of Isa−, two sets of solutions were prepared with [Isa−]T = 0.050 and 0.100 M, where [OH−]T was varied systematically from 0.00 to 1.00 M.
To examine the behavior of Isa− in the presence of Ca2+ in highly alkaline medium, solutions containing [Isa−]T = 0.20 M, [OH−]T = 0.50 M and [Ca2+]T = 0.00, 0.05, 0.10, 0.25 and 0.50 M were prepared.
To reveal the structure of the complex formed between Isa− and Ca2+ in alkaline solutions, the temperature dependence of the 1H NMR spectra was recorded in the temperature range of 0–50 °C for a solution containing [Isa−]T = 0.20 M, [OH−]T = 0.20 M and [Ca2+]T = 0.10 M.
Nonlinear fitting of the 13C NMR chemical shifts as a function of [NaOH]T was performed using the PSEQUAD program.43
Potentiometric titrations
Potentiometric titrations were carried out at constant ionic strength (I = 1 M NaCl) using a Metrohm 794 Titrando instrument.The complexation between Ca2+ and Isa− in neutral medium was studied via using a Ca-ion selective electrode (Metrohm). All measurements were carried out in a titration cell thermostated to (25.0 ± 0.1) °C, and the samples were stirred continuously during the reactions. For the calibration of the electrode, a solution containing 10−4 M CaCl2 as the initial concentration and 45 ml as the initial volume was titrated with 0.0650 M CaCl2 up to 120 ml. The response of the Ca-ISE was found to be nonlinear in the −4.0 < log([Ca2+]/M) < −1.5 range, thus a nonlinear calibration procedure was used by fitting splines into the calibration curve using the Spline Calculus program.44 Several sets of measurements were performed with solutions containing [Ca2+]T = 10−4 M and [Isa−]T = 0.011, 0.020, 0.030, 0.059, 0.099, 0.150, 0.194, 0.243 M using the same titrant as in the calibration.
The complex formation between Ca2+ and Isa− in highly alkaline medium was studied by pH-potentiometric titrations, following the reactions with a H2/Pt electrode in the pH range of 11.6–12.9. The full electrochemical cell contained a platinized-platinum hydrogen electrode and a thermodynamic Ag/AgCl reference electrode, and was constructed as follows:
| Pt|H2|test sol., I = 1 M (NaCl) | 1 M NaCl|1 M NaCl|AgCl|Ag |
Within the employed pH range the response of the electrode was found to be linear with a Nernstian slope (59.0–59.2 mV). The titration cell was externally thermostated to (25.0 ± 0.1) °C. Potentiometric titrations of systems containing both Ca2+ and Isa− were performed with the initial NaOH concentration of 0.0102 M and V0 = 20 cm3. The titrant was 1.0136 M NaOH in each case. The initial [Isa−]T concentration was 0.100 M, while the initial [Ca2+]T concentration was set to 0.024 and 0.051 M.
During the data processing, the log([Ca2+]/M) or E/mV values for the measurements performed in neutral and alkaline media, respectively, were fitted as a function of added volume of the titrant using PSEQUAD software.
ESI-MS measurements
ESI-MS measurements in positive ion mode were performed using a Micromass Q-TOF Premier (Waters MS Technologies, Manchester, UK) mass spectrometer equipped with an electrospray ion source. Samples were introduced into the MS by using the direct injection method: the built-in syringe pump of the instrument with a Hamilton syringe was used. The electrospray needle was adjusted to 3 kV and N2 was used as the nebulizer gas.Quantum chemical structure optimizations
The geometry optimizations of the CaIsa+ and CaIsaH−10 complexes were performed using the Gaussian 09 software package45 at the B3LYP/6-311++g(d,p) level. The structures were first optimized in vacuo, and then further optimization was performed on the thus obtained structures considering implicit solvation. For these calculations, the Conductor-like Polarizable Continuum Model (CPCM)46 was utilized at the same theoretical level and with the same basis set (using water as the solvent). During computations, different coordination isomers for CaIsa+ and CaIsaH−10 were considered in order to find the most probable structure.Results and discussion
Ca2+ complexation of Isa− in neutral solution
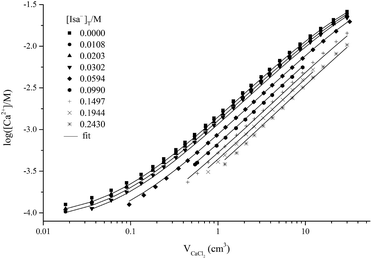
The Ca-ISE potentiometric titration curves of Isa− containing solutions are shown in Fig. 1. The observed cell potential values are systematically shifted towards smaller [Ca2+] values with increasing [Isa−]T indicating complexation. The maximum difference is about 10 mV between the cell potentials obtained for solutions containing 0 and 0.24 M Isa−, respectively. The titration curves were fitted assuming solely the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (represented by the solid lines in Fig. 1). The optimized value for log
1 complex (represented by the solid lines in Fig. 1). The optimized value for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,0 (conditional stability constant relating to I = 1.0 M (const.) ionic strength) with its ±SD value was found to be 1.12 ± 0.02. In general, βp,q,r can be defined as
β1,1,0 (conditional stability constant relating to I = 1.0 M (const.) ionic strength) with its ±SD value was found to be 1.12 ± 0.02. In general, βp,q,r can be defined as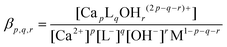 | (1) |
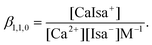 | (2) |
This stability constant corresponds to the significant (up to 60%) formation of the complex CaIsa+ (Fig. S1†). At T = 22 °C and I = 0.2 M, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,0 was found to be 1.25 from potentiometry and 1.29 ± 0.02 from ion-exchange,6 while a value of 1.44 ± 0.07 was suggested from solubility measurements.18
β1,1,0 was found to be 1.25 from potentiometry and 1.29 ± 0.02 from ion-exchange,6 while a value of 1.44 ± 0.07 was suggested from solubility measurements.18
Under the experimental conditions identical to ours (T = 25 °C, I = 1.0 M NaCl), Ca2+ and Gluc− were found to form both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (log
1 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,0 = 1.08 ± 0.01) and 1
β1,1,0 = 1.08 ± 0.01) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (log
2 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,2,0 = 1.65 ± 0.03) complexes,47 where
β1,2,0 = 1.65 ± 0.03) complexes,47 where
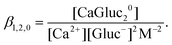 | (3) |
In the case of Isa−, a surprisingly high formation constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,2,0 = 5.40) was proposed for the CaIsa20 complex,48 however, it was further neglected from the comprehensive model describing the Ca2+/Isa− system in the 2–14 pH range.18 Additionally, its formation was neither observed by us nor reported in other literature sources as well.5–7
β1,2,0 = 5.40) was proposed for the CaIsa20 complex,48 however, it was further neglected from the comprehensive model describing the Ca2+/Isa− system in the 2–14 pH range.18 Additionally, its formation was neither observed by us nor reported in other literature sources as well.5–7
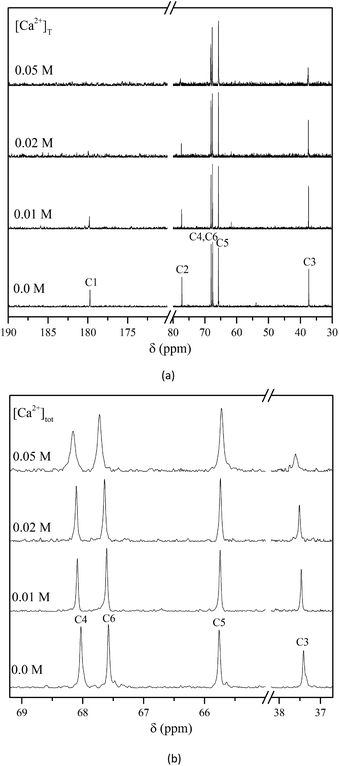
The difference in the composition of the solution species in the Ca2+/Isa− and Ca2+/Gluc− systems is most probably associated with the differences between the structures of the two ligands. The optimum geometry of the CaIsa+ complex obtained from DFT quantum chemical calculations is shown in Fig. 2. The Ca2+ ion sits in the nest of three O atoms (one carboxylate oxygen on C1, and the OH oxygens on C6 and C4). From single crystal X-ray diffraction measurements49 similar binding mode is present in Ca(Isa)2. Analogous calculations for the CaGluc+ complex43 suggested binding of Ca2+ to O atoms on C1, C2, C3 and C6. This binding mode seems to be the governing coordination motif for both ligands resulting in an almost identical association constant for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species.
1 species.
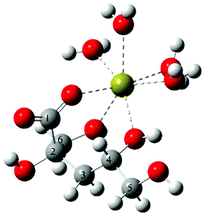 | ||
| Fig. 2 The optimum geometry calculated for CaIsa+ at the B3LYP/6-311++G(d,p) level using the PCM model and explicit water molecules. | ||
In contrast to CaGluc+, there is no binding to the alcoholic OH closest to the carboxylate (the latter two rather establish an intramolecular hydrogen bond) in the CaIsa+ species. Moreover, only one freely rotating C–C bond is present in this rigid structure. Consequently, the binding of a second anion and the simultaneous dehydration of Ca2+ are difficult compared to the more flexible Gluc−. This may be the reason why the CaIsa20 complex has lower stability than CaGluc20 and why the former was not possible to detect experimentally.
Acid–base properties of Isa− in hyperalkaline solutions
The proton dissociation constant of Isa− (corresponding to the deprotonation of one or more alcoholic OH groups) taking place in hyperalkaline solutions can be defined as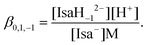 | (4) |
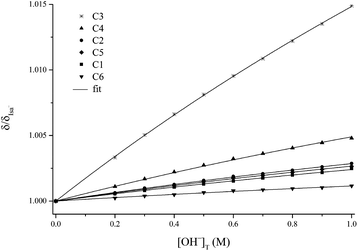
This deprotonation process causes a significant downfield shift in each 13C NMR signal of Isa− (see Fig. 3, in which the peak assignations shown in Scheme 1 are used; they were constructed on the basis of the average proton coupling constants of Isa− shown in Table S1† and from the two-dimensional 1H–13C HSQC NMR spectrum of Isa−). The extent of this variation is 0.08–0.55 ppm and it can be described using saturation curves with the increasing NaOH concentration. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0,1,−1 dissociation constant extracted from the data points obtained for a solution series with I = 1 M NaCl (const.) was found to be −14.5 ± 0.1 (using −13.76 as log
β0,1,−1 dissociation constant extracted from the data points obtained for a solution series with I = 1 M NaCl (const.) was found to be −14.5 ± 0.1 (using −13.76 as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kw, the ionic product of water, for 1 M NaCl50). From this dissociation constant, the degree of deprotonation is ca. 20% at pH = 14 (Fig. S2†).
Kw, the ionic product of water, for 1 M NaCl50). From this dissociation constant, the degree of deprotonation is ca. 20% at pH = 14 (Fig. S2†).
The 1H NMR signals of Isa− exhibited an upfield shift with increasing NaOH concentration. This small but detectable variation (Δδ < 0.1 ppm) supports the deprotonation of the anion, but the magnitude of these changes makes the 1H NMR spectra unsuitable for extracting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0,1,−1. The almost uniform variation in the chemical shifts on each proton signal upon increasing NaOH concentration indicates the deprotonation of the alcoholic OH groups without a favored position for the deprotonation. In this respect, 1H NMR observations analogous to those found for Isa− were made for Gluc−.1
β0,1,−1. The almost uniform variation in the chemical shifts on each proton signal upon increasing NaOH concentration indicates the deprotonation of the alcoholic OH groups without a favored position for the deprotonation. In this respect, 1H NMR observations analogous to those found for Isa− were made for Gluc−.1
Ca2+ complexation of Isa− in alkaline to hyperalkaline solutions
The 1H NMR spectra of aqueous solutions containing [Isa−]T = 0.20 M, [OH−]T = 0.50 M and varying amounts of added Ca2+ (0–0.10 M) are shown in Fig. 4(a). For comparison, the spectra of solutions with identical compositions, but with Gluc− in place of Isa− are also shown (Fig. 4(b)).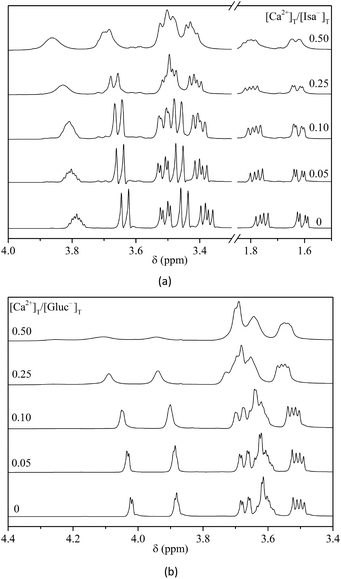 | ||
| Fig. 4 1H NMR spectra of Isa− (a) or Gluc− (b) solutions (0.20 M) in the presence of [Ca2+]T = 0–0.10 M and at [OH−]T = 0.50 M. I = 1 M (NaCl), T = (25 ± 1) °C. | ||
Addition of Ca(II) ions to the system causes minor but detectable effects in the 1H NMR spectrum of Isa−: the peaks are shifted downfield and broadened; the highest change occurred in the signal of H4. Both experimental observations indicate the interaction between the metal ion and Isa−. Many more dramatic effects are seen for identical solutions containing Gluc−, the displacement of the NMR peaks is significantly larger and the extent of line broadening is so extensive that at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 metal-to-ligand ratio, some peaks (H2 and H3) vanish in the baseline. The profound difference between the two spectral series in Fig. 3 strongly suggests that under these experimental conditions, calcium ions form complexes more readily with Gluc− than with Isa−. To further enhance the experimental effect seen in Fig. 4(a), the metal-to-ligand ratio should be increased; in this concentration range Ca(Isa)2(S) precipitation occurred in the system right after solution preparation. (The precipitate formation was also observed at lower total concentrations too, as it is exemplified in Fig. S3,† however, the spectra exhibited variation only after the onset of the precipitation. Before that, the spectra are independent of the time elapsed since solution preparation. This indicates that the simultaneous solution equilibria are very rapidly established between the solution species even in supersaturated solutions.)
2 metal-to-ligand ratio, some peaks (H2 and H3) vanish in the baseline. The profound difference between the two spectral series in Fig. 3 strongly suggests that under these experimental conditions, calcium ions form complexes more readily with Gluc− than with Isa−. To further enhance the experimental effect seen in Fig. 4(a), the metal-to-ligand ratio should be increased; in this concentration range Ca(Isa)2(S) precipitation occurred in the system right after solution preparation. (The precipitate formation was also observed at lower total concentrations too, as it is exemplified in Fig. S3,† however, the spectra exhibited variation only after the onset of the precipitation. Before that, the spectra are independent of the time elapsed since solution preparation. This indicates that the simultaneous solution equilibria are very rapidly established between the solution species even in supersaturated solutions.)
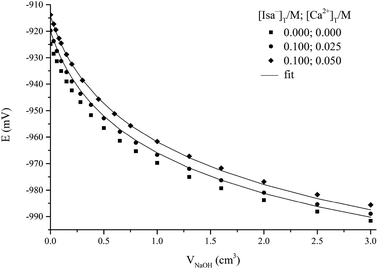
Although the experimental effects observed in the 1H NMR spectra undoubtedly proved the complex formation between Ca2+ and Isa−, they were not sufficiently large for the quantitative determination of the composition and structure of the complexes formed. Accordingly, the interaction between Ca2+ and Isa− in alkaline solutions was studied via potentiometric titrations using the H2/Pt electrode (Fig. 5).
The observed cell potentials are shifted towards the less negative values for solutions containing both calcium and Isa−. This corresponds to some OH− consuming complexation process resulting in a decrease in [OH−]. However, the experimental effect (i.e., the potential difference between the calibration and the titration in question at the same added base volume) is at most ∼12 mV. A much larger effect (up to 50 mV) and a unique curvature were seen on the titration curves analogous to these ones but with Gluc− as the complexing ligand (see Fig. 1 in ref. 1). This confirms the semi-quantitative statement derived from the 1H NMR measurements (Fig. 4) on the formation of more stable Ca2+ complexes with Gluc− than with Isa−.
During the data processing, the formation constants of IsaH−12− and CaIsa+ (see previous sections), the ionic product of water, pKw (13.76, taken from the literature50) and the formation constants of the CaOH+ and Ca(OH)20 solution species51 (with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,0,1 = 0.18 ± 0.02 and log
β1,0,1 = 0.18 ± 0.02 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,0,2 = 0.67 ± 0.02, respectively) were kept constant. Assumption of only one mononuclear complex, CaIsaH−10 with log
β1,0,2 = 0.67 ± 0.02, respectively) were kept constant. Assumption of only one mononuclear complex, CaIsaH−10 with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,−1 = −11.36 ± 0.02, where
β1,1,−1 = −11.36 ± 0.02, where
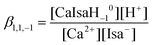 | (5) |
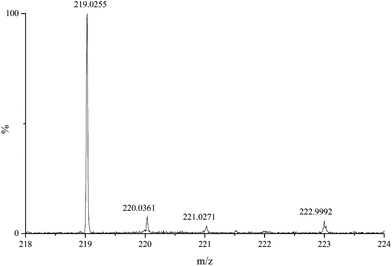
ESI-MS measurements were performed to obtain further information on the composition of the solution species present in the Ca2+/Isa−/OH− systems. The spectrum of the sample containing Ca2+ (0.025 M), Isa− (0.050 M) and NaOH (0.100 M) was recorded in positive ion mode (Fig. 6). As uncharged complexes are invisible in ESI-MS, the peaks referring to the solution species appeared in the spectrum gaining positive charge(s) via “binding” one (or more) proton(s). Therefore, the peaks referring to CaIsaH−10 are expected to appear at 219.03 m/z. Polynuclear complexes with compositions similar to those found for the Ca2+/Gluc−/OH− systems are expected to appear at around 257 and 475 m/z values. For the Ca2+/Isa−/OH− system, the experimentally observed mass spectrum was practically empty in this range.
It is interesting to note that the stability constant of the direct association of Ca2+ and IsaH−12− is defined as
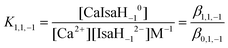 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K1,1,−1 = 3.13. This is considerably larger than that of the CaGlucH−10 complex (2.74
K1,1,−1 = 3.13. This is considerably larger than that of the CaGlucH−10 complex (2.74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); this difference in the formation constants is most probably due to the stronger basicity of IsaH−12− than GlucH−12−.
1); this difference in the formation constants is most probably due to the stronger basicity of IsaH−12− than GlucH−12−.
The binding sites of Isa− in the CaIsaH−10 complex
To identify the Ca2+-binding sites of Isa− in the CaIsaH−10 complex, 1H and 13C NMR measurements were performed. From the temperature dependence of the 1H NMR spectrum of an alkaline solution containing Ca2+ and Isa− (Fig. S6†), the chemical exchange between the various forms of the ligand at low temperatures (0–5 °C) is slow on the NMR time scale, while by increasing the temperature to 30–35 °C, the chemical exchange becomes fast. Below 5 °C, the signals of free Isa− and those of its Ca2+ complex(es) appear separately (Fig. S7†). The largest change (splitting at low temperatures, displacement and broadening at higher ones) is seen in the 1H NMR peak of H4 indicating that the alcoholic OH group on C4 (most probably in the form of alcoholate) participates in calcium binding. Because of the complexity of the 1H NMR spectra and the overlap of various peaks, it is not possible to unambiguously locate further binding sites in the molecule.The 13C NMR spectra of alkaline Isa− solutions containing various amounts of added calcium are shown in Fig. 7. With increasing Ca2+ concentration, the signals of C1, C2, and C3 significantly broaden to an extent that those of C1 and C2 vanish in the baseline at the highest calcium concentration ([Ca2+]T = 0.05 M, corresponding to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 metal-to-ligand ratio). Less spectacular but still significant broadening is seen on the peak corresponding to C4, and those of C5 and C6 are the least affected by calcium binding.
4 metal-to-ligand ratio). Less spectacular but still significant broadening is seen on the peak corresponding to C4, and those of C5 and C6 are the least affected by calcium binding.
 | ||
| Fig. 7 Normalized 13C NMR spectra of solutions containing [Isa−]T = 0.2 M, [OH−]T = 0.2 M and [Ca2+]T = 0–0.05 M, T = (25 ± 1) °C. | ||
These observations indicate that in alkaline solutions Isa− acts as a multidentate ligand in the CaIsaH−10 complex; this feature is similar to that of Gluc−, as it is shown in ref. 1. Furthermore, the peak broadening and loss of intensity imply that the chemical exchange is slower than at neutral pH, since for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of the Gluc− and Hpgl− ions1,8 the chemical exchange was proven to be fast. This implies stronger interaction between the metal ion and the ligand and can be explained by the binding of an alcoholate group. This reaction takes place most probably on C2–OH since this is the closest to the carboxylate anchor and the ionization of the O–H group may be facilitated by an intramolecular hydrogen bond (Fig. 2).
1 complex of the Gluc− and Hpgl− ions1,8 the chemical exchange was proven to be fast. This implies stronger interaction between the metal ion and the ligand and can be explained by the binding of an alcoholate group. This reaction takes place most probably on C2–OH since this is the closest to the carboxylate anchor and the ionization of the O–H group may be facilitated by an intramolecular hydrogen bond (Fig. 2).
Profound differences, however, are seen in the binding arrangement around the calcium ion in CaIsaH−10 compared to CaGlucH−10. In the latter, beside the carboxylate oxygens on C1, the alcoholate groups on both the C2 and C3 carbons adjacent to the carboxylate participate in Ca2+ binding. This results in the formation of two bonding isomers containing five- or six-membered chelate rings.1 These arrangements are similar to those observed in analogous systems with neutral and slightly alkaline pH (that is, in the CaGluc+ solution species).8
In CaIsaH−10, unlike in CaGlucH−10, the donor group(s) further away from the carboxylate moiety are most probably involved in the calcium binding. This is strongly supported by the broadening of the C3 signal upon calcium addition (Fig. 7). Of the two alcoholic OH groups of Isa− adjacent to the carboxylate (on C2 and C6) only the one on C2 participates in the metal ion binding, while that on C6 does not. In the bonding isomers of CaIsaH−10 a carboxylate oxygen on C1 and the alcoholate groups on C2 or C4 coordinate. It is expected that the chelate ring with C1 and C2 oxygens is energetically more favored (5 membered) than that with C1 and C4, which is a 7 membered chelate. The OH on C6 is a non-coordinating group. This is supported not only by the 13C NMR spectra shown in Fig. 7 (the carbon signal barely changes with the increasing calcium concentration), but also by the 1H NMR spectra shown in Fig. S7† (the proton signal corresponding to H6 and H6′ does not change with temperature).
Structural models for the CaIsaH−10 complex were also built (Fig. 8 and S8†). From the calculations, the formation of four binding isomers can be proposed. In the two lowest energy bidentate arrangements, Ca2+ is bound to the oxygen on C1 and the alcoholate on C2 (Fig. 8a) or C2 and C4 (Fig. 8b); the latter is only 0.7 kJ mol−1 higher in energy. In the third structure, oxygens on C1, C4 (alcoholate) and C6 (alcohol) bind Ca2+ (Fig. S8a†), while the fourth isomer (Fig. S8b†) with binding oxygens on C1, C6 (alcoholate) and C4 (alcohol) does not. The formation of these complexes is less probable, since their energies are 2.2 and 2.4 kJ mol−1 higher. From these calculations, the bidentate arrangement with Ca2+ is bound to the oxygen on C1 and the alcoholate on C6 is one of the least energetically favored (14.9 kJ mol−1 higher in energy).
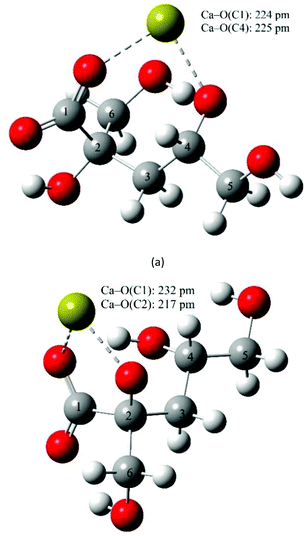 | ||
| Fig. 8 The optimum geometries calculated for CaIsaH−10 at the B3LYP/6-311++G(d,p) level using the PCM model and explicit water molecules. | ||
Conclusions
The structure of the two ligands (Scheme 1) is similar in the sense that both contain one carboxylate group and several (4 or 5) alcoholic OH groups. On Isa− next to the –COO− group, there are two –OH moieties on C2 and C6; these motifs are practically the same on Gluc− (i.e., the –OH groups on C2 and C3). The structure of Isa− is branched (contains one tertiary C atom), while that of Gluc− can be regarded more like linear (only primary and secondary C atoms are present). Accordingly, Gluc− is expected to be much more flexible than Isa−. In the middle of an Isa− anion, there is a methylene group (C3) forming a hydrophobic “bridge” between the two hydrophilic sides of the molecule (comprising of C1, C2 and C6 on one end and C4 and C5 on the other). This hydrophobic motif is completely missing in Gluc−, and it is likely to be associated with the difference between the solubility of their calcium salts (pKsp values reported for Ca(Gluc)2 and Ca(Isa)2 are 4.19 ± 0.05 and 6.53 ± 0.02, respectively40).In neutral solutions weak complexes are formed with Ca2+ (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,0 = 1.12 and 1.08 for CaIsa+ and CaGluc+ at I = 1 M NaCl and at T = 25 °C, respectively). The almost identical formation constants imply the involvement of similar coordinating groups (i.e., carboxylate O and one or two OH). Isa− does not form a 1
β1,1,0 = 1.12 and 1.08 for CaIsa+ and CaGluc+ at I = 1 M NaCl and at T = 25 °C, respectively). The almost identical formation constants imply the involvement of similar coordinating groups (i.e., carboxylate O and one or two OH). Isa− does not form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex with calcium, while at appreciable excess ligand excess, there is unambiguous experimental proof for the formation of the CaGluc2(aq.) solution species. There are indications that the positions of binding sites in CaIsa+ and CaGluc+ are different: in CaIsa+, the OH on C2 does not take part in the metal ion binding, while in CaGluc+, both the OH and C2 and that on C3 are capable of coordinating (based on calculations). Either of these features is most probably connected to the rigidity of Isa− compared to Gluc−.
2 complex with calcium, while at appreciable excess ligand excess, there is unambiguous experimental proof for the formation of the CaGluc2(aq.) solution species. There are indications that the positions of binding sites in CaIsa+ and CaGluc+ are different: in CaIsa+, the OH on C2 does not take part in the metal ion binding, while in CaGluc+, both the OH and C2 and that on C3 are capable of coordinating (based on calculations). Either of these features is most probably connected to the rigidity of Isa− compared to Gluc−.
The proton dissociation constants of Isa− and Gluc− are also somewhat different (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0,1,−1 = −14.5 ± 0.1 and −13.85 ± 0.02 for Isa− and Gluc−, respectively). Isa− is a significantly weaker acid than Gluc−, which is due to the presence of an electron withdrawing group (i.e., OH) on C3 of Gluc−. Based on the statistical effect of the number of OH groups, the pK of Isa− would only be 0.3 unit higher52 which points out the importance of the steric factor as well.
β0,1,−1 = −14.5 ± 0.1 and −13.85 ± 0.02 for Isa− and Gluc−, respectively). Isa− is a significantly weaker acid than Gluc−, which is due to the presence of an electron withdrawing group (i.e., OH) on C3 of Gluc−. Based on the statistical effect of the number of OH groups, the pK of Isa− would only be 0.3 unit higher52 which points out the importance of the steric factor as well.
On the basis of the difference between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0,1,−1 overall proton dissociation constants, IsaH−12− should form more stable Ca2+-complex, than GlucH−12−, which is reflected in the difference of the stepwise formation constants (log
β0,1,−1 overall proton dissociation constants, IsaH−12− should form more stable Ca2+-complex, than GlucH−12−, which is reflected in the difference of the stepwise formation constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,−1 = 3.15 and 2.74 for Isa− and Gluc−, respectively). The higher acidity of Gluc− indicates that the CaGluc+ complex undergoes deprotonation at a lower pH (the pK of the complex is log
β1,1,−1 = 3.15 and 2.74 for Isa− and Gluc−, respectively). The higher acidity of Gluc− indicates that the CaGluc+ complex undergoes deprotonation at a lower pH (the pK of the complex is log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,0 − log
β1,1,0 − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,1,−1 = 12.02) than does CaIsa+ (pK = 12.48). This remarkable difference was found previously for Th(OH)4GlucH−12−; an analogous complex with Isa− in place of Gluc− could not be observed in the same pH range.19
β1,1,−1 = 12.02) than does CaIsa+ (pK = 12.48). This remarkable difference was found previously for Th(OH)4GlucH−12−; an analogous complex with Isa− in place of Gluc− could not be observed in the same pH range.19
A more striking difference is seen between the composition and structure of the Ca2+-complexes forming in strong alkaline solutions. In Isa−-containing solutions, no polynuclear complexes were detected, and under hyperalkaline conditions, the only species is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1 complex. Under identical conditions, solutions with Gluc− are predominated by 2
−1 complex. Under identical conditions, solutions with Gluc− are predominated by 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −3 and 3
−3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −4 polynuclear complexes with a 1
−4 polynuclear complexes with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1 mononuclear complex as a minor species. In the polynuclear complexes, the flexibility of Gluc− makes the simultaneous participation of the alcoholate groups on C2 and C3 in the calcium ion binding possible, and this feature is a prerequisite for the formation of the multinuclear species (see Fig. 6 in ref. 1). As we have shown via using multinuclear NMR and molecular modelling calculations, this condition does not hold for Isa−; it binds Ca2+ only with one alcoholate adjacent to the carboxylate (i.e., on C2). The participation of the other adjacent oxygen donor on C6 is hindered, due to the unfavorable arrangement of the COO−, C2–OH and C6–OH groups (Fig. S8†).
−1 mononuclear complex as a minor species. In the polynuclear complexes, the flexibility of Gluc− makes the simultaneous participation of the alcoholate groups on C2 and C3 in the calcium ion binding possible, and this feature is a prerequisite for the formation of the multinuclear species (see Fig. 6 in ref. 1). As we have shown via using multinuclear NMR and molecular modelling calculations, this condition does not hold for Isa−; it binds Ca2+ only with one alcoholate adjacent to the carboxylate (i.e., on C2). The participation of the other adjacent oxygen donor on C6 is hindered, due to the unfavorable arrangement of the COO−, C2–OH and C6–OH groups (Fig. S8†).
Because of this structural difference, it is not expected that Isa− and Gluc− behave identically (or even similarly) in hyperalkaline solutions containing Ca2+ ions and furthermore, higher valent cations, such as various actinides and lanthanides, i.e., under conditions relevant to radioactive waste repositories. It is also expected that the thermodynamics and structure of ternary complexes comprising Ca2+, L− and various radionuclides depend strongly on whether L− = Isa− or Gluc−. Taking this into account, a detailed study, similar to the present one, on the hyperalkaline aqueous chemistry of β-D-isosaccharinate would also be warranted. Birjkumar et al. stated that “caution should be exercised when using gluconate as a thermodynamic model for isosaccharinate in uranyl(VI) chemistry”.53 In that sense, our investigations led to similar conclusions with regard to certain aspects of the chemistry of aqueous solutions containing Isa− and calcium.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the technical assistance provided by Ilona Halasiné-Varga, Petronella Medvegy and Orsolya Orbán-Gyapai. Research leading to this contribution was financed by GINOP-2.3.2-15-2016-00013 and NKFIH K 124 265 grants. All these supports are highly appreciated.Notes and references
- A. Pallagi, É. G. Bajnóczi, S. E. Canton, T. Bolin, G. Peintler, B. Kutus, Z. Kele, I. Pálinkó and P. Sipos, Environ. Sci. Technol., 2014, 48, 6604–6611 CrossRef CAS PubMed.
- A. Pallagi, Z. Csendes, B. Kutus, E. Czeglédi, G. Peintler, P. Forgó, I. Pálinkó and P. Sipos, Dalton Trans., 2013, 42, 8460–8467 RSC.
- D. T. Sawyer, Chem. Rev., 1964, 64, 633–695 CrossRef CAS.
- H. A. Tajmir-Riahi, J. Inorg. Biochem., 1990, 39, 33–41 CrossRef CAS.
- K. Vercammen, M. A. Glaus and L. R. Van Loon, Acta Chem. Scand., 1999, 53, 241–246 CrossRef CAS.
- L. R. Van Loon, M. A. Glaus and K. Vercammen, J. Solution Chem., 2004, 33, 1573–1583 CrossRef CAS.
- K. Vercammen, Complexation of Calcium, Thorium and Europium by α-Isosaccharinic Acid under Alkaline Conditions, PhD dissertation, Swiss Federal Institute of Technology, Zurich, 2000 Search PubMed.
- A. Pallagi, P. Sebők, P. Forgó, T. Jakusch, I. Pálinkó and P. Sipos, Carbohydr. Res., 2010, 345, 1856–1864 CrossRef CAS PubMed.
- K. Blomqvist and E. R. Still, Anal. Chem., 1985, 57, 749–752 CrossRef CAS.
- G. M. Escandar and L. F. Sala, Can. J. Chem., 1992, 70, 2053–2057 CrossRef CAS.
- G. M. Escandar, J. M. Salas Peregrin, M. Gonzalez Sierra, D. Martino, M. Santoro, A. A. Frutos, S. I. Garcia, G. Labadié and L. F. Sala, Polyhedron, 1996, 15, 2251–2261 CrossRef CAS.
- N. A. Kostromina, Zh. Neorg. Khim., 1966, 11, 381–385 CAS.
- S. Giroux, P. Rubini, B. Henry and S. Aury, Polyhedron, 2000, 19, 1567–1574 CrossRef CAS.
- S. Giroux, S. Aury, B. Henry and P. Rubini, Eur. J. Inorg. Chem., 2002, 1162–1168 CrossRef CAS.
- Z. Zhang, B. Bottenus, S. B. Clark, G. X. Tian, P. Zanonato and L. F. Rao, J. Alloys Compd., 2007, 444, 470–476 CrossRef.
- A. D. Moreton, N. J. Pilkington and C. J. Tweed, Mater. Res. Soc. Symp. Proc., 1993, 294, 753–758 CrossRef CAS.
- K. Vercammen, M. A. Glaus and L. R. Van Loon, Radiochim. Acta, 2001, 89, 393–401 CrossRef CAS.
- D. Rai, N. J. Hess, Y. Xia, L. Rao, H. M. Cho, R. C. Moore and L. R. Van Loon, J. Solution Chem., 2003, 32, 665–689 CrossRef CAS.
- A. R. Felmy, G. Choppin and D. A. Dixon, Development of fundamental data on chemical speciation and solubility for strontium and americium in high level waste: predictive modelling of phase partitioning during tank processing, EMSP Project 73749, PNNL, USA, 2001 Search PubMed.
- K. L. Nash, M. Borkowski, M. Hancock and I. Laszak, Sep. Sci. Technol., 2005, 40, 1497–1512 CrossRef CAS.
- J. Tits, E. Wieland and M. H. Bradbury, Appl. Geochem., 2005, 20, 2082–2096 CrossRef CAS.
- Z. Zhang, S. B. Clark, G. Tian, P. L. Zanonato and L. Rao, Radiochim. Acta, 2006, 94, 531–536 CAS.
- X. Gaona, V. Montoya, E. Colàs, M. Grivé and L. Duro, J. Contam. Hydrol., 2008, 102, 217–227 CrossRef CAS PubMed.
- Z. Zhang, G. Helms, S. B. Clark, G. X. Tian, P. Zanonato and L. F. Rao, Inorg. Chem., 2009, 48, 3814–3824 CrossRef CAS PubMed.
- E. Colàs, M. Grivé and I. Rojo, J. Solution Chem., 2013, 42, 1545–1557 CrossRef.
- E. Colàs, M. Grivé, I. Rojo and L. Duro, J. Solution Chem., 2013, 42, 1680–1690 CrossRef.
- T. Bechtold, E. Burtscher and A. Turcanu, J. Chem. Soc., Dalton Trans., 2002, 2683–2688 RSC.
- F. R. Venema, J. A. Peters and H. van Bekkum, Recl. Trav. Chim. Pays-Bas, 1993, 112, 445–450 CrossRef CAS.
- J. Tits, E. Wieland, M. H. Bradbury, P. Eckert and A. Schaible, The uptake of Eu(III) and Th(IV) by calcite under hyperalkaline conditions, PSI Bericht 02-03, Paul Scherrer Institut, Villigen, Switzerland, 2002 Search PubMed.
- M. J. Keith-Roach, Sci. Total Environ., 2008, 396, 1–11 CrossRef CAS PubMed.
- U. R. Berner, Waste Manage., 1992, 12, 201–209 CrossRef CAS.
- C. Bube, V. Metz, E. Bohnert, K. Garbev, D. Schild and B. Kienzler, Phys. Chem. Earth, 2013, 64, 87–94 CrossRef.
- M. A. Glaus and L. R. Van Loon, Environ. Sci. Technol., 2008, 42, 2906–2911 CrossRef CAS PubMed.
- G. N. Richards and H. H. Sephton, J. Chem. Soc., 1957, 51, 4492–4499 RSC.
- M. A. Glaus, L. R. Van Loon, S. Achatz and A. Chodura, Anal. Chim. Acta, 1999, 398, 111–122 CrossRef CAS.
- C. J. Knill and J. F. Kennedy, Carbohydr. Polym., 2003, 51, 281–300 CrossRef CAS.
- L. R. Van Loon and M. A. Glaus, Experimental and theoretical studies on alkaline degradation of cellulose and its impact on the sorption of radionuclides, PSI Bericht 98-07, Paul Scherrer Institut, Villigen, Switzerland, 1998 Search PubMed.
- L. R. Van Loon, M. A. Glaus, S. Stallone and A. Laube, Mater. Res. Soc. Symp. Proc., 1997, 506, 1009–1010 CrossRef.
- M. A. Glaus, A. Laube and L. R. Van Loon, Waste Manage., 2006, 26, 741–751 CrossRef CAS PubMed.
- L. R. Van Loon, M. A. Glaus and K. Vercammen, Acta Chem. Scand., 1999, 53, 235–240 CrossRef CAS.
- R. L. Whistler and J. N. BeMiller, Reactions of Carbohydrates, in Methods in carbohydrate chemistry, ed. M. L. Wolfrom and J. N. BeMiller, Academic Press, New York, 1963, vol. 2, pp. 477–479 Search PubMed.
- P. Sipos, G. Hefter and P. M. May, Analyst, 2000, 125, 955–958 RSC.
- L. Zékány, I. Nagypál and G. Peintler, PSEQUAD for Chemical Equilibria, Update 5–5.10, Hungary, 2000–2008 Search PubMed.
- G. Peintler, Spline Calculus, Version 2.12a, University of Szeged, Szeged, Hungary, 2008 Search PubMed.
- Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- B. Kutus, D. Ozsvár, N. Varga, I. Pálinkó and P. Sipos, Dalton Trans., 2017, 46, 1065–1074 RSC.
- D. Rai, L. Rao and Y. Xia, J. Solution Chem., 1998, 27, 1109–1122 CrossRef CAS.
- A. Ishizu, Acta Chem., Scand., 1968, 22, 1395–1403 CrossRef.
- R. Näsänen and P. Meriläinen, Suom. Kemistil. B, 1960, 33, 149–151 Search PubMed.
- B. Kutus, A. Gácsi, A. Pallagi, I. Pálinkó, G. Peintler and P. Sipos, RSC Adv., 2016, 6, 45231–45240 RSC.
- D. D. Perrin, B. Dempsey and E. P. Serjeant, pKa Prediction for organic acids and bases, Springer, 2012 Search PubMed.
- K. H. Birjkumar and N. D. Bryan, Dalton Trans., 2012, 41, 5542–5552 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Distribution diagram for the Ca2+–Isa− neutral system (Fig. S1), the structure of the CaIsa+ complex in aqueous solution (Fig. S2), the values of J-coupling constants for the Isa− protons (Table S1), the distribution diagram of Isa−/IsaH−12− at pH = 12–14 (Fig. S3), time dependent 1H NMR spectra of an alkaline solution supersaturated with respect to Ca(ISA)2 (Fig. S4), the distribution diagram of the Ca2+–Isa− and Ca2+–Gluc− alkaline systems (Fig. S5 and S6, respectively), temperature dependent 1H NMR spectra in 0.2 M NaOH (Fig. S7 and S8) and the structure of the CaIsaH−10 complex with O(C6) as a binding site. See DOI: 10.1039/c7dt03120c |
| This journal is © The Royal Society of Chemistry 2017 |