Solid state structures and properties of free-base 5,10,15-triphenylcorrole (TPCor) anions obtained by deprotonation and reduction. Effective magnetic coupling of spins in (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂

Abstract

The reduction of 5,10,15-triphenylcorrole (H₃TPCor) with decamethylchromocene yields (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1). It is accompanied by the deprotonation of H₃TPCor and the formation of planar H₂TPCor˙²⁻ radical dianions. Complex 1 manifests a band at about 750 nm observed in the solution spectra of H₂TArylCor˙²⁻ and demonstrates an EPR signal attributed to the reduced corrole macrocycle. The magnetic moment of 1 of 4.10μ_B at 300 K indicates the contribution of Cp*₂Cr⁺ (S = 3/2) and H₂TPCor˙²⁻ (S = 1/2). These paramagnetic species alternate in the π-stacks providing rather effective antiferromagnetic coupling of spins at the Weiss temperature of −31 K. To distinguish the H₂TPC˙²⁻ dianions from the deprotonated H₂TPCor⁻ anions, we also studied the {cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) salt with deprotonated corrole anions. In this case, a planar macrocycle was formed as well. However, the properties of H₂TPCor⁻ in 2 differ from those of H₂TPCor˙²⁻ in 1.

---

Introduction

Metal macroheterocycles are effective components for the design of optical, magnetic and conducting materials. Some phthalocyanine (Pc) and porphyrin (Porph) derivatives can be used as sensors, as materials for optical and electronic devices, and in photoelectronics.¹ Conducting compounds were obtained by the oxidation of free-base and metal-containing phthalocyanines using iodine or the electrochemical oxidation of axially substituted phthalocyanine [M^IIIPcL₂]⁻ anions (M = Co, Fe; L = CN, Cl, Br).² Since metal phthalocyanines can contain paramagnetic metals, they have also been used as active components in the design of magnetic assemblies.³ For example, polymeric compounds with alternating (Mn^IIIPc)⁺ or (Mn^IIIPorph)⁺ and tetracyanoethylene (TCNE˙⁻) ions show ferrimagnetic ordering of spins.^3a,b The reduction of iron(II) phthalocyanine using decamethylchromocene (Cp*₂Cr) allows one to obtain the complex with π-stacks of alternating [Fe^I(Pc²⁻)]⁻ (S = 1/2) and Cp*₂Cr⁺ (S = 3/2) ions which shows ferrimagnetic ordering of spins below 5 K.^3c The charge transfer complex (Cp*₂Cr⁺)(H₂Pc˙⁻)·4C₆H₄Cl₂ of free-base phthalocyanine (H₂Pc) with Cp*₂Cr has similar π-stacks of alternating ions but no essential magnetic coupling was found in this complex (the Weiss temperature is −4 K) most probably due to ineffective π–π interactions between H₂Pc˙⁻ and the Cp* ligand.^3d Nevertheless, this work shows that free-base macroheterocycles can also be used in the design of magnetic assemblies.

meso-Substituted 5,10,15-triarylcorroles (H₃TArylCor) are related to meso-substituted 5,10,15,20-tetraarylporphyrins but one aryl-C fragment is removed from the macrocycle (Scheme 1).⁴ Free-base triarylcorroles have complicated reduction chemistry.⁵ They are reduced in benzonitrile (BN) at about −1.03 V vs. SCE (for aryl = Ph(CF₃)₂) but this reduction is accompanied by deprotonation and the formation of the H₂TArylCor⁻ anions. The deprotonation becomes easier in basic solvents like pyridine (Py) and the H₂TArylCor⁻ anions are formed under these conditions even without reduction in some cases. Therefore, the H₃TArylCor˙⁻ radical anions are not stable in solution due to deprotonation. Nevertheless, paramagnetic radical H₂TArylCor˙²⁻ dianions can be obtained by the reduction of the H₂TArylCor⁻ anions at −1.40 V in BN and at −1.60 V in Py vs. SCE.⁵ Decamethylchromocene with E_ox = −1.04 V vs. SCE in CH₃CN has strong donor properties⁶ and potentially can generate anionic species of 5,10,15-triarylcorroles. Now corroles and their metal complexes have been intensively studied in different fields⁴ but anionic species of these macrocycles neither have been obtained nor studied in solid form so far. The H₂TArylCor⁻ and H₂TArylCor˙²⁻ anions were only generated by the electrochemical reduction of free-base triarylcorroles in BN or Py and their optical properties were studied in solution.⁵

Scheme 1

In this work, we obtained the first crystalline charge transfer complex of free-base 5,10,15-triphenylcorrole with decamethylchromocene (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1) and analyzed its structure, and optical and magnetic properties. Cp*₂Cr reduces a free-base corrole but the H₃Cor˙⁻ radical anion loses a proton to form the H₂TPCor˙²⁻ radical dianions. Alternation of two paramagnetic Cp*₂Cr⁺ and H₂TPCor˙²⁻ ions in the π-stacks of 1 provides rather effective magnetic coupling between them. To understand the difference between reduced and deprotonated (H₂TPCor˙²⁻) and deprotonated (H₂TPCor⁻) anions, we also obtained the crystalline {cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) salt. The comparison of these anions shows that they have different optical and magnetic properties.

Results and discussion

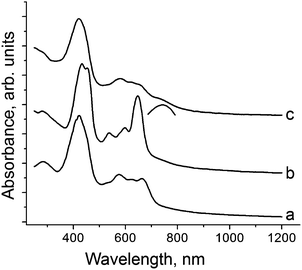
Starting H₃TPCor was synthesized⁸ by the benzaldehyde–pyrrole condensation in the water–methanol mixture in the presence of HCl followed by oxidative cyclization using p-chloranil in boiling chloroform. The product was purified by column chromatography. H₃TPCor is well soluble in o-dichlorobenzene to produce a blue-green solution. The addition of an excess of Cp*₂Cr under anaerobic conditions resulted in a color change to red-green. Slow mixing of the obtained solution with n-hexane over 1.5 months precipitated crystals on the walls of the diffusion tube. The solvent was decanted and crystals were washed with n-hexane to give elongated black planks in 43% yield. The crystals are very air sensitive, and their composition determined from X-ray diffraction on a single crystal is (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1). Hydrogen atoms bonded to nitrogen cannot be unambiguously localized in the structure analysis of 1. Nevertheless, the attempts to geometrically insert three hydrogen atoms in the planar corrole macrocycle result in very short H⋯H contacts between them (less than 1.4 Å). Hence, we suppose that only two hydrogen atoms remain in the center of the macrocycle and the third proton is removed. Starting H₃TPCor is stable in o-dichlorobenzene and interaction with Cp*₂Cr should provide the H₃TPCor˙⁻ radical anion which is not stable and loses a proton to form the radical H₂TPCor˙²⁻ dianion. Deprotonated H₂TPCor⁻ anions are not formed in 1 as we show below. To obtain salt 2 with the H₂TPCor⁻ anions, H₃TPCor was deprotonated by NaOH in o-dichlorobenzene in the presence of one equivalent of cryptand[2,2,2]. In spite of the fact that NaOH is completely insoluble in this solvent, cryptand[2,2,2] forms a stable complex with Na⁺ allowing exactly one equivalent of NaOH to be dissolved to deprotonate H₃TPCor and form greenish brown solution with the H₂TPCor⁻ anions. Slow mixing of the obtained solution with n-hexane over one month produced black blocks of {cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) whose composition was determined from X-ray diffraction analysis on a single crystal and was confirmed by elemental analysis (ESI†).

The solid state spectra of H₃TPCor, 1 and 2 in the UV-visible-NIR range are shown in Fig. 1. Starting H₃TPCor manifests absorption bands at 424 nm (the Soret band) and the split Q-band in the visible range at 575, 618 and 662 nm (Fig. 1a). Deprotonation results in essential modification of the optical spectrum. For 2, the intense Soret band is split into two bands positioned at 432 and 450 nm and the Q-band (537, 597 and 647 nm) becomes more pronounced since the intensity of the lowest energy band at 647 nm increases strongly (Fig. 1b). The spectra of deprotonated triarylcorrole anions (H₂TArylCor⁻) in Py show very similar features in the visible range including strongly increased intensity of the band at 643 nm.⁵ However, the Soret band remains unsplit in the solution spectra of H₂TArylCor⁻ and is observed at 439–440 nm ⁵ (its position is approximately intermediate between 432 and 450 nm).

Fig. 1 Spectra of starting H₃TPCor (a); salt {cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) (b); and complex (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1) (c) in the UV-visible-NIR range measured in KBr pellets prepared under anaerobic conditions.

The solid state spectrum of 1 differs from that of 2. It shows an intense Soret band at 421 nm and split Q-bands at 579, 614 and 644 nm (Fig. 1c). The band at 644 nm is of essentially lower intensity (Fig. 1c) than that in the spectrum of 2. The lowest energy band in the spectrum of 1 is observed as a shoulder with an approximate maximum at 750 nm (shown by an arc in Fig. 1c). On the whole, the spectrum of 1 is similar to that of electrochemically generated radical H₂TArylCor˙²⁻ dianions which shows a Soret band at 418 nm, relatively weak bands at 570–650 nm and the lowest energy band at 755 nm.⁵ Thus, the optical spectra allow one to suppose the formation of H₂TPCor˙²⁻ and H₂TPCor⁻ anions in 1 and 2, respectively, and their spectra are to a certain extent similar to the solution spectra of these anions.⁵

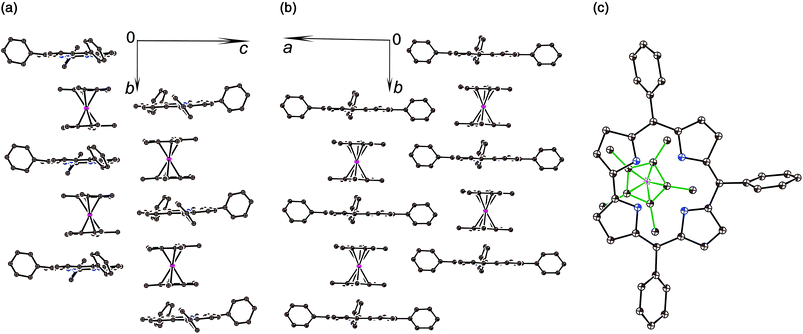
The crystal structures of 1 and 2 were analyzed at 110 K. The H₃TPCor macrocycles have a smaller coordination core in comparison with porphyrins, and the presence of three hydrogen atoms in this core results in essential repulsion between them. To avoid short H⋯H contacts, the macrocycle in a neutral state adopts a strongly nonplanar conformation.⁹ In contrast, the corrole macrocycle in H₂TPCor˙²⁻ is nearly planar in 1 with a slight deviation of only pyrrole nitrogen atoms from the 23-atom plane by 0.029–0.185 Å (Fig. 2a and b). Three hydrogen atoms cannot be inserted into the center of the planar corrole macrocycle due to very short H⋯H contacts (less than 1.4 Å). Therefore, we suppose that only two hydrogen atoms are preserved in H₂TPCor˙²⁻. In this case, the H⋯H distance of 2.152 Å indicates the absence of noticeable repulsion between hydrogen atoms. Most probably, the third proton can be localized in the structure of 1 as a counter cation.

Fig. 2 Crystal structure of complex 1: views on the π-stacks of alternating radical H₂TPCor˙²⁻ dianions and the Cp*₂Cr⁺ cations along the a- (a) and c-axes (b); projection of one half of the Cp*₂Cr⁺ cations (bonds are shown by green lines) on the TPCor plane (c). Hydrogen atoms are not shown.

The H₂TPCor˙²⁻ radical dianions and the Cp*₂Cr⁺ cations form π-stacking columns along the b axis (Fig. 2a and b). There is effective overlapping between the corrole and the Cp* ligand in 1 since the interplanar distance between them is only 3.42 Å and a dihedral angle is 0.95°. As a result, multiple van der Waals C,N⋯C,N contacts are formed between them in the 3.44–3.56 Å range. The relative orientation of half of the Cp*₂Cr⁺ cations to the TPCor macrocycle is shown in Fig. 2c. The Cp*₂Cr⁺ cations have a staggered conformation in 1 typical of decamethylmetallocenes. The average Cr–C(Cp*) bond length is 2.201(5) Å. This value is close to that of the Cp*₂Cr⁺ cations (the average Cr–C(Cp*) bond length is 2.176(3)–2.198(3) Å).^3c,d,11 These bonds are noticeably longer than those in neutral Cp*₂Cr (2.152(4) Å ¹²).

The deprotonation of H₃TPCor in 2 also provides a nearly planar shape of the H₂TPCor⁻ macrocycle since all atoms are positioned in the 23-atom corrole plane with maximal deviations of pyrrole nitrogen atoms by 0.005–0.110 Å. No essential repulsion is observed between the hydrogen atoms of H₂TPCor⁻ due to the 2.308–2.352 Å distances between them. Therefore, repulsion between the three hydrogen atoms of H₃TPCor is a reason for the non-planar shape of neutral free-base corrole macrocycles. Deprotonation restores its planar shape. Corrole planes form channels in 2 occupied by bulky cryptand[2,2,2](Na⁺) cations and arranged approximately along the a axis (Fig. S2†).

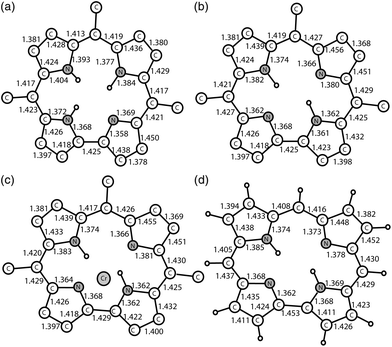
Previously, the alternation of the C–N(imine) and C–C(meso) bonds was found for the reduced phthalocyanine macrocycles in H₂Pc˙⁻ and {M(Pc˙³⁻)}˙⁻ and for the porphyrin radical trianions in Al^III(THF)₂(Porph˙³⁻), respectively.^3d,7,10 This alternation is realized in the H₂Pc˙⁻ radical anions (Fig. 4a) by such a way that short and long bonds belong to two oppositely located isoindole units. The difference between the short and long bonds is about 0.04 Å. This alternation is explained by the partial disruption of aromaticity of the Pc macrocycle during the transition from a stable 18 π-electron system of H₂Pc to a less stable 19 π-electron system of H₂Pc˙⁻.^3d,7 The lengths of the C–C and C–N bonds in neutral H₃TPCor,⁹ H₂TPCor⁻ and H₂TPCor˙²⁻ are shown in Fig. 3. It is seen that the alternation of the C–C(meso) bonds is also observed in H₂TPCor˙²⁻ with the appearance of short and long bonds (Fig. 4b). The short and long bonds are positioned similarly to those in H₂Pc˙⁻ (Fig. 4a) but one short bond is absent in H₂TPCor˙²⁻ (Fig. 4). The difference between the short and long bonds for H₂TPCor˙²⁻ (0.02 Å) is about two times smaller than that for H₂Pc˙⁻ (0.04 Å). The alternation is not observed for the deprotonated H₂TPCor⁻ anion (Fig. 3b) as well as for the deprotonated HPc⁻ anion⁷ due to the preservation of 18 π-electron systems in these anions. At the same time, pristine H₃TPCor also shows some alternation of the C–C(meso) bonds (Fig. 3a). Since H₃TPCor has a strong non-planar shape due to the repulsion of hydrogen atoms, we suppose that the partial disruption of aromaticity is also possible in this macrocycle.

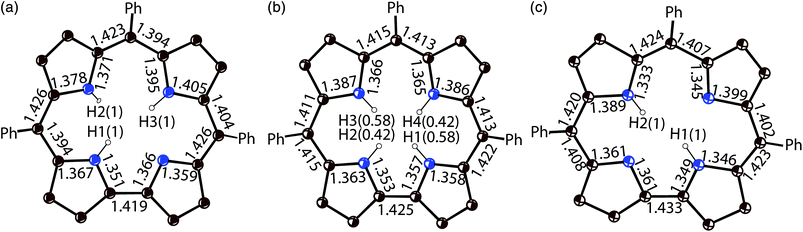Fig. 3 Bond length, position and occupancy (in parentheses) of hydrogen atoms in the center of the macrocycle for: (a) pristine H₃TPCor according to ref. 3; (b) deprotonated H₂TPCor⁻ anion in {cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) with two hydrogen atoms occupying four positions with the 0.58/0.42 occupancies; and (c) the radical H₂TPCor˙²⁻ dianion in (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1). Phenyl substituents of TPCor are omitted.

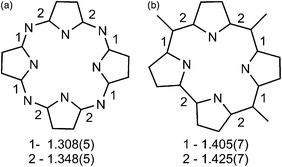Fig. 4 (a) Alternation of the C–N(imine) bonds in the H₂Pc˙⁻ radical anions according to ref. 7; (b) Alternation of the C–C(meso) bonds in the H₂TPCor˙²⁻ radical dianions in 1. The lengths of short (type 1) and long (type 2) bonds are also shown.

Fig. 5 shows the calculated structures of the meso-substituted H₃TPCor macrocycle (a), its deprotonated form (b), the structure of the H₂TPCor˙²⁻ macrocycle in the (H₂TPCor˙²⁻)(Cp*₂Cr⁺) complex (c) and the H₂Cor˙²⁻ radical dianion (d) (see the ESI† for details). The calculated structure of isolated H₃TPCor (Fig. 5a) is in good agreement with the experimental data of the molecular crystal (Fig. 3a). The average values of the C–N and C–C bonds are greater than the experimental values by 0.002 and 0.007 A, respectively. This difference remains at the same level for the deprotonated H₂TPCor⁻ anion (Fig. 5b). The geometry of the H₂TPCor˙²⁻ radical dianion was calculated in the complex with Cp*₂Cr⁺ to take into account the Coulomb field of the surrounding counterions (Fig. 5c). In this structure, only a small change of the mean values of the C–N and C–C bonds of 0.001 (−0.006) and 0.000 (0.000) Å, respectively, is observed (the experimental values are given in parentheses). In contrast, the larger divergence of the C–N and C–C bonds is observed in the calculated structure of isolated H₂TPCorr˙²⁻ (Fig. S3†), 0.012 and 0.021 Å, respectively, with respect to the experimental data. This calculation indicates an increase of the difference between the short and long C–C(meso) bonds in the macrocycle during the transition from H₂TPCorr⁻ to H₂TPCorr˙²⁻ from 0.060 (0.006) to 0.010 (0.020) Å (the experimental values are given in parentheses).

Fig. 5 Calculated structures of pristine H₃TPCor (a), the deprotonated H₂TPCor⁻ anion (b); the H₂TPCor˙²⁻ radical dianion in the (H₂TPCor˙²⁻)(Cp*₂Cr⁺) complex (c) and the H₂Cor˙²⁻ radical dianion for comparison (d).

The comparison of the geometry of the radical H₂Cor˙²⁻ and H₂TPCor˙²⁻ dianions (Fig. 5d and 5c, respectively) shows that the introduction of phenyl groups results in the systematic elongation of C–C(meso) bonds by 0.005 Å as the average. The excess electron in the radical dianions appears on the antibonding π-orbitals. As we discussed above for H₂Pc˙⁻ that provides the alternation of the C–C(meso) bonds due to partial disruption of the macrocycle aromaticity. The main geometric differences between H₂Cor˙²⁻ and H₂TPCor˙²⁻ are due to the stronger alternation of the C–C(meso) bonds for H₂Cor˙²⁻ (0.018 Å) than that for H₂TPCor˙²⁻ (0.010 Å). In fact, that is a consequence of a different electron density distribution for the meso-substituted form since approximately half of the additional negative charge in H₂TPCor˙²⁻ is distributed among the phenyl substituents. As a result, the effect of population of the antibonding π-orbitals on the macrocycle decreases. This effect can decrease the alternation of the C–C(meso) bonds in H₂TPCor˙²⁻ in comparison with H₂Cor˙²⁻ and even H₂Pc˙⁻. A similar effect is observed for the {Cu^II(F₁₆Pc˙³⁻)}˙⁻ radical anions in which an excess of negative charge is to a great extent delocalized among the acceptor fluoro-substutients.¹³ Another anomaly is the significant difference in the lengths of the C–N bonds within one pyrrole ring of H₂TPCor˙²⁻ in 1, reaching 0.054 Å (Fig. 3c). The common reason for this phenomenon is the lability of the electron system of the radical dianion and the significant effect of the Coulomb field of the surrounding counterions.

Two counter cations are required for the electroneutrality of 1 with the radical H₂TPCor˙²⁻ dianions. One cation is Cp*₂Cr⁺ and the other cation should be H⁺ removed from the macrocycle. The reaction was carried out under very dry conditions and in a base (B) free medium to stabilize H⁺ in the hydronium (H₃O⁺) or HB⁺ cations (residual electron density in 1 is too small (0.87 e) to be attributed to H₃O⁺). Therefore, most probably, the proton is localized somewhere in the structure of 1. One of the possible positions is near the two chloride substituents of o-C₆H₄Cl₂. In this case, the Cl–H⁺ distance would be about 1.715 Å, which is reasonable for the interaction of such a type. The (Cl⋯H⋯Cl)⁻ anions with strong (Cl⁻)⋯(H⁺) hydrogen bonds are known and have close Cl–H⁺ distances of 1.56–1.64 Å.¹⁴ According to our calculations, the binding of a proton to o-C₆H₄Cl₂ leads to the formation of strong Cl⋯(H⁺) hydrogen bonds of 1.573 Å length and the elongation of the C–Cl bonds in this molecule by about 0.036 Å. These data agree with the experimental results since the C–Cl bonds for the o-C₆H₄Cl₂ molecules in 1 forming hydrogen bonds with H⁺ are elongated by 0.03 Å in comparison with those for the nonbonded o-C₆H₄Cl₂ molecules. In addition, the formation of strong Cl⋯(H⁺) hydrogen bonds leads to the appearance of new broad absorption bands in the theoretical IR spectrum at 770 and 1050 cm⁻¹. Indeed, broad bands are observed at about 800 and 1040 cm⁻¹ in the experimental IR spectrum of 1 (Fig. S1†). The calculation of the structure of the H₃TPCor˙⁻ radical anion shows its nonplanar character as expected. This calculation allows one to find the proton affinity for the H₂TPCor˙²⁻ radical dianion which is equal to 16.8 eV. This value significantly exceeds the affinity for the proton of the o-C₆H₄Cl₂ molecule, 7.2 eV. A logical question arises is to how such a weak base as o-C₆H₄Cl₂ can hold a proton in the presence of a stronger H₂TPCor˙²⁻ base. One of the explanations is that the acceptance of the proton by the o-C₆H₄Cl₂ molecule is energetically favorable due to the gain in the Coulomb energy for the crystal lattice.

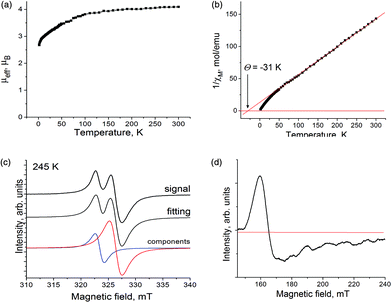
The magnetic properties of 1 were studied by EPR and SQUID techniques. The effective magnetic moment is equal to 4.10μ_B at 300 K (Fig. 6a), which is close to the calculated magnetic moment for a system of non-interacting S = 3/2 spins from Cp*₂Cr⁺ and S = 1/2 spins from H₂TPCor˙²⁻ (μ_eff = 4.24μ_B)_. The magnetic moment decreases below 120 K (Fig. 6a) most probably due to the antiferromagnetic coupling of spins. The reciprocal molar magnetic susceptibility of 1 is linear in the 50–300 K range allowing the Weiss temperature to be determined as −31 K (Fig. 6b). This value indicates a strong antiferromagnetic coupling of spins in the π-stacks containing alternating Cp*₂Cr⁺ and H₂TPCor˙²⁻ ions. However, long-range magnetic ordering is not observed in 1 down to 1.9 K. It should be noted that the observed magnetic coupling in 1 is essentially stronger than that in the previously studied (Cp*₂Cr⁺)(H₂Pc˙⁻)·4C₆H₄Cl₂ complex with free-base phthalocyanine radical anions which also contains π-stacks of alternating Cp*₂Cr⁺ and H₂Pc˙⁻ ions.^3d From this viewpoint, free-base corroles can be more effective magnetic mediators than free-base phthalocyanines.

Fig. 6 Magnetic data of 1: temperature dependencies of the effective magnetic moment (a) and reciprocal molar magnetic susceptibility (b). EPR signals are attributed to the H₂TPCor˙²⁻ dianions (c) and the Cp*₂Cr⁺ cations with the S = 3/2 spin state (d).

The EPR spectra of polycrystalline 1 confirm the presence of two paramagnetic species. An intense and relatively narrow signal is observed at 323–325 mT. This signal contains two lines with g₁ = 1.9971 and the linewidth (ΔH) of 1.58 mT and g₂ = 1.9790 and ΔH = 2.28 mT at 292 K (Fig. 6c shows this signal at 245 K) and can be attributed to the paramagnetic radical H₂TPCor˙²⁻ dianions. Both signals are preserved down to 4.2 K. Below 90 K, the abrupt decrease of g-factors is observed, and both lines are broadened and shifted to higher g-factor values at T < 30 K (Fig. S4a and S4b†) due to the antiferromagnetic coupling of spins. Obviously, both lines originate from the same paramagnetic species since they show similar temperature dependencies of g-factors and linewidths (Fig. S4a and S4b†). It should be noted that the EPR signal from H₂TPCor˙²⁻ is broader (ΔH = 1.5–2.3 mT) than those from the H₂Pc˙⁻ radical anions (ΔH = 0.2–0.6 mT).^3d,10a,b At the same time, complex 1 as well as the H₂Pc˙⁻ salts do not display the super hyperfine splitting characteristic of some oxidized porphyrins and explained by the interaction of spins with four coordinated nitrogen atoms.¹⁵ Most probably, the measurement of the diluted samples is needed to observe such splitting.

The Cp*₂Cr⁺ cations show a broad asymmetric EPR signal with the main component at g₃ = 3.88 and ΔH = 12.0 mT at 292 K (signal at 245 K is shown in Fig. 3d). The strong asymmetry of the signal could be explained by the polycrystallinity of the sample. Generally, the Cp*₂Cr⁺ cations with the S = 3/2 spin state manifest similar EPR signals in the complexes with different anions, and the strong asymmetry of the signal is also observed in some cases.¹⁶ The signal from Cp*₂Cr⁺ has a nearly temperature independent g-factor and a linewidth down to 4.2 K.

Crystals of 2 were also studied by the EPR technique at room temperature and at 4.2 K. They are EPR silent at both temperatures due to the diamagnetism of deprotonated H₂TPCor⁻ anions. Similarly, the deprotonated HPc⁻ anions were diamagnetic and EPR silent.⁷ The removal of one proton from the macrocycle does not change the number of π-electrons and preserves the diamagnetic state of the macrocycle.

Experimental

Materials

Free-base 5,10,15-triphenylcorrole (H₃TPCor) was synthesized according to ref. 8. Decamethylchromocene (Cp*₂Cr, >95%) was purchased from Strem. Cryptand[2,2,2] was purchased from TCI Reagents. o-Dichlorobenzene (C₆H₄Cl₂, Acros) was distilled over CaH₂ under reduced pressure and n-hexane was distilled over Na/benzophenone. Solvents were degassed and stored in an MBraun 150B-G glove box. Salt 1 was synthesized and stored in the glove box under a controlled atmosphere containing less than 1 ppm of water and oxygen. KBr pellets used for the IR and UV-visible-NIR analyses were prepared in the glove box. Magnetic measurements were performed on polycrystalline samples of 1 and 2 sealed in a 2 mm quartz tube in anaerobic conditions under ambient pressure.

General

UV-visible-NIR spectra were recorded in KBr pellets on a PerkinElmer Lambda 1050 spectrometer in the 250–2500 nm range. FT-IR spectra were obtained in KBr pellets on a PerkinElmer Spectrum 400 spectrometer (400–7800 cm⁻¹). EPR spectra were recorded for a polycrystalline sample of 1 from room temperature (RT) down to 4.2 K and for a polycrystalline sample of 2 at RT and 4.2 K on a JEOL JES-TE 200 X-band ESR spectrometer equipped with a JEOL ES-CT470 cryostat. A Quantum Design MPMS-XL SQUID magnetometer was used to measure the static magnetic susceptibility of 1 at 100 mT magnetic field under cooling and heating conditions in the 300–1.9 K range. A sample holder contribution and core temperature independent diamagnetic susceptibility (χ_d) were subtracted from the experimental values. The χ_d values were estimated by the extrapolation of the data in the high-temperature range by fitting the data using the following expression: χ_M = C/(T − Θ) + χ_d, where C is the Curie constant and Θ is the Weiss temperature. The effective magnetic moment (μ_eff) was calculated using the following formula: μ_eff = (8·χ_M·T)^1/2.

Synthesis

Crystals of 1 and 2 were obtained by the diffusion technique. A reaction mixture was filtered into a 1.8 cm-diameter, 50 mL glass tube with a ground glass plug, and then 30 mL of n-hexane was layered over the solution. Slow mixing of the solutions resulted in the precipitation of crystals over 1–1.5 months. The solvent was then decanted from the crystals, and they were washed with n-hexane. The composition of the obtained compound was determined from X-ray diffraction analysis on a single crystal. Several crystals from one synthesis were found to consist of a single crystalline phase.

Crystals of (Cp*₂Cr⁺)(H⁺)(H₂TPCor˙²⁻)·C₆H₄Cl₂ (1) were obtained via the reaction of H₃TPCor (22 mg, 0.042 mmol) with an excess of Cp*₂Cr (20 mg, 0.0562 mmol) in 16 mL of o-dichlorobenzene upon stirring at 80 °C for 24 hours. The color of the solution changed from blue-green to red-green. The obtained solution was cooled down to room temperature and filtered into the tube for diffusion. Black planks of 1 were obtained in 43% yield.

{Cryptand[2,2,2](Na⁺)}(H₂TPCor⁻)·0.5C₆H₄Cl₂ (2) was obtained via the reaction of H₃TPCor (22 mg, 0.042 mmol) with an excess of powdered NaOH (30 mg, 0.75 mmol) and one equivalent of cryptand[2,2,2] (16 mg, 0.042 mmol) in 16 mL of o-dichlorobenzene upon stirring at 80 °C for 24 hours. The color of the solution changed from blue-green to greenish brown. The obtained solution was cooled down to RT and filtered into the tube for diffusion. Black blocks of 2 were obtained in 79% yield. The composition of 2 was determined from X-ray diffraction on a single crystal and was confirmed via elemental analysis: anal. calcd for C₅₈H₆₃ClN₆NaO₆, M_r = 998.58: C 69.76, H 6.30, N 8.41, Cl 3.55; found: C 69.54, H 6.24, N 8.21, Cl 3.36.

X-ray crystal structure determination

Crystal data of 1 at 110(1) K: C₆₃H₅₉Cl₂CrN₄, M_r = 995.04 g mol⁻¹, black plank, monoclinic, C2/c, a = 26.245(3), b = 10.6383(6), c = 36.765(3) Å, β = 90.065(8)°, V = 10 265.0(15) ų, Z = 8, d_calc = 1.288 g cm⁻³, μ = 0.372 mm⁻¹, F(000) = 4184, 2θ_max = 52.742°, reflections measured 44 240, unique reflections 9723, reflections with I > 2σ(I) = 5747, parameters refined 669, restraints 271, R₁ = 0.0787, wR₂ = 0.1959, G.O.F. = 1.015, CCDC 1552215.†

Crystal data of 2 at 110(1) K: C₅₈H₆₃ClN₆NaO₆, M_r = 998.58 g mol⁻¹, black block, monoclinic, P2₁/n, a = 13.0302(2), b = 18.0323(3), c = 21.3928(4) Å, β = 96.142(2)°, V = 4997.69(15) ų, Z = 4, d_calc = 1.327 g cm⁻³, μ = 0.145 mm⁻¹, F(000) = 2116, max. 2θ_max = 54.206°, reflections measured 55 350, unique reflections 11 012, reflections with I > 2σ(I) = 9172, parameters refined 674, restraints 246, R₁ = 0.0462, wR₂ = 0.1332, G.O.F. = 1.032, CCDC 1552216.†

X-ray diffraction data of 1 and 2 at 110(1) K were collected on an Oxford diffraction “Gemini-R” CCD diffractometer with graphite monochromated MoK_α radiation using an Oxford Instrument Cryojet system. Raw data reduction to F² was carried out using CrysAlisPro, Oxford Diffraction Ltd. The structures were solved by direct methods and refined by the full-matrix least-squares method against F² using SHELX-2013.¹⁷ Non-hydrogen atoms were refined anisotropically. The positions of hydrogen atoms were calculated geometrically. One solvent C₆H₄Cl₂ molecule with the 0.5 occupancy is positioned in both 1 and 2 in the inversion centers and is statistically disordered between two orientations. The positions of hydrogen atoms in the center of H₂TPCor˙²⁻ in 1 were calculated geometrically. The insertion of three hydrogen atoms in the center of the corrole macrocycle results in very short H⋯H contacts (less than 1.4 Å). Therefore, we suppose that only two hydrogen atoms are positioned in the center of the corrole macrocycle in 1. The third hydrogen atom can be present in the crystal structure of 1 as a countercation but its exact position could not be unambiguously determined. Therefore, this hydrogen atom was omitted from the cif file. Hydrogen atoms in the center of H₂TPCor⁻ in 2 are found at two positions near two oppositely located pyrrole nitrogen atoms with the 0.58(2)/0.48(2) occupancies (as shown in Fig. 3b). To keep the anisotropic thermal parameters of the disordered fragments within the reasonable limits, the displacement components were restrained using the ISOR, SIMU and DELU SHELXL instructions. This resulted in 271 and 246 restraints used for the refinement of the crystal structures of 1 and 2.

Theoretical calculations

Theoretical calculations were performed using the PBE density functional method¹⁸ and the Λ2 basis¹⁹ of cc-pVTZ quality. Atomic distribution of charge was determined by the Hirschfeld method.²⁰ All calculations were performed using the PRIRODA program package²¹ at the Joint Supercomputer Center of the Russian Academy of Sciences.

Conclusions

In conclusion, two types of anionic forms of 5,10,15-triphenylcorroles were obtained and studied in the crystalline state for the first time: diamagnetic deprotonated H₂TPCor⁻ anions and paramagnetic deprotonated and reduced H₂TPCor˙²⁻ dianions. In both cases, deprotonation provides a nearly planar shape of the corrole macrocycle unlike the neutral corrole, which has a non-planar shape due to the strong repulsion of hydrogen atoms.⁹ The H₃TPCor˙⁻ radical anions cannot be obtained in the solid state due to their instability. Paramagnetic radical H₂TPCor˙²⁻ dianions are synthetically available when strong reductants like decamethylchromocene are used. Therefore, corroles can also be used in the design of magnetic and probably conducting assemblies in the reduced form. Until now, such assemblies have been developed with phthalocyanines and porphyrins only.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Russian Science Foundation grant no. 17-13-01215, JSPS KAKENHI Grant Number JP26288035, and the JST (ACCEL) 27 (100150500010) project.

Notes and references

1. (a) C. G. Claessens, W. J. Blau, M. Cook, M. Hanack, R. J. M. Nolte, T. Torres and D. Wöhrle, Monatsh. Chem., 2001, 132, 3–11; (b) D. Wöhrle, G. Schnurpfeil, S. G. Makarov, A. Kazarin and O. N. Suvorova, Macroheterocycles, 2012, 5, 191–202.
2. (a) J. L. Petersen, C. S. Schramm, D. R. Stojakovic, B. M. Hoffman and T. J. Marks, J. Am. Chem. Soc., 1977, 99, 286–288; (b) H. Hasegawa, T. Naito, T. Inabe, T. Akutagawa and T. Nakamura, J. Mater. Chem., 1998, 8, 1567–1570; (c) T. Inabe and H. Tajima, Chem. Rev., 2004, 104, 5503–5534.
3. (a) J. S. Miller, C. Vazquez, J. C. Calabrese, R. S. McLean and A. J. Epstein, Adv. Mater., 1994, 6, 217–221; (b) W. Hibbs, D. K. Rittenberg, K.-I. Sugiura, B. M. Burkhart, B. G. Morin, A. M. Arif, L. Liable-Sands, A. L. Rheingold, M. Sundaralingam, A. J. Epstein and J. S. Miller, Inorg. Chem., 2001, 40, 1915–1925; (c) D. V. Konarev, L. V. Zorina, S. S. Khasanov, E. U. Hakimova and R. N. Lyubovskaya, New J. Chem., 2012, 36, 48–51; (d) D. V. Konarev, S. S. Khasanov, M. Ishikawa, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Dalton Trans., 2017, 46, 3492–3499.
4. (a) I. Aviv and Z. Gross, Chem. Commun., 2007, 1987–1999; (b) R. Paolesse, Synlett, 2008, 15, 2215–2230; (c) R. Orłowski, D. Gryko and D. T. Gryko, Chem. Rev., 2017, 117, 3102–3137.
5. J. Shen, J. Shao, Z. Ou, W. E. B. Koszarna, D. T. Gryko and K. M. Kadish, Inorg. Chem., 2006, 45, 2251–2265.
6. J. L. Robbins, N. Edelstein, B. Spencer and J. C. Smart, J. Am. Chem. Soc., 1982, 104, 1882–1893.
7. D. V. Konarev, S. S. Khasanov and R. N. Lyubovskaya, Asian J. Org. Chem., 2017, 6, 1028–1033.
8. B. Koszarna and D. T. Gryko, J. Org. Chem., 2006, 71, 3707–3717.
9. (a) T. Ding, J. D. Harvey and C. J. Ziegler, J. Porphyrins Phthalocyanines, 2005, 9, 22–27; (b) R.-B. Du, C. Liu, D.-M. Shen and Q.-Y. Chen, Synlett, 2009, 2701–2705.
10. (a) D. V. Konarev, L. V. Zorina, S. S. Khasanov, A. L. Litvinov, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Dalton Trans., 2013, 42, 6810–6816; (b) D. V. Konarev, A. V. Kuzmin, M. A. Faraonov, M. Ishikawa, Y. Nakano, S. S. Khasanov, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Chem. – Eur. J., 2015, 21, 1014–1028; (c) J. A. Cissell, T. P. Vaid and A. L. Rheingold, Inorg. Chem., 2006, 45, 2367–2369.
11. (a) J. S. Miller, R. S. Mclean, C. Vazquez, J. C. Calabrese, F. Zuo and A. J. Epstein, J. Mater. Chem., 1993, 3, 215–218; (b) D. V. Konarev, S. S. Khasanov, A. Otsuka and G. Saito, J. Am. Chem. Soc., 2002, 124, 8520–8521.
12. J. Blümel, M. Herker, W. Hiller and F. H. Köhler, Organometallics, 1996, 15, 3474–3476.
13. D. V. Konarev, S. S. Khasanov, A. V. Kumin, Y. Nakano, M. Ishikawa, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Inorg. Chem., 2017, 56, 1804–1813.
14. (a) J. S. Swanson and J. M. Williams, Inorg. Nucl. Chem. Lett., 1970, 6, 271–276; (b) J. L. Atwood, S. G. Bott, A. W. Coleman, K. D. Robinson, S. B. Whetstone and C. M. Means, J. Am. Chem. Soc., 1987, 109, 8100–8101.
15. D. V. Konarev, S. S. Khasanov, G. Saito, A. Otsuka, Y. Yoshida and R. N. Lyubovskaya, J. Am. Chem. Soc., 2003, 125, 10074–10083.
16. (a) A. Fidalgo-Marijuan, G. Barandika, B. Bazán, M. K. Urtiaga, E. S. Larrea, M. Iglesias, L. Lezamab and M. I. Arriortua, Dalton Trans., 2015, 44, 213–222; (b) G. Nandia and S. Sarkar, J. Porphyrins Phthalocyanines, 2014, 18, 1–8.
17. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–120.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
19. D. N. Laikov, Chem. Phys. Lett., 2005, 416, 116–120.
20. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
21. D. N. Laikov, Chem. Phys. Lett., 1997, 281, 151–156.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1552215 and 1552216. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02901b

---