Open Access Article
Open Access ArticleMono-BHT heteroleptic magnesium complexes: synthesis, molecular structure and catalytic behavior in the ring-opening polymerization of cyclic esters†
I. E.
Nifant'ev
 *ab,
A. V.
Shlyakhtin
a,
V. V.
Bagrov
a,
M. E.
Minyaev
b,
A. V.
Churakov
c,
S. G.
Karchevsky
d,
K. P.
Birin
e and
P. V.
Ivchenko
*ab,
A. V.
Shlyakhtin
a,
V. V.
Bagrov
a,
M. E.
Minyaev
b,
A. V.
Churakov
c,
S. G.
Karchevsky
d,
K. P.
Birin
e and
P. V.
Ivchenko
 ab
ab
aM.V. Lomonosov Moscow State University, Department of Chemistry, Moscow, Russian Federation. E-mail: inif@org.chem.msu.ru; ilnif@yahoo.com
bA.V. Topchiev Institute of Petrochemical Synthesis, Russian Academy of Sciences, Moscow, Russian Federation
cN.S. Kurnakov Institute of General and Inorganic Chemistry, Russian Academy of Sciences, 31 Leninsky Prospect, 119991, Moscow, Russian Federation
dInstitute of Petroleum Refining and Petrochemistry of the Republic of Bashkortostan, 12 Iniciativnaya Str., 450065, Ufa, Russian Federation
eA.N. Frumkin Institute of Physical Chemistry and Electrochemistry, Russian Academy of Sciences, 31 Leninsky Prospect, Building 4, 119071, Moscow, Russian Federation
First published on 29th August 2017
Abstract
Numerous heteroleptic 2,6-di-tert-butyl-4-methylphenolate (BHT) magnesium complexes have been synthesized by treatment of (BHT)MgBu(THF)2 with various alcohols. Molecular structures of the complexes have been determined by X-ray diffraction. The magnesium coordination number in [(BHT)Mg(μ-OBn)(THF)]2 (3) and [(BHT)Mg(μ-O-tert-BuC6H4)(THF)]2 (4) is equal to 4. Complexes formed from esters of glycolic and lactic acids, [(BHT)Mg(μ-OCH2COOEt)(THF)]2 (5) and [(BHT)Mg(μ-OCH(CH3)COOCH2COOtBu)(THF)]2 (6) contain chelate fragments with pentacoordinated magnesium. Compounds 3–6 contain THF molecules coordinated to magnesium atoms. Complex {(BHT)Mg[μ-O(CH2)3CON(CH3)2]}2 (7) does not demonstrate any tendency to form an adduct with THF. It has been experimentally determined that complexes 3 and 5 are highly active catalysts of lactide polymerization. The activity of 4 is rather low, and complex 7 demonstrates moderate productivity. According to DOSY NMR experiments, compounds 3 and 5 retain their dimeric structures even in THF. The free energies of model dimeric [(DBP)Mg(μ-OMe)(Sub)]2 and monomeric (DBP)Mg(OMe)(Sub)2 products on treatment of [(DBP)Mg(μ-OMe)(THF)]2 with a series of σ-electron donors (Sub) have been estimated by DFT calculations. These results demonstrate that the substitution of THF by Sub in a dimeric molecule is an energetically allowed process, whereas the dissociation of dimers is energetically unfavorable. DFT modeling of ε-CL and (DL)-lactide ROP catalyzed by dimeric and monomeric complexes showed that a cooperative effect of two magnesium atoms occurs within the ROP for binuclear catalytic species. A comparison of the reaction profiles for ROP catalyzed by binuclear and mononuclear species allowed us to conclude that the binuclear mechanism is favorable in early stages of ROP initiated by dimers 3 and 5.
Introduction
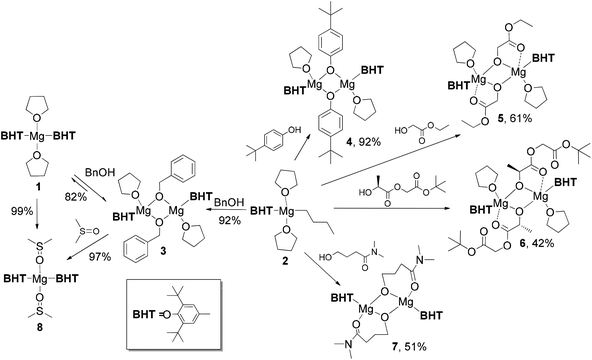
Research and development of biodegradable and biocompatible polymers are of great interest from the perspective of designing new materials, which could reduce adverse environmental and health effects associated with their manufacture, use, and end-of-life properties.1–10 Their applications span a wide field, ranging from green wrapping materials and fibres11–13 to surgical polymers, tissue engineering, drug delivery and other biomedical applications.5,14–18 The most frequently used biomedical polymers comprise homo- and copolymers of poly(lactic acid) (PLA), poly(glycolic acid) (PGA) and poly-(ε-caprolactone) (PCL).19–24 Their synthesis via ring-opening polymerization (ROP) is most commonly conducted with tin(II) 2-ethylhexanoate Sn(Oct)2.25–28 Due to potential toxicity and unknown long-term effects of Sn2+ in tissues, the search for non-toxic and effective ROP catalysts for the purpose of biopolymer synthesis is of great interest. Derivatives of “biometals”, i.e., Mg, Ca, Al and Zn, attract research attention due to their synthetic availability, low toxicity, and variable catalytic properties.29–37Among “biometal” complexes, various magnesium alkoxides attract attention due to their high productivity38,39 and facile synthesis from readily available organomagnesium compounds. The main problem in obtaining and using Mg-based ROP catalysts is the tendency of magnesium alkoxides to aggregate and form oligomeric and polymeric structures (Scheme 1).40–43 Various types of chelating ligands are usually applied to prevent aggregation.38,39,44–47 Alternatively, the aggregation can be prevented using bulky phenols as ligands at the magnesium atom (Scheme 1). 2,6-Di-tert-butyl-4-methylphenol (butylated hydroxytoluene, BHT) seems the most attractive phenol due to its availability. Bis-aryloxy complex (BHT)2Mg(THF)2 (1)48 activated by alcohols was effectively used in the ROP of lactide,49 ε-caprolactone50 and ω-pentadecalactone.51,52
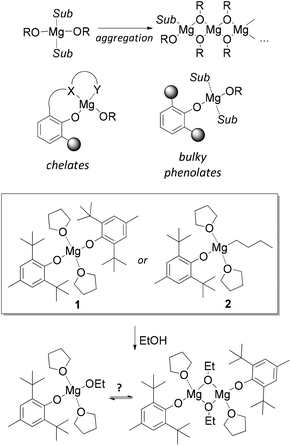 | ||
| Scheme 1 Top: Magnesium alkoxide aggregation and prospective types of alkoxy-Mg catalysts. Middle and bottom: Monomeric and dimeric BHT-ethoxy magnesium complexes. | ||
In our recent work,53 we reported the synthesis, molecular structure and catalytic properties of the first well-defined dimeric heteroleptic BHT-alkoxy magnesium complex [(BHT)Mg(μ-OEt)(THF)]2 and compared its catalytic properties with those of the monomeric heteroleptic complex (BHT)Mg(OR)(THF)2, which can be generated in situ by interaction of EtOH either with 1 or with (BHT)MgBu(THF)2 (2) (Scheme 1). We determined that the catalytic properties of well-defined dimeric and generated monomeric species differ greatly. However, the chemical origin of this difference, the geometry of heteroleptic BHT-derived magnesium complexes and their tendency toward monomeric or dimeric structure formation remained unclear.
The present work is devoted to the synthesis of heteroleptic BHT-Mg-OR complexes containing various types of alkoxide ligands (RO) and to elucidation of their molecular structure in the solid state and in solution. Experimental study is complimented with evaluation of the thermodynamics of ligand exchange at the magnesium center and of the dissociation of dimeric complexes. Moreover, we performed comparative DFT modeling of ε-CL and DL-lactide ROP catalyzed by dimeric and monomeric BHT-Mg complexes. These results demonstrated the feasibility of both mechanisms of ROP of cyclic esters and allowed us to explain some of our experimental data.
Experimental
(BHT)2Mg(THF)2 (1) was prepared using the modified method of Ittel.48 [(BHT)Mg(n-Bu)(THF)2] (2) and [(BHT)Mg(n-Bu)]2 were synthesized according to the literature procedure.53Synthetic protocols and NMR spectra of BHT magnesium complexes 3–8 as well as polymerization experiment details are given in ESI.†
Corresponding CCDC numbers are 1463808, 1545641–1545643, 1545645, 1545646, 1545648, and 1545650† (for details see ESI†).
Results and discussion
Synthesis and solid state structures of BHT magnesium complexes
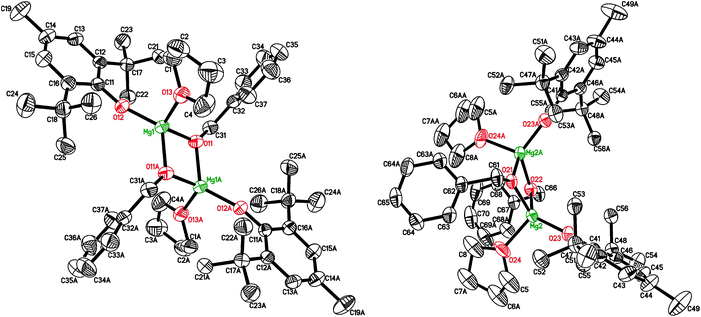
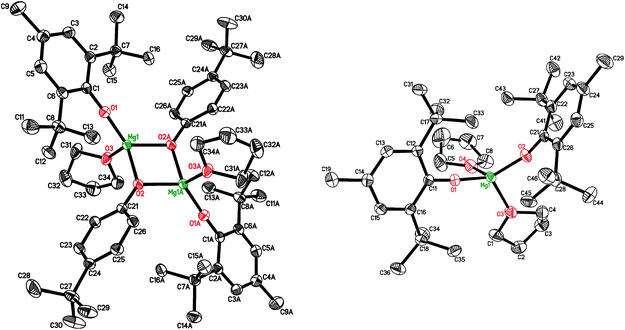
Earlier, we elaborated two alternative approaches to synthesize dimeric complex [(BHT)Mg(μ-OEt)(THF)]2 by using either reversible reaction between (BHT)2Mg(THF)2 (1) and EtOH (yield 66%) or an irreversible reaction of the heteroleptic aryloxy–alkyl complex (BHT)Mg(n-Bu)(THF)2 (2) with ethanol (yield 94%).53 In the present work, we have determined that a structurally analogous benzyloxy derivative, [(BHT)Mg(μ-OBn)(THF)]2 (3), can be obtained according to these two methods in yields of 82% and 92%, respectively (Scheme 2). Product 3, obtained via reaction of 1 with BnOH, contained an admixture of benzyl alcohol and needed additional purification by recrystallization. Therefore to prepare compounds 4–7 we have used a method based on alcoholysis of the BHT-Mg-butyl complex 2 (Scheme 1). Complexes 4–7 were isolated in high yields as crystalline substances, which allowed us to study them by X-ray analysis.The crystal structure of [(BHT)Mg(μ-OBn)(THF)]2 (3) contains two different isomers (Fig. 1, see ESI† for details) with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the crystal lattice. In both dimeric molecules, the Mg atoms are in a distorted tetrahedral environment, possessing magnesium coordination number CNMg = 4. Two bridging benzyl groups connect two Mg atoms, forming a flat Mg2O2 rhomboid core. Both molecules exhibit the shortest distances for Mg–OBHT bonds, and the longest for Mg–OTHF (see ESI†). The trans-conformer 3 (Fig. 1, left) is structurally similar to previously published [(BHT)Mg(μ-OEt)(THF)]2
1 ratio in the crystal lattice. In both dimeric molecules, the Mg atoms are in a distorted tetrahedral environment, possessing magnesium coordination number CNMg = 4. Two bridging benzyl groups connect two Mg atoms, forming a flat Mg2O2 rhomboid core. Both molecules exhibit the shortest distances for Mg–OBHT bonds, and the longest for Mg–OTHF (see ESI†). The trans-conformer 3 (Fig. 1, left) is structurally similar to previously published [(BHT)Mg(μ-OEt)(THF)]2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 and dimeric BHT-guanidine complexes.54
53 and dimeric BHT-guanidine complexes.54
Bis(aryloxy) magnesium heteroleptic complex [(BHT)Mg(μ-OC6H4tertBu)(THF)]2 (4) was obtained in 92% yield via reaction of 2 with 4-tert-butylphenol in the presence of THF (Scheme 2). The molecular structures of 4 (Fig. 2, left) and the symmetric bis-aryloxy-complex (BHT)2Mg(THF)2 (1) (Fig. 2, right) were determined by X-ray diffraction. For both complexes CNMg = 4. The X-ray data for the closest analogue of 1, (DBP)2Mg(THF)2 (DBP is the 2,6-di-tert-butylphenoxide anion), have been published.55 The key structural parameters of complex 1 and (DBP)2Mg(THF)2 are nearly identical.
 | ||
| Fig. 2 Molecular structures of [(BHT)Mg(μ-OC6H4tertBu)(THF)]2 (4, left) and (BHT)2Mg(THF)2 (1, right). | ||
Unlike [(ArO)Mg(μ-ArO)]2 (ArO = BHT, DBP), which form mononuclear complexes [(ArO)2Mg(THF)2] upon solvation with THF,48 less sterically hindered [(BHT)Mg(μ-OC6H4tertBu)(THF)]2 (4, Fig. 2) has a flat Mg2O2 rhomboid core (for details see ESI†) and does not display any tendencies toward monomer formation even in the presence of THF. The molecule is similar to trans-[(BHT)Mg(μ-OBn)(THF)]2 (3, Fig. 1, left) described above.
The reaction of 2 with ethyl glycolate, HO-CH2COOEt, yielded a dimeric complex [(BHT)Mg(μ-OCH2COOEt)(THF)]2 (5, Scheme 2). According to the X-ray data (Fig. 3, ESI†), complex 5 contains an ethyl glycolate fragment in the μ–κ1O:κ2O,O′-semi-bridging coordination mode: the oxygen atom of the hydroxy group is bound to both Mg atoms, whereas the O-atom of the carboxy group is coordinated to only one of the magnesium atoms, making CNMg = 5. To the best of our knowledge, 5 is the first example of an aryloxy-glycolate magnesium complex characterized by X-ray diffraction.
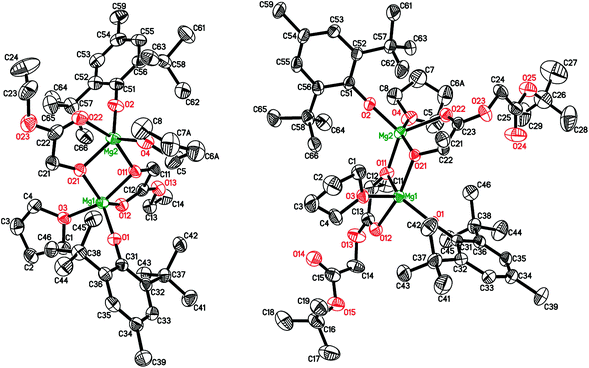 | ||
| Fig. 3 Molecular structures of [(BHT)Mg(μ-OCH2COOEt)(THF)]2 (5, left) and [(BHT)Mg(μ-OCH(CH3)COOCH2COOtBu)(THF)]2 (6, right). | ||
The structure of the complex formed by the reaction of 2 with HO-CH2COOEt depends on the reaction conditions. The slow diffusion of THF solutions of 2 and HOCH2COOEt yielded crystals of [Mg6(BHT)2(OCH2COOEt)10](THF)3 possessing an unusual Mg6O10 tetracubic core. The yield of this product was only 14%. However, due to poor crystal data, its crystal structure (see ESI†) was not deposited to the CSD.56,57
During lactide polymerization, various coordination modes of the growing polymeric chain to the metal atom are possible. Formation of such chelates is critically important for understanding the mechanism of coordination catalysis for the ROP of lactides.58 The molecular structure of glycolate and lactate complexes of Al,59–64 Mg,65 Ga,66 Y,67 and Zn68 have been determined for the “X-ray modeling” of the lactide polymerization mechanism. As it has been earlier determined by X-ray diffraction analysis for Al complexes, the μ–κ1:κ2 coordination type of the O-CHMeC(O)OCHMeCOOR fragment with a formation of five-membered chelates is observed in lactide ring-opening products.61,64 To determine the coordination mode in lactide polymerization by BHT-Mg complexes, we have synthesized in 42% yield crystalline dimer 6 (Scheme 2) – a product of the interaction of 2 with (RS) HO-CHMeCOOCH2COOtBu. The structure of 6 (Fig. 3) shows that the preferable product is a five-membered chelate fragment with coordination of the closest carbonyl group to the magnesium atom. Compounds 5 and 6 have two non-coordinating solvent molecules in crystal channels. The non-coordinating molecules in crystals of 5 are highly disordered, therefore they have been deleted from the crystallographic model by the SQUEEZE method. 1H and 13C{1H} NMR studies have confirmed that these molecules are THF and hexane in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.
1 ratio.
The CNMg in chelate heteroleptic complexes apparently depends on the geometry and the donor properties of the RO ligand. We reacted 2 with N,N-dimethyl-γ-hydroxybutyramide in a non-coordinating solvent (toluene) and in the presence of THF. Dimeric crystalline products [(BHT)Mg(μ-OCH2CH2CH2CONMe2)]2 (7) and [(BHT)Mg(μ-OCH2CH2CH2CONMe2)]2(THF)3 (7′) were isolated from the reaction mixtures (Scheme 2). We studied both complexes by X-ray diffraction and determined that molecule 7 has a μ–κ1O:κ2O,O′ semibridging ligand coordination mode (Fig. 4) similar to that of 5 and 6. Surprisingly, complex 7′ (for the ORTEP drawing see ESI†), synthesized in the presence of THF, does not contain coordinated solvent molecules, and CNMg = 4. Conformations of {(BHT)Mg[O(CH2)3CON(CH3)2]}2, in 7 and 7′ are nearly identical. Non-coordinating THF molecules in complex 7′ are in the outer sphere, filling the crystal channels. The various modes of coordination in dimeric complexes formed by glycolate/lactate and γ-hydroxybutyroylamide can be explained by steric factors (a longer γ-butyroyloxy fragment hinders THF coordination) and by the higher Lewis base strength of amides in comparison with esters. Typically, the Gutmann donor numbers for amides are double the donor numbers of ketones and esters.69 An argument in favor of a higher donor ability of the oxygen-coordinated amide fragment is that the Mg–OC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are noticeably shorter in 7 and 7′ in comparison to those in 5 or 6.
O bonds are noticeably shorter in 7 and 7′ in comparison to those in 5 or 6.
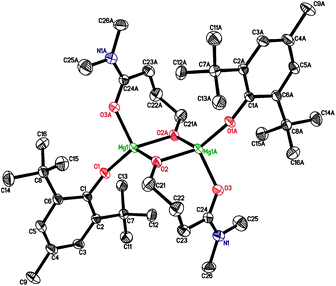 | ||
| Fig. 4 Molecular structures of {(BHT)Mg[μ-O(CH2)3CON(CH3)2]}2 (7). Symmetry code (A) to generate equivalent atoms: −x, −y + 1, −z + 1. | ||
During synthesis of complexes 3–7 we used THF as a donor solvent. Considering the importance of the reaction media when using BHT complexes in coordination catalysis, we studied the interaction of donor solvents and dimeric complex 3. In the reaction of 3 with DMSO, we observed a disproportionation with a formation of (BHT)2Mg(DMSO)2 (8), and the latter was isolated by crystallization in 97% yield based on BHT. This product is also formed in quantitative yield by the reaction of 1 with 2 eq. DMSO. We determined the structure of 8 by X-ray diffraction and found that despite significant differences in the donor properties of THF and DMSO, the basic geometric parameters of 1 and 8 are very close (for details, see ESI†).
Several observations and conclusions can be made regarding the results of experiments on the synthesis of BHT-derived magnesium complexes and their structural investigation. First, the stability of dimeric heteroletpic complexes depends on the Mg environment, such as BHT and RO ligands. The bridging position between Mg atoms is more efficiently taken up by relatively unhindered RO fragments, which is illustrated by the dimeric structure of the sterically less hindered phenolate [(BHT)Mg(μ-OC6H4tertBu)(THF)]2 (4) in comparison to the monomeric structure of complex (BHT)2Mg(THF)2 (1) containing bulky phenolates only. Second, we suppose that the THF molecule mimics a coordinated cyclic ester molecule at the catalytic site within ROP. Therefore, one can conclude that the complexes with coordinated THF could be effective catalysts of ROP and conversely, complexes that cannot coordinate THF should be less active in ROP, especially in the beginning of the process. We see from the X-ray data that complexes 3 and 5 have THF coordinated to the Mg center, whereas complex 7 does not have this even though it possesses THF molecules in the crystal channels! Thus, we suppose that 7 should be less active than 3 and 5 at least at the beginning of the process. The catalytic activity of aryloxy-complex 4, which contains coordinated THF molecules, depends on whether the aryloxy-group can initiate ROP. It has been shown that Mg phenolates can only initiate ROP of lactide at high temperatures (100–140 °C),70 therefore, one can expect a modest initiation activity in ROP for complex 4 under mild conditions. Third, the magnesium coordination number in the “normal” alcoholates (3, 4, 7) is equal to 4, and CNMg in glycolates (5, 6) is equal to 5 due to chelate formation with the ester group of the glicolate. Assuming that the structure of 3 models the structure of the catalytic species of ROP of lactones, while the structures of 5 and 6 model the structure of the catalytic species of ROP of lactide, one can conclude that ROP of lactides and lactones should proceed via different mechanisms at least with dimeric BHT-magnesium catalysts.
Polymerization of ε-caprolactone and (DL)-lactide catalyzed by BHT-Mg complexes
In the current work, we started studying catalytic properties of heteroleptic BHT-Mg complexes with comparison of the catalytic behavior of monomeric complex (BHT)Mg(OBn)(THF)2, which can be generated in situ by interaction of BnOH with (BHT)MgBu(THF)2 (2) (Scheme 1), and of its well-defined dimer [(BHT)Mg(μ-OBn)(THF)]2 (3) in the ROP of ε-CL and (DL)-LA ([Mon]/[Cat] = 200, 25 °C, [monomer] = 1 M). We have found that polymerization of both ε-CL and (DL)-lactide proceeds faster, when a monomeric catalyst, generated from 2/BnOH, is used, and is almost completed in 2 min under the given conditions (Table 1, runs 1 and 4). Dimeric catalyst 3 demonstrates slightly lower activity (Table 1, runs 2 and 5). In its presence, the reaction is almost completed in 10 min. It should be noted that catalysts 2/BnOH and 3 outperform in catalytic activity widely known coordination catalysts such as tin(II) octanoate (typical reaction conditions: bulk, 120–180 °C temperature range) and aluminum(III) isopropoxide.71,72| Run | Cat. | Mon. | [Mon]/[Cat] | React. time, min | Conv., % | M n × 103 (theor)a | M n × 103 (SEC)b | Đ M | M n × 103 (NMR)c |
|---|---|---|---|---|---|---|---|---|---|
| a M n (theor) = MWM × [M]0/[I]0 × conversion + MWI, MWM – molecular weights of monomers (114.14 for εCL, 144.13 for rac-LA), MWI – molecular weight of initiator, [M]0/[I]0 – monomer to initiator initial concentration ratio. b Determined by SEC vs. polystyrene standards and corrected by a factors of 0.56 (εCL) and 0.58 (rac-LA). c Determined by the analysis of 1H NMR spectra by the ratio of integral intensities of signals attributed to polymer OCH2 (εCL) or CHMe (rac-LA) and initiator fragments. d Activated by 1 eq. of BnOH. e No data. | |||||||||
| 1 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
ε-CL | 200 | 2 | 97 | 22.3 | 22.0 | 1.34 | 23.8 |
| 2 | 3 | ε-CL | 200 | 2 | 64 | 14.7 | 14.1 | 1.21 | 15.8 |
| 3 | 3 | ε-CL | 200 | 10 | 93 | 21.3 | 20.0 | 1.26 | 21.7 |
| 4 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
rac-LA | 200 | 2 | 95 | 27.5 | 25.6 | 1.41 | 27.8 |
| 5 | 3 | rac-LA | 200 | 2 | 76 | 22.0 | 20.8 | 1.37 | 22.2 |
| 6 | 3 | rac-LA | 200 | 10 | 94 | 27.2 | 25.4 | 1.38 | 26.9 |
| 7 | 3 | rac-LA | 75 | 2 | 96 | 10.4 | 11.1 | 1.33 | 10.9 |
| 8 | 3 | rac-LA | 75 | 10 | >99 | 10.8 | 12.2 | 1.30 | 11.9 |
| 9 | 5 | rac-LA | 75 | 2 | 95 | 10.3 | 10.6 | 1.28 | 9.8 |
| 10 | 5 | rac-LA | 75 | 10 | >99 | 10.8 | 10.9 | 1.24 | 10.1 |
| 11 | 7 | rac-LA | 75 | 2 | 65 | 7.0 | —e | —e | 11.5 |
| 12 | 7 | rac-LA | 75 | 10 | 98 | 10.6 | 16.4 | 1.38 | 15.9 |
| 13 | 4 | rac-LA | 75 | 10 | 18 | 1.9 | —e | —e | —e |
| 14 | 4 | rac-LA | 75 | 600 | >99 | 10.8 | 29.4 | 1.54 | 30.7 |
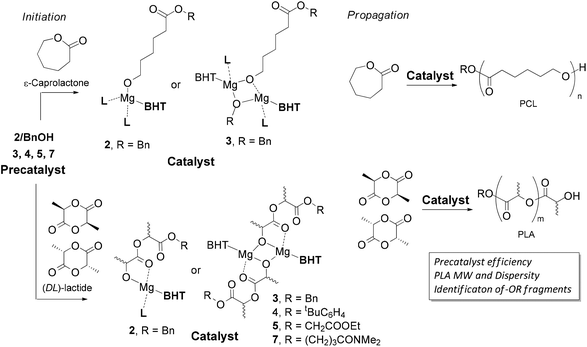
To experimentally verify our suppositions regarding the influence of the structure of complex 3, 4, 5 and 7 on their catalytic properties, we studied (DL)-LA polymerization catalyzed by these precatalysts. The experiments were conducted at moderate monomer-catalyst ratios (75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to conclusively identify by NMR the fragments of the initiator –OR in PLA (Scheme 3) under mild conditions (20 °C). The results of polymerization experiments are summarized in Table 1. Assuming that the catalytic particles produced from 3, 4, 5 and 7 should be equal in activity (molecular structure of 6 indicates that there is no coordination between the Mg-center and the “second” ester fragment), the difference between the integral catalytic productivity of 3, 4, 5 and 7 depends strongly on the rate of the catalyst's formation within the initiation step (Scheme 3). If the initiation rate for any of precatalysts 3, 4, 5 or 7 is lower than the propagation rate, one could expect that the Mn and ĐM values for PLAs would exceed their theoretical estimations.
1) to conclusively identify by NMR the fragments of the initiator –OR in PLA (Scheme 3) under mild conditions (20 °C). The results of polymerization experiments are summarized in Table 1. Assuming that the catalytic particles produced from 3, 4, 5 and 7 should be equal in activity (molecular structure of 6 indicates that there is no coordination between the Mg-center and the “second” ester fragment), the difference between the integral catalytic productivity of 3, 4, 5 and 7 depends strongly on the rate of the catalyst's formation within the initiation step (Scheme 3). If the initiation rate for any of precatalysts 3, 4, 5 or 7 is lower than the propagation rate, one could expect that the Mn and ĐM values for PLAs would exceed their theoretical estimations.
We have found that complexes 3 and 5, which contain THF coordinated to magnesium atoms, are effective catalysts of (DL)-lactide ROP (Table 1, runs 7–10). Monomer conversion for both catalysts after 2 minutes exceeded 90%. The full conversion was achieved in 10 minutes. The molecular weights of the polymers obtained by NMR (see ESI, Fig. S28–S36†) and SEC correspond to the theoretical values. Complex 7 demonstrated a significantly lower activity (Table 1, runs 11 and 12). Presumably, the relatively low activity of 7 is addressed by its modest predisposition to bind the monomer due to internal coordination of the Mg-center with the amide group of the pendant OR fragment. The difference between initiation and propagation rates leads to broadening of the molecular weight distribution of PLA and to a deviation between theoretical and experimental Mn values. This deviation becomes more significant in the case of aryloxy complex 4, which has demonstrated extremely low initial catalytic activity. Upon hydrolysis after 10 minutes of the reaction, the 1H NMR spectrum contained signals of 4-tert-butylphenol and BHT-H, products of decomposition of catalyst 4, as well as (DL)-LA and PLA in a ratio of ca. 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (see ESI, Fig. S35†). Almost full conversion was achieved after 10 hours. The molecular weight of PLA, which was obtained in the presence of 4, is three times higher than Mn (theor). The product demonstrates a broader polydispersity (Table 2, run 14). Presumably, this is owing to lower nucleophilicity of the magnesium phenolate in comparison with magnesium alcoholates 3, 5 and 7. The rate of initiation by tert-butyl phenolate is an order of magnitude lower than the polymerization rate, so only a third of the molecules of 4 acts as catalytic particles. Therefore, the catalytic experiments confirmed in general our suppositions regarding the structure–activity relationship of BHT-Mg complexes.
1 (see ESI, Fig. S35†). Almost full conversion was achieved after 10 hours. The molecular weight of PLA, which was obtained in the presence of 4, is three times higher than Mn (theor). The product demonstrates a broader polydispersity (Table 2, run 14). Presumably, this is owing to lower nucleophilicity of the magnesium phenolate in comparison with magnesium alcoholates 3, 5 and 7. The rate of initiation by tert-butyl phenolate is an order of magnitude lower than the polymerization rate, so only a third of the molecules of 4 acts as catalytic particles. Therefore, the catalytic experiments confirmed in general our suppositions regarding the structure–activity relationship of BHT-Mg complexes.
| DOSY NMR | X-ray data | DFT calc. | ||||
|---|---|---|---|---|---|---|
Δlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D D |
R S(dimer)/RS(1) | R Weq | R Weq (dimer)/RWeq(1) | R Weq | R Weq/RWeq(1) | |
| a No data. | ||||||
| (BHT)2Mg(THF)2 (1) | —a | — | 5.138 | — | 5.220 | — |
| (BHT)Mg(OBn)(THF)2 | 0.076 | 1.191 | — | — | 4.838 | 0.927 |
| [(BHT)Mg(OBn) | ||||||
| (THF)]2 (3) (trans) | 5.685 | 1.107 | 5.773 | 1.106 | ||
| (BHT)Mg(OCH2COOEt) | ||||||
| (THF)2 | 0.078 | 1.197 | — | — | 4.542 | 0.870 |
| [(BHT)Mg(OCH2COOEt) (THF)]2 (4) | 5.628 | 1.095 | 5.714 | 1.095 | ||
Examination of the behavior of BHT-Mg complexes in solution
We have determined by X-ray diffraction that complexes [(BHT)Mg(OBn)(THF)]2 (3) and [(BHT)Mg(OCH2COOEt)(THF)]2 (5) are dimers in the crystal with different CNMg. When discussing catalytic processes with 3 and 5 it is important to know whether the dimeric structure of these compounds is retained in solution, and in the presence of a large excess of electron-donating molecules, for example, THF. To experimentally verify whether complexes 3 and 5 are present in THF solution as monomers or dimers, we have used the method of diffusion-ordered NMR spectroscopy (DOSY NMR).73It is known that for spherical molecules the diffusion coefficient (D) is related to molecule size via the Stokes–Einstein equation (eqn (1)),74 where k is the Boltzmann constant, T – temperature, η – dynamic viscosity, RS – hydrodynamic molecular radius. Methods of DOSY NMR allow evaluating the diffusion coefficient of the molecule and thus the molecular size of Mg-BHT derivatives according to eqn (1) and (2). The DOSY NMR spectrum is registered with coordinates chemical shift/lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D, which allows us to experimentally determine lg
D, which allows us to experimentally determine lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D and, consequently, gauge the RS of BHT-Mg derivatives in solution (eqn (2)).
D and, consequently, gauge the RS of BHT-Mg derivatives in solution (eqn (2)).
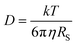 | (1) |
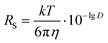 | (2) |
The abovementioned equations refer to molecules of spherical shape. Nevertheless, they can be used for other types of molecules if the rotational rate exceeds the rate of progressive motion of the molecule. It can be gathered from eqn (2) that the observed RS in the DOSY NMR experiment is inversely proportional to the dynamic viscosity of the specific BHT-Mg derivative solution being examined. This value depends on the viscosity of the solvent and on the concentration of the studied compound, and cannot always be predicted or measured with adequate accuracy for the concentrated solutions required to register DOSY NMR spectra of good quality. As a result, the observed accuracy of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BHT-Mg derivative solutions is inadequate for accurately calculating RS. Thus, the DOSY experiments we conducted under formally identical conditions for complex [(BHT)Mg(μ-OBn)(THF)]2 in THF-d8 gave lg
D for BHT-Mg derivative solutions is inadequate for accurately calculating RS. Thus, the DOSY experiments we conducted under formally identical conditions for complex [(BHT)Mg(μ-OBn)(THF)]2 in THF-d8 gave lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values from −9.086 to −9.191, which corresponds to a 27% error in RS determined by eqn (2). To remove this uncertainty in calculating dynamic viscosity, we propose to use an internal standard,73,75,76 which can be a chemically inert compound of similar nature and size. To study complexes 3 and 4, we used (BHT)2Mg(THF)2 (1) as such a standard, possessing a monomeric structure in THF media.48 According to this approach and eqn (2), the difference Δlg
D values from −9.086 to −9.191, which corresponds to a 27% error in RS determined by eqn (2). To remove this uncertainty in calculating dynamic viscosity, we propose to use an internal standard,73,75,76 which can be a chemically inert compound of similar nature and size. To study complexes 3 and 4, we used (BHT)2Mg(THF)2 (1) as such a standard, possessing a monomeric structure in THF media.48 According to this approach and eqn (2), the difference Δlg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = lg
D = lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(1) − lg
D(1) − lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(dimer) is connected with the ratio of hydrodynamic radii RS(dimer)/RS(1) by a simple equation that excludes such values as T and η, because the measurement of lg
D(dimer) is connected with the ratio of hydrodynamic radii RS(dimer)/RS(1) by a simple equation that excludes such values as T and η, because the measurement of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(dimer) and lg
D(dimer) and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D(1) occurs in the same experiment (eqn (3)),
D(1) occurs in the same experiment (eqn (3)),
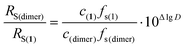 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D and the RS(dimer)/RS(1) ratios (see Table 2).
D and the RS(dimer)/RS(1) ratios (see Table 2).
We compared the obtained data with the RWeq values determined from the X-ray diffraction experiments for 1, 3 and 5, as well as from the DFT data for molecular structures of dimeric complexes 1, 3, 5 and hypothetical monomeric complexes (BHT)Mg(OBn)(THF)2 and (BHT)Mg(OCH2COOEt)(THF)2 (see Table 2). The RWeq(dimer)/RWeq(1) values for dimeric complexes 3 and 4 calculated and confirmed by X-ray diffraction are in good agreement with the experimental values, while the RWeq/RWeq(1) ratios for calculated hypothetical monomeric structures (BHT)Mg(OBn)(THF)2 and (BHT)Mg(OCH2COOEt)(THF) (0.927 and 0.870, respectively) correspond to the regions of the DOSY NMR spectrum where no signals are observed. Therefore, we can state that complexes 3 and 4 possess a dimeric structure in THF solution.
DFT modeling of ligand exchange and dissociation for dimeric BHT-Mg complexes
The tendency of heteroleptic BHT-magnesium complexes to form dimers is confirmed by the results of X-ray analysis of compounds 3–7, as well as DOSY NMR spectra of complexes 3 and 5. Complexes of formula [(BHT)Mg(μ-OR)(THF)]2 are precursors of ROP catalysts and can form two principally different types of catalytic particles under treatment with a molecule of cyclic ester (Scheme 4):- Binuclear catalytic species are formed as a result of substitution of THF with a molecule of cyclic ester – an ROP substrate (Sub);
- Mononuclear catalytic species are formed during the dissociation of BHT-alkoxy dimers with parallel solvation with two Sub molecules.
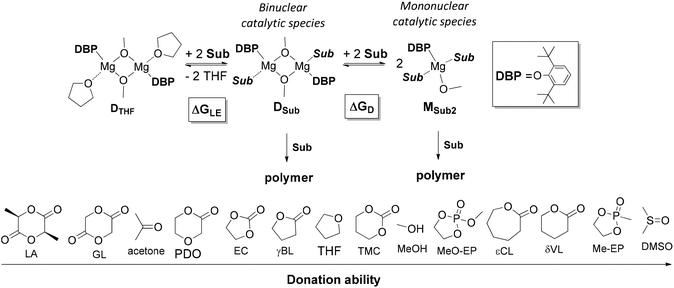 | ||
| Scheme 4 Ligand exchange and dissociation of model DBP-methoxy complexes. Sub donation ability range. | ||
We determined whether the thermodynamics are favorable for the formation of both types of catalytic particles. We calculated the free energy 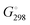 of the interaction of model compound [(DBP)Mg(μ-OMe)(THF)]2 (DTHF) with one and two equivalents of Sub (per mol of Mg) – monomers used in ROP and typical solvents (Scheme 4). The change in free energy during ligand exchange (per mol of Mg) ΔGLE was calculated as the difference in free energies of [(DBP)Mg(μ-OMe)(Sub)]2 (DSub) and DTHF with the free energies of Sub and THF considered using the formula
of the interaction of model compound [(DBP)Mg(μ-OMe)(THF)]2 (DTHF) with one and two equivalents of Sub (per mol of Mg) – monomers used in ROP and typical solvents (Scheme 4). The change in free energy during ligand exchange (per mol of Mg) ΔGLE was calculated as the difference in free energies of [(DBP)Mg(μ-OMe)(Sub)]2 (DSub) and DTHF with the free energies of Sub and THF considered using the formula 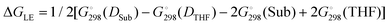 . The values of ΔGLE (Table 3) characterize the relative ability of Sub to coordinate to the Mg atom in a dimeric DBP-methoxy complex. Coordination with the examined complexes is not sterically hindered, therefore, ΔGLE can be viewed as a measure of ligand donor ability, an analogue of the Gutmann donor number, an experimentally determined characteristic of ligands and solvents (Table 3).69,81 The comparison of ΔGLE for various substrates Sub allows us to form a range of donor abilities (Scheme 4). As shown in Table 3, THF is in the middle of this range, therefore, its replacement with Sub during ROP in the presence of excess Sub is thermodynamically permissible.
. The values of ΔGLE (Table 3) characterize the relative ability of Sub to coordinate to the Mg atom in a dimeric DBP-methoxy complex. Coordination with the examined complexes is not sterically hindered, therefore, ΔGLE can be viewed as a measure of ligand donor ability, an analogue of the Gutmann donor number, an experimentally determined characteristic of ligands and solvents (Table 3).69,81 The comparison of ΔGLE for various substrates Sub allows us to form a range of donor abilities (Scheme 4). As shown in Table 3, THF is in the middle of this range, therefore, its replacement with Sub during ROP in the presence of excess Sub is thermodynamically permissible.
| S | ΔGLE, kcal mol−1 | ΔGD, kcal mol−1 | Donor number |
|---|---|---|---|
| a No data. b For trimethyl phosphate. | |||
| LA | 3.01 | 16.88 | —a |
| GL | 2.78 | 16.83 | — |
| Acetone | 1.38 | 14.90 | 17 |
| PDO | 0.90 | 15.24 | — |
| EC | 0.82 | 18.52 | 16.4 |
| γBL | 0.60 | 15.06 | 18 |
| THF | 0.00 | 17.99 | 20 |
| TMC | −0.87 | 15.17 | — |
| MeOH | −1.49 | 11.12 | 19 |
| MeO-EP | −1.81 | 13.49 | 23b |
| εCL | −2.04 | 15.66 | — |
| δVL | −2.06 | 15.30 | — |
| Me-EP | −5.47 | 9.51 | — |
| DMSO | −7.41 | 7.75 | 29.8 |
Table 3 also contains the free energies ΔGD of monomeric complex MSub2 formation (Scheme 4). As a hypothetical structure of the monomeric complex we chose tetrahedral (DBP)Mg(μ-OMe)(Sub)2, which is isostructural to (BHT)Mg(Bu)(THF)2.53 The calculation was made according to the formula 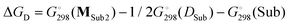 . We found that the formation of monomeric complexes is energetically unfavorable for all solvating substrates (ΔGD > 0). The dissociation energy for all Sub except for DMSO and Me-EP is higher than 13 kcal mol−1, which prevents this reaction under mild conditions.
. We found that the formation of monomeric complexes is energetically unfavorable for all solvating substrates (ΔGD > 0). The dissociation energy for all Sub except for DMSO and Me-EP is higher than 13 kcal mol−1, which prevents this reaction under mild conditions.
DFT modeling of ROP catalyzed by monomeric and dimeric BHT-alkoxy magnesium species
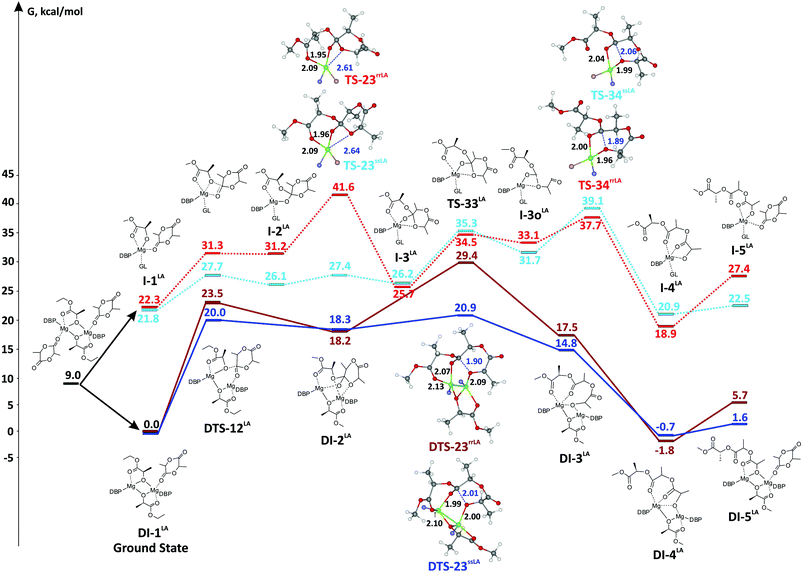
Using X-ray diffraction analysis, DOSY NMR experiments and DFT calculations of ligand exchange and dissociation processes, we have determined that the dimeric structure for heteroleptic BHT-alkoxy magnesium complexes is more favorable in both the solid state and solution. During the next stage of our work we conducted a DFT study of the polymerization mechanism. For BHT-alkoxy-Mg complexes two principally different ROP mechanisms are possible: a traditional mononuclear coordination–insertion mechanism, which is realized if the dimeric complex is dissociated beforehand with formation of monomeric BHT-alkoxy catalyst species, and the alternative and novel binuclear ROP mechanism with direct involvement of dimeric bimetallic catalytic particles. To determine which mechanism is more favorable, we analyzed the reaction profiles of lactone and lactide polymerization for monomeric and dimeric catalyst species. εCL was chosen as the substrate during modeling of the lactone ROP reaction profile, whereas DL-lactide was used to model lactide ROP.Polymerization of εCL
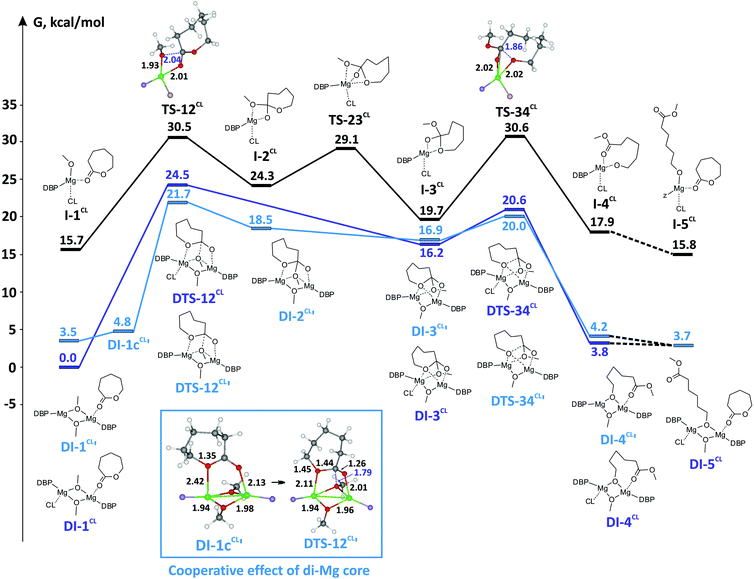
Earlier, we determined by DFT calculations that BHT-Mg-OMe complexes containing one or three molecules of coordinated monomer (CNMg = 3 and 5, respectively), are significantly higher in energy than tetrahedral complexes.90 In this work, we used the tetrahedral complex (DBP)Mg(OMe)(εCL)2 as a model catalytic particle and starting stationary point on the mononuclear reaction profile, I-1CL. The calculations showed that during the first stage from I-1CL, through the transition state TS-12CL, a hemi-acetal complex I-2CL is formed. Then, the bond between Mg–OMe and the endocyclic oxygen atom coordinated to Mg is cleaved (viaTS-23CL), which leads to formation of I-3CL. This reaction is followed by cleavage of the (O)C–O bond, which corresponds to the transition state TS-34CL. The concomitant dissociation of the M⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OR)– in I-4CL can occur with the coordination of a second molecule of εCL. The process occurs via the low-energy “dispersed” TS-45CL, the exact geometry of which we could not determine (the relative energy of TS-45CL obtained by scanning the potential energy surface was 5–6 kcal mol−1). The product I-5CL formed during the coordination of the second molecule of εCL is a structural analog of I-1CL. Stationary points I-1CL–I-5CL and transition states TS-12CL, TS-23CL and TS-34CL form the reaction profile of the single-center ROP of εCL (Fig. 5). The activation barrier of this reaction is 14.8 kcal mol−1.
C(OR)– in I-4CL can occur with the coordination of a second molecule of εCL. The process occurs via the low-energy “dispersed” TS-45CL, the exact geometry of which we could not determine (the relative energy of TS-45CL obtained by scanning the potential energy surface was 5–6 kcal mol−1). The product I-5CL formed during the coordination of the second molecule of εCL is a structural analog of I-1CL. Stationary points I-1CL–I-5CL and transition states TS-12CL, TS-23CL and TS-34CL form the reaction profile of the single-center ROP of εCL (Fig. 5). The activation barrier of this reaction is 14.8 kcal mol−1.
This process requires only 1.3 kcal mol−1, but the formation of DI-1cCL′ obviously increases the Arrhenius pre-exponential factor for a binuclear mechanism. For DI-1CL, this type of intermediate is not fixed. Therefore, we can assume that on the main reaction pathway DI-1CL loses one molecule of εCL, with the formation of DI-1cCL′. The energy of the first transition state DTS-12CL′ between DI-1cCL′ and DI-2CL is significantly (2.8 kcal mol−1) lower than the energy of DTS-12CL. A possible reason for this is that in DTS-12CL′ the degree of constraint between the Mg atom and the endocyclic oxygen atom of εCL is increased (dMg–O 2.11 vs. 2.23 Å). As we expected, the cleavage of the Mg–μ-OMe bond in binuclear DTS-12CL′ requires more close contact between the methoxy oxygen atom and the carbon atom of εCL. The distance d[MeO–C(O)] in DTS-12CL′ is only 1.78 Å; this distance in mononuclear TS-12CL is 2.04 Å. As a result, DTS-12CL′ is characterized by a higher relative energy: 21.7 kcal mol−1vs. 14.8 kcal mol−1 for TS-12CL.
Because DI-2CL′ possesses an endocyclic oxygen atom coordinated to Mg, the transition to DI-3CL′ occurs with low activation energy. Re-coordination of εCL at this stage leads to the intermediate DI-3CL, the energy of which is 0.7 kcal mol−1 lower than that of DI-3CL′. Transition states of the ring opening for particles containing one (DTS-34CL′) and two (DTS-34CL) molecules of εCL are similar in energy. The product of ring opening DI-4CL is more stable, and the additional coordination of εCL is accompanied by the dissociation of the Mg⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OR) bond and leads to DI-5CL.
C(OR) bond and leads to DI-5CL.
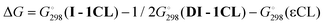 is equal to 15.7 kcal mol−1. For the mononuclear mechanism, the activation energy taking I-1CL as the stationary point is equal to 14.8 kcal mol−1. For the “pure” binuclear mechanism the activation barrier through DTS-12CL′ taking DI-1CL as the starting stationary point is equal to 21.7 kcal mol−1. ROP starting from DI-1CL and going through mononuclear TS-12CL is much less favorable (the activation barrier is equal to 30.5 kcal mol−1). Therefore, we can conclude that lactone polymerization initiated by the dimeric magnesium complex 3 should proceed via the binuclear mechanism. However, when we generate the monomeric catalyst species of the type I-1CL, for example, by alcoholysis of monomeric complexes 1 or 2, the mononuclear mechanism becomes the preferable reaction pathway (assuming that dimerization of I-1CL in viscous and diluted solution is relatively slow). This conclusion correlates strongly with the recently published results53 and experiments reported in this article. While studying lactone ROP we found that the initial polymerization rate of the processes initiated by the catalyst obtained in situ from the monomeric complex (BHT)Mg(Bu)(THF)2 is three times faster than that of the reaction catalyzed by bimetallic [(BHT)Mg(μ-OR)(THF)]2.
is equal to 15.7 kcal mol−1. For the mononuclear mechanism, the activation energy taking I-1CL as the stationary point is equal to 14.8 kcal mol−1. For the “pure” binuclear mechanism the activation barrier through DTS-12CL′ taking DI-1CL as the starting stationary point is equal to 21.7 kcal mol−1. ROP starting from DI-1CL and going through mononuclear TS-12CL is much less favorable (the activation barrier is equal to 30.5 kcal mol−1). Therefore, we can conclude that lactone polymerization initiated by the dimeric magnesium complex 3 should proceed via the binuclear mechanism. However, when we generate the monomeric catalyst species of the type I-1CL, for example, by alcoholysis of monomeric complexes 1 or 2, the mononuclear mechanism becomes the preferable reaction pathway (assuming that dimerization of I-1CL in viscous and diluted solution is relatively slow). This conclusion correlates strongly with the recently published results53 and experiments reported in this article. While studying lactone ROP we found that the initial polymerization rate of the processes initiated by the catalyst obtained in situ from the monomeric complex (BHT)Mg(Bu)(THF)2 is three times faster than that of the reaction catalyzed by bimetallic [(BHT)Mg(μ-OR)(THF)]2.
Polymerization of LA
DFT modeling of lactide polymerization by “biometal” complexes performed via a mononuclear coordination–insertion mechanism has been discussed in tens of publications. The work94 examines a binuclear mechanism for the initiation and propagation stages of lactide polymerization in the presence of benzyloxy Zn complex. As opposed to a several publications devoted to the mononuclear mechanism of PLA formation,58,89,95–97 including catalysis by Mg complexes,58,96 the paper94 does not consider the chelate formation ability of a lactate fragment. In any case, the binuclear mechanism concept is a new idea in lactide polymerization initiated by Mg-alkoxy complexes. Here, we performed DFT calculations of reaction profiles of lactide ROP for mononuclear and binuclear mechanisms to determine which reaction pathway is preferable, and to ascertain the reasons for heterotactic polymer formation during catalysis by BHT-Mg complexes.In conclusion, we note that catalytic systems based on BHT-magnesium complexes studied by us53 and other colleagues,49–52 regardless of the “living” nature of the polymerization, leads to formation of polymers with a relatively high ĐM – ∼1.2–1.5. The deviation of ĐM from theoretical values of ∼1.0 for living coordination polymerization is usually explained by transesterification. We propose that for BHT-Mg complexes, broadening of the molecular weight distribution can be explained by the fact that the real catalyst can be a mixture of monomeric and dimeric particles. Moreover, molecules of cyclic esters and donor solvent can take part in formation of both types of catalytic particles. When modeling εCL polymerization via the binuclear mechanism we determined the similarity of energy profiles for processes with catalytic particles of different amounts of coordinated substrate molecules. This leads to the diversification of the catalytic system; formation of single-type but different catalytic particles with similar but not the same geometry and energy.
Conclusion
We synthesized a series of heteroleptic BHT-Mg-OR complexes containing various types of alkoxide ligands (RO) and studied their molecular structure by X-ray diffraction. We found that complexes prepared from a primary alcohol ([(BHT)Mg(μ-OBn)(THF)]2 (3), {(BHT)Mg[μ-O(CH2)3CON(CH3)2]}2 (7)), from an unhindered phenol ([(BHT)Mg(μ-O-tert-BuC6H4)(THF)]2 (4)), as well as from esters of glycolic ([(BHT)Mg(μ-OCH2COOEt)(THF)]2 (5)) and lactic ([(BHT)Mg(μ-OCH(CH3)COOCH2COOtBu)(THF)]2 (6)) acids all have dimeric structures, with a Mg-(μ-OR)2-Mg core. Surprisingly, the BHT-Mg-derivatives of glicolate and lactate have pentacoordinated magnesium whereas the CNMg in other BHT-Mg alcoholates is equal to 4. It has been experimentally determined that 3 and 5 are highly active catalysts of LA polymerization.Using DOSY NMR we determined that 3 and 5 retain their dimeric structure even in a solvating solvent (THF). DFT-calculations of free energies of model dimeric [(DBP)Mg(μ-OMe)(Sub)]2 and monomeric (DBP)Mg(OMe)(Sub)2 complexes for a wide spectrum of solvating solvents and substrates (Sub) has shown that THF substitution with Sub in a dimeric complex is a feasible process, whereas dimer dissociation by treatment of Sub is energetically unfavorable, with an energy loss of 8–18 kcal molMg−1 depending on the solvent.
We performed a comparative DFT modeling of ε-CL and (DL)-lactide ROP catalyzed by dimeric and monomeric BHT-Mg catalysts. We concluded that the binuclear mechanism is more favorable for both lactones and lactides in the initial stages of reactions catalyzed by dimeric complexes 3 and 5.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Russian Science Foundation (Grant No. 16-13-10344) is gratefully acknowledged. The NMR DOSY measurements were made at the Shared Facility Centers of the Institute of Physical Chemistry and Electrochemistry, RAS, and Institute of General and Inorganic Chemistry, RAS.Notes and references
- H. Tian, Z. Tang, X. Zhuang, X. Chen and X. Jing, Prog. Polym. Sci., 2012, 37, 237–280 CrossRef CAS.
- R. T. Martin, L. P. Camargo and S. A. Miller, Green Chem., 2014, 16, 1768–1773 RSC.
- J. N. Hoskins and S. M. Grayson, Polym. Chem., 2011, 2, 289–299 RSC.
- R. P. Brannigan and A. P. Dove, Biomater. Sci., 2017, 5, 9–21 RSC.
- N. G. Ricapito, C. Ghobril, H. Zhang, M. W. Grinstaff and D. Putnam, Chem. Rev., 2016, 116, 2664–2704 CrossRef CAS PubMed.
- K. Fukushima, Biomater. Sci., 2016, 4, 9–24 RSC.
- A. Gandini and T. M. Lacerda, Prog. Polym. Sci., 2015, 48, 1–39 CrossRef CAS.
- R. Klein and F. R. Wurm, Macromol. Rapid Commun., 2015, 36, 1147–1165 CrossRef CAS PubMed.
- J. Rydz, W. Sikorska, M. Kyulavska and D. Christova, Int. J. Mol. Sci., 2015, 16, 564–596 CrossRef CAS PubMed.
- Y. Zhu, C. Romain and C. K. Williams, Nature, 2016, 540, 354–362 CrossRef CAS PubMed.
- G.-Q. Chen and M. K. Patel, Chem. Rev., 2012, 112, 2082–2099 CrossRef CAS PubMed.
- S. S. Bari, A. Chattarjee and S. Mishra, Polym. Rev., 2016, 56, 287–328 CrossRef CAS.
- J.-W. Rhim, H.-M. Park and C.-S. Ha, Prog. Polym. Sci., 2013, 38, 1629–1652 CrossRef CAS.
- B. D. Ulery, L. S. Nair and C. T. Laurencin, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 832–864 CrossRef CAS PubMed.
- H. R. Lakkireddy and D. Bazile, Adv. Drug Delivery Rev., 2016, 107, 289–332 CrossRef CAS PubMed.
- Z. Sheikh, S. Najeeb, Z. Khurshid, V. Verma, H. Rashid and M. Glogauer, Materials, 2015, 8, 5744–5794 CrossRef PubMed.
- M. Guvendiren, J. Molde, R. M. D. Soares and J. Kohn, ACS Biomater. Sci. Eng., 2016, 2, 1679–1693 CrossRef CAS PubMed.
- A. J. T. Teo, A. Mishra, I. Park, Y.-J. Kim, W.-T. Park and Y.-J. Yoon, ACS Biomater. Sci. Eng., 2016, 2, 454–472 CrossRef CAS.
- S. Farah, D. G. Anderson and R. Langer, Adv. Drug Delivery Rev., 2016, 107, 367–392 CrossRef CAS PubMed.
- E. Castro-Aguirre, F. Iñiguez-Franco, H. Samsudin, X. Fang and R. Auras, Adv. Drug Delivery Rev., 2016, 107, 333–366 CrossRef CAS PubMed.
- M. Santoro, S. R. Shah, J. L. Walker and A. G. Mikos, Adv. Drug Delivery Rev., 2016, 107, 206–212 CrossRef CAS PubMed.
- E. A. Rainbolt, K. E. Washington, M. C. Biewer and M. C. Stefan, Polym. Chem., 2015, 6, 2369–2381 RSC.
- J.-M. Raquez, Y. Habibi, M. Murariu and P. Dubois, Prog. Polym. Sci., 2013, 38, 1504–1542 CrossRef CAS.
- G. Narayanan, V. N. Vernekar, E. L. Kuyinu and C. T. Laurencin, Adv. Drug Delivery Rev., 2016, 107, 247–276 CrossRef CAS PubMed.
- A.-C. Albertsson and I. K. Varma, Biomacromolecules, 2003, 4, 1466–1486 CrossRef CAS PubMed.
- S. Ruengdechawiwat, R. Somsunan, R. Molloy, J. Siripitayananon, V. J. Franklin, P. D. Topham and B. J. Tighe, Adv. Mater. Res., 2014, 894, 172–176 CrossRef.
- L. Wang, V. Poirier, F. Ghiotto, M. Bochmann, R. D. Cannon, J.-F. Carpentier and Y. Sarazin, Macromolecules, 2014, 47, 2574–2584 CrossRef CAS.
- J.-M. Raquez, R. Mincheva, O. Coulembier and P. Dubois, in Polymer Science: A Comprehensive Reference, ed. K. Matyjaszewski and M. Möller, 2012, vol. 4, pp. 761–778 Search PubMed.
- R. H. Platel, L. M. Hodgson and C. K. Williams, Polym. Rev., 2008, 48, 11–63 CrossRef CAS.
- C. A. Wheaton, P. G. Hayes and B. J. Ireland, Dalton Trans., 2009, 4832–4846 RSC.
- C. M. Thomas, Chem. Soc. Rev., 2010, 39, 165–173 RSC.
- M. J. Stanford and A. P. Dove, Chem. Soc. Rev., 2010, 39, 486–494 RSC.
- R. Jianming, X. Anguo, W. Hongwei and Y. Hailin, Des. Monomers Polym., 2014, 17, 345–355 CrossRef.
- B. Calvo, M. G. Davidson and D. García-Vivó, Inorg. Chem., 2011, 50, 3589–3595 CrossRef CAS PubMed.
- W. Yi and H. Ma, Inorg. Chem., 2013, 52, 11821–11835 CrossRef CAS PubMed.
- J. Zhang, J. Xiong, Y. Sun, N. Tang and J. Wu, Macromolecules, 2014, 47, 7789–7796 CrossRef CAS.
- A. Duda and A. Kowalski, in Handbook of ring-opening polymerization, ed. P. Dubois, O. Coulembier and J.-M. Raquez, 2009, pp. 1–52 Search PubMed.
- L. Wang and H. Ma, Macromolecules, 2010, 43, 6535–6537 CrossRef CAS.
- S. Song, H. Ma and Y. Yang, Dalton Trans., 2013, 42, 14200–14211 RSC.
- J.-C. Wu, B.-H. Huang, M.-L. Hsueh, S.-L. Lai and C.-C. Lin, Polymer, 2005, 46, 9784–9792 CrossRef CAS.
- Y. Gao, Z. Dai, J. Zhang, X. Ma, N. Tang and J. Wu, Inorg. Chem., 2014, 53, 716–726 CrossRef CAS PubMed.
- Y. Wang, W. Zhao, X. Liu, D. Cui and E. Y.-X. Chen, Macromolecules, 2012, 45, 6957–6965 CrossRef CAS.
- H.-J. Chuang, H.-L. Chen, J.-L. Ye, Z.-Y. Chen, P.-L. Huang, T.-T. Liao, T.-E. Tsai and C.-C. Lin, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 696–707 CrossRef CAS.
- C.-Y. Sung, C.-Y. Li, J.-K. Su, T.-Y. Chen, C.-H. Lin and B.-T. Ko, Dalton Trans., 2012, 41, 953–961 RSC.
- J. Ejfler, K. Krauzy-Dziedzic, S. Szafert, L. B. Jerzykiewicz and P. Sobota, Eur. J. Inorg. Chem., 2010, 3602–3609 CrossRef CAS.
- M. H. Chisholm, J. Gallucci and K. Phomphrai, Inorg. Chem., 2002, 41, 2785–2794 CrossRef CAS PubMed.
- P. Brignou, S. M. Guillaume, T. Roisnel, D. Bourissou and J.-F. Carpentier, Chem. – Eur. J., 2012, 18, 9360–9370 CrossRef CAS PubMed.
- J. Calabrese, M. A. Cushing Jr. and S. D. Ittel, Inorg. Chem., 1988, 27, 867–870 CrossRef CAS.
- H.-Y. Chen, L. Mialon, K. A. Abboud and S. A. Miller, Organometallics, 2012, 31, 5252–5261 CrossRef CAS.
- H.-J. Fang, P.-S. Lai, J.-Y. Chen, S. C. N. Hsu, W.-D. Peng, S.-W. Ou, Y.-C. Lai, Y.-J. Chen, H. Chung, Y. Chen, T.-C. Huang, B.-S. Wu and H.-Y. Chen, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 2697–2704 CrossRef CAS.
- J. A. Wilson, S. A. Hopkins, P. M. Wright and A. P. Dove, Polym. Chem., 2014, 5, 2691–2694 RSC.
- J. A. Wilson, S. A. Hopkins, P. M. Wright and A. P. Dove, Macromolecules, 2015, 48, 950–958 CrossRef CAS.
- I. E. Nifant'ev, A. V. Shlyakhtin, A. N. Tavtorkin, P. V. Ivchenko, R. S. Borisov and A. V. Churakov, Catal. Commun., 2016, 87, 106–111 CrossRef.
- J. D. Monegan and S. D. Bunge, Inorg. Chem., 2009, 48, 3248–3256 CrossRef CAS PubMed.
- K. W. Henderson, G. W. Honeyman, A. R. Kennedy, R. E. Mulvey, J. A. Parkinson and D. C. Sherrington, Dalton Trans., 2003, 1365–1372 RSC.
- C. R. Groom and F. H. Allen, Angew. Chem., Int. Ed., 2014, 53, 662–671 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., 2016, 72, 171–179 CrossRef CAS PubMed.
- E. L. Marshall, V. C. Gibson and H. S. Rzepa, J. Am. Chem. Soc., 2005, 127, 6048–6051 CrossRef CAS PubMed.
- J. Lewiński, J. Zachara and I. Justyniak, Chem. Commun., 1997, 1519–1520 RSC.
- J. Lewiński, J. Zachara and I. Justyniak, Organometallics, 1997, 16, 4597–4605 CrossRef.
- J. Lewiński, P. Horeglad, K. Wójcik and I. Justyniak, Organometallics, 2005, 24, 4588–4593 CrossRef.
- N. Nomura, R. Ishii, Y. Yamamoto and T. Kondo, Chem. – Eur. J., 2007, 13, 4433–4451 CrossRef CAS PubMed.
- K. Phomphrai, P. Chumsaeng, P. Sangtrirutnugul, P. Kongsaeree and M. Pohmakotr, Dalton Trans., 2010, 39, 1865–1871 RSC.
- S. Dagorne, F. Le Bideau, R. Welter, S. Bellemin-Laponnaz and A. Maisse-François, Chem. – Eur. J., 2007, 13, 3202–3217 CrossRef CAS PubMed.
- V. Balasanthiran, M. H. Chisholm, K. Choojun and C. B. Durr, Dalton Trans., 2014, 43, 2781–2788 RSC.
- P. Horeglad, P. Kruk and J. Pécaut, Organometallics, 2010, 29, 3729–3734 CrossRef CAS.
- J. S. Klitzke, T. Roisnel, E. Kirillov, O. de L. Casagrande Jr. and J.-F. Carpentier, Organometallics, 2014, 33, 309–321 CrossRef CAS.
- H. Wang, Y. Yang and H. Ma, Macromolecules, 2014, 47, 7750–7764 CrossRef CAS.
- V. Gutmann, Coord. Chem. Rev., 1976, 18, 225–255 CrossRef CAS.
- S. Ghosh, P. K. S. Antharjanam and D. Chakraborty, Polymer, 2015, 70, 38–51 CrossRef CAS.
- O. Dechy-Cabaret, B. Martin-Vaca and D. Bourissou, Chem. Rev., 2004, 104, 6147–6176 CrossRef CAS PubMed.
- P. Degée, P. Dubois, R. Jerôme, S. Jacobsen and H.-G. Fritz, Macromol. Symp., 1999, 144, 289 CrossRef.
- A. Macchioni, G. Ciancaleoni, C. Zuccaccia and D. Zuccaccia, Chem. Soc. Rev., 2008, 37, 479–489 RSC.
- A. Einstein, Investigations on the Theory of the Brownian Movement, Dover Publications Inc., Mineola, NY, 1956 Search PubMed.
- D. Li, G. Kagan, R. Hopson and P. G. Williard, J. Am. Chem. Soc., 2009, 131, 5627–5634 CrossRef CAS PubMed.
- G. Kagan, W. Li, R. Hopson and P. G. Williard, Org. Lett., 2009, 11, 4818–4821 CrossRef CAS PubMed.
- B. M. Schulze, D. L. Watkins, J. Zhang, I. Ghiviriga and R. K. Castellano, Org. Biomol. Chem., 2014, 12, 7932–7936 CAS.
- D. Jędrzkiewicz, J. Ejfler, N. Gulia, Ł. John and S. Szafert, Dalton Trans., 2015, 44, 13700–13715 RSC.
- A. Gierer and K. Wirtz, Z. Naturforsch., A: Astrophys. Phys. Phys. Chem., 1953, 8, 532–538 Search PubMed.
- H. C. Chen and S. H. Chen, J. Phys. Chem., 1984, 88, 5118–5121 CrossRef CAS.
- F. Cataldo, Eur. Chem. Bull., 2015, 4, 92–97 CAS.
- M. Kuzdrowska, L. Annunziata, S. Marks, M. Schmid, C. G. Jaffredo, P. W. Roesky, S. M. Guillaume and L. Maron, Dalton Trans., 2013, 42, 9352–9360 RSC.
- E. E. Marlier, J. A. Macaranas, D. J. Marell, C. R. Dunbar, M. A. Johnson, Y. DePorre, M. O. Miranda, B. D. Neisen, C. J. Cramer, M. A. Hillmyer and W. B. Tolman, ACS Catal., 2016, 6, 1215–1224 CrossRef CAS PubMed.
- K. Ding, M. O. Miranda, B. Moscato-Goodpaster, N. Ajellal, L. E. Breyfogle, E. D. Hermes, C. P. Schaller, S. E. Roe, C. J. Cramer, M. A. Hillmyer and W. B. Tolman, Macromolecules, 2012, 45, 5387–5396 CrossRef CAS.
- M.-C. Chang, W.-Y. Lu, H.-Y. Chang, Y.-C. Lai, M. Y. Chiang, H.-Y. Chen and H.-Y. Chen, Inorg. Chem., 2015, 54, 11292–11298 CrossRef CAS PubMed.
- M. O. Miranda, Y. DePorre, H. Vazquez-Lima, M. A. Johnson, D. J. Marell, C. J. Cramer and W. B. Tolman, Inorg. Chem., 2013, 52, 13692–13701 CrossRef CAS PubMed.
- J. Jitonnom, R. Molloy, W. Punyodom and W. Meelua, Comput. Theor. Chem., 2016, 1097, 25–32 CrossRef CAS.
- J. Wei, M. N. Riffel and P. L. Diaconescu, Macromolecules, 2017, 50, 1847–1861 CrossRef CAS.
- S. Vogt-Geisse, R. A. Matac and A. Toro-Labbé, Phys. Chem. Chem. Phys., 2017, 19, 8989–8999 RSC.
- I. E. Nifant'ev, P. V. Ivchenko, A. V. Shlyakhtin and A. V. Ivanyuk, Polym. Sci., Ser. B, 2017, 59, 147–156 CrossRef.
- I. del Rosal, P. Brignou, S. M. Guillaume, J.-F. Carpentier and L. Maron, Polym. Chem., 2015, 6, 3336–3352 RSC.
- I. del Rosal, P. Brignou, S. M. Guillaume, J.-F. Carpentier and L. Maron, Polym. Chem., 2011, 2, 2564–2573 Search PubMed.
- C. Sattayanon, W. Sontising, W. Limwanich, P. Meepowpan, W. Punyodom and N. Kungwan, Struct. Chem., 2015, 26, 695–703 CrossRef CAS.
- C. Fliedel, D. Vila-Viçosa, M. J. Calhorda, S. Dagorne and T. Avilés, ChemCatChem, 2014, 6, 1357–1367 CrossRef CAS.
- S. Tabthong, T. Nanok, P. Sumrit, P. Kongsaeree, S. Prabpai, P. Chuawong and P. Hormnirun, Macromolecules, 2015, 48, 6846–6861 CrossRef CAS.
- P. V. Ivchenko, A. V. Shlyakhtin and I. E. Nifant'ev, Mendeleev Commun., 2017, 27, 278–280 CrossRef CAS.
- C. Robert, T. E. Schmid, V. Richard, P. Haquette, S. K. Raman, M.-N. Rager, R. M. Gauvin, Y. Morin, X. Trivelli, V. Guérineau, I. del Rosal, L. Maron and C. M. Thomas, J. Am. Chem. Soc., 2017, 139, 6217–6225 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic, X-ray and polymerization experimental details, NMR spectra, DFT calculations data. CCDC 1463808, 1545641–1545643, 1545645, 1545646, 1545648 and 1545650. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02469j |
| This journal is © The Royal Society of Chemistry 2017 |