Open Access Article
Open Access ArticleThe first lead cobalt phosphite, PbCo2(HPO3)3†
Vadim M.
Kovrugin
 *abc,
Marie
Colmont
*abc,
Marie
Colmont
 a,
Oleg I.
Siidra
a,
Oleg I.
Siidra
 b,
Sergey V.
Krivovichev
b,
Sergey V.
Krivovichev
 b,
Silviu
Colis
d and
Olivier
Mentré
b,
Silviu
Colis
d and
Olivier
Mentré
 *a
*a
aUnité de Catalyse et Chimie du Solide (UCCS), UMR 8181 CNRS, Université Lille 1 Sciences et Technologies, 59655 Villeneuve d'ASCQ, France. E-mail: kovrugin_vm@hotmail.com; olivier.mentre@ensc-lille.fr
bDepartment of Crystallography, Institute of Earth Sciences, St. Petersburg State University, 199034 St. Petersburg, Russian Federation
cLaboratoire de Réactivité et Chimie des Solides (LRCS), UMR 7314 CNRS, Université de Picardie Jules Verne, 80039 Amiens Cedex, France
dInstitut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), UMR 7504 UDS-CNRS (UDS-ECPM), 67034 Cedex 2 Strasbourg, France
First published on 30th August 2017
Abstract
Single crystals of a new lead cobalt phosphite, PbCo2(HPO3)3, have been synthesized using mild hydrothermal techniques and characterized by X-ray diffraction analysis, SQUID magnetic measurements, IR spectroscopy, UV/vis spectroscopy, thermogravimetric analysis, and scanning electron microscopy. PbCo2(HPO3)3 crystallizes in the non-centrosymmetric (NCS) R3m space group, a = 5.3145(15) Å, c = 25.494(7) Å, V = 623.6(4) Å3. The crystal structure of PbCo2(HPO3)3 is based upon 2D heteropolyhedral blocks built up from Co2O9 octahedral dimers and HPO3 pseudo-tetrahedra. Lead cations reside in the interlayer space of the structure. Here, the NCS character results reasonably from the cooperative Pb2+ lone electron pair arrangements, by analogy to the centrosymmetric compound (NH4)2Co2(HPO3)3 with similar but disordered blocks. A local twisting of specific HPO3 groups arises due to unreasonably short H⋯H contacts between two phosphite oxoanions. In terms of the magnetic behavior, the new PbCo2(HPO3)3 phase demonstrates weak antiferromagnetic interactions inside the Co2O9 dimers between cobalt ions as expected from the phosphite μ-O bridges.
1. Introduction
Nowadays, interest in transition metal phosphites is focused mainly on hybrid organic/inorganic compounds since they favor the formation of microporous materials with open-framework zeolite-type structures, which may find various applications in ion-exchange, separation, and catalysis.1–3 Dealing with “pure” inorganic chemistry, the specific intrinsic bonding scheme of phosphite [HPO3]2− groups and tridentate ligand species offer other interesting possibilities to achieve original topologies between transition metals, compared to common tetradentate phosphate [PO4]3− groups. Both having tetrahedral geometry, they exhibit a similar structural chemistry, but with important differences due to the smaller charge within an asymmetric charge distribution in [HPO3]2−. For instance, it was demonstrated that the pseudo-tetrahedral phosphite oxoanions can replace the phosphate groups in novel open crystal structures as reported for zinc phosphites.4,5 Also note that the strongly covalent P–H bond in HPO3 negatively polarizes the Hδ− corner. Thus, it plays a role analogous to that of the lone electron pair E in specific oxoanions such as ESe4+O3, as demonstrated by the recent report on Fe2(SeO3)3versus Fe2(HPO3)3.6 The co-presence of asymmetric anionic groups and stereochemically active lone electron pairs of cations (e.g. Sn2+, Pb2+, Sb3+, Bi3+) in solids appears as a promising route to non-centrosymmetric polar crystal structures,7–10 very attractive in terms of their possible applications in optics, asymmetric catalysis and enantioselective separation processes.11,12 The Co-containing systems are an important group of this kind of materials mainly owing to their ability to achieve various coordination environments (tetrahedral, bipyramidal, and octahedral) and versatile valence states. The Co-containing compositions combined with organic ligands can also be used for the preparation of metal–organic frameworks with higher surface areas, higher porosity, and various atomic arrangements.13 Moreover, the Co-containing materials based on HPO3 anionic groups may exhibit particular magnetic14,15 or photosensitive properties.16,17 Particularly, due to the weak aptitude of phosphite as magnetic transmitters,6,14 they can form ideal diamagnetic spacers. Despite the report of about twenty different hybrid organic/inorganic cobalt phosphite phases, the structural chemistry of inorganic cobalt phosphites remains poorly explored. There are only a few reported cobalt phosphites, namely, NaCo(H2PO3)3(H2O),18 Co(HPO3)(H2O),19 Co11(HPO3)8(OH)6,20 and Na2Co(HPO3)2.21 In order to fill up the gap in the structural chemistry of inorganic cobalt-based phosphites, we report on the synthesis, structural characterization, and magnetic properties of the first cobalt phosphite containing lead, i.e., PbCo2(HPO3)3 which turns out to be non-centrosymmetric, as expected.2. Experimental
2.1 Synthesis
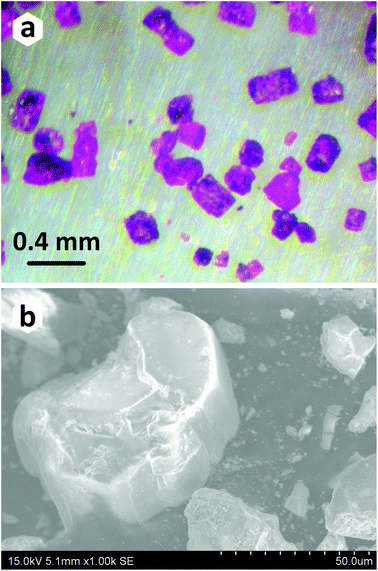
Commercial PbO (crystalline powder, 99.9% Aldrich), Co3O4 (crystalline powder, 95%, Alfa Aesar), and H3PO3 (crystalline powder, 98%, Acros Organics) were used as received.The title compound has been prepared under mild hydrothermal conditions. The main reasons for choosing the method based on crystallization from aqueous solutions are the high hygroscopicity of phosphorous acid (H3PO3), and its decomposition into phosphoric acid (H3PO4) and phosphine (PH3) at a relatively low temperature around 200 °C. Although several attempts were made to obtain a pure polycrystalline sample by combining the stoichiometric amounts of starting reactants, secondary phases always accompanied the title compound (Table 1). To grow single crystals of the novel PbCo2(HPO3)3 composition suitable for the X-ray diffraction analysis, a mixture of PbO (0.1488 g, 0.67 mmol), Co3O4 (0.0803 g, 0.33 mmol), and H3PO3 (0.1639 g, 2.0 mmol) was dissolved in 6 ml of distilled water. The hydrothermal reaction was performed in a 23 ml Teflon-lined steel autoclave heated to 160 °C in a mechanical convection oven. The temperature of the oven was held constant for two days, followed by slow cooling to room temperature for 48 hours. Pink pseudo-hexagonal prismatic blocks (Fig. 1a and b) of the title compound were observed in association with transparent platy crystals of PbHPO4.22,23 The crystals of the PbCo2(HPO3)3 compound were carefully washed with ethanol to remove the unwanted admixture of PbHPO4 and then dried in air.
| No. | Precursors (+6 ml H2O) | Products | Ref. |
|---|---|---|---|
| a This work. | |||
| 1 | PbO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co3O4 Co3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H3PO3 = 0.67 H3PO3 = 0.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.33 0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.00 2.00 |
i. PbCo2(HPO3)3 | |
| ii. PbHPO4 | 22 and 23 | ||
| 2 | PbO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co3O4 Co3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H3PO3 = 1.00 H3PO3 = 1.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.67 0.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.00 3.00 |
i. PbCo2(HPO3)3 | |
| ii. PbHPO3 | 24 | ||
| iii. Pb3(PO4)2 | 25 and 26 | ||
| 3 | PbO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CoO CoO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H3PO3 = 1.00 H3PO3 = 1.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.00 2.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.00 3.00 |
i. PbCo2(HPO3)3 | |
| ii. PbHPO4 | 22 and 23 | ||
| iii. PbHPO3 | 24 | ||
2.2 Single crystal X-ray diffraction studies
Single crystals of PbCo2(HPO3)3 were mounted on thin glass fibers for X-ray diffraction (XRD) analysis and tested using a Bruker X8 APEX II X-ray diffractometer with a fine-focus X-ray tube delivering a MoKα radiation, λ = 0.71073 Å at 50 kV and 40 mA. More than a hemisphere of three-dimensional XRD data was collected with frame widths of 0.5° in ω, and a 30 s count time for each frame. The diffraction data were integrated and corrected for the absorption using a multi-scan type model integrated in the APEX2 and SADABS Bruker programs. The unit cell parameters of PbCo2(HPO3)3 (R3m, a = 5.3145(15) Å, c = 25.494(7) Å, V = 623.6(4) Å3, Z = 3) were determined and refined by least-squares techniques on the basis of 3265 reflections with 2θ in the range between 4.8 and 63.48°. The crystal structure of PbCo2(HPO3)3 was solved in the non-centrosymmetric R3m space group by direct methods and refined to R1 = 0.015 (wR2 = 0.030) for 534 reflections with |Fo| ≥ 4σF by using the SHELXL–2013 program implemented in the WinGX program package.27 The final model included coordinates and anisotropic displacement parameters for all non-hydrogen atoms. The “ideal” hydrogen atoms of the (HPO3)2− groups were localized from the difference Fourier maps. Data collection refinement parameters and detailed crystallographic information are provided in Table 2. Fractional atomic coordinates, atomic displacement parameters, and selected bond distances are listed in Tables 3 and 4. CSD 433061 contains the supplementary crystallographic information for PbCo2(HPO3)3. This data can be obtained from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany, http://www.fiz-karlsruhe.de/.| a R 1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2; GoF = {∑[w(Fo2 − Fc2)]/(n − p)}1/2, where n is the number of reflections, and p is the number of refined parameters. | |
|---|---|
| Crystal data | |
| Chemical formula | PbCo2(HPO3)3 |
| Formula weight (g) | 564.98 |
| Crystal system | Trigonal |
| Space group | R3m (no. 160) |
| a (Å) | 5.3145(15) |
| c (Å) | 25.494(7) |
| V (Å3) | 623.6(4) |
| Z | 3 |
| ρ calc (g cm−3) | 4.514 |
| Crystal size (mm) | 0.20 × 0.15 × 0.13 |
| Data collection | |
| Diffractometer | Bruker X8 APEX II (CCD) |
| Radiation, λ (Å) | MoKα, 0.71073 |
| μ (mm−1) | 24.75 |
| F (000) | 768 |
| θ range (°) | 2.4–32.0 |
| No. of measured reflections | 3590 |
| Total reflections (Rint) | 534 (0.029) |
| Unique reflections with |Fo| ≥ 4σF | 534 |
| Refinement | |
| Refinement method | Full-matrix least-squares on F2 |
| Weighting coefficients a, b | 0.0063, 0 |
| Data/restraints/parameters | 534/4/41 |
| R 1, wR2 (|Fo| ≥ 4σF) | 0.0147, 0.0298 |
| R 1, wR2 (all data) | 0.0147, 0.0298 |
| GoF | 1.034 |
| Largest diff. peak and hole (e Å−3) | 1.485, −0.555 |
| Atom | Wyck. | x | y | z | U iso*/Ueq | Charge ±q |
|---|---|---|---|---|---|---|
| Pb1 | 3a | 0 | 0 | 0.16209(2) | 0.01761(10) | +0.74757 |
| Co1 | 3a | 0 | 0 | 0.28985(5) | 0.0099(2) | +0.89371 |
| Co2 | 3a | 1/3 | 2/3 | 0.07026(5) | 0.0096(3) | +0.92617 |
| P1 | 3a | 2/3 | 1/3 | 0.09927(11) | 0.0098(5) | +0.39751 |
| P2 | 3a | 1/3 | 1/3 | 0.32927(9) | 0.0089(4) | +0.43115 |
| P3 | 3a | 1/3 | 2/3 | 0.25226(11) | 0.0086(5) | +0.43475 |
| O1 | 9b | 0.3478(10) | 0.1739(5) | 0.34537(15) | 0.0137(8) | −0.41732 |
| O2 | 9b | 0.5100(5) | 0.0199(9) | 0.11827(17) | 0.0185(9) | −0.40610 |
| O3 | 9b | 0.6523(9) | 0.8262(5) | 0.23647(15) | 0.0147(9) | −0.40187 |
| H1 | 3a | 2/3 | 1/3 | 0.049(2) | 0.022* | −0.05623 |
| H2 | 3a | 2/3 | 1/3 | 0.273(3) | 0.022* | −0.03701 |
| H3 | 3a | 1/3 | 2/3 | 0.303(2) | 0.022* | −0.06166 |
| Distance | Å | Distance | Å |
|---|---|---|---|
| Pb1–O3 | 3 × 2.481(4) | P1–O2 | 3 × 1.522(4) |
| Pb1–O2 | 6 × 2.8841(18) | P2–O1 | 3 × 1.524(4) |
| <Pb1–O> | 2.6963 | P3–O3 | 3 × 1.522(4) |
| <P–O> | 1.523 | ||
| Co1–O3 | 3 × 2.101(4) | ||
| Co1–O1 | 3 × 2.137(4) | P1–H1 | 1.282(4) |
| Co2–O2 | 3 × 2.035(4) | P2–H2 | 1.435(4) |
| Co2–O1 | 3 × 2.183(4) | P3–H3 | 1.294(4) |
| <Co–O> | 2.114 | <P–H> | 1.337(4) |
| Co1–Co2 | 2.900(2) | H1–H3 | 2.023(4) |
2.3 Powder X-ray diffraction studies
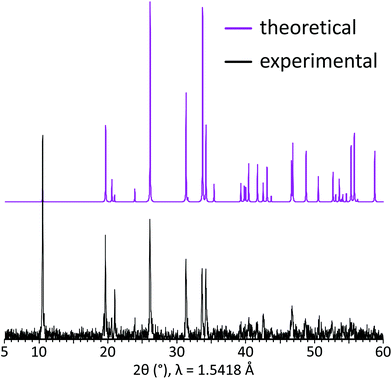
The grown single crystals were crushed using an agate mortar and then used for the powder X-ray diffraction analysis performed at room temperature in the 2θ range of 10–60° with a scan step width of 0.02° using a D8 Advance Bruker AXS diffractometer (CuKα radiation, λ = 1.5418 Å). Difference of the XRD peak intensities between two patterns implies preferred orientation along [00l] as the XRD pattern was collected using crushed single crystals on a silicon crystal sample holder. A good coincidence between experimental and theoretical powder XRD patterns for the title compound is shown in Fig. 2.2.4 IR spectroscopy
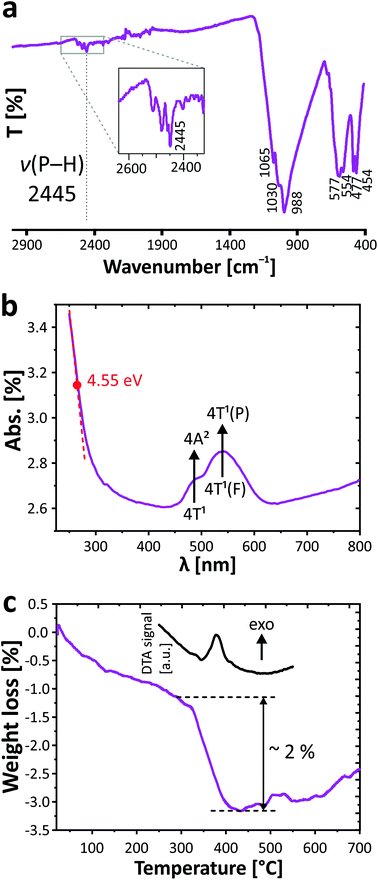
The infrared spectrum of PbCo2(HPO3)3 was obtained between 4000 and 400 cm−1 with a PerkinElmer Spectrum Two spectrometer equipped with a diamond attenuated total reflectance (ATR) accessory. The vibrational bands of phosphite groups have been established in the studied range. Stretching vibrations and deformation modes of phosphite oxoanions in PbCo2(HPO3)3 are divided between the following modes: ν(P–H): 2445 cm−1, δas(P–H): 1030, 988 cm−1; δs(P–O3): 1065, 988 cm−1, δs(P–O3): 588–577, 554 cm−1, δas(P–O3): 477, 454 cm−1. The presence of the typical P–H bond was preliminarily verified by infrared spectroscopy with evidence of the vibrational band at 2445 cm−1 (Fig. 3a). The observed values are similar to those found in other related compounds containing the phosphite ion.6,282.5 UV/vis spectroscopy
The UV/vis absorbance spectrum was collected at room temperature with a PerkinElmer Lambda 650 spectrophotometer in the 250–800 nm range using an integration sphere designed for the characterization of solids. The spectrum is given in Fig. 3b. Beyond the band gap estimated at 4.55 eV of an insulating regime, it demonstrates the typical d–d transition of Co2+ in a high spin configuration. The main transition and the shoulder at lower energy are assigned to the 4T1(F) to 4T1(P) and 4T1 to 4A2 transitions. The resulting broad doublet between 450 and 600 nm (green to orange absorption) justifies the pink color of the crystal, i.e., its complementary spectral color.2.6 Thermogravimetric analysis
The thermogravimetric experiments have been carried out on a thermoanalyzer TGA 92 SETARAM under air atmosphere with a heating rate of 5 °C min−1 from room temperature up to 700 °C. The TGA curve (Fig. 3c) shows a constant weight loss assigned to moisture, while a sudden step occurs from both TGA and DTA at 380 °C, signing the phase decomposition. The corresponding loss of ca. 2% is hard to assign due to the poor crystalline residue after TGA. However as expected from the phosphite reactivity,29 it most plausibly includes the removal of all H atoms with loss of water molecules (1.5 H2O, i.e., −4.7% mass loss) together with the partial oxidation by ca. one O atom (i.e., 2.8% mass uptake), which is in good agreement with the experimental total weight loss of 2%. The latter is pursued at higher temperature with a constant mass increase and can be assigned to the oxidation of both the Co2+ and P3+ species. The final residue is black colored.2.7 Magnetic measurements
The magnetic characterization of the new PbCo2(HPO3)3 phase was performed on the crushed single crystals using a MPMS SQUID-VSM (Quantum Design) magnetometer in a temperature and field range of 1.8–400 K and 0–7 T, respectively. The temperature dependence of the magnetization was determined under various magnetic fields after cooling the sample in a field (FC, field cooling) or in a zero field (ZFC, zero-field cooling).3. Results and discussion
3.1 Crystal structure
The new PbCo2(HPO3)3 compound crystallizes in the R3m non-centrosymmetric space group. It is built up from alternating 2D layered blocks composed of (HPO3)2− and (CoO6)10− structural units separated by Pb2+ cations in the interlayer space (Fig. 4a). The crystal structure of PbCo2(HPO3)3 contains two Co2+, one Pb2+, and three P3+ cations, which are crystallographically independent.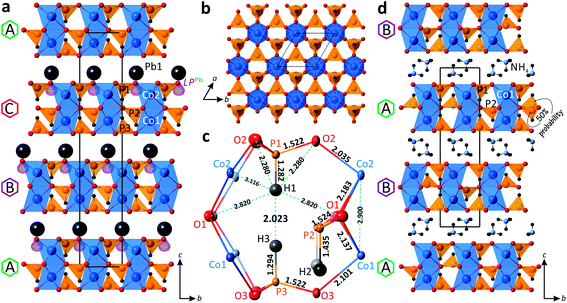 | ||
Fig. 4 General projections of the crystal structures of PbCo2(HPO3)3 (a) and (NH4)Co2(HPO3)3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (d) along the a-axis; [Co2(HPO3)3]2− 2D block in PbCo2(HPO3)3 projected on the ab plane (b); the atomic arrangement in the internal space of the 2D block (c). 30 (d) along the a-axis; [Co2(HPO3)3]2− 2D block in PbCo2(HPO3)3 projected on the ab plane (b); the atomic arrangement in the internal space of the 2D block (c). | ||
Both cobalt positions are located in the face-sharing octahedral dimers, with a Co⋯Co distance of 2.900 Å. The octahedral coordination of Co atoms is rather regular with the average Co–O bond lengths of 2.118 Å and 2.109 Å for the Co1 and Co2 sites, respectively. The calculated bond valence sums give 1.89 and 1.98 v.u. (valence units) for Co1 and Co2, respectively, in good agreement with Co2+ species.
All three pseudo-tetrahedral HPO3 oxoanions share all their O corners with adjacent cobalt octahedral dimers leading to 2D layered blocks in the ab plane (Fig. 4b). Thus, each phosphite pseudo-tetrahedron has three crystallographically identical P–O contacts (1.522 Å, 1.523 Å, and 1.522 Å for P1, P2, and P3, respectively) and a short hydrogen P–H bond (1.282 Å, 1.435 Å, and 1.294 Å for P1, P2, and P3, respectively). Note also the too short P1–H1 and P3–H3 bond lengths (≈ 1.29 Å) compared to the P2–H2 (≈ 1.44 Å) and the short H1⋯H3 contact of 2.023 Å, as a result of the orientation of the HP1O3 and HP3O3 pseudo-tetrahedra toward each other inside the 2D blocks, which may lead to local twisting of these polyhedra. The latter suggested resolving the crystal structure with off-centered one third occupied H sites (see below). The atomic arrangement in the internal space of the 2D block is demonstrated in Fig. 4c.
In the crystal structure of PbCo2(HPO3)3, the unique Pb2+ cation adopts an irregular coordination with three equivalent short Pb–O bonds (2.481 Å) in the first coordination sphere and six identical longer bonds (2.884 Å) in the second coordination sphere. The observed asymmetric environment of the Pb polyhedra clearly indicates that the 6s2 lone pair is stereochemically active (Fig. 4a). Divalent lead cations reside in the interlayer space of the structure and balance the charge of the negatively charged 2D blocks of the title compound. The non-centrosymmetric symmetry results from the “down” only orientation of the HP2O3 groups in the crystal structure.
Similar 2D blocks have been reported in the crystal structure of (NH4)2Co2(HPO3)3.30 The main difference between these two compounds lies in the packing sequence of the 2D blocks and interlayer species between them, i.e., double layers of NH4+ ions in (NH4)2Co2(HPO3)3 and single layers of Pb2+ in PbCo2(HPO3)3 (Fig. 4d). The most interesting structural feature of the (NH4)2Co2(HPO3)3 phase is the HP2O3 site, which is split into two half-occupied positions located above or below the mirror plane of the 2D blocks in the centrosymmetric P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1c space group. Clearly, in the title compound the cooperative displacement of the lone pair on Pb2+ cations between the layers leads to the unique orientation of HP2O3 in a non-centrosymmetric mode. We also note too-short H⋯H contacts (1.85 Å) in the blocks of (NH4)2Co2(HPO3)3, but this observation was not commented on in the original publication.
1c space group. Clearly, in the title compound the cooperative displacement of the lone pair on Pb2+ cations between the layers leads to the unique orientation of HP2O3 in a non-centrosymmetric mode. We also note too-short H⋯H contacts (1.85 Å) in the blocks of (NH4)2Co2(HPO3)3, but this observation was not commented on in the original publication.
The determination of partial charges using scales of atomic non-empirical electronegativity and hardness was carried out using Henry's method.31,32 The average negative charge of −0.052 was found for the H atoms in PbCo2(HPO3)3 (Table 3), which clearly indicates the hydride character of the terminal H in phosphite anions. The latter lies in accordance with an observed weak Pδ+–Hδ− polarization in various inorganic phases containing (HPO3)2− groups as reported in ref. 6.
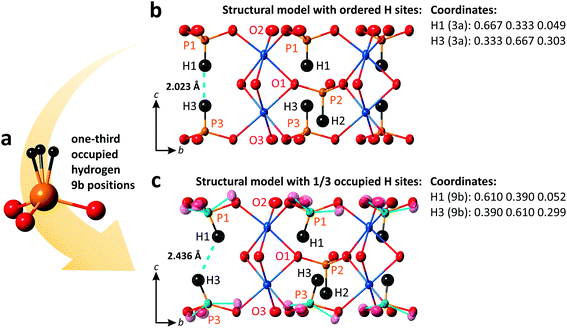
3.2 Structural model with 1/3 occupied off-centered H sites
As mentioned in the previous section, inside the 2D blocks of the structure of PbCo2(HPO3)3, two crystallographically inequivalent phosphite groups point toward each other leading to the unreasonably short H1⋯H3 = 2.023 Å, as refined in the R3m space-group symmetry. Note that it is close to the H⋯H contact in the PH3 phosphorous trihydride, i.e., H⋯H = 2.07 Å,33 but significantly shorter than the sums of the van der Waals radii of H atoms. This abnormally short contact between two HPO3 groups most plausibly denotes local off-centering of the H1 and H3 positions out of their ideal special 3a positions. The model of splitting of H1 and H3 into plausible x, 2x, and z positions (1/3rd occupied, see Fig. 5a) did not converge. However, the large thermal parameters of the coordinating oxygen atoms suggest local tilting around the c-axis to preserve the rigid HPO3 configuration, as depicted in Fig. 5b and c. Similar features are observed in (NH4)Co2(HPO3)3,30 which suggests the occurrence of similar local disorder.For instance, setting H1 and H3 on the 9b sites (H1: 0.61, 0.39, 0.052 and H3: 0.39, 0.61, 0.299), one may get a reasonable length of 2.436 Å for the H⋯H contacts and P–H distances of 1.332 Å and 1.330 Å for P1 and P3, respectively.
3.3 Magnetic properties
One of the characteristics of phosphite (HPO3)2− groups acting as ligands between transition metal ions is the strong tendency towards weak magnetic exchanges which denotes a poor ability for magnetic connections compared to standard tetrahedral ligands such as phosphate (PO4)3− groups, despite similar P–O bond distances and P–O–P angles. Especially, it was shown in several compounds that the phosphite μ-O bridge between two metal centers gives rise to very weak exchanges, even for dimeric units with short Co⋯Co distances.14 In Fe2(HPO3)3 with face-sharing Fe dimers similar to those in the title compound, i.e., three μ2–η1 bridging modes (which mean three M–O–M paths with one single oxygen bridging two metal atoms in each) that the intra-dimer exchanges are ten times weaker than the inter-dimer exchanges.6It mostly leads to extended Curie–Weiss (CW) thermal regimes down to low temperature in the absence of long-range magnetic ordering above 10 K. For instance, the behaviors reported for AI[MIII(HPO3)2] (A = K, NH4, Rb; M = V, Fe)28 show smooth deviation from the CW law, and Néel temperatures occur only for Fe3+ (S = 5/2) phases below TN = 9 K at maximum.
For the new PbCo2(HPO3)3 compound, the system obeys a Curie–Weiss law χ = C/(T − θCW) (C = 7.01 emu K Oe−1; μeff = 7.48μB per FU; θCW = −69.4 K) down to 22 K which suggests weak spin exchanges. The magnetic susceptibility data for PbCo2(HPO3)3 are provided in Fig. 6. The effective moment reflects a strong spin orbit coupling as expected for anisotropic Co2+ ions, i.e., the rough approximation μeff = g√[S(S + 1)] gives g = 2.73 instead of 2 for a spin-only contribution. It was not possible to fit χ using the analytical expression for dinuclear Co2+ (S = 3/2) compounds due to the strong spin–orbit interaction and other parameters inherent to high spin Co2+,34 even after correction from a temperature independent term describing a residual paramagnetic contribution (see ref. 35). Once again, the structural analogy of the magnetic M–O–M paths with those found in Fe2(HPO3)3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 suggests very weak intra-dimer exchanges, in good agreement with the χ(T) shape with smooth deviations from the Curie–Weiss law. The magnetic exchange coupling can be roughly estimated using the mean-field approximation:
6 suggests very weak intra-dimer exchanges, in good agreement with the χ(T) shape with smooth deviations from the Curie–Weiss law. The magnetic exchange coupling can be roughly estimated using the mean-field approximation:
| J/kB = 3θCW/[2zS(S + 1)] = −69 K, |
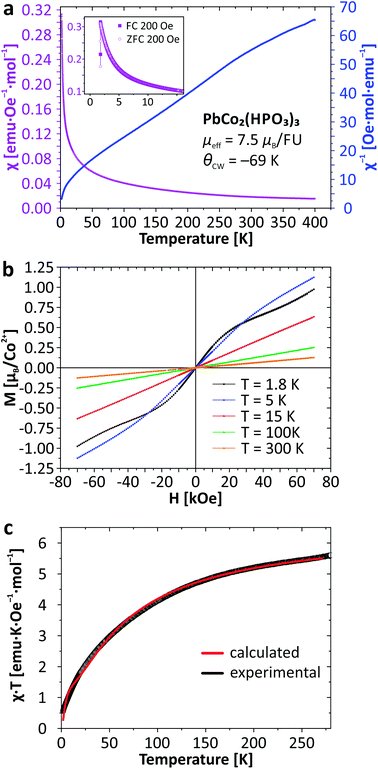 | ||
| Fig. 6 Thermal evolution of the magnetic susceptibility (a); magnetization as a function of applied field (b), and temperature dependence of χT (c) for PbCo2(HPO3)3. | ||
The bi-exponential phenomenological equation given below can be used to describe the χT(T) product for the interplay of two thermally activated phenomena (Fig. 6c), for instance weak AFM occurrence in an antiferromagnetic matrix:35,36
χT = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E1/kT) + B exp(−E1/kT) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E2/kT), exp(−E2/kT), |
4. Conclusion
The first lead cobalt phosphite PbCo2(HPO3)3 has been prepared using mild hydrothermal techniques. Its non-centrosymmetric crystal structure is consistent with the stereoactive lone-pair effect of Pb2+ ions arranged cooperatively in the structure. It is built up from alternating 2D blocks composed of Co2O9 dimers and HPO3 groups, which share common O corners. Divalent lead cations with stereochemically active lone electron pairs reside in the interlayer space between the 2D blocks and balance the charge. Similar blocks have been observed in the centrosymmetric structure of (NH4)Co2(HPO3)3,30 which is distinguished from the title compound by a different sequence of stacking of the layered cobalt phosphite blocks. Another structural feature of PbCo2(HPO3)3 is the evidence of an unreasonably short H⋯H contact (2.02 Å) between two HPO3 groups oriented toward each other inside the 2D block. A local twisting of the HPO3 oxoanions and off-centering of the H sites around the average special position with 1/3rd occupancy may give a more reasonable distance of 2.44 Å for the H⋯H contacts. The measurement of the magnetic properties of PbCo2(HPO3)3 reveals weak antiferromagnetic interactions between the cobalt ions inside the Co2O9 dimers due to the weak μ-O magnetic connectors with the bridging oxygen part of the phosphite groups. This aspect reinforces the interest of phosphite ligands as strong diamagnetic spacers ideally residing between compact metal center clusters.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ANR (grant no. ANR 2011-JS-08 00301) and carried out within the framework of the international French–Russian co-tutorial Ph.D. program funded by the Embassy of France in the Russian Federation, the French Government and the Agency CampusFrance. The Fonds Européen de Développement Régional (FEDER), the CNRS, the Région Nord Pas-de-Calais, and the Ministère de l'Education Nationale de l'Enseignement Supérieur et de la Recherche are acknowledged for funding the X-ray diffractometers. The authors would like to acknowledge Mrs Nora Djelal for her technical assistance with the TGA analyses and SEM images. V. M. K. has been also supported by the Russian Foundation for Basic Research (grant 16-35-00191 mol_a). O. I. S. acknowledges financial support of the Saint-Petersburg State University through its internal grant 3.38.238.2015. The authors also wish to thank Prof. Myung-Hwan Whangbo (North Carolina State University) for the fruitful discussion concerning the structural model with local off-centering of the H positions in the reported compound.References
- M. Plabst, L. B. McCusker and T. Bein, J. Am. Chem. Soc., 2009, 131, 18112–18118 CrossRef CAS PubMed.
- S. Natarajan and S. Mandal, Angew. Chem., Int. Ed. Engl., 2008, 47, 4798–4828 CrossRef CAS PubMed.
- T. Rojo, J. L. Mesa, J. Lago, B. Bazan, J. L. Pizarro and M. I. Arriortua, J. Mater. Chem., 2009, 19, 3793 RSC.
- C. Y. Ortiz-Avila, P. J. Squattrito, M. Shieh and A. Clearfield, Inorg. Chem., 1989, 28, 2608–2615 CrossRef CAS.
- M. Shieh, K. J. Martin, P. J. Squattrito and A. Clearfield, Inorg. Chem., 1990, 29, 958–963 CrossRef CAS.
- V. M. Kovrugin, E. E. Gordon, E. E. Kasapbasi, M.-H. Whangbo, M. Colmont, O. I. Siidra, S. Colis, S. V. Krivovichev and O. Mentré, J. Phys. Chem. C, 2016, 120, 1650–1656 CAS.
- V. M. Kovrugin, M. Colmont, O. I. Siidra, S. V. Krivovichev and O. Mentré, Cryst. Growth Des., 2016, 16, 3113–3123 CAS.
- X.-L. Cao, F. Kong, C.-L. Hu, X. Xu and J.-G. Mao, Inorg. Chem., 2014, 53, 8816–8824 CrossRef CAS PubMed.
- A. Aliev, V. M. Kovrugin, M. Colmont, C. Terryn, M. Huvé, O. I. Siidra, S. V. Krivovichev and O. Mentré, Cryst. Growth Des., 2014, 14, 3026–3034 CAS.
- V. M. Kovrugin, M. Colmont, C. Terryn, S. Colis, O. I. Siidra, S. V. Krivovichev and O. Mentré, Inorg. Chem., 2015, 54, 2425–2434 CrossRef CAS PubMed.
- X. Liu, Y. Xing, X. Wang, H. Xu, X. Liu, K. Shao and Z. Su, Chem. Commun., 2010, 46, 2614 RSC.
- A. Baiker, Curr. Opin. Solid State Mater. Sci., 1998, 3, 86–93 CrossRef CAS.
- S. Zheng, X. Li, B. Yan, Q. Hu, Y. Xu, X. Xiao, H. Xue and H. Pang, Adv. Energy Mater., 2017, 1602733 CrossRef.
- J. Fan, G. T. Yee, G. Wang and B. E. Hanson, Inorg. Chem., 2006, 45, 599–608 CrossRef CAS PubMed.
- X. Liu, Y. Xing and X. Liu, CrystEngComm, 2010, 12, 383–386 RSC.
- X.-M. Jing, Y.-B. Tan, L.-W. Xiao and Y.-L. Liu, Inorg. Chem. Commun., 2015, 57, 75–77 CrossRef CAS.
- J. Zhang, Z. Yao, S. Liao, J. Dai and Z. Fu, J. Mater. Chem. A, 2013, 1, 4945–4948 CAS.
- B. Kratochvíl, J. Podlahová, S. Habibpur, V. Petříček and K. Malý, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 2436–2438 CrossRef.
- F. Sapiña, P. Gómez-Romero, M. D. Marcos, P. Amorós, R. Ibanez and D. Beltrán-Porter, Eur. J. Solid State Inorg. Chem., 1989, 26, 603–617 Search PubMed.
- M. D. Marcos, P. Amorós, A. Beltrán-Porter, R. Martinez-Manez and J. P. Attfield, Chem. Mater., 1993, 5, 121–128 CrossRef CAS.
- W. Liu, H.-H. Chen, X.-X. Yang and J.-T. Zhao, Eur. J. Inorg. Chem., 2005, 2005, 946–951 CrossRef.
- H. Effenberger and F. Pertlik, TMPM, Tschermaks Mineral. Petrogr. Mitt., 1986, 35, 157–166 CrossRef CAS.
- A. Katrusiak and R. J. Nelmes, J. Phys.: Condens. Matter, 1989, 1, 10165–10174 CrossRef CAS.
- B. Liu, D. Li and C. Che, Rare Met. Mater. Eng., 2003, 32, 862–865 CAS.
- U. Keppler, Z. Kristallogr. - Cryst. Mater., 1970, 132, 228–235 CrossRef CAS.
- H. N. Ng and C. Calvo, Can. J. Phys., 1975, 53, 42–51 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- F. Hamchaoui, V. Alonzo, D. Venegas-Yazigi, H. Rebbah and E. Le Fur, J. Solid State Chem., 2013, 198, 295–302 CrossRef CAS.
- H. Y. Asl, K. Ghosh, M. P. Vidal Meza and A. Choudhury, J. Mater. Chem. A, 2015, 3, 7488–7497 CAS.
- C.-C. Cheng, W.-K. Chang, R.-K. Chiang and S.-L. Wang, J. Solid State Chem., 2010, 183, 304–309 CrossRef CAS.
- M. Henry, ChemPhysChem, 2002, 3, 561–569 CrossRef CAS PubMed.
- M. Henry, in Advances in quantum chemical bonding structures, ed. M. V. Putz, Transworld Research Network, Kerala, India, 2008, pp. 153–211 Search PubMed.
- T. Shimanouchi, I. Nakagawa, J. Hiraishi and M. Ishii, J. Mol. Spectrosc., 1966, 19, 78–107 CrossRef CAS.
- Z. Tomkowicz, S. Ostrovsky, S. Foro, V. Calvo-Perez and W. Haase, Inorg. Chem., 2012, 51, 6046–6055 CrossRef CAS PubMed.
- L. Cui, G.-P. Yang, W.-P. Wu, H.-H. Miao, Q.-Z. Shi and Y.-Y. Wang, Dalton Trans., 2014, 43, 5823–5830 RSC.
- X.-Y. Wang and S. C. Sevov, Inorg. Chem., 2008, 47, 1037–1043 CrossRef CAS PubMed.
- J.-M. Rueff, N. Masciocchi, P. Rabu, A. Sironi and A. Skoulios, Eur. J. Inorg. Chem., 2001, 2001, 2843–2848 CrossRef.
- L.-L. Liang, S.-B. Ren, J. Wang, J. Zhang, Y.-Z. Li, H.-B. Du and X.-Z. You, CrystEngComm, 2010, 12, 2669–2671 RSC.
- R. L. Carlin, Magnetochemistry, Springer-Verlag, Berlin, Heidelberg, 1986 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7dt02279d |
| This journal is © The Royal Society of Chemistry 2017 |