Raman spectral titration method: an informative technique for studying the complexation of uranyl with uranyl(vi)–DPA/oxalate systems as examples†
Abstract
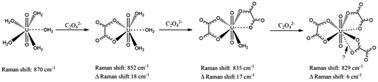
The Raman band at about 870 cm−1 originating from the symmetric stretch vibration (ν1) of uranyl, UO22+, has proven to be very informative for investigating the complexation of uranyl using perchlorate or nitrate of known concentration as internal standards. The concentration of uranyl can be conveniently calculated by using the ratio of the directly read band intensities of uranyl and the added reference, ClO4−, with a factor of 1.72. While with NO3− of concentration lower than 1.8 M as the reference, a factor of 0.85 should be used. Furthermore, with added internal standards, the linear relationship between the Raman intensity and the concentration of the corresponding species is illustrated by the spectral titration of U(VI) with a very strong ligand, dipicolinic acid (DPA); and the application of a spectral titration method with Raman spectroscopy in studying the complexation of uranyl is demonstrated by the titration of U(VI) with oxalate. The stepwise changes in the Raman shift of 18, 17, and 6 cm−1, corresponding to the three oxalate anions successively bonding to UO22+, imply that the coordination modes are different. In the 1 : 1 and 1 : 2 ratios of metal to ligand complexes, the oxalate anions bond to the uranyl ion in side-on bidentate mode, but in the 1 : 3 complex the third oxalate bonds in head-on mode, which is much weaker than the first two.
- This article is part of the themed collection: Frontiers in Spectroscopic Techniques in Inorganic Chemistry


 Please wait while we load your content...
Please wait while we load your content...